1 Introduction

Chemical mechanical polishing has been a critical process for achieving surface planarization in electronics and is commonly used as an intermediate fabrication step for devices such as integrated circuits [25], light-emitting diodes [26, 28] and magnetic hard disk read/write heads [9]. Although CMP is a common practice in the precision manufacturing industry, the tribological mechanism of the process is not completely understood. This is primarily due to the complex nature of the interactions between the wafer, pad and the abrasive particles.

Several models have been proposed to explain the wear action in the CMP process, ignoring one or more of the physical phenomena involved. Some of the earlier studies presented empirical models based on results from CMP experiments. Preston in his landmark paper [17] presented the first mechanical model relating the material removal rate to the work done by the frictional force. This approach though reasonable under certain restrictions, does not reveal insights into the wear mechanism. Zhao and Chang [27] and Luo and Dornfeld [12] published seminal wear models based on the real contact area between the pad and wafer interface and the calculation of active particles. Both models gave an accurate fraction of “active” particles, as shown by [14], thus resulting in reasonable wear prediction. However, both works acknowledged the fact that the slurry flow behavior would play an important role in the polishing mechanism, something that both models neglected. Another group of authors such as Sundararajan et al. [21] have approached CMP with fluid hydrodynamics to calculate wear by calculating the hydrodynamic pressure. Their models, as opposed to the previously mentioned category of models, captured the behavior of the slurry quite well, but ignored the effect of contact between the pad and wafer surfaces, thus neglecting the possibility of abrasive wear. The final approach builds up on the theories of contact mechanics and fluid hydrodynamics. Shan et al. [20] presented a one-dimensional model to predict interfacial fluid pressure under the wafer by solving an average flow Reynolds equation by introducing mixed lubrication (the lubrication process where the load is being carried by the fluid, together with a solid–solid contact) into CMP. Higgs et al. [5] extended that work to two dimensions with a stationary wafer and determined the equilibrium orientation for calculating the hydrodynamic pressure and contact stress. Similar work was done by Jin et al. [7] following the theory of elasto-hydrodynamic lubrication (EHL). However, the seminal EHL or mixed lubrication studies for CMP were just oriented toward predicting the interfacial lubrication process and did not address the material removal aspect of CMP.

All the approaches mentioned above were set up at the wafer scale and did not predict the presence of defects at feature scale, namely dishing, erosion and micro-scratching. Identifying a phenomenon they called particle-augmented mixed lubrication (PAML), Terrell and Higgs [22] presented an asperity-scale deterministic model that can overcome these shortcomings of the wafer-scale modeling approach. However, due to the high computational costs, even with a small domain, the model was computationally quite expensive. The present study, similar to the earlier PAML study, integrates the effect of slurry fluid flow, the mechanics of wafer and pad contact, and includes abrasive wear of particles for the process of polishing. The approach here is presented as a wafer-scale analysis, intended to capture the wafer-scale defects such as inter-die polishing differences.

2 Modeling Scheme

The philosophy of the proposed modeling scheme has two parts: determining the quasi-equilibrium orientation of the wafer over the polishing pad and calculating the material removal in that orientation. The state of quasi-equilibrium of the wafer is achieved when the net forces and moments acting on the wafer vanish. Due to apparent circular symmetry in the process, the net horizontal force (in X and Y directions) is assumed negligible. For the same reason, the vertical moment (in Z-direction) is also neglected in the present analysis. As a result, the only conditions required to satisfy, for dynamic equilibrium, are \(F_z = 0\), \(M_x = 0\) and \(M_y = 0\).

The major forces acting on the wafer during CMP are the hydrodynamic pressure applied by the slurry, the contact pressure applied by the pad asperities, and the external load applied on the wafer carrier. The slurry flow is assumed to be incompressible and Newtonian, and the pad material is assumed to be linear-elastic and isotropic. Based on these assumptions, a comprehensive model is presented here that accounts for the effect of the slurry, solid–solid contact between the wafer and the pad and wear due to the abrasive particles in the slurry. The following sections describe the major components of the model.

2.1 Hydrodynamic (Slurry) Modeling

The effect of the slurry on CMP has been widely acknowledged previously, even by the authors who excluded the slurry from their models [12, 27]. Some authors have claimed that the chemical erosion is the dominant material removal mechanism in CMP and have hence focused their entire approach toward accurate prediction of the hydrodynamic behavior of the slurry [19, 21].

The authors of the present study also acknowledge the effect of the slurry on the polishing process and have thus integrated the effect of the slurry as an important part of the analysis. The slurry has several chemical additives that are intended to enhance its polishing performance. The additives adsorb and react with the surface of the wafer, altering its thermo-mechanical properties, and thus affecting the material removal rate. However, for the purpose of this work, the analysis of the slurry has been restricted to its mechanical or hydrodynamic behavior only. In the presented model, the hydrodynamic pressure acting on the wafer plays an important role in determining the equilibrium orientation of the wafer. Similar to previously mentioned studies [5, 20, 21], the Reynolds equation has been solved to calculate the hydrodynamic pressure acting on the wafer surface. Due to the cylindrical geometry of the interface, the cylindrical polar form of Reynolds equation [eq. (1)] given by Beschorner and Higgs [1] has been used in the current model.

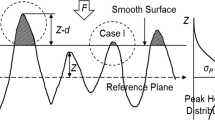
$$\begin{aligned} \frac{1}{12\eta } \left[ \frac{\partial }{\partial r}\left( rh^3\frac{\partial p}{ \partial r}\right) + \frac{\partial }{r \partial \theta }\left( h^3\frac{\partial p}{\partial \theta}\right) \right] &= - rv_{r({\text{ w}})}\frac{\partial h}{\partial r} - v_{\theta ({\text{ w}})}\frac{\partial h}{\partial \theta } \\& \quad + \frac{\partial }{\partial r}\left(\frac{v_{r({\text{p}})} + v_{r({\text{w}})}}{2} rh \right) +\frac{\partial }{\partial \theta }\left( \frac{v_{\theta ({\text{p}})} + v_{\theta ({\text{w}})}}{2}h \right) \end{aligned}$$
(1)

The primary quantity dictating the fluid pressure (p) in the Reynolds equation [eq. (1)] is the film thickness ‘h’. The film thickness in this model has been approximated as the separation between the smooth wafer surface and the mean plane of the pad asperities. The individual contribution of the nominal clearance (\(\delta _0\)), rolling angle (\({\alpha }\)) and pitching angle (\(\beta\)) has been superposed to give the effective film thickness at a point (Fig. 1). The resultant film thickness can be written as shown in (2).

$$\begin{aligned} h(r,\theta ) = \delta _0 + r \sin \alpha \cos \theta + r \sin \beta \sin \theta \end{aligned}$$
(2)
Fig. 1
figure 1

Superposition of individual variables to calculate the film thickness. a Angle with X-axis. b Angle with Y-axis. c Displacement in Z-direction

Full size image

The velocities have been calculated with the wafer’s center as the origin, following the work of previous studies by Park et al. [16], Cho et al. [4] and Beschorner and Higgs [1], shown in Fig. 2 and can be given as in (3)

$$v_{r({\mathrm{p}})} = r_{\rm wp} \sin \theta \varOmega _{\rm p}$$
(3a)
$$v_{\theta ({\mathrm{p}})} = (r + r_{\rm wp} \cos \theta ) \varOmega _{\mathrm{p}}$$
(3b)
$$v_{r({\mathrm{w}})} = 0$$
(3c)
$$v_{\theta ({\mathrm{w}})} = r\varOmega _{\mathrm{w}}$$
(3d)
Fig. 2
figure 2

Different velocities in the system

Full size image

2.2 Wafer–Pad Contact

In a regular CMP setup, the pad is made of a soft polymeric material placed on top of a rigid metallic platen. The wafer typically is a metallic, metalloid or ceramic material and is much tougher than the polymeric pad. Thus, the solid–solid contact between the wafer and the pad can be modeled through a Winkler elastic foundation [8] which approximates the softer material as a mattress, constructed by assembling a set of parallel springs. In this case, each spring represents a collection of, or a single asperity, occupying a rectangular area, and representing the average height of that area. It is assumed that these springs deform vertically, without influencing their neighbors. This provides a relationship [eq. (4)] between the stress and normal deflection for each spring, as has been described by Johnson [8]

$$\begin{aligned} \sigma (x,y) = K \frac{u(x,y)}{\tau } \end{aligned}$$
(4)

where \(\sigma\) is the contact pressure, \(\tau\) is the initial height of the foundation, and u is the deformation at the surface. The following assumptions were made to determine the proportionality constant:

  • Tangential deflection of the asperities is neglected

  • The effect of the tangential loads on the normal deflection is neglected

With the above assumptions, the equations of elasticity for the pad can be condensed to eq. (5)

$$\begin{aligned} \sigma (x,y) = \frac{E_{\rm pad}(1-\nu _{\rm pad})}{(1-2\nu _{\rm pad})(1+\nu _{\rm pad})} \frac{u(x,y)}{\tau } \end{aligned}$$
(5)

This expression explicitly relates the normal stress \(\sigma (x,y)\) to the normal deflection u(x, y) of an asperity. As a result, the calculation of contact pressure can be obtained through O(N) operations, which is critical to maintaining the speed and memory efficiency of the model.

2.3 Equilibrium Orientation

The fluid and contact pressure fields are used to formulate three equations in three independent variables mentioned earlier, the nominal clearance \((\delta _0)\), rolling angle \(({\alpha })\) and pitching angle \((\beta )\). The three equations correspond to the equilibrium conditions of no normal force \((F_z = 0)\) and no tangential moments \((Mx = 0\), \(My = 0)\) on the wafer. The equations are nonlinear, implicit equations and, hence, an analytical solution is not possible. A novel root-finding method based on a homotopy algorithm has been designed to solve the equations, which is described next.

The algorithm starts with an initial guess, sufficiently far from the expected solution. One of the variables is fixed at the initial value, and the remaining two variables are varied to satisfy two of the equations. The first variable is then modified slightly, and the other two variables are again varied to satisfy two equations, starting with the previous iteration’s roots as the initial guesses. This process is repeated until the third equation is also satisfied by the values of the three variables.

For the step at solving the two equations, the conjugate gradient method was employed to ensure stability and consistency. As all the equations are nonlinear and highly complex, traditional root-finding algorithms such as Newton–Raphson, Secant method or Broyden method were found incapable of yielding consistent results.

It is important to note that the equilibrium being discussed here is a quasi-steady equilibrium. As the pad and wafer rotate, the hydrodynamic pressure and the contact stress change and a new equilibrium orientation appears at every time step.

Fig. 3
figure 3

Root-finding algorithm

Full size image

2.4 Wear

Abrasive wear has been widely accepted as the predominant wear mechanism during CMP. Following the definition of abrasive wear, a “wafer-wear” event only occurs when an abrasive particle, trapped within the contact of a pad and a wafer asperity, indents into the wafer surface, due to force applied by the pad asperity. The method used for calculating wear over a wafer asperity is based on the formulation described by Luo and Dornfeld [12, 13]. The aggregate plastic deformation in both wafer and pad \((\Updelta )\) can be written as:

$$\begin{aligned} \Updelta = \Updelta _{\rm w} + \Updelta _{\rm p} \end{aligned}$$
(6)

where the subscripts ‘w’ and ‘p’ refer to the wafer and the pad, respectively. The particle sizes are assumed to follow normal distribution, with the probability distribution function defined as in eqs. (7) and (8).

$$\begin{aligned} p\{d = d_{\rm a}\}= & {} \frac{1}{\sqrt{2\pi }} \exp \left[ -\frac{1}{2}\left( \frac{d-d_{\rm avg}}{\sigma _d}\right) ^2\right] \end{aligned}$$
(7)
$$\begin{aligned} p\{d \le d_{\rm a}\}= & {} \frac{1}{\sqrt{2\pi }} \int _{-\infty }^{(d_{\rm a}-d_{\rm avg})/\sigma _d} \hbox {e}^{-(1/2)t^2}\hbox {d}t \end{aligned}$$
(8)

Every particle having diameter larger than \(\Updelta\) will cause plastic deformation and hence lead to wear. Following this principle, the number of active particles can be calculated as eq. (9).

$$\begin{aligned} N_{\rm active}&= N_{\rm total} - N_{d < \Updelta } \nonumber \\&= N_{\rm total} \left( p\{d \le d_{\rm max}\} - p\{d \le \Updelta \} \right) \end{aligned}$$
(9)

Here, following the work of ref. [12], it is assumed that the average diameter of the active particles is independent of the down pressure, as in most cases, only the largest particles would be participating in wear. \(N_{\rm total}\) is the total number of particles trapped in the interface, which can be calculated through the slurry concentration.

Also, in most cases, \((d_{\rm max} - d_{\rm avg})/\sigma \approx 3\) and \(p\{d \le d_{\rm max}\} \approx 1\). The total volume removed at every asperity contact is calculated by adding the volume removed by every active particle, which in turn is approximated as the product of the number of active particles and volume removed by one average-sized active particle. Volume removed by one particle is written as eq. (10).

$$\begin{aligned} \hbox {Vol}_{\rm avg} = \Updelta _{\rm w} a_{\rm w} v_{\rm rel} \end{aligned}$$
(10)

where \(\Updelta _{\rm w}\) is the particle indentation depth into the wafer surface, \(a_{\rm w}\) is the radius of contact area between the particle and the wafer surface, and \(v_{\rm rel}\) is the velocity with which the particle is being dragged across the wafer, which in this case is the relative velocity between the pad and the wafer at that location. Assuming the contact between the particle and the wafer is completely plastic, as shown by ref. [12], \(\Updelta _{\rm w}\) and \(a_{\rm w}\) can be calculated as (11) and (12), respectively.

$$\begin{aligned} \Updelta _{\rm w}&= \frac{2F}{\pi d_{\mathrm{avg-a}} H_{\rm w}} \end{aligned}$$
(11)
$$\begin{aligned} a_{\rm w}&= \sqrt{\frac{2F}{\pi H_{\rm w}}} \end{aligned}$$
(12)

Using eqs. (11) and (12), we can rewrite (10) as (13).

$$\begin{aligned} \hbox {Vol}_{\rm avg} = \frac{1}{d_{\rm avg-a}} \left( \frac{2F}{\pi H_{\rm w}}\right) ^{3/2} v_{\rm rel} \end{aligned}$$
(13)

Here, F can be calculated using the contact stress given by eq. (5) and \(v_{\rm rel}\) can be obtained using eq. (3). As mentioned earlier, \(d_{\rm avg-a}\) is independent of the down pressure and has been approximated as being close to the size of the largest particles.

2.5 Differences Between the Current Work and Previous Work by Terrell and Higgs [22]

An approach similar to the current work was presented by the co-author in another paper [22] in the past. However, the present solution is significantly different from the previous work, in the following ways:

  • The hydrodynamic pressure field was solved using the Reynolds lubrication equation for cylindrical polar contacts, whereas [22] solved the three-dimensional Navier–Stokes equations

  • Even though both models utilized the elastic foundation model, contrary to the present work, [22] did not account for the topography of the entire pad and limited its focus on a small, microscopic domain

  • High-resolution Lagrangian–Eulerian formulation was used to model the particle–fluid interactions in [22]. Their model assumed that all particles trapped between a wafer and pad asperities were contributing to material removal or were “active.” Although the present work makes assumptions regarding particle transport, it accounts for the probability of particles being inactive while still being trapped in the solid–solid contact zone.

  • The wafer orientation from [22] only aimed to achieve a quasi-equilibrium using the solid contact force. The current work achieves a three-dimensional load and moment balance at each time step, which incorporates both the solid and fluid load-carrying capacity.

While [22] used higher fidelity modeling treatments, the framework was computationally expensive and thus limited to a microscopic wafer–pad interface simulated over microseconds. The present work, on the other hand, can study the entire wafer–pad interface and simulate real CMP conditions in a practical timescale.

Table 1 Model parameters
Full size table

3 Results

The Reynolds Equation was solved numerically using the wafer center as the origin. The entire region under the wafer was discretized into a polar rectangular grid. The pad was independently discretized into another polar grid, originating at its own center. For calculating the contact stress, a pad surface was generated with a mean height and average roughness specified in Table 1. The pad was assumed to be a Rodel IC1000, and the wafer was assumed to be a blanket Cu surface. The slurry was assumed to be an aqueous alumina suspension.

Fig. 4
figure 4

Flowchart of the modeling process

Full size image

Figure 3 shows the overall algorithm that was followed in the model for the transient analysis. As shown, the equilibrium hydrodynamic pressure and contact stress profiles are calculated at every time step, as is the wafer wear. Note that the model provides a wear “field” as an output, which is then averaged over the entire region for comparing with other studies, which typically give an average material removal rate in terms of reduction in thickness of the wafer (Fig. 4).

3.1 Fluid Pressure

The model can predict the evolution of the hydrodynamic pressure profile over the course of a simulation. Over the entire simulation, no steady state pressure profile is observed. This is not surprising as the surface of the pad affects the equilibrium orientation, which in turn governs the distribution of fluid pressure. As the surface of the pad is rough with significantly different topographies interacting with the wafer in consecutive time steps, a new equilibrium orientation and thus a new pressure profile are expected at every time step. However, an “average fluid pressure field” can still be calculated by averaging the pressure field over one whole rotation of the pad. This average pressure was compared against the measured fluid pressure reported by Osorno [15] for conditioned pads in Fig. 5. The experimental measurements were taken through wireless point probes that rotated with the wafer. These discrete values reported by the point probes were then interpolated to construct a pressure contour. Ignoring the zigzag nature of the pressure distribution which appears to be the artifact of the spatial interpolation, good agreement can be observed between the model and the experiments.

Fig. 5
figure 5

Dynamic fluid pressure profile for a well-conditioned pad. a Dynamic pressure measurement conducted by Osorno [15]. b Average pressure calculated over one pad rotation

Full size image

3.2 Polishing Load

The effect of the polishing load on the material removal rate was compared against the numerical and experimental results given by Terrell and Higgs [22], as shown in Fig. 6. It can be seen that for lower loads (less than 16 psi), the model is in good agreement with the experimental measurements and is closer than the numerical results generated by the PAML model [22]. However, for higher loads, the deviation between the experimental results and the current model becomes much greater, which can be attributed to the approach taken to model the contact mechanics in this work. As discussed in 2.2, the pad has been modeled to act as an assembly of independent voxels that do not influence each other while deforming under stress. As the springs (and hence the representative voxels) act independently, they only come in contact when the applied load is large enough to cause deformation in all the asperities taller than themselves. Because of this, as the load increases, patches of pad start to appear that have been deformed completely flat, i.e., no difference in the heights of the deformed voxels. This leads to the fluid slowly getting squeezed out of the interface. This in turn results in diminishing fluid load carrying capacity, and, unrealistically large fraction of the load being supported through the solid–solid contact between the wafer and the pad. Such high contact stresses would lead to much higher material removal as is seen in Fig. 6. Fortunately, more and more applications now seek very low after-polish roughness values. The general strategy to achieve such low roughnesses is to apply very low loads during polishing. In such cases, the present model can provide excellent predictions.

Fig. 6
figure 6

Effect of polishing load on the material removal rate

Full size image

3.3 Particle Size and Concentration

The effect of the abrasive particles in the slurry was also studied through the model. The material removal rate predictions of the model have been compared against the experimental data reported by Bielmann et al. [2] who studied the effect of different particle sizes and solid concentration on the MRR. Figure 7 plots the variation in the MRR as a function of solids loading. For the lower concentrations (less than 15 %), the linear increase in the MRR with increasing solid concentration matches well with the experimental observation by Bielmann et al. (shown in the inset). However, two major differences can be noted between the two set of results.

Firstly, in the experimental data, one can observe the saturation of MRR for smaller particles above the concentration of 10 %. It has been explained in detail by [11] that at higher concentrations, the MRR saturates and does not increase with increasing solid loading. After the saturation point, in the absence of exposed wafer surface, additional abrasive particles cannot come in contact with the wafer and hence fail to cause any additional wear. Thus, a larger fraction of available abrasives remains “inactive” and possibly enhances lubrication, similar to lubrication enhancement caused by granular media [6, 24]. As the current model fails to account for the inactivity in a larger fraction of particles beyond a certain point, similar phenomena is not reflected in the predictions.

Secondly, although the variation in MRR in the experimental data is linear [Fig. 7 (inset)], there appears to be a nonzero y-intercept to all the curves plotted. On the other hand, the present model shows that all the curves pass through the origin, thus resulting in zero intercept. This difference can be explained by the assumption made for the present model which ignores all wear mechanisms except abrasive wear. This means that there would be no wear predicted by the model when the solid concentration goes to zero, i.e., in an abrasive-free slurry. During the experiments, however, some material removal may still be possible in the absence of particles as a result of chemical erosion which has been neglected in this study.

The dependence of MRR on mean abrasive particle diameter has also been studied. As noted by Bielmann et al. [2] and followed on by [13], the material removal rate drops exponentially with the increase in the abrasive particle diameter. Similar behavior has been observed in the present study as shown in Fig. 8a. The MRR averaged over concentration values in the linear region in Fig. 7 (2, 5 and 10 %) has been plotted against mean abrasive particle diameter.

Although trend-wise similarity has been observed in both of these comparisons, quantitatively, the values reported by the present study have been off by a factor of 3–4. This can be explained by the uncertainty in the values of the input parameters required for the model. For this comparison, most common values have been used for the material properties of the wafer and the pad and operating parameters were estimated from the limited information available in Bielmann et al.’s paper [2]. If the model predictions are multiplied by a constant scaling factor to account for all these uncertainties, an excellent match can be obtained between the predicted values and the experimental measurements, as shown in Fig. 8b. Similar approach has been followed by [13] while comparing their modeling approach against the experimental data reported by [2]. In the present work, the scaling thus accounts for two factors: the uncertainty in the values of the input parameters and the chemical action during the process. Detailed in-house experimentation can help us avoid the use of scaling for the former. However, to accurately incorporate the latter, large-scale modifications would be required in the model.

Fig. 7
figure 7

Material removal rate with varying abrasive concentration in the slurry, plotted for various mean abrasive diameters. Inset Data presented by Bielmann et al. [2]

Full size image
Fig. 8
figure 8

Material removal rate as a function of average particle size. a Experimental measurement and corresponding model predictions of MRR for different average particle sizes. b Experimental measurement and scaled model predictions (same curves as in (a) with smaller y-axis)

Full size image

3.4 Parametric Studies

Now that experimental evidence supporting the model predictions has been presented, parametric studies were conducted to understand the effect of parameters that are difficult to study experimentally.

3.4.1 Slurry Viscosity

Several researchers have reported several degrees of temperature increase during polishing [3, 10, 23]. Thus, the performance of the slurry can differ significantly with such changes in temperature. One of the most prominent effects of the increase in temperature can be seen by a sharp decrease in the slurry viscosity. Through the present model, the effect of such change in viscosity has been studied and the result is shown in Fig. 9. It can be seen that material removal rate decreases rapidly with increases in viscosity. This is expected, as with increase in viscosity the load-carrying capacity of the fluid increases, resulting in reduced solid–solid contact stress between the wafer and the pad. The increase in the fluid load-carrying capacity can also be monitored by the fluid pressure in the interface. Figure 10 shows the time-averaged fluid pressure distribution in the interface for three of the studied viscosity values (the Z-axis limits have been adjusted for each plot to show the pressure profile). Even though the pressure profile remains similar, a steady increase in the pressure values can be observed as the viscosity increases. To demonstrate the differences in magnitudes of pressure values, Fig. 10 is replotted with the same pressure limits across the viscosity plots, in Fig. 11 that shows the sharp increase in the pressure more clearly.

In the absence of any solid–solid contact, as might be the case with the slurry viscosity equal to 0.01, there would be virtually no material removal (once again, here we are assuming that particle abrasion is the only mechanism for wafer wear and effects of erosive material removal have been neglected). As the temperature rises with time during the polish, thus resulting in lower viscosities, one can expect faster material removal than at initial, ambient temperatures.

Fig. 9
figure 9

Effect of Newtonian slurry viscosity on the material removal rate

Full size image
Fig. 10
figure 10

Average fluid pressure as a function of viscosity (locally adjusted Z-axis). a Viscosity = 0.0005 Pa s, b viscosity = 0.001 Pa s, c viscosity = 0.005 Pa s

Full size image
Fig. 11
figure 11

Average fluid pressure as a function of viscosity. Plots with the same data as in Fig. 10, but with common Z-axis limits across a viscosity = 0.0005 Pa  s, b viscosity = 0.001 Pa s and c viscosity = 0.005 Pa s

Full size image

3.4.2 Particle Size Distribution

Controlling the abrasive particle shape and size is a very difficult task due to the inherent nature of the process by which they are produced. Also, it is extremely difficult to study the effect of degree of deviation from the mean abrasive size experimentally, as the deviation itself is not a controlled parameter but a result of inefficient manufacturing. This is where computational tools like the present model can provide invaluable insight. Assuming all the particles are spherical, the effect of deviation from the mean value of the particle diameter was studied. Figure 12 shows the variation in material removal rate with change in the standard deviation of the diameter of the particles. One expects the change in standard deviation to not cause much variation in MRR, since with increasing the standard deviation, two counteracting effects come into picture. Firstly, for a particle size distribution with large standard deviation, the active particles would have larger diameter than the distribution with smaller standard deviation. For the same pad–wafer asperity contact stress, these larger active particles would result in larger material removal per particle. However, as the volume of the particle is larger for larger standard deviation, there would also be less number of active particles, assuming the concentration to be constant.

As seen in Fig. 12, a larger variation in particle sizes indicated by a larger standard deviation of particle diameter results in slightly higher average material removal rate. Unless the standard deviation values are extremely small, which represents extremely high size control on very fine particles (very hard to achieve in manufacturing), the growing size of the particles overcomes the decrease in the number of particles (as shown by [13]), thus increasing the material removal rate. However, the wafer polished with a slurry having a larger variation in particle sizes would have a higher probability of resulting with polishing defects such as micro-scratching and pitting [18]. On the other hand, even though we would get much more control on the surface quality with a very small variation in particle sizes, the cost of such control might be prohibitive and would also result in a much slower polish. Thus, aiming for a median standard deviation value in particle sizes would be easier to achieve and would also yield an acceptable surface quality.

Fig. 12
figure 12

Effect of particle size distribution on the material removal rate, for a mean particle size of 150 nm

Full size image

4 Conclusion

A new wafer-scale multi-physics model based on the hypothesis of abrasive wear and particle-augmented mixed lubrication was developed for modeling CMP. The model integrated the effects of mixed lubrication in the wafer–pad–slurry interface and wear caused by the abrasive particles in the slurry.

The proposed framework was then compared against experimental measurements available in the literature. A variety of temporal and time-averaged quantities can be obtained as the output of the model. The average fluid pressure distribution obtained from the model matches well with the experiments conducted by [15]. The effect of variation in polishing load on the material removal rate also agrees with the experiments conducted by the co-author in the past [22]. Finally, the effect of abrasive particle diameter and solid loading of the slurry also matches with papers published in the past [2, 13].

The model can capture wafer-scale defects such as differential polishing across the wafer and over-polishing close to the wafer edge. With the model’s capability to capture multi-physical interactions, the effect of several material or operational parameters can be studied. The model can thus provide invaluable insights in the cases where the parameter of interest cannot be studied experimentally. This capability was demonstrated through two example cases of variation in slurry viscosity and abrasive particle size distribution. Therefore, the current model can facilitate design and evaluation of the next generation of polishing equipment and consumables, thus bringing the cost of electronic devices down.