1 Introduction

In the present work, we explore the use of anisotropic constitutive materials within the context of topology optimization. The choice of wording is purposefully broad as we aim at proposing a fairly general approach for design optimization considering local material orientations alongside with the topology.

Section 1 presents the motivation toward the optimization of structures using anisotropic materials and reviews existing approaches. Section 2 describes the mathematical model chosen to represent and simulate designs containing the given material models. In Section 3 we address the numerical optimization schemes developed for tailoring material orientation layouts in the context of topology optimization. Finally, Section 4 is dedicated to various numerical experiments, analyzing the results of the present approach and its applicability to industrial design scenarios.

1.1 Motivation

Bakelite was the first artificial fiber reinforced plastic and was synthesized in 1907. However, composite materials have been a staple of mechanical engineering for centuries prior to that. Naturally occurring materials like wood have long been used in construction, specifically for their anisotropic properties granted by continuous fibers. Today, composite materials like reinforced concrete, plywood or fiberglass are commonly used in a wide variety of industrial applications. Advanced synthetic anisotropic materials perform routinely on aircraft and spacecraft in demanding environments.

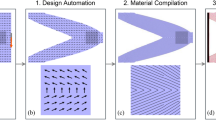
Producing components consisting of composite materials is typically challenging and multiple manufacturing processes have been developed to tackle this challenge (Gao 2018; Kabir et al. 2020). Figure 1 shows examples of such processes with emphasis on the use of continuous fiber reinforcements.

Fig. 1
figure 1

Examples of manufacturing processes applying continuous fiber composites. (a) Filament deposition-based additive manufacturing using continuous fibers fused with a thermoplastic polymer matrix. (b) Continuous fiber winding. (c) Continuous fiber tape laying (Gao 2018).

Full size image

We observe a rapid progress of additive manufacturing capabilities which already enables the production of structures with spatially varying fiber orientations. The local orientation of fibers in a given manufacturing process directly affect the anisotropic material properties. In turn, these properties play a major role in the physical performance and characteristics of the manufactured designs. It is worth noting that whether it is in a single component and/or in a subcomponent assembled in a full structure, the anisotropic behavior of the material can affect a wide variety of physical phenomena, e.g., total mass, stiffness, strength, stability, robustness, dynamics, heat conduction, acoustics, and electromagnetics.

We aim at devising a method for material orientation optimization compatible with industrial requirements in order to leverage the recent progress in AM technologies for composite materials. Consequently, we will be addressing 2D and 3D structural optimization with the aim of keeping the core of the material orientation formulation agnostic of the physical phenomenon driving the optimization. In other words the material orientations will affect the behavior of the structure, but the orientation formulation itself should be compatible with stiffness, heat conduction, or other physical phenomena without any fundamental modifications.

In the following, we numerically optimize orientation fields knowing that manufacturing processes are for the most part not yet capable of producing such objects with fiber orientations freely varying in 3D. There are however existing approaches for additive manufacturing of frame structures departing from the classical 2D layer-by-layer paradigm (Huang et al. 2016) where 3D orientation of fibers could be considered. It is then reasonable to expect that more general purpose manufacturing capabilities for oriented fibered materials will become a reality in the future, at which point the industry would want to benefit from it immediately without having to wait for the engineering design tools to be available. Moreover, a separate class of approaches consider the optimization of material 3D orientations as a first step before projection of fine-scale anisotropic microstructures either in a high resolution density field (Groen and Sigmund 2018; Allaire et al. 2019) or as a conformal lattice structure (Wu et al. 2019). This class of methods can already allow the fabrication of objects with truly 3D anisotropic meta-material of varying orientations and also rely on the optimization of smooth material orientation fields.

We will be addressing smoothly oriented fiber reinforcement and therefore focus on transverse isotropic material properties in 2D and 3D, respectively. Another consequence of optimizing fiber orientation is that the regularity and continuity of the material orientation field will be paramount to ensure the validity of the generated structures for industrial applications. Thus, a major part of this work is dedicated to the regularization techniques and length-scale control. We also require the ability to handle multiple load cases. This requirement is one of the main motivators for the use of sensitivity driven numerical optimization schemes. Indeed, it is known that under a single load case, the optimal orientations of an orthotropic material for elastic stiffness are given by the principal stresses (Pedersen 1989). However, this statement is no longer valid under multiple load cases since the stress and strain tensors have different values for each load case. Considering that industrial design specifications are seldom restricted to a single load case but instead commonly include several loading scenarios applied for various physics, then it is natural to express the material orientation as a numerical optimization problem.

1.2 Context

Topology optimization is a general form of structural optimization whose history can be traced back to seminal work from Martin Philip Bendsøe in the 1980s (Bendsøe 1983, 1988, 1989) as a material distribution problem in a so-called design space. Nowadays, topology optimization has developed in many different directions with the most common methods known as “density-based,” “level-set,” “topological derivatives,” “phase field” and “evolutionary” approaches (Sigmund and Maute 2013; Bendsøe and Sigmund 2003). The present work extends the density-based method known as the Solid Isotropic Material with Penalization (SIMP) approach (Bendsøe and Sigmund 1999).

This approach describes the effective Young modulus Y of an element E in the design space Ω as a function of the element density ρE penalized by an exponent γ yielding

$$ Y(\rho_{E}) = Y_{min} + \rho_{E}^{\gamma} \left( Y_{0} - Y_{min}\right), \quad 0 < Y_{min} \ll Y_{0} $$
(1)

The design problem is formulated as an optimization of the design variables ρ under constraints as follows

$$ \setlength{\jot}{4pt} \begin{aligned} \arg\min_{\boldsymbol{\rho}} \quad &J(\boldsymbol{\rho}) = \boldsymbol{f}^{T} \boldsymbol{u}\\ s.t.\quad &\boldsymbol{K}(\boldsymbol{\rho})\boldsymbol{u} = \boldsymbol{f}\\ &0 \leq \rho_{E} \leq 1, \quad \forall E \in \boldsymbol{\Omega}\\ &G_{tot}(\boldsymbol{\rho}) = \frac{1}{G_{tot}^{\star} \cdot v_{\boldsymbol{\Omega}}}\sum\limits_{E\in\boldsymbol{\Omega}}\left( \rho_{E} v_{E}\right) -1 \leq 0 \end{aligned} $$
(2)

with the objective function J defined as the total strain energy, the state equation depending on the stiffness matrix K of the design, u and f respectively the nodal displacement and force vectors, and Gtot the total volume constraint depending on the elements volumes vE.

For ensuring a well-posed optimization problem, it is necessary to apply a control on the length scale of the density field (Díaz and Sigmund 1995). This is commonly achieved through the use of filters (Sigmund and Petersson 1998; Sigmund and Maute 2012).

1.3 Existing work and approaches

The use of spatially varying fiber orientations promises gains in structural stiffness that could be leveraged in the field of mechanical and material engineering. Nevertheless, the manufacturing capabilities for continuous fiber printing are still in their infancy. Consequently, there seem to be a lack of approaches for general purpose sensitivity-based topology optimization methods enforcing smooth fiber orientations.

The original work by Bendsøe and Kikuchi (1988) optimized orthotropic material distribution and orientation using the homogenization method. This early work did not produce solid/void designs nor included length-scale control on the densities or regularization on the material orientations. As reviewed by Bendsøe and Sigmund (2003), subsequent work applied this approach to 2D and 3D applications. These methods generally focus on a multiscale representation where the final geometry is projected at a fine scale (Groen and Sigmund 2018).

The method proposed by Safonov (2019) is another example of approach aiming at generating structures constituted of orthotropic material through topology optimization. This approach is limited to single load cases and runs a traditional density-based topology optimization. At each design update the orthotropic material is aligned with the principal directions of stress obtained by evaluating the stress tensor of each element.

The principal stress directions naturally exhibit smooth transitions and alignment for material orientations, and are trivially extended to 3D optimization problems. However, the limitation of working exclusively with single load case problems is too restrictive for industrial applications. Similarly, relying exclusively on a unique stress tensor for material orientation excludes working with other problem formulation such as strength, dynamics or multiphysics.

Liu and Yu (2017) propose a level set-based approach for concurrent optimization of topology and in-plane deposition path orientation. The local orthotropic behavior of the material is modeled according to studies of typical in-plane raster, in-plane transverse and build direction properties in layer-based 3D printing. The deposition paths are defined by consecutive isolevels of the level set representation and can thus be seen as analogous to offsets of the boundary.

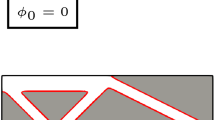
Fernandez et al. (2019) propose a method focused on enforcing the manufacturing constraints of a specific printing process into the fiber orientation optimization. Especially, they target the Direct Ink Writing process which builds the object layer by layer by filling each slice with an extruded mixture of thermoset resin and short carbon fibers. Since the short fibers tend to settle in a direction aligned with the printing path, they aim at devising a path generation algorithm fulfilling constraints like the absence of paths overlaps, orientation and spacing regularity, and low path curvature. To that effect, they opt for paths obtained as level sets of a given function and then link these isolevel curves together yielding a single continuous extruder path. The approach operates on a predetermined 2D design topology and smoothly deforms an initial hatching pattern to produce optimized printing paths (Fig. 2).

Fig. 2
figure 2

(a) Illustration of the level sets of an arbitrary function defining curved, evenly spaced paths with no overlap. (b) Diagram of a simple loading scenario. (c) Level sets linked as a single manufacturable printing path (Fernandez et al. 2019)

Full size image

The method proposed by Nomura et al. (2015) and Lee et al. (2018) offers a promising alternative to the fiber orientation problem. This work aims at devising a topology optimization scheme where both the density and orientation of material are optimized simultaneously. To do so, a vector parameterization is used to encompass both variables at the same time, where the vector direction represents the fiber orientation and the vector magnitude encodes for the material density. Consequently, the fiber orientations become part of the design variables. They also propose an extension to this process were the orientations are discretized in uniform patches through isoparametric projection.

The main advantage of this approach is that the design variables in vector space exhibit fairly few local minima during the numerical optimization. On the other hand, this approach has not been applied to 3D fiber orientation and the tight coupling of the density and orientation parameters makes the method less versatile when working with other additional design variables or physics due to their interdependence.

Recent work by Jiang et al. (2019) presents an approach for topology optimization with densities and fiber orientations as separate design variables. It demonstrates handling 2D and very low-resolution 3D problems but the fiber orientation are still constrained to a XY -plane (Fig. 3) and have no length-scale control. The thesis (Jiang 2017) also shows an example with two symmetric load cases.

Fig. 3
figure 3

Visualization of the first 3 layers of a 6 layer cantilever design with optimized material orientation displayed as a short white segment for each element (Jiang et al. 2019)

Full size image

This last approach is the closest to what we will propose in the present. However, we also aim at tackling the previously mentioned issues. Specifically, the proposed method aims at fulfilling the following criteria:

  • Local material orientation varying in 2D or 3D

  • Smooth variation of material fiber orientation

  • Sensitivity-based orientation optimization

  • Multiple load cases optimization scenarios

  • Scalability to high resolution meshes

  • Separate design variables for density and orientation

  • Synchronous or asynchronous optimization of density and orientation

2 Mathematical modeling

This section describes the mathematical model chosen for the physical simulation using finite element analysis. We first specify the properties of the material through its constitutive law. Then, we describe the transformation matrices allowing the variation of material orientation on an element-based level. Finally, we show some numerical experiments to validate the model and study the effect of combined density topology optimization with differentiable non-uniform material orientations.

2.1 Constitutive law

Section 1.2 described the numerical model commonly used for isotropic density-based topology optimization. Therefore the present section presents the constitutive material law as well as the process allowing local material orientation variation throughout the design domain.

An orthotropic material for 3D is defined according to its three orthogonal principal directions. Thus, the material needs nine physical properties to be fully described. These physical constants are the three principal Young moduli Y1, Y2 and Y3 corresponding to the stiffness along each principal direction, the three Poisson ratios ν12, ν13 and ν23, and the three shear moduli μ12, μ13 and μ23. For a complete description of the material, the three other Poisson ratios ν21, ν31 and ν32 can be deduced from these nine physical constants by symmetry.

Given the strain vector [ε] and stress vector [σ], the constitutive law in stiffness form is formulated as

$$ \boldsymbol{[\sigma]} = \boldsymbol{C} \boldsymbol{[\varepsilon]} $$
(3)

where C is the inverse of the constitutive matrix defined in compliance form as follows:

$$ \boldsymbol{C} = \left[\begin{array}{cccccc} \frac{1}{Y_{1}} & \frac{-\nu_{21}}{Y_{2}} & \frac{-\nu_{31}}{Y_{3}} & 0 & 0 & 0\\ \frac{-\nu_{12}}{Y_{1}} & \frac{1}{Y_{2}} & \frac{-\nu_{32}}{Y_{3}} & 0 & 0 & 0\\ \frac{-\nu_{13}}{Y_{1}} & \frac{-\nu_{23}}{Y_{2}} & \frac{1}{Y_{3}} & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{1}{2\mu_{12}} & 0 & 0\\ 0 & 0 & 0 & 0 & \frac{1}{2\mu_{13}} & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2\mu_{23}}\\ \end{array}\right]^{-1} $$
(4)

with the factor 2 applied to the shear coefficients resulting from the difference between shear strain and engineering shear strain. Transverse isotropic material for the representation of fibers is modeled by using the same properties for two of the three principal directions.

2.2 Material orientation as design variables

We now choose a representation to express the orientation for each element. For our purpose in 3D, we use a form of spherical coordinate system based on two angles α and 𝜃 referred to as the azimuth and elevation, respectively as shown in Fig. 4. Since we are only interested in orientation, the radius component of spherical coordinates is irrelevant and omitted here.

Fig. 4
figure 4

Diagram of spherical coordinates notations used for the definition of material orientation with two angle variables α and 𝜃

Full size image

Note that the angle α rotates in the YZ plane. Moreover 𝜃 is negative as it approaches the X+ semi-axis and positive as it approaches the X− semi-axis. The reason for these unconventional choices is purely due to computational and implementation considerations. Indeed, this formulations facilitates the use of the same code for 2D and 3D problems while minimizing the RAM fragmentation of the data arrays being stored in X-major Z-minor ordering.

Given the right set of bounds and disregarding the radius component, one can easily transform between these spherical coordinates and classical Cartesian coordinates using the following relations:

$$ \begin{cases} x =& -\sin(\theta)\\ y =& \cos(\theta)*\cos(\alpha) \Longleftrightarrow \begin{cases} \alpha =& \text{arctan2}(z,y)\\ \theta =& -\arcsin(x)\\ \end{cases}\\ z =& \cos(\theta)*\sin(\alpha) \end{cases}\\ $$
(5)

In certain circumstances, a vector description of the fiber orientation will be more practical. Thus depending on the situation, we will use these relations to swap for the most appropriate coordinate system.

We now devise a series of transformations T applied to the constitutive law matrix C in order to rotate it for both angles α and 𝜃. Thus, we define the rotated matrix RE for any given element E in the design domain Ω as

$$ \boldsymbol{R_{E}}(\alpha_{E}, \theta_{E})= \boldsymbol{T_{\alpha}}(\alpha_{E}) \boldsymbol{T_{\theta}}(\theta_{E}) \boldsymbol{C} \boldsymbol{T_{\theta}^{T}}(\theta_{E}) \boldsymbol{T_{\alpha}^{T}}(\alpha_{E}) $$
(6)

The 6 × 6 matrices Tα(αE) is written as

$$ \begin{aligned} \boldsymbol{T_{\alpha}}(\alpha_{E}) =& \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & c_{\alpha}^{2} & s_{\alpha}^{2} & 0 & 0 & -2c_{\alpha}s_{\alpha}\\ 0 & s_{\alpha}^{2} & c_{\alpha}^{2} & 0 & 0 & 2c_{\alpha}s_{\alpha}\\ 0 & 0 & 0 & c_{\alpha} & -s_{\alpha} & 0\\ 0 & 0 & 0 & s & c & 0\\ 0 & c_{\alpha}s_{\alpha} & -c_{\alpha}s_{\alpha} & 0 & 0 & c_{\alpha}^{2}-s_{\alpha}^{2}\\ \end{array}\right]\\ \text{ with }& \begin{cases} c_{\alpha}= \cos(\alpha_{E})\\ s_{\alpha}= \sin(\alpha_{E})\\ \end{cases} \end{aligned} $$
(7)

Similarly T𝜃(𝜃E) is written as

$$ \begin{aligned} \boldsymbol{T_{\theta}}(\theta_{E}) =& \left[\begin{array}{cccccc} c_{\theta}^{2} & s_{\theta}^{2} & 0 & -2c_{\theta}s_{\theta} & 0 & 0\\ s_{\theta}^{2} & c_{\theta}^{2} & 0 & 2c_{\theta}s_{\theta} & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ c_{\theta}s_{\theta} & -c_{\theta}s_{\theta} & 0 & c_{\theta}^{2}-s_{\theta}^{2} & 0 & 0\\ 0 & 0 & 0 & 0 & c_{\theta} & -s_{\theta}\\ 0 & 0 & 0 & 0 & s_{\theta} & c_{\theta} \end{array}\right]\\ \text{ with }& \begin{cases} c_{\theta}= \cos(\theta_{E})\\ s_{\theta}= \sin(\theta_{E})\\ \end{cases} \end{aligned} $$
(8)

Since the material orientations are carried by these rotation matrices, and in order to clarify the notations without any loss of generality, we will now assume that the base material before rotation has its three principal directions aligned with the X, Y and Z-axes. Consequently the nine physical constants will be denoted Yx, Yy, Yz, νxy, νxz, νyz, μxy, μxz, μyz. For the purpose of the following numerical experiments, we define the three sets of physical constants each defining a different material.

(9)

The material Mat1 exhibit isotropic properties whereas the materials Mat2 and Mat3 exhibit transverse isotropic properties having their stiffest direction aligned with the Y axis. Specifically, Mat2 and Mat3 have their first principal direction 5 and 25 times stiffer than their second principal direction. In this work focusing of the optimization of fibers with smooth orientations, the stiffest direction corresponds to the fiber direction, whereas the lower stiffness in the transverse plane corresponds to the “matrix” material.

2.3 Element stiffness matrix

Having defined the fiber orientation transformations, we can combine these orientation fields with the previously described density field. Therefore, for any given element E in the design domain Ω, we can assemble the element stiffness matrix KE of dimensions 24 × 24 as a function of the element density ρE and the element orientation (αE,𝜃E). Recalling that γ is the penalization exponent of the density-based topology optimization, we define KE as

$$ \begin{aligned} \boldsymbol{K_{E}}(\rho_{E}, \alpha_{E}, &\theta_{E}) = \rho_{E}^{\gamma} \boldsymbol{{K_{E}^{0}}}(\alpha_{E}, \theta_{E})\\ \rho_{min} \leq \rho_{E}& \leq 1, \quad \forall E \in \boldsymbol{\Omega}\\ -\pi \leq \alpha_{E}& \leq \pi, \quad \forall E \in \boldsymbol{\Omega}\\ -\pi/2 \leq \theta_{E}& \leq \pi/2, \quad \forall E \in \boldsymbol{\Omega}\\ \end{aligned} $$
(10)

We are using 8-node regular hexahedral elements in 3D. Consequently, we compute the element stiffness matrix through Gaussian integration using classical linear shape functions. The matrix \(\boldsymbol {{K_{E}^{0}}}\) can be assembled as the following

$$ \boldsymbol{{K_{E}^{0}}} = \iiint \boldsymbol{{B_{E}^{T}}} \boldsymbol{R_{E}}(\alpha_{E}, \theta_{E}) \boldsymbol{B_{E}}d\boldsymbol{\Omega} $$
(11)

where BE is the 6 × 24 matrix defined as

$$ \boldsymbol{B_{E}} = \left[\boldsymbol{B_{E0}} \boldsymbol{B_{E1}} \boldsymbol{B_{E2}} \boldsymbol{B_{E3}} \boldsymbol{B_{E4}} \boldsymbol{B_{E5}} \boldsymbol{B_{E6}} \boldsymbol{B_{E7}}\right] $$
(12)

with the eight sub matrices BEi the containing the element shape functions for the three axes \(\mathcal {N}_{Ei, x}\), \(\mathcal {N}_{Ei, y}\) and \(\mathcal {N}_{Ei, z}\) as

$$ \boldsymbol{B_{Ei}} = \left[\begin{array}{ccc} \mathcal{N}_{Ei,x} & 0 & 0\\ 0 & \mathcal{N}_{Ei,y} & 0\\ 0 & 0 & \mathcal{N}_{Ei,z}\\ \mathcal{N}_{Ei,y} & \mathcal{N}_{Ei,x} & 0\\ \mathcal{N}_{Ei,z} & 0 & \mathcal{N}_{Ei,x}\\ 0 & \mathcal{N}_{Ei,z} & \mathcal{N}_{Ei,y}\\ \end{array}\right] $$
(13)

Having the element stiffness matrix defined means that for a given set of density and orientation fields ρ, α and 𝜃 we can aggregate all the coefficients into the global stiffness matrix K using

$$ \boldsymbol{K}(\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta}) = \bigwedge_{E \in \boldsymbol{\Omega}} \boldsymbol{K_{E}}(\rho_{E}, \alpha_{E}, \theta_{E}) $$
(14)

then write the state equation as an equality constraint in the optimization formulation similarly to (2).

2.4 General orthotropic material

Note that the optimization of a general orthotropic material with 3 different Young moduli would involve an additional angle variable to allow rotation in the transverse plane. This additional angle would be modeled with transformation matrices in the same manner as for the α and 𝜃 fields. Furthermore, the gradients used in the optimization of this third orientation variable would also be obtained via adjoint sensitivity analysis as shown in the next section. Similarily, the regularization scheme described later would be applied on tensors of rank-2 instead of rank-1.

3 Optimization

The previous section presented the mathematical model for simulating the elastic deformation of structures consisting of non-uniformly oriented transverse isotropic constitutive material. The aim of the present section is to leverage this model by developing a numerical optimization scheme responsible for the automated optimization of the material orientations throughout the design domain. Initially we develop the computation of the derivatives allowing the use of sensitivity-based optimization methods. Afterwards, we evaluate the behavior of the optimization scheme through several numerical experiments. Lastly, we discuss the purpose and impact of regularization and filtering of design variables as an important approach for obtaining a smoothly varying material orientation field.

3.1 Sensitivity analysis

The derivatives of the compliance objective function J with respect to the design variables ρ, α and 𝜃 can be obtained by adjoint sensitivity analysis.

$$ \begin{aligned} \frac{\partial J}{\partial \rho_{E}}&= -\gamma\rho_{E}^{\gamma-1} \boldsymbol{u_{E}}^{T} \boldsymbol{{K_{E}^{0}}} \boldsymbol{u_{E}} ,\quad \forall E \in \boldsymbol{\Omega}\\ \frac{\partial J}{\partial \alpha_{E}}&= -\rho_{E}^{\gamma} \boldsymbol{u_{E}}^{T} \frac{\partial \boldsymbol{{K_{E}^{0}}}}{\partial \alpha_{E}} \boldsymbol{u_{E}} ,\quad \forall E \in \boldsymbol{\Omega}\\ \frac{\partial J}{\partial \theta_{E}}&= -\rho_{E}^{\gamma} \boldsymbol{u_{E}}^{T} \frac{\partial \boldsymbol{{K_{E}^{0}}}}{\partial \theta_{E}} \boldsymbol{u_{E}} ,\quad \forall E \in \boldsymbol{\Omega}\\ \end{aligned} $$
(15)

with γ the penalization term defined in (1). In order to obtain the partial derivatives of \(\boldsymbol {{K_{E}^{0}}}\) with respect to αE we differentiate (11) as follows

$$ \begin{aligned} \frac{\partial \boldsymbol{{K_{E}^{0}}}}{\partial \alpha_{E}} &= \iiint \boldsymbol{{B_{E}^{T}}} \frac{\partial \boldsymbol{R_{E}}(\alpha_{E}, \theta_{E})}{\partial \alpha_{E}} \boldsymbol{B_{E}}d\boldsymbol{\Omega}\\ \frac{\partial \boldsymbol{R_{E}}}{\partial \alpha_{E}} &= \frac{\partial \boldsymbol{T_{\alpha}}}{\partial \alpha_{E}} \boldsymbol{T_{\theta}} \boldsymbol{C} \boldsymbol{T_{\theta}^{T}} \boldsymbol{T_{\alpha}^{T}} \!\! + \boldsymbol{T_{\alpha}} \boldsymbol{T_{\theta}} \boldsymbol{C} \boldsymbol{T_{\theta}^{T}} \frac{\partial \boldsymbol{T_{\alpha}^{T}}}{\partial \alpha_{E}} \end{aligned} $$
(16)

Similarly, the partial derivatives of \(\boldsymbol {{K_{E}^{0}}}\) with respect to 𝜃E are obtained as

$$ \begin{aligned} \frac{\partial \boldsymbol{{K_{E}^{0}}}}{\partial \theta_{E}} &= \iiint \boldsymbol{{B_{E}^{T}}} \frac{\partial \boldsymbol{R_{E}}(\alpha_{E}, \theta_{E})}{\partial \theta_{E}} \boldsymbol{B_{E}}d\boldsymbol{\Omega}\\ \frac{\partial \boldsymbol{R_{E}}}{\partial \theta_{E}} &= \boldsymbol{T_{\alpha}} \left( \frac{\partial \boldsymbol{T_{\theta}}}{\partial \theta_{E}} \boldsymbol{C} \boldsymbol{T_{\theta}^{T}} + \boldsymbol{T_{\theta}} \boldsymbol{C} \frac{\partial \boldsymbol{T_{\theta}^{T}}}{\partial \theta_{E}} \right) \boldsymbol{T_{\alpha}^{T}} \end{aligned} $$
(17)

Finally, we calculate the derivatives of the transformation matrix Tα with respect to the design variables αE. This is achieved by differentiating the matrix defined in (7) as follows

$$ \frac{\partial \boldsymbol{T_{\alpha}}}{\partial \alpha_{E}} = \left[\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 0\\ 0 & -2c_{\alpha}s_{\alpha} & 2c_{\alpha}s_{\alpha} & 0 & 0 & -2(c_{\alpha}^{2}-s_{\alpha}^{2})\\ 0 & 2c_{\alpha}s_{\alpha} & -2c_{\alpha}s_{\alpha} & 0 & 0 & 2(c_{\alpha}^{2}-s_{\alpha}^{2})\\ 0 & 0 & 0 & -s_{\alpha} & -c_{\alpha} & 0\\ 0 & 0 & 0 & c_{\alpha} & -s_{\alpha} & 0\\ 0 & c_{\alpha}^{2}-s_{\alpha}^{2} & s_{\alpha}^{2}-c_{\alpha}^{2} & 0 & 0 & -4c_{\alpha}s_{\alpha}\\ \end{array}\right] $$
(18)

Similarly, we obtain the derivative of T𝜃 with respect to the design variables 𝜃E by differentiating (8) as follows and T𝜃 as

$$ \frac{\partial \boldsymbol{T_{\theta}}}{\partial \theta_{E}} = \left[\begin{array}{cccccc} -2c_{\theta}s_{\theta} & 2c_{\theta}s_{\theta} & 0 & -2(c_{\theta}^{2}-s_{\theta}^{2}) & 0 & 0\\ 2c_{\theta}s_{\theta} & -2c_{\theta}s_{\theta} & 0 & 2(c_{\theta}^{2}-s_{\theta}^{2}) & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ c_{\theta}^{2}-s_{\theta}^{2} & s_{\theta}^{2}-c_{\theta}^{2} & 0 & -4c_{\theta}s_{\theta} & 0 & 0\\ 0 & 0 & 0 & 0 & -s_{\theta} & -c_{\theta}\\ 0 & 0 & 0 & 0 & c_{\theta} & -s_{\theta}\\ \end{array}\right] $$
(19)

The implementation of a gradient-based numerical optimization scheme also requires the gradients of the constraint Gtot with respect to the design variables ρ, α and 𝜃. Recalling the definition of the constraint Gtot as

$$ G_{tot}(\boldsymbol{\rho}) = \frac{1}{G_{tot}^{\star} \cdot v_{\boldsymbol{\Omega}}}\sum\limits_{E\in\boldsymbol{\Omega}}\left( \rho_{E} v_{E}\right) -1 \leq 0 $$
(20)

it is clear that this constraint is independent of the material orientation variables. This makes intuitive sense considering that the mass of the structure should be the same regardless of the orientation of the material within it. This lets us write the required gradients as

$$ \begin{aligned} \frac{\partial G_{tot}}{\partial \rho_{E}} &= \frac{v_{E}}{G_{tot}^{\star} \cdot v_{\boldsymbol{\Omega}}}, \quad \forall E \in \boldsymbol{\Omega}\\ \frac{\partial G_{tot}}{\partial \alpha_{E}} &= 0, \quad \forall E \in \boldsymbol{\Omega}\\ \frac{\partial G_{tot}}{\partial \theta_{E}} &= 0, \quad \forall E \in \boldsymbol{\Omega}\\ \end{aligned} $$
(21)

3.2 Design variable update scheme

Having introduced the orientation design variables in the problem, we obtain the following optimization formulation

$$ \setlength{\jot}{4pt} \begin{aligned} \arg\min_{\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta}} \quad &J_{sm}(\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta}) = \left( \sum\limits_{i \in \boldsymbol{LC}}\left( \boldsymbol{f_{i}}^{T} \boldsymbol{u_{i}}\right)^{n}\right)^{1/n}\\ s.t.\quad &\boldsymbol{K_{i}}(\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta})\boldsymbol{u_{i}} = \boldsymbol{f_{i}} ,\quad \forall i \in \boldsymbol{LC}\\ &\rho_{min} \leq \rho_{E} \leq 1, \quad \forall E \in \boldsymbol{\Omega}\\ &-\pi \leq \alpha_{E} \leq \pi, \quad \forall E \in \boldsymbol{\Omega}\\ &-\pi/2 \leq \theta_{E} \leq \pi/2, \quad \forall E \in \boldsymbol{\Omega}\\ &G_{tot}(\boldsymbol{\rho}) = \frac{1}{G_{tot}^{\star} \cdot v_{\boldsymbol{\Omega}}}{\sum}_{E\in\boldsymbol{\Omega}}\left( \rho_{E} v_{E}\right) -1 \leq 0 \end{aligned} $$
(22)

with Jsm the objective function, one equality constraint in the form of the state equation, three box constraints specifying the lower and upper bounds for the optimization variable fields ρ, α and 𝜃, and one inequality constraint on the total material volume fraction. Note, we use a n-norm aggregation method to combine the respective compliance of each load case i ∈LC into the differentiable soft max function Jsm.

We can now formulate a gradient-based optimization scheme to iteratively update the design variables. The design variables for density and orientation have been purposefully formulated to be separate, thus allowing executing their update synchronously or asynchronously. We can use the Method of Moving Asymptotes optimization scheme (MMA) introduced by Svanberg (1987). The advantage is that this approach will also handle bounds and convergence rates for all the considered design variables. The MMA algorithm is also known to be robust and reliable even when working with optimization formulations having multiple non-linear constraints.

However, it is worth noting that the design variables for material orientations are independent of the mass constraint in this optimization problem formulation. Consequently, the use of a simpler optimization scheme is worth considering to study the convergence behavior. For this first set of numerical experiments we use a modified implementation of the gradient descent update scheme. For stability the gradients of both optimization variables are rescaled and a numerical damping factor ζ is added. Moreover, we introduce move limits mα and m𝜃 which act as a restriction to the maximum amplitude of change for a design variable in a given update step. The update scheme then becomes

$$ \begin{array}{@{}rcl@{}} \alpha_{E} \!\!&\leftarrow&\!\! \min\left( \!\max\left( \!\alpha_{E} - \frac{\zeta}{J_{sm}}\frac{\partial J_{sm}}{\partial \alpha_{E}} , \alpha_{E} - m_{\alpha}\!\right), \alpha_{E} + m_{\alpha}\!\right)\\ \theta_{E} \!\!&\leftarrow&\!\! \min\left( \!\max\left( \!\theta_{E} - \frac{\zeta}{J_{sm}}\frac{\partial J_{sm}}{\partial \theta_{E}} , \theta_{E} - m_{\theta}\!\right), \theta_{E} + m_{\theta}\!\right) \end{array} $$
(23)

Note, contrary to the update rule of the density variables ρ, no explicit bounds are needed to maintain the orientation variables α and 𝜃 in the range specified by (22) due to the π-periodicity of the orientation.

3.3 Numerical experiments

The present formulation allows modeling 2D or 3D transverse isotropic material fields parameterized by their local densities and orientations. This section is dedicated to the execution of numerical experiments highlighting the capabilities and shortcomings of the method. Then, we propose improvements to the update scheme for handling design variable initialization and non-convexity of the optimization problem.

Throughout this article, we will visualize material orientation fields in 2D and 3D. This is accomplished by representing these orientations as short color-coded segments inside each voxel. In order to help with visualization, the coloration of each segment is chosen by converting the absolute magnitudes of the X, Y, and Z components of the vector field directly into the R, G, and B color components as follows: (R;G;B) = (|X|;|Y |;|Z|). For example, the 3D vector [0;0;1] will be displayed as blue, whereas the 3D vector [− 0.7;0;0.7] will be purple.

3.3.1 Orientation regularization

Optimizing both density and orientation field on a 2D cantilever scenario yields results as shown in Fig. 5(a) using the material properties Mat2 from (9). The overall shape resembles a typical cantilever optimized solution using density field optimization. However the material orientation field shows irregularities and 90∘ misalignments due to the non-convexity of the optimization problem which will be discussed in the next section. In order to improve the regularity of the material orientation field we introduce a minimum length scale where the angle design variable fields α and 𝜃 are filtered throughout the optimization process yielding results as shown in Fig. 5b.

Fig. 5
figure 5

Cantilever design obtained using synchronous optimization of the material density and orientation fields on a 48 × 30 mesh. The designs (a) and (b) are obtained without and with filtering using a radius of 1.5 voxels, respectively

Full size image

The filtering process should not be executed as a simple convolution on both scalar fields α and 𝜃 separately for two reasons. Firstly, such convolution would not properly handle the periodicity of the orientation variables. Secondly, both angles are strongly interdependent in the definition of the rotated constitutive material RE(αE,𝜃E), and thus cannot be treated as separate entities.

Consequently, the filtering is a modified version for vector parameterization based upon the method introduced in Bruns and Tortorelli (2001) and Bourdin (2001). Using the relationship described in (5), each couple \(\left (\alpha _{E}; \theta _{E}\right )\) is transformed into vector space as a single unit vector ϕE for each element E in Ω. The proposed regularization filter yields the smoothed vector field \(\boldsymbol {\tilde \phi }\) as follows

$$ \begin{aligned} &\boldsymbol{\tilde\phi_{E}} = \frac{{\sum}_{e \in \boldsymbol{\omega}} \left( v_{e} w_{E, e} \boldsymbol{\hat\phi_{e}}\right)} {{\sum}_{e \in \boldsymbol{\omega}} \left( v_{e} w_{E, e} \right) } ,\quad \forall E \in \boldsymbol{\Omega}\\ \text{ where } &\boldsymbol{\hat\phi_{e}} = \begin{cases} -\boldsymbol{\phi_{e}} \text{ if } \boldsymbol{\phi_{E}} \cdot \boldsymbol{\phi_{e}} \leq 0\\ \boldsymbol{\phi_{e}} \text{ otherwise}\\ \end{cases}\\ \end{aligned} $$
(24)

with the weighted mask wE,e defined as a linearly decaying function of radius R on the neighboring elements e in the set ω and their positions x as follows

$$ w_{E, e} = R - \| \boldsymbol{x_{E}} - \boldsymbol{x_{e}} \| $$
(25)

After filtering the orientation variables in vector space, the field \(\widetilde {\boldsymbol {\phi }}\) is the transformed back into spherical coordinates to provide the regularized angle fields updating α and 𝜃 for the next optimization iteration. Figure 6 plots the evaluated compliance for the first 60 optimization iterations leading to the designs shown in Fig. 5.

Fig. 6
figure 6

Compliance evaluated at each iteration of the design optimization resulting in the two designs shown in Fig. 5

Full size image

As expected, the material orientation regularization improves the vector field continuity leading to smoothly changing fiber paths. We also note that filtering helps reaching results with significantly lower compliance by reducing sudden changes of material direction between elements. The filtering of orientation variables allows controlling the length scale of the vector field, analogously to the regularization of the density variables through filtering and will be discussed in Section 4.4. Consequently, this filtering of design variables prevents the solution to fall in noisy local minima early in the optimization process.

3.3.2 Orientation initialization

The following numerical experiment is a 2D bridge optimization scenario with five distinct load cases. The purpose of the present test is to evaluate the behavior of the optimization workflow with respect to the initial orientation vector field. Figure 7 shows the side-by-side comparison of the optimized structure obtained when the initial fibers are aligned vertically or horizontally in the 2D bridge scenario.

Fig. 7
figure 7

Comparison of the optimized density and fiber orientation fields on a 64 × 40 mesh obtained using initial fibers aligned vertically (a) or horizontally (b) in the 2D bridge scenario with 5 load cases

Full size image

We observe from the two designs that the optimization workflow presented here displays a high degree of dependence upon the initial material orientation field. This can be explained as a feedback loop happening in the early iterations of the topology optimization. If the fibers are initially all set in a given direction, then the optimization scheme will preferentially adjust the density field in order to produce beams along the length of these fibers due to the higher stiffness of this direction. Similarly, if the density field mostly describes beams along a certain direction, then the fiber orientations will be directed to align with this same direction in order to give a higher stiffness to the beam. This feedback effect between the design variables ρ and (α;𝜃) during their simultaneous optimization is the reason why the designs in Fig. 7 exhibit a structural layout mostly oriented along the initial orientations.

This effect is suppressed by providing an initial orientation field without any preferential direction, i.e., with a random orientation for each element. The convergence history of three 2D bridge designs with different initialization strategies is shown in Fig. 8.

Fig. 8
figure 8

Convergence history for three variants of the 2D bridge design obtained with various strategies of initial material orientations

Full size image

We observe that for this specific optimization scenario, the vertical direction is an excellent initial guess for the orientation field, yielding an initial and final compliance more than 2.5 times lower than the initial guess using horizontal direction. On the other hand, knowledge of such appropriate initial guess is impossible for general applications with arbitrary optimization scenarios.

Synchronous optimization of the material density and orientation using a random initial orientation field yields designs with less uniform fiber directions. Moreover, running multiple separate topology optimizations of the same problem starting from different random material orientation fields reveals that, while the designs differ, they exhibit similar overall shape and compliances. This will be demonstrated in Section 4.5. As a result, the random initialization, achieving a final compliance almost as low, appears to be a valid initialization strategy for general purpose setup aiming at reducing dependence to initial material orientations.

3.3.3 Non-convexity

As observed in the previous sections, optimized designs involving local material orientations often contain regions with seemingly sub-optimal alignment. This difficulty encountered by the optimization scheme is the result of the non-convexity of the objective function when considering anisotropic materials. By definition, an element with orthotropic material in tension or compression will have multiple orthogonal minima corresponding to each principal directions of the material. In order to illustrate how this non-convexity affects optimization problems with more design variables, we use the test case illustrated in Fig. 9 where a 2D plate is fixed on one edge and a uniform load is applied at the opposite edge.

Fig. 9
figure 9

Load case of a 2D plate fixed at the bottom edge and subjected to a uniform tension load (a) and shear load (b) at the opposite edge

Full size image

The design space is divided into two regions describing adjacent horizontal patches. Each region of the two regions has its material orientation defined by one uniform angle and we evaluate the design compliance for each pair of values. Figure 10 shows the design responses as a surface parameterized by the two design variables, each changing from 0∘ to 360∘ independently.

Fig. 10
figure 10

Plot of the design responses for a 2D plate submitted to tension and shear deformation with respect to two material orientation variables defining the fiber direction of two adjacent sets of elements

Full size image

First we observe that the design responses exhibit the expected 180∘-periodicity, therefore all angles values given below will be considered mod 180∘. Secondly, we observe that in the tension load case the design response has a local minimum when the two angles take values of \(\left (0^{\circ }; 90^{\circ }\right )\), \(\left (90^{\circ }; 0^{\circ }\right )\) and \(\left (90^{\circ }; 90^{\circ }\right )\) and the global minimum for \(\left (0^{\circ }; 0^{\circ }\right )\). The number of local minima in the design response increases exponentially with the number of design variables. Thirdly, the shear load case exhibits multiple equivalent local minima with a material orientation of 36∘ and 144∘. Note that formulating an optimization problem with multiple load cases can further worsen the situation. To illustrate this point, we consider the three aggregation strategies sum, max and soft max to formulate the objective function considering both the tension and shear load cases. Figure 11 shows the design responses with respect to the two design variables under these different aggregation strategies.

Fig. 11
figure 11

Design responses for a 2D plate submitted to both tension and shear load cases using different aggregation function strategies

Full size image

The sum aggregation results in the overall smoothest design response. Nevertheless, industrial scenarios often require using so-called MinMax formulation which prioritizes the worst case scenario, i.e., minimize the maximum compliance (or maximum displacement, stress, etc.). The max function is notoriously non-differentiable, as seen in Fig. 11, which explains the use of the soft max aggregation strategy as an alternative. Regardless of the number of design variables, load cases and choice of aggregation function, the orientation of any anisotropic material is a fundamentally non-convex optimization problem.

This issue is circumvented by modifying the update rule to introduce a continuation scheme and a global optimum search strategy similar to the simulated annealing process. The iterative optimization scheme is then a hybrid process controlled by two components. The search direction is defined by the gradient of the objective function, similarly to a classical gradient descent algorithm. The step size along that direction is conditioned by initially large and progressively decreasing move limits mα and m𝜃. In our experiments, the move limits mα and m𝜃 start at 45∘ and decay exponentially at a rate of 0.9 at each optimization iteration. The term ζ in (23) allows introducing an artificial “energy” thereby preventing the solution to settle in a local minimum early in the optimization iterations. In later examples this strategy is also employed for the MMA optimization scheme by applying the same continuation scheme and the ζ term on the design sensitivities. The global convergence of this modified scheme is discussed in Section 4.5.

4 Results and analysis

The previous sections described a mathematical model and numerical optimization framework for generating structures with oriented orthotropic material. Especially, we discussed the need for a regularization scheme on the orientation field providing length-scale control. We also studied the dependency of the optimization scheme to initial conditions as well as the non-convexity of the underlying design response functions. Therefore, the present section uses the components described so far in various scenarios and analyze the results to numerically validate the proposed method.

4.1 Simple 3D test case

As a first test we use a simple 3D scenario with 3 loads involving the synchronous optimization of both material density field ρ and orientation fields (α;𝜃). We will use the Mat2 material properties from (9), subject to a total volume constraint set to 10% of the design space volume. The initial design variables are given by a uniform density field with random 3D material orientations. The structure is optimized according to the final numerical optimization scheme described in the previous section yielding the result shown in Fig. 12.

Fig. 12
figure 12

Optimization convergence a logarithmic scale of the objective function of a simple 3D structure with oriented fibers. Both densities and material directions are optimized at each iteration for a volume fraction constraint of 10% on a 32 × 32 × 32 mesh. The state of the design variables is visualized at iteration 0, 2, 10 and 40, respectively

Full size image

Even with a purely random initial orientation field, the convergence plot shows that most elements have their material aligend with the orientation of tension after the second iteration. We recall that segments in red, green and blue correspond to material orientations aligned with the X, Y and Z axes, respectively. After 5 to 10 optimization iterations, the initial drop in compliance is done and the remaining iterations only cause minor adjustments to the design variables. In this second phase of the optimization, the tight move limits combined with the regularization scheme ensure that the final design exhibits a well-defined topology with smoothly varying material orientations.

4.2 Performance of isotropic and transverse isotropic materials

To follow-up on the previous result, we aim at quantifying the efficiency of using a material with optimized orientations compared with a classical isotropic material. Anisotropic and isotropic materials cannot be directly compared as they are fundamentally different in performance and cost. However, we observe that most metals are by nature polycrystalline structures with very small grains each having anisotropic mechanical properties but the random arrangement of these grains makes the material exhibit isotropic behavior on large scales.

Consequently, we can imagine a fair comparison where we generate two structures consisting of the same transverse isotropic material. The first structure has random material orientations and only the density field is optimized, thus exhibiting pseudo-isotropic properties. The second structure starts with the same random material orientations but both orientation and density fields are optimized.

We use a 2D cantilever load case on a 512 × 256 grid resolution with a total volume constraint of 40%. A sufficiently high mesh resolution and total volume constraint are necessary to allow the averaging effect of random orientations leading to pseudo-isotropic macroscopic properties. The outcome of this comparison is summarized in Fig. 13 showing the compliance history over the optimization iterations for these two structures using the material properties Mat2 and Mat3, respectively.

Fig. 13
figure 13

Comparison of the convergence history of a pseudo-isotropic model with optimized density field and a transverse isotropic model with optimized density field and material orientations on a logarithmic scale

Full size image

We observe that all four designs exhibit a typical smooth convergence curve. As expected, the design with optimized element orientations achieve a much lower final compliance after convergence than its pseudo-isotropic counterpart for both Mat2 and Mat3 materials. Specifically these structures are 2.9 and 6.5 times stiffer with optimized material orientations under the specified load, respectively.

In addition, we can also see the computational efficiency of the proposed numerical optimization method compared with the classical SIMP approach. Firstly, by allowing the modification of material orientations we introduce a new set of design variables in the formulation. Nevertheless, numerical experiments showed that in practice the number of optimization iterations required to achieve convergence stays generally the same. Secondly, the introduction of an anisotropic material in the system matrix tends to increase its condition number proportionally to the ratio of Young moduli between the principal directions of that material. As a consequence, when solving the state equation for the displacements, the iterative solver does apply a larger number of iterations to sufficiently reduce the solution’s residual error even if the number of unknowns stays unchanged. Finally, the material orientation potentially changing for each element at each optimization step means that the elemental stiffness matrices cannot be computed in advance for the voxel mesh, thereby making the system matrix assembly more costly.

4.3 Large-scale optimization

The proposed numerical optimization framework is compatible and stable with high resolution structural design problems. We set up a test scenario illustrated in Fig. 14, where the design domain is a cube with all corners being fully clamped. Multiple different load cases are generated in the form of point-forces each with a random position, direction and magnitude.

Fig. 14
figure 14

Test case for high resolution topology optimization using a cube design domain having all its corners fully clamped and multiple randomly generated load cases

Full size image

On this test scenario, we generate three optimization problems with different mesh resolutions and number of load cases. All three problems are conducted as a synchronous optimization of the density and material orientation fields with a constraint on the total volume fraction of 10% and using the material Mat2. Solving the state equation for each load case is done using a single NVIDIA Quadro RTX6000 GPU. The rest of the optimization workflow, including the design variables update using the hybrid gradient-based simulated annealing optimization procedure, is executed on a 20 Cores 2.40GHz Intel Xeon Gold6148 CPU. The problem specifications and achieved runtimes are summarized in the following.

(26)

The 3 structures are shown in Fig. 15 as isosurfaces on the density fields and the highest resolution example is displayed as a vector field in Fig. 16.

Fig. 15
figure 15

Isosurfaces of the density fields for the three optimized structures on meshes with resolution 643 (a), 1283 (b) and 1603 (c)

Full size image
Fig. 16
figure 16

Material orientation vector field for the optimized 160 × 160 × 160 grid mesh

Full size image

At the end of the design optimization, the sub-structures consist mainly of beams and hub connections forming an intricate geometrical network. These geometrical features are characteristic of 3D topology optimization scenarios with multiple load cases. Close examination of the material orientation vector field shows smooth transitions near junctions. In particular, the regularization of both density and orientations result in a structure having a geometric surface without sharp corners and with continuous internal material directions. However, it is also clear that at this resolution, the visualization of 3D scalar and vector fields is difficult. Consequently, we also display the final structure as a transparent volume render and as streamlines in Fig. 17.

Fig. 17
figure 17

Transparent volume render and streamlines computed for the optimized 160 × 160 × 160 grid mesh

Full size image

The streamlines are calculated using the 4th-order Runge-Kutta integrator generally referred to as the RK4 method (Runge 1895; Kutta 1901; Tan and Chen 2012). The local truncation error is on the order of \(\mathcal {O}(h^{5})\) and the total accumulated error is on the order of \(\mathcal {O}(h^{4})\) where h is the integration step size. This is a simple yet effective visualization technique to study the smoothness of the material orientation field. Indeed, streamlines are widely used for the visualization of Computational Fluid Dynamics (CFD) results because they allow quickly locating and estimating certain phenomena like field continuity, oscillations, divergence and curl. Thus, the generation of streamlines helps verifying the quality of the fiber orientations in our 3D topology optimization results.

In the present numerical test, we used the sum aggregation strategy to produce the differentiable objective function. The convergence history of all eight individual compliances for the 160 × 160 × 160 grid mesh is shown in Fig. 18.

Fig. 18
figure 18

Compliances of 8 load cases on a logarithmic scale evaluated at each iteration during the generation of the optimized 160 × 160 × 160 grid mesh with a 10% volume fraction constraint, and visualization of the corresponding streamlines at iteration 0, 5, 10 and 120, respectively

Full size image

We observe that the optimization traces a typical convergence behavior for compliance with a sharp drop in the first few iterations followed small design variable adjustments in the following optimization iterations. However, it is worth noting that the compliances for this specific case are lowest around the 15th iteration and slightly increases in the subsequent iterations. This seemingly unintuitive outcome is a result of the regularization scheme used in the optimization workflow for the material orientations. Indeed, while the measured compliance at the 15th iteration is low, the design variable fields ρ and \(\left (\boldsymbol {\alpha }; \boldsymbol {\theta }\right )\) still show irregularities and intermediate densities. These irregularities are however corrected in the subsequent optimization iteration, yielding a satisfying design after the 40th to 50th iterations with a well a defined topology and smooth material orientations. This observation was supported by the visualization of the numerical results as continuous streamlines.

4.4 Mesh independence

Mesh independence is a known challenge in topology optimization and many studies have discussed how approaches like filters, projections schemes, morphology operators or perimeter control can reduce the dependence of the optimized density field to the finite element mesh and especially to the element sizes. This section shows how the regularization scheme applied on the material orientation field in (24) allows controlling its length scale in a similar manner. Figure 19 shows multiple variants of a 2D cantilever design and displays the behavior of the fiber paths in a curved regions for different mesh sizes and filter radii.

Fig. 19
figure 19

Mesh dependence experiments on a 2D cantilever. Five designs are optimized with different mesh resolutions and filter sizes (in number of elements). Examples (a), (c) and (d) show mesh independence due to consistent filter radius relative to the mesh resolution. Examples (b) and (d) show mesh dependence as only the mesh resolution increases

Full size image

As expected, we observe that the fiber path curvature is tied to the radius of the regularization filter. Consequently, by keeping the filter radius consistent with the mesh resolution, we prevent the optimization scheme from creating tighter fiber turns by exploiting the smaller element sizes.

4.5 Global convergence

Even for the simplest density-based compliance topology optimization, the solution space is known to be non-convex when applying multiple load cases, penalization, discretization or restrictions in the design space. Moreover, as shown by the Mitchell truss structure (Michell 1904) for optimal layout in continuum space (i.e., infinite number of members), the optimal result of a simple discrete cantilever problem will necessarily be tied to the underlying mesh topology and resolution. Nevertheless, despite the absence of theoretical guarantees, the general consensus is that initializing all densities to “gray” material combined with length-scale control is usually enough to prevent the optimization to fall in a poor local minimum.

In Section 3.3.3 we show that introducing material orientation as design variables increases the non-convexity of the solution space. Consequently, the proposed optimization scheme applies a continuation scheme to induce initially large and progressively decreasing changes in the material orientation design variables. Our empirical experiments on various test scenarios showed that combining random initial orientations and length-scale control allows this process to consistently converge to optimized designs of the same quality in approximately 40 and 25 optimization iterations in 2D and 3D, respectively. Figure 20 shows the compliance history of nine optimized variants of the 3D cantilever scenario with different initial orientations.

Fig. 20
figure 20

Compliance history on a logarithmic scale of nine optimized variants of the 3D cantilever scenario on a 30 × 60 × 30 mesh with different initial orientations. Xinit, Yinit and Zinit correspond to initial orientations aligned with the X, Y and Z axes, respectively. RandXY, RandXZ and RandYZ correspond to random initial orientations in the XY, XZ and YZ planes, respectively. Rand0, Rand1 and Rand2 correspond to purely random initial orientations in 3D

Full size image

We observe that the convergence rate is similar for all designs, and despite the differences in initial compliance, the final compliance are within a few percent of each other. Oscillations in the first optimization iterations are caused by the initially large move limits in our continuation scheme. Equation (27) reports the final compliances for the nine designs:

(27)

This empirical experiment shows that fully random initial orientations led to both the lowest final compliance and lowest variations in final compliance. Tests using other optimization scenarios (multiple load cases in 2D and 3D) led to the same numerical findings and we conclude that the proposed optimization scheme successfully avoids poor quality local minima despite the non-convexity of the solution space.

4.6 Industrial design scenario

We apply the proposed approach to the optimization of a mechanical part from an industrial design problem. The chosen scenario is the General Electric (GE) jet engine bracket challenge announced on the GrabCAD Community website in 2013 (GrabCAD 2013). This design problem involves multiple load cases applied on a restricted design space. The structure with synchronous optimization of density and orientation fields is shown in Fig. 21.

Fig. 21
figure 21

Isosurface of the optimized bracket design in the design space

Full size image

We enforce 6 prescribed regions around the bolt and load rings. Such functional regions are considered in the analysis and their material orientations are optimized. Moreover, using the signed distance field to the input design space, specific bounds are placed on the density variables to perfectly follow the shape of the input design space while also allowing a seamless connection with the optimized structural regions. The design domain consists of 2.7M hexahedral elements yielding 8.1M design variables. The final material orientation field after 60 optimization iterations is displayed in Fig. 22.

Fig. 22
figure 22

Optimized GE bracket model with smoothly varying material orientation displayed as streamlines colored by their angular velocity

Full size image

The streamlines displayed on the bracket design are calculated with the RK4 method and color coded based on their local angular velocity. This display allows immediately locating the locations with fiber paths of highest curvature. The highest streamline curvatures are detected near the boundary of the input design space. This is expected as the density field has to follow the predefined outer shape of the corner. Nevertheless the material orientation field is still tied to the length-scale control applied by the regularization scheme. Consequently, the streamlines trace smooth paths even in those regions.

4.7 Compliant mechanisms

Compliant mechanism design is a type of optimization problem where optimal material orientation may not be aligned with local stress tensors regardless of the number of load cases. Therefore, we apply the proposed method on the force inverter problem (Sigmund 1997). Both material density and orientations are optimized simultaneously and the resulting design is shown in Fig. 23.

Fig. 23
figure 23

Optimized material orientation field of a compliant force inverter design on a 100 × 100 mesh

Full size image

During the optimization, we observe oscillations of the material orientations in the narrow hinge regions due to the concentrated strain. However, the combination of regularization and continuation scheme on the move limits stabilize the convergence and yield a smooth final material orientation field.

4.8 Compatibility with porosity constraint

As mentioned in the introduction, one of the goals of the proposed method is to provide the ability of optimizing material with spatially varying directions, while also maintaining the orientation design variables separate in the formulation. The motivation behind this requirement is to facilitate the combination of this method with other extensions to the traditional topology optimization approach. In this section we combine the present formulation with a constraint controlling a local volume leading to porosity in the final structural layout (Wu et al. 2018; Schmidt et al. 2019).

Both the material orientation design variables and porosity constraint are compatible allowing us to formulate the new optimization formulation as

$$ \begin{aligned} \arg\min_{\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta}} \quad &J_{sm}(\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta}) = \left( \sum\limits_{i \in \boldsymbol{LC}}\left( \boldsymbol{f_{i}}^{T} \boldsymbol{u_{i}}\right)^{n}\right)^{1/n}\\ s.t.\quad &\boldsymbol{K_{i}}(\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta})\boldsymbol{u_{i}} = \boldsymbol{f_{i}} \quad \forall i \in \boldsymbol{LC}\\ &\rho_{min} \leq \rho_{E} \leq 1, \quad \forall E \in \boldsymbol{\Omega}\\ &-\pi \leq \alpha_{E} \leq \pi, \quad \forall E \in \boldsymbol{\Omega}\\ &-\pi/2 \leq \theta_{E} \leq \pi/2, \quad \forall E \in \boldsymbol{\Omega}\\ &G_{tot}(\boldsymbol{\rho}) = \frac{1}{G_{tot}^{\star} \cdot |\boldsymbol{\Omega}|}\sum\limits_{E\in\boldsymbol{\Omega}}\rho_{E} -1 \leq 0\\ &G_{dyn}(\boldsymbol{\rho}) = \left( \frac{1}{|\boldsymbol{\Omega}|}\sum\limits_{E\in\boldsymbol{\Omega}}\frac{\overline{\rho_{E}}^{p}}{G_{dyn, E}^{\star \quad p}}\right)^{1/p}\!-1 \leq 0 \end{aligned} $$
(28)

with the aggregated objective function Jsm parameterized by the material density field ρ and orientation field \(\left (\boldsymbol {\alpha }; \boldsymbol {\theta }\right )\), and the porosity constraint Gdyn(ρ). The partial derivatives of the additional porosity constraint with respect to the material orientation variables are trivially derived as

$$ \frac{\partial G_{dyn}}{\partial \alpha_{E}} = \frac{\partial G_{dyn}}{\partial \theta_{E}} = 0, \quad \forall E \in \boldsymbol{\Omega}\\ $$
(29)

since the local density \(\overline {\rho _{E}}\) is independent of material orientation. Using this formulation, we execute a topology optimization of a 2D bridge model with 3 load cases and obtain the result shown in Fig. 24.

Fig. 24
figure 24

Optimized bridge structure combining oriented material and porosity constraint on a 240 × 160 mesh. The boundary conditions consist of two fully clamped regions in the lower left and right corners and three load cases shown in red at the top

Full size image

Due to the effect of the porosity constraint, the number of geometrical sub-components in the structure is increased. This introduces more junction points throughout the density field layout. In addition, the scenario is 2D meaning that the material orientation problem is particularly challenging as there is no straightforward way to handle the multiple crossing points without out-of-plane orientations. Nevertheless, the final optimized structure contains smoothly varying fiber orientations. This demonstrates the compatibility of the proposed material orientation optimization workflow with other constraints.

4.9 Varying ratios of anisotropy

Previously, we observed that certain beam-like geometrical features have clearly defined optimal fiber orientations. Conversely, regions like the junction of multiple beams would sometimes prove to be more challenging with respect to the continuity of their material orientations. This observation is a direct consequence of the fact that the most appropriate material in such regions would often be isotropic due to the multiaxial stress state at these locations. Therefore, we develop an extension to the numerical optimization scheme by introducing a new design variable τE parameterizing the ratio of anisotropy of each element E in the design domain Ω. We thereby reformulate C in (6) as an interpolation between Caniso and Ciso, the constitutive laws for two sets of material properties with transverse isotropic and isotropic behaviors, respectively. Similarly to the traditional SIMP topology optimization workflow, intermediate values for the ratio of anisotropy τ would complicate physical interpretation. Therefore, we introduce a penalization exponent q = 3 which yields the elemental constitutive law as a function of τ as

$$ \boldsymbol{C_{E}}(\boldsymbol{\tau}) = \left( {\tau_{E}^{q}}\boldsymbol{C_{aniso}}+ (1-\tau_{E})^{q}\boldsymbol{C_{iso}}\right) $$
(30)

We then write the optimization problem formulation as

$$ \begin{aligned} \arg\min_{\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta}, \boldsymbol{\tau}} \quad &J_{sm}(\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta}, \boldsymbol{\tau}) = \left( \sum\limits_{i \in \boldsymbol{LC}}\left( \boldsymbol{f_{i}}^{T} \boldsymbol{u_{i}}\right)^{n}\right)^{1/n}\\ s.t.\quad &\boldsymbol{K_{i}}(\boldsymbol{\rho}, \boldsymbol{\alpha}, \boldsymbol{\theta}, \boldsymbol{\tau})\boldsymbol{u_{i}} = \boldsymbol{f_{i}} ,\quad \forall i \in \boldsymbol{LC}\\ &\rho_{min} \leq \rho_{E} \leq 1, \quad \forall E \in \boldsymbol{\Omega}\\ &-\pi \leq \alpha_{E} \leq \pi, \quad \forall E \in \boldsymbol{\Omega}\\ &-\pi/2 \leq \theta_{E} \leq \pi/2, \quad \forall E \in \boldsymbol{\Omega}\\ &0 \leq \tau_{E} \leq 1, \quad \forall E \in \boldsymbol{\Omega}\\ &G_{tot}(\boldsymbol{\rho}) = \frac{1}{G_{tot}^{\star} \cdot |\boldsymbol{\Omega}|}{\sum}_{E\in\boldsymbol{\Omega}}\rho_{E} -1 \leq 0\\ \end{aligned} $$
(31)

The derivatives of the objective function and constraint with respect to the design variables are the same as before with the exception of the following additional terms

$$ \begin{aligned} \frac{\partial \boldsymbol{C_{E}}}{\partial \tau_{E}} &= q\left( \tau_{E}^{q-1}\boldsymbol{C_{aniso}} - (1-\tau_{E})^{q-1}\boldsymbol{C_{iso}}\right)\\ \frac{\partial G_{tot}}{\partial \tau_{E}} &= 0\\ \end{aligned} $$
(32)

Then we can run a topology optimization using all four design variable fields ρ, α, 𝜃 and τ. Note that we need to choose reasonable values for Caniso and Ciso to create a compromise between isotropic and transverse isotropic material. In this numerical experiment we use the materials Mat1 and Mat2 of (9). The materials Mat1 was chosen to be similar to the effective pseudo-isotropic behavior of Mat2 on a high resolution mesh with random local fiber orientations. Moreover, we introduce length-scale control of the design variable field τ using a smoothing filter. Using this formulation, we optimize a 2D bridge model with three load cases and a 3D cantilever model as shown in Fig. 25.

Fig. 25
figure 25

Optimized designs with spatially varying ratio of anisotropy. A 2D bridge design with 3 load cases on a 240 × 160 mesh (a) and a 3D cantilever design on a 120 × 60 × 60 mesh (b). The material orientation field is shown on the left and the ratio of anisotropy field is shown on the right where transverse isotropic and isotropic materials are colored in green and red, respectively

Full size image

We observe that the optimization procedure predominantly applied transverse isotropic material throughout the design domain, except for junctions between beam members where isotropic material was deemed more efficient for optimal stiffness. This numerical experiment shows that density, orientation and type of material (in the form of a variable ratio of anisotropy) are optimized simultaneously using the proposed formulation. Moreover this result is in accordance with the initial statement of this section: The optimization scheme generates structures consisting of transverse isotropic beam members under with uniaxial stress in compression or tension connected by isotropic hubs under multiaxial stress.

5 Conclusion

The present work addresses topology optimization using orientation of transverse isotropic material as additional design variables. We developed a sensitivity-based procedure for full-3D material orientation optimization considering multiple load cases. The issue of orientation field continuity is discussed and a regularization filter is proposed to enforce a minimum length scale in the orientation field thereby controlling path curvature. We analyze the non-convexity of the solution space and propose a hybrid gradient-based simulated annealing optimization approach which successfully avoids poor quality local minima. The proposed method is applied on large-scale optimization problems with millions of design variables and multiple load cases yielding topologically optimized structures with smooth fiber orientations in approximately 50 optimization iterations. We also demonstrate the compatibility of this approach with compliant mechanism optimization as well as the local volume constraints recently introduced in the literature. Finally, we extend this formulation with yet another design variable allowing the optimization scheme to choose between isotropic or transverse isotropic material for each element of the design domain. Here it is shown that the topology optimization automatically produces geometrical networks of transverse isotropic beams connected by isotropic hubs. Further work will involve expanding the types of constitutive material laws considered. We also intend to explore methods relying on the projection of fine-scale anisotropic microstructures onto the optimized orientation field.