Concurrent level set topology and fiber orientation optimization of fiber-reinforced composite structures

Abstract

By altering the structural shape and fiber orientation, this research aims to optimize the design of Fiber-Reinforced Composite (FRC) structures. The structural geometry is represented by a level set function approximated by quadratic B-spline functions. The fiber orientation field is parameterized with quadratic/cubic B-splines on hierarchically refined meshes. Different levels for B-spline mesh refinement for the level set and fiber orientation fields are studied to resolve geometric features and to obtain a smooth fiber layout. To facilitate FRC manufacturing, the parallel alignment and smoothness of fiber paths are enforced by introducing penalty terms referred to as "misalignment penalty" and "curvature penalty". A geometric interpretation of these penalties is provided. The material behavior of the FRCs is modeled by the Mori–Tanaka homogenization scheme and the macroscopic structure response is predicted by linear elasticity under static multiloading conditions. The governing equations are discretized by a Heaviside-enriched eXtended IsoGeometric Analysis (XIGA) to avoid the need to generate conformal meshes. Instabilities in XIGA are mitigated by the face-oriented ghost stabilization technique. This work considers mass and strain energy in the formulation of the optimization objective, along with misalignment and curvature penalties and additional regularization terms. Constraints are imposed on the volume of the structure. The resulting optimization problems are solved by a gradient-based algorithm. The design sensitivities are computed by the adjoint method. Numerical examples demonstrate with two-dimensional and three-dimensional configurations that the proposed method is efficient in simultaneously optimizing the macroscopic shape and the fiber layout while improving manufacturability by promoting parallel and smooth fiber paths.

1 Introduction

Fiber-Reinforced Composites (FRCs) are materials that are made up of a matrix (the continuous phase) and fibers (the dispersed phase). The fibers are embedded in the matrix and provide the composite material with enhanced mechanical properties, such as increased stiffness, strength, and fatigue resistance. FRCs exhibit a superior stiffness-to-weight ratio compared to conventional isotropic homogeneous materials.

In the early stages of FRC design, the primary emphasis was on determining the orientation of fibers for given structural shapes like beams or plates, as noted in Nikbakt et al. (2018). These designs typically assumed a constant fiber orientation throughout each ply. However, advancements in composite manufacturing techniques, such as continuous fiber fused filament fabrication (CF4) (Wang et al. 2021), allow for spatially varying fiber angles, increasing structural performance if the local angles are chosen appropriately. Moreover, if the structural shape can be designed alongside the fiber orientation, further performance improvements can be expected. This paper introduces a design optimization framework for the simultaneous optimization of the structural shape and fiber orientation in FRC structures.

To optimize the structural shape, this paper uses Topology Optimization (TO), which is a reliable method for finding the optimal layout of a structure. It provides a systematic way to alter the topology and shape of a structure and effectively eliminate unnecessary material. TO does not require a close-to-optimal design to initialize the optimization process and can significantly reduce a structure's weight and cost.

In this work, design optimization is used to determine not only the topology of the structure but also the fiber orientation to achieve a desired set of mechanical properties. There have been several attempts to optimize fiber orientation and topology simultaneously in the literature, most of which are summarized in the review paper by Gandhi and Minak (2022). Concurrent topology and fiber orientation optimization involve two main components: representation of structural shape and parameterization of fibers. The past work differs mainly in the latter component.

To represent the shape of the structure, most of the methods proposed in the literature employ the density method which represents the material distribution as a volume fraction field, ranging from 0 (indicating void) to 1 (indicating solid). The material properties are typically interpolated using the Solid Isotropic Material with Penalization (SIMP) approach, often in conjunction with filtering and projection techniques. These additional steps are crucial for controlling feature size and accurately delineating the solid-void boundary interface, as exemplified in Sigmund and Maute (2013). Conversely, the Level Set Method (LSM) addresses the challenge of defining this interface, offering a precise description of structural shape throughout the optimization process and eliminating the need for a material interpolation scheme, as discussed by Van Dijk et al. (2013). In this work, the LSM is selected to describe the structural shape.

Methods for FRC optimization vary by the type of design parameters which may include fiber orientation, fiber volume fraction, and other fiber properties. The focus of this paper is on FRC structures with designable spatially varying fiber orientation. Depending on the manufacturing techniques, different levels of spatial variability of the fiber orientation can be realized. For example, CF4 allows for a continuously varying fiber orientation, whereas other manufacturing techniques such as automated tape layout only allow for a discrete set of fiber orientation values. In the context of continuous fiber orientation optimization of FRCs, maintaining a continuous and smooth fiber trajectory is crucial for two primary reasons: Firstly, interruptions in fiber alignment can lead to stress concentrations, weakening the composite structure. Secondly, a continuous, smooth, and parallel fiber path is a prerequisite for most manufacturing techniques.

In discrete parameterization approaches to fiber orientation optimization, the orientation is treated as a discrete variable, limited to a predefined set of angles. This approach, known as Discrete Material Optimization (DMO), was initially introduced in the work of Stegmann and Lund (2005). Subsequent advancements, akin to those in Kiyono et al. (2017), expanded the methodology by augmenting the discrete angle set with angles selected from a normal distribution. However, DMO’s inherent constraint of limiting fiber orientations to a predefined set makes it less suitable for manufacturing techniques like CF4. Such techniques offer broader design freedoms, which DMO does not exploit due to its discrete nature.

To leverage the design capabilities of Additive Manufacturing (AM) methods such as the CF4 method, it is essential to allow for continuous variation in fiber orientation. The initial approach in this field, the stress/strain-based design, was introduced by Pedersen (1989) and further developed by Gea and Luo (2004). This method aligns fiber orientations with the principal stress or strain directions. This method does not apply to problems with multiple load cases and does not treat fiber orientation as an optimization variable that is updated by an optimization algorithm, further restricting its applicability to a broader class of optimization problems.

Treating fiber angle as a continuous design variable was initially introduced in the context of laminate composites allowing for a range of fiber angles from $[0, \pi ]$; see, for example, Sun and Hansen (1988), Mateus et al. (1991), Thomsen and Olhoff (1993), Bruyneel and Fleury (2002), and Hirano (2012). Considering manufacturing limitations, this approach often necessitates a smooth fiber layout. To address this requirement, several studies, such as Papapetrou et al. (2020), Brampton et al. (2015), Bruyneel and Zein (2013), and Fernandez et al. (2019), have aligned fibers along iso-contours of a level set field or streamlines. This method produces parallel, equidistant fibers, simplifying the post-processing steps required for their manufacturing. However, this method restricts the design space, potentially leading to sub-optimal designs, as discussed in Tian et al. (2021).

Feature-based parametrization is another technique for obtaining spatially continuous fiber orientation. This approach involves designing bars reinforced with continuous fibers aligned along the bars, see Smith and Norato (2021), and Greifenstein et al. (2023). While effective, this method also imposes limitations on the design space, links fiber orientation with the structure’s geometry, and does not take full advantage of the design freedom offered by AM.

The isoparametric transformation method is a continuous fiber orientation optimization approach adopting parameterization concepts of density TO. Introduced by Nomura et al. (2015), it converts the fiber angle into a Cartesian vector with two independent components. These components along with a density variable are used in the SIMP method for interpolating properties of anisotropic materials. This method, although effective in creating a smooth fiber field through filtering and projection, doubles the number of design variables and requires a constraint for maintaining the unit norm of the angle vector. It also faces challenges similar to the density method, such as clearly defining interfaces and boundaries. Follow-up studies by Kim et al. (2020), Jung et al. (2022), and Smith and Norato (2022) have further developed Nomura et al. (2015)’s method. To ensure fiber path smoothness, these methods typically adjust filter radius and constrain design variable derivatives, as explored by Greifenstein and Stingl (2016). Additionally, some researchers, including Papapetrou et al. (2020), Boddeti et al. (2020), Fedulov et al. (2021), and Fernandes et al. (2021), have investigated post-processing techniques to achieve smooth and parallel fiber layouts from optimized orientation fields to bridge the gap between the optimized fiber orientation field and the final manufacturable structure’s fiber layout.

Most manufacturing methods impose constraints on the maximum curvature of the fiber path. Approaches for constraining the curvature differ based on the parameterization of the fiber orientation field. For instance, using iso-contours of a level set field, where the level set equation defines the fiber path, the curvature of the fiber orientation field can be controlled directly by constraining the curvature of the level set field; see, for example, Nagendra et al. (1995), Setoodeh et al. (2006), Haddadpour et al. (2012), Ding et al. (2022), and Zhang et al. (2024). Explicit curvature constraints can also be formulated when the fiber path is represented by a spline (Lemaire et al. 2015; Fernandez et al. 2019). Conversely, methods based on isoparametric transformations often utilize filtering to limit the curvature, where the fiber path curvature correlates with the filter radius (Jantos et al. 2020; Schmidt et al. 2020; Mei et al. 2021). Particularly relevant to the work in this paper, where fiber orientation is an explicit design variable, are the studies that determine fiber path curvature from spatial changes in the fiber orientation field. For example, Tian et al. (2019) and Shafighfard et al. (2019) approximate the curvature by the change in fiber orientation across neighboring elements in a Finite Element (FE) mesh. While effective, this discrete approach is not well suited for shape optimization and 3D problems due to reliance on a fixed geometry and mesh size. In this paper, we introduce a continuous formulation of the fiber path curvature in terms of the fiber orientation field. This formulation is directly applicable to shape optimization problems in two and three dimensions.

A design optimization methodology is presented in this paper to address the shortcomings discussed above. The structural shape is represented using level sets, ensuring a clear interface definition throughout the optimization. To enhance design flexibility, the fiber orientation is described explicitly by a continuous field that is parametrized by higher-order B-splines with adjustable refinement levels. The B-spline coefficients are considered optimization variables. B-spline functions promote smooth designs, prevent the appearance of spurious features, and eliminate the need for further filtering techniques, as discussed by Noël et al. (2020). The fiber orientation field is filtered implicitly by adjusting the refinement level and polynomial order of the B-spline.

Misalignment and curvature penalties are introduced to promote parallel and smooth fiber alignment. These penalties control the first-order derivative of the fiber orientation field in an anisotropic manner and are incorporated into the formulation of the objective function. A detailed geometric interpretation is provided to explain how these penalty terms facilitate the creation of smooth and parallel fiber layouts. While some post-processing of the optimized structure is still necessary to generate a manufacturable design, these penalties reduce the difference between the optimized fiber orientation field and the final, manufactured fiber paths.

In this study, the structural behavior is modeled using static linear elasticity, and the microscopic behavior of the FRC is captured through the Mori–Tanaka homogenization scheme (Mori and Tanaka 1973). The weak form of the governing equations is discretized by the eXtended IsoGeometric Analysis (XIGA). Nitsche’s method (Nitsche 1971) is employed to weakly enforce Dirichlet boundary conditions. Furthermore, numerical instabilities due to XIGA are mitigated by face-oriented ghost stabilization. The level set and fiber orientation fields are discretized by higher-order B-splines, and the displacement field is approximated by linear B-splines. The optimization problems are solved by the Globally Convergent Method of Moving Asymptotes (GCMMA). The gradients of the objective and constraint functions with respect to the optimization variables are computed by the adjoint method.

The remainder of this paper is organized as follows: Sect. 2 discusses the parameterization of the level set and fiber orientation fields. Section 3 provides a brief description of XIGA and its building blocks as well as the weak form of the governing equations. An overview of the formulation of the optimization problem and detailed descriptions of the misalignment and curvature penalties are provided in Sect. 4. Section 5 presents numerical examples where the effects of misalignment and smoothing penalties and parameterization of the fiber orientation field on the optimized design are discussed. Section 6 summarizes the findings of this study and draws conclusions about the developed method.

2 Design variable representation

In this study, the structural shape and the local fiber orientation are considered design parameters. Section 2.1 details the shape parametrization and Section 2.2 discusses the parametrization of the fiber orientation field.

2.1 Geometry representation

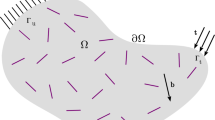
The shape of the structure and material interfaces are described by a level set function (LSF), $\phi$; see for example Van Dijk et al. (2013) and references therein. The interface and external boundaries are defined as the zero iso-level of the LSF. The LSF is a scalar function that discriminates between the two material domains, $\varOmega _1$ and $\varOmega _2$, by assigning positive and negative values, respectively, with $\varGamma _{12}$ representing the boundary. Note that one of these domains may represent void. Formally, the LSF at a spatial point with coordinates $\textbf{x}$ within the computational domain is given by

$$\begin{aligned} \phi (\textbf{x}) = {\left\{ \begin{array}{ll} < 0, &{} \text {for all } \textbf{x} \in \varOmega _1, \\ > 0, &{} \text {for all } \textbf{x} \in \varOmega _2, \\ = 0, &{} \text {for all } \textbf{x} \in \varGamma _{12}. \end{array}\right. } \end{aligned}$$

(1)

Figure 1 illustrates the LSF’s application in defining the geometry of a two-phase solid/void design domain, with $\varOmega _1$ indicating the solid structure, $\varOmega _2$ the void, and $\varGamma _{12}$ the interface between them.

Fig. 1

Geometric description of solid ($\varOmega _1$)/void ($\varOmega _2$) design domain using the LSF

The LSF is discretized on a computational mesh which may be independent of the state variable mesh. In this work, the LSF is approximated by B-spline basis functions $B_k(\textbf{x})$ and their corresponding coefficients $\phi _k$ as

$$\begin{aligned} \phi (\textbf{x}) \approx \phi ^h(\textbf{x}) = \sum _{k} B_k(\textbf{x}) \phi _k, \end{aligned},$$

(2)

where $\phi ^h(\textbf{x})$ denotes the discretized LSF.

In the work of Sethian and Wiegmann (2000), optimization with the level set method involves evolving the LSF through the Hamilton-Jacobi equation. In contrast, the current study follows the work of Noël et al. (2020) and defines the LSF coefficients $\phi _k$ explicitly as functions of the design variables, represented by vector $\varvec{s}$ of length $N_s$. These coefficients are updated via a gradient-based algorithm employing shape sensitivities. This approach simplifies managing multiple constraints.

2.2 Fiber orientation

This work considers FRCs in two dimensions with one spatially varying fiber direction and three dimensions with two spatially varying fiber angles. Figure 2 illustrates the geometrical definitions of the fiber angles $\theta _{xy}$ and $\theta _z$. The tangent vector $\textbf{t}$ along a fiber’s path is projected onto the x–y plane, establishing $\theta _{xy}$ as the first angle. Conversely, $\theta _z$ is defined as the angle between the fiber’s tangent and its projection onto the x–y plane. Utilizing these definitions, the fiber’s tangent vector is expressed in two and three dimensions as follows:

Fig. 2

Fiber angle definitions in 3D ($\theta _{xy}$,$\theta _z$)

$$\begin{aligned} \textbf{t}_{2D} = \begin{bmatrix} \cos (\theta _{xy}) \\ \sin (\theta _{xy}) \end{bmatrix}, \quad \textbf{t}_{3D} = \begin{bmatrix} \cos (\theta _{xy})\cos (\theta _z) \\ \sin (\theta _{xy})\cos (\theta _z) \\ \sin (\theta _z) \end{bmatrix}. \end{aligned}$$

(3)

In this study, we focus on continuously varying fiber orientation and to leverage the design potential offered by advanced manufacturing processes, we adopt a field-based approach. This approach represents fiber orientation as a continuous field in the computational domain, unlike the iso-contours approach of Bruyneel and Zein (2013) or feature-mapping approach of Greifenstein et al. (2023) where fibers are aligned with bars.

Considering field-based methods, Nomura et al. (2015) convert the fiber orientation field into a Cartesian vector field, addressing the $2\pi$ periodicity issue where angles like 0 and $2\pi$ represent the same orientation. In our approach, where the fiber angle is directly utilized as a design variable, we extend the bounds beyond the conventional $[0,2\pi ]$ range. Notably, as discussed in the numerical examples in Sect. 5, the fiber orientation does not reach the prescribed upper and lower bounds. It is important to note that the Cartesian transformation does not resolve the $\pi$-periodicity in the elastic properties of materials, resulting in identical material properties for angles differing by $\pi$. Employing a continuous interpolation method may create a transition zone between angles associated with $\pi$-periodicity, resulting in sub-optimal designs.

Most field-based methods, including those of Almeida Jr et al. (2023) and Smith and Norato (2022), are typically paired with the density method and adopt the same interpolation for fiber orientation as the density variables. Other parametrization approaches exist, as shown by Tian et al. (2019), where fiber orientation is constant within each element in the FE mesh. In this work, we interpolate the fiber orientation field by B-splines, chosen for their smoothness.

For 2D problems, only one B-spline discretization suffices to describe the tangent vector field; see Eq. (3). 3D problems necessitate two independent B-spline discretizations, one for the $\theta _{xy}$ and another for the $\theta _z$. The fiber orientation fields are discretized on a mesh that may differ in polynomial order and refinement level from those used for state variables and geometry. This discretization of the fiber orientation field, $\theta$, is achieved through B-spline basis functions as

$$\begin{aligned} \theta (\textbf{x}) \approx \theta ^h(\textbf{x}) = \sum _{k} B_k(\textbf{x}) \theta _k, \end{aligned}$$

(4)

where $B_k(\textbf{x})$ denotes the B-spline basis functions and $\theta _k$ the coefficients of the approximating function. In Eq. (4), $\theta$ represents either $\theta _{xy}$ or $\theta _z$. Analogous to the LSF, these B-spline coefficients are considered optimization variables and updated via a gradient-based algorithm using material parameter sensitivities.

Figure 3 illustrates the overlay of the geometry with the fiber orientation. The top left and top right sections of this figure depict B-spline surfaces, representing the LSF and fiber orientation, respectively. The lower part of the figure illustrates the superposition of these two B-spline surfaces, showcasing the resulting structure’s geometry and its fiber orientation.

Fig. 3

Illustration of the LSF for a truss structure (top left), the B-spline surface parameterizing the fiber orientation field (top right), and the resulting fiber orientation and geometry (bottom)

3 Structural analysis

In the present work, the structural response is predicted by XIGA. This immersed finite element method builds upon the traditional eXtended Finite Element Method (XFEM) framework by incorporating B-spline basis functions, as discussed by Noël et al. (2022). XFEM itself is a variant of the classical Finite Element Method (FEM), using immersed geometry descriptions. XFEM can be seamlessly combined with level set TO to manage evolving design interfaces, eliminating the need for generating conformal meshes. This combination maintains the crisp definition of the interface, as represented by the LSF, within the physical FEM model. XFEM and XIAG augment the standard FEM approximation spaces with additional basis functions and Degrees Of Freedom (DOFs), an approach termed "enrichment", to capture the physical response near interfaces and boundaries. The following subsections summarize the enrichment strategy and present the weak formulation of the governing equations.

3.1 Enrichment strategy

This work utilizes the generalized Heaviside enrichment strategy described in Noël et al. (2022). This enrichment approach accommodates a variety of material phases, intersection configurations, and basis function supports.

Consider the configuration in Fig. 4 which shows a region covered by two material phases ($\varOmega _1$ and $\varOmega _2$) and the support of the basis function, $B_k$, indicated by dashed red lines. The basis support consists of three distinct subregions. To accurately represent the physical response in these subregions without spurious coupling, the same basis function is weighted by three different independent coefficients, i.e., DOFs. Phase 1 occupies subregions $l=1$ and $l=3$, which are topologically disconnected, while phase 2 occupies the subregion $l=2$. The set of all subregions is denoted by $\{ \varOmega _k^{\ell } \}_{\ell =1}^{L_k}$, where $L_k$ is the total number of these subregions. In general, the $i^{th}$ component of the discretized vector-valued state variable field, denoted as $\textbf{u}_i$, which corresponds to displacement in this study, is expressed as

$$\begin{aligned} \textbf{u}_i(\textbf{x}) = \sum _{k=1}^{K} \sum _{\ell =1}^{L_k} \varphi _k^{\ell }(\textbf{x})\, B_k(\textbf{x})\, u_{i,k}^{\ell }, \end{aligned}$$

(5)

where the total number of background basis functions is denoted by K. The coefficients ${u}^{l}_{i,k}$ are the DOFs associated with the basis function $B_k$ and subregions $\varOmega _{k}^{\ell }$.

The indicator function $\varphi _k^{\ell }(\textbf{x})$ is a binary-valued function which indicates membership of $\textbf{x}$ in $\varOmega _k^{\ell }$ and is defined as

$$\begin{aligned} \varphi _k^{\ell }(\textbf{x}) = I_{\varOmega _k^{\ell }}(\textbf{x}) = \left\{ \begin{array}{ll} 1, &{} \displaystyle \text{ if }\ \textbf{x} \in \varOmega _k^{\ell },\\ 0, &{} \displaystyle \text{ otherwise }. \end{array} \right. \end{aligned}$$

(6)

Fig. 4

Enrichment strategy in XIGA

3.2 Governing equations

The enrichment strategy is applied to the weak form of the governing equations, modeling the static linear elastic response of a structure in this paper. The residual equation is broken down into the following four separate components:

$$\begin{aligned} \mathcal {R} = \mathcal {R} ^{ U }+ \mathcal {R} ^{ D }+ \mathcal {R} ^{ G } + \mathcal {R} ^{ S } =0. \end{aligned}$$

(7)

The bulk contribution and Neumann boundary contribution are included in $\mathcal {R} ^{ U }$, the Dirichlet boundary condition is represented by $\mathcal {R} ^{ D }$, the face-oriented ghost stabilization term added through $\mathcal {R} ^{ G }$, and $\mathcal {R} ^{ S }$ represents a stabilization term to suppress rigid body motions of material not connected to mechanical supports.

Assuming linear elasticity without body forces under static loading conditions, the bulk and Neuman contributions are as follows:

$$\begin{aligned} \mathcal {R} ^{ U }= \int _{\varOmega ^m} \varvec{\varepsilon }(\delta {\textbf{u}}): \varvec{\sigma } d \varOmega -\int _{\varGamma _{N}} \delta {\textbf{u}} \cdot {\textbf{f}} _N d \varGamma , \end{aligned}$$

(8)

where ${\textbf{u}}$ and $\delta {\textbf{u}}$ are the displacement trial and test functions, respectively. The traction, ${\textbf{f}} _N$, is applied to the boundary $\varGamma _N$. The Cauchy stress tensor, $\varvec{\sigma }$, is defined as $\varvec{\sigma } = \varvec{C}_{eff} \varvec{\varepsilon }$ assuming linear elasticity. The infinitesimal strain is denoted by $\varvec{\varepsilon }$, and $\varvec{C}_{eff}$ is the homogenized elasticity tensor obtained from Mori–Tanaka homogenization discussed in Sect. 3.3.

Using Nitsche’s unsymmetric formulation, the Dirichlet boundary condition is weakly imposed along the boundary $\varGamma _D$ as follows:

$$\begin{aligned} \begin{aligned} \mathcal {R}^D =&-\int _{\varGamma ^{D}} \delta {\textbf{u}} \cdot \sigma ( {\textbf{u}} ) {\textbf{n}} _{\varGamma } d \varGamma \\&+\int _{\varGamma ^{D}} \mathbf \sigma (\delta {\textbf{u}} ) {\textbf{n}} _{\varGamma } \cdot \left( {\textbf{u}} - {\textbf{u}} _D\right) d \varGamma \\&+ \gamma _{D} \int _{\varGamma ^{D}} \delta {\textbf{u}} \cdot \left( {\textbf{u}} - {\textbf{u}} _D\right) d \varGamma , \end{aligned} \end{aligned}$$

(9)

where ${\textbf{u}} _D$ is the prescribed displacement vector and ${\textbf{n}} _{\varGamma }$ denotes the normal pointing outward from the boundary $\varGamma _{D}$. The penalty factor depends on the mesh size and is obtained as follows:

$$\begin{aligned} \gamma _{D}=c_{D} \frac{E_{eff}}{h}, \end{aligned}$$

(10)

where $c_{D}$ is a parameter that controls the accuracy of the Dirichlet enforcement, and $E_{eff}$ denotes the effective Young’s modulus of the FRC material, computed by homogenization.

The term $\mathcal {R}^G$ denotes the face-oriented ghost stabilization contribution. When the LSF intersects background elements, it may create small subdomains such that some basis functions have diminishing support. This can lead to ill-conditioning of the linear system and potentially degrade the accuracy of the state variables and their gradient approximations. To mitigate this issue, this work adopts the approach of Noël et al. (2022) for stabilizing XIGA and introduces the following ghost stabilization term:

$$\begin{aligned}{} & {} \mathcal {R}^G = \nonumber \\{} & {} \quad \sum _{i=1}^{N_{F}} \sum _{j \in J_{F,i}} \Bigg [ \sum _{k=1}^{p} \int _{F} \gamma _{G}^{\textbf{a}}\, \llbracket \partial ^{k}_{n}\, \delta \textbf{u} \rrbracket \cdot \llbracket \partial ^{k}_{n}\, \textbf{u} \rrbracket \, d\varGamma \ \Bigg ], \end{aligned}$$

(11)

where $J_{F,i}$ denotes the set of facets subject to the ghost penalty, $N_{F}$ is the total number of such facets, and $p$ represents the order of approximation. $\gamma _{G}^{\textbf{a}}$ is the ghost penalty parameter, $\partial ^k_n$ is the $k^{th}$ order derivative in the normal direction of the facet, and $\llbracket \ \rrbracket$ is the jump operator measuring the difference across a ghost facet. The residual term (11) penalizes discontinuities in the derivatives of the state variables across the entire element facet.

In the optimization process, the LSF may evolve to create subregions that are disconnected from the mechanical supports and thus exhibit rigid body modes. Unlike the approach of Wei et al. (2010) where the void phase is modeled as a soft material, we adopt the approach of Geiss and Maute (2018) and introduce a weak elastic bedding for disconnected subregions. Identification of these subregions is achieved by solving an auxiliary thermal convection problem, where the temperature is prescribed at mechanical boundaries. The convection effect ensures that all isolated regions assume ambient temperature which is used to activate the elastic bedding. The formulation for the elastic bedding residual is as follows:

$$\begin{aligned} \mathcal {R}^{S} = \int _{\varOmega ^m} \gamma _s \kappa _s (\delta \textbf{u}) \textbf{u} \, d\varOmega , \end{aligned}$$

(12)

where $\kappa _s = \frac{E_{eff}}{h^2}$, with $E_{eff}$ representing effective Young’s modulus and $h$ the mesh size. The coefficient $\gamma _s$ activates the elastic bedding and is defined as a smooth transition function of the auxiliary temperature, in the interval of $[0,T_{pre}]$ where $T_{pre}$ denotes the prescribed temperature.

3.3 Mori–Tanaka homogenization

To predict the physical response of the FRC, the Mori–Tanaka (MT) homogenization scheme (Mori and Tanaka 1973) is employed. MT is a mean-field homogenization technique that assumes uniformly dispersed inhomogeneities in the matrix and builds on Eshelby’s elasticity method. Figure 5 shows the idealized Representative Volume Element (RVE) for the MT homogenization scheme. It considers the properties of the individual phases, as well as the geometry and arrangement of the phases within the composite material. These properties include Young’s modulus of the matrix and fiber,

Fig. 5

Matrix fiber layout for MT

$E_m, E_f$, Poisson ratio of the fiber and matrix, $\nu _m, \nu _f$, volume fraction, $V_f$, and aspect ratio, $AR = \frac{d}{l}$. The rotation angles, $\theta _{xy}$ and $\theta _z$, are used to construct the rotation tensor which transforms the stiffness tensor from the local coordinate system, aligned with the fiber orientation, to the global coordinate system. The effective constitutive tensor, $\varvec{C}_{eff}$, is expressed as a function of the fiber and matrix’s material properties as well as the fiber orientation as

$$\begin{aligned} \varvec{C}_{eff}&= \textbf{Q}^T(\theta _{xy},\theta _z)\nonumber \\&\cdot \textbf{C}_{MT}(E_m, E_f,\nu _m,\nu _f,V_f,AR) \cdot \textbf{Q}(\theta _{xy},\theta _{z}), \end{aligned}$$

(13)

where the rotation tensor is denoted by $\textbf{Q}$.

4 Optimization framework

The optimization problems addressed in this study are described by the following general formulation:

$$\begin{aligned} \begin{aligned} \min _{\textbf{s}}&\quad z(\textbf{s}, \textbf{u}(\textbf{s})) \\ \text {s.t.}&\quad g_j(\textbf{s}, \textbf{u}(\textbf{s})) \le 0, \quad j=1,\ldots ,N_g, \\&\quad \underline{s} \le s_i \le \overline{s}, \quad i=1,\ldots ,N_s, \end{aligned} \end{aligned}$$

(14)

where $\textbf{s}$ denotes the vector of optimization variables of dimension $N_s$, constrained between lower bounds $\underline{\textbf{s}}$ and upper bounds $\overline{\textbf{s}}$. The state variable vector $\textbf{u}(\textbf{s})$ denotes the structural displacements. The objective function is represented by $z(\textbf{s}, \textbf{u}(\textbf{s}))$, with $g_j(\textbf{s}, \textbf{u}(\textbf{s}))$ as the constraint functions. The focus of this paper is on the minimization of compliance, augmented by regularization terms. The objective function is defined as follows:

$$\begin{aligned} \begin{aligned} z(\textbf{s}, \textbf{u}(\textbf{s}))&= w_f \frac{\mathcal {F}(\textbf{s}, \textbf{u}(\textbf{s}))}{\mathcal {F}^0(\textbf{s}, \textbf{u}(\textbf{s}))} + w_p \frac{\mathcal {P}_{p}(\textbf{s})}{\mathcal {P}^0_{p}(\textbf{s})} + w_g \frac{\mathcal {P}_{g}(\textbf{s})}{\mathcal {P}^0_{g}(\textbf{s})} \\&\quad + w_{\text {par}} \frac{\mathcal {P}_{\text {par}}(\textbf{s})}{\mathcal {P}^0_{\text {par}}(\textbf{s})} + w_{\text {Lcur}} \frac{\mathcal {P}_{\text {Lcur}}(\textbf{s})}{\mathcal {P}^0_{\text {Lcur}}(\textbf{s})} \\&\quad + w_{\text {Gcur}} \frac{\mathcal {P}_{\text {Gcur}}(\textbf{s})}{\mathcal {P}^0_{\text {Gcur}}(\textbf{s})}, \end{aligned} \end{aligned}$$

(15)

where $\mathcal {F}(\textbf{s}, \textbf{u}(\textbf{s}))$ denotes the strain energy. The optimization problem is regularized by perimeter and level set gradient penalties, $\mathcal {P}_{p}$ and $\mathcal {P}_{g}$, with the weights $w_p$ and $w_g$, respectively. The alignment and curvature of the fiber orientation fields are controlled by $\mathcal {P}_{\text {par}}$, $\mathcal {P}_{\text {Lcur}}$ , and $\mathcal {P}_{\text {Gcur}}$, representing the parallel misalignment penalty, local curvature penalty, and global curvature penalty, with $w_{\text {par}}$, $w_{\text {Lcur}}$ , and $w_{\text {Gcur}}$ being the associated weights. All terms in the objective function are normalized by reference values denoted by the superscript $0$. Subsequent subsections discuss these penalties in detail.

4.1 Regularization of the level set

Haber et al. (1996) introduced a constraint on the perimeter of the solid-void interface to discourage irregular geometrical features. Following this approach, a perimeter penalty term is incorporated into the objective function as follows:

$$\begin{aligned} \mathcal {P}_{p} = \frac{1}{\mathcal {P}_0} \int _{\varGamma _I}\, d\varGamma , \end{aligned}$$

(16)

where $\mathcal {P}_0$ denotes the initial perimeter value.

In addition, a regularization term, $\mathcal {P}_{g}$, is employed to stabilize the gradient of the LSF in proximity to the interface. This term promotes uniform spatial gradients of the LSF in the vicinity of zero iso-contour. As the LSF evolves throughout the optimization process, convergence to upper and lower bounds is encouraged away from the interface. This approach prevents the LSF from becoming excessively flat or steep which may cause oscillations in the optimization process. The regularization approach outlined by Geiss et al. (2019) introduces a smoothed target field with uniform gradients along the interface. Deviations from this target field in terms of function values and gradients incur a penalty in the objective function:

$$\begin{aligned} \mathcal {P}_{r} = \frac{\int _{\varOmega } w_{\phi } \left( \phi -\tilde{\phi } \right) ^2 d\varOmega }{\int _{\varOmega } \phi _{Bnd}^2\, d\varOmega } + \frac{\int _{\varOmega } w_{\nabla \phi } \left| \nabla \phi - \nabla \tilde{\phi } \right| ^2 d\varOmega }{\int _{\varOmega } d\varOmega }, \end{aligned}$$

(17)

where $\tilde{\phi }$ denotes the corresponding smoothed target field. The penalty weights $w_{\phi }$ and $w_{\nabla \phi }$ are responsible for penalizing deviations in the level set values and its gradient, respectively. These weights are adjusted based on the proximity to the interface. The level set lower bound is denoted by $\phi _{Bnd}$, and the target field $\tilde{\phi }$ is constructed as a truncated signed distance field through a sigmoidal function:

$$\begin{aligned} \tilde{\phi } = \left( \frac{2}{1+\exp ({-2\, \phi _{D}} / { \phi _{Bnd}})} -1 \right) \, \phi _{Bnd}, \end{aligned}$$

(18)

with $\phi _{D}$ as the signed distance field, computed by the "heat method" of Crane et al. (2017).

As discussed by Geiss et al. (2019), it is advantageous to disregard the sensitivity of the signed distance field with respect to the interface location, as including these sensitivities can lead to premature convergence of the optimization process. Thus, only the sensitivities of the design LSF are considered when computing the sensitivities of the regularization term. However, this approach results in inconsistent sensitivities of the regularization term, potentially affecting the convergence of the optimization process. To address this issue, Barrera et al. (2020) recommend using small values for the weights of the regularization terms, yet sufficiently large to achieve the desired regularization effect.

4.2 Parallel misalignment penalty

This section introduces a key contribution of the paper, the misalignment penalty term, which facilitates the generation of locally parallel fiber paths. Such parallelism minimizes the need for post-processing the optimization results, required to transform the fiber orientation field into continuous, manufacturable fiber paths.

Geometrically, parallel curves can be defined in several different ways. Two curves are parallel if the distance between them is constant. Alternatively, two curves within the same plane can be considered parallel if they have identical tangent vectors at corresponding points along their respective lengths. This study takes advantage of the second definition, and curves are defined as parallel when the tangent does not change in the normal direction of the curve.

Fig. 6

Parallel fiber path

Consider Fig. 6 which presents three geometrically parallel curves. Traversing from point q in the normal direction, $\varvec{n}$, leads to point p. The tangent vectors in both points are identical. Consequently, the tangent vector $\varvec{t}$ remains invariant in the direction of the normal vector $\varvec{n}$. In mathematical terms, the directional derivative of $\varvec{t}$ with respect to $\varvec{n}$ vanishes such that

$$\begin{aligned} \nabla \varvec{t} \cdot \varvec{n} = \varvec{0}. \end{aligned}$$

(19)

Figure 7 illustrates the fiber orientation field’s layout at the top, with each line depicting a fiber tangent as defined by Eq. (3). The corresponding $\nabla \varvec{t} \cdot \varvec{n}$ values for the fiber orientation field are shown in the contour plot at the bottom. These values are zero in regions with parallel fiber paths and non-zero where fibers intersect.

Fig. 7

Misalignment penalty visualization for a specific fiber orientation field

For a 2D problem, based on the parameterization of the fiber orientation in Eq. (3), there is a direct relationship between the tangent vector and the normal vector as well as the angle value. As the tangent and normal are constructed from $\theta _{xy}$, for parallel curves, one can infer that the change in $\theta _{xy}$ in the direction of ${\textbf{n}}$ is zero, i.e.,

$$\begin{aligned} \nabla \varvec{t} \cdot \varvec{n} \equiv \nabla \varvec{n} \cdot \varvec{n} \equiv \nabla \theta _{xy} \cdot \varvec{n} = \varvec{0}. \end{aligned}$$

(20)

In 3D, with two angles defining the tangent, and the normal vector being non-unique, the condition $\nabla \varvec{t} \cdot \varvec{n} = 0$ still applies, but $\varvec{n}$ could be any vector with its normal vector being $\varvec{t}$. A vector in this plane can be decomposed into two linearly independent vectors $\varvec{n}_1$ and $\varvec{n}_2$ with arbitrary coefficients $a$ and $b$ as $\varvec{n} = a \varvec{n}_1 + b \varvec{n}_2$. Subsequently, Eq. (19) can be reformulated as

$$\begin{aligned} \nabla \varvec{t} \cdot \varvec{n} = a \left( \nabla \varvec{t} \cdot \varvec{n_1} \right) + b \left( \nabla \varvec{t} \cdot \varvec{n_2} \right) = \varvec{0}, \end{aligned}$$

(21)

By following the right-hand rule for $\varvec{n}_1$, $\varvec{n}_2$, and $\varvec{t}$, with $\varvec{n}_1$ arbitrarily chosen to be orthogonal to $\varvec{t}$, and $\varvec{n}_2$ obtained from their cross product, the parallel condition can be satisfied.

The parallel misalignment penalties for 2D and 3D structures are defined as

$$\begin{aligned} \begin{aligned} \mathcal {P}_{\text {par}}^{\text {2D}}&= \int _\varOmega \Vert \nabla \varvec{t} \cdot \varvec{n} \Vert _2^2 dV, \\ \mathcal {P}_{\text {par}}^{\text {3D}}&= \int _\varOmega \Vert \nabla \varvec{t} \cdot \varvec{n_1} \Vert _2^2 dV + \int _\varOmega \Vert \nabla \varvec{t} \cdot \varvec{n_2} \Vert _2^2 dV. \end{aligned} \end{aligned}$$

(22)

A simple optimization problem is presented to illustrate the impact of the parallel misalignment penalty. Here, the fiber orientation is the sole design parameter field, and the sole objective is to minimize parallel misalignment penalty $\mathcal {P}_{\text {par}}$. The algorithmic setting uses the parameters outlined in Sect. 5.

Figure 8 shows the initial and optimized fiber layouts for both 2D and 3D cases. For visualization purposes, the fiber paths are generated by equally spaced streamlines. The initial layout is generated by the function $\theta _{xy}(x,y,z) = \theta _z(x,y,z) = \sin (\pi x)\sin (\pi y)\sin (\pi z)$ for 3D, and $\theta _{xy}(x,y) = \sin (\pi x)\sin (\pi y)$ for 2D. Visual inspection suggests that the parallel penalty effectively aligns the fiber paths. The normalized objective value (parallel misalignment penalty), relative to the initial design, reduces from 1.0 to $8.1\cdot 10^{-5}$ for the 2D case, and from 1.0 to $5.1\cdot 10^{-6}$ in the 3D case.

Fig. 8

Minimization of the parallel misalignment penalty for 2D and 3D: initial layout (left) and optimized layout (right)

4.3 Curvature penalty

The misalignment penalty introduced in Eq. (22) promotes the parallel fiber paths but does not control the curvature of the fibers. To account for potential manufacturing constraints and to avoid excessive bending of the fibers, a penalty term is introduced that limits the curvature of the fiber path. The curvature $\kappa (l)$ for a curve parameterized by arc length $l$ is

$$\begin{aligned} \kappa (l) = \frac{\Vert \varvec{r}'(l) \times \varvec{r}''(l) \Vert }{\Vert \varvec{r}'(l) \Vert ^3 }, \end{aligned}$$

(23)

where the position vector is denoted by $\varvec{r}(l)$, with $\varvec{r}'(l)$ and $\varvec{r}''(l)$ representing its first- and second-order derivatives with respect to the arc length, respectively. The second-order derivative of the position vector, derived using the chain rule, is $\varvec{r}''(l) = \frac{D \varvec{r}'(l)}{D \varvec{x}} \cdot \varvec{r}$. For fiber paths generated from fiber orientation field(s), the first-order derivative of the position vector $\varvec{r}'$ is equal to the tangent vector $\varvec{t}$, given in Eq. (3), i.e., $\varvec{r}' =\varvec{t}$. Using the chain rule, the second derivative of the position vector is computed as: $\varvec{r}'' = \varvec{t}' = \frac{D \varvec{t}}{D \varvec{x}} \cdot \varvec{t}$.

Given the unit magnitude of the tangent vector, $\Vert \textbf{t} \Vert = 1,$ the curvature of the fiber path is subsequently calculated as

$$\begin{aligned} \kappa ^{2D,3D} = \Vert \varvec{M} \varvec{t} \times \varvec{t} \Vert , \end{aligned}$$

(24)

where the matrix $\varvec{M}$ represents the spatial derivative of the tangent vector field and is defined as $\varvec{M} = \frac{D \varvec{t}}{D \varvec{x}}$. For 2D problems, $\varvec{M}$ is a function of $\theta _{xy}(x,y),$ while for 3D problems, it depends on both $\theta _{xy}(x,y,z)$ and $\theta _{z}(x,y,z)$.

In Fig. 9, the upper section displays the configuration of the fiber orientation field, where individual lines denote fiber tangents as defined in Eq. (3). The corresponding $\kappa ^2$ values for the fiber orientation field are shown at the bottom. These values are zero in regions with straight fibers and non-zero where fibers exhibit bending, as illustrated by the blue and red magnified insets in the figure, respectively.

Fig. 9

Curvature penalty visualization for a specific fiber orientation field

To ensure that the local curvature does not exceed a maximum manufacturing limit defined by $\kappa _{\text {max}}$, the following penalty term is incorporated into the objective function:

$$\begin{aligned} \mathcal {P}_{\text {Lcur}}^{\text {2D,3D}} = \int _\varOmega \left( \left( \kappa ^2 - \kappa _{\text {max}}^2 \right) ^{+} \right) ^2 dV, \end{aligned}$$

(25)

where ${{\left( \cdot \right)}^{+}}=\max (0,\cdot )$. The penalty term agglomerates the local point-wise curvature constraint into a global constraint which is applied as a penalty term in the objective function.

While the local curvature penalty aims to lessen sharp turns in fiber paths, a global curvature penalty can be formulated to enhance overall smoothness, discouraging wavy fibers. The global curvature penalty is defined as follows:

$$\begin{aligned} \mathcal {P}_{\text {Gcur}}^{\text {2D,3D}} = \int _\varOmega \kappa ^2 dV. \end{aligned}$$

(26)

In 2D problems, the curvature is simplified by substituting the tangent vector from Eq. (3) into Eq. (25), yielding $\nabla \theta _{xy} \cdot \varvec{t}$. This represents the rate of change in the fiber angle along the tangent, capturing the fiber path’s curvature. With this simplification, the following relation holds:

$$\begin{aligned} \Vert \nabla \theta _{xy} \Vert ^2 = \Vert \nabla \theta _{xy} \cdot \varvec{t} \Vert ^2 + \Vert \nabla \theta _{xy} \cdot \varvec{n} \Vert ^2. \end{aligned}$$

(27)

This demonstrates that combining misalignment and curvature penalties with equal weights effectively penalizes the first-order derivative of the fiber orientation field. Adjusting the weights or using anisotropic penalties can produce outcomes not achievable through penalization of the first derivative alone. This effect is illustrated in the previous section, where the parallel misalignment penalty was minimized, and further explored subsequently.

To demonstrate the curvature penalty’s effect on fiber layout smoothness, we consider an optimization problem where the algorithmic setting uses the parameters outlined in Sect. 5. Here, the objective is to minimize the global curvature penalty, with the fiber orientation being the only design variable.

The initial and optimized fiber layouts are illustrated in Fig. 10. The optimization results in straight fiber paths with zero curvature, as evident by the figure, with the normalized objective value with respect to the initial design reducing from $1.0$ to $1.2\cdot 10^{-5}$ in 2D case and from $1.0$ to $7.6\cdot 10^{-6}$ in 3D case. It is important to note that while the optimized fiber path is straight, it is not parallel due to the exclusion of the parallel misalignment penalty in the optimization problem.

Fig. 10

Minimization of the curvature penalty for 2D and 3D: initial layout (left) and optimized layout (right)

5 Numerical optimization examples

The subsequent subsections study the interplay between shape and fiber orientation field and the efficacy of the proposed methodology for achieving parallel and smooth fiber orientation configurations. First, a 2D optimization problem is presented with fiber orientation as the sole design parameter to isolate the impact of misalignment and curvature penalties. This example further explores the effect of the polynomial order of the fiber orientation parameterization. Subsequently, a 2D problem optimizing both structural shape and fiber orientation is considered, investigating the influence of the B-spline refinement and the initial fiber orientation on the optimization results. Lastly, two 3D cases are examined to optimize shape and fiber orientation simultaneously, analyzing the effect of misalignment and curvature penalties in 3D settings.

Table 1 Matrix and fiber material properties

Table 1 provides the material properties used in the numerical examples. This includes the matrix and fiber Young’s moduli, their respective Poisson’s ratios, fiber aspect ratio, and volume fraction. While the stiffness ratio is high and the volume fraction is low, a rather small aspect ratio is chosen for demonstration purposes. These material parameters yield a moderate material anisotropy which facilitates an intricate interplay between shape and fiber orientation. Units are omitted as they are consistent throughout the study.

In this study, our computational domains are defined on rectangular grids, utilizing uniform B-spline meshes for discretizing level set, fiber orientation, and state variable fields. Mesh refinement is conducted by recursively subdividing each element into four elements in 2D and into eight elements in 3D until the specified level of refinement is attained.

The state variable field, i.e., the displacement field is discretized using bi-linear B-splines with quadrilateral elements for 2D, and tri-linear B-splines with hexahedral elements in 3D. The LSF is discretized with bi-quadratic (2D) and tri-quadric (3D) B-splines on a mesh that is twice as coarse as the state variable mesh. The fiber orientation field is discretized on a mesh that is either two or four times coarser than the state variable mesh, utilizing linear, quadratic, and cubic B-splines. As discussed by Noël et al. (2020), defining the design variables fields on coarser and higher-order B-spline meshes has a smoothing effect, suppressing spurious geometric features and oscillating fiber orientation fields.

For the evaluation of the governing equations, the weak Dirichlet boundary condition penalty, $\gamma _D$, is assigned a value of 10.0, while the ghost penalty, $\gamma _G$, is chosen to be 0.01. The discretized governing equations and adjoint sensitivity equations for 2D problems are solved using the direct solver PARDISO (Schenk et al. 2001). In 3D problems, the linear systems are solved using a Generalized Minimal RESidual (GMRES) method, with an ILUT (dual threshold incomplete LU factorization) preconditioner. The convergence tolerance for the GMRES algorithm, i.e., the required drop in relative preconditioned residual, is set to $1\cdot 10^{-9}$.

The optimization problem is solved using a gradient-based algorithm, the Globally Convergent Method of Moving Asymptotes (GCMMA) referenced in Svanberg (2002), utilizing two inner iterations. In cases where the local curvature penalty is applied and both geometry and fiber orientation are treated as design variables, it was observed that the use of inner iterations resulted in designs that stagnated at local minima. For such cases, the optimization initially progresses without inner iterations for a specified number of steps, after which inner iterations are activated. The optimization is considered to have converged when the relative change in objective function values between two successive iterations falls below $1 \cdot 10^{-5}$. In the GCMMA algorithm, the parameters for adapting the initial, shrinking, and expanding asymptotes are set to 0.5, 0.7, and 1.2, respectively. The design sensitivities are computed by the adjoint method, see Sharma et al. (2017) for more details on the adjoint method for XFEM problems.

Fiber orientation design variable fields, $\theta _{xy}$ and $\theta _z$, are bounded by the box-constraints $\left[ -3\pi , 3\pi \right]$ for all the examples. The value for the maximum feasible curvature $\kappa _{\text {max}}$ is selected to demonstrate the effectiveness of the local curvature penalty in reducing fiber path curvature. This value is not representative of a specific manufacturing method but is set to a value much lower than the curvature values observed when only the parallel misalignment penalty is applied. Thus, the maximum feasible curvature used in the numerical examples below intentionally differs from curvature constraints of common manufacturing techniques; see, for example, Lemaire et al. (2015).

We employ continuation strategies to regulate the influence of the penalty terms in the objective function. By repeatedly renormalizing these terms, their contributions are kept at a target level which is controlled through the penalty weights and chosen such that the strain energy is the predominant term in the objective function. The strain energy and the perimeter and level set regularization penalties are normalized against their initial values. As the fiber paths are initialized to be horizontal or vertical across the domain, unless stated otherwise, the initial misalignment and curvature penalty values are zero. Therefore, the misalignment and global curvature penalty terms are normalized based on their values at the tenth optimization iteration. Renormalization occurs at every 10th outer iteration step. The weights for the misalignment and global curvature penalties are set at 0.05 and 0.01, respectively. The weights for the perimeter and level set regularization penalties are each set at 0.01. Based on the authors’ experience, these or similar values for the penalty weights result in a good balance between mechanical performance and control of the shape and the fiber orientation.

The local curvature penalty weight is initialized with 0.1. This low starting value ensures that the strain energy predominantly influences the optimization process. However, to ensure that the local curvature penalty effectively enforces the agglomerated, point-wise constraints, the penalty weight needs to be sufficiently large, and thus it is multiplied by a factor of 4.0 every 20 optimization steps.

5.1 Post-processing for fiber paths

In our methodology, the fiber orientation field is directly used as a design variable in the optimization process. However, this parametrization does not immediately provide a geometrical description of the continuous fiber paths. Therefore, a post-processing step is needed to convert the fiber orientation field into a geometric description of the fiber path while preserving the volume fraction. We employ the methodology of Boddeti et al. (2020) to determine continuous fiber paths. This process uses the stripe patterns algorithm of Knöppel et al. (2015), which positions evenly spaced and parallel stripes along a specified vector field on a surface, with singularities introduced as needed to maintain parallelism and even spacing.

We visualize the fiber orientation fields via stripe patterns, in addition to displaying the fiber orientation via streamlines. In the latter case, the tangents to the fiber fields are plotted, where the length of the tangent vector does not have any physical meaning. The stripe pattern visualization provides a more realistic illustration of the fiber paths. However, it is important to note that in this work the stripe patterns are not meant to represent the microscopic fiber layout and are not intended to define the final fiber geometry, ready for fabrication.

5.2 Short plate under shear

Fig. 11

Short plate configuration

This example investigates how various combinations of misalignment and curvature penalties affect the optimized fiber layout. We explore different scenarios employing linear, quadratic, and cubic polynomial orders of the fiber orientation B-spline discretization. The sole design parameter in this problem is the fiber orientation, while the structural shape remains unchanged. This example minimizes the compliance of the short plate shown in Fig. 11 under plane stress conditions. The plate is fixed at the bottom and a load ($P = 0.01$) is applied at the top. The short geometry of the plate induces a shear-dominated structural response.

With the structural shape fixed, the formulation of the optimization problem in Eq. (15) is simplified to an unconstrained optimization problem as follows:

$$\begin{aligned} \begin{aligned} \underset{\theta _{xy}}{min} \varPi =&w_{f} \frac{\mathcal {F}}{\mathcal {F}^0} + \frac{w_{\text {par}}}{\mathcal {P}_{\text {par}}^{0} } \mathcal {P}_{\text {par}} + \\&\frac{w_{\text {Lcur}}}{\mathcal {P}_{\text {Lcur}}^{0} } \mathcal {P}_{\text {Lcur}} + \frac{w_{\text {Gcur}}}{\mathcal {P}_{\text {Gcur}}^{0} } \mathcal {P}_{\text {Gcur}}. \end{aligned} \end{aligned}$$

(28)

The first term in Eq. (28) captures the strain energy of the system and $\mathcal {F}^{0}$ denotes the initial strain energy. The rest of the terms correspond to the misalignment and curvature penalties defined in Eq. (22), Eq. (25), and Eq. (26). All terms are normalized by reference values indicated by the superscript $0$. The maximum allowable curvature is set to $\kappa _{\text {max}} = 1.0$.

To analyze the effects of the misalignment and curvature penalties, four different penalization cases are considered:

• Case NP: No penalties applied - $w_{\text {par}} = 0.0$, $w_{\text {Lcur}} = 0.0$, $w_{\text {Gcur}} = 0.0$.

• Case MP: Only the misalignment penalty is applied - $w_{\text {par}} = 0.05$, $w_{\text {Lcur}} = 0.0$, $w_{\text {Gcur}} = 0.0$.

• Case MLCP: Both misalignment and local curvature penalties are applied - $w_{\text {par}} = 0.05$, $w_{\text {Lcur}} \ne 0.0$, $w_{\text {Gcur}} = 0.0$.

• Case MCP: All penalties, including misalignment, local curvature, and global curvature, are applied - $w_{\text {par}} = 0.05$, $w_{\text {Lcur}} \ne 0.0$, $w_{\text {Gcur}} = 0.01$.

The fiber orientation field is discretized on linear, quadratic, or cubic B-spline meshes. To obtain a filtering effect, these B-spline meshes are coarser than the linear B-spline meshes used to discretize the displacement field. In this example, the fiber orientation mesh is selected to be two times coarser than the displacement mesh, which uses a resolution of $64 \times 256$ elements for all testing configurations. Consequently, the fiber orientation mesh resolution is set to $16 \times 64$. The initial fiber orientation is set to be vertical across the domain.

Figure 12 presents the optimized fiber path for a quadratic B-spline discretization under Case NP, where no penalty is applied, and Table 2 displays the absolute values for the penalty terms, strain energy, and maximum curvature. This configuration acts as the reference for subsequent analyses.

Table 2 Absolute values of objective components and maximum curvature for quadratic B-splines discretization of the fiber orientation field under Case NP

Fig. 12

Streamline visualization of the optimized fiber path for quadratic B-splines discretization of the fiber orientation field for Case NP

Figure 13 shows the optimized fiber layouts obtained using quadratic B-splines for all cases, incorporating different penalty combinations. The corresponding strain energy value and penalty values, $\mathcal {P}_{\text {par}}$, $\mathcal {P}_{\text {Lcur}}$ , and $\mathcal {P}_{\text {Gcur}}$, all normalized against the reference case and maximum curvature are displayed in Table 3. Figure 14 presents the local value of the misalignment penalty and curvature values across different penalization cases, processed with $max\left( \log _{10}(\cdot ), 0.0\right)$ for better visualization. The 0.0 threshold in the visualization function for curvature corresponds to $\log _{10}(\kappa _{max}) = \log _{10}(1.0) = 0.0$, whereas the threshold for the misalignment penalty is selected purely for visualization purposes.

Fig. 13

Streamline visualization of the optimized fiber layout of the short plate for different penalization cases with quadratic B-splines discretization of the fiber orientation field

Table 3 Objective components, normalized against the reference case, and maximum curvature for different penalization cases with a quadratic B-spline fiber orientation field

Fig. 14

Misalignment penalty and curvature contour plots for different penalization cases for a quadratic B-spline fiber orientation field

It is observed that the misalignment penalty effectively aligns the fibers, reducing intersections of the fiber paths, as highlighted in the magnified insets in Fig. 13. The comparison of the parallel misalignment penalty in Table 3, $\mathcal {P}_\text {par}$, shows a substantial decrease in cases where the penalty is applied, indicating a higher degree of parallelism in fiber paths. This observation is further substantiated by the contour plots of the misalignment penalty in Fig. 14, which not only show decreased penalty values but also a reduction in regions of fiber intersection.

Incorporating local curvature penalty reduces the bending in the fiber paths, as illustrated in the magnified insets in Fig. 13, and decreases the curvature values close to the maximum allowable curvature value of 1.0 as demonstrated in Table 3. Contour plots of the curvature values for Case MLCP and MCP in Fig. 14 demonstrate that curvature values, processed with the function $max\left( \log _{10}(\cdot ), 0.0\right)$, are close to zero. This implies that curvature values across the computational domain fall below or are very close to 1.0, indicating that the local curvature constraint is well satisfied.

The global curvature penalty further makes the fiber paths more uniform and straighter, as evident from the magnified insets of the fiber path in Fig. 13 and the contour plots in Fig. 14. When comparing the curvature penalty values, $\mathcal {P}_{Lcur}$ and $\mathcal {P}_{Gcur}$, presented in Table 3, it is evident that the two curvature penalties are interconnected; applying one results in a decrease in the other.

The addition of either misalignment or curvature penalties results in an asymmetric fiber layout, as can be seen in the magnified insets in Fig. 13. This non-symmetry arises because the penalty terms are not symmetric, resulting in non-symmetric gradients. For instance, for a symmetric function $\theta (x,y) = x^2 + y^2$ in the computational domain $\varOmega = [-1,1] \times [-1,1]$, the misalignment penalty $\nabla \theta \cdot \varvec{n} = 2x \cdot \cos \left( x^{2}+y^{2}\right) + 2y \cdot \sin \left( x^{2}+y^{2}\right)$ creates a non-symmetric objective function, which leads to non-systematic gradients.

Comparing strain energy values across different cases presented in Table 3 reveals that the addition of the misalignment and curvature penalties to the objective leads to increased strain energy. In a pure shear problem, optimal compliance corresponds to fiber orientations at $\frac{\pi }{4}$ and $\frac{3\pi }{4}$, aligning with the principal directions of stress. The constitutive tensor’s shear components are identical at these angles. Given the shear-dominated nature of this problem, angles close to these values are observed in the optimized fiber layout for all cases with a continuous transition between these angles. This can be seen in the magnified insets in Fig. 13.

Fig. 15

Streamline visualization of the optimized fiber layout of the short plate for different polynomial orders of the fiber orientation field

Table 4 Objective components normalized against the reference case and maximum curvature for different penalization cases and discretization orders

To examine the impact of the polynomial order, we consider Cases MP and MLCP and conduct simulations with varying discretization orders for the fiber orientation field. Figure 15 shows the optimized fiber layouts using linear, quadratic, and cubic B-splines with a mesh size of $16 \times 64$. The corresponding objective components, normalized against the reference case and maximum curvature, are presented in Table 4.

No visual distinctions are noted between the fiber paths in the quadratic and cubic cases, whereas the linear case demonstrates a different non-symmetry resulting from the incorporation of penalties. The fiber layouts across all cases appear smooth, which can be attributed to the coarser B-spline discretization of the fiber orientation field relative to the state variable mesh.

Comparing the strain energy values in Table 4 reveals slight variations among the discretization orders, with linear exhibiting the highest energy and cubic the lowest, a consequence of the increased number of design variables in higher-order discretizations. These discretizations have slightly lower misalignment and curvature values compared to the linear case.

The higher-order discretization’s smoothness becomes evident when evaluating the local curvature values which are using derivatives of the fiber orientation field. Figure 16 shows local curvature values for Case MLCP across different discretization orders, revealing discontinuities in the linear case within the contour plot, while quadratic and cubic cases exhibit smoother curvature distributions.

Fig. 16

Curvature values for Case MLCP with varying polynomial order of the fiber orientation field discretization

This example illustrated the effectiveness of misalignment and curvature penalties in achieving smoother and more parallel fiber arrangements. The optimization results also revealed the influence of the polynomial order of fiber orientation field discretization on the optimized fiber layout. Although the strain energy was largely unaffected, higher-order discretizations produce smoother first-order spatial derivatives which are subsequently used for calculating curvature and misalignment penalties.

5.3 Cantilever beam under bending

This example considers simultaneous optimization of the structural shape and fiber orientation in 2D, considering various penalization cases. This study extends the optimization problem of the previous subsection to include the LSF as a design parameter. Furthermore, the influence of the initial fiber orientation on the final optimized layout is examined.

Fig. 17

Initial Configuration for concurrent topology and fiber orientation optimization, 2D

Fig. 18

Streamline visualization of the concurrent geometry and fiber orientation optimized designs of a cantilever beam under bending for different mesh sizes and penalization cases

The objective is to minimize the compliance of the structure illustrated in Fig. 17, which is subjected to two different loading cases under plane stress conditions. The cantilever beam is fixed on the left side, with non-design domains indicated by darker semicircles that transfer the loads. To ensure the fiber orientations are not solely dictated by principal stress directions, the problem is formulated with two loading scenarios. Loads are applied alternately at $\varGamma _{t,1}$ and $\varGamma _{t,2}$ with the values of $P_{\varGamma _{t,1}} = 0.1$ and $P_{\varGamma _{t,2}} = 0.125$. The optimization problem is formally expressed as follows:

$$\begin{aligned} \begin{aligned} \underset{\theta _{xy}, LS }{min} \varPi =&w_{f} \left< \frac{\mathcal {F}}{\mathcal {F}^0} \right> + \frac{w_p}{\mathcal {P}^0_p} \mathcal {P}_p + \frac{w_g}{\mathcal {P}^0_g} \mathcal {P}_{g} +\\&\frac{w_{\text {par}}}{\mathcal {P}_{\text {par}}^{0} } \mathcal {P}_{\text {par}} + \frac{w_{\text {Lcur}}}{\mathcal {P}_{\text {Lcur}}^{0} } \mathcal {P}_{\text {Lcur}} \\ \text{ s.t }&\quad V \le \frac{1}{2}V_0. \end{aligned} \end{aligned}$$

(29)

Eq. (29) components represent the averaged strain energy, alongside penalties for perimeter and regularization of the LSF introduced in Sect. 4.1. The misalignment and local curvature penalties, as defined in Eqs. (22) and (25), are also included. The operator $\langle \cdot \rangle$ denotes the average of the strain energy over both load cases. The terms in the objective function are normalized by reference values denoted by superscript 0. The optimization is constrained by limiting the structural volume to no more than 50% of the volume computational domain. The value of $\kappa _{\text {max}}$ is set to 10.0.

We consider two penalization cases:

• Case MP with only the parallel misalignment penalty ($w_{\text {par}} = 0.05$, $w_{\text {Lcur}} = 0.0$).

• Case MLCP with both misalignment and local curvature penalties ($w_{\text {par}} = 0.05$, $w_{\text {Lcur}} \ne 0.0$).

The state variables are discretized on a $256 \times 128$ mesh, while the LSF is discretized on a coarser $64 \times 32$ mesh. For the fiber orientation field, quadratic B-spline discretizations are utilized, with two and four times coarser meshes. This results in meshes with dimensions of $64 \times 32$ and $16 \times 8$ elements for the fiber orientation, respectively. The initial LSF is created by seeding an array of holes arranged in a $7 \times 3$ grid, each with a radius of 0.12. The fiber orientation field is initialized to a constant value of zero, corresponding to horizontal fiber paths.

Figure 18 shows the optimized fiber layouts for various penalization cases and mesh sizes for the fiber orientation field. Table 5 shows the corresponding strain energy and penalty values, normalized against Case MP with a mesh size of $16 \times 8$, and the maximum curvature for each case.

Table 5 Objective components, normalized against Case MP with $16 \times 8$ Mesh size, and maximum curvature for different penalization cases and mesh sizes

All cases in Fig. 18 exhibit parallel fiber layouts, as anticipated due to the addition of the parallel penalty. The introduction of the curvature penalty results in smoother fiber paths. While this smoothness is not immediately evident for the configuration using a $16 \times 8$ mesh, it becomes more pronounced when using the $64 \times 32$ mesh. Additionally, the maximum curvature value observed in Table 5 for Case MLCP closely aligns with the maximum allowable curvature and is lower than the curvatures observed in Case MP. The high value of the curvature penalty in Case MP with the finer mesh size, $64 \times 32$, is due to the kinks in the fiber path which results in a high curvature value. The strain energy values in Table 5 show that Case MLCP has higher strain energy than Case MP across different mesh sizes. This increase is due to the addition of another penalty term, which decreases the strain energy’s relative contribution to the objective.

Investigating the influence of the discretization of the fiber orientation fields shows that a finer mesh leads to smaller strain energy values. However, the coarser $16 \times 8$ B-spline mesh leads to a smoother fiber orientation field and, consequently, a more uniform fiber layout. The values for the parallel misalignment and curvature penalties are notably lower for the coarser mesh compared to the finer one, indicating enhanced smoothness.

Figure 19 illustrates the post-processed fiber paths for the optimized designs for Case MLCP for two different mesh sizes. The fiber paths are generated according to the process detailed in Boddeti et al. (2020). The resulting stripe patterns are compared against the streamline visualization of the optimized fiber paths. This figure illustrates that applying the parallel penalty reduces fiber intersections, while the curvature penalty minimizes fiber bending. Consequently, these penalties align the optimization results more closely with continuous, post-processed fiber paths. As shown in the magnified insets of Fig. 19, utilizing a finer mesh size reveals short branches within the fiber path after creating continuous paths. This issue arises from the challenge of maintaining parallel fiber paths. The stripe pattern algorithm introduces singularity points to preserve parallelism and uniform spacing, a problem that can be alleviated by using a coarser mesh, resulting in smoother outcomes as depicted in the insets. Additionally, it may be necessary to introduce discrete discontinuous boundaries and divide the structure into subregions to achieve parallel, manufacturable fiber paths. The study by Zhou et al. (2018) explores an initial method to address this issue using the isoparametric transformation approach, segmenting the geometry into areas where fiber paths can be parallel and manufactured as individual segments.

To evaluate the mechanical performance of the post-processed results, we construct a fiber orientation field from the stripes by calculating their slope along the fiber paths and interpolating at points between the stripes. Using the optimized LSF and the interpolated fiber orientation, we perform an XIGA analysis to compute the strain energies for both load cases. This analysis yields a minor increase of less than 5% in total strain energy compared to the one obtained for the optimized fiber orientation field. The difference is attributed to the slightly enhanced smoothness and parallelism of the stripe patterns. This comparison shows good agreement in the mechanical performance of the structures with optimized and post-processed fiber orientation fields.

Fig. 19

Post-processed and streamline visualization of the fiber paths for Case MLCP with quadratic B-spline discretization and two different mesh sizes

To assess the influence of the initial design of the fiber orientation field on the optimization results, the initial fiber layout is changed to vertical fiber paths, keeping the initial LSF unchanged. For Case MP, the optimization results are then compared to those obtained from designs initiated with horizontal fiber paths in Fig. 18. Figure 20 shows the optimized fiber layouts initialized with different angles. Table 6 shows the corresponding strain energy and penalty values, normalized against the top left case in Fig. 18, as well as the absolute value of the maximum curvature for each case.

Designs initiated with horizontal fibers tend to retain more horizontal orientation in the optimized layout, and likewise, those starting with vertical fibers show a predominance of vertical fibers. When considering the strain energy of these results, it is observed that the values are slightly lower for designs initialized with vertical fibers than those starting with horizontal fibers. However, this difference is below 2%. Thus, while having a significant impact on the fiber layout in some regions, the initial fiber orientation does not significantly affect the strain energy in this example.

Fig. 20

Streamline visualization of the concurrent geometry and fiber orientation optimized designs

Table 6 Objective components, normalized against the reference case, and maximum curvature for different initial fiber orientation angles

This example demonstrated the effectiveness of the misalignment and curvature penalties in generating more parallel and smoother fiber layouts for concurrent topology and fiber orientation optimization. The investigations into the parameterization of the fiber orientation field suggest the refinement level of the B-spline mesh plays an important role in the optimized fiber layouts. The results also highlighted the impact of the initial choice of fiber orientation on the final optimized layout.

5.4 Support structure for a plate under uniform pressure

This example minimizes the compliance of a 3D support structure for a plate, where both the structural shape and fiber orientations are considered design parameters. The example examines the effects of misalignment and curvature penalties in cases where either a single fiber orientation, $\theta _{xy}$, or both fiber orientations, $\theta _{xy}$ and $\theta _z$, are treated as design variable fields. The design problem is illustrated in Fig. 21, showing the plate’s top surface subjected to a uniform load of $p=0.01$. Dirichlet boundary conditions are applied at the left and right sides, marked as $\varGamma _D$ in the figure. The symmetry planes are shown by dashed lines. The plate, acting as the load-bearing component, is considered a non-design domain ($0.95 \le z \le 1.0$), while the space beneath the plate is the design domain.

Fig. 21

Support structure for a plate under uniform pressure

Utilizing the symmetry in the $x-y$ and $x-z$ planes, the simulation is conducted on a quarter of the structure. To ensure the symmetry of the fiber orientation field, a penalty term is applied in the symmetry planes such that on the $x-y$ symmetry plane $\theta _z = 0$ and on the $x-z$ symmetry plane $\theta _{xy} = 0$. The quadratic mesh, used for discretizing the level set and fiber orientation fields, has dimensions of $32 \times 16 \times 16$, making it twice as coarse as the linear mesh for state variables, which is $128 \times 64 \times 64$.

The optimization problem is formulated as follows:

$$\begin{aligned} \begin{aligned} \underset{\theta _{xy}, (\theta _{z}), LS }{min} \varPi =&w_{f} \frac{\mathcal {F}}{\mathcal {F}^0} + \frac{w_p}{\mathcal {P}_{p}^{0} } \mathcal {P}_p + \frac{w_g}{\mathcal {P}_{g}^{0} } \mathcal {P}_{g} + \\&\frac{w_{\text {par}}}{\mathcal {P}_{\text {par}}^{0} } \mathcal {P}_{\text {par}}+ \frac{w_{\text {Lcur}}}{\mathcal {P}_{\text {Lcur}}^{0} } \mathcal {P}_{\text {Lcur}} + \frac{w_{sym}}{\mathcal {P}_{sym}^{0} } \mathcal {P}_{sym} \\&\text{ s.t } \quad V \le \frac{1}{4}V_0. \end{aligned} \end{aligned}$$

(30)

In Eq. (30), the terms represent the system’s strain energy, perimeter and regularization penalties for the LSF, and the misalignment and local curvature penalty for fiber orientation field(s). The last penalty term enforces a symmetric fiber layout. Each term is normalized by reference values, indicated by the superscript 0. The optimization is constrained to ensure the volume of the optimized design does not surpass 25% of the computational domain’s total volume. The maximum curvature is set to 5.0. The initial LSF creates an array of holes arranged in a $7 \times 3 \times 3 \times 3$ grid, each with a radius of 0.12. The initial fiber orientation field(s) is set to a constant value of zero, corresponding to horizontal fiber paths parallel to the x-axis.

We define two cases to evaluate the effects of misalignment and local curvature penalty with different fiber orientation configurations as design variables:

• Case 1 considers solely $\theta _{xy}$ as the design variable field, while $\theta _z$ remains constant. A misalignment penalty with a weight of 0.05 is applied. This setup mirrors the sequential, layer-wise printing process used in some FRC manufacturing techniques.

• Case 2 incorporates both fiber orientations, $\theta _{xy}$ and $\theta _z$, as design variable fields, with a misalignment penalty weight of 0.05.

Figure 22 presents the optimized geometries for the two cases. The geometries display notable similarities, with slight variations primarily in the areas where the support structure connects to the plate. Figure 23 illustrates the optimized shape and fiber layout for the specified cases, along with a cross-sectional slice at $z=0$. The fiber layout is similar for both cases, showing only slight variations in geometry within the slices.

Fig. 22

Optimized shape of the plate support structure for predefined cases

Fig. 23

Streamline visualization of the optimized fiber layout and shape of the plate support structure for different cases

Table 7 presents the objective components, normalized against Case 1 and maximum curvature. In both cases, the maximum curvature is close to the allowable limit of 5.0. In Case 2, controlling curvature becomes more challenging due to the potential alignment of fiber paths outside the $x-y$ plane. This is reflected by the higher curvature penalty value and the larger maximum curvature observed in this case. It is noteworthy that the absolute curvature penalty is below $10^{-9}$ for both cases ensuring the local curvature constraint is tightly satisfied. Notably, Case 2 has a lower strain energy than Case 1, which is attributed to its expanded design space involving two design parameter fields ($\theta _{xy}$ and $\theta _z$), compared to Case 1’s singular design parameter field ($\theta _{xy}$).

Table 7 Objective components and maximum curvature for cases

This example extended the misalignment and curvature penalties to 3D concurrent topology and fiber orientation optimization and demonstrated their effectiveness in generating smoother and more parallel fiber layouts. Similar to the 2D configurations, the shape of the design domain was simple, i.e., it was rectangular.

5.5 Cylinder with variable cross-section under torsion

Fig. 24

Cylindrical design domain with variable cross-section

This example examines concurrent topology and fiber orientation optimization for a complex 3D geometric configuration, featuring a design domain with a spatially variable circular cross-section and circumferential fiber orientation field. The objective is to minimize strain energy, with both the level set and fiber orientation fields serving as design variables.

Figure 24 illustrates the problem setup, where the axis-symmetric design domain is defined by an inner and an outer radius as follows: $r_{\textrm{in}} = 0.15 + 0.2 z - 0.4 z^2 + 0.16 z^3$, and $r_{\textrm{out}} = r_{\textrm{in}} + 0.05$. A torque of $T = 0.05$ is uniformly applied over the cross-section at $z=2$, while the left end of the cylinder is clamped. A solid, non-design domain is placed at the cylinder’s right end ($1.9< z < 2$) to facilitate load transfer. This design domain is embedded into a rectangular computational domain. The geometry of the design domain is defined via the following LSFs:

$$\begin{aligned} \begin{aligned} \phi _{1}(x,y,z)&= r_{\text {out}} - \sqrt{x^2 + y^2}, \\ \phi _{2}(x,y,z)&= r_{\text {in}} - \sqrt{x^2 + y^2}, \end{aligned} \end{aligned}$$

(31)

where $r_{\text {out}}$ and $r_{\text {out}}$ represent the outer and inner radii, respectively, and (x, y, z) specify the spatial coordinates within the computational domain.

A B-spline discretized design LSF is used to describe the shape of the solid within the design domain. Given that the fibers are arranged circumferentially, the angle $\theta _{xy}$ is obtained from the spatial coordinates using $\theta _{xy} = {{\,\textrm{atan2}\,}}(y,x)$, hence it is not a design parameter. Conversely, $\theta _{z}$ is treated as a design parameter. A quadratic B-spline mesh of size $16 \times 16 \times 64$ is used to discretize the design LSF and fiber orientation field, while a linear B-spline mesh of size $64 \times 64 \times 256$ is used to discretize the displacement field.

The optimization problem is formally defined as

$$\begin{aligned} \begin{aligned} \underset{\theta _{z}, LS }{min} \varPi =&w_{f} \frac{\mathcal {F}}{\mathcal {F}^0} + \frac{w_p}{\mathcal {P}^0_p} \mathcal {P}_p + \frac{w_g}{\mathcal {P}^0_g} \mathcal {P}_{g} \\&\frac{w_{\text {par}}}{\mathcal {P}_{\text {par}}^{0} } \mathcal {P}_{\text {par}} + \frac{w_{\text {Lcur}}}{\mathcal {P}_{\text {Lcur}}^{0} } \mathcal {P}_{\text {Lcur}} \\&\text{ s.t } \quad V \le \frac{1}{2}V_0, \end{aligned} \end{aligned}$$

(32)

where the terms represent the system’s strain energy, perimeter and regularization penalties for the level set, and misalignment and local curvature penalties for the fiber orientation field. All terms in the objective function are normalized by the reference values indicated by the superscript 0. A volume constraint is imposed, restricting the structural volume to 50% of the design domain. The weight for the parallel misalignment penalty is set to $w_{\text {par}} = 0.05$, and $\kappa _{\text {max}}$ is assigned a value of 30.0. This value is higher than the values in the previous examples because the circumferential initialization of the fiber path means that the maximum curvature is $max(\kappa ) = \frac{1}{r_{\text {min}}} = 18.12$, with $r_{\text {min}}$ being the minimum radius across the cross-section in the initial design.

Figure 25 illustrates the initial design for both the geometry and fiber orientation fields. The design LSF is initialized to create a pattern of radially symmetric holes, and the initial $\theta _{z}$ values are set to zero, resulting in concentric fiber paths.

Fig. 25

Initial design for the cylinder with variable cross-section

Figure 26 shows the optimized design cropped with the plane $z=0.5$, and the corresponding cross-section. Since the optimization aims to minimize compliance, it effectively seeks to maximize the torsional rigidity of the structure by creating a cross-section that has a nearly uniform torsional stiffness along the length of the cylinder. For a thin circular cross-section, torsional rigidity is described by $J=\frac{2}{3} \pi r^3t$, with r the radius and t thickness. The figure demonstrates that the variation in thickness along the z-axis is inversely proportional to the radius, consistent with the torsional rigidity equation for a thin circular cross-section. Consequently, in areas with a larger radius, the structure is thinner, whereas in the central region with a smaller radius, the thickness increases, occupying more of the design domain.

Fig. 26

Optimized design geometry for the cylinder with variable cross-section

Figure 27 shows the optimized fiber layout visualized with streamlines alongside the post-processed continuous fiber layout. The fiber layouts are depicted by projecting the design’s outer boundary surface onto a plane. Note that since a surface with non-zero Gaussian curvature is mapped into a plane, distortion increases progressively away from the central line of the plane.

In a state of uniform torsion, the outer boundary elements of the structure are subjected to pure shear, resulting in principal stress directions to align at $\frac{\pi }{4}$ and $\frac{3\pi }{4}$. Since this problem is shear-dominated, fiber angles alternate between orientations near $\frac{\pi }{4}$ and $\frac{3\pi }{4}$ with transition regions between them. The figure also indicates that the penalty terms assist in aligning and smoothing the optimized fiber paths, making them more closely resemble the post-processed continuous fiber paths.

Fig. 27

Streamline and post-processed fiber layout for the optimized design of the cylinder with variable cross-section

The absolute values of the objective components and maximum curvature for the optimized design are presented in Table 8. As it can be seen, the maximum curvature is close to the allowable limit of 30.0, and the local curvature penalty is below $10^{-5}$, indicating that the local curvature constraints imposed by the local curvature penalty are tightly satisfied.

Table 8 Absolute values of objective components and maximum curvature for the optimized design of the cylinder with variable cross-section

6 Conclusions

In this study, we presented an approach for the concurrent optimization of shape and fiber orientation for FRC structures. The structural shape is represented by a LSF approximated by quadratic B-splines, while the fiber orientation fields are discretized with linear, quadratic, and cubic B-splines on coarser meshes. Employing LSFs for geometry definition ensures precise boundary definition. Utilizing higher-order, coarse B-splines for the discretization of the level set and fiber orientation fields promotes smoother designs. The structural response is predicted by XIGA, adopting a generalized Heaviside enrichment and face-oriented ghost stabilization for improved stability and robustness. FRCs’ material behavior is modeled with linear elasticity, with the elasticity tensor derived from Mori–Tanaka homogenization.

Novel penalty terms were introduced to promote parallel and smooth fiber paths. These terms anisotropically constrain the fiber orientation field’s first-order derivative, and are integrated into the optimization problem formulation via the penalty terms. The geometric interpretation of these penalties was explored by considering simplified optimization problems to assess their impact on a hypothetical fiber path and their efficacy in creating parallel and smooth paths.

This study considered compliance minimization problems and examined the interplay between geometry and fiber orientation for different penalty combinations. The influence of the discretization of the fiber orientation field in terms of polynomial order and B-spline mesh size and its influence on the optimized structure were studied.

Numerical experiments with various penalty combinations demonstrated the effectiveness of the parallel misalignment penalty in aligning fiber paths in both 2D and 3D settings. Simultaneously, the curvature penalties were found to be efficient in controlling bending and waviness in the fiber paths. Incorporating the misalignment and curvature penalties in the optimization problem formulation led to an increase in optimized strain energy values. The strain energy increase was more pronounced as additional penalty terms were introduced, indicating that increased parallelism and smoothness in the fiber paths lead to higher strain energy values.

The numerical examples suggested that the polynomial order of fiber orientation did not significantly influence strain energy, yielding similar outcomes across all polynomial orders. While linear B-splines failed to produce smooth curvature variations, this lack of smoothness was not noticeable when visualizing the fiber paths via streamlines. Coarser discretization of the fiber orientation fields leads to a smoother fiber layout by reducing localized features. However, this smoothness comes at the cost of increased strain energy values.

Optimized fiber paths, characterized by their parallel alignment and smoothness, simplify the post-processing efforts and narrow the difference between the optimized layout and the post-processed, uniformly spaced fiber path. However, additional research is needed to seamlessly integrate the design and manufacturing processes. This study focused primarily on parallelism and curvature as manufacturing constraints. Yet, other factors such as preventing internal loops and accounting for no-sag constraints also require careful consideration.

In the two-scale optimization framework explored in this study, the strain energies of designs with optimized and post-processed fiber orientation fields were very similar. Conducting full-scale simulations could provide insight into the validity of the two-scale homogenization scheme and identify differences between the optimized results and their stripe pattern interpretation at full scale. Such an analysis would involve developing FE models that resolve fibers at the microscopic scale, instead of approximating the micro-scale response with the Mori–Tanaka homogenization scheme used in this study.

While the numerical experiments render the proposed method promising, a fundamental problem remains to be addressed. Although $\pi$-periodicity issues did not arise in the numerical examples studied in this paper, a similar issue was encountered in the shear-dominated examples, see Sect. 5.2 and 5.5. In a state of pure shear, the fiber angles $\frac{\pi }{4}$ and $\frac{3\pi }{4}$ result in the same stiffness. The optimization process may create regions where the fiber orientation is $\frac{\pi }{4}$ and nearby regions where the fiber orientation is $\frac{3\pi }{4}$. The continuous interpolation of the fiber orientation field used in the proposed method necessitates transition regions where the fiber angles vary between $\frac{\pi }{4}$ and $\frac{3\pi }{4}$. Thus, in these transition regions, the angle is not optimal, affecting the performance of the design. A similar issue may arise for general loading scenarios due to the $\pi$-periodicity. In future studies, the proposed method needs to be enhanced to avoid the need for these transition regions by, for example, allowing for a locally discontinuous fiber orientation field.