Topology optimization of easy-removal support structures for additive manufacturing

Abstract

This paper presents a density-based topology optimization approach to design easy-removal support structures for additive manufacturing (AM). First, a multi-field structural parameterization is proposed for topology optimization by considering AM filtering technique that ensures the physical design being self-support. An easy-removal constraint is developed to generate porous structural patterns in the contact region between the support structures and its surroundings. An improved formulation is further proposed to prevent obtaining impractical solutions which contain one-node connection in the structural members. Besides, an overhang constraint and a design-dependent self-weight load are considered. As a result, the optimized support structures are self-support, able to support the overhang regions of the given prototype and possesses excellent mechanical properties to bear the self-weight of the entire AM part. It can be easily removed from both the prototype and the baseplate. Numerical examples and discussions are given to demonstrate its effectiveness and applicability.

1 Introduction

With the fast development of additive manufacturing (AM) techniques, mechanical parts with complex geometries can be fabricated in a much easier way. The market needs and the volume of AM production grow rapidly nowadays as the processes are becoming more efficient. An additively manufactured part (e.g., by powder-bed-based selective laser melting) generally consists of two parts, the functional part and the support structures. The latter is used to support the overhang features of the functional design during an AM process to ensure the overall manufacturability, while it must be removed afterwards by a manual or machining post-process. Due to inevitable machining and human errors, the risk of damaging the functional part is high in the post-process if the support structures are badly designed or too complicated to be removed. The cost of post-process contributes significantly to an AM activity. Hence, it is preferable to design easy-removal and cost-effective AM support structures with enough stiffness to support the overhangs of the functional prototype.

Many works have been done to design support structures for AM (Jiang et al. 2018) and the most common strategy is based on utilizing predefined geometric patterns. For a given prototype, designers may choose geometric primitives such as lattice (Hussein et al. 2013; Strano et al. 2013), straight thin wall (Krol et al. 2012), sloping wall (Huang et al. 2009), or tree-like (Lantada et al. 2017) geometric primitives to support the overhang regions of a prototype. Although most of the geometric patterns are porous and self-support, the AM support structures are generally designed based on engineers’ experiences and it is difficult in practice to realize a balance between the geometric complexity, mechanical property (e.g., stiffness), material usage, and the cost of post-processing.

Topology optimization (Bendsøe and Kikuchi 1988; Sigmund and Maute 2013; Xia and Shi 2016; Xia et al. 2019) is an effective design approach to generate structures that possess effective mechanical properties such as optimized stiffness to weight ratio. For AM-oriented structural topological design, one of the hot topics in recent years is to design self-support structures using the topology optimization techniques. Langelaar (2016) and Langelaar (2017) developed an AM filtering method that can ensure the optimized structure being self-support. Gaynor and Guest (2016) proposed a projection-based strategy in a similar way to achieve a self-support structural design. Zhang and Zhou (2018) used polygon holes as design primitives to control the overhang angle. Moreover, a polygon modification and re-optimization strategy was used to avoid the unprintable V-shape areas. Qian (2017) proposed a projected perimeter-based formulation to control the overhang angle. A grayness constraint was used at the same time to prevent the appearance of gray density. Guo et al. (2017) achieved self-support structural design based on the moving morphable components (MMC) and moving morphable voids (MMV) frameworks. Zhang et al. (2019) proposed an overhang angle constraint and a hanging feature constraint to achieve self-support structural design. In addition, Allaire et al. (2017a, 2017b, ??) solved the overhang issue by considering the mechanical property of the intermediate structure in the layer-by-layer additive manufacturing process. By using the above methods, the functional structure is self-support and it reduces the manufacturing cost of using additional support structures. However, the mechanical property (e.g., stiffness) of the functional structure degrades substantially due to the self-support design requirement comparing with that without such a constraint.

In order to obtain a well-behaved functional part with as low manufacturing cost as possible, another design strategy is to optimize the support structures for a given functional prototype rather than generating self-support prototype with degraded structural performance.¹Mezzadri et al. (2018) designed support structures by applying evenly distributed pressure load in the need-support surface of the functional structure for a compliance minimization problem. Zhou et al. (2019) proposed a topology optimization approach to design support structures that can dissipate thermal energy efficiently and also support the overhang surface of the given prototype. Langelaar (2018) proposed an approach to optimize the functional part, the support structures, and the AM building direction at the same time. Allaire and Bogosel (2018) proposed several models to optimize the stiffness or the heat dissipation ability of the support structures and the functional prototype. However, the focuses of above studies are mainly on the mechanical property and material usage of the support structures without considering the easy-removal issue.

One way to obtain easy-removal support structures is by preventing bulky material conglomerating in the contact regions between the support structures and its surroundings including the prototype and the baseplate. Previously, Liu et al. (2019) proposed a method by changing the gravity of the functional structure into several point loads and then applying these loads on the top surface of designable domain for structural design optimization. In doing so, the optimized support structure near the top surface can be easily separated. However, in Liu’s model, the stiffness of the functional structure is neglected while in practice the self-gravity and the overall structural stiffness including both the prototype and the support structures shall be preferably considered. Kuo et al. (2017) proposed a repulsion index function to measure the element connection. By incorporating the repulsion index function into a multi-objective optimization problem, the layout of easy-removal support structures can be obtained. However with their solution, there is a large amount of gray elements in the contact region and the support structures cannot fully support the overhangs of the functional structure.

In this paper, a density-based topology optimization method is proposed to design easy-removal AM support structures for a given non-designable functional structure. The support structure will not only have enough stiffness to bear the gravity of the functional prototype and itself but can also fully support the overhangs of the prototype, ensuring the overall manufacturability. The AM filter proposed by Langelaar (2017) is firstly utilized in parameterization strategy so that the support structure is self-support. A geometric constraint proposed by Zhou et al. (2019) is further utilized to make sure that the overhang feature of the given prototype can be fully supported. More importantly, a local volume constraint proposed by Wu et al. (2018) is employed in the contact region between the support structure and its surroundings and thus the support structure can be easily removed from the prototype and the baseplate. Furthermore, an improved formulation is further proposed to prevent obtaining impractical design solutions that exhibiting one-node connection in the structural members.

The remainder of this paper is organized as follows. In Section 2, a topology optimization model is proposed to design easy-removal support structure. The key technologies including the AM filtering, the overhang constraint and the easy-removal constraint are introduced. A numerical example is then given to discuss the one-node connection issue. Afterwards, an improved formulation is proposed to address the issue, which is followed by successful design cases of easy-removal support structures in Section 4. Discussions and conclusions are given in Section 5.

2 Topology optimization model for easy-removal AM support structures

2.1 Structural parameterization

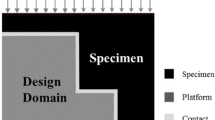
In this section, a density-based topology optimization model is proposed to design easy-removal support structures for a given functional prototype. As shown in Fig. 1e, the building chamber Ω which consists of a non-designable domain Ω_N (blue color) and the rest designable domain Ω_D is discretized by square finite elements. Each element is annotated with a physical variable $\check {\phi }_{e}(e=1:N)$ indicating whether it is solid ($\check {\phi }_{e}=1$) or void ($\check {\phi }_{e}=0$), where e is the element index. The physical variables are dependent on design variables ϕ_e ∈ [0,1](e = 1 : N) through a series of filtering operations.

Fig. 1

Parameterization of topology optimization for AM with four different filters (blue color, non-designable domain Ω_N; red color, overhang region). a Design variable. b–d Intermediate variable. e Physical variable

First, a density filter (Bruns and Tortorelli 2001; Bourdin 2001) is applied to avoid the mesh-dependent and check-board issues (Bendsøe and Sigmund 2003):

$$ \bar{\phi}_{e}=\frac{1}{\sum\limits_{i\in N_{e,r}}H_{ei}}\sum\limits_{i\in N_{e,r}}H_{ei}\phi_{i}, $$

(1)

where N_e,r = {i|∥χ_e − χ_i∥≤ r,i ∈Ω_D} is the set containing elements near element e within the filter radius r. χ_i and χ_e are the center positions of elements i and e, respectively. $H_{ei}=\max \limits (0,r-\|\chi _{e}-\chi _{i}\|)$ is the weight function.

Second, a Heaviside projection is used (Guest et al. 2004; Sigmund 2007; Wang et al. 2010) to have a clear solid-void design as follows:

$$ \tilde{\phi}_{e}=\frac{\tanh(\beta\eta)+\tanh(\beta(\bar{\phi}_{e}-\eta))}{\tanh(\beta\eta)+\tanh(\beta(1.0-\eta))}, $$

(2)

where β controls the sharpness of the differentiable function and η is the threshold.

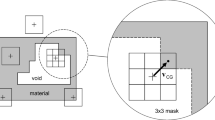
In order to guarantee the support structure being self-support, an AM filter (Langelaar 2017) is further applied to remove the overhang feature of the overall structure including the design domain for support structures and the non-design domain for the given prototype. The idea of the AM filter is shown in Fig. 2. For an element at position (i,j), the nearest three elements under it with index (i − 1,j − 1), (i − 1,j), and (i − 1,j + 1) are defined as the support region of the element (i,j). If no material exists in the support region of the element (i,j), the element is unprintable and will be removed by the AM filter. Otherwise, the element at (i,j) is supported by the underlying structure. By applying the AM filter, the unprintable overhang structure will be removed and the remaining structure $\hat {\phi }$ is self-support under a 45^o overhang constraint. The formulation of the AM filter is given as follows:

$$ \hat{\phi}_{(i,j)}=\left\{ \begin{array}{lr} \min(\tilde{\phi}_{(i,j)},\xi_{(i,j)}), &i>1 \\ \tilde{\phi}_{(i,j)}, &i=1 \end{array} \right., with $$

(3)

$$ \xi_{(i,j)}=\max(\hat{\phi}_{(i-1,j-1)},\hat{\phi}_{(i-1,j)},\hat{\phi}_{(i-1,j+1)}), $$

(4)

and differentiable form is given as:

$$ \hat{\phi}_{(i,j)} = \left\{ \begin{array}{lr} \frac{1}{2}(\tilde{\phi}_{i,j} + \xi_{(i,j)} - \sqrt{(\tilde{\phi}_{(i,j)}-\xi_{i,j})^{2}+\varepsilon_{m}}+\sqrt{\varepsilon_{m}}), &i>1 \\ \tilde{\phi}_{(i,j)}, &i=1 \end{array} \right., with $$

(5)

$$ \xi_{i,j}=(\hat{\phi}_{(i-1,j-1)}^{P} + \hat{\phi}_{(i-1,j)}^{P} + \hat{\phi}_{(i-1,j+1)}^{P})^{\frac{1}{Q}}, $$

(6)

where P = 40, $Q=P+\frac {\ln 3}{\ln 0.5}$, and ε_m = 10^− 4 are used as suggested in Langelaar (2017).

Fig. 2

Support region of element (i,j)

One issue of applying the AM filter to entire domain is that some parts of the non-designable functional structure are removed as shown in Fig. 1d. In order to keep the non-designable domain unchange in the optimization process, an extra feature-preserving filter is applied afterwards to recover the eroded functional structure (Zhou et al. 2019):

$$ \check{\phi}_{e}=\left\{ \begin{array}{lr} \hat{\phi}_{e}, &e\in {\Omega}_{D} \\ 1, &e\in {\Omega}_{N} \end{array} \right.. $$

(7)

2.2 Overhang constraint

With the above parameterization, the support structure in designable domain Ω_D is guaranteed to be self-support and the functional structure in non-designable domain Ω_N remains unchanged during the optimization process. However, some parts of the functional structure may not be supported by the underlying support structure as shown in Fig. 1e. Hence, an overhang constraint proposed by Zhou et al. (2019) is leveraged here to make sure that the overhangs of the prototype are fully supported.

As shown in Fig. 3, by applying the ideal AM filter (3-4) to the cantilever beam without having any supports, the need-support (NS) region Ω_NS of the functional structure is defined as the area wherever is removed by the AM filtering operation as shown in green color. A indicator function G is then used to calculate the volume of the non-supported overhang regions in Ω_NS as:

$$ \begin{array}{@{}rcl@{}} G&=& \sum\limits_{e\in {\Omega}_{NS}}(1-\hat{\phi}_{e})V_{e}\\ &=& (\textbf{I}^{T}\cdot\textbf{l}_{NS}-\hat{\boldsymbol{\phi}}^{T}\cdot\textbf{l}_{NS})V_{e}, \end{array} $$

(8)

where l_NS is a vector related to Ω_NS. If an element belongs to Ω_NS, the corresponding element in l_NS is equal to 1. Otherwise, it is equal to 0. I is a unit vector with values of 1. The overhang constraint is given as follows:

$$ G\leq\varepsilon_{r}, $$

(9)

where $\varepsilon _{r}=10^{-4}\times \textbf {I}^{T}\cdot \textbf {l}_{NS}V_{e}$ is a small value according to Zhou et al. (2019).

Fig. 3

The need-support region (marked in green) of a cantilever beam

2.3 Easy-removal constraint

The key idea to design easy-removal support structures is herein to ensure that connections between the supports to its surroundings are porous and easy-to-break, rather than a bulky structural bond.

As shown in Fig. 4, a contact region Ω_C around the prototype and the baseplate with thickness t_C inside the designable domain Ω_D is firstly defined. For each element e ∈Ω_C, the local volume fraction in the neighborhood is calculated by:

$$ \bar{v}_{e}= \frac{{\Sigma}_{i \in N_{e,R}}\check{\phi}_{i}}{{\Sigma}_{i \in N_{e,R}}1}, e \in {\Omega}_{C}, $$

(10)

where N_e,R = {i : ∥χ_e − χ_i∥≤ R,i ∈Ω_C} is the set containing elements around element e within the distance R. A local volume constraint proposed by Wu et al. (2018) is applied in Ω_C to restrict the material usage inside, and hence resulting in porous and easy-removal structural pattern in the contact region. The ideal local volume constraint is given by:

$$ \max_{e \in {\Omega}_{C}}\bar{v}_{e} \leq \alpha_{l} , $$

(11)

where α_l is the maximum allowable local volume fraction. A differentiable p-norm-based formulation is given as follows to approximate the above function:

$$ V_{l} = \left( \frac{1}{M}\sum\limits_{e \in {\Omega}_{C}}\bar{v}_{e}^{P_{l}}\right)^{1/P_{l}} \leq \alpha_{l} , $$

(12)

where P_l = 16 is used as suggested in (Wu et al. 2018). $M={\sum }_{e \in {\Omega }_{C}}1$ is the total number of elements in the contact region Ω_C. With the proposed design constraint, easy-removal support structures can be realized as will be demonstrated in later sections.

Fig. 4

The contact region (marked in red) of a cantilever beam

2.4 Material interpolation and optimization model

Besides the easy-removal and support-to-overhang properties, the support structures must be stiff enough to bear the gravity of itself and the functional prototype. The gravity load of the non-designable functional structure is fixed while that of the support structures is design-dependent. The gravity acceleration g for elements with intermediate densities is interpolated by a linear function:

$$ g_{e}=\check{\phi}_{e}g_{0}, $$

(13)

where g₀ = 1 is the gravity acceleration for solid elements. Moreover in this work, the Young modulus E of the elements with intermediate physical densities is interpolated using rational approximation of material properties (RAMP) (Stolpe and Svanberg 2001):

$$ E_{e}=E_{min}+\frac{\check{\phi}_{e}}{1+q(1-\check{\phi}_{e})}(E_{0}-E_{min}), $$

(14)

where E₀ = 1 and E_min = 10^− 9 are used for the solid and void, respectively. q = 10 is the penalty factor.

With the above parameterization and constraints, a topology optimization model for easy-removal support structures is proposed as:

$$ \begin{array}{ll} \min\limits_{\boldsymbol{\phi}}& : C={\boldsymbol{F}}^{T}\cdot \boldsymbol{U}\\ s.t.& : V\leq\alpha V_{0}\\ & : V_{l} \leq \alpha_{l}\\ & : G \leq \varepsilon_{r}\\ & : \boldsymbol{K}\boldsymbol{U }=\boldsymbol{F}\\ & : 0\leq \phi_{e}\leq1 ,e=1,2,...,N \end{array}, $$

(15)

where C is the compliance of the overall structure subject to gravity loads and a fixed baseplate boundary condition. $V=\sum \limits _{e\in {\Omega }_{D}}\check {\phi }_{e}$ is the volume of support structures. V₀ is the volume of designable domain Ω_D. α is the allowable upper bound for the volume fraction. K, U, and F are the stiffness matrix, the displacement vector, and the force vector, respectively. The method of moving asymptotes (MMA) (Svanberg 1987) is used to solve the above optimization problem.

2.5 Topology optimization workflow

The workflow of the topology optimization approach is shown in Fig. 5 and the solution procedure is given as follows:

• Step 1: Setup the designable domain Ω_D and the non-designable domain Ω_N. Initialize the design variables and β.

• Step 2: Perform density filtering, projection, AM filtering, and feature-preserving filtering.

• Step 3: Solve the FEA model and calculate design responses.

• Step 4: Calculate the sensitivity for each design response.

• Step 5: Use the MMA method to update design variables.

• Step 6: Check the condition for β continuation. If the change rate of the objective function is less than 0.005 in 10 continuous iterations, β < β_max are both satisfied, then double the value of β and turn to Step 2. Otherwise, turn to Step 7.

• Step 7: Check the convergence. If the change rate of the objective function is less than 0.005 in 10 continuous iterations and all the constraints are satisfied, stop the optimization process. Otherwise, turn to Step 2.

Fig. 5

Workflow of topology optimization

2.6 Numerical example

A benchmark topology optimization example is used here to study the proposed solution. It is to design the support structures for the cantilever beam shown in Fig. 3, which is discretized by a mesh of 400 × 200 square elements. The optimization parameters are set as follows: the maximum allowable volume fraction for the support structure α = 0.3, the allowable local volume fraction is α_l = 0.6, the neighborhood distance R = 6, the thickness of contact region t_C = 3, and the threshold value η = 0.5. Besides, a continuation approach is used by setting β = 1 initially and doubling its value up to 32 until convergence.

The optimized result is shown in Fig. 6 and the support structure in the contact region exhibits a porous structural layout, indicating that it can be removed easily. Besides, all the overhang regions of the functional structure are well supported by the optimized supports. However, several one-node connected bars are observed in the optimized design, of which the enlarged snapshots are given in Fig. 6. These one-node connections exist as it indeed satisfies the overhang constraint. However, due to the discretization of using square elements and impractical finite element modeling, it neither can provide any stiffness nor can be manufactured in practice. Hence, such a design is impractical and meaningless.

Fig. 6

Optimized support structure for a cantilever bean (red color, the optimized support structure in the contact region), (a–c) enlarged details

3 Manufacturable design solution

The support structure optimized in the previous section contains porous structural features in the contact regions between itself and the surroundings, which can be easily removed from the prototype and the baseplate after AM processing. However, the design exhibits one-node connection which is impractical from manufacturing viewpoint. An improved solution is introduced herein to avoid such a issue.

As shown in Fig. 7, three projected fields are considered in the improved solution where the filtered field $\bar {\phi }$ is projected to eroded $\tilde {\phi }^{ero}$, intermediate $\tilde {\phi }^{int}$, and dilated field $\tilde {\phi }^{dil}$ respectively:

$$ \tilde{\phi}_{e}^{ero}=\frac{\tanh(\beta\eta^{ero})+\tanh(\beta(\bar{\phi}_{e}-\eta^{ero}))}{\tanh(\beta\eta^{ero})+\tanh(\beta(1.0-\eta^{ero}))}, $$

(16)

$$ \tilde{\phi}_{e}^{int}=\frac{\tanh(\beta\eta^{int})+\tanh(\beta(\bar{\phi}_{e}-\eta^{int}))}{\tanh(\beta\eta^{int})+\tanh(\beta(1.0-\eta^{int}))}, $$

(17)

$$ \tilde{\phi}_{e}^{dil}=\frac{\tanh(\beta\eta^{dil})+\tanh(\beta(\bar{\phi}_{e}-\eta^{dil}))}{\tanh(\beta\eta^{dil})+\tanh(\beta(1.0-\eta^{dil}))}, $$

(18)

where different projection threshold values η^ero = 0.7, η^int = 0.5, and η^dil = 0.3 are chosen in this work. To ensure the property of being self-support and to recover the non-designable functional prototype, the AM filter and the feature-preserving filter are applied to the projected fields, similarly to the previous section, which are in turn represented as $\hat {\phi }^{ero}$, $\hat {\phi }^{int}$$\hat {\phi }^{dil}$ and the physical fields $\check {\phi }^{ero}$, $\check {\phi }^{int}$ (the blueprint design to be manufactured), and $\check {\phi }^{dil}$.

Fig. 7

Improved structural parameterization

For topology optimization problems involving only stiffness and structural weight, a minimum length scale can be imposed on the intermediate design if one considers the eroded design as the measure for stiffness and the dilated design for structural weight, provided that eroded design has the the worst stiffness and the dilated design has the highest structural volume ratio (Lazarov et al. 2016). Such an idea is employed in the current work and it is found effective in avoiding the one-node connection issue in the blueprint design. The improved formulation is given as follows:

$$ \begin{array}{ll} \min\limits_{\boldsymbol{\phi}}& : C^{ero}=({\boldsymbol{F}}^{ero})^{T}\cdot \boldsymbol{U}^{ero}\\ s.t.& : V^{dil}(\check{\boldsymbol{\phi}}^{dil})\leq\alpha V_{0}\\ & : V_{l}(\check{\boldsymbol{\phi}}^{int}) \leq \alpha_{l}\\ & : G(\check{\boldsymbol{\phi}}^{ero}) \leq \varepsilon_{r}\\ & : \boldsymbol{K}(\check{\boldsymbol{\phi}}^{ero})\boldsymbol{U }^{ero}=\boldsymbol{F}^{ero}\\ & : 0\leq \phi_{e}\leq1 ,e=1,2,...,N \end{array}, $$

(19)

where the objective functional, the overhang constraint, and the state equation are defined on the eroded design. The corresponding design-dependent gravity acceleration is given as:

$$ g_{e}^{ero}=\check{\phi}^{ero}_{e}g_{0}. $$

(20)

The overhang constraint is imposed in the eroded design, which has the thinnest structural members and the worst ability to support the functional structure. As a result, the support structures in the intermediate design will satisfy the overhang constraint naturally. The constraint is given as:

$$ G(\check{\boldsymbol{\phi}}^{ero})\leq\varepsilon_{r}, $$

(21)

where the volume of overhang features in Ω_NS is calculated by:

$$ \begin{array}{@{}rcl@{}} G(\check{\boldsymbol{\phi}}^{ero})&=& \sum\limits_{e\in {\Omega}_{NS}}(1-\hat{\phi}_{e}^{ero})V_{e} \\ &=& (\textbf{I}^{T}\cdot\textbf{l}_{NS}-(\hat{\boldsymbol{\phi}}^{ero})^{T}\cdot\textbf{l}_{NS})V_{e}. \end{array} $$

(22)

Since the intermediate design $\check {\phi }^{int}$ is the blueprint to be manufactured, the easy-removal constraint is defined on it as:

$$ V_{l}(\check{\boldsymbol{\phi}}^{int}) = \left( \frac{1}{M}{\sum}_{e \in {\Omega}_{C}}(\bar{v}_{e}^{int})^{P_{l}}\right)^{1/P_{l}} \leq \alpha_{l}, $$

(23)

where $\bar {v}_{e}^{int}$ is the local volume fraction of element e for intermediate design:

$$ \bar{v}_{e}^{int}= \frac{{\Sigma}_{i \in N_{e,R}}\check{\phi}_{i}^{int}}{{\Sigma}_{i \in N_{e,R}}1}, e \in {\Omega}_{C}. $$

(24)

Moreover, the volume fraction constraint is defined on the dilated design as:

$$ V^{dil}(\check{\boldsymbol{\phi}}^{dil})=\sum\limits_{e\in {\Omega}_{D}}\check{\phi}_{e}^{dil}\leq\alpha V_{0}. $$

(25)

In order to impose a desirable volume fraction α^∗ to the intermediate design, the parameter α is updated at least 10 design iterations after the last change, provided that the current volume constraint satisfied. The update rule is based on the square root of the ratios between the desirable volume fraction and that of the intermediate design:

$$ \alpha^{(new)}=\alpha^{(old)}\sqrt{\frac{\alpha^{*}}{V^{int}}}, $$

(26)

where α^(old) and α^(new) are the upper volume fraction for dilated design before and after the update, respectively. This strategy drives the volume fraction of the intermediate design to the desired volume fraction α^∗ indirectly.

The workflow of the improved topology optimization model is almost the same as that described in Section 2.5, except that the α parameter adaptation is added between Step 3 and Step 4.

4 Numerical examples

4.1 Support structure design for a cantilever beam

The first example is to redesign the support structures with the improved optimization formulation for the cantilever beam shown in Fig. 3. The optimized designs with different allowable volume fraction from 0.25 to 0.4 are shown in Fig. 8.

Fig. 8

Optimized results for cantilever beam with different volume fractions. aα = 0.25. bα = 0.3. cα = 0.35. dα = 0.4

The optimization parameters are set the same for all the cases as follows: the filter radius of the density filter in (1) r = 2.5, contact thickness t_C = 3, the neighborhood distance R = 6, the local volume fraction α_l = 0.6. For each case, the compliance (C), volume ratio (α), and the number of remaining overhang elements (OE) are compared. The overall compliance is decreasing as the allowable material increases. Besides, the low numbers of OE show that proposed optimization is able to generate effective structure to support the overhang of a given prototype. Note that the OE value is obtained by applying the AM filter (3–4) to the optimized result and then summing up the number of removed elements in Ω_NS.

For all the results shown in Fig. 8, the previously seen one-node connection issue is resolved. The optimized designs show that the material tends to accumulate in the bottom of design domain because of the self-weight load. Such a tendency becomes more clear as the volume fraction α increases. Besides, the support structures in contact regions resemble a pattern of dashed line, which can be easily removed comparing with a full-material and bulky connection. However, a precise minimum length scale cannot be defined by the proposed solution and parameterization. The topic of length-scale control is out of the scope of the current work and one may leverage other techniques, e.g., geometric constraints (Zhou et al. 2015) for such a purpose.

Moreover, two geometry-based support structures are generated for comparison as shown in Fig. 9. Both the optimized support structures by the proposed method and the geometry-based support structures can support the overhang features of the functional part. However, when the material usage for the support structures is the same, the support structure optimized by the proposed method in Fig. 8a has a lower compliance value.

Fig. 9

Geometry-based support structures for comparison

4.2 Support structure design for a MBB model

The second example is to design support structures for a MBB beam sized 150 × 450 as shown in Fig. 10, where the corresponding need-support regions are marked in green. The optimization parameters are given as follows: the volume fraction α = 0.25, the radius of density filer r = 2.5, the neighborhood distance R = 6, the local volume fraction α_l = 0.6.

Fig. 10

The given MBB beam (left) and the corresponding need-support region (right)

The optimized result with the local volume constraint applied in the overall designable domain is given in Fig. 11a. For comparison, the optimized results with contact thickness t_C = 9,6,3 are shown in Fig. 11b–d and the optimized result without using the easy-removal constraint is given in Fig. 11e. The compliance value becomes lower as the thickness of the contact region decreases. Among these structures, the optimized result with the easy-removal constraint applied in the overall designable domain has the largest compliance value while the one without the constraint exhibits the most stiff design.

Fig. 11

a optimized result with local volume constraint applied in the overall designable domain; b–d optimized results with contact thickness t_C = 9,6,3; e optimized result without easy-removal constraint

4.3 Support structure design for a complex model

The third example is presented to design support structures for a geometric prototype consisting of four English letters SJTU (the capital initials of Shanghai Jiao Tong University) as shown in Fig. 12, where the corresponding need-support regions are highlighted. The size of domain is 650 × 350. The optimization parameters for this example are set as follows: the allowable volume fraction for the support structures α = 0.3, the filter radius of the density filter r = 2.5, contact thickness t_C = 3, the neighborhood distance R = 6, and the local volume fraction α_l = 0.6.

Fig. 12

The given letter figure (left) and the corresponding need-support region (right)

As shown in Fig. 13a, the model is fully supported by the optimized supports and the contact region exhibits a porous feature. In order to illustrate the necessity of the supports between the letters “S” and “J,” a modified support structure without any supports between “S” and “J” is constructed for comparison as shown in Fig. 13b. The latter structure has a higher compliance value, indicating that the removed supports indeed help increase the stiffness of the overall structure. Furthermore, three other different printing directions are also considered and the corresponding optimized supports with the same material usage as that in Fig. 13a are given in Fig. 14. As a comparison, the optimized design shown in Fig. 14a has the highest stiffness value. It can be seen that the proposed approach can be applied to generate easy-removable support structures with optimized mechanical property. Besides, the printing direction is found to be an important variable in AM design optimization. By selecting an appropriate printing direction, the stiffness of the overall AM part can be significantly enhanced.

Fig. 13

(a) The optimized support structure for “SJTU.” (b) A modified support structure by removing a portion of supports

Fig. 14

Optimized results with different building directions. a build from bottom; b build from left; c build from right

5 Conclusions

This paper proposes a density-based topology optimization method to design easy-removal support structure for additive manufacturing . The underlying structural parametrization takes the AM filtering technique into account to ensure the support structure being self-support, which is necessary for AM support structures. The overhang constraint helps reduce the overhang features of the given functional prototype. Besides, the local volume constraint in contact region is utilized to ensure that the porous pattern in specific region can be easily removed after AM. Structural member size is also effectively controlled by an improved formulation and thus the entire manufacturability is guaranteed. Numerical examples show that the proposed method can generate optimized support structures that possess the characteristics of self-support, efficient mechanical property, and manufacturability. To cope with the practical scenario in additive manufacturing, design-dependent gravity loads are considered in the current work for structural stiffness maximization.

However, there is one issue remaining in the current solution that worthy further investigation. It is observed that the number of overhang elements in the optimized design is not vanish but a small number even though the overhang constraint is satisfied. In the current implementation, the threshold ε_r is set to a small value rather than zero, which is otherwise difficult to be satisfied. It is because according to (5–6), the value of $\hat {\phi }_{e}^{ero}$ may be slightly larger than 1 and $1-\hat {\phi }_{e}^{ero}<0$ in (8). The summation counteracts a positive value of $1-\hat {\phi }_{e}^{ero}$ in (8), leaving the elements where $1-\hat {\phi }_{e}^{ero}\geq 0$ unsupported and thus the number of overhang elements in overall structure cannot reach zero. This issue will be addressed in a separate future work. Besides, extension of the proposed approach to 3D application will be targeted as a separate future work.