Reliability-based multi-scale design optimization of composite frames considering structural compliance and manufacturing constraints

Abstract

The paper proposes an efficient methodology for concurrent reliability-based multi-scale design optimization (RBMDO) of composite frames to minimize structural cost subjecting to compliance constraint. Two types of variables are systematically considered in RBMDO, which are deterministic design variables of the frame components, the discrete fiber winding angles at the two geometrical scales, and random parameters of material properties and loading conditions in both magnitude and direction. To overcome the difficulty of highly nonlinear compliance constraint when using fiber winding angles as design variables and improve efficiency and accuracy of RBMDO of composite frames, the improved single loop and single vector (SLSV) approach based on modified chaos control (MCC) scheme, which is abbreviated hereafter as SLSV-MCC, is proposed, and sensitivities at the current design point are utilized to further increase accuracy of the proposed SLSV-MCC. Six types of specific manufacturing constraints are explicitly considered in the proposed RBMDO to reduce the risk of local failure in the laminated composite. The deterministic multi-scale design optimization (DMDO) model is also presented and utilized for comparison to distinguish differences between deterministic and reliability-based optimization results. Efficiency and accuracy of the proposed SLSV-MCC are compared with the first-order reliability method (FORM) and conventional SLSV approach. Meanwhile, the Monte Carlo simulation (MCS) method is further utilized to validate the accuracy of the proposed RBMDO. The discrete material optimization (DMO) approach is utilized to couple two geometrical scales: macroscopic topology and microscopic material selection. Capabilities of the proposed RBMDO are demonstrated by optimization of 2D and 3D composite frames. Numerical study reveals that the uncertainties in material properties and loading conditions will lead to different macroscopic sizing and topology configurations for deterministic and reliability-based solutions.

1 Introduction

Concurrent multi-scale design optimization provides a competitive approach to realize innovative structure configuration and lightweight design through macro-scale structural topology and micro-scale material selection. Pioneering work of the multi-scale optimization on hierarchical structure and material design is found in Rodrigues et al. (2002). Then, the hierarchical model has been extended to investigate concurrent material and topology optimization of three-dimensional structures and bone tissue adaptation (Coelho et al. 2008). State-of-the-art researches for multi-scale design optimization of structures with cellular and porous material can be found in Liu et al. (2008), Yan et al. (2008), Niu et al. (2009), Zuo et al. (2013), Andreasen and Sigmund (2012), and Deng et al. (2013).

Laminated fibrous composite materials have been widely used, especially in aerospace, automotive, advanced shipping, and civil engineering, due to their superior material properties for high specific strength and stiffness. As architecture material, laminated composites offer a good opportunity to tailor the material properties by adjusting the fiber ply parameters. Thus, many researchers have recently carried out excellent works on multi-scale lightweight design optimization of composite structures. Ferreira et al. (2013) adopted the DMO (Stegmann and Lund 2005; Hvejsel and Lund 2011) approach to perform a hierarchical optimization of laminated composite structures considering both fiber orientation and cross-section size/shape. For more researches about the deterministic multi-scale design optimization (DMDO) of composite material and structure, readers can refer to Gao et al. (2013), Sørensen et al. (2014), Duan et al. (2015), Yan et al. (2017), Duan et al. (2018, 2019a, b), Wu et al. (2019) and Ma et al. (2020).

Uncertainties are inevitable and pervasive in simulation, modeling, manufacturing processes, material properties, and loading environments. Without considering uncertainties in optimization, the optimum design will have a high risk of failure. Hence, reliability-based design optimization (RBDO) has been applied to structural design optimization with multi-scale materials such as laminated composites to guarantee reliability and robustness (Guo et al. 2009; 2015; António and Hoffbauer, 2009; Deng and Chen 2017; Shimoda et al. 2019). Recently, it should be pointed out that Sohouli et al. (2018) investigated RBMDO of variable stiffness composite structures with sequential optimization and reliability assessment (SORA), and hybrid RBDO decoupled scheme to determine material and fiber orientation. Xu et al. (2019) proposed a non-deterministic robust topology optimization of ply orientation for multiple fiber-reinforced plastic (FRP) materials under loading uncertainties with both random magnitude and random direction.

Efficient but accurate reliability analysis needs to be performed in reliability-based multi-scale design optimization (RBMDO) of composite structures with many deterministic and random design variables. Commonly, reliability analysis is classified into two types: (1) sampling methods such as MCS (Papadrakakis and Lagaros 2002; Cho et al. 2016), importance sampling (IS) (Denny 2001), and latin hypercube sampling (Helton and Davis 2003) and (2) analytical methods or most probable point (MPP)-based methods including first-order reliability method (FORM) (Chiralaksanakul and Mahadevan 2005; Shin and Lee 2014), second-order reliability method (SORM) (Kiureghian et al. 1987; Lee et al. 2012), and MPP-based dimension reduction method (Lee et al. 2008, 2010; Kang et al. 2017; Jung et al. 2019). Recently, Imani et al. (2018, 2019) investigated general nonlinear state-space and data-poor environment problems with Bayesian method. Xie et al. (2017) proposed a linear discriminant analysis classification rule to investigate nonstationary data problem. To improve the computational efficiency of conventional RBDO, Chen et al. (1997) proposed the single loop single vector approach (SLSV), and Jeong and Park (2017) improved SLSV by proposing the single loop single vector conjugate gradient (SLSVCG) approach using the conjugate gradient at MPP of the previous cycles.

There are three major challenges in applying RBMDO to composite frames: (1) the number of design variables dramatically increases as the number of components in the composite frames increases since both cross-sections of the beams in the macro-scale and fiber winding angles in the micro-scale are considered as independent design variables in RBMDO. (2) When fiber winding angles are used as design variables directly, the convexity of the objective function is not guaranteed (Foldager et al. 1998; Duan et al. 2019a, b), which may lead to instability and inaccuracy in convergence during reliability analysis. (3) In practical applications, design guidelines or rules, referred to as manufacturing constraints, must be considered to reduce local failure risk in the composite structure (Bailie et al. 1997; Yan et al. 2017).

Consequently, the purpose of this paper is to propose an efficient RBMDO for composite frames under uncertainties in material properties and loading conditions. To enhance the stability of structural performance in a real operational environment, load uncertainties in both magnitude and direction are considered in RBMDO. The DMO approach for multi-scale optimization of laminated composites is adopted in RBMDO of composite frames to overcome the non-convexity and high non-linearity. Based on MCC scheme (Yang and Yi 2009; Meng et al. 2015), the SLSV-MCC approach which utilizes sensitivities at the current design point is proposed for more efficient RBMDO of composite frames with manufacturing constraints.

The rest of the paper is organized as follows. Review of RBDO related to the proposed method is presented in Sect. 2. The proposed SLSV-MCC is explained in Sect. 3. Concept and mathematical formulation of RBMDO are introduced along with DMDO in Sect. 4. Section 5 presents the parameterization of the DMO approach and sensitivity analysis for the proposed RBMDO. Explicit mathematical expressions for specific manufacturing constraints as well as two solution strategies are briefly described in Sect. 6. Numerical study with 2D and 3D composite frames is performed using RBMDO and DMDO in Sect. 7. Finally, Sect. 8 concludes the paper.

2 Review of reliability-based design optimization

2.1 Reliability-based design optimization

In comparison with deterministic design optimization, RBDO takes into account uncertainties for variables and parameters that may influence the structural response. In the present research, RBDO with random parameters and deterministic design variables can be mathematically formulated as

$$ {\displaystyle \begin{array}{c}\underset{\boldsymbol{d}}{\min }C\left(\boldsymbol{d}\right)\\ {} Subject\ to:\left\{\begin{array}{c}\mathit{\Pr}\left[{G}_l\left(\boldsymbol{d},\boldsymbol{P}\right)>0\right]\le {P}_{f_l}^{Tar}\ \left(l=1\cdots nc\right)\\ {}{\boldsymbol{d}}^{\boldsymbol{L}}\mathbf{\le}\boldsymbol{d}\mathbf{\le}{\boldsymbol{d}}^{\boldsymbol{U}}\end{array}\right.\end{array}} $$

(1)

where C(d) is the objective function; d is the deterministic design variable vector with the upper bounds d^U and lower bounds d^L, the design spaces of d are the macro-scale inner tube radius and micro-scale artificial material density in the two geometrical scales in this paper; P represents the random vector; Pr[∙] is the probability function; ${P}_{f_l}^{Tar}$ is the target probability of failure for the l-th constraint; nc is the number of the limit functions or probabilistic constraints; and G_l(d, P) is the l-th limit state function such that G_l(d, P) > 0 is defined as failure. The purpose of RBDO is to find the optimum that the probability of failure in each constraint has to be less than the target probability of failure. In (1), the probability of failure in reliability analysis can be calculated using a multi-dimensional integral as

$$ {P}_f\equiv \mathit{\Pr}\left[{G}_l\left(\boldsymbol{d},\boldsymbol{P}\right)>0\right]=\int \cdots {\int}_{G\left(\boldsymbol{d},\boldsymbol{P}\right)>0}{f}_{\boldsymbol{P}}\left(\boldsymbol{p}\right)d\mathbf{p} $$

(2)

where P_f is the probability of failure and f_P(p) is the joint probability density function (PDF) of random parameter P. The limit-state function is generally transformed from the original space (X-space) to the standard normal space (U-space) (Rosenblatt 1952) for easy integration. Then, the integration in (2) can be rewritten as

$$ {P}_f=\mathit{\Pr}\left[{G}_i\left(\boldsymbol{d},\boldsymbol{P}\right)>0\right]=\int \cdots {\int}_{g\left(\boldsymbol{u}\right)>0}{f}_{\boldsymbol{U}}\left(\boldsymbol{u}\right)d\mathbf{u} $$

(3)

where f_U(u) is the joint PDF of the standard normal variables U and g(u) is the limit-state function in U-space. For efficient computation of (3), FORM linearizes g(u) at u^∗, which is MPP in U-space obtained through the Rosenblatt transformation, as

$$ g\left(\boldsymbol{u}\right)\cong g\left({\boldsymbol{u}}^{\ast}\right)+\nabla {g}^T\left({\boldsymbol{u}}^{\ast}\right)\left(\boldsymbol{U}-{\boldsymbol{u}}^{\ast}\right) $$

(4)

where ∇g^T(u^∗) is the gradient of g(u) at u^∗ and T stands for transpose. u^∗ is obtained by solving

$$ {\displaystyle \begin{array}{c}\underset{\boldsymbol{u}}{\min}\left\Vert \boldsymbol{u}\right\Vert \\ {} Subject\ to:{g}_l\left(\boldsymbol{u}\right)=0\kern0.5em \left(l=1\cdots nc\right)\end{array}} $$

(5)

A reliability index β_l is defined as the distance from the origin to u^∗, that is,

$$ {\beta}_l=\left\Vert {\boldsymbol{u}}^{\ast}\right\Vert ={\left({{\boldsymbol{u}}^{\ast}}^T{\boldsymbol{u}}^{\ast}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} $$

(6)

FORM estimates the probability of failure using the reliability index as Φ(−β_l).

Using performance measure approach (PMA) (Youn et al. 2003), (5) can be rewritten to find MPP as

$$ {\displaystyle \begin{array}{c}\underset{\boldsymbol{u}}{\max }{g}_l\left(\boldsymbol{u}\right)\\ {} Subject\ to:\left\Vert \boldsymbol{u}\right\Vert ={\beta}_l^t=-{\Phi}^{-1}\left({P}_{f_l}^{Tar}\right)\end{array}} $$

(7)

where ${\beta}_l^t$ is the target reliability index obtained from the target probability of failure ${P}_{f_l}^{Tar}$. By applying the Lagrange multiplier method in (7), the general updating formula for MPP search is derived as

$$ {\boldsymbol{u}}^{\left(\varsigma +1\right)}={\beta}_l^t\frac{\nabla \mathrm{g}\left({\boldsymbol{u}}^{\left(\varsigma \right)}\right)}{\left\Vert \nabla \mathrm{g}\left({\boldsymbol{u}}^{\left(\varsigma \right)}\right)\right\Vert } $$

(8)

where ς is the iteration for MPP search.

2.2 Single loop single vector approach

To eliminate the inner loop, that is, the reliability analysis loop for MPP search, SLSV approximates MPP by utilizing the sensitivity of a performance function in the previous design (Chen et al. 1997), and thus, the MPP updating formula in (8) can be replaced in SLSV as

$$ {\displaystyle \begin{array}{c}{\boldsymbol{u}}^{\left(\varsigma \right)}={\boldsymbol{\mu}}_{\boldsymbol{p}}+{\beta}_l^t{\boldsymbol{\sigma}}_{\boldsymbol{p}}^{\boldsymbol{T}}{\boldsymbol{\alpha}}^{\left(\varsigma -1\right)}\\ {} where\ {\boldsymbol{\alpha}}^{\left(\varsigma -1\right)}=\frac{{\boldsymbol{\sigma}}_{\boldsymbol{p}}^{\boldsymbol{T}}\nabla \mathrm{g}\left({\boldsymbol{u}}^{\left(\varsigma -1\right)}\right)}{\left\Vert {\boldsymbol{\sigma}}_{\boldsymbol{p}}^{\boldsymbol{T}}\nabla \mathrm{g}\left({\boldsymbol{u}}^{\left(\varsigma -1\right)}\right)\right\Vert}\end{array}} $$

(9)

where μ_p and σ_p are the mean vector of p and the standard deviation of p, respectively. Since the approximated MPP is found using the gradient from the previous design, MPP search iteration is not necessary in SLSV. Therefore, SLSV significantly improves computational efficiency of RBDO by eliminating the inner loop. RBDO using SLSV is formulated as

$$ {\displaystyle \begin{array}{c}\underset{\boldsymbol{d}}{\min } Cost\left(\boldsymbol{d}\right)\\ {} Subject\ to:\left\{\begin{array}{c}{g}_l\left(\boldsymbol{d},{\boldsymbol{p}}_{l, MPP}^{(k)}\right)\le 0\ \left(l=1\cdots nc\right)\\ {}{\boldsymbol{p}}_{l, MPP}^{(k)}={\boldsymbol{\mu}}_{\boldsymbol{p}}+{\beta}_l^t{\boldsymbol{\sigma}}_{\boldsymbol{p}}^{\boldsymbol{T}}{\boldsymbol{\alpha}}_l^{\left(k-1\right)}\\ {}{\boldsymbol{\alpha}}_l^{\left(k-1\right)}={\left.\left[\frac{{\boldsymbol{\sigma}}_{\boldsymbol{p}}^{\boldsymbol{T}}\nabla {g}_l\left({\boldsymbol{u}}^{\left(k-1\right)}\right)}{\left\Vert {\boldsymbol{\sigma}}_{\boldsymbol{p}}^{\boldsymbol{T}}\nabla {g}_l\left({\boldsymbol{u}}^{\left(k-1\right)}\right)\right\Vert}\right]\right\rceil}_{\boldsymbol{p}={\boldsymbol{p}}_{l, MPP}^{\left(k-1\right)}}\\ {}{\boldsymbol{d}}^{\boldsymbol{L}}\mathbf{\le}\boldsymbol{d}\mathbf{\le}{\boldsymbol{d}}^{\boldsymbol{U}}\end{array}\right.\end{array}} $$

(10)

where ${\boldsymbol{p}}_{l, MPP}^{\left(k-1\right)}$ is the MPP at the (k-1)-th iteration for the l-th constraint and ${\boldsymbol{\alpha}}_l^{\left(k-1\right)}$ is the normalized gradient vector of the l-th constraint. Due to the MPP approximation, the number of function evaluations in SLSV may be similar with computational demands in deterministic optimization. However, the approximation may cause large error and divergence in case of highly nonlinear performance functions because exact MPP search is replaced with the approximation by gradient vector of previous MPP. Therefore, these difficulties need to be alleviated while maintaining the advantages of SLSV.

3 Improved SLSV for efficient RBDO

As discussed in Sect. 2.2, one of the weaknesses in the single loop RBDO using SLSV is inaccurate MPP approximation for highly nonlinear performance functions. To maintain efficiency of SLSV and overcome its inaccuracy, the modified SLSV based on MCC is proposed to solve concurrent multi-scale design optimization of composite frame where uncertain parameters such as material properties and loading conditions are considered, and the cross-sections of the beam at the macro-scale and the discrete fiber winding angles at the micro-scale are deterministic. Accordingly, since only random parameters exist in the design formulation, the gradient of a performance function with respect to the random parameter is not necessary for an optimizer since it is invariant during the optimization. SLSV is modified to utilize the sensitivity obtained in current design point without requiring additional function evaluations, and the concept of MCC is adopted to increase the accuracy of reliability analysis.

3.1 Improved SLSV approach based on MCC

To overcome the convergence problem in reliability analysis for highly nonlinear functions, Yang and Yi (2009) proposed the chaos control (CC) method. With considering the weakness of CC in convex or concave performance measure functions, Meng et al. (2015) proposed MCC by extending the iterative point of the CC method to the constraint boundary to investigate double-loop RBDO. Some new developments of MCC can be found in Keshtegar et al. (2017) and Yang et al. (2018) where the self-adaptive modified chaos control (SMCC) method and the accelerated stability transformation method (ASTM) of chaos control are proposed, respectively. In this research, the SLSV-MCC approach is proposed to fully exploit the potential of MCC and SLSV on accuracy and efficiency, respectively. In MCC, new direction of MPP is estimated as

$$ \overset{\sim }{\boldsymbol{n}}\left({\boldsymbol{u}}^{\varsigma +1}\right)={\boldsymbol{u}}^{\varsigma }+\lambda \boldsymbol{C}\left(f\left({\boldsymbol{u}}^{\varsigma}\right)-{\boldsymbol{u}}^{\varsigma}\right),0<\lambda <1 $$

(11-a)

$$ {\boldsymbol{u}}^{\varsigma +1}={\beta}_l^t\frac{\overset{\sim }{\boldsymbol{n}}\left({\boldsymbol{u}}^{\varsigma +1}\right)}{\left\Vert \begin{array}{c}\overset{\sim }{\boldsymbol{n}}\end{array}\left({\boldsymbol{u}}^{\varsigma +1}\right)\right\Vert } $$

(11-b)

where

$$ f\left({\boldsymbol{u}}^{\varsigma}\right)=-{\beta}_l^t\frac{\nabla_Ug\left(\boldsymbol{d},{\boldsymbol{u}}^{\varsigma}\right)}{\left\Vert {\nabla}_Ug\left(\boldsymbol{d},{\boldsymbol{u}}^{\varsigma}\right)\right\Vert } $$

(12)

where a stabilization factor λ is determined according to eigenvalues of the original system’s Jacobian matrix, and C is the involutory matrix with only one element in each row and size of n × n where n is the number of random variables. In this study, an identity matrix is selected for C, and λ is set to be 0.7 based on heuristically. Note that the superscript ς in (12) stands for the iteration in MPP search.

By adopting the concept of MCC with the stabilization factor λ in SLSV, the MPP updating formula in (10) can be rewritten in the proposed SLSV-MCC as

$$ {\boldsymbol{u}}^k={\boldsymbol{\mu}}_{\boldsymbol{p}}+{\beta}_t{\boldsymbol{\sigma}}^T\overset{\sim }{\boldsymbol{n}}\left({\boldsymbol{u}}^k\right) $$

(13)

where

$$ \overset{\sim }{\boldsymbol{n}}\left({\boldsymbol{u}}^k\right)={\boldsymbol{u}}^{\left(k-1\right)}+\lambda \boldsymbol{C}\left(f\left({\boldsymbol{u}}^k\right)-{\boldsymbol{u}}^{k-1}\right) $$

(14)

and

$$ f\left({\boldsymbol{u}}^k\right)=-{\beta}_t{\left[\frac{\nabla_Ug\left({\boldsymbol{d}}^k,{\boldsymbol{u}}^{k-1}\right)}{\left\Vert {\nabla}_Ug\left({\boldsymbol{d}}^k,{\boldsymbol{u}}^k-1\right)\right\Vert}\right]}_{\boldsymbol{u}={\boldsymbol{u}}_{MPP}^{\left(k-1\right)}} $$

(15)

Note that k is iteration for design optimization of SLSV-MCC. Since SLSV has a single loop for design optimization without inner loop for MPP search, deterministic design variable d is changed as the optimization proceed denoted as superscript. Hence, MPP is approximated in the SLSV-MCC using the gradient at the current MPP denoted as ${\left.{\nabla}_Ug\left({\boldsymbol{d}}^k,{\boldsymbol{u}}^{k-1}\right)\right|}_{\boldsymbol{u}={\boldsymbol{u}}_{MPP}^{\left(k-1\right)}}$ and the previous MPP vector denoted as u^k − 1.

Figure 1 illustrates differences between conventional SLSV and the proposed SLSV-MCC specialized for RBDO problems with random parameters only. There are two major differences compared with conventional SLSV: (1) utilization of gradient when deterministic design vector is d^k instead of d^k − 1 and (2) application of stabilization factor λ with MCC approach to prevent significant error on estimating MPP induced by high nonlinearity. In Fig. 1, k means the iteration number for single-loop optimization. Specifically, k-th MPP is approximated by the gradient obtained from the (k-1)-th iteration in conventional SLSV. However, in this research, the gradient obtained in the k-th iteration can be directly used since there is no random design variable. Meanwhile, to avoid oscillation in MPP search and increase accuracy, the stabilization factor used in MCC is adopted. Hence, the approximated MPP based on the previous MPP vector and gradient at the current MPP by SLSV is obtained as shown in Fig. 1b.

Fig. 1

Approximation of MPP at each design point: a conventional SLSV and b proposed SLSV-MCC

The advantage of using the gradient vector in k-th iteration rather than (k-1)-th iteration is the improvement of better approximation on MPP. However, the gradient of performance on current design point cannot be applied without further function evaluations if random design variables exist since sensitivity analysis is required at MPP.

3.2 Process of SLSV-MCC

The main difference between SLSV and SLSV-MCC is how to obtain a new MPP using gradient vectors as shown in green boxes of Fig. 2 which shows a detailed procedure for SLSV and SLSV-MCC. In SLSV, the new MPP is approximated by the previous information only, and in the proposed SLSV-MCC, sensitivity analysis with respect to random parameters at the current design point is performed in prior to approximate the new MPP by MCC. Notably, the number of function evaluations required in both algorithms is identical since there is no random variable.

Fig. 2

Flowchart of a SLSV and b proposed SLSV-MCC

4 Reliability-based multi-scale design optimization of composite frames

4.1 Concept of RBMDO

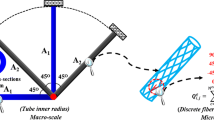
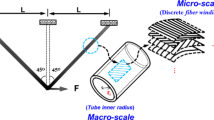
The concept of RBMDO under uncertainties related to material properties and loading conditions is shown in Fig. 3.

Fig. 3

Schematic diagram of RBMDO of composite frames (adapted from Duan et al. 2019a, b)

In the macroscopic level as shown in the left part of Fig. 3, load uncertainties in both magnitude and direction are considered in this study to consider a real operational environment. The inner radii of circular cross-sections (r_i as shown in Fig. 3) of beam components in the frame are considered as macroscopic deterministic design variables. The ground structure approach (Bendsøe and Sigmund 2013) is adopted where the tube is deleted from the original ground frame structure when its radius reaches the specified lower limit. Thus, both sizing and topology optimization of macroscopic structural configuration can be achieved.

In the microscopic level as shown in the right part of Fig. 3, composite material properties, i.e., longitudinal stiffness E₁₁, transverse modulus E₂₂, and shear modulus G₁₂, are considered to be random parameters since they have the strongest relation with structure compliance as pointed by Sohouli et al. (2018). The DMO approach, which will be explained in Sect. 5.1, is adopted in the microscopic level to realize selection of discrete fiber winding angles to overcome difficulty of non-convexity and high non-linearity when the fiber winding angles are directly recognized as design variables. Considering cost and process requirements, the most commonly used discrete fiber ply angles in industrial applications, i.e., [0^°, ∓45^°, 90^°], are adopted. Composite tubes are mostly manufactured by filament winding process (Martins et al. 2014). Mallick (2007) suggested that 0^° and 90^° fiber winding angles in the filament winding process should be implemented by 5^° and 85^° fiber winding angles, respectively. In this paper, assembly of [5^°, ∓45^°, 85^°] is considered as a set of candidate composite fiber winding angles. The fiber winding angle is assumed to be constant in a given ply. It should be noted that the joints connecting composite tubes can transfer moments, and are assumed to be infinitely stiff for the composite frames in this study.

4.2 Mathematical formulation for DMDO and RBMDO of composite frames

Mathematical formulations of DMDO and RBMDO for composite frames to minimize structural cost while satisfying structural compliance and manufacturing constraints are explained in this section. For both DMDO and RBMDO, manufacturing constraints (MC1 − MC6) which will be briefly explained in Sect. 6.1 are considered and it is assumed that damping is neglected. The convergence measure given in Stegmann and Lund (2005) and explained in Appendix A is utilized for the convergence criterion in this study. As shown in Fig. 3, the macro-scale inner tube radius (r_i) and micro-scale artificial material density (x_{i, j, c}) related to discrete fiber winding angles are set to be independent design variables to realize topology and stacking sequence optimization of the two geometrical scales simultaneously. Thus, DMDO for composite frames can be formulated as

$$ {\displaystyle \begin{array}{c}\underset{r_i}{\min}\mathrm{V}\left({r}_i\right)=\sum \limits_{i=1}^{{\mathrm{N}}^{\mathrm{tub}}}\uppi \left[{t_i^{\overset{\sim }{tot}}}^2+2{r}_i{t}_i^{\overset{\sim }{tot}}\right]{L}_i\\ {} Subject\ to:\left\{\begin{array}{c}\mathrm{C}\left(\boldsymbol{UK}\left({\boldsymbol{D}}_{\mathrm{n}}^{\mathrm{e}}\left({r}_i,{x}_{i,j,c}\right)\right)\boldsymbol{U}\right)\le {\mathrm{C}}^{Tar}\ \\ {}\mathrm{S}.\mathrm{T}.\boldsymbol{K}\left({\boldsymbol{D}}_{\mathrm{n}}^{\mathrm{e}}\left({r}_i,{x}_{i,j,c}\right)\right)\boldsymbol{U}=\boldsymbol{F}\\ {}{r}_i\in \left[{\mathrm{r}}_{\mathrm{min}},{\mathrm{r}}_{\mathrm{max}}\right]\\ {}{x}_{i,j,c}\in \left[0,1\right]\ \\ {}i=1,2,\dots, {\mathrm{N}}^{\mathrm{tub}},j=1,2,\dots, \raisebox{1ex}{${\mathrm{N}}^{\mathrm{lay}}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,c=1,2,\dots, {\mathrm{N}}^{\mathrm{can}}\\ {}\mathrm{Manufacturing}\ \mathrm{Constraints}\ \left( MC1- MC6\ \right)\end{array}\right.\end{array}} $$

(16)

where V is the structure cost of the composite frames; r_i is the inner radius of the composite tube; ${t}_i^{\overset{\sim }{tot}}$ and L_i are the current total thickness after punishment as presented in Sect. 6.2.2 and length of the i-th tube, respectively; x_{i, j, c} is the artificial density of DMO candidate materials whose subscripts i, j, and c denote the number of tubes, layers, and candidate materials, respectively; C and C^Tar denote the structure compliance and its target, respectively; U and K are the displacement vector and stiffness matrix; ${\boldsymbol{D}}_{\mathrm{n}}^{\mathrm{e}}$ is the element constitutive matrix for the n-th element; N^tub, N^lay, and N^cand denote the total number of tubes, layers, and candidate materials, respectively; the ground structure approach (Bendsøe and Sigmund 2013) is adopted to realize the topology optimization. The lower bound on the inner radius, r_min, is set to be 0.1 mm to avoid any possible singularity of stiffness matrix for the equilibrium function;

r_max is the upper bound of the inner radius. Because of symmetry constraints applied on the micro-scale design variables, only half of layers are considered as design variables, and thus $j=1,2,\dots, \raisebox{1ex}{${\mathrm{N}}^{\mathrm{lay}}$}\!\left/ \!\raisebox{-1ex}{$2.$}\right.$

Unlike (16), mathematical formulation of RBMDO for composite frames under uncertainties can be formulated as

$$ {\displaystyle \begin{array}{c}\ \underset{r_i}{\min}\mathrm{V}\left({r}_i\right)=\sum \limits_{i=1}^{{\mathrm{N}}^{\mathrm{tub}}}\uppi \left[{t_i^{\overset{\sim }{tot}}}^2+2{r}_i{t}_i^{\overset{\sim }{tot}}\right]{L}_i\\ {} Subject\ to:\left\{\begin{array}{c}\Pr \left[{G}_C\left({r}_i,{x}_{i,j,c},{\mathrm{R}}_{\mathrm{mat},\kern0.5em \upzeta},{\mathrm{R}}_{\mathrm{loa},\upeta}\right)\le 0\right]\le {P}_{fC}^{Tar}\ \\ {}\mathrm{S}.\mathrm{T}.\boldsymbol{K}\left({\boldsymbol{D}}_{\mathrm{n}}^{\mathrm{e}}\left({r}_i,{x}_{i,j,c},{\mathrm{R}}_{\mathrm{mat},\kern0.5em \upzeta}\right)\right)\boldsymbol{U}=\boldsymbol{F}\left({\mathrm{R}}_{\mathrm{loa},\upeta}\right)\\ {}{r}_i\in \left[{\mathrm{r}}_{\mathrm{min}},{\mathrm{r}}_{\mathrm{max}}\right]\\ {}{x}_{i,j,c}\in \left[0,1\right]\ \\ {}i=1,2,\dots, {\mathrm{N}}^{\mathrm{tub}},j=1,2,\dots, \raisebox{1ex}{${\mathrm{N}}^{\mathrm{lay}}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,c=1,2,\dots, {\mathrm{N}}^{\mathrm{can}}\\ {}\upzeta =1,2,\dots, {\mathrm{N}}^{{\mathrm{R}}_{\mathrm{mat}}},\upeta =1,2,\dots, {\mathrm{N}}^{{\mathrm{R}}_{\mathrm{loa}}}\\ {}\mathrm{Manufacturing}\ \mathrm{Constraints}\ \left( MC1- MC6\ \right)\end{array}\right.\end{array}} $$

(17)

where G_C(r_i, x_{i, j, c}, R_mat, ζ, R_{loa, η}) is the limit state function of structure compliance which is expressed as C(r_i, x_{i, j, c}, R_mat, ζ, R_{loa, η})-C^Tar; R_mat, ζ and R_{loa, η} represent the ζ-th and η-th random parameter of material properties and loading condition, respectively; ${\mathrm{N}}^{{\mathrm{R}}_{\mathrm{mat}}}$ and ${\mathrm{N}}^{{\mathrm{R}}_{\mathrm{loa}}}$ are the number of random parameters for material properties and loading conditions, respectively; ${P}_{fC}^{Tar}$ is the target probability of failure for the compliance constraint. For the numerical examples in Sect. 7, the same C^Tar is used for both DMDO and RBMDO.

Structural analysis of composite frames in (16) and (17) is performed using the modified beam finite element tool called BEam Cross Section Analysis Software (BECAS) by Duan et al. (2018, 2019a, b) to apply to composite frames combined with DMO. BECAS is an analysis tool of cross sections developed by Blasques and Lazarov (2012) for anisotropic and inhomogeneous beam sections with arbitrary geometry.

5 Discrete material optimization and sensitivity analysis

5.1 Fundamental DMO theory

Fundamental theory of DMO used to perform DMDO and RBMDO in (16) and (17), respectively, is briefly introduced in this section. The DMO approach is implemented in a finite element framework. Then, the element constitutive matrix per layer ${\boldsymbol{Q}}_{i,j}^e$ can be expressed as a weighted sum of the constitutive matrices Q_{i, j, c} of the candidate ply angles where the superscript e refers to “element”, and the subscripts i, j, and c refer to the i-th tube, j-th layer, and c-th candidate ply angles, respectively. In general, for multi-layer laminates, interpolation scheme can be implemented layer-wise for all layers in all elements. The constitutive relationship for the j-th layer can be expressed as a sum over the number of candidate ply angles N^cand as

$$ {\boldsymbol{Q}}_{i,j}^e=\sum \limits_{c=1}^{{\mathrm{N}}^{\mathrm{cand}}}{\omega}_{i,j,c}{\boldsymbol{Q}}_{i,j,c} $$

(18)

where ω_{i, j, c} is the weighting function with the bound of 0 and 1 since no stiffness or mass matrix can contribute more than the physical material properties, and negative contribution is physically meaningless. Generalized solid isotropic material with penalization (SIMP) for multi-material interpolation schemes (Hvejsel and Lund 2011) is used in this paper to push the weighting function to either 0 or 1 to obtain distinct material selection. Then, the weighting function can be expressed as

$$ {\omega}_{i,j,c}={\left({x}_{i,j,c}\right)}^p $$

(19)

where p is the penalty parameter and x_{i, j, c} is the artificial material density of candidate ply angles which satisfies

$$ \sum \limits_{c=1}^{{\mathrm{N}}^{\mathrm{cand}}}{x}_{i,j,c}=1 $$

(20)

5.2 Design sensitivity analysis

The global structure cost in (16) and (17) is a function of r_i only. Thus, its sensitivity with respect to r_i considering the winding layer thickness punitive strategy is given by

$$ \frac{\partial V\left({r}_i\right)}{\partial {r}_i}=2\pi {r}_i\frac{t_i^{tot}}{r_i^0}\left(\frac{t_i^{tot}}{r_i^0}+2\right){L}_i $$

(21)

where ${t}_i^{tot}$ is the initial total thickness of the i-th tube. The manufacturing constraints in this study are formulated as a series of linear inequalities or equalities. Thus, sensitivities of all manufacturing constraints are obtained explicitly without further derivation.

For sensitivity analysis of the structure compliance constraint, the semi-analytical method (SAM) (Cheng & Olhoff, 1993; Lund 1994; Blasques and Lazarov 2012) is adopted in this work instead of directly deriving analytical sensitivities due to its ease of derivation and implementation. SAM is computationally efficient and thus often used for sensitivity analysis of finite element models. This section only presents the compliance constraint sensitivity analysis with respect to deterministic micro-scale design variable x_{i, j, c}. Sensitivities of the compliance with respect to deterministic macro-scale design variable r_i can be easily obtained in a similar manner. Assume that applied static loads are design independent, then sensitivities of the structure compliance C in (16) and (17) with respect to x_{i, j, c} are given as

$$ \frac{\mathrm{\partial C}}{\partial {x}_{i,j,c}}=\sum \limits_{n=1}^{{\mathrm{N}}^{\mathrm{ele}}}\left(\frac{\partial {\boldsymbol{U}}_n^T}{\partial {x}_{i,j,c}}{\boldsymbol{K}}_n{\boldsymbol{U}}_n+{\boldsymbol{U}}_n^T\left(\frac{\partial {\boldsymbol{K}}_n}{\partial {x}_{i,j,c}}{\boldsymbol{U}}_n+{\boldsymbol{K}}_n\frac{\partial {\boldsymbol{U}}_n}{\partial {x}_{i,j,c}}\right)\right) $$

(22)

where U_n is the displacement vector of element n and K_n is the corresponding element stiffness matrix. Furthermore, using the equilibrium conditions K_nU_n = F, (22) can be simplified (see Bendsøe and Sigmund 2013) as

$$ \frac{\mathrm{\partial C}}{\partial {x}_{i,j,c}}=-\sum \limits_{n=1}^{{\mathrm{N}}^{\mathrm{ele}}}{\boldsymbol{U}}_n^T\frac{\partial {\boldsymbol{K}}_n}{\partial {x}_{i,j,c}}{\boldsymbol{U}}_n $$

(23)

It is possible to rewrite (23) using the element stiffness matrix given by ${\boldsymbol{K}}_n={\int}_{\Omega^{\mathrm{n}}}{\boldsymbol{B}}^{\mathrm{T}}{\boldsymbol{D}}_n\boldsymbol{B}\mathrm{d}{\Omega}^n$ where B is the strain-displacement matrix and Ωⁿ is the volume of the n-th finite element as

$$ \frac{\mathrm{\partial C}}{\partial {x}_{i,j,c}}=-\sum \limits_{n=1}^{{\mathrm{N}}^{\mathrm{ele}}}{\boldsymbol{U}}_n^T{\int}_{\varOmega^n}{\boldsymbol{B}}^{\mathrm{T}}\frac{\partial {\boldsymbol{D}}_n\left({x}_{i,j,c},{r}_i\right)}{\partial {x}_{i,j,c}}\boldsymbol{B}\mathrm{d}{\varOmega}^n\ {\boldsymbol{U}}_n $$

(24)

The SAM approach is computationally more efficient than the overall finite difference (OFD) method since factorization of the global stiffness matrix, which is the most time consuming part in the computation, is calculated once for N design variables whereas the stiffness matrix needs to be assembled and factored N + 1 times for N design variables in OFD. Then, $\frac{\partial {\boldsymbol{D}}_n\left({x}_{i,j,c},{r}_i\right)}{\partial {x}_{i,j,c}}$ are calculated using central difference as

$$ \frac{\partial {\boldsymbol{D}}_n\left({x}_{i,j,c},{r}_i\right)}{\partial {x}_{i,j,c}}\approx \frac{{\boldsymbol{D}}_n\left(\left({x}_{i,j,c}+{\Delta x}_{i,j,c},{r}_i\right)\right)-{\boldsymbol{D}}_n\left({x}_{i,j,c}-{\Delta x}_{i,j,c},{r}_i\right)}{2\Delta {x}_{i,j,c}} $$

(25)

where ∆x_{i, j, c} is a small perturbation of x_{i, j, c}.

The accuracy of SAM has been compared with the overall finite difference (OFD) method with a small perturbation of deterministic design variables. The sensitivities of compliance constraint with respect to deterministic design variables are not exactly obtained but the accuracy is desirable enough.

For MPP approximation in SLSV-MCC, it is necessary to perform sensitivity analysis of the compliance constraint with respect to random parameters (R_mat, ζ, R_{loa, η}), i.e., $\frac{\mathrm{\partial C}}{\partial {\mathrm{R}}_{\mathrm{mat},\kern0.5em \upzeta}}$ and $\frac{\mathrm{\partial C}}{\partial {\mathrm{R}}_{\mathrm{loa},\upeta}}$. In this study, they are calculated using the central difference method.

6 Typical manufacturing constraints and solution strategies

Manufacturing constraints in (16) and (17) labeled as MC1 − MC6 are briefly introduced in this section. Explicit linear equality and inequality equations for the manufacturing constraints are expressed in terms of x_{i, j, c} in DMO. For more detailed explanation on six typical manufacturing constraints of laminated fibrous composite structures, readers can refer to Yan et al. (2017) and Duan et al. (2019a, b).

6.1 Manufacturing constraints and numerical solution steps

The first manufacturing constraint is contiguity constraint with contiguity limit of CL ∈ N and is formulated as a linear inequality as

$$ {x}_{i,j,c}+\cdots +{x}_{i,j+\mathrm{CL},c}\le \mathrm{CL},\kern0.5em j+\mathrm{CL}\le {\mathrm{N}}^{\mathrm{lay}},\kern0.5em MC1 $$

(26)

For any i ∈ N^tub, j ∈ N^lay, and c ∈ N^cand, it should follow(Imani et al., 2018), and the loop should meet the dimension of j + CL ≤ N^lay. For example, if a composite tube has 20 layers, i.e., N^lay = 20, and every layer has four candidate materials, i.e., N^cand = 4, then, the total number of contiguity constraints should be calculated as (N^lay − CL) × N^cand = (20 − 1) × 4 = 76, when CL = 1.

The second manufacturing constraint is the 10% rule, which means that a minimum of 10% of plies of each candidate angle (5^°, ∓ 45^°, 85^°) is required. It is frequently adopted in engineering applications and expressed as

$$ \sum \limits_{j=1}^{{\mathrm{N}}^{\mathrm{lay}}}{x}_{i,j,c}\ge 0.1{\mathrm{N}}^{\mathrm{lay}}, MC2 $$

(27)

The third manufacturing constraint is balance constraint, which means that angle plies (those at any angle other than 5^∘ and 85^∘) should occur only in balanced pairs with the same number of +θ^∘and −θ^∘ plies. The parameterized linear equality constraint with respect to x_{i, j, c} can be expressed as

$$ \sum \limits_{j=1}^{{\mathrm{N}}^{\mathrm{lay}}}{x}_{i,j,+c}-\sum \limits_{j=1}^{{\mathrm{N}}^{\mathrm{lay}}}{x}_{i,j,-c}=0,\kern0.5em c\ne \left({5}^{\circ}\cup {85}^{\circ}\right),\kern0.5em MC3 $$

(28)

where x_{i, j, + c} and x_{i, j, − c} denote a positive and an accompanied negative angle, respectively.

The fourth manufacturing constraint is damage tolerance constraint, which means that 5^∘ ply along the axial direction cannot be selected in the inner and outer layers. This constraint can be expressed as the artificial density of 5^∘ candidate material in the outer surface which is set to be zero, and the same as in the inner surface, i.e., ${x}_{i,1,c}=0;{x}_{i,{\mathrm{N}}^{\mathrm{lay}},c}=0,\kern0.5em \left(c\in \left[{5}^{\circ}\right]\right)$, which are combined into one equality constraint as

$$ {x}_{i,1,c}+{x}_{i,{\mathrm{N}}^{\mathrm{lay}},c}=0,c\in \left[{5}^{\circ}\right],\kern0.5em MC4 $$

(29)

As an alternative strategy, MC4 constraint can be also realized through the micro-scale DMO material interpolation strategy which means that the candidate material set of the outer and inner surfaces does not contain 5^∘ candidate material.

The fifth manufacturing constraint is symmetry constraint, which means that the fiber winding sequence should be symmetric with respect to the mid-plane. In the case of the composite tube in this study, the mid-plane specifically refers to the average radius plane of the tube. Then, the symmetry constraint can be formulated as a linear equality as

$$ {x}_{i,j,c}={x}_{i,{N}^{lay}-j+1,c},\kern0.5em MC5 $$

(30)

The sixth manufacturing constraint (MC6) is the normalization constraint in (20) to keep physical meaning in the case of a volume constraint or eigenfrequency optimization.

A flowchart for numerical implementation of RBMDO with SLSV-MCC in design optimization of composite frames in this paper is shown in Fig. 4. The detailed process of SLSV-MCC to approximate the MPP can be referred to Fig. 2b.

Fig. 4

Flowchart of RBMDO with SLSV-MCC in design optimization of composite frames under structural compliance and manufacturing constraints

6.2 Solution strategies

6.2.1 Continuation strategy

In order to obtain discrete designs in the micro-scale, a continuation strategy for the penalization parameter p in (19) is adopted in this paper. The initial penalty parameter p is set to be 1. It has been shown by Hvejsel and Lund (2011) that p larger than 3 will not help too much to penalize intermediate values of design variables. Hence, p linearly increases in this study with slope of 0.5 in every ten iterations from 1 to 3.

6.2.2 Winding layer thickness punitive strategy

To realize topology optimization in the macro-structural scale and reduce the number of design variables, a linear punitive relationship between micro winding layer thickness and macro-scale tube radius is adopted as

$$ \tilde{t}_{i}=\frac{r_i}{r_0}\times {t}_0,i\in {N}^{Tub}\ if{r}_i<{r}_0 $$

(31)

where $\tilde{t}_{i}$ is the single layer thickness of the i-th tube after punishment, t₀ is the initial layer thickness, and r₀ is the initial inner radius of the tube. In (31), the layer thickness will change as the inner radius changes when r_i < r₀. Otherwise, the layer thickness will be kept as t₀. Based on the ground structure approach of topology optimization, small r_i means that the tube has lower contribution to stiffness of the whole structure, so that more material can be allocated in other tubes to improve the stiffness. For more discussion on this strategy, readers can refer to Duan et al. (2018, 2019a, b).

7 Numerical examples and discussions

In this section, two 2D and one 3D numerical examples are investigated to validate effectiveness of the proposed RBMDO with SLSV-MCC in design optimization of composite frames. In three numerical examples, DMDO and RBMDO with FORM and SLSV are performed as well for comparison. MCS is utilized to validate accuracy of these methods in two 2D examples.

The specific manufacturing constraints are considered in both DMDO and RBMDO. Considering practical engineering applications, it is assumed that each composite tube has the same number of layers, i.e., N^lay = 20, and the 20 layers have identical thickness of 0.1 mm in the initial design, i.e., ${t}_i^{tot}/{\mathrm{N}}^{\mathrm{lay}}=0.1\ \mathrm{mm}$. The initial value of the inner radius is r_init = 25 mm, and the upper and lower limits are r_max = 75 mm and r_min = 0.1 mm, respectively. The contiguity limit CL is set as CL = 2. The fiber candidate materials are carbon fiber-reinforced epoxy (CFRE) with orthotropic properties as shown in Table 1. Table 2 lists uncertainty information of three composite material properties, E₁₁, E₂₂, and G₁₂, and two loading conditions, magnitude and direction.

Table 1 Material properties of the uni-directional CFRE

Table 2 Uncertainty information in material properties and loading conditions

In three numerical examples, the target probability of failure is set as ${P}_{fC}^{Tar}=5\%$. The number of finite element analysis (FEA) evaluations is used as a measure of efficiency. MCS with 10⁵ samples is performed considering computational costs in engineering problems. In all methods, the same initial design variables and convergence criteria are used. Considering all the manufacturing constraints explained in Sect. 6.1, the number of design variables in each tube is 40 which contains 1 sizing design variable (r_i) and 39 candidate material density design variables (x_{i, j, c}). It should be noted that x_{i, j, c}=$\left(\raisebox{1ex}{${\mathrm{N}}^{\mathrm{lay}}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\times {\mathrm{N}}^{\mathrm{cand}}=10\times 4=40$ from the symmetry constraint, and the damage tolerance constraint (MC4) is realized through the micro-scale DMO material interpolation strategy. Thus, the actual number of x_{i, j, c} becomes 39.

There are seven types of constraints: one reliability compliance constraint related with random parameters and six manufacturing constraints that are independent of random parameters. The symmetry constraint (MC5) and damage tolerance constraint (MC4) are realized by design variable linking and DMO material interpolation without 5^∘ candidate material, respectively. Hence, there are total 47 manufacturing constraints in each tube: 32 contiguity constraints (MC1) since CL = 2, 4 10% rule constraints (MC2), 10 DMO normalization constraints (MC6), and 1 balance constraint (MC3). With the first 2D 4-beam composite frame as example, the total number of manufacturing constraints is 94. The detailed convergent results are presented in form of fiber winding angles and schematic diagram as in Fig. 7.

7.1 2D 4-beam composite frame

For the first example, a simple 2D 4-beam composite frame is introduced for RBMDO. Its initial geometric sizes, loading, and bounndary conditions for DMDO and RBMDO are shown in Fig. 5a and b. Four tubes are divided into two groups as labeled A₁ and A₂ in different colors. The total numbers of deterministic design variables, manufacturing constraints, compliance constraints, and random parameters are 80, 94, 1, and 5, respectively. The initial structural cost is V = 0.01759.

Fig. 5

Initial configuration of 2D 4-beam composite frame for a DMDO with deterministic load and b RBMDO with uncertainties in loading magnitude and direction, F = 10000; + and − denote positive and negative uncertain loading direction

For RBMDO, three reliability analysis methods—FORM, SLSV, and SLSV-MCC—are utilized for comparison. Table 5 presents detailed optimization results of DMDO and RBMDO with three methods, and optimized topology configurations of DMDO and RBMDO are shown in Fig. 6. From Table 3 and Fig. 6, four observations can be made:

• (1) The proposed SLSV-MCC shows much better efficiency and accuracy than FORM (6410 vs 1088) and SLSV (18.37% vs 1.78%).

• (2) The proposed SLSV-MCC shows similar efficiency and accuracy as SLSV (1024 vs 1088) and FORM (2.10% vs 1.78%).

• (3) Figure 6 shows that the optimized topology configurations can be categorized into two types: 2-beam structure in DMDO and SLSV and 4-beam structure in FORM and SLSV-MCC. The detailed values of r_i in all the optimum designs are presented in Table 4.

• (4) MPPs for loading direction in FORM and SLSV-MCC (− 4.8224° and − 5.2212°) show that horizontal loading is considered in RBMDO with FORM and SLSV-MCC yielding 4-beam optimal structure with thicker A₂ tubes and thinner A₁ tubes. On the other hand, SLSV with relatively small MPP value in loading direction (− 2.7659°) and DMDO with no consideration of horizontal loading yield 2-beam optimal structure where A₁ tubes reached the lower limit and thus are eliminated.

Fig. 6

Optimized topology configurations of DMDO and RBMDO for 4-beam example: a DMDO, b RBMDO with FORM, c RBMDO with SLSV, and d RBMDO with SLSV-MCC

Table 3 Comparison of optimization results obtained using DMDO and RBMDO

Table 4 Optimum designs of macroscopic radii in DMDO and RBMDO

Iteration histories of the cost and compliance constraint for DMDO and RBMDO are presented in Figs. 7 and 8 where histories of the initial 25 iterations are shown for clearer demonstration. In Fig. 8, compliance constraints of RBMDO are evaluated at MPP. As observed in the figures, RBMDO utilizes more structure cost to satify the compliance constraint with ${P}_{fC}^{Tar}=5\%$. The objective function of DMDO is reduced by 27.29% from the initial cost V = 0.01759, but the DMDO optimum will have higher risk of failure under uncertainties of material properties and loading conditions. All the optimum designs of DMDO and RBMDO well converged strictly satisfying the compliance constraint.

Fig. 7

Iteration history of the objective function for DMDO and RBMDO

Fig. 8

Iteration history of the compliance constraint for DMDO and RBMDO

Detailed optimal results of θ_{i, j} are presented in Table 5 which shows that all the micro-scale fiber winding angles strictly follow the specific manufacturing constraints. Figure 9 shows detailed manufacturing constraints on micro-scale design variables using A₂ tubes of SLSV-MCC. Because the outer and inner layers cannot contain 5^∘ candidate material, there is no 5^∘ ply placed in the outer layer of the laminate. Since CL = 2, more 5^∘ candidate fiber winding angles are selected because they are beneficial to improve axial stiffness of the structure. However, larger CL may lead to crack propagation in the laminate ultimately. So in most engineering applications, CL is set between 2 and 3, especially in aerospace engineering. Without the 10% rule constraint, 85^∘ fiber winding angles may not appear. The 10% rule effectively avoids a single fiber angle to dominate excessively to make the laminate more robust in the sense that they are less susceptible to weaknesses associated with highly orthotropic laminates.

Table 5 Optimum designs of microscopic fiber winding angles for DMDO and RBMDO

Fig. 9

Detailed manufacturing constraints in A₂ tubes of SLSV-MCC

7.2 2D 14-beam composite frame

To further verify capability of the proposed SLSV-MCC, a 2D 14-beam composite frame is investigated. Its initial geometric sizes, loading, and bounndary conditions for DMDO and RBMDO are shown in Fig. 10a and b, respectively. The total numbers of deterministic design variables, manufacturing constraints, compliance constraints, and random parameters are 560, 658, 1, and 5, respectively, with the initial structure cost of V = 0.05127.

Fig. 10

Initial configuration of 2D 14-beam composite frame for a DMDO with deterministic load. b RBMDO with uncertainties in loading magnitude and direction, F = 10000

Table 6 presents detailed optimization results of DMDO and RBMDO with three methods, and optimized topology configurations of DMDO and RBMDO are shown in Fig. 11. For convenience of discussion, the optimized tubes are divided into three groups which are labeled with dashed line in green (1st-3rd tubes), blue (4th, 6th, 7th, 10th, 12nd, 13rd tubes), and red (8th, 9th, 11th, 14th tubes), respectively.

Table 6 Comparison of optimization results obtained using DMDO and RBMDO

Fig. 11

Optimized topology configurations of DMDO and RBMDO for 14-beam example: a DMDO, b RBMDO with FORM, c RBMDO with SLSV, d RBMDO with SLSV-MCC

Similarly with Example 1,

• (1) FEA calls of SLSV-MCC is 808, which is much less than FORM (# of FEA calls = 9280) with saving the computational cost about 91.28% while maintaining its accuracy since the relative error compared with MCS is 2.15%.

• (2) Compared with SLSV, SLSV-MCC is more accurate and even more efficient since it has less number of design iterations.

• (3) Figure 11 shows that the optimized topology configurations are identical for DMDO and RBMDO. However, their optimal designs are quite different as can be seen from Table 7. The 5th tube has reached the lower limit for all the approaches. To satisfy the reliability constraint, the optimized radii of RBMDO are thicker than those of DMDO.

Table 7 Optimum designs of macroscopic radii in DMDO and RBMDO

Iteration histories of the cost and compliance constraint for DMDO and RBMDO are presented in Figs. 12 and 13 where histories of the initial 50 iterations are shown for clearer demonstration. From Figs. 12 and 13 and Table 6, it can be seen that DMDO, FORM, SLSV, and SLSV-MCC reduced the structural cost by 64.87%, 53.15%, 53.85%, and 53.40%, respectively. Figure 13 also shows that all the optimum designs of DMDO and RBMDO well converged while strictly satisfying the compliance constraint. Detailed optimal results of θ_{i, j} are presented in Table 8 which shows that all the micro-scale fiber winding angles strictly follow the specific manufacturing constraints. It should be pointed out that combination of winding sequences is limited due to the layer number limit and contiguity limit.

Fig. 12

Iteration history of the objective function for DMDO and RBMDO

Fig. 13

Iteration history of the compliance constraint for DMDO and RBMDO

Table 8 Optimum designs of microscopic fiber winding angles for DMDO and RBMDO

7.3 Spatial 120-beam composite frame

Multi-scale design optimization of a spatial 120-beam composite is introduced for the last example. Its boundary conditions and geometric sizes are modeled according to Huu et al. (2018) and are categorized into seven groups in different colors as shown in Fig. 14. The total number of deterministic design variables, manufacturing constraints, and compliance constraints are 280, 329, and 1, respectively, with the initial structure cost of V = 2.11494. The number of random parameters is 6: 3 random material properties, 1 loading magnitude, and 2 loading directions. In this example, comparison between DMDO and SLSV-MCC is performed.

Fig. 14

Initial configuration of spatial 120-beam composite frame for DMDO and RBMDO: a the top view of 120-beam composite frame, b the side view of 120-beam composite frame for DMDO with deterministic load, and c uncertainty in loading magnitude and directions (θ₁, θ₂), F₁ = 10,000

Detailed optimization results and configurations of DMDO and RBMDO with SLSV-MCC are shown in Table 9 and Fig. 15, respectively. Table 9 shows that very accurate optimization result is obtained using RBMDO with SLSV-MCC, and MPP value of θ₁ is much larger than that of θ₂. This is reasonable because the structure is rotationally symmetrical, and thus, uncertainty of θ₂ will not affect the structural failure significantly. Optimal designs of DMDO and RBDMO with SLSV-MCC are presented in Table 10. The structural cost of SLSV-MCC is about 19.21% higher than that of DMDO. The optimal radii of group 1 for DMDO are much larger than those from SLSV-MCC and other groups. The optimal structures use more material in group 2 and group 5 in ring-in direction and group 4 and group 6 in radial direction.

Table 9 Comparison of optimization results between DMDO and RBMDO with SLSV-MCC

Fig. 15

Optimized topology configurations of DMDO and RBMDO with SLSV-MCC for 120-beam example: a DMDO and b RBMDO with SLSV-MCC

Table 10 Optimum designs of DMDO and RBMDO with SLSV-MCC

Iteration histories of the cost and compliance constraint for DMDO and RBMDO with SLSV-MCC are presented in Figs. 16 and 17. As observed in Fig. 16 and Table 9, the optimized structural cost of DMDO and SLSV-MCC are reduced by 38.48% and 26.62%, respectively. Figures also show that both DMDO and SLSV-MCC are well converged and strictly follow the compliance constraint.

Fig. 16

Iteration history of the objective function for DMDO and SLSV-MCC

Fig. 17

Iteration history of the compliance constraint for DMDO and SLSV-MCC

8 Conclusion

This paper proposes an efficient reliability analysis methodology, SLSV-MCC, to realize RBMDO of composite frames with considering uncertainties of material properties and loading conditions. Efficiency and accuracy of SLSV-MCC are compared with FORM and SLSV approaches, and the MCS method is utilized to validate accuracy of these approaches. Planar and spatial numerical examples show effectiveness of the proposed SLSV-MCC for structural optimization to minimizing the cost and subjecting to compliance constraint compared with FORM and SLSV. It is shown from the numerical examples that the optimized structure configurations between DMDO and RBMDO are indeed different. It is also shown that specific manufacturing constraints are strictly kept in all the numerical examples.

Appendix A: Evaluation of convergence

The convergence measure given in Stegmann and Lund (2005) is adopted to describe whether the optimization has converged to a satisfactory result, i.e., a single candidate material has been chosen in a specified element and all other materials have been discarded. For each layer, the following inequality is evaluated as

$$ {\omega}_{i,j,c}\ge \upvarepsilon \sqrt{\omega_{i,j,1}^2+{\omega}_{i,j,2}^2+\cdots +{\omega}_{i,j,{\mathrm{N}}^{\mathrm{cand}}}^2} $$

(A-1)

where ε is the tolerance, typically, ε ∈ [0.95~0.99]. If the inequality in (A-1) is satisfied for any ω_{i, j, c} in the j-th layer, then the layer is flagged as converged. The convergence assessment criterion H_ε is defined as the ratio between the number of converged layers ${N}_c^{l, tot}$ and the total number of layers N^{l, tot}. N^lay is the number of layers in each tube, and it is assumed that each tube has the same number of layers in the paper. N^tub is the number of tubes in the frame structure. Thus, N^{l, tot} can be expressed as the number of tubes multiplied by the number of layers in a tube, that is, N^{l, tot} = N^tub ∙ N^lay. Then, the convergence assessment H_ε can be expressed as

$$ {H}_{\varepsilon }=\frac{N_c^{l, tot}}{N^{l, tot}} $$

(A-2)

If the tolerance is 0.95 and the optimization is fully converged, i.e., H_{ε = 0.95} = 1, all layers have a single weight factor that contributes more than 95% to the Euclidian norm of the weight factors. More discussion about convergence criteria can be found in the references (Xu et al. 2019; Duan et al. 2015).