1 Introduction

Since the seminal work of Bendsøe and Kikuchi (1988), a huge amount of contributions have allowed to establish topology optimization as a practical design tool. The method looks for the optimal material distribution within a design space by minimizing an objective function subject to a set of design constraints. The concept is developed in many approaches, see, e.g., Sigmund and Maute (2013) and Deaton and Grandhi (2014), where density-based stands out due to the easy adaptation to finite element codes. The process is iterative and illustrates the metamorphosis of the design space, a gradual change in each iteration that converts the design space into an innovative, complex, and high-performance structure. However, mainly due to technological limitations, the optimized structure sometimes is solely a conceptual design idea since the solution can not be manufactured. For this reason, manufacturing constraints became one of the important topics in topology optimization, since they impose the appearance of manufacturable designs and reduce the need of postprocessing. Perhaps, the most important manufacturing constraint is the minimum size because it is related to the resolution allowed by the fabrication process. The reader is referred to the work of Lazarov et al. (2016) for a deeper insight on the subject.

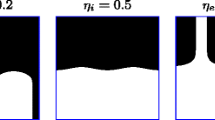
Length scale control could be owed not only to manufacturing limitations, but also to include indirect desired properties on the design. For example, the maximum size of the solid phase could be a tool for designers to deal with overheating-related problems in additive manufacturing by restricting the size of bulky parts Thompson et al. (2016), or to improve the performance of structures under local damage by diversification of the load path with the appearance of redundant members Jansen et al. (2014). In addition, the maximum size could be required for aesthetic reasons due to its ability to produce surprising changes in the material distribution, as exemplified in Fig. 1. Applications of the maximum size in fluid flows are mentioned in the pioneering work of Guest (2009a), where the reader is referred for a more complete discussion. In his work, the maximum size control is enforced by local constraints which restrict the amount of material in the neighborhood of each point in the design domain. The method proves to be robust in the context of structural and fluid topology optimization, but it demands a big computational cost due to the large number of constraints that are introduced in the optimization problem. Then Zhang et al. (2014) reduce the amount of constraints by collecting those that belong to the structural skeleton. The main drawback is the neglected sensitivity of the skeleton which makes the solution more likely to fall into a local optima. Later, Lazarov and Wang (2017) present two methods to impose maximum size. The first one applies band-pass filters on the frequency domain after a Fourier transform. The method produces manufacturable black and white designs but the maximum size is loosely controlled. The second method is based on morphological operators and provides more control over the geometry. Their method shows a satisfactory performance for compliance minimization and the compliant mechanism design. However, Lazarov and Wang (2017) encounter some geometrical difficulties in the optimized design: a large number of hollow circles in the structure and a wavy pattern in the vicinity of the connections between solid structural elements, which can lead to a lost of manufacturability and a reduction of performance. More recently. Carstensen and Guest (2018) propose a projection-based method to control the maximum length scale. The method is based on the multiple phase projection strategy (Guest 2009b), but they reduce the number of design variables using weighting functions. They report multiple 2D benchmark problems satisfying the desired length scale. The disadvantage of the multiple phase projection method is that it uses a series of weighting and projection functions that make the method highly non-linear.

Fig. 1
figure 1

Christmas tree-like domain for compliance minimization. In a solution with minimum size control. In b the maximum size of the solid phase is included. The volume fraction is set to 0.8 in both cases

Full size image

Aggregation functions are well known in the field of stress constraints in topology optimization. They were initially introduced by Yang and Chen (1996) to reduce the size of highly constrained problems. Among the popular functions in topology optimization are the KS (Kreisselmeier – Steinhauser) function, p-norm, and p-mean (see for instance, Yang and Chen 1996; Duysinx and Sigmund 1998). These are smooth and differentiable approximations of the max(⋅) function to resort to gradient-based optimizers. Unfortunately, the smooth approximation brings numerical issues, e.g., the non-linearity of the method increases as the function approaches the maximum value, which is essential to capture the critical constraints. In the last decade, a large amount of contributions have addressed this issue. Among others, we can cite the work of París et al. (2010). They proposed to aggregate the constraints by groups; this increases the number of global constraints but reduces the non-linearity of the problem. Despite the known drawbacks, the successful idea of the aggregation is still applied in the field since it is an efficient way to solve large and highly constrained problems in a reasonable amount of time.

However, to the best of our knowledge, aggregation functions have not been successfully applied in the maximum size field. Among the few works that can be found in the literature, we can cite Guest (2009a) and Wu et al. (2017, 2018). In the pioneering work, Guest (2009a) highlights the need of using aggregation functions to reduce the computation time. Motivated by this fact, Guest mentions that barrier functions were tested but results were not encouraging enough to be reported. More recently, Wu et al. (2017, 2018) use p-mean function to aggregate a local volume constraint and produce sparse structures that mimic bone-like porous structures. Their method is related to the length scale problem presented by Guest (2009a) but differs from an exact formulation of the maximum size. This will be discussed with more details later.

In this work, we take over the maximum size formulation proposed by Guest (2009a) to perform an efficient aggregation of the local constraints. The challenge of this task is exposed in detail as well as the proposed strategy to address it. In addition, we introduce another test region to limit the amount of material which reduces the hollow circles introduced by the constraint. The developments are validated on 2D domains in classical linear problems such as compliance minimization, heat transfer problem, and the compliant mechanism design.

The paper is organized as follows. In Section 2, we describe the formulation of the topology optimization problems addressed in this work. In Section 3, we recall the Guest’s formulation to impose the maximum size. Then we introduce a new test region to count the amount of material. Section 4 presents the aggregation functions used in this work, the difficulties of aggregating the maximum size constraints, and the proposed strategy. Section 5 gathers the results and discussions, Section 6 the final conclusions of this work, and Section 7 provides some indications to facilitate the replication of results.

2 Problem formulation and definition of test cases

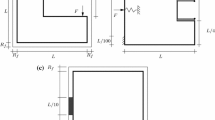
The proposed method to introduce maximum size control in topology optimization is tested on usual problems of literature, i.e., the compliance minimization, the minimum thermal compliance, and the compliant mechanism design. In each problem, we solve some of the well-known test cases, i.e., the MBB beam, the squared heat sink, and the compliant force inverter, which are depicted in Fig. 2. These domains are discretized using four-node quadrilateral elements and they are extended on the boundaries to facilitate the treatment of the filter (Sigmund 2007). The extension is represented with white squares outside the design domain in Fig. 2. Here, we define Ψ as the set of indexes that contains all the element numbers in the design domain including those on the extended domain, while Φ contains only the indexes whose elements belong to the optimizable design space, thus Φ ⊂ Ψ as shown in Fig. 2.

Fig. 2
figure 2

Design domains included in this work to solve a the compliance minimization problem, b the heat transfer problem, and c the compliant mechanism. In this work, L = 1

Full size image

The methods presented in this work were implemented in the free PolyTop MATLAB code (Talischi et al. 2012), which is slightly modified to solve the heat transfer problem and the compliant mechanism design, as well as to include the Method of Moving Asymptotes as solver (Svanberg 1987). The MATLAB environment is well known in the topology optimization community because of the free access codes that are available, see, e.g., Sigmund (2001), Andreassen et al. (2011), and Talischi et al. (2012). It is also known that the best performance is obtained with loop vectorization and memory preallocation. Thus, throughout the article, the equations will be presented in such a way to allow an efficient use of the software. In addition with this paper, a sample MATLAB implementation of the maximum size constraint is provided for use with PolyTop (Talischi et al. 2012) but it can be adapted to other topology optimization scripts.

Since the aforementioned problems share a common basis, we present a generic formulation of the optimization problem given as:

$$ \begin{array}{@{}rcl@{}} &{\min_{\rho}} &\quad \boldsymbol{t}^{\intercal} \boldsymbol{u} \end{array} $$
(1a)
$$ \begin{array}{@{}rcl@{}} &{s.t.:} &\quad \mathbf{K}(\boldsymbol{\rho}) \boldsymbol{u}=\boldsymbol{f} \end{array} $$
(1b)
$$ \begin{array}{@{}rcl@{}} &&\quad\bar{ \boldsymbol{\rho}}^{\intercal} \boldsymbol{v} \leq V^{*} \end{array} $$
(1c)
$$ \begin{array}{@{}rcl@{}} &&\quad G_{\text{ms}} \leq 0 \end{array} $$
(1d)
$$ \begin{array}{@{}rcl@{}} &&\quad 0 \leq {\rho_{e}} \leq1 \ \hspace{3mm} , \hspace{3mm} \forall e \in {\Phi} \end{array} $$
(1e)
$$ \begin{array}{@{}rcl@{}} &&\quad{\rho_{i}} = 0 \hspace{11mm} , \hspace{3mm} \forall i \in {\Psi} \text{and} i \notin {\Phi} \end{array} $$
(1f)

The objective is the linear function \(\boldsymbol {t}^{\intercal }\boldsymbol {u}\) defined in (1a). For compliance minimization and heat conduction problems, t represents the input force/heat flux over the domain, i.e., is equal to the array f. For the compliant mechanism, t is an array that contains value 1 at the output degree of freedom and 0 otherwise. The array u contains the nodal displacements/temperatures which are obtained after solving the state equation (1b).

The design variables on the extended design domain are set to 0 in (1f). For other design variables, we use a three-field scheme (see Sigmund and Maute 2013) which utilizes the design field ρ, a filtered field \(\tilde {\boldsymbol {\rho }}\), and a physical field \(\bar {\boldsymbol {\rho }}\). The filtered field \(\tilde {\boldsymbol {\rho }}\), used to ensure mesh independency and checkerboard-free solutions, is computed as:

$$ \tilde{\boldsymbol{\rho}} = \mathbf{D}_{\mathrm{I}}\boldsymbol{\rho} , $$
(2)

where DI is the matrix that contains the linear weights of the filter. Its components are defined as:

$$ \mathrm{D}_{\mathrm{I}_(i,j)} = \left\{\begin{array}{ll} \frac{\displaystyle v_{j} w_{i,j}}{\sum\limits_{k\in {\Psi}} v_{k} w_{i,k}} & , \text{if} i \in {\Phi} \vspace{5mm} \\ 0 & , \mathrm{otherwise.} \end{array}\right. $$
(3)
$$ w_{(i,j)} = \left\{\begin{array}{ll} 1-\frac{\displaystyle 2 \Vert x_{i}-x_{j} \Vert} {\displaystyle d_{\text{fil}}} & , \text{if} 2 \Vert x_{i}-x_{j} \Vert \leq d_{\text{fil}} \vspace{3mm} \\ 0 & , \mathrm{otherwise.} \end{array}\right. $$
(4)

Here, wi, j represents the linear weight of the variable j in the filtering of variable i. dfil is the diameter of the filtering region. xi and xj are the locations at the centroid of the elements i and j, respectively, where i and j ∈Ψ. The condition applied in (3) avoids the computation of the filter on the passive elements. Without this treatment, the DI matrix would be identical to the P matrix presented by Talischi et al. (2012).

The physical field \(\bar {\boldsymbol {\rho }}\) is obtained from the filtered field \(\tilde {\boldsymbol {\rho }}\) using a smoothed Heaviside projection defined as:

$$ {\bar{\rho}}_{i} = \frac {{\tanh}(\beta \mu)+{\tanh}(\beta (\tilde{\rho}_{i}-\mu))} {{\tanh}(\beta \mu)+{\tanh}(\beta ( 1 -\mu))} \quad , \quad \forall i \in {\Psi} , $$
(5)

where β and μ control the steepness and the threshold of the projection, respectively. The projection (5) is suited for the robust design approach (Wang et al. 2011). However, here, it is used because it offers smoother convergence than the classic projection proposed by Guest et al. (2004).

The aim of the projection (5) in this work is to reduce the amount of gray elements. This in turns promotes the minimum size of the solid phase. However, as shown by (Wang et al. 2011), simple projection strategies do not ensure minimum length scale control since they do not prevent small local features as the well-known one-node connected hinges. Therefore, results in this work are not exempt from small structural details that do not fulfil minimum size. Knowing this, in this work we call dmin the theoretical minimum size obtained by the smoothed Heaviside projection. As shown by Wang et al. (2011), dmin depends on the filter diameter dfil and on the threshold parameter μ. In this work, we use μ = 0.25, therefore, dmin = 0.5dfil (for further details, see Wang et al. 2011; Qian and Sigmund 2013).

The global stiffness/conductivity matrix K is assembled from the local stiffness matrices defined as ki = Eik0. Here, k0 denotes the element stiffness matrix of base material. Ei is the material stiffness/conductivity obtained by using the modified SIMP (Sigmund 2007) given as:

$$ E_{i} = E_{{\min}}+\bar{\rho}^{\eta}_{i}(E_{0}-E_{{\min}}) , $$
(6)

where η is the penalization of the material interpolation law. For the three problems, the parameters η and β are defined by a continuation method. This is a common practice in topology optimization as it is known to help avoid convergence to undesirable local minima (see for instance, Sigmund and Maute 2013; Rojas-Labanda and Stolpe 2015). E0 is the stiffness/conductivity of the solid phase equal to 1 in all three problems. Emin is a small number to avoid the numerical singularity issue in the finite element analysis. For the compliance minimization and force inverter problems, Emin = 10− 6, while for the heat sink Emin = 10− 3.

The volume constraint is in (1c), where V∗ is the upper bound of the constraint and v the array that gathers the volume of all the elements. The maximum size is imposed through the global constraint Gms in (1d).

3 Local maximum size constraint

The method to restrict the amount of material and impose a maximum size was originally proposed by Guest (2009a). As mentioned before, the method showed to be robust in the context of structural and fluid topology optimization and, therefore, it is selected as the fundamental formulation in this work. The local constraint is defined as:

$$ g_{e} = \varepsilon - \frac {\displaystyle\sum\limits_{k\in{\Omega}_{e}} v_{k} (1-\bar{\rho})^{\eta}} {\displaystyle\sum\limits_{k\in{\Omega}_{e}} v_{k}} \leq 0 , \forall e \in {\Phi} , $$
(7)

where Ωe is the maximum size region of the element e and ε is a small positive number used for relaxing the problem. In this work, we use ε = 0.05. The most usual approach in literature is to define the test region Ωe as a circle around the element e. This is shown in Fig. 3a and is defined as:

$$ {\Omega}_{e}^{(\mathrm{c})} = \{ x_{i} \vert 2 \Vert x_{e} - x_{i} \Vert \leq d_{{\max}} , \forall i \in {\Psi} \} , $$
(8)

where dmax represents the maximum size defined by the user.

Fig. 3
figure 3

Circular (a) and annular (b) test regions to count the amount of material

Full size image

The constraint (7) restricts the amount of material around the element e by imposing, at least, the amount ε of void in Ωe. Since gray elements contribute to the void counting, they must be penalized. To this end, we use the same SIMP exponent η as suggested by Guest (2009a). Equation (7) must be evaluated at every design point; therefore, it is convenient to vectorize the computation of the local constraints as follows:

$$ \boldsymbol{g} = \varepsilon-\mathbf{D}_{\text{II}} \boldsymbol{\delta} \leq 0 , $$
(9)

where DII is the matrix that stores the maximum size neighborhoods and δ the array containing the measure of void. These entities are defined in (10) and (12), respectively. In the Appendix, the DII matrix is assembled in lines 36–44 and δ is computed in line 26.

$$ \mathrm{D_{II}}_{(e,i)} = \frac{v_{i} l_{e,i}}{{\sum}_{k\in{\Psi}}v_{k} l_{e,k}} , \forall e \in {\Phi} \text{and} i \in {\Psi} $$
(10)
$$ l_{e,i}= \left\{\begin{array}{ll} 1 & , \text{if} x_{i} \in {\Omega}_{e} \vspace{3mm} \\ 0 & , \text{otherwise}. \end{array}\right. $$
(11)
$$ \delta_{i} = (1-\bar{\rho}_{i})^{\eta} $$
(12)

3.1 New test region for maximum size

The maximum size constraint splits the bulky material during the optimization process by introducing void in each test region Ωi. In 2D, void introduced by the constraint can form circular or channel-shaped cavities. Designers may prioritize a cavity type depending on the manufacturing process. For instance, if the purpose of the constraint is to produce bar-like structures, then channel-shaped cavities must be prioritized over circular ones.

We have noticed in 2D that most circular cavities tend to be placed in the connection of bars. To illustrate this, consider Fig. 4a which shows the connection of two bars during the optimization process. The red circle shows the neighborhood of a potentially violated constraint. There, to satisfy the constraint and keep the connection at the same time, two possibilities are presented: either introduce a hole as in Fig. 4b or remove the edges as in Fig. 4c. Thus, aiming to reduce the introduction of small circular holes, we propose to take the internal zone out of the analysis, as Fig. 4d shows. We consider as inner zone the minimum size region imposed through the Heaviside projection (see Fig. 3b). Therefore, the proposed test region is defined as:

$$ \begin{array}{@{}rcl@{}} {\Omega}_{e}^{(\mathrm{r})} &= & \left\{ x_{i} \vert \right. \Vert x_{e} - x_{i} \Vert \leq \tfrac{d_{{\max}}}{2} \quad \text{and} \\ && \left. \hspace{7.9mm} \Vert x_{e} - x_{i} \Vert > \tfrac{{d}_{{\min}}}{2}, \forall e \in {\Phi} \text{and} i \in {\Psi} \right\}. \end{array} $$
(13)
Fig. 4
figure 4

Representation of a connection with maximum size constraints during the optimization process. In a the circular test region. In b and c, two possibilities to satisfy the maximum size constraint and keep the material connectivity. In d, the inner zone is removed from the circular test region to avoid the introduction of a hole

Full size image

Even if a circular hole is introduced in the middle of the connection when using the annular region, the cavity is expected to be of size dmin, so that void elements can pass into the annular zone through the inner diameter of the ring.

It is important to note that the annular test region does not affect the maximum size imposed by the user. The only difference with the circular region is that void elements are forced to be placed in the outer ring.

4 Aggregation of local constraints

4.1 Aggregation functions

Two aggregation functions are tested in the context of maximum size, p-mean and p-norm. These are defined as follows:

$$ P_{\mathrm{m}} = \left( \frac{1}{N} \displaystyle{\sum\limits_{e \in {\Phi}}(s_{e})^{p}} \right)^{\frac{1}{p}} , $$
(14)
$$ P_{\mathrm{n}} = \left( \displaystyle{{\sum}_{e \in {\Phi}}(s_{e})^{p}} \right)^{\frac{1}{p}} , $$
(15)

where Pm and Pn are the p-mean and p-norm functions, respectively. N is the total amount of design variables in Φ, p is the exponent that controls the accuracy of the aggregation, and se is the quantity of interest (QoI) that is being aggregated.

For positive values of se and large p exponents, it is known that both aggregation functions converge to the maximum value of the data set (see for instance, Duysinx and Sigmund 1998). It is widely known also that the main difference between these functions is that p-norm overestimates the maximum value while p-mean underestimates it. However, within the context of topology optimization and to the best of our knowledge, it has not been mentioned that these functions are also highly dependent on the data distribution. This can be clearly seen by comparing the aggregation curves of two sets of data, such as those shown in Fig. 5a. The aggregation of those sets using p-mean and p-norm is shown in Fig. 5b. For this particular case, it is interesting to note that p-norm, with p > 12, provides a better approximation of the maximum when data is located mostly at low values (set 1). But the opposite occurs when data is located at higher values. In this configuration (set 2), p-mean provides a better approximation of the maximum, even for low p exponents. This also shows that p-mean is less sensitive to the exponent p when data is placed at higher values, since the approximation of p-mean is slightly improved with the increment of p.

Fig. 5
figure 5

In a are the histograms of two randomly produced sets of data with values between 0 and 1. In b are the aggregation curves using p-mean and p-norm. In c is the aggregation of the set 2 with different number of variables. In d is the sensitivity information using p-norm for data set 2. In the latter, sensitivities are incrementally sorted and normalized

Full size image

Another interesting observation is their dependency to the amount of data. As Fig. 5c shows, the greater the amount of data, the lower the performance of the p-norm function. This does not apply for p-mean, since it has the scaling factor N− 1 that places the function around the arithmetic mean, regardless the quantity of data. The same situation arises when comparing the KS and the lower bound KS (see for instance Verbart et al. 2017, for definitions). The latter has the scaling factor N− 1 and therefore it is less sensitive to the amount of aggregated data.

The main attractiveness of these aggregation functions is that they provide sensitivity information, which is essential for gradient-based optimizers. Unfortunately, as shown in Fig. 5d, as p increases the sensitivities of the smooth aggregation function resemble those of the max(s) function, for which only one value of the sensitivities is different from zero. This issue affects the linearization performed by gradient-based optimizers since sensitivity information tends to be lost for closer approximations of the max(s) function. In this situation, few local constraints are being considered by the optimizer and when updating design variables, a new set of local constraints will stand out as critical. A common practice to reduce oscillations, which is also adopted in this work, is to limit the maximum change of the design variables (see for instance, Yang and Chen 1996). Being ml the move limit, the maximum change of the design variables is controlled as follows:

$$ {\max}(0,\rho_{e}-m_{l}) \leq \rho_{e} \leq {\min}(1,\rho_{e}+m_{l}) $$
(16)

4.2 Adopted aggregation strategy

Given that the constraint gi ∈ [ε-1, ε], the QoI is chosen such that si ∈ [0, 1]. Therefore, QoI is defined as follows:

$$ s_{i}=g_{i}+1-\varepsilon . $$
(17)

Considering Pm/n as either p-mean or p-norm, the global constraint Gms is recovered as follows:

$$ G_{\text{ms}} = P_{m/n} \left( \boldsymbol{s} \right) -1+\varepsilon . $$
(18)

The purpose of the aggregation is to catch the most critical constraints from the set (9), i.e., the maximum size constraints with positive values. The main difficulty of this task is that few constraints are being violated at every iteration. These ones are located in the narrow band [0, ε] shown in the histogram of Fig. 6a. This small band is a difficult target for the aggregation functions. As shown in Fig. 6b, large p values are required to catch the band [0, ε].

Fig. 6
figure 6

Information of two iterations of the MBB beam for compliance minimization with maximum size constraints. In a is the histogram of local maximum size constraints, in b the aggregation curves, and in c the sensitivity information

Full size image

The band [0, ε] is narrow because ε must be small. The ε parameter acts as a buffer of voids in the maximum size constraint. It should be big enough to split the bulky material but small enough to avoid affecting the length scale. As big value ε reduces the allowable amount of solid material within the test region, therefore it reduces the maximum size defined by the user. In addition, in the connection of bars, the Heaviside projection and the maximum size constraint act in opposition. As shown in Fig. 7a, the maximum size constraint tries to introduce amount ε of void, but the Heaviside projection tries to introduce material. This contradiction compromises the convergence of the problem.

Fig. 7
figure 7

Two situations when a large ε is chosen. In a, the maximum size constraint acts in opposition to the Heaviside projection. In b, the minimum size of the solid phase does not compromise the material connectivity

Full size image

The attractiveness of using big ε values, for example greater than 0.2, is that the aggregation process becomes easier since the band [0, ε] is no longer narrow. But this approach works only if the minimum size of the solid phase is sufficiently small to not contradict the maximum size constraint, as shown in Fig. 7b. The previous condition forms part of the method proposed by Wu et al. (2018) to produce infill structures. The difference between the later method and the method that controls the maximum size can be seen in Fig. 8. There, both solutions have the same maximum size diameter dmax, but ε in Fig. 8a is 10 times bigger than in Fig. 8b. The attached code computes the maximum size constraint with the method proposed in the following section, but it can be easily adapted to obtain the method that produces infill structures, for which the reader is referred to Section 7.

Fig. 8
figure 8

Solutions of the MBB beam domain for compliance minimization with maximum size constraints. In a solution using ε = 0.4% and in b using ε = 0.04%. The volume constraint is 60% in both cases. Black symbols next to each solution represent \(d_{{\min }}\) and Ω

Full size image

The adopted strategy in this paper uses (17) as QoI and a large p value (greater than 100) to ensure the capturing of the band [0, ε]. The non-linearity of the constraint is addressed in the optimizer by restricting the maximum change of the design variables. However, the slow evolution of the design variables demands a big number of iterations, being this the main drawback of the method. Each example reported in this article is solved using 450 iterations, with a continuation method defined as follows. In the three problems, the SIMP exponent η is initialized at 1.0 and is increased in increments of 0.25 to a maximum of 3.0. The Heaviside parameter β is initialized at 1.5 and is increased by a factor 1.5 to a maximum of 38. The continuation procedure includes 50 iteration between parameters increment.

We have noticed that at the beginning of the optimization process, when η is still smaller than 3, a large ml can be used without compromising the convergence of the objective function. This is probably due to the fact that a significantly larger amount of sensitivities are different from 0 at earlier stages of the optimization problem, as shown in Fig. 6c where p = 100. As the optimization progresses and the values of μ and β rise, smaller ml should be used for avoiding the divergence of the optimization process. In practice, we start the optimization with ml = 0.3 and finish with ml = 0.05. During the optimization process, a linear interpolation sets ml as follows:

$$ m_{l} = \frac{0.3-0.05}{3-1} (3-\eta)+0.05 . $$
(19)

This scheme is preferable than introducing a small ml from the beginning of the optimization problem because the slow evolution of the design variables can demand even a larger amount of iterations or promote the design topology get locked in the early stages of the optimization. In the later situation, we have observed designs with disconnected material, or designs that do not use all the allowed material. A similar observation is described by Lazarov and Wang (2017).

Figure 9 shows the evolution of the objective function \(\boldsymbol {t}^{\intercal } \boldsymbol {u}\) and of the constraint Gms. The problem corresponds to the solution shown in Table 2, using p = 100 and N = 30000. The picks on the objective and on the constraint come from the abrupt increase of the parameters η and β. It is worth mentioned that problems shown in this article start from an uniform initial guess satisfying both the volume and the maximum size constraint.

Fig. 9
figure 9

Convergence plot of the MBB beam design shown in Table 2, obtained with p = 100 and N = 30000

Full size image

4.3 Sensitivity analysis

Taking into account that we use column arrays, the sensitivity expression of the global constraint is obtained by applying the chain rule as follows:

$$ \frac{\mathrm{d} G_{\text{ms}}}{\mathrm{d} \boldsymbol{\rho}} = \frac{\mathrm{d}\tilde{\boldsymbol{\rho}}}{\mathrm{d}\boldsymbol{\rho}} \frac{\mathrm{d}\bar{\boldsymbol{\rho}}}{\mathrm{d}\tilde{\boldsymbol{\rho}}} \frac{\mathrm{d}\boldsymbol{\delta}}{\mathrm{d}\bar{\boldsymbol{\rho}}} \frac{\mathrm{d}\boldsymbol{g}}{\mathrm{d}\boldsymbol{\delta}} \frac{\mathrm{d}\boldsymbol{s}}{\mathrm{d}\boldsymbol{g}} \frac{\mathrm{d}P_{m/n}}{\mathrm{d}\boldsymbol{s}} \frac{\mathrm{d}G_{\text{ms}}}{\mathrm{d}P_{m/n}} , $$
(20)
$$ \frac{\mathrm{d} G_{\text{ms}}}{\mathrm{d} \boldsymbol{\rho}} = - \mathbf{D}_{\mathrm{I}}^{\mathrm{\intercal}} {J}_{\bar{\rho}} {J}_{\delta} \mathbf{D}_{\text{II}}^{\mathrm{\intercal}} {J}_{s} \frac{\boldsymbol{s}^{p-1}}{N} \left( \frac{ {\displaystyle{\sum\limits_{e \in {\Phi}}}}{s_{e}}^{p}}{N} \right)^{\frac{1}{p}-1} . $$
(21)

The sensitivities in (21) consider p-mean as aggregation function. The expression using p-norm is identical to (21) but without the term N− 1. Here, \(J_{\bar {\rho }}\), Jδ, and Js respectively represent the Jacobian matrix of the smoothed Heaviside projection, the measure of void, and the QoI to aggregate. These matrices are defined as:

$$ \begin{array}{@{}rcl@{}} J_{\bar{\rho}} & = &\text{diag}(\bar{\rho}_{1}^{\prime}(\tilde{\rho}_{1}),...,\bar{\rho}_{N_{t}}^{\prime}(\tilde{\rho}_{N_{\Psi}})) ,\\ J_{{\delta}} & =& \text{diag}(\delta_{1}^{\prime}(\bar{\rho}_{1}),...,\delta_{N_{t}}^{\prime}(\bar{\rho}_{N_{\Psi}})) , \\ J_{{s}} & = &\text{diag}(s_{1}^{\prime}(g_{1}),...,s_{N}^{\prime}(g_{N})) , \end{array} $$
(22)

with \(\bar {\rho }^{\prime }\), δ′, and s′ being the derivatives of (5), (12), and (17), respectively, and NΨ being the total number of elements in Ψ.

5 Numerical examples and discussion

The problems addressed here were introduced in Section 2. These ones are implemented in the PolyTop code (Talischi et al. 2012) as well as the proposed developments related to the maximum size constraint. In the Appendix, it is attached a sample MATLAB code that includes the formulation of the constraint and its sensitivities. This code is intended for integration with PolyTop and as a supporting material of the theoretical details discussed in this paper.

In this section, the reported objective values Obj are normalized with respect to the solution that does not consider the maximum size constraint. In addition, a measure of discreteness Mnd (Sigmund 2007) is also provided for each result. The measure is defined as follows:

$$ M_{\text{nd}}=\frac{\displaystyle{\sum\limits_{i \in {\Phi}}4v_{i} \bar{\rho}_{i}(1-\bar{\rho}_{i})}}{\displaystyle\sum\limits_{i \in {\Phi}} v_{i}} \times 100 . $$
(23)

When two topologies are compared, a topology equality index is provided which is defined in (24), where VTot is the total volume of the design domain. \(\bar {\boldsymbol {\rho }}^{(a)}\) and \(\bar {\boldsymbol {\rho }}^{(b)}\) are the two density maps being compared. For two identical maps Teq = 100, and for two totally different maps, Teq = 0.

$$ T_{\text{eq}} = 100 - \frac{ \boldsymbol{v}^{\intercal} \left | \bar{\boldsymbol{\rho}}^{(a)}-\bar{\boldsymbol{\rho}}^{(b)} \right| } {{\min}(2 V^{^{*}},V_{Tot})} \times 100 . $$
(24)

5.1 Comparison of test regions

The three optimization problems introduced in Section 2 are solved using the circular and annular test regions. For the MBB beam, V∗ = 40%, dfil = 0.08L, and dmax = 0.06L. For the force inverter, V∗ = 30%, dfil = 0.03L, and dmax = 0.025L. And for the heat sink, V∗ = 30%, dfil = 0.025L, and dmax = 0.031L. The maximum size constraint is formulated using p-mean function with p = 200. Table 1 gathers the results.

Table 1 Optimization problems with maximum size constraint including the circular and annular test regions
Full size table

Teq, reported in parenthesis, shows that designs obtained with different test regions share more than 76% of the topology. The main difference between them is that the circular region introduces more hollow circles into the topology. These are highlighted with red lines in the Table 1. The annular region introduces more channel-shaped cavities than circular ones. In addition, circular cavities in the designs obtained with the annular region are larger in diameter. These slight changes in the topology reduce the complexity of the component, which improves manufacturing. We observed a similar effect of the annular region, but less noticeable, with the inverse projection proposed by Almeida et al. (2009), i.e., when weights le, i decrease as they approach the center of the circular test region.

The annular test region improved structural performance in the MBB beam, but in the other test cases it was detrimental to the mechanical performance. However, the objective functions were affected by less than 0.7%, which can be considered negligible compared to the topological change. Therefore, changing the test region from Ω(c) to Ω(r) reduces the number of cavities in the design, having a greater impact on the topology than on the structural performance.

Another attractiveness of the annular region is that it makes possible to alleviate the memory load when dealing with large-scale topology optimization. There, maximum size neighborhoods easily come to contain thousands of elements, so removing the internal zone has a significant impact on the required memory to store the weights le, i in DII matrix.

5.2 Mesh dependency

In this example, the compliance minimization and the force inverter problems are solved using different discretizations. For the MBB beam, V∗ = 40%, dmax = 0.06L, dmin = 0.04L, and dfil = 0.08L. For the force inverter, V∗ = 30%, dmax = 0.04L, dmin = 0.02L, and dfil = 0.04L. For both problems, the annular test region Ω(r) is used to compute the local maximum size constraint. Solutions using p-mean and p-norm are summarized in Tables 2 and 3, respectively. Designs for two different p values are shown in each Table. The number of elements N is found on top of each solution, next to the indicator Teq that compares solutions obtained with different p values but same aggregation function. Comments about the essential differences between the chosen aggregation functions are listed below.

  • p-mean promotes mesh independence: When comparing topologies obtained with different discretizations but same p, it can be seen that the position and length of the larger bars are practically the same when using p-mean. For instance, taking into account the bar labelling shown in the MBB beam design with p-mean, p = 100 and N = 7500, it can be seen that bars 1 to 8 are easily recognizable in all discretizations. In the force inverter, the number of bars that compose the right diagonal structure is 3 in all discretizations. The main difference is in the central bar which tends to shrink as the number of elements in the discretization increases. However, in the designs obtained with p-norm, it is difficult to recognize a common topology. The internal number of bars in the MBB beam is different in all topologies, and in the force inverter, the right diagonal structure does not have the same number of bars in all discretizations.

Table 2 Effect of the p-mean function on the mesh dependency
Full size table
Table 3 Effect of the p-norm function on the mesh dependency
Full size table

Figures 10 and 11 were obtained from the MBB beam designs shown in Table 2, using p-mean with p = 100. These Figures display the constraints information of two different iterations, an early one and the last one. It can be seen that the local formulation of the maximum size constraint allows nearly the same data distribution, regardless of the discretization. It is precisely this property of the maximum size constraint that allows p-mean to promote mesh independence, because, as discussed in Section 4.1, for the same data distribution, the amount of data does not affect the p-mean function. Since histograms of different discretizations are not exactly the same, small differences between aggregation curves are expected. This probably justifies the subtle differences between the topologies obtained with p-mean, for instance, the absence of bar 7 in the MBB beam design obtained with p-mean, p = 300 and N = 120000.

  • p-mean underestimates: Because p-mean underestimates the most critical restriction, it introduces a lower penalization in the design. This is why the designs obtained with p-mean have a better structural performance than those obtained with p-norm. Increasing p when using p-mean increases the penalization and reduces structural performance, as can be seen in the objective values in Table 2 for designs obtained with different p. Although p-mean with p = 100 underestimates a significant fraction of critical restrictions, as can be seen in Fig. 11, it also divides the bulky material. There, the violated restrictions are mainly found in the union of bars, as can be seen in Fig. 11a. This is interesting since the restriction limits the maximum size of the bars but allows a rigid bond between them.

  • p-norm overestimates: Overestimating the local constraint (7) is equivalent to increasing ε. For this reason, p-norm places more voids in the test region Ω resulting in designs with larger cavities, with greater number of structural elements and thinner too. Having more partitioned material increases the perimeter of the design, this is why most of the results using p-norm have a greater Mnd.

  • p-mean is less parameter dependent: The disadvantage of the aggregation strategy is that it adds additional parameters to the optimization problem, which must be tuned by the user. In the context of maximum size constraints, we have observed that when p-mean is used, the parameters that most influence the final topology are the move limits ml and the chosen continuation procedure. Compared to these, the value of p has a smaller effect. As can be seen in Table 2, the results obtained with different p are very similar. These share about 80% of the topology. This is consistent with Section 4.1, which shows that the p-mean function is less sensitive to p than the p-norm.

  • Minimum length scale: As mentioned in Section 2, the adopted projection strategy does not guarantee complete control of the minimum size, i.e., local mesh convergence is not reached, especially in the areas where bulky material is divided by a thin layer composed of void and gray elements. As can be seen in Tables 2 and 3, small hinges are introduced as the number of elements in the discretization increases. This undesirable feature could be avoided by adding the geometric constraints proposed by Zhou et al. (2015) to impose the minimum size of the solid and void phases, or, as shown in the following example, by using the robust design approach (Wang et al. 2011).

Fig. 10
figure 10

Information of an early iteration of the MBB beam with maximum size constraints using p-mean. In a are the histograms and constraints map. In b are the aggregation curves

Full size image
Fig. 11
figure 11

MBB design with maximum size constraint using p-mean. In a are the histograms and constraints map for different discretizations. In b are the aggregation curves. Iterations obtained from a maximum size–constrained problem using p-mean function

Full size image

5.3 Maximum and minimum length scale controls

This example is simply to analyze the performance of the maximum size constraint on a problem with minimum size control. The three problems are solved using the robust design approach. To this end, three designs are obtained in the projection stage, named as eroded \(\bar {\boldsymbol {\rho }}_{\text {ero}}\), intermediate \(\bar {\boldsymbol {\rho }}_{\text {int}}\), and dilated \(\bar {\boldsymbol {\rho }}_{\text {dil}}\). The objective function considers the design that offers the worst performance (for further details see Wang et al. 2011). The volume constraint is evaluated on the dilated design only since the projection strategy adds more material in \(\bar {\boldsymbol {\rho }}_{\text {dil}}\) than in the other two fields. Given that \(\bar {\boldsymbol {\rho }}_{\text {int}}\) is the design intended for manufacturing, the upper bound of the volume constraint \(V^{*}_{\text {dil}}\) is updated according to the desired volume constraint \(V^{*}_{\text {int}}\) of the intermediate design. For the latter, we use the strategy adopted by Amir and Lazarov (2018). The maximum size is imposed in the dilated design only, i.e., \(G_{\text {ms}}(\bar {\boldsymbol {\rho }}_{\text {dil}})\). For the sake of brevity, the effect on the length scale from restricting the dilated field is omitted.

In this example, we use μero = 0.75, μint = 0.50 and μdil = 0.25 to obtain \(\bar {\boldsymbol {\rho }}_{\text {ero}}\), \(\bar {\boldsymbol {\rho }}_{\text {int}}\), and \(\bar {\boldsymbol {\rho }}_{\text {dil}}\), respectively. Here, differently from the previous examples, the length scale is linearly changed within the design domain. This is just to highlight the fact that it is not necessary to introduce extra constraints to impose, simultaneously, different maximum and minimum sizes. This task just requires assembling the \(\mathbb {\mathrm {D_{I}}}\) and \(\mathbb {\mathrm {D_{II}}}\) matrices with the desired neighborhoods. The minimum and maximum sizes, dmin and dmax, are given next to each solution, which are shown in Fig. 12. Since the thresholds μero and μdil are symmetric with respect to μint, the theoretical minimum size of the solid and void phases are equal. The p-mean function with p = 300 is used to aggregate the constraints and the remaining optimization parameters are kept as in the previous examples.

Fig. 12
figure 12

Topology optimization problems with different length scale. In aV∗ = 40%, Obj = 1.551, and Mnd = 2.7. In bV∗ = 50%, Obj = 2.931 and Mnd = 3.7. In cV∗ = 30%, \(O_{\text {bj}}^{-1}=1.277\) and Mnd = 1.7

Full size image

It can be seen in the MBB beam that there are two portions of material disconnected from the structure. These are pointed with two arrows in Fig. 12a. We have observed that this issue can be avoided by increasing the total number of iterations, or by changing the move limit ml to be less conservative.

As expected, by imposing the minimum size, it is possible to avoid the small hinges. For this reason, compared to previous examples, designs obtained with the robust design approach have approximately 1.5% less gray elements, which contributes to improve the manufacturability of the optimized design.

Unlike the examples in previous sections, the designs in Fig. 12 have a considerably lower performance than the reference solution. This is associated with the additional penalization introduced by the minimum size control, which avoids gray elements and increases the separation distance between the bars.

It is worth mentioning that after the work of Yan et al. (2018), it is known that needle-like structures in thermal compliance offer a better performance that tree-like structures. This was also observed in the context of maximum size by Carstensen and Guest (2018). However, in the thermal compliance designs shown in this work, the maximum size restriction did not improve the performance of the component despite of promoting needle-like structures, as shown in Fig. 12b. The reason is that a large portion of the material is removed from the area near the heat sink, interrupting the heat conduction towards the cold zone.

5.4 3D cantilever beam

The MATLAB code in the Appendix is transcribed into the free access code TopOpt (Aage et al. 2015), to solve the 3D cantilever beam for compliance minimization with maximum size constraints. The design domain is shown in Fig. 13a and the parameters are in the notes of Table 4. Most of these are defined by default in the TopOpt code. The maximum size constraint is formulated with the annular test region, which in 3D takes the form of a spherical shell of thickness (dmax − dmin)/2. The p-mean function is used to aggregate the local constraints with p = 300.

Fig. 13
figure 13

In a the cantilever beam domain with a maximum size test region that exceeds the design space. In b the portion of the test region that remains inside, and c the portion that exceeds the design space

Full size image
Table 4 3D cantilever beam for compliance minimizationa. Solutions include 2 views, one removes a portion of the component and the other one shows multiple sections. The displayed elements meet \(\bar {\rho }_{i} \geq 0.1\)
Full size table

Differently from the 2D case, the treatment of the filter is performed numerically since an extension of the design domain is computationally expensive when it comes to large-scale topology optimization. With a regular mesh, it is possible to redefine the filter and the maximum size matrices as:

$$ \begin{array}{@{}rcl@{}} \mathrm{D}_{\mathrm{I}_(i,j)} & =&\frac{\displaystyle v_{j} w_{i,j}}{c_{\mathrm{I}}} , i,j \in {\Phi}, \end{array} $$
(25a)
$$ \begin{array}{@{}rcl@{}} c_{\mathrm{I}} & = &{\max}(\boldsymbol{w} \boldsymbol{v}) , \end{array} $$
(25b)
$$ \begin{array}{@{}rcl@{}} \mathrm{D}_{\text{II}_(i,j)} & =& \frac{\displaystyle v_{j} l_{i,j}}{c_{\text{II}}} , i,j \in {\Phi}, \end{array} $$
(26a)
$$ \begin{array}{@{}rcl@{}} c_{\text{II}} & =& {\max}(\boldsymbol{l} \boldsymbol{v}) , \end{array} $$
(26b)

where w and l are matrices containing the weights. These are defined in (4) and (11), respectively. Then, the local maximum size constraint considering a numerical extension of the design domain is computed as:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{g} &=& \varepsilon - (\mathbf{D}_{\text{II}} \boldsymbol{\delta} + \boldsymbol{c}_{\boldsymbol{g}}) \leq 0 , \end{array} $$
(27a)
$$ \begin{array}{@{}rcl@{}} \boldsymbol{c}_{\mathbf{g}} &=& \mathbf{1} - \mathbf{D}_{\text{II}} \mathbf{1} , \end{array} $$
(27b)

where 1 is an all-one array. cg contains the fraction of the test regions that remains outside the design domain. For instance, the test region of an element located at the edge of the design domain (see Fig. 13a) has a cgi = 0.75 which represents the portion shown in Fig. 13c.

Table 4 summarizes the results. The first column shows the reference solution and the second column shows the solution with maximum size control. It can be observed that in this example, differently from the 2D case, the constraint promotes plate-like structures rather than bar-like structures. Where plates bond, a long-narrow-closed circular cavity is present, which hinders manufacturing if, for example, additive manufacturing technologies are considered. This suggests that the maximum size constraint may demand other methods to reduce the geometric complexity of the design.

In the 3D example, the computation time is increased by 7%, which can be considered negligible. However, the additional computation time and memory required to store the DII matrix could be considerably high if larger test regions Ω are used.

6 Conclusion

This article presents the aggregation of maximum size constraints. In particular, it is used the formulation that limits the amount of material within a test region of each element in the design domain. A detailed analysis of this constraint and a comparison between the studied aggregation functions lead to the following conclusions:

  • For large p-exponents, the sensitivity information of the aggregation function resembles that of the max(⋅) function, for which only one value of the sensitivities is different from zero. In this situation, oscillations are expected since few local constraint are being considered by the optimizer. Here, more conservative updating strategies are necessary to guaranty the convergence of the problem.

  • The aggregation of the maximum size constraints can be eased by increasing the amount of void within the test regions, since smaller p-exponents can be used to catch the critical constraints. However, this strategy limits the minimum size of the solid phase because of a contradiction between the smoothed Heaviside projection and the maximum size constraint.

  • Some aggregation functions, such as p-norm, are sensitive to the amount of aggregated data. Therefore, they are sensitive to different discretizations of the same optimization problem.

  • The aggregation functions are sensitive to the data distribution. This suggests that it is advisable to check the distribution of the constraints for a proper selection of the aggregation function.

In addition, it is observed that by removing the inner zone of the circular test region, less holes are introduced in the topology. This can contribute to improve manufacturability of maximum size–constrained components.

7 Replication of results

The attached code can be easily integrated into the PolyTop MATLAB code (Talischi et al. 2012). To facilitate its implementation and make it easy to read, some strategies have been simplified. For example, the PolyTop code by default does not include any treatment for the filter with respect to the boundaries, and the smoothed Heaviside projection is not threshold commanded. By default, it is solved the compliance minimization problem subject to volume and maximum size constraints, and the design is discretized using polygonal elements.

Some indications are given below to ease the replication of results.

  • The proposed strategy: The attached code includes by default the proposed aggregation strategy that uses (17) as QoI and (21) to obtain sensitivities. A big p exponent is set line 21, therefore a small move limit ml must be used.

  • Infill structures: As explained in Section 4.1, the maximum size constraint is related to the method that produces infill structures. To obtain a result similar to Fig. 8a, the attached code must be changed as described in lines 20, 21, 22, and 39.

  • Comparison of test regions: By default, the code in the Appendix assembles the DII matrix using the annular test region, but it is possible to recover the circular one by commenting the line 40.

  • p-mean and p-norm: By default the attached code uses p-mean as aggregation function, but it is possible to get p-norm simply by defining N = 1 in line 23.