Many-objective differential evolution optimization based on reference points: NSDE-R

Abstract

Design methodologies of today require the solution of several many-objective optimization problems. The last two decades have seen a surge in several algorithms capable of solving multi-objective optimization problems. It was only in the past 5 years that new algorithms capable of coping with a large number of objectives have been introduced. This work presents a new differential evolution algorithm (NSDE-R) capable of efficiently solving many-objective optimization problems. The algorithms make use of reference points evenly distributed through the objective function space to preserve diversity and aid in multi-criteria-decision-making. The proposed NSDE-R was applied to test problems from the DTLZ and WFG suite, having three to 15 objectives. Two mutation donor operators were investigated for their ability to converge to the analytical Pareto front while maintaining diversity. The ability of NSDE-R to converge to a user-specified region of the Pareto front is also investigated. The proposed NSDE-R algorithm has shown to have a higher rate of convergence and better convergence to the analytical Pareto front.

1 Introduction

Evolutionary and heuristic optimization methods have been extensively exploited for their ability to explore and exploit vast design and objective function space. The last two decades have given rise to several multi-objective optimization algorithms capable of finding a well-converged and well-diversified Pareto set of a two to three objective optimization problems. The optimization problems faced today require the solution of five to 10+ objectives (Chikumbo et al. 2012; Coello Coello and Lamont 2004) and are typically referred to as many-objective optimization problems. This leads to a challenging increase in size or the restriction placed on the objective functions space. The current algorithms suffer from solution clustering in certain regions of the objective function space and are not able to preserve diversity in the Pareto solutions. The need for the solution of these large scale optimization problems has led to the development of several many-objective optimization algorithms in the last 5 years.

A typical multi-objective optimization problem can be stated as

$$ {\displaystyle \begin{array}{l}\min\;\overrightarrow{f}\left(\overrightarrow{x}\right)\\ {}\overrightarrow{f}=\left\{{f}_1\left(\overrightarrow{x}\right),\dots, {f}_l\left(\overrightarrow{x}\right)\right\}\\ {}\overrightarrow{x}=\left\{{x}_1,\dots, {x}_m\right\}\\ {}\mathrm{subject}\kern0.17em \mathrm{to}:x\in \left[{a}_i,{b}_i\right]\kern0.96em i=1,\dots, m\end{array}} $$

(1)

subject to a number of inequality and equality constraints. These optimizers typically use various niching techniques to preserve diversity and typically use either decomposition based or indicator based methods. Decomposition based algorithms make use of reference points or reference directions to guide the search to scarce areas of the Pareto fronts. Algorithms using decomposition based approach include Non-dominated Sorting Genetic Algorithm (NSGA-III) (Deb and Jain 2014), Many-objective Optimization Evolutionary Algorithm based on Dominance and Decomposition (MOEA-DD) (Li et al. 2015), and Strength Pareto Evolutionary Algorithm (SPEA-R) (Jiang and Yang 2017). Indicator-based algorithms use certain performance metrics to quantify the superiority of one solution over another and control the recombination and selection operators. Some indicator-based algorithms include Indicator Based Evolutionary Algorithm (IBEA) (Zitzler and Künzli 2004) and Hypervolume-Based Estimation Algorithm (HypE) (Bader and Zitzler 2011a). The indicator-based algorithms are heavily influenced by the accuracy of the indicators used and by the computational times required to compute the indicators. Decomposition-based algorithm does not make use of indicators in the search process, thereby reducing the number of operations required for each generation.

This work presents a Non-dominated Sorting Differential Evolution algorithm based on reference points (NSDE-R). The effects of two different recombination operators on the performance on the NSDE-R algorithm are also investigated. The algorithm uses the recombination operator to create a candidate design, non-dominated sorting to find the non-dominated front, and a reference point–based niching strategy for environmental selection.

The performance of NSDE-R algorithm is evaluated against the performance of NSGA-III and MOEA/DD algorithms. The test problems were taken from the DTLZ and WFG test suites and feature three to 15 objectives. The performance is quantified utilizing the widely used Inverted Generalized Distance (IGD) and Hypervolume (HV) measures. The best, average, and worst IGD and HV metrics are presented for each algorithm.

2 Related work

There have been significant developments in the area of genetic evolutionary algorithms when solving many-objective optimization problems. The previously mentioned NSGA-III, MOEA/DD, and SPEA-R all use simulated binary crossover (Deb and Agrawal 1994) and polynomial mutation (Deb and Goyal 1996) to create offspring/candidate solutions. Therefore, they are closer to genetic algorithms in their algorithm structure. Whereas the development in genetic algorithms has progressed steadily over the decade, there has not been a differential evolution (DE) algorithm that is able to cope with large numbers of simultaneous objectives.

The differential evolution algorithm was first introduced by Storn and Price (Storn and Price 1997) in 1997 for single-objective problems. Das and Suganthan (Das and Suganthan 2011) recently performed a comprehensive review of the advances in differential evolution algorithm. They have shown that there did not exist a differential evolution algorithm for many-objective optimization. Robic and Filipic (Robic and Filipic 2005) presented the most popular differential evolution algorithm for multi-objective optimization (DEMO) (Robic and Filipic 2005). This algorithm uses the same Pareto ranking and crowding distance ranking scheme as NSGA-II (Deb et al. 2002) and, therefore, also underperforms when solving many-objective optimization problems. Recent work of He et al. (He et al. 2014) proposed a DE algorithm for many-objective optimization based on ranking (MODER). However, the MODER was shown to consistently perform worse than the NSGA-III algorithm. Denysiuk et al. (Denysiuk et al. 2013) also presented a many-objective version of the DE algorithm, but only compared its performance to multi-objective optimization algorithms.

To minimize the computing time in many-objective optimization problems, the algorithms should utilize the users’ preferences within their search procedures rather than insisting on uniform accuracy and details of the search. The proposed NSDE-R algorithm is able to incorporate the users’ preferences when performing the search and performs better for many-objective problems than the aforementioned algorithms.

3 Proposed NSDE-R algorithm

The basic framework of the proposed algorithm is presented in Algorithm 1. The NSDE-R starts with an initial population set P_i, and reference points set, R. The reference points can be uniformly distributed through objective function space or can be biased towards particular regions. At each generation, the NSDE-R algorithm then selects three members and performs its mutation operator. The parent population and offspring population, O, are then combined and normalized. Each individual in the combined population is then associated with the closest reference points. Then, an environmental selection procedure is applied to select individuals for the next generation that can aid convergence and preserve diversity. The following sections present each operation in the NSDE-R algorithm.

3.1 Generation of reference points

The proposed NSDE-R algorithm uses reference points to guide the search and preserve diversity. The reference points can be uniformly distributed through the objective function space or can be biased towards a particular region of interest. Results from both approaches are presented in this work. Two approaches can be used to uniformly distribute reference points through the objective function space. The first approach uses Das and Dennis’ (Das and Dennis 1998) systematic approach to place points on a normalized unit hyperplane. This is shown in Fig. 1a. This method guarantees uniform distribution of reference points, but suffers from the curse of dimensionality. Using this approach, for d divisions along each objective axis, the total number of reference points N in M-objective space is given by (2).

$$ N=\left(\begin{array}{c}M+d-1\\ {}d\end{array}\right)=\frac{\left(M+d-1\right)!}{\left(M-1\right)!d!} $$

(2)

Fig. 1

Das and Dennis’ method applied using a standard approach and b two-layer approach

For example, given eight divisions (d = 8) along each objective of a 10-objective problem (M = 10), the total number of points produced by Das and Dennis’ approach is 24,310. This drastically increases the computational cost when associating the designs with the reference points. The number of points can be significantly reduced using a two-step approach where an outer layer is first created followed by an inner layer as shown in Fig. 1b. Consider a 3-objective case with two divisions along the outer layer and one division along the inner layer. Then, the two-step systematic approach will yield a total of 9 points.

An alternative method for uniformly distributing reference points in high dimensional space is to utilize a random number generator. A pseudo-random sequence that uniformly distributes points in M-dimensional space can be used. One can utilize Uniform Latin Hypercube Sampling (Wyss and Jorgensen 1998). Figure 2 shows such distribution of 20 points for a 3-objective problem.

Fig. 2

Randomly distributed reference points on a unit hyperplane

3.2 Selection and recombination

The traditional DE algorithm selects three random, unique parents and combines them to create an offspring. At the end of each generation, each individual in the current population is compared to remaining members of the population to identify its uniqueness. An individual I is said to be unique, in design variable space, to a set A of size N_A, if

$$ {\left\Vert \overrightarrow{I}-{\overrightarrow{A}}_i\right\Vert}_{i\in \left\{1,\dots, {N}_A\right\}}\ge \varepsilon $$

(3)

This means that the L² norm between the variables defining individual $\overrightarrow{I}$ and the variables of every individual in $\overrightarrow{A}$ must be greater than some specified tolerance, ε. All required parent population that must satisfy uniqueness is selected from this unique archive, U. A new archive U is constructed every generation. For each individual i in parent population P, three parents are randomly selected from the unique archive (Alg. 1: Step 1) to perform mutation and crossover. Two different mutation operators are investigated for the NSDE-R algorithm (Alg. 1: Step 2). The most common used mutation operator in DE algorithms is the “rand/1/bin” (R1B) (Storn and Price 1997) given by

$$ {\overrightarrow{V}}_i={\overrightarrow{X}}_{r_1}+F\left({\overrightarrow{X}}_{r_2}-{\overrightarrow{X}}_{r_3}\right) $$

(4)

where i = 1…, N_P, $\overrightarrow{V}$_i = [v_i,1,…,v_i,N] and {r_j}_{j = 1,..,3}∈U ≠ i . The factor F determines the scaling of the difference between two random parents. In the above mutation, parent r₃ is taken as a donor parent. The R1B approach selects the donor vector randomly from the unique archive, U. Fan et al. (Fan et al. 2010) proposed using a convex sum of the three parents to create a donor vector. The combination is given as

$$ donor=\sum \limits_{k=1}^3{\mu}_k{\overrightarrow{X}}_{r_k} $$

(5)

where μ is a random number. Different distributions of the parameter μ result in different mutation scheme. Here, μ is assumed to be a uniformly distributed random number μ∈[0,1] which leads to the Donor3 (D3) scheme given by

$$ donor3=\sum \limits_{k=1}^3\frac{\mu_k{\overrightarrow{X}}_{r_k}}{\sum_{j=1}^3{\mu}_j} $$

(6)

The complete D3 mutation scheme can then be given by

$$ {\overrightarrow{V}}_i=\sum \limits_{k=1}^3\frac{\mu_k{\overrightarrow{X}}_{r_k}}{\sum_{j=1}^3{\mu}_j}+F\left({\overrightarrow{X}}_{r_2}-{\overrightarrow{X}}_{r_3}\right) $$

(7)

The crossover operation is then performed using the mutated vector and the ith individual. The offspring o is then given by

$$ {\left.{o}_j=\Big\{\begin{array}{c}{v}_j\\ {}{x}_{i,j}\end{array}\begin{array}{c}\mathrm{if} \operatorname {rand}\le {\mathrm{C}}_{\mathrm{r}}\vee j=k\\ {}\mathrm{otherwise}\end{array}\right|}_{j=1,\dots, N} $$

(8)

where C_r is the crossover probability. An offspring is created for each individual i in the parent population, P. The parent population and offspring population are then combined (Alg. 1: Step 3) to create the combined population, C, and the NSDE-R algorithm proceeds to objective normalization. The complete selection and recombination procedure is given in Algorithm 2.

3.3 Objective normalization

Normalization of the population members at each generation allows for diversity preservation and solution of differently scaled optimization problems. The normalization procedure is given in Algorithm 3.

The first step is to find the ideal point of the combined population, C, such that | C | = N_P. The approximate ideal point, z^min = (f₁^min,…, f_M^min) is calculated by

$$ {f}_j^{\mathrm{min}}={\min}_{i\in C}{f}_j\left({x}_i\right),j=1,\dots, M $$

(9)

Each member in C is then translated by z^min as f’ = f - z^min, such that the ideal point is now the zero vector. The extreme solutions from the translated population are then found. A solution i in C is extreme for axis i if the solution i makes the achievement scalarizing function (ASF) minimum (Figueiredo et al. 2016). The extreme solutions are then used to build a hyperplane, whose intercepts a_i are then used to normalize the population C as

$$ {f}_i^n=\frac{f_i^{\hbox{'}}(x)}{a_i},\kern0.36em i=1,\dots, M $$

(10)

This normalized objective function is then used to perform the association procedure.

3.4 Member association

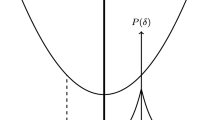
The association procedure associates each individual in the set to a single reference point. A member is associated with the reference point that has the shorted perpendicular distance between that individual and a line passing through the reference point and the origin. All distances are computed in the normalized objective space. This can be seen as a measure of density in the vicinity of the reference point. That is, the more individuals that are associated with a reference point, the denser (more crowded) that region will become. Figure 3 illustrates this association procedure, where the black dots are the reference points, the red squares are the individuals in the normalized objective functions’ space, and the blue lines are the rays connecting the reference points and the origin. It should be noted that a reference point may have one or more individuals associated with it or it may have none. The algorithm for association is given in Algorithm 4.

Fig. 3

Association of population members with reference points

3.5 Non-dominated sorting

The combined population C is then sorted into its non-dominated front levels using the usual non-dominated sorting approach (Chankong and Haimes 1983). Members of the first l front levels are added to S_t such that | S_t | ≤ N. If | S_t | = N, then no further operations are needed and the next generation is started with P_i + 1 = S_t. If | S_t | > N, then members from the first l – 1 fronts are added to S_l. The current population for the next generation is given by ${P}_{i+1}={\cup}_{i-1}^{l-1}{F}_i$. The remaining (K = N_P- | S_t |) population is selected from the lth front, F_l, using the niching procedure.

3.6 Niching procedure

The niching procedure aims to select a diverse population to carry into the next generation. Non-dominated sorting and niching are used together to carefully select a total of |N_p| individuals from a combined population C of size 2|N_p|. The niching procedure is given in Algorithm 5.

As previously stated, a reference point can have one or more members associated with it or it can have no individuals associated with it. Let us denote the niche count, ρ_j, of the jth reference point as the number of individuals associated with that reference point. The reference point with the highest niche count is the most crowded reference point.

The points to carry over into the next generation are selected as follows. The least used reference point is first identified. This will be the reference point with the lowest niche count. In the case of multiple such reference points, one is selected at random.

If ρ_j = 0, two scenarios are possible. First, there exists one or more solutions in F_l associated with reference point j. For this scenario, the individual in F_l with the shortest perpendicular distance to reference point j is added to P_i + 1. The niche count for reference point j is then incremented by 1 and the previously selected individual from F_l is excluded from further consideration. The second scenario is that there are no individuals in F_l associated with reference point j. In this case, reference point j is excluded from further consideration.

If ρ_j ≥ 1 and there exists one or more solutions in F_l associated with reference point j, then one is selected at random from F_l and added to P_i + 1. The niche count of the reference point j is incremented by 1. If there are no individuals in F_l associated with the reference point j, then this reference point is excluded from further consideration. The procedure is repeated until the population set has been filled.

4 Experiments on many-objective optimization

The ability of NSDE-R to solve many-objective optimization problems is investigated on a total of 14 test problems with three, five, eight, 10, and 15 objectives. This section presents optimization problem formulations and algorithm setup used to validate the NSDE-R algorithm.

4.1 Test problems

The test problems used to assess the performance of NSDE-R are taken from the DTLZ (Deb et al. 2005) and WFG (Huband et al. 2006) test suites. Table 1 gives the properties of each of the test problems selected. A total of 14 test problems, featuring three, five, eight, 10, and 15 objectives were used. The total number of variables for the DTLZ cases are N = M + k – 1, where M is the number of objectives, and k = 5 for DTLZ1, while k = 10 for DTLZ2, DTLZ3, and DTLZ4. Then, number of input variables for the WFG suite were N = k + l, where l = 20 and k = 2 × (M – 1). The many-objective test functions used in this paper can be scaled to any number of objectives and any number of design variables. They provide a diverse set of objective function topologies that the optimization algorithm can be validated against. Their analytical Pareto fronts are also known, which allows for the convergence analysis of the algorithms.

Table 1 Characteristics of DTLZ and WFG test problems

4.2 Indicator of performance

This work utilizes two metrics of accuracy for two different test suites of problems. The two metrics both measure diversity and convergence of the algorithms.

4.2.1 Inverted generalized distance (Bosman and Thierens 2003)

For each of the previously stated DTLZ test problems, the analytical Pareto front is known. Because the reference point–guided algorithms drive the search towards the reference points, only the analytical Pareto points closest to the reference points, called targeted Pareto points, should be used to construct the accuracy measure. Since the analytical Pareto front is known, one can find the targeted Pareto point, Z_tar, by finding the intersection between the analytical Pareto front and the reference line connecting the reference points and the origin. The accuracy measure should then use these targeted Pareto points and the approximate Pareto point obtained from the optimization algorithms. This work makes use of the Inverted Generalized Distance (IGD) measure given by

$$ \mathrm{IGD}\left(\mathrm{P},{\mathrm{Z}}_{\mathrm{tar}}\right)=\frac{1}{\mid {\mathrm{Z}}_{\mathrm{tar}}\mid}\sum \limits_{i=1}^{\mid {\mathrm{Z}}_{\mathrm{tar}}}\underset{j=1}{\overset{\mathrm{P}\mid }{\min }}\kern0.24em d\left({\mathrm{z}}_i,{\mathrm{p}}_i\right) $$

(11)

where d (z_i, p_i) = || z_i, p_i||₂. The IGD metric measures both the convergence to the analytical Pareto front and the diversity of the Pareto solutions. The smaller the value of the IGD, the better the approximated Pareto solution.

4.2.2 Hypervolume (Zitzler and Thiele 1999)

For the WFG suite of test cases, the analytical Pareto front is often difficult to obtain. It is even more difficult to uniformly distribute the analytical Pareto solution on this analytical Pareto front. For this reason, a metric that does not require the analytical Pareto front to be known is used for the WFG test suite. Hypervolume measures the size of the objective function space dominated by solutions S and bounded by z^r, where z^r is a reference point dominated by all Pareto-optimal solutions. The hypervolume is computed as

$$ HV(S)= Vol\left({}_{\mathrm{x}\in S}\left[{f}_1(x),{z}_1^r\right]\times \dots \left[{f}_M\left(\mathrm{x}\right),{z}_M^r\right]\right) $$

(12)

where Vol(·) is the Lebesgue measure. A larger value of HV indicates a better converged and more diversified solution set.

The reference point used for each test problem is given in Table 2. The HV is normalized to [0,1] by diving by $z={\prod}_{i=1}^M{z}_i^r$. For three to 10-objective test problems, the exact HV is calculated using the WFG algorithm (While et al. 2012). For test problems with the number of objectives greater than 10, the HV is approximated using Monte Carlo sampling (Bader and Zitzler 2011b). The sampling size was held constant, as recommended, at 10,000 (Bader and Zitzler 2011b).

Table 2 Hypervolume reference point used for each problem

4.3 Compared algorithms

The proposed NSDE-R algorithm is compared to two other state-of-the-art, popular, and powerful many-objective optimization algorithms: NSGA-III (Deb and Jain 2014) and the MOEA/DD (Li et al. 2015). They have been shown to outperform several indicator-based and other decomposition-based many-objective optimization algorithms. The basic principles of operation for these two algorithms are given below.

NSGA-III (Deb and Jain 2014)

It is an upgraded version of the popular NSGA-II algorithm. NSGA-III uses the same crossover and mutation operators as NSGA-II, but makes use of reference points to preserve diversity using niche preservation.

MOEA/DD (Li et al. 2015)

It is an extension of the MOEA/D algorithm. Unlike the original algorithm that only uses decomposition methods, the MOEA/DD algorithm also makes use of domination principle and was shown to converge faster to the analytical Pareto front for several test functions.

4.4 Parameter settings

The parameters used for each algorithm and each test problem are presented in this section. Table 3 shows the number of generations and the population sizes for the test problems. The number of reference points is equal to the population size. Each algorithm was run 20 times on each test problem.

Table 3 Population size and generations for test problems

The algorithmic parameter settings for each algorithm are given below.

NSGA-III

The crossover probability, p_c, and mutation probability p_m are 1.0 and 1/N respectively. The crossover distribution indexη_c and mutation distribution index η_m are set to 30 and 20 respectively.

MOEA/DD

The crossover and mutation parameters are the same as for the NSGA-III algorithm. The penalty parameter θ in PBI is set to 5.0. The neighborhood size, T, is set to 20 and the probability, δ, used to select in the neighborhood is chosen to be 0.9.

NSDE-R

The scaling factor F in (4) is held constant at 0.5 and the crossover probability Cr is also held constant at 0.5. Both the “rand/1/bin” and “donor3” mutation operators will be investigated.

It can be observed that the NSDE-R algorithm requires significantly fewer parameters to be specified. Since the choice of mutation donor does not affect the number of parameter needed, the NSDE-R algorithm requires at most two parameters, as opposed to four required by NSGA-III and seven required by MOEA/DD. In the upcoming sections, the DE algorithm using “rand/1/bin” mutation donor will be referred to as NSDE-R, while the DE algorithm using the “donor3” mutation operator will be referend to as NSDE-D3.

5 Empirical results and discussions

5.1 Performance comparisons using DTLZ test suite

A comparison of the four algorithms on the four DTLZ test problems having a different number of objectives is presented. As previously mentioned, each algorithm was run 20 times on each test problem. The best, average, and worst case IGD values from the 20 runs are presented in Table 4. The shaded, bold cells indicate that the algorithm is superior to others for that particular test problem.

Table 4 Best, average, and worst IGD values for the DTLZ test problems. Best performance is bold-italic

Table 4 shows that the NSDE family of algorithms is consistently on par if not better than the NSGA-III and MOEA/DD algorithms. For certain test cases, such as lower dimensional DTLZ1, the IGD values for the NSDE family differ by an order of magnitude from the NSGA-III and MOEA/DD. Moreover, Table 4 shows that NSDE-R consistently outperforms NSDE-D3 for DTLZ1 and DTLZ3, whereas NSDE-D3 outperforms NSDE-R in DTLZ2 and DTLZ4 test cases. This suggests that the “rand/1/bin” mutation is more robust for a multi-modal test problem and the “donor3” mutation is more robust for a concave test problem. Although NSDE-D3 outperforms NSDE-R for DTLZ2 and DTLZ4, it is not by much, as their performance measures are very similar. It can also be seen that the NSGA-III consistently performs better than the other three algorithms for the DTLZ4 problems which are of the concave, biased type. For the DTLZ2 and DTLZ4 problems, the IGD values of all algorithms are of the same order of magnitude.

Table 5 shows the percent of total DTLZ test cases for which a particular algorithm was able to outperform the others. It can be seen that the NSDE family performs better than the other algorithms in a larger set of test cases. In the best case, average, and worst case scenario, the NSDE family outperforms the other two in 75%, 60%, and 55% of the test cases, respectively. It can be deduced that for the DTLZ test cases, the “rand/1/bin” mutation is more robust than the “donor3” mutation. If the “donor3” results are omitted, the “rand/1/bin” mutation outperforms the others in 62% of the test runs.

Table 5 Percent of DTLZ cases that each algorithm outperforms others (best performance is bold-italic)

Figure 4 a shows the variation of the IGD metrics obtained using the four algorithms for a random 10-objective DTLZ1 test problem run. It can be seen that at the beginning, the convergence rate of the NSDE-R is comparable to that of MOEA/DD. However, the NSDE-R algorithm not only maintains its higher convergence rate, but also arrives at a much lower IGD value than the other three algorithms. The plateau in IGD metric experienced by the MOEA/DD and the NSDE-D3 algorithms seen here and also in (Deb and Jain 2014) indicates convergence to a local Pareto front, whereas the NSDE-R and NSGA-III algorithms are able to escape this local Pareto front.

Fig. 4

Convergence histories: variations of IGD with the four algorithms for a random 10-objective run of a DTLZ1 test problem, b DTLZ2 test problem, and c DTLZ4 test problems

Figure 4 b shows the IGD convergence for the DTLZ2 test problem. It can be seen that the IGD values of all four algorithms continually decreases. DTLZ2 is a concave problem with no local Pareto front. Again the IGD values of NSGA-III and MOEA/DD follow similar pattern as the one presented in (Deb and Jain 2014). Figure 4 b shows that performances of NSDE-R and NSDE-D3 are almost indistinguishable from each other for this test case.

Figure 4 b shows the IGD convergence for a 10-objective DTLZ4 run. It can be seen that the IGD of all four algorithms is monotonically decreasing as it did for the DTLZ2 test problem. It should be noted that both DTLZ2 and DTLZ4 are concave test problems, and that DTLZ3 would have similar behavior to DTLZ1 test problem as they are both multi-modal. It can be seen that the NSDE family of algorithms consistently leads to similar IGD values if not lower. They also feature a higher convergence rate than the NSGA-III and MOEA/DD algorithms.

Having assessed the convergence to the analytical Pareto front, the diversity of the Pareto solutions obtained using the four algorithms is now investigated.

Figure 5 shows the parallel value plot obtained using the four algorithms on a random run of a 10-objective DTLZ1 test problem. It can be seen that the NSDE-R and NSGA-III are both able to find the minimum and maximum values of each objective. The NSDE-D3 and MOEA/DD, however, were not able to find the limits of each objective function. Comparing Fig. 5a and Fig. 5b it can be seen that the “donor3” mutation does not perform well for a multi-modal test function. Similar conclusion can be made about the MOEA/DD algorithm by comparing Fig. 5b and Fig. 5d. Figure 5 shows that NSDE-R and NSGA-III are able to converge well to the analytical Pareto front while maintaining diversity. This is also evident in the IGD values given in Table 5.

Fig. 5

Parallel value plots obtained for a random run of a 10-objective DTLZ1 test problem using a NSDE-R, b NSDE-D3, c NSGA-III, and d MOEA/DD

The parallel value plot obtained for a random run of a 15-objective DTLZ3 test problem is shown in Fig. 6. The DTZL3 problem combines the multi-modal feature of DTLZ1 and the concave property of DTLZ2.

Fig. 6

Parallel value plots obtained for a random run of a 15-objective DTLZ3 test problem using a NSDE-R, b NSDE-D3, c NSGA-III, and d MOEA/DD

Figure 6 a shows that the NSDE-R algorithm is again able to both converge well and maintain solution diversity for a high dimensional, multi-modal, concave problem. The NSDE-D3, NSGA-III, and MOEA/DD all fail to fully converge and preserve diversity for this challenging test problem. This reaffirms that NSDE-R can outperform the other algorithms in a broad range of test problems that have various properties, whereas the NSDE-D3 performs well only on concave problems.

Figure 7 shows the parallel value plot obtained using the four algorithms on a random run of a 10-objective DTLZ4 test problem. All four algorithms were able to find the maximum and minimum values of each objective. It can be seen that both the “donor3” mutation and MOEA/DD perform well for concave test problems. For the DTLZ4 problem, all four algorithms produced evenly distributed solutions with MOEA/DD having the most uniformly distributed solutions.

Fig. 7

Parallel value plots obtained for a random run of a 10-objective DTLZ4 test problem using a NSDE-R, b NSDE-D3, c NSGA-III, and d MOEA/DD

5.2 Performance comparisons on the WFG test suite

The WFG test suite combines several properties of objective function space (non-separability, multi-modality, biasing) into a single test problem, making it very difficult for algorithms to obtain well-converged and well-distributed Pareto solutions.

A comparison of the four algorithms tested on the nine WFG test problems having a different number of objectives is presented. As previously mentioned, each algorithm was run 20 times on each test problem. The best, average, and worst case HV values from the 20 runs are presented in Table 6. The shaded, bold cells indicate that the algorithm is superior to others for that particular test problem.

Table 6 Best, average, and worst HV values for the WFG test problems. Best performance is bold-italic

WFG1 test case investigates the algorithms’ performance for biased and mixed Pareto fronts. It can be seen that for lower dimensional WFG1 problems, the NSGA-III algorithms, performs best, but for higher dimensional problems, the NSDE-D3 algorithm performs better. It should be noted that although NSGA-III performs well for lower dimensional problems, the performance of the NSDE-D3 is also just as good. The NSDE-R, however, is not able to cope with the difficulties of the WFG1 test function. It should be mentioned however, that the other algorithms are only slightly better.

WFG2 test case investigates the algorithms’ ability to cope with convex, disconnected, multi-modal, and non-separable problems. The two DE algorithms perform best for the WFG2 problem. For lower dimensional problems, the performance of NSDE-R is comparable to that of NSDE-D3, but for higher dimensional problems, the NSDE-R performs significantly better.

WFG3 test case represents a connected version of WFG2. Its features are linear, degenerate, and non-separable. For this problem, the NSDE-D3 performs better for lower dimensional problems, while NSGA-III performs better for higher dimensional problems. The NSGA-III algorithm is more robust for the WFG3 test problem. The NSDE-R algorithm is the least robust for the WFG3 test case. This suggests that the “rand/1/bin” mutation is not ideal for degenerate type problems.

WFG4 to WFG9 test cases all have a hyperelliptic Pareto front with radii r_i = 2i, where i∈{1…, M}. They are all concave problems featuring additional properties given in Table 1. The NSDE-D3 algorithm performs best on the WFG4 test problem, which features a concave, multi-modal space. The HV values for most algorithms are slightly below that of NSDE-D3 algorithm, but are still comparable.

The WFG5 test problem features a concave, deceptive landscape. The NSGA-III performs significantly better than the other three algorithms for the WFG5 test function. The HV values for the NSGA-III are significantly and consistently higher.

WFG6 test case investigates the algorithms’ ability to deal with concave and non-separable problem. The NSDE-D3 algorithm consistently performs better than the other three algorithms. The HV values of NSDE-D3 algorithm are significantly higher than those of the other three algorithms. The NSDE-R algorithm performs slightly worse than the NSDE-D3 algorithm. It performs slightly, but consistently better than the NSGA-III and MOEA/DD algorithms, especially for higher dimensional problems. This suggests both DE mutations are able to cope with non-separable problems.

WFG7 test case investigates the algorithms’ abilities to deal with concave and biased problems. NSDE-D3 again performed better for most objectives. For five- and eight-objective problems, where the NSGA-III was better, the HV values of NSDE-D3 are on par with those for the NSGA-III algorithm. This shows that for the WFG7 test functions, the NSDE-D3 is significantly more robust. The NSDE-R preformed consistently better than the MOEA/DD algorithm, but was less robust than NSGA-III for higher dimensional problems. This suggests that the “rand/1/bin” mutation is not able to cope with biased problems. This was also seen in the case of the DTLZ4 test case.

WFG8 test case investigates algorithms’ ability to cope with concave, biased, non-separable problems. The NSGA-III algorithm performed consistently better than the other three algorithms. The HV values of the NSGA-III were also consistently and significantly higher than those of the other algorithms. The HV values of NSDE-D3 algorithm were only slightly lower than those of the NSGA-III algorithm and consistently higher than those of the MOEA/DD algorithm. The NSDE-R algorithm was again less robust than NSDE-D3 due to the biased nature of the test case.

In WFG9 test case, the NSDE-D3 performed consistently better. However, the HV values of the NSGA-III were also on par with NSDE-D3 for most objectives cases that were run. The HV values of the NSDE-R were also comparable to those of the NSDE-D3, but only for lower dimensional problems. The NSDE-R algorithm performed consistently better than the MOEA/DD algorithm, but slightly worse than the NSGA-III algorithm. This is again due to the biased characteristic of the WFG9 test case.

Table 7 shows by how many percent of the total WFG test problems was a particular algorithm able to outperform the others. For each case, “best-case,” “averaged-case,” and “worst-cases,” there were a total of 45 test instances (# test problems × # of objectives). Meaning, for each of the nine WFG test cases, the percent was calculated over 45 samples. It can be seen that the “best-case scenario”, the NSDE-D3 algorithm performs best in 56% of the test cases. In the “averaged-case” scenario, the NSDE-D3 is successful in 56% of the test cases. In the “best-case” and “averaged-case”, the success rate of NSDE-D3 is significantly higher than that of the other three algorithms. In the “worst-case” scenario, the NSDE-D3 is again the best performing with a success rate of 44%.

Table 7 Percent of nine WFG test cases that each algorithm performs best in (best performance is bold-italic)

It is interesting to note that, unlike in the DTLZ comparison (Table 5), the NSDE-R algorithm consistently underperforms for the WFG suite. This is primarily because the “rand/1/bin” mutation is unable to cope with the biased characteristic present in the large number of WFG test cases. The “donor3” mutation however performs significantly better in a large number of WFG test cases.

5.3 Performance comparisons of optimization algorithms on the DTLZ and WFG test suites

In the previous sections, Tables 4 and 6 showcased the performance of each algorithm on each test problem. This section presents a more condensed comparison between algorithms over all test cases. It presents the success rate of one algorithm over another over all test suites. This method of comparison provides a more conclusive result when comparing algorithms.

Table 8 shows the success rate for the four algorithms on the DTLZ test suite. It shows that the NSDE-R is comparable to NSDE-D3, with both having a success rate of almost 50% over each other. The NSDE-R algorithm is better in 72% and 65% of the DTLZ family of test problems over the NSGA-III and MOEA/DD algorithms, respectively. It can be deduced that the NSDE-R algorithm is more robust for the DTLZ test suite as it is consistently better in more than 50% of the test problems over the other algorithms.

Table 8 Success rate of each algorithm over another for the four DTLZ test problems

Table 9 shows the success rate of the four algorithms on the WFG test suite. The previously robust NSDE-R algorithm is the least robust on the WFG suite. The NSDE-D3 is better than NSDE-R in 80% of the test functions. The NSDE-D3 performs better in 61% and 79% of the WFG test problems over the NSGA-III and MOEA/DD algorithms, respectively. For the WFG family of test problems, NSDE-D3 has shown to be the most robust algorithm.

Table 9 Success rate of each algorithm over another for the nine WFG test problems

5.4 Reference points to aid multi-criteria-decision-making

Often in multi-criteria-decision-making (MCDM), the user is interested in finding solutions in a particular region of the Pareto front. It was previously mentioned that the reference point based approach can be used to guide the search to particular regions of interest. This section presents the results of reference point assisted MCDM on a three-objective and 15-objective DTLZ1 and DTLZ4 test problems obtained using the NSDE-R algorithm.

Figure 8 a shows the distribution of the reference points for three-objective problems. These reference points are biased towards the extreme values of each objective. Figure 8 b and c show the converged Pareto front obtained using these reference points and the NSDE-R algorithm. It can be seen that the search for both the multi-modal and concave problem is driven to the region of the reference points.

Fig. 8

Pareto fronts obtained using biased placement of reference points a for a three-objective test problem: b DTLZ1 problem and c DTLZ4 problem

Figure 9 shows results of the reference point guided approach on 15-objective test problems. Figure 9 a shows the distribution of the reference points on a unit hyperplane. The reference points for this problem were biased towards the 15th objective. Figure 9 b and c show the distribution obtained on the DTLZ1 and DTLZ4 test problems. It can be seen that both algorithms were able to find the minimum and maximum values for each objective. For the DTLZ1 problem, the NSDE-R algorithm was able to drive the search in the region of the reference points and was also able to converge in that particular region. For the DTLZ4 problem, NSDE-R was again able to drive the search towards the reference points. It can also be seen from Fig. 9c that the algorithm was able to converge not only to the region, but also to the analytical Pareto front.

Fig. 9

Parallel value plot of Pareto fronts obtained using biased placement of reference points a for 15-objective test problem: b DTLZ1 problem and c DTLZ4 problem

Table 10 shows the IGD values obtained using NSDE-R on the two test problems for two different numbers of objectives. As previously stated, the IGD metric measures both convergence and diversity of a solution. It can be seen that the IGD values are relatively low, indicating that well-converged and well-diversified Pareto sets were reached in these test cases.

Table 10 Best, average, and worst IGD values obtained using biased reference points

5.5 Randomly varying algorithm properties

All evolutionary algorithms are heavily influenced by the parameters used by them. Some of these properties are given in Section 4, D. It is very well known that the values of F and Cr greatly impact the search process of differential evolution algorithms. Often, users of the algorithm select these parameters either based on their experience or by trial-and-error (Storn and Price 1997). Others (Pedersen 2012) have proposed using meta-optimization to determine the values for these parameters. Some works (Das et al. 2008; Konar et al. n.d.) have proposed randomly varying the algorithm parameters within a specified bound. It was previously shown (Inclan and Dulikravich 2017) that for single-objective optimization, randomly varying these parameters significantly improves convergence. The effects of this adaption on the NSDE-R and NSDE-D3 for many-objective problems are investigated here.

The scaling factor F and crossover probability Cr will both vary uniformly within [0.3, 0.7] and [0.3, 0.7], respectively. The effects of random variation of the DE parameters were investigated on both the “rand/1/bin” and “donor3” mutation schemes. The algorithms were again run on the DTLZ test suite. The algorithms’ number of runs, number of generations, population size, and number of reference points were kept the same as for the previous DTLZ runs.

Table 11 shows the best, average, and worst case IGD values for the DE algorithms with randomly varying algorithm properties. The IGD values of NSDE-R and NSDE-D3 refer to the previous case where F and Cr were both set at 0.5, while the NSDE-R* and NSDE-D3* are runs with randomly varying parameters. It can be seen that the NSDE-R and NSDE-D3 outperform their stochastic counterparts for the DTLZ1 and DTLZ3 problems, suggesting that the chaotic search pattern caused by random values of the parameter should be avoided for multi-modal problems. The values of NSDE-D3* performs well for the concave problems such as DTLZ2 and DTLZ4. That being said, the original NSDE-R and NSDE-D3 both produce similar results to their stochastic versions for concave problems.

Table 11 Best, average, and worst IGD values for the DTLZ test problems. Best performance is bold-italic

It can again be seen that the NSDE-R algorithm is more robust than the other three algorithms since its performance is on par, if not better, for all test problems studied here. It is recommended that for many-objective problems, the DE parameters not be varied randomly each generation, especially for multi-modal functions, as this leads to an overly chaotic search. The cases with static values of algorithm parameters produce well-converged results in average and in worst case scenarios.

5.6 Performance of NSDE-R on problems with more objectives

It was previously shown that the NSDE-R algorithm is able to converge and preserve diversity in most of the test problems analyzed. The ability of NSDE-R to converge for problems with more objectives was then investigated on a 20-objective DTLZ1, DTLZ2, DTLZ3, and WFG4 test problems. These problems feature linearity, concavity, and multi-modality in their objective functions. The NSDE-R algorithm was run for 1500 generation of each of these test problems with a population size and reference point set size of 230.

The obtained Pareto front in parallel value plot format is shown in Fig. 10. It should be noted that the Pareto points plotted are not normalized and that they represent the actual value of the objective functions. It can be seen in Fig. 10a that for the linear, multi-modal DTLZ1 test case, the Pareto set obtained using NSDE-R are not only diverse, but are also well converged. The convergence is seen in the value of the objective functions, as the Pareto front of the DTLZ1 is a half-unit hyperplane.

Fig. 10

Parallel value plots of Pareto fronts obtained using NSDE-R on a random run of a 20-objective problems: a DTLZ1, b DTLZ2, c DTLZ3, and d WFG4

The NSDE-R algorithm was also able to preserve diversity and converge well for the concave DTLZ2 test problem. The Pareto set of the DTLZ2 problem is a unit hypersphere. Figure 10 b shows that the NSDE-R algorithm is able to find the minimum and maximum values of each objective.

Figure 10 c shows the Pareto front obtained for the concave, multi-modal DTLZ3 test problem. The Pareto sets for the DTLZ2 and DTLZ3 test cases were the same.

It can be seen that even in this difficult test problem, the NSDE-R is not only able to converge to the analytical Pareto front but also preserved population diversity. The proposed algorithm was able to find minimum and maximum values of each objective for all three test problems and therefore can be used for the estimation of the ideal point and the Nadir point.

The WFG4 test case also has the same properties as the DTLZ3 test function. The Pareto set of this problem is a hyperellipse. Figure 10 d shows that the NSDE-R algorithm was again able to converge while preserving diversity for this challenging problem, and that it performed well for 20 simultaneous objectives over a range of problem types. It can be seen that the maximum and minimum values of the Pareto front found by NSDE-R define the hyperelliptic Pareto front of the WFG4 problem.

6 Crashworthiness design of vehicles for complete trade-off front

The crashworthiness problem was first described in (Liao and Li 2008) and aims at the optimization of the frontal structure of a vehicle. The design variables are the reinforced members around the frontal structure and the mass of the vehicle, deceleration during frontal crash, and toe-board intrusion in the offset-frontal crash were the three objective functions, all of which were to be minimized. The deceleration is directly proportional to biomechanical injuries cause to the occupants, while the toe-board intrusion accounts for the structural integrity of the vehicle. In (Liao and Li 2008), a design of experiments using Latin Hypercube and a full non-linear FEA analysis was performed and a stepwise regression model was fitted to the data. The optimization in this work and in (Deb and Jain 2014) was performed using this stepwise regression surrogate model. For this three-objective test problem, the same algorithm settings were used as for other three-objective problems. The total number of generations was set at 1000.

Figure 11 shows the Pareto front obtained using the four algorithms after 1000 generations. It can be seen that the NSDE-R and NSDE-D3 algorithms both produce uniformly distributed Pareto fronts, while the MOEA/DD produces the least diverse Pareto set. Comparing NSDE algorithms and the NSGA-III, it can be seen that both NSDE algorithms outperform the NSGA-III, since in Fig. 11c, a region of the Pareto front is shared by more than one design.

Fig. 11

Pareto front found for the crashworthiness problem using a NSDE-R, b NSDE-D3, c NSGA-III, and d MOEA/DD

7 Conclusion

This work introduced two differential evolution algorithms for many-objective optimization. The proposed DE algorithms have been tested on problems from the DTLZ and WFG test suites with the number of simultaneous objectives ranging from three to 20. Both differential evolution algorithms use reference point based niching to preserve diversity among Pareto solutions. The proposed algorithms were compared against two state-of-the-art algorithms, NSGA-III and MOEA/DD. The following conclusions can be drawn from the performances on each test suite.

DTLZ

It was seen that the differential evolution using “rand/1/bin” mutation performed best on the DTLZ test suite. The NSDE-R has shown to have a higher convergence rate than the other algorithms, converged well to the analytical Pareto front and was able to maintain diversity in the Pareto solution. The NSDE-D3 algorithm was able to converge well for concave, uni-modal problems, but failed for multi-modal test functions. The NSDE-R, however, performed well for both uni-modal and multi-modal problems. The NSDE-R algorithm performed better than NSGA-III in 72% of the test problems and better than MOEA/DD in 65% of the test problems. The NSDE-R algorithm was shown to be more robust when applied to the DTLZ suite of test problems.

WFG

For this set of test problems, NSDE-D3 was shown to be more robust. It was shown that the NSDE-D3 algorithm performs better for higher dimensional problems, while its performance for lower dimensional problems is on par with the other three algorithms. It was again observed that the NSDE-D3 performed well for the concave, non-separable problems, but did not work well on the concave, biased, non-separable WFG8 test problem. The NSDE-R algorithm was only able to solve the WFG2 test problem and lower dimensional WFG5 problem. It was observed that for the WFG test suite, the NSDE-R is the least robust algorithm. The NSDE-D3 outperformed NSDE-R in 80% of the WFG test cases. The NSDE-D3 algorithm also outperformed the NSGA-III and MOEA/DD algorithms in 61% and 79% of the test cases respectively.

It was shown that the DE algorithms can aid in multi-criteria-decision-making. The ability of the proposed NSDE-R algorithms to find a preferred part of the Pareto front was demonstrated. It was shown that the NSDE-R is able to guide the search towards the reference point even for high dimensional problems. This ability was showcased on both uni-modal and multi-modal, linear and concave test problems.

The effects of randomly varying algorithm parameters on the performance of the DE algorithms were also investigated. It was shown that the performance of the DE algorithm deteriorates for multi-modal problems when the parameters are randomly varied. It was also noticed that the solution of the concave DTLZ2 and DTLZ4 problems are less sensitive to the variation in the algorithm parameters.

Finally, the performance of NSDE-R was investigated for high dimensional problems. Its performance on multi-modal, uni-modal, biased and concave test problems were investigated. Results showed that the NSDE-R algorithm is not only able to converge well for 20-objective problems but was also able to preserve diversity. The NSDR-R algorithm was also tested on a practical design problem for vehicle crashworthiness.

The two proposed DE algorithms have shown to be robust for a variety of test problems. They consistently perform better than the state-of-the-art NSGA-III and MOEA/DD algorithms.