1 Introduction

Additive manufacturing (AM) processes are cutting-edge technologies that have transformed industrial and mechanical design. Prototypes can be easily printed using AM processes, improving efficiency and convenience in developing new products. Moreover, AM facilitates manufacturing of mechanical structures with complicated shapes that could not be produced using conventional forging, casting, or machining methods (AM-platform 2014; Huang et al. 2015; Gibson et al. 2015).

However, as with other well-developed manufacturing techniques, AM has its own drawbacks and constraints. One critical problem relates to manufacturing overhanging parts of specimens. Unwanted thermo-induced phenomena such as sag, warp, and shrinkage can reduce product quality during fabrication according to different melting schemes or material properties. These thermo-induced effects are crucial for the two most commonly used AM processes selective laser melting (SLM) and fused deposition modeling (FDM), and FDM even cannot ignore the gravity effect. Generally speaking, most of the physical distortions can be mitigated on the basis of a certain geometrical manufacturing rule during the AM processes (EOS GmbH Application Notes n.d.; Crucible Design Ltd. 2015; Stratasys Ltd. 2018; Ultimaker 2018). Adding supporting structures and redesign the specimen with proper overhang angle are the two most common suggestions for the manufacturability.

To ensure that specimens with overhangs can be produced to an acceptable quality, extra supporting structures are required to maintain the specimen profile during SLM or FDM. These extra supporting structures can be classified into internal and external supports. The external support is vital for maintaining the specimen profile during SLM or FDM, and it should be removed after fabrication. However, external supports require extra materials, time, and energy consumption as well as additional effort during postprocessing to remove it from the specimen (Mirzendehdel and Suresh 2016; Kuo et al. 2018; Strano et al. 2013; Vanek et al. 2014). Internal support structures are used not only for maintaining the profile during fabrication but also for enhancing the structural strength of a specimen. Studies have shown that the need for external supports can be lessened or entirely removed owing to well-designed internal supports (Cheng et al. 2017; Li et al. 2018; Panesar et al. 2018; Wang et al. 2017; Wang et al. 2018).

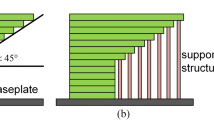
The overhanging part of a specimen cannot be printed without supports if its inclination remains below a minimal value (e.g., 45° in the most general case) with respect to the baseplate. By contrast, if the part with its inclination (i.e., the overhang angle) is larger than this minimal value, it is said to be self-supporting. Therefore, the overhang angle becomes a constraint in designing specimens for manufacturing using an AM process.

A specimen with mostly self-supporting parts can certainly be produced cost effectively and efficiently. However, the minimal value of the overhang angle varies according to the material and manufacturing parameters in the AM process. This study focused on how to incorporate overhang angle constraints of AM within density-based topology optimization for self-supporting structural design, which is a typical problem of designing for manufacturability in AM.

Incorporating self-supporting constraint in topology optimization aiming for AM was initiated by Leary et al. (2014). They made support-free structures by attaching additional materials onto regions that do not meet the self-supporting criteria after topology optimization; however, this method means that the volume constraint is violated, and the final layouts might not be mechanically optimal. A filter-like Heaviside projection function proposed by Gaynor and Guest (2016) enforces the structure elements that should be supported from its below elements in a specific overhang region as defined by the filter. This method was successfully demonstrated using the Messerschmidt-Bölkow-Blohm (MBB) beam and cantilever as examples.

Another scheme that can apply self-supporting constraint during structure optimization is to estimate the layer-wise relation between the supported and supporting elements during finite-element analysis. Langelaar (2016, 2017) was the first to propose a layer-wise filter that effectively excludes unprintable geometries from the design space. Smooth minimum and maximum operators are introduced to provide the overhang constraint and necessary gradient information for the density-based topology optimization. Zhao et al. (2017) proposed a simple quadratic function to represent the overhang constraint. By using an efficient element detection method based on discrete convolution, the total number of unsupported elements is forced to be zero through the defined overhang angle. Although the self-supporting identification is mostly processed by logic judgment instead of typical sensitivity analysis, the resulting topology is reasonable. Moreover, Zhao’s method can easily be extended to a general overhang angles as in the aforementioned work by Gaynor and Guest (2016) and Langelaar (2017).

van de Ven et al. (2018) proposed a method in detecting the overhang region using the anisotropic front propagation and updating arrival times by ordered upwind method (OUM). The sensitivity filter for arbitrary overhang angles is then established according to this propagation. The resulting 2D topology layout satisfied different overhang angle constraint but might have a zigzag structure.

Besides adding additional constraint or transforming constraint into a filter based on adjoint method, the self-supporting design approaches based on feature-driven topology optimization are also reported. Zhang and Zhou (2018) proposed polygon features which directly constrained the overhang angle by geometry descriptions. Guo et al. (2017) presented two kinds of explicit geometry parameter sets, moving morphable components (MMC) and moving morphable voids (MMV), to optimize the structural topology for the satisfaction of the general overhang angles.

A Heaviside projection–based integral (HPI) proposed by Qian (2017) can reduce the undercut region requiring supporting structures in AM through density-based topology optimization. This method can also control the minimal overhang angle during structure optimization. However, a grayness constraint is also required for a clear topology according to the characteristic of the density filter based on Heaviside functions. In addition, the parameters corresponding to the grayness filter threshold and the precise perimeter require more experience.

Many studies have attempted to define an index that may quantify the degree of self-support in a target specimen for AM while adopting topology optimization. However, not all can directly or easily obtain the corresponding sensitivity of the self-supporting index during topology optimization. Based on the same element-wise geometrical relation of overhang angle used in Langelaar (2017) and Zhao et al. (2017), herein, a polynomial-based logistic aggregate function is proposed that can not only quantify the degree of self-support in a specimen but also easily be differentiated for the associated sensitivity during optimization.

Comparing this study with Langelaar (2017) and Zhao et al. (2017), the geometrical relations between supporting and supported elements are the same; however, the transformation from the self-supporting condition to the mathematical equations is quite different. All three methods can be applied with existing density-based topology optimization method without modifying the procedure. The comparisons of self-supporting schemes referred from Zhao et al. are listed in Table 1. Besides, all these three methods implement the self-supporting condition from three different aspects, so which one is better requires more studies and it is also beyond the scope of this study. Nevertheless, comparisons of these three methods are provided as a review of these three studies.

Table 1 Comparison of self-supporting manipulations
Full size table

This study provides each element a self-supporting index that can be directly utilized as a manufacturing constraint equation in an optimization problem. Langelaar (2017) proposed a filter-like module that redistributes the sensitivities for satisfying the overhang constraint by adjoint method. Zhao et al. (2017) used the discrete convolution method to identify which elements are out of support according to 0–1 design results by Heaviside filter, and then directly eliminated those unsupported density to zero in the constraint. From formulation point of view, this study is similar to Zhao et al. in that both studies implement self-supporting condition as constraint in optimization. However, this study considers the self-supporting relations with sensitivity analysis as Langelaar’s work instead of only eliminating the unsupported elements as Zhao et al.

From numerical programming point of view, Zhao et al. (2017) provided a highly efficient program under a limited prerequisite in meshing the design domain because the fixed convolution mask may not work anymore when the non-uniform free meshes are encountered. Langelaar (2017) used smooth approximation function with radicands which may be more time consuming in sensitivity analysis as compared to the polynomial function adopted in this study. On the other hand, the filter-like implementation might ignore certain convergence problem than adding additional constraint function as Zhao et al.

Figure 1 illustrates three overhang angles in AM: 26.6°, 45°, and 63.4°. To assess the characteristics of the proposed self-supporting index, this study first focused on the overhang angle of 45° because it is the manufacturing limitation for most FDM–based machines. However, design examples including overhang angles of 26.6° and 63.4° are also presented to demonstrate the extensibility of the proposed self-supporting index.

Fig. 1
figure 1

Elements with different overhang angles: a 45°, b 63.4°, and c 26.6°

Full size image

This paper is structured as follows. In Section 2, a logistic aggregate function is introduced for use as an index, hereafter called the self-supporting index (SSI), to quantify the degree of self-support in a specimen. This proposed SSI is intentionally used as the overhang angle constraint in the topology optimization of self-supporting structure. Section 3 presents three different schemes for determining the sensitivity of SSI with respect to the element density. Using a cantilever as an example, the topology layouts with different overhang angle constraints resulting from these gradient schemes are compared and discussed. Section 4 investigates the reliability of using the proposed SSI as the overhang angle constraint, and the self-supporting topology optimization of an MBB beam in different orientations is also demonstrated. Finally, the investigation of the self-supporting structure design for additive manufacturing by using the proposed logistic aggregate function is concluded in Section 5.

The topology optimization including finite-element analysis and optimization program were coded using MATLAB, and the topology optimization method in this study is the same as the previous work (Kuo et al. 2018) (i.e., SIMP with CAMD and optimized using GCMMA with the continuation method). The length scale control is not utilized in this study.

2 Quantifying the degree of self-support

This section introduces a logistic aggregate function that is proposed to quantify the degree of self-support for each finite element in a targeted design domain during optimization. This logistic aggregate function is conceptually based on the repulsion index (RI) proposed by Kuo et al. (2018), and it can be extended to a more general function that is introduced in the next section.

RI is originally used to meet the easy removal requirement of external supporting structures by penalizing the adjacent layer–wise elements for encouraging the topology layout to be a twig-like structure. This RI can be extended and rewritten in a more general form LA(ρ) called the logistic aggregate (LA) function:

$$ LA\left({\boldsymbol{\uprho}}_{te}\right)=T\frac{\prod_{t=1}^T{\rho_t}^q}{\sum_{t=1}^T{\rho_t}^q},\mathrm{for}\;0\le {\rho}_t\le 1\ \mathrm{and}\;q\in \Re $$
(1)

where ρte is an T × 1 density vector, q is the power for modifying the convexity of the function, and T is the number of elements involved for aggregate. Note that LA is 1 if all ρt = 1, and it is 0 if any of ρt = 0 (i.e., it is a continuous logical conjunction function that can be analogue to N multiple Boolean “and” operators). This function can be either convex or concave according to the value of q. With this property, LA function can be easily modified to satisfy the associate optimization problem. In addition, this function can be regarded as a “softand” function which smoothly approximates the logistic “and” operators using a continuous function similar to the “softmax” function.

Figure 1 illustrates the geometrical relation of three different overhang angles in Zhao et al.: (a) 45°, (b) 63.4°, and (c) 26.6°. For deriving the overhang angle as the element relation that can be directly applied to optimal constraint without additional mathematical transformations, a continuous convex function is indispensable. A logistic function SFte(ρte) quantifying the degree of supporting of ρt0 by each ρte is defined as

$$ S{F}_{te}\left({\boldsymbol{\uprho}}_{te}\right)=2\frac{{\left(1-{\rho}_{te}\right)}^r{\rho_{t0}}^s}{{\left(1-{\rho}_{te}\right)}^r+{\rho_{t0}}^s},{\boldsymbol{\uprho}}_{te}=\left[{\rho}_{t0},{\rho}_{te}\right],\forall e\ne 0 $$
(2)

where SFte(ρte) varies between 0 and 1, and ∀e ≠ 0 represents the number of supporting elements. The subscribe e in (2) can be extended to the general overhang angles including those listed in Fig. 1 (i.e., e = 1~3 for 45° and 63.4°, and e = 1~7 for 26.6°). If ρt0 is full but its underneath ρte is a void element, then SFte(ρte) = 1, which represents an unsupported situation (i.e., ρt0 = 1 and ρte = 0). The functions of SFte(ρte) for r = s = 1 and r = s = 2 are illustrated in Fig. 2a and b, respectively. The powers r and s play similar roles as the power q for each ρt in (1).

Fig. 2
figure 2

Value of SFte(ρte), where a is r = s = 1 and b is r = s = 2

Full size image

Because of its simplicity and frequent occurrence, a 45° overhang angle (Fig. 1a) is first selected as an example to determine whether the element ρt0 is supported adequately by its underneath supporting elements ρt1, ρt2, and ρt3. Now, both the logistic and aggregate properties of (1) are used here by assuming q = 1 and replacing ρt in (1) with SFte(ρte) from (2):

$$ S{F}_n\left({\boldsymbol{\uprho}}_t\right)=3\frac{\prod_{e=0}^3S{F}_{te}\left({\boldsymbol{\uprho}}_{te}\right)}{\sum_{e=0}^3S{F}_{te}\left({\boldsymbol{\uprho}}_{te}\right)},{\boldsymbol{\uprho}}_t=\left[{\rho}_{t0},{\rho}_{t1},{\rho}_{t2},{\rho}_{t3}\right] $$
(3)

where SFn(ρt) is the proposed SSI for ρt0 ranging between 0 and 1. Notably, element ρt3 = 0 if it is located on the right edge of a design domain. Figure 3 presents a plot of SSI according to (3) with different values of r and s with ρt3 = 0. Each figure from Fig. 3a–d has three surfaces, from top to bottom corresponding to ρt0 = 1, 0.5, and 0, respectively. The vertical edges in Fig. 3 illustrated by the dotted line indicate that the SFn(ρt) depends only on ρt0 and s when ρt1 = ρt2 = 0. These three lines are compared in Fig. 3e, which shows that SSI gradually changes from the concave to convex function with an increase in s. Comparing Fig. 3d with the rest of Fig. 3, the SFn(ρt) value is small for any ρte when ρt0 is below 0.5. Consequently, the gradient is insensitive with respect to the change of ρ1 and ρ2, which makes Fig. 3d inadequate as an SSI for topology optimization. Therefore, after testing r and s from 1 to 3 respectively and examining the resulting convex surfaces and curves for better convergence, r = 3 and s = 2 as illustrated in Fig 3a are selected to be the default values for the following self-supporting constraints.

Fig. 3
figure 3

Value of SFn(ρt) when ar = 3 and s = 2, br = s = 1, cr = s = 2, dr = s = 3, and eρt1 = ρt2 = ρt3 = 0

Full size image

For sensitivity analysis, Fig. 4 shows three gradient schemes of SSI: the gradient is required only for the supported element, the supporting elements, and for both the supported and supporting elements, as respectively illustrated in Fig. 4a, b, and c. From a mathematical perspective, Fig. 4a shows that variation in the supported element ρt0 depends on whether the supporting element ρte exists during the optimization, whereas Fig. 4b shows the opposite (i.e., the variation in the supporting element ρte depends on the supported element ρt0). Last, Fig. 4c illustrates that both the gradients of supported and supporting elements are taken into consideration during optimization.

Fig. 4
figure 4

Three different schemes for determining the sensitivity of self-supporting constraints

Full size image

According to the sensitivity analysis and the associated demonstration from Gaynor and Guest (2016), the upper/supported element can exist only if the lower/supporting elements can provide enough support. One way to meet this overhang angle constraint is to modify the upper/supported elements (i.e., similar with Fig. 4a in this study). On the other hand, according to the sensitivity analysis from Langelaar (2017), the lower/supporting elements can be modified during the optimization to provide enough support for the upper/supported one, which leads to the similar element modification as shown in Fig. 4b in this study.

Comparing with Gaynor and Guest (2016) and Langelaar (2017), the topology optimization method used in this study can meet the overhang constraint based on the proposed gradient scheme involving both supported and supporting elements. This means if the supported element need support, supporting elements have chance to increase the density. On the other hand, the supporting elements might be dropped out if the supported one does not exist. This is why we present and compare all three schemes in this study.

The sensitivity of SSI from Fig. 4 is illustrated as follows:

$$ \frac{\partial SF\left(\boldsymbol{\uprho} \right)}{\partial {\boldsymbol{\uprho}}_n}=\frac{\sum_{n=1}^N\partial S{F}_n\left({\boldsymbol{\uprho}}_t\right)}{\partial {\boldsymbol{\uprho}}_n} $$
(4)

where ρ is a N × 1 density vector of the whole design domain, N is the number of elements involved for topology optimization, and ρn is the element that will be updated according to the gradient schemes illustrated in Fig. 4. ρn varies in different schemes: ρn = [ρt0] in Fig. 4a, ρn = [ρt1, ρt2, ρt3] in Fig. 4b, and ρn = [ρt0, ρt1, ρt2, ρt3] in Fig. 4c.

3 Characteristics of SSI using a cantilever

Figure 5 illustrates a cantilever with a size of 0.03 × 0.09 m2, and it is fixed at its bottom. The design domain is meshed using 4-node square finite elements with a size of 0.5 × 0.5 mm2, the Young’s modulus is 70 GPa, and the Poisson’s ratio is 0.3. This beam is subjected to a horizontal force of 50 Nt acting on the center of its free top end. The objective is to minimize the total strain energy c, or equivalently the compliance, with a 50% volume reduction of the design domain. The fabrication process of printing this cantilever is from bottom to top, and the self-supporting requirement must be satisfied. The formulation based on topology optimization without including the gravity effect is written as follows:

$$ \mathit{\operatorname{Minimize}}:\kern0.5em c\left(\boldsymbol{\uprho} \right)={\mathbf{F}}^T\mathbf{u}={\mathbf{u}}^T\mathbf{Ku} $$
(5a)
$$ Subject\ to:\kern0.5em \sum \limits_{n=1}^N{\rho}_n{v}_n\le {\mathrm{V}}_{\mathrm{t}} $$
(5b)
$$ \frac{SF\left(\boldsymbol{\uprho} \right)}{{\mathrm{SF}}_0}=\frac{\sum_{n=1}^NS{F}_n\left({\boldsymbol{\uprho}}_t\right)}{{\mathrm{SF}}_0}\le \varepsilon $$
(5c)
$$ {10}^{-4}={\rho}_{\mathrm{min}}\le {\rho}_n\le 1 $$
(5d)
$$ \mathbf{Ku}=\mathbf{F} $$
(5f)

where the objective function c(ρ) is the total strain energy of the design domain, u is the displacement vector of each node, K is the global stiffness matrix, F is the force vector, and Ku = F is the force equilibrium equation that is also required to calculate the sensitivity during optimization. vn is the volume of each element, Vt is the value of total volume constraint (i.e., 50% in this practice), and ρmin is the lower bound of the density that prevents singularity during the finite-element analysis. The continuation method that progressively increases p from 1 to 3 with an increment of 0.125 is adopted here to encourage a 0–1 design that might keep the objective close to the global optimum (Petersson and Sigmund 1998).

Fig. 5
figure 5

Design domain of cantilever beam for performing self-supporting structure topology optimization

Full size image

SF(ρ) is the summation of all the elemental SSIs SFn(ρt), and SF0 is the value of SF(ρ) when all the elements are in the poorest supporting condition (i.e., all of the elements have the same penalty index equal to value 1). According to (5c), the overhang constraint is satisfied by approximating the normalized summation SSIs to 0 (i.e., ε is close to 0). Normalizing SF(ρ) with respect to SF0 smooths the sensitivity of the self-supporting constraint, and therefore the topology layout is able to converge during optimization. Figure 6 shows the resulting cantilever with and without normalization under a 45° angle constraint. The resulting cantilever topology becomes too sparse and over-constrained if (5c) has not been normalized.

Fig. 6
figure 6

Cantilever after topology optimization a with and b without normalization

Full size image

3.1 Topology layout comparisons from different gradient schemes

Figure 7a–d show the resulting topology layouts with and without 45° self-supporting constraints, whereas Fig. 7e–h show the corresponding SSI distributions in the gray scale. Figure 7b–d show the resulting topology layouts with the three different gradient schemes previously mentioned. The SSI distribution in Fig. 7e–h represents the degree of self-support, where the darker gray denotes larger SSI.

Fig. 7
figure 7

Topology layout of cantilever with and without self-supporting constraint and their corresponding SSI: a and e without self-supporting constraint, b and f with gradients only on the supported elements, c and g with gradients only on supporting elements, and d and h with gradients on both supporting and supported elements

Full size image

The topology resulting from using only the supported element gradient as in Fig. 4a appears to be a sufficiently sharp layout, even though the Heaviside filter (Sigmund 2007) has not been adopted. This shows that 95% of all elements in the design domain are less than 0.1 or larger than 0.9. However, a more detailed examination reveals that parts of the internal structure are not properly self-supported for a 45° overhang angle. As can be seen in Fig. 7f, the four portions of the design domain, two near the top and the other two in the middle of the cantilever, have SSI values larger than 0.14, which indicates that they are not properly self-supporting. This poor self-support is improved when the gradient scheme is changed to involve only the supporting element gradient, as illustrated in Fig. 4b. Figure 7c shows only two small portions near the top of the cantilever with SSI values larger than 0.14. The gradients of both the supported and supporting elements are displayed in Fig. 7d. All SSIs in Fig. 7h are smaller than 0.0452, which indicates that all the structures in the design domain are self-supporting. Presenting the SSI distribution in gray scale as in Fig. 7e–h helps to identify whether the structure is self-supporting during the AM process.

Table 2 compares the compliance c, SF(ρ), and SSI in the design domain from each topology layout in Fig. 7. The compliance of the topology without self-supporting constraint is used as a baseline denoted by Cref. Comparing the topology layouts from the results involving self-supporting constraint in the optimization, the compliance is positively correlated to the quantity of twigs. The more twig-like ribs in the structure, the higher the total strain energy is. Using only the supporting elements’ gradient during optimization, the layout tends to have more twig-like structures, as shown in Fig. 7c; whereas with only the supported elements’ gradient, the resulting topology appears to have more trunk-like structures.

Table 2 Self-supporting index and compliance of Fig. 7
Full size table

The maximum value of SSI in Fig. 7h is at least three times smaller than the others. In this study, the threshold is not explicitly defined to determine whether elements are self-supporting; however, the SSI truly reflects the relative degree of self-supporting in a specific structure. The normalized summation SSIs (5c), SF(ρ)/SF0, numerically approximates to a very small number close to zero. It indicates that results optimized by GCMMA are numerically convergent and acceptable with the proposed overhang constraint. The standard deviation (SD) of the SSI listed in Table 2 quantifies the distribution of the SSI for each topology layout. The SSI distribution of the topology layout without self-supporting constraint spreads out over a wider range, and the SD is an order larger than those with self-supporting constraint. This result shows that when the SSI distribution tends to be less dispersive, the self-supporting constraint effectively restricts the overhang in the prescribed angle (45° in this example). Figure 7d shows a compromise between the compliance and the self-supporting requirement because the compliance of the topology without the self-supporting constraint is the smallest.

Comparing with Gaynor and Guest (2016) and Langelaar (2017) mentioned in the end of Section 2, the topology optimization method used in this study can meet the overhang constraint based on the proposed gradient scheme involving both supported and supporting elements.

3.2 Self-supporting structures with general overhang angle constraints

To validate the proposed LA function–based SSI that can be employed for general overhang angle constraints, three different overhang angles, as shown in Fig. 1, were applied to the same cantilever model.

A comparison between Fig. 1a and b denotes that the quantity of supporting elements ρte and the derivation of SF(ρ) are the same even though the supporting configuration is different. In contrast to Fig. 1a and b, Fig. 1c is different in both supporting configuration and the supporting element numbers. However, simply changing e in (3) from 3 to 7 yields Fig. 1c. In general, the proposed LA function SFn(ρt) can be used for any arbitrary overhang angle regardless of the number of supporting elements ρte.

Figure 8a shows a resulting cantilever after topology optimization without overhang constraint, whereas Fig. 8 b–d display the same cantilever problem with three different overhang angle constraints: 26.6°, 45°, and 63.4°, respectively. Figure 8e–h show the SSI distribution on the gray scale. All the cantilevers shown in Fig. 8 result from topology optimization with the gradient of both supporting and supported elements. In order for an easier examination, the small triangles illustrated in each figure are added to represent the specific overhang angle for each result (i.e., 26.6° in the right half of Fig. 8a and 45° in the left half, 26.6° in Fig. 8b, 45° in Fig. 8c, and 63.4° in Fig. 8d). Some of the non-overhanging beams have light gray color in Fig. 8e with 45° SSI detection; however, they have a magnitude at least an order smaller than the highest values. These blur elements in Fig. 8e correspond to the blur boundary of those ribs’ profile in Fig. 8a. The severity of blur distributions can be mitigated with the proposed overhang constraint as can be seen in the self-supporting results in this study.

Fig. 8
figure 8

Cantilevers after topology optimization with different overhang angle constraints and their corresponding SSI: a and e are without overhang angle constraint, b and f have an overhang angle constraint of 26.6°, c and g)have a 45° constraint, and d and h have a 63.4° constraint

Full size image

Figure 8a shows that parts of the internal rib-like structure inside the cantilever have angles less than 26.6°, which might not be possible to manufacture using AM. Topology layouts with self-supporting constraints, as illustrated in Fig. 8b–d, meet their respective angle constraint. For example, the layout shown in Fig. 8a looks similar to that in Fig. 8b. However, upon further examination, every internal rib–like structure inside the cantilever in Fig. 8b has angles larger than 26.6°, which guarantees that the cantilever satisfies the overhang constraint. The maximum SSIs of Fig. 8a–d are 0.18518, 0.000023, 0.04513, and 0.08095, which indicates that the maximum SSIs with the overhang constraints are at least two times smaller than that without overhang constraint.

Figure 9 plots the convergence history for both the compliance and the normalized summation SSIs from results of Fig. 8. In Fig. 9a, the compliance from the topology layout without overhang constraint and that with 26.6° overhang angle constraint converges to the value close to each other. Consequently, their corresponding topology layouts illustrated in Fig. 8a and b look alike. With the increase in the overhang angle, the topology layout evolves to have more twig-like ribs. Nevertheless, the compliance from the topology layout converges after 60 iterations. Figure 9b shows that all the normalized summation SSI from the results with overhang angle constraints approximate to 0 after 100 iterations.

Fig. 9
figure 9

Optimization history for different overhang angles: a are the objective values from (5a) and b are the normalized SSI values from (5c)

Full size image

Table 3 lists the SSI and the compliance of Fig. 8. The SD of SSIs without overhang constraint is larger than those with overhang constraint. It indicates that the SSI values with overhang constraint distribute more concentration with a smaller maximum value. Although the summation of SSIs, SF(ρ), corresponding to the overhang constraint of 63.4° is larger than that without constraint, the maximum SSI, Max SFn(ρt), is at least twice smaller. The larger value of SF(ρ) is because the more twig-like ribs the more blur element appearing in the topology layout. Nevertheless, Fig. 8d still satisfies the overhang angle constraint.

Table 3 Self-supporting index and compliance of Fig. 8
Full size table

Figure 10a and b displays the FDM practices comparing workpiece quality with and without overhang angle constraint (e.g., Fig. 7a and d). Both FDM processes were realized using Ultimaker 2+ with the suggested optimal process parameters in Cura 3.2. The structures with overhang angles smaller than 45° can still be printed. Nevertheless, Fig. 10a shows that some portions of the structure as indicated by the rectangular boxes significantly have flash, especially at the bottom of branches whose angles are less than 45°. By contrast, the four solid lines with angles of 45° as shown in Fig. 10b indicate that every part of the structure satisfies the required overhang constraint, and consequently, the resulting structure has a high-quality surface at the bottom of every branch.

Fig. 10
figure 10

Topologically optimal cantilever print obtained using the FDM machine a without and b with a 45°overhang angle constraint

Full size image

4 Topology layout comparisons from general workpiece orientations

To further prove that the proposed SSI can be generally applied to different structure designs oriented in arbitrary directions, a symmetric MBB beam model was selected with the same dimension as that of Langelaar (2017). Figure 10 illustrates a 90 × 30 mm2 half-MBB beam meshed by 0.5 × 0.5 mm2 4-node square elements with a 70 GPa Young’s modulus and 0.3 Poisson’s ratio. The beam is subjected to a vertical 50 N concentrated force on the left top corner, and it is fixed horizontally on its left side due to the symmetry. The formulation is the same as that in (5) with a 45° overhang angle constraint.

Figure 12 illustrates the topology layout with and without self-supporting constraints. All the MBB beams are built from bottom to top in the AM process, as indicated by the arrow at the corner in each figure. The SSI distributions are illustrated next to their corresponding topology layout. Fig. 12a is the only layout without the overhang angle constraints, whereas the others have 45° overhang angle constraints. Figure 12a and b is the same orientation as Fig. 11, whereas Fig. 12c is a horizontal reflection of Fig. 11. Figure 12d is a 90° counterclockwise rotation of Fig. 11, and Fig. 12e is a horizontal reflection of Fig. 12d.

Fig. 11
figure 11

Design domain of half-MBB beam for performing self-supporting structure topology optimization

Full size image
Fig. 12
figure 12

Half of MBB beam in different orientations after topology optimization with and without 45° overhang angle constraint: a the only set without overhang constraint, in the same position as Fig. 11; b same orientation as (a) but with overhang constraint; c the horizontal reflection of (b); d 90° counterclockwise rotation from (a); and e horizontal reflection of (d)

Full size image

Table 4 compares the compliance, SF(ρ), and SSI in the design domain from each topology layout in Fig. 12. Because CAMD was applied instead of the Heaviside filter, the quantity of relatively high-value SSI correlates as much to the quantity of blur elements as it does to the twig quantity. This phenomenon leads to the SF(ρ) in Fig. 12b and c being almost twice as high as those in Fig. 12d and e, even though the four maximum SSIs corresponding respectively to Fig. 12b–e are closed to each other in magnitude, as listed in Table 4. In addition, comparing the compliance of the topology with and without self-supporting constraints, the more twigs that appear in the structure, the more compliant the structure is, as can be seen in Table 2.

Table 4 Self-supporting index and compliance of Fig. 12
Full size table

5 Conclusion

This study proposed a continuous LA function that can be employed not only in quantifying the degree of self-support for each element through the topology layout but also for satisfying arbitrary overhang angle requirements. The proposed LA function does not require additional mathematical transformations for optimization formulation, and it can be directly applied in sensitivity analysis. This formulation can make the resulting topology layouts meet the overhang angle constraint for general orientations of the deposition direction, as specified for AM.

So far, there is no threshold or critical value of SSI for estimating whether each element is self-supporting in this study. As an alternative, the maximum value and the standard deviation of SSI are utilized for assessing the effectiveness of proposed self-supporting constraint. Every portion of the resulting topology layout in Figs. 8 and 12 guarantees satisfying the self-supporting requirement with the proposed self-supporting constraint. Therefore, the threshold value of SSI is not required, and the maximum and SD of SFn(ρt) proves to be sufficient to determine whether the element is well-supported during the optimization. The proposed SSI includes design for manufacturability requirements in the topology design by using FDM practices according to the topology layout results.