An efficient multi-objective optimization method for uncertain structures based on ellipsoidal convex model

Abstract

Compared with the interval model, the ellipsoidal convex model can describe the correlation of the uncertain parameters through a multidimensional ellipsoid, and whereby excludes extreme combination of uncertain parameters and avoids over-conservative designs. In this paper, we attempt to propose an efficient multi-objective optimization method for uncertain structures based on ellipsoidal convex model. Firstly, each uncertain objective function is transformed into deterministic optimization problem by using nonlinear interval number programming (NINP) method and a possibility degree of interval number is applied to deal with the uncertain constraints. The penalty function method is suggested to transform the uncertain optimization problem into deterministic non-constrained optimization problem. Secondly, the approximation model based on radial basis function (RBF) is applied to improve computational efficiency. For ensuring the accuracy of the approximation models, a local-densifying approximation technique is suggested. Then, the micro multi-objective genetic algorithm (μMOGA) is used to optimize design parameters in the outer loop and the intergeneration projection genetic algorithm (IP-GA) is used to treat uncertain vector in the inner loop. Finally, two numerical examples and an engineering example are investigated to demonstrate the effectiveness of the present method.

1 Introduction

Uncertainties of material properties, manufacturing errors, and bound conditions are often involved in engineering structure optimization problems; however, these uncertain parameters are treated as deterministic parameters in traditional optimization problems (Lagaros et al. 2005; Liu et al. 2008; Lin et al. 2010; Xia et al. 2018), which will induce non-economical structural design. Therefore, the effective uncertain optimization methods should be developed for uncertain structure optimization problems. In order to deal with uncertain optimization problems, the probability model (Rackwitz and Fiessler 1978; Liang et al. 2007; Tsai et al. 2013; Bobby et al. 2017) is applied to describe the uncertainty of the parameters. In this model, the uncertainty is described by random parameter for which the probability distribution should be known. Unfortunately, it is difficult to get accurate probability distribution in actual engineering problem. Furthermore, the probability distribution is very sensitive to the optimization results. The literature (Ben-Haim and Elishakoff 1990) has shown that even small deviations of probability distributions of the uncertain parameters may cause large errors of the computational results.

Although the precise probability distribution is difficult to be obtained, a small quantity of information on the uncertain parameters could be confirmed according to the practical engineering experiences. To remedy the deficiencies of the traditional probability method, therefore, non-probability convex model (Ben-Haim 1994; Adduri and Penmetsa 2007; Jiang et al. 2011) has been well-developed based on the limited knowledge of the uncertain parameters. The frequently used convex models are the interval model and the ellipsoidal convex model. In the interval model, the fluctuation of the uncertain parameter is expressed by an interval (Qiu and Elishakoff 1998; Du 2007; Jiang et al. 2008a). Furthermore, uncertain parameters vary independently and may reach their extreme values simultaneously, which would induce an over-conservative description of the system variability. Comparing to the interval model, the ellipsoidal convex model can describe the correlation of the uncertain parameters through a multidimensional ellipsoid (Luo et al. 2009; Liu and Zhang 2014), which excludes extreme combination of uncertain parameters and avoids over-conservative designs. Thus, the uncertain optimization method based on the ellipsoidal convex model seems more significant in practical engineering application (Kang and Luo 2010).

Simultaneously, many uncertain optimization problems involve more than one objective, which are treated as uncertain multi-objective optimization (U-MOO) problems. On the best knowledge of the authors, Stancu-Minasian (Stancu-Minasian 1984) seems the first attempt to study the stochastic multi-objective programming problem which opens the door for U-MOO research. Kaushik (Kaushik 2007) presented a methodology for reliability-based multi-objective optimization of large-scale engineering systems based on two first-order reliability method. Liu et al. (Liu et al. 2017) proposed a multi-objective optimization method based on interval model to obtain the Pareto optimal set (Deb 2001) of the uncertain multi-objective optimization problems; however, these works all focus on the U-MOO problem containing the independent uncertain parameters, namely, not considering the correlation of the uncertain parameters. Yet in practice, engineering problems often present correlations between uncertain parameters, hence the interest of exploring the ellipsoidal convex model in the context of U-MOO.

It should be noted that the uncertain multi-objective optimization method based on the ellipsoidal convex model generally belong to the two-loop nesting optimization problem. Furthermore, the objective and constraint functions do not have straightforward mathematical expressions in many engineering problems. They are treated as black-box functions (i.e., complex finite element models) whose evaluation is very time-consuming. When such models are involved, it will lead to extremely low efficiency and influence the practicability of the uncertain multi-objective optimization method. For this reason, the approximation techniques (Queipo et al. 2005) have been widely applied to alleviate the computational burden, based on which the approximation value of the objective and constraint functions could be obtained quickly. Among existing approximation techniques, polynomial (Jin et al. 2001), radial basis function (RBF) (Fang et al. 2005), and Kriging (Simpson et al. 2001; Hawchar et al. 2018; Dubourg et al. 2011) are the most widely used and a series of prominent work in this filed has been carried out and reported. Simultaneously, in order to improve the accuracy of approximation model and the computational efficiency, Li et al. (Li et al. 2013) developed an adaptive Kriging approximation model to achieve the interval-based uncertain multi-objective optimization. Zhao et al. (Zhao et al. 2010) proposed a local-densifying approximation technique to improve the efficiency of uncertain optimization. The results show that the local-densifying approximation technique can procure a higher accuracy of the approximate model with fewer sample points. Hence, to push the U-MOO method based on ellipsoidal convex model into practical applications, its computational efficiency and corresponding efficient algorithms with approximation technique should be both developed.

This paper aims to develop an efficient multi-objective optimization method based on the ellipsoidal convex model. In the following contents, four sections are included. The uncertain multi-objective optimization problem based on ellipsoidal convex model is introduced in Section 2. In Section 3, the solutions of the uncertain multi-objective optimization method are proposed and the local-densifying approximation technique is presented in order to improve computation efficiency. Three numerical examples are investigated to demonstrate the effectiveness of the present method in Section 4. Finally, some conclusions are summarized in Section 5.

2 Statement of the problem

Generally, a multi-objective problem is described as follows:

$$ {\displaystyle \begin{array}{c}\\ {}\mathrm{Subject}\ \mathrm{to}\\ {}\end{array}}\kern0.5em {\displaystyle \begin{array}{c}\underset{\mathbf{X}}{\min }{f}_i\left(\mathbf{X}\right),\cdot i=1,2,...,s\\ {}{g}_k(X)\le {v}_k,\cdot k=1,2,...,m\\ {}\mathbf{X}\in {\varOmega}_{\mathbf{X}}^n\end{array}} $$

(1)

where X is an n-dimension design vector. f and g stand for the objective function and constraint function with the total number of s and m, respectively. v_k represents an allowable value of the kth constraint. In the process of solving above multi-objective problem, there often exists a set of optimal solutions, no solutions from which can be said to be better than any other without any further information. This set is known as the non-dominated set or the Pareto optimal set and its corresponding tradeoff in objective space is known as the Pareto optimal frontier which are made up of the Pareto optimal points (Deb 2001).

When the objective function f_i and constraint g_k contain correlated uncertain variables, the ellipsoidal convex model could be used to describe the variables and the corresponding uncertain multi-objective optimization problem can be expressed as follows:

$$ {\displaystyle \begin{array}{cc}& \underset{X}{\min }{f}_i\left(X,U\right),\cdot i=1,2,...,s\\ {}\mathrm{Subject}\ \mathrm{to}& \\ {}& {g}_k\left(X,U\right)\le {v}_k^I=\left[{v}_k^{lo},{v}_k^{up}\right],\cdot k=1,2,...,m\\ {}& \mathbf{X}\in {\varOmega}_{\mathbf{X}}^n,\cdot \mathbf{U}\in {\varOmega}_{\mathbf{U}}^p=\left\{\mathbf{U}|{\left(\mathbf{U}-{\mathbf{U}}^c\right)}^{\mathbf{T}}{G}_{\mathbf{U}}\left(\mathbf{U}-{\mathbf{U}}^c\right)\le {\varepsilon}^2\right\}\\ {}& \mathbf{U}=\left({U}_1,{U}_2,...,{U}_p\right),\cdot {U}_q\in {U}_q^I=\left[{U}_q^{lo},{U}_q^{up}\right],\cdot q=1,2,...,p\end{array}} $$

(2)

where U is a p-dimension uncertain vector which is restricted within the multi-ellipsoid ${\varOmega}_{\mathbf{U}}^p$. It is noted that for each single uncertain variable U_q which is called the marginal interval variable in this paper, its possible values will constitute an interval denoted by ${U}_q^I=\left[{U}_q^{lo},{U}_q^{up}\right]$ whose superscripts I, lo, and up denote interval, lower, and upper bounds of interval, respectively. G_U represents the characteristic matrix of the multi-ellipsoid convex model, which is a real positive-definite symmetric matrix. U^c denotes the center point of the ellipsoid. ${v}_k^I$ represents allowable interval that can be defined by the engineering requirement. Considering the fluctuation of uncertain vector U, the traditional optimization methods have limitations to solve such uncertain optimization problems. In the following sections, an uncertain multi-objective optimization method based on ellipsoidal convex model will be suggested to solve the above problem.

3 An efficient uncertain multi-objective optimization method based on ellipsoidal convex model

3.1 Treatments of the uncertain objective functions

Because of the existence of the uncertain vector U, for each specific X, the possible values of the objective function or a constraint will form an interval instead of a real number. According to nonlinear interval number programming (NINP) method (Jiang et al. 2008b), hence, the order relation ≤_mw is applied to compare the interval of objective function, which is used to qualitatively determine whether an interval is better than another interval. It should be noted that the order relation A≤_mwB implies that the interval number B is better than A but not that B is larger than A, namely, the interval B is better than A only if the midpoint and radius of B are both smaller than A. By using this order relation ≤_mw, the midpoint and radius value of the interval are chosen as the objective function. Therefore, the objective function f_i in Eq. (2) can be transformed into deterministic optimization problem as follows:

$$ \underset{\mathbf{X}}{\min}\left(c\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right),w\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)\right) $$

(3)

where.

${\displaystyle \begin{array}{c}c\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)=\frac{1}{2}\left({f}_i^{lo}\left(\mathbf{X}\right)+{f}_i^{up}\left(\mathbf{X}\right)\right)\\ {}w\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)=\frac{1}{2}\left({f}_i^{lo}\left(\mathbf{X}\right)-{f}_i^{up}\left(\mathbf{X}\right)\right)\\ {}i=1,2,...,s\end{array}}$

where c and w are the midpoint and radius value of the interval. ${f}_i^{lo}\left(\mathbf{X}\right)$ and ${f}_i^{up}\left(\mathbf{X}\right)$ are used to describe the bounds of the objective function f_i. The bounds ${f}_i^{lo}\left(\mathbf{X}\right)$ and ${f}_i^{up}\left(\mathbf{X}\right)$ in Eq. (3) can be calculated as follows:

$$ {\displaystyle \begin{array}{c}{f}_i^{lo}\left(\mathbf{X}\right)=\underset{\mathbf{U}}{\min }{f}_i\left(\mathbf{X},\mathbf{U}\right),\cdot {f}_i^{up}\left(\mathbf{X}\right)=\underset{\mathbf{U}}{\max }{f}_i\left(\mathbf{X},\mathbf{U}\right)\\ {}i=1,2,...,s\end{array}} $$

(4)

where the vector X is considered as a constant and the lower and upper bounds of the objective function f_i can be obtained.

In order to facilitate the calculation of Eq. (3), a linear combination method is applied to transform Eq. (3) into as follows:

$$ {\displaystyle \begin{array}{c}\underset{\mathbf{X}}{\min }{f}_{d_i}\left(\mathbf{X}\right)\\ {}\mathrm{where}\kern0.75em {f}_{d_i}\left(\mathbf{X}\right)=\left(1-{\beta}_i\right)\left(c\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)+{\gamma}_i\right)/{\phi}_i+{\beta}_i\left(w\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)+{\gamma}_i\right)/{\varphi}_i\\ {}i=1,2,...,s\end{array}} $$

(5)

where 0 ≤ β_i ≤ 1 is a weighting factor which imply the decision makers’ preference. γ_i is a number to make c(f_i(X, U)) + γ_i and w(f_i(X, U)) + γ_i non-negative. The parameters ϕ_i and φ_i are two normalization factors, which could be calculated as follows:

$$ {\displaystyle \begin{array}{c}{\phi}_i=\underset{\mathbf{X}}{\min}\left(c\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)+{\gamma}_i\right)\\ {}{\varphi}_i=\underset{\mathbf{X}}{\min}\left(w\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)+{\gamma}_i\right)\end{array}}. $$

(6)

In practical applications, the parameters γ_i, ϕ_i, and φ_i could be chosen according to the same order of magnitude of each individual objective function.

3.2 Treatments of the uncertain constraints

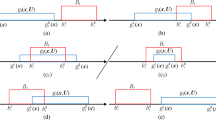
According to the interval mathematics (Jiang et al. 2008b; Moore 1979), the possibility degree can be used to quantitatively represent an extent that one interval is superior or inferior to another. For intervals A^I and B^I, there exist a total of six possible positional relations as shown in Fig. 1 (Jiang et al. 2008b), and based on these a possibility degree P(A^I ≤ B^I) is constructed:

$$ P\left({A}^I\le {B}^I\right)=\Big\{{\displaystyle \begin{array}{l}0\kern21.5em {A}^{lo}\ge {B}^{up}\\ {}0.5\cdot \frac{B^{up}-{A}^{lo}}{A^{up}-{A}^{lo}}\cdot \frac{B^{up}-{A}^{lo}}{B^{up}-{B}^{lo}}\kern12.75em {B}^{lo}\le {A}^{lo}<{B}^{up}\le {A}^{up}\\ {}\frac{B^{lo}-{A}^{lo}}{A^{up}-{A}^{lo}}+0.5\cdot \frac{B^{up}-{B}^{lo}}{A^{up}-{A}^{lo}}\kern12.5em {A}^{lo}<{B}^{lo}<{B}^{up}\le {A}^{up}\\ {}\frac{B^{lo}-{A}^{lo}}{A^{up}-{A}^{lo}}+\frac{A^{up}-{B}^{lo}}{A^{up}-{A}^{lo}}\cdot \frac{B^{up}-{A}^{up}}{B^{up}-{B}^{lo}}+0.5\cdot \frac{A^{up}-{B}^{lo}}{A^{up}-{A}^{lo}}\cdot \frac{A^{up}-{B}^{lo}}{B^{up}-{B}^{lo}}\kern0.5em {A}^{lo}<{B}^{lo}\le {A}^{up}<{B}^{up}\\ {}\frac{B^{up}-{A}^{up}}{B^{up}-{B}^{lo}}+0.5\cdot \frac{A^{up}-{A}^{lo}}{B^{up}-{B}^{lo}}\kern12.25em {B}^{lo}\le {A}^{lo}<{A}^{up}<{B}^{up}\\ {}1\kern21.25em {A}^{up}<{B}^{lo}\end{array}}\partial $$

(7)

Fig. 1

Six positional relations between intervals A and B

Here, intervals A^I and B^I are treated as random variables $\tilde{A}$ and $\tilde{B}$ with uniform distributions, and the probability for random variable $\tilde{A}$ smaller than $\tilde{B}$ is regarded as P(A^I ≤ B^I). In Eq. (7), P(A^I ≤ B^I) = 0 or 1 means that interval A^I is absolutely larger or smaller than B^I.

In this section, the possibility degree is applied to deal with the uncertain constraints. Based on the possibility degree, the constraints in Eq. (2) could be expressed as:

$$ {\displaystyle \begin{array}{cc}& P\left({g}_k^I\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I\right)\ge {\lambda}_k\\ {}\mathrm{where}& {g}_k^I\left(\mathbf{X},\mathbf{U}\right)=\left[{g}_k^{lo}\left(\mathbf{X}\right),{g}_k^{up}\left(\mathbf{X}\right)\right],{v}_k^I=\left[{v}_k^{lo},{v}_k^{up}\right]\\ {}& k=1,2,...,m\end{array}} $$

(8)

where the possibility degree $P\left({g}_k^I\left(\mathbf{X},\mathrm{U}\right)\le {v}_k^I\right)$ means the interval ${g}_k^I\left(\mathbf{X},\mathbf{U}\right)$ is smaller than the given interval ${v}_k^I$. λ_k is a predetermined possibility degree level of the kth constraint and the value of possibility degree $P\left({g}_k^I\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I\right)$ must be larger than λ_k. The bounds ${g}_k^{lo}\left(\mathbf{X}\right)$ and ${g}_k^{up}\left(\mathbf{X}\right)$ can be calculated as follows:

$$ {\displaystyle \begin{array}{c}{g}_k^{lo}\left(\mathbf{X}\right)=\underset{\mathbf{U}}{\min }{g}_k\left(\mathbf{X},\mathbf{U}\right)\\ {}{g}_k^{up}\left(\mathbf{X}\right)=\underset{\mathbf{U}}{\max }{g}_k\left(\mathbf{X},\mathbf{U}\right)\end{array}} $$

(9)

Through Eq. (9), the uncertain vector U is eliminated, and the transformed constraints Eq. (8) become deterministic. λ_k can be adjusted to control the feasible field of X.

3.3 Deterministic optimization problem

In order to transform the above Eq. (2) into deterministic non-constrained optimization problem, the penalty function method is applied for the constrains. Thus, a multi-objective and non-constraint deterministic optimization problem can be finally formulated as follows:

$$ \underset{\mathbf{X}}{\min }\ {f}_{p_i}\left(\mathbf{X}\right),i=1,2,...,s $$

(10)

where

$$ {\displaystyle \begin{array}{l}{f}_{p_i}\left(\mathbf{X}\right)={f}_{d_i}\left(\mathbf{X}\right)+{\sigma}_i\left(\sum \limits_{k=1}^m\mu \left(P\left({g}_k^I\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I\right)-{\lambda}_k\right)+\psi \right)\\ {}=\left(1-{\beta}_i\right)\left(c\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)+{\gamma}_i\right)/{\phi}_i+{\beta}_i\left(w\left({f}_i\left(\mathbf{X},\mathbf{U}\right)\right)+{\gamma}_i\right)/{\varphi}_i+{\sigma}_i\left(\sum \limits_{k=1}^m\mu \left(P\left({g}_k^I\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I\right)-{\lambda}_k\right)+\psi \right)\end{array}} $$

where ${f}_{p_i}\left(\mathbf{X}\right)$ is penalty function and σ_i stands for the penalty factor which is usually specified as a large value. μ and ψ can be expressed as follows:

$$ \mu \left(P\left({g}_k^I\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I\right)-{\lambda}_k\right)={\left(\max \left(0,-\left(P\left({g}_k^I\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I\right)-{\lambda}_k\right)\right)\right)}^2 $$

(11)

$$ \psi ={\left(\max \left(0,\left({\left(\mathbf{U}-{\mathbf{U}}^c\right)}^{\mathrm{T}}{G}_{\mathbf{U}}\left(\mathbf{U}-{\mathbf{U}}^c\right)-{\varepsilon}^2\right)\right)\right)}^2 $$

(12)

According to the above mathematical transformation, the primal U-MOO problem as Eq. (2) is converted into the non-constraint deterministic optimization problem as Eq. (10); however, it belongs to the two-loop nesting optimization problem. When the simulation models are time-consuming in practical engineering application, the expensive computational cost will be resulted. Hence, the approximate model technique will be used to improve the optimization efficiency in this paper.

3.4 The construction of the approximation models

In this section, the local-densifying approximation technique based on radial basis function (RBF) is used to solve the above uncertain multi-objective optimization problem. In the optimization process, Latin Hypercube Design (Queipo et al. 2005) is applied to obtain the initial samples of the design vector X and uncertain vector U. Then, the RBF is applied to construct the approximation models of the uncertain objective functions and constraints. Thus, Eq. (2) can be transformed as follows:

$$ {\displaystyle \begin{array}{cc}& \underset{\mathbf{X}}{\min }{\tilde{f}}_i\left(\mathbf{X},\mathbf{U}\right),\kern0.36em i=1,2,...,s\\ {}\mathrm{Subject}\ \mathrm{to}& \\ {}& {\tilde{g}}_k\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I=\left[{v}_k^{lo},{v}_k^{up}\right],\kern0.48em k=1,2,...,m\\ {}& \mathbf{X}\in {\varOmega}_{\mathbf{X}}^n,\kern0.36em \mathbf{U}\in {\varOmega}_{\mathbf{U}}^p=\left\{\mathbf{U}|{\left(\mathbf{U}-{\mathbf{U}}^c\right)}^{\mathbf{T}}{G}_{\mathbf{U}}\left(\mathbf{U}-{\mathbf{U}}^c\right)\le {\varepsilon}^2\right\}\\ {}& {U}_q\in {U}_q^I=\left[{U}_q^{lo},{U}_q^{up}\right],\kern0.36em q=1,2,...,p\end{array}} $$

(13)

where ${\tilde{f}}_i$ and ${\tilde{g}}_k$ are approximation models of the objective function and the kth constraint, respectively. They are both explicit functions with respect to X and U. Based on the interval mathematics and penalty function method, Eq. (13) can be transformed into the following optimization problem:

$$ \underset{\mathbf{X}}{\min }\ {\tilde{f}}_{p_i}\left(\mathbf{X}\right),\kern0.36em i=1,2,...,s $$

(14)

where

${\displaystyle \begin{array}{l}{\tilde{f}}_{p_i}\left(\mathbf{X}\right)={\tilde{f}}_{d_i}\left(\mathbf{X}\right)+{\sigma}_i\left(\sum \limits_{k=1}^m\mu \left(P\left({\tilde{g}}_k^I\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I\right)-{\lambda}_k\right)+\psi \right)\\ {}=\left(1-{\beta}_i\right)\left(c\left({\tilde{f}}_i\left(\mathbf{X},\mathbf{U}\right)\right)+{\gamma}_i\right)/{\phi}_i+{\beta}_i\left(w\left({\tilde{f}}_i\left(\mathbf{X},\mathbf{U}\right)\right)+{\gamma}_i\right)/{\varphi}_i+{\sigma}_i\left(\sum \limits_{k=1}^m\mu \left(P\left({\tilde{g}}_k^I\left(\mathbf{X},\mathbf{U}\right)\le {v}_k^I\right)-{\lambda}_k\right)+\psi \right).\end{array}}$For the above approximation U-MOO problem, the bounds of objective functions and constraints are usually most concerned. While the local-densifying method is an updating strategy of sampling method focusing the limited sample resources on the local regions we concerned, namely more samples are expected to be densified into the local regions where the minimal and maximal responses of objective and constraints occur. If the approximation model precision of local regions where the bounds of objective functions and constraints could be guaranteed, the optimization results can be more reliable. Therefore, the local-densifying approximation technique is used to ensure the approximation models have small approximate errors in the bounds. When the approximation bounds of the objective function and constraints are obtained in each iterative step, the RBF approximation models are reconstructed using local densified samples for the next iteration until the stopping criteria are reached.

3.5 Iterative mechanism

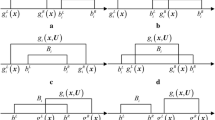
Because the above uncertain multi-objective optimization problem belongs to the two-loop nesting optimization problem, the micro multi-objective genetic algorithm (μMOGA) (Liu et al. 2008) is used to optimize design vector X in the outer loop and the intergeneration projection genetic algorithm (IP-GA) (Liu and Han 2003) is used to compute the bounds of the objective functions and constraints in the inner loop. The flowchart of the U-MOO method with local-densifying approximation technique is shown in Fig. 2 and the iterative process of the algorithm can be considered as follows:

• (1) Obtain the initial samples by Latin Hypercube Design within the hybrid space Ω and calculating the response values f_i(X, U) and g_k(X, U). Giving allowable error δ > 0 and making the iterative step a = 1.

Fig. 2

The flowchart of uncertain multi-objective optimization method with local-densifying approximation technique

$$ \boldsymbol{\Omega} =\left\{\left(\mathbf{X},\mathbf{U}\right)/{\mathbf{X}}^{lo}\le \mathbf{X}\le {\mathbf{X}}^{up},{\left(\mathbf{U}-{\mathbf{U}}^c\right)}^{\mathbf{T}}{G}_{\mathbf{U}}\left(\mathbf{U}-{\mathbf{U}}^c\right)\le {\varepsilon}^2\right\} $$

(15)

• (2) Construct the approximation model of objective functions and constraints with the samples and obtaining the approximate optimization problem as Eq. (14). The micro multi-objective genetic algorithm and the intergeneration projection genetic algorithm are used to solve the approximate optimization problem as Eq. (14) and obtain the Pareto optimal set of approximate penalty functions $\left\{{\tilde{f}}_{p_i}^{(a)}\left({\mathbf{X}}^{(z)}\right)\right\}$, z = 1, 2, ..., t, where ${\tilde{f}}_{p_i}^{(a)}\left({\mathbf{X}}^{(z)}\right)$ represents the zth Pareto solution of the Pareto optimal set in step a.

According to the Pareto optimal set $\left\{{\tilde{f}}_{p_i}^{(a)}\left({\mathbf{X}}^{(z)}\right)\right\}$, the response interval of the objective functions $\left[{\tilde{f}}_i^{lo}\left({\mathbf{X}}^{(z)}\right),{\tilde{f}}_i^{up}\left({\mathbf{X}}^{(z)}\right)\right]$ and constraints $\left[{\tilde{g}}_k^{lo}\left({\mathbf{X}}^{(z)}\right),{\tilde{g}}_k^{up}\left({\mathbf{X}}^{(z)}\right)\right]$ can be obtained:

$$ {\displaystyle \begin{array}{c}{\tilde{f}}_i^{lo}\left({\mathbf{X}}^{(z)}\right)={\tilde{f}}_i\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{lo}}^{(z)}\right),{\tilde{f}}_i^{up}\left({\mathbf{X}}^{(z)}\right)={\tilde{f}}_i\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{up}}^{(z)}\right)\\ {}{\tilde{g}}_k^{lo}\left({\mathbf{X}}^{(z)}\right)={\tilde{g}}_k\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{lo}}^{(z)}\right),\kern0.36em {\tilde{g}}_k^{up}\left({\mathbf{X}}^{(z)}\right)={\tilde{g}}_k\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{up}}^{(z)}\right)\end{array}}. $$

(16)

That means the approximate objective function and constraints achieve the minimum and maximum at the combinations $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{lo}}^{(z)}\right)$, $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{up}}^{(z)}\right)$, $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{lo}}^{(z)}\right)$, and$\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{up}}^{(z)}\right)$, respectively.

• (3) Based on the real model, computing the corresponding interval $\left[{f}_i^{lo}\left({\mathbf{X}}^{(z)}\right),{f}_i^{up}\left({\mathbf{X}}^{(z)}\right)\right]$ and $\left[{g}_k^{lo}\left({\mathbf{X}}^{(z)}\right),{g}_k^{up}\left({\mathbf{X}}^{(z)}\right)\right]$ at the combinations $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{lo}}^{(z)}\right)$, $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{up}}^{(z)}\right)$, $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{lo}}^{(z)}\right)$, and $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{up}}^{(z)}\right)$, respectively.

$$ {\displaystyle \begin{array}{l}{f}_i^{lo}\left({\mathbf{X}}^{(z)}\right)={f}_i\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{lo}}^{(z)}\right),\kern0.36em {f}_i^{up}\left({\mathbf{X}}^{(z)}\right)={f}_i\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{up}}^{(z)}\right)\\ {}{g}_k^{lo}\left({\mathbf{X}}^{(z)}\right)={g}_k\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{lo}}^{(z)}\right),\kern0.36em {g}_k^{up}\left({\mathbf{X}}^{(z)}\right)={g}_k\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{up}}^{(z)}\right)\end{array}} $$

(17)

• (4) Calculate the maximum error Δ_max:

$$ {\displaystyle \begin{array}{l}\kern11.15999em {\varDelta}_{\mathrm{max}}=\max \left\{{\varDelta}_z\right\},\kern0.5em z=1,2,...,t\\ {}{\varDelta}_z=\max \left\{|\frac{f_i^{lo}\left({\mathbf{X}}^{(z)}\right)-{\tilde{f}}_i^{lo}\left({\mathbf{X}}^{(z)}\right)}{f_i^{lo}\left({\mathbf{X}}^{(z)}\right)}|,|\frac{f_i^{up}\left({\mathbf{X}}^{(z)}\right)-{\tilde{f}}_i^{up}\left({\mathbf{X}}^{(z)}\right)}{f_i^{up}\left({\mathbf{X}}^{(z)}\right)}|,|\frac{g_k^{lo}\left({\mathbf{X}}^{(z)}\right)-{\tilde{g}}_k^{lo}\left({\mathbf{X}}^{(z)}\right)}{g_k^{lo}\left({\mathbf{X}}^{(z)}\right)}|,|\frac{g_k^{up}\left({\mathbf{X}}^{(z)}\right)-{\tilde{g}}_k^{up}\left({\mathbf{X}}^{(z)}\right)}{g_k^{up}\left({\mathbf{X}}^{(z)}\right)}\right\}\end{array}} $$

(18)

• (5) If Δ_max ≤ δ, then {X^(z)} is selected as the final optimal design vector and the iteration terminates. Otherwise, $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{lo}}^{(z)}\right)$, $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{f}}_i^{up}}^{(z)}\right)$, $\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{lo}}^{(z)}\right)$, and$\left({\mathbf{X}}^{(z)},{\mathbf{U}}_{{\tilde{g}}_k^{up}}^{(z)}\right)$ will be added to the sample point space, which is used to construct the new approximate models of objective functions and constraints. Set a = a + 1 and turn to step (2).

4 Numerical examples and discussion

In this section, two numerical examples and one engineering example will be investigated. The computational efficiency and optimization accuracy of the present method are tested by the first two ones. In order to exhibit the applicability of the algorithm to practical engineering problem, the present method is also used to optimize occupant restraint system in full vehicle frontal impact.

4.1 Numerical example 1

A numerical example with two objective functions and three constraints is given as:

$$ {\displaystyle \begin{array}{cc}& {f}_1\left(\mathbf{X},\mathbf{U}\right)={U}_1{\left({X}_1+{X}_2-7.5\right)}^2+{U}_2^2{\left({X}_2-{X}_1+3\right)}^2/4a\\ {}& {f}_2\left(\mathbf{X},\mathbf{U}\right)={U}_1^3{\left({X}_1-1\right)}^2/4+{U}_2^2{\left({X}_2-4\right)}^2/2\\ {}\mathrm{Subject}\ \mathrm{to}& {g}_1\left(\mathbf{X},\mathbf{U}\right)={U}_1\left({X}_1-2\right)/2+{U}_2{X}_2-2.5\le \left[-1,1\right]\\ {}& {g}_2\left(\mathbf{X},\mathbf{U}\right)={U}_1{X}_2+{U}_2{X}_1-3.85\le \left[-1,1\right]\\ {}& {g}_3\left(\mathbf{X},\mathbf{U}\right)={U}_1\left({X}_1-0.6\right)/4+{U}_2{X}_2-0.3\le \left[1,3\right]\\ {}& \mathbf{X}={\left({X}_1,{X}_2\right)}^{\mathbf{T}},0\le {X}_1\le 3,0\le {X}_2\le 3,{\left(\mathbf{U}-{\mathbf{U}}^c\right)}^{\mathbf{T}}{G}_{\mathbf{U}}\left(\mathbf{U}-{\mathbf{U}}^c\right)\le 0.002\end{array}} $$

(19)

where X is the design vector. U = (U₁, U₂)^T stands for the uncertain vector whose intervals are denoted by:

$$ {U}_1\in \left[0.9,1.1\right],{U}_2\in \left[0.9,1.1\right] $$

(20)

U^c = (1.0, 1.0)^T denotes the center point of the ellipsoid. ${G}_{\mathbf{U}}=\left(\begin{array}{cc}1& 0.29\\ {}0.29& 1\end{array}\right)$ is the characteristic matrix to describe the level of the uncertainty. In the optimization process, the possibility degrees of inequality constraints λ₁, λ₂, and λ₃ are both set to 0.6. The weighting factors β₁ and β₂ are both set to 0.5. In principle, the parameter γ_i should make c(f_i(X, U)) + γ_i and w(f_i(X, U)) + γ_i non-negative. The parameters ϕ_i and φ_i should be calculated as Eq. (6). In practical applications, the parameters γ_i, ϕ_i, and φ_i could be chosen according to the same order of magnitude of each individual objective function. Therefore, the corresponding computation parameters are set as listed in Table 2. For the inner IP-GA and outer μMOGA, the population size are both set to 5.0. The probability of crossover are set to 0.5 and 0.6, respectively. The maximum generations are both specified as 100. In the following text, the above problem will be analyzed based on three cases.

4.1.1 The computational efficiency and optimization errors

In this case, the computational efficiency and optimization errors of presented method are discussed. The number of initial samples is 10, which are used to construct the approximation models for the uncertain objectives and constraints. The numbers of samples in different iterative steps are listed in Table 1. According to the optimization results of different iterative steps as shown in Fig. 3, the Pareto optimal set of approximate penalty functions ${\tilde{f}}_{p_1}$ and ${\tilde{f}}_{p_2}$ is far from the actual penalty function ${f}_{p_1}$ and ${f}_{p_2}$ at the beginning steps. The maximal bound error of the uncertain objective functions and constraints has reached 79.18%, which means the approximation models of the uncertain objective functions and constraints are relatively coarse. With increasing of the sampling points, the approximate penalty functions are close to the actual penalty function. In step 3, the maximal bound error of the uncertain objective functions and constraints is equal to 1.76% which is less than allowable error δ = 5%. It shows that the maximal bound error decreases obviously with the increasing of the local-densifying samples and the optimization results could achieve a high accuracy after several iterative steps.

Table 1 The number of samples in different iterative steps (numerical example 1)

Fig. 3

The optimization results of different iterative steps (numerical example 1)

The comparison of the proposed method with the uncertain multi-objective optimization method based on interval model (Liu et al. 2017) is also illustrated in Fig. 4. When using the ellipsoid convex model to describe the correlation of the uncertain parameters, the range of penalty function 1 varies from 8.15 to 17.54 and penalty function 2 varies from 1.11 to 2.8; however, when using the interval model to describe the uncertainty of the parameters, the range of penalty function 1 varies from 8.287 to 19.083 and penalty function 2 varies from 1.057 to 3.697. The results demonstrate that the domain of Pareto optimal solutions obtained by ellipsoid convex model is narrower than the domain obtained by interval model. It is because the uncertain multi-objective optimization method in reference (Liu et al. 2017) uses the interval model to describe the uncertainty of the parameters, namely, uncertain parameters vary independently and may reach their extreme values simultaneously, which would induce an over-conservative description of the system variability. In proposed method, the correlation of uncertain variables is fully considered through a multidimensional ellipsoid. Comparing to the interval model, the ellipsoidal convex model can describe the correlation of the uncertain parameters, which excludes extreme combination of uncertain parameters and avoids over-conservative designs. Thus, the uncertain optimization method based on the ellipsoidal convex model seems more significant in practical engineering application.

Fig. 4

The optimization results based on different models

4.1.2 The influence of different possibility degree levels

In order to analyze the influence of different possibility degree levels, the possibility degree levels λ₁, λ₂, and λ₃ are varied between 0.2 and 1.0 in steps of 0.2. The other computation parameters remain unchanged. The corresponding optimization results under different possibility degree levels are illustrated in Fig. 5. It can be found that Pareto optimal set of the penalty functions are divided into several levels with different possibility degree levels. It is because that possibility degree level stands for the strength of the constraint. With the possibility degree levels increasing, the feasible field of Pareto optimal set will become smaller. The optimization results also indicate that the design objective and possibility degrees of the constraints are always contradictive. Thus, the possibility degree levels of the constraints should be regulated according to actual engineering problems.

Fig. 5

Pareto optimal points under different possibility degree levels

4.1.3 The influence of different penalty parameters

In order to analyze the influence of different penalty parameters, the penalty factors σ₁ and σ₂ are both set to 10⁶ and 10⁸. The other computation parameters remain unchanged. The corresponding optimization results of the third iterative step under different penalty factors are illustrated in Figs. 6 and 7. When the penalty factors σ₁ and σ₂ are both set to 10⁶ and 10⁸, the maximal bound error of the uncertain objective functions and constraints have reached 28.41% and 61.77% in step 3, respectively. It also indicates that the approximation models of the uncertain objective functions and constraints are relatively coarse and three iterative steps cannot guarantee the desired accuracy of the optimization results. When the penalty factors σ₁ and σ₂ are both set to 10⁷, however, the maximal bound error of the uncertain objective functions and constraints is 1.76% in step 3 as shown in Fig. 3, which demonstrate that the approximation models are close to the actual numerical models and the optimization result is also consistent with the accuracy requirement. According to the above computational results, it can be found that the selection of penalty factors will directly affect the superiority and inferiority of the optimization results. An appropriate penalty factor will be helpful to solve the optimization problem.

Fig. 6

The optimization results in step 3 (penalty factors )

Fig. 7

The optimization results in step 3 (penalty factors )

4.2 Numerical example 2

Then the benchmark problem of the cantilever as shown in Fig. 8 is considered which is modified from the numerical example in reference (Du 2007). The maximum von Misses stress σ_max and the cantilever tube volume V are considered as objective functions. The four parameters t, θ₁, θ₂, and L₂ are treated as design variables. The external forces F₁, F₂, and P, torsion T, length L₁, and diameter d are treated as the uncertain variables, whose correlation is described through a multidimensional ellipsoid G_Q. The area A, bending moment M, and moment of inertia I are limited in the allowable intervals, respectively. Therefore, the uncertain multi-objective optimization problem of cantilever tube can be formulated as follows:

$$ {\displaystyle \begin{array}{cc}& {\sigma}_{\mathrm{max}}=\sqrt{{\left(\frac{P+{F}_1\sin {\theta}_1+{F}_2\sin {\theta}_2}{A}+\frac{Md}{2I}\right)}^2+3{\left(\frac{Td}{4I}\right)}^2}\\ {}& V=\frac{\pi \left[{d}^2-{\left(d-2t\right)}^2\right]}{4}\cdot {L}_1\\ {}\mathrm{Subject}\ \mathrm{to}& \\ {}& A=\frac{\pi }{4}\left[{d}^2-{\left(d-2t\right)}^2\right]\le \left[800,1000\right]\\ {}& I=\frac{\pi }{64}\left[{d}^4-{\left(d-2t\right)}^4\right]\le \left[1.1\times {10}^5,1.2\times {10}^5\right]\\ {}& M={F}_1{L}_1\cos {\theta}_1+{F}_2{L}_2\cos {\theta}_2\le \left[5.5\times {10}^5,6\times {10}^5\right]\\ {}& 5.0\mathrm{mm}\le t\le 8.0\mathrm{mm},0\le {\theta}_1\le {10}^{\circ },{2}^{\circ}\le {\theta}_2\le {15}^{\circ },\kern0.36em 50\mathrm{mm}\le {L}_2\le 70\mathrm{mm}\\ {}& {\left(\mathbf{Q}-{\mathbf{Q}}^c\right)}^{\mathbf{T}}{G}_{\mathbf{Q}}\left(\mathbf{Q}-{\mathbf{Q}}^c\right)\le 1.5\times {10}^5\end{array}} $$

(21)

where Q = (F₁, F₂, T, P, L₁, d)^T stands for the uncertain vector whose intervals are denoted by:

$$ {\displaystyle \begin{array}{l}{F}_1\in \left[3000\mathrm{N},3050\mathrm{N}\right],\kern0.36em {F}_2\in \left[3000\mathrm{N},3050\mathrm{N}\right],\kern0.36em T\in \left[81\mathrm{N}\cdotp \mathrm{m},89\mathrm{N}\cdotp \mathrm{m}\right]\\ {}P\in \left[12000\mathrm{N},13000\mathrm{N}\right],\kern0.36em {L}_1\in \left[110\mathrm{mm},130\mathrm{mm}\right],\kern0.36em d\in \left[40\mathrm{mm},43\mathrm{mm}\right].\\ {}{G}_{\mathbf{Q}}=\left(\begin{array}{cccccc}2& -0.25& 0.36& -0.67& 0.26& 0.28\\ {}-0.25& 2& -0.12& 0.29& 1& 0.35\\ {}0.36& -0.12& 1& 0.45& 0.34& 1.3\\ {}-0.67& 0.29& 0.45& 2& 0.23& 0.29\\ {}0.26& 1& 0.34& 0.23& 2& 0.63\\ {}0.28& 0.35& 1.3& 0.29& 0.63& 1\end{array}\right).\end{array}} $$

(22)

Fig. 8

A cantilever tube

Q^c = (3025, 3025, 85, 12500, 120, 41.5)^T denotes the center point of the ellipsoid. The characteristic matrix G_Q is described as follows.

$$ {G}_{\mathbf{Q}}=\left(\begin{array}{cccccc}2& -0.25& 0.36& -0.67& 0.26& 0.28\\ {}-0.25& 2& -0.12& 0.29& 1& 0.35\\ {}0.36& -0.12& 1& 0.45& 0.34& 1.3\\ {}-0.67& 0.29& 0.45& 2& 0.23& 0.29\\ {}0.26& 1& 0.34& 0.23& 2& 0.63\\ {}0.28& 0.35& 1.3& 0.29& 0.63& 1\end{array}\right). $$

(23)

In the optimization process, the possibility degrees of inequality constraints λ₁, λ₂, and λ₃ are both set to 0.6. The weighting factors β₁ and β₂ are both set to 0.5. The corresponding computation parameters are set as listed in Table 2. For the inner IP-GA and outer μMOGA, the population sizes are both set to 5.0. The probability of crossover are set to 0.5 and 0.6, respectively. The maximum generations are specified as 100 and 200, respectively. In the following text, the above problem will be analyzed based on three cases.

Table 2 The computation parameter setting

4.2.1 The computational efficiency and optimization errors

In this case, the local-densifying approximation technique is used to improve the optimization efficiency for the cantilever tube design problem. The numbers of samples in different iterative steps are listed in Table 3 and the process of the local-densifying approximation technique is shown in Fig. 9. In step 1, the 50 initial samples are adopted to construct the approximation models. The maximal bound error of the uncertain objective functions and constraints is 10.96%, which means the accuracy of approximation models of the uncertain objective functions and constraints need to be further improved. With increasing of the sampling points, the Pareto optimal set based on actual function model are close to the solution set with the local-densifying approximation technique. In step 3, the bound error of the uncertain objective functions and constraints is 4.73% which is less than allowable errors = 5%. It shows that the optimization results could satisfy the design requirement.

Table 3 The number of samples in different iterative steps (numerical example 2)

Fig. 9

The optimization results of different iterative steps (numerical example 2)

4.2.2 The convergence performance

To analyze the convergence performance of the present method, the maximum generations is specified as 100 for inner IP-GA and different maximum generations with 100, 200, 300, and 400 are investigated for outer μMOGA, respectively. The other computation parameters remain unchanged. The Pareto optimal set of the penalty functions under different maximum generations are shown in Fig. 10. It can be found that the Pareto optimal set of the penalty functions has exhibited a better convergence performance when the generation number of outer μMOGA is 200. Comparing with the results of generation number 200, the results of generation number 100 has greater fluctuation, and it implies that 100 generations are not enough to reach the fine optimums. For generation number from 300 to 400, the optimization results are nearly equal to the ones of generation number 200. It is because that generation number 200 is enough to obtain the stable global optimums for this problem and the present method has a better convergence performance.

Fig. 10

Pareto optimal points under different iterative generations

4.2.3 The influence of different characteristic matrixes

In this case, three different characteristic matrixes ${G}_{{\mathbf{Q}}_1}$, ${G}_{{\mathbf{Q}}_2}$, and ${G}_{{\mathbf{Q}}_3}$ as listed in Table 4 are adopted to test the difference of optimization results. The other computation parameters remain unchanged. As shown in Fig. 11, it can be found that the value of the penalty functions varies with the change of the characteristic matrix. It is because that the characteristic matrix stands for the uncertain level of the correlated uncertain variables. The different levels of uncertainty will inevitably lead to the change of the optimization results. Therefore, a characteristic matrix should be specified beforehand according to the practical problem and engineers’ experience.

Table 4 The different characteristic matrixes (numerical example 2)

Fig. 11

Pareto optimal points under different matrixes (numerical example 2)

4.3 Application to the uncertain optimization of occupant restraint system

Occupant restraint system is an important part of the vehicle safety design. When the car crash occurs, the occupant restraint system could avoid secondary collisions so as to protect the safety of occupant. Hence, the presented method is applied to uncertain optimization of occupant restraint system in full vehicle frontal impact. The simulation model of occupant restraint system is established in MADYMO software as shown in Fig. 12. The model consists of dummy model, seat model, safety belt, and simplified model of the driver space with toeboard and windshield.

Fig. 12

The numerical model of occupant restraint system

To ensure protection performance of occupant restraint system, the head injury index () and the chest injury index () (Viano and Arepally 1990) are adopted as objective functions. The chest deflection , axial pressure of left thigh , and axial pressure of right thigh are considered as constraint functions. During the design process, the protection performance of occupant restraint system could be improved by adjusting D-ring position , anchor position , and belt extensibility . Thus, the above three parameters are chosen as design variables. Considering the errors of manufacture process, the initial strain of belt and stiffness of driver’s seat are treated as uncertain variables. Therefore, the U-MOO problem of occupant restraint system can be obtained as follows:

$$ {\displaystyle \begin{array}{cc}& \underset{\mathbf{X}}{\min}\left\{{f}_{\mathrm{HIC}}\left(\mathbf{X},\mathbf{U}\right),{f}_{{\mathrm{C}}_{3\mathrm{ms}}}\left(\mathbf{X},\mathbf{U}\right)\right\}\\ {}\mathrm{Subject}\ \mathrm{to}\ & \\ {}& {g}_1\left(\mathbf{X},\mathbf{U}\right)\le 75\ \mathrm{mm}\\ {}& {g}_2\left(\mathbf{X},\mathbf{U}\right)\le 10\ \mathrm{kN}\\ {}& {g}_3\left(\mathbf{X},\mathbf{U}\right)\le 10\ \mathrm{kN}\\ {}& {\left(\mathbf{U}-{\mathbf{U}}^c\right)}^{\mathbf{T}}{G}_{\mathbf{U}}\left(\mathbf{U}-{\mathbf{U}}^c\right)\le 0.006\\ {}& \begin{array}{l}\mathbf{X}={\left({X}_1,{X}_2,{X}_3\right)}^{\mathbf{T}},\kern0.36em 0.82\mathrm{m}\le {X}_1\le 0.92\mathrm{m},\kern0.36em -0.01\mathrm{m}\le {X}_2\le 0.02\mathrm{m},0.06\\ {}\le {X}_3\le 0.15\end{array}\end{array}} $$

(24)

where U = (U₁, U₂)^T stands for the uncertain vector whose intervals are denoted by:

$$ {U}_1\in \left[-0.05,0.0\right],\kern0.36em {U}_2\in \left[0.9,1.0\right]. $$

(25)

U^c = (−0.025, 0.95)^T denotes the center point of the ellipsoid and ${G}_{\mathbf{U}}=\left(\begin{array}{cc}1& 0.29\\ {}0.29& 1\end{array}\right)$ is the characteristic matrix.

In the optimization process, the possibility degrees of inequality constraints λ₁, λ₂, and λ₃ are both set to 0.6. The weighting factors β₁ and β₂ are both set to 0.5. The penalty factors σ₁ and σ₂ are both set to 1000. The allowable error δ is set to 10%. The other computation parameters are set as listed in Table 2. For the inner IP-GA and outer μMOGA, the population size are both set to 5.0. The probability of crossover are set to 0.5 and 0.6, respectively. The maximum generations are both specified as 100.

The number of initial samples is 80, which are used to construct the approximation models for the uncertain objective and constraint. Through ten local-densified samples, the final optimization results as shown in Fig. 13 are obtained, which satisfy the design requirement. It can be found that the maximum error of the objective functions and constraints is 6.69%, which is less than the allowable error 10%. Eight solutions are chosen from the Pareto optimal set as listed in Table 5. Indeed, the Pareto set provide designer with a large number of optimal solutions and the attitude of the designer will also influence the selection of the Pareto optimal set. Take Table 5 as an example, the decision-maker could choose the eighth solution if the head injury index is most cared. While if the decision-maker emphasizes the chest injury index, the first solution would be considered. Thus the designer should make a tradeoff between head injury index and chest injury index. It should be noted that each solution stands for a different compromise among design objectives, no solutions from which can be said to be better than any other without any further information. This set is known as the non-dominated set or the Pareto optimal set.

Fig. 13

The optimization results with local-densifying approximation technique

Table 5 Pareto solutions of the uncertain optimization of occupant restraint system

5 Conclusion

This paper suggests an efficient multi-objective optimization method for uncertain structures based on ellipsoidal convex model. In the method, the correlated uncertain variables can be described by the ellipsoidal convex model. By using nonlinear interval number programming (NINP) method, the uncertain objective functions can be converted into deterministic optimization problem. To deal with uncertain constraints, the possibility degree of interval is applied to make the inequality constraints satisfied with a possibility degree level. Simultaneously, the approximation models based on radial basis function (RBF) is applied to replace the actual objective functions and constraints, and the local-densifying approximation technique is used to improve the efficiency and accuracy of the optimization. Considering the original optimization problem belongs to the two-loop nesting optimization problem, the intergeneration projection genetic algorithm and the micro multi-objective genetic algorithm are employed as inner and outer optimization solvers, respectively. The simulation results of two test functions demonstrate that the present method can efficiently find the Pareto optimal set. The present method is also applied to solve the uncertain multi-objective optimization problem of vehicle occupant restraint system. The fine optimization results exhibit the applicability of the present method to practical engineering problems. It should be noted that the accuracy of the optimization results is guaranteed by the local-densifying approximation technique. When the high nonlinear simulation models are involved, the approximation models need to be reconstructed through more local-densifying iterations. It will influence computational efficiency and the engineering practicability. Hence, we will consider this above-mentioned problem in our future work.