Robust optimization of uncertain structures based on interval closeness coefficients and the 3D violation vectors of interval constraints

Abstract

In this paper, a novel direct interval robust optimization approach is proposed so that the robust optimal design vectors for structures with interval uncertainties can be achieved. A new concept of interval closeness coefficient is proposed to describe the relative positional relationship between the boundaries of two intervals. Subsequently, the explicit formulae for calculating the four interval closeness coefficients between the boundaries of an interval constraint mechanical performance index and those of its corresponding given interval constant are put forward. Consequently, the 3D violation vectors of different interval constraints can be calculated, and the feasibility of a design vector can be evaluated by its total 3D violation vector of all interval constraints. Finally, various design vectors are directly ranked according to the preferential guidelines considering the robustness of all the mechanical performance indices of uncertain structures, which is realized by integrating the Kriging technique and nested genetic algorithm. Unlike the traditional robust optimization of structures involving interval uncertainties, the proposed method can avoid the complicated model transformation process and ensure the robustness of all the mechanical performance indices of the optimal solution. Two examples are thoroughly investigated, the results of which demonstrate the applicability and advantages of the proposed approach.

1 Introduction

Uncertainties such as variations in material properties, manufacturing errors, and load fluctuations ubiquitously exist in engineering structures, which will inevitably lead to the fluctuations of their mechanical performance indices. To achieve the robust optimal mechanical performance indices of engineering structures, it is necessary to develop robust structural optimization approaches with considerations of various uncertainties (Muscolino and Sofi 2013; Chen et al. 2016; Peng et al. 2017; Zheng et al. 2018; Yin et al. 2018; Chu et al. 2018; Zhang et al. 2018).

The traditional robust design optimization was developed in the probabilistic framework with known statistical information of uncertain parameters (Richardson et al. 2015; Peng et al. 2018a; Sun et al. 2018). For example, Doltsinis et al. (2005) formulated the robust optimization model of nonlinear structures and solved it by a gradient-based algorithm. Tang and Périaux (2012) proposed a robust optimization method for drag minimization problems in aerodynamics by integrating the Pareto and Nash game strategies with the adjoint method. Zhao and Wang (2014) investigated the robust topology optimization under loading uncertainty based on linear elastic theory and orthogonal diagonalization of symmetric matrices. Martínez-Frutos et al. (2016) realized the robust shape optimization of continuous structures via the level set method. However, it is often quite difficult to achieve the precise probabilistic distributions of uncertain parameters due to the data insufficiency in realistic engineering applications (Muscolino et al. 2013; Yang et al. 2015; Santoro et al. 2015; Jiang et al. 2015; Wu et al. 2016; Peng et al. 2018b).

To address the robust optimization problems where the probabilistic distributions of uncertain parameters are unknown, a number of scholars have proposed various nonprobabilistic modeling approaches (Sofi et al. 2015a; Ni et al. 2016, 2018). Takewaki and Ben-Haim (2005) proposed an info-gap robust design method for structures with load and model uncertainties. Kang and Bai (2013) investigated the robust design optimization of truss structures considering the variations of the cross-sectional areas, Young’s moduli, and loads based on nonprobabilistic ellipsoid convex model. Hanks et al. (2017) investigated the robust goal programming method on the basis of the norm-based and ellipsoidal uncertainty sets. However, the abovementioned uncertainty modeling methods will be very complex when the structural responses cannot be analytically expressed as the functions of design variables and uncertain parameters, which significantly restrict their applications in realistic engineering problems.

Due to the advantages of simple calculation and low requirement for uncertain data, robust optimization based on the interval modeling of uncertainties has recently attracted wide attention from scientific community (Guo and Lu 2015; Sofi et al. 2015b; Sofi and Romeo 2016; Cheng et al. 2017). Hladík (2016) proposed an approach for locating the robust optimal solutions to interval linear programming problems. Lievens et al. (2016) investigated the robust design of tuned mass damper for the vibration serviceability of footbridge based on multi-interval approach. However, it is obvious that these approaches cannot address realistic engineering problems. Li et al. (2015) investigated the actuator placement robust optimization approach for vibration control system with interval parameters. Karer and Skrjanc (2016) proposed an interval global optimization framework for improving the robust stability and performance of PID controllers. However, these engineering-oriented interval robust optimization approaches are indirect ones, which firstly transformed the interval models into deterministic ones and then solved the resulting models by deterministic optimization algorithms. The shortcomings of such indirect robust optimization approaches are similar to the indirect ones for solving conventional interval optimization models (Jiang et al. 2007; Li et al. 2013). Specifically, different weighting and normalization factors for the objective functions or different penalty factors for the interval constraints utilized in the model transformation process will result in different optimal solutions to an interval optimization model. Moreover, the transformation of interval models into deterministic ones also deviates from the original intention of modeling the optimization problems based on interval theory.

In this paper, a new direct interval robust optimization approach is proposed to improve the mechanical performance indices of realistic engineering structures and ensure their global robustness against uncertainties. Unlike the traditional indirect robust optimization approaches for uncertain structures with interval uncertainties, the proposed method can avoid the complicated transformation process from interval models to deterministic ones and directly achieve the optimal designs with globally robust mechanical performance indices. With the introduction of a novel concept of interval closeness coefficient for describing the relative positional relationship between two interval boundaries, the relative position between an interval constraint performance index and its corresponding given interval constant can be described by four interval closeness coefficients. Meanwhile, a 3D violation vector composed of three interval closeness coefficients is constructed to describe the violation degree of an interval constraint. Thus, the feasibility of a design vector can be determined by the total 3D violation vector of all interval constraints. Subsequently, the “constraint first objective next” preferential guidelines considering the global robustness of all the mechanical performance indices in the robust optimization model are proposed for directly ranking various design vectors. And finally, a direct interval robust optimization algorithm is developed based on Kriging technique and nested genetic algorithm (GA) to locate the robust optimal design of complex uncertain structure. Since the transformation of an interval model into a deterministic one is avoided and all the mechanical performance indices of the uncertain structure are calculated by their corresponding Kriging models, the proposed algorithm can efficiently locate the optimal design with robust mechanical performance indices and it is applicable to various realistic engineering structures regardless of their geometrical complexities and strong nonlinearities of optimization problems. Therefore, the applicability of robust design optimization is further broadened by the improved universality of the proposed direct interval robust optimization approach.

The rest of the paper is organized as follows. Section 2 introduces the interval robust optimization model of an uncertain structure. Section 3 firstly presents the novel concept of interval closeness coefficient and then introduces the detailed formulae for calculating different interval closeness coefficients between interval boundaries. Section 4 introduces the method for determining the 3D violation vectors corresponding to different interval constraints. Section 5 firstly puts forward the preferential guidelines considering global robustness, then realizes the direct interval robust optimization algorithm by integrating Kriging technique and nested GA, and finally demonstrates the validity of the proposed algorithm by a numerical example. Subsequently, a realistic engineering example is investigated in Sect. 6 to illustrate the applicability and versatility of the proposed robust structural optimization approach. Finally, the conclusions are drawn in Sect. 7.

2 Interval robust optimization model of an uncertain structure

When the uncertain parameters are modeled as interval parameters, the mechanical performance indices of an uncertain structure are the functions of design variables and interval parameters. Supposing that the center and width of the most important mechanical performance index of the uncertain structure are described as objective functions while the requirements on the other mechanical performance indices are described as constraint functions, the interval robust optimization model of an uncertain structure can be described as

$$ {\displaystyle \begin{array}{l}\underset{\boldsymbol{x}}{\min}\left\{{f}^C\left(\boldsymbol{x}\right),{f}^W\left(\boldsymbol{x}\right)\right\}=\underset{\boldsymbol{x}}{\min}\left\{\left({f}^R\left(\boldsymbol{x}\right)+{f}^L(x)\right)/2,{f}^R\left(\boldsymbol{x}\right)-{f}^L\left(\boldsymbol{x}\right)\right\}\\ {}\mathrm{s}.\mathrm{t}.\kern1.75em {G}_i\left(\boldsymbol{x}\right)=\left[{g}_i^L\left(\boldsymbol{x}\right),{g}_i^R\left(\boldsymbol{x}\right)\right]\le \left(\ge \right){B}_i=\left[{b}_i^L,{b}_i^R\right],i=1,2,\cdots, l;\\ {}\mathrm{where}\kern0.75em {f}^R\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\max }f\left(\boldsymbol{x},\boldsymbol{U}\right),{f}^L\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\min }f\left(\boldsymbol{x},\boldsymbol{U}\right);\\ {}\kern3em {g}_i^R\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\max }{g}_i\left(\boldsymbol{x},\boldsymbol{U}\right),{g}_i^L\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\min }{g}_i\left(\boldsymbol{x},\boldsymbol{U}\right);\\ {}\kern3em \boldsymbol{x}=\left({x}_1,{x}_2,\cdots, {x}_n\right);\\ {}\kern3em \boldsymbol{U}=\left({U}_1,{U}_2,\cdots, {U}_m\right),{U}_j=\left[{u}_j^L,{u}_j^R\right],j=1,2,\cdots, m.\end{array}} $$

(1)

where x denotes the n-dimensional design vector; U denotes the m-dimensional interval parameter vector; f(x, U) and g_i(x, U) denote the objective and constraint mechanical performance indices of the uncertain structure, which are usually the implicit functions of x and U; f^C(x) and f^W(x) denote the center and width of the objective performance index f(x, U) while f^L(x) and f^R(x) denote its left and right bounds; and B_i denotes the given interval constant corresponding to the ith interval constraint performance index g_i(x, U). It is worth to mention that some constraint mechanical performance indices may degenerate into deterministic ones when they are independent of interval parameters and that their corresponding interval constants may also degenerate into real numbers.

3 Interval closeness coefficients

In the first part of this section, a new concept of interval closeness coefficient between two interval boundaries is put forward so that the relative position between an interval constraint mechanical performance index and its corresponding given interval constant can be determined by four interval closeness coefficients. Then, the detailed formulations for calculating four different interval closeness coefficients are explicitly introduced in the second part of the section.

3.1 The concept of interval closeness coefficient

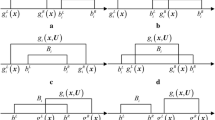
There are six relative positional relationships between the ith interval constraint mechanical performance index g_i(x, U) in (1) and its corresponding given interval constant B_i, see Fig. 1 for illustration. Supposing that ${g}_i^W\left(\boldsymbol{x}\right)={g}_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)$ and ${b}_i^W={b}_i^R-{b}_i^L$ are the interval widths of the ith constraint mechanical performance index g_i(x, U) and interval constant B_i respectively, there is ${g}_i^W\left(\boldsymbol{x}\right)>{b}_i^W$ for the relative positional relationship shown in Fig. 1(c₁) and ${g}_i^W\left(\boldsymbol{x}\right)<{b}_i^W$ for that shown in Fig. 1(c₂). According to the frequency that the boundaries of interval constraint mechanical performance index g_i(x, U) cross over those of interval constant B_i, the relative positional relationships between g_i(x, U) and B_i can be classified as follows: (a) no boundary crossing; (b) one boundary crossing, namely, ${g}_i^R\left(\boldsymbol{x}\right)$ crosses over ${b}_i^L$; (c) two-boundary crossings, namely, ${g}_i^R\left(\boldsymbol{x}\right)$ crosses over both ${b}_i^L$ and ${b}_i^R$ as shown in Fig. 1(c₁) or both ${g}_i^R\left(\boldsymbol{x}\right)$ and ${g}_i^L\left(\boldsymbol{x}\right)$ cross over ${b}_i^L$ as shown in Fig. 1(c₂); (d) three-boundary crossings, that is, ${g}_i^R\left(\boldsymbol{x}\right)$ cross over both ${b}_i^L$ and ${b}_i^R$ while ${g}_i^L\left(\boldsymbol{x}\right)$ crosses over ${b}_i^L$; and (e) four boundary crossings, namely, both ${g}_i^R\left(\boldsymbol{x}\right)$ and ${g}_i^L\left(\boldsymbol{x}\right)$ cross over ${b}_i^L$ and ${b}_i^R$.

Fig. 1

Relative positional relationships between interval constraint mechanical performance index g_i(x, U) and given interval constant B_i

A new concept of interval closeness coefficient is proposed to describe the relative positional relationship between the interval constraint mechanical performance index g_i(x, U) and the given interval constant B_i. Specifically, there are the following four interval closeness coefficients with regard to the interval constraint mechanical performance index g_i(x, U) and interval constant B_i: (1) the interval closeness coefficient cc_i^RL(x) reflecting the capability of ${g}_i^R\left(\boldsymbol{x}\right)$ approaching and crossing over ${b}_i^L$, (2) the interval closeness coefficient cc_i^LL(x) reflecting the capability of ${g}_i^L\left(\boldsymbol{x}\right)$ approaching and crossing over ${b}_i^L$, (3) the interval closeness coefficient cc_i^RR(x) reflecting the capability of ${g}_i^R\left(\boldsymbol{x}\right)$ approaching and crossing over ${b}_i^R$, and (4) the interval closeness coefficient cc_i^LR(x) reflecting the capability of ${g}_i^L\left(\boldsymbol{x}\right)$ approaching and crossing over ${b}_i^R$.

The value of every interval closeness coefficient is a real number, which monotonously increases from 0 to 1 when the boundary of interval constraint mechanical performance index g_i(x, U) gradually approaches that of the given interval constant B_i and keeps the value of 1 after the boundary of constraint mechanical performance index g_i(x, U) crosses over that of interval constant B_i. As a result, the relative positional relationship between the interval constraint mechanical performance index g_i(x, U) and interval constant B_i can be precisely determined by the values of four interval closeness coefficients cc_i^RL(x), cc_i^LL(x), cc_i^RR(x), and cc_i^LR(x).

3.2 Calculation of different interval closeness coefficients

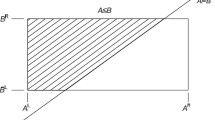
Supposing that the value of interval closeness coefficient cc_i^RL(x) continuously increases from 0 to 1 when ${g}_i^R\left(\boldsymbol{x}\right)$ is approaching ${b}_i^L$ under the condition that ${b}_i^L-{g}_i^R\left(\boldsymbol{x}\right)\le {b}_i^W$ (namely, ${g}_i^R\left(\boldsymbol{x}\right)\ge {b}_i^L-{b}_i^W$) and there is cc_i^RL(x) ≡ 1 when ${g}_i^R\left(\boldsymbol{x}\right)\ge {b}_i^L$, see Fig. 2 for illustration, the formula for calculating cc_i^RL(x) can be constructed as (2). It is obvious that there is cc_i^RL(x) ≡ 1 for all the relative positional relationships between g_i(x, U) and B_i except the case shown in Fig. 1(a).

$$ c{c_i}^{RL}\left(\boldsymbol{x}\right)=\max \left(0,\frac{b_i^W-\left({b}_i^L-{g}_i^R\left(\boldsymbol{x}\right)\right)}{b_i^W+\mid {b}_i^L-{g}_i^R\left(\boldsymbol{x}\right)\mid}\right)=\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-\left({b}_i^L-{b}_i^W\right)}{b_i^W+\mid {b}_i^L-{g}_i^R\left(\boldsymbol{x}\right)\mid}\right). $$

(2)

Fig. 2

Variation of cc_i^RL(x) with the right bound of interval constraint mechanical performance index

Supposing that the value of interval closeness coefficient cc_i^LL(x) continuously increases from 0 to 1 when ${g}_i^L\left(\boldsymbol{x}\right)$ is approaching ${b}_i^L$ under the condition that ${b}_i^L-{g}_i^L\left(\boldsymbol{x}\right)\le {g}_i^W\left(\boldsymbol{x}\right)$ (namely, ${g}_i^L\left(\boldsymbol{x}\right)\ge {b}_i^L-{g}_i^W\left(\boldsymbol{x}\right)$ or ${g}_i^R\left(\boldsymbol{x}\right)\ge {b}_i^L$) and there is cc_i^LL(x) ≡ 1 when ${g}_i^L\left(\boldsymbol{x}\right)\ge {b}_i^L$ (namely, ${g}_i^R\left(\boldsymbol{x}\right)\ge {b}_i^L+{g}_i^W\left(\boldsymbol{x}\right)$), see Fig. 3 for illustration, the formula for calculating cc_i^LL(x) can be constructed as (3). It is obvious that there is cc_i^LL(x) ≡ 0 for the relative positional relationship between g_i(x, U) and B_i shown in Fig. 1(a) and cc_i^LL(x) ≡ 1 for the cases shown in Fig. 1(c₂), (d), (e).

$$ c{c_i}^{LL}\left(\boldsymbol{x}\right)=\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^L}{g_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)+\mid {b}_i^L-{g}_i^L\left(\boldsymbol{x}\right)\mid}\right). $$

(3)

Fig. 3

Variation of $c{c}_i^{LL}\left(\mathbf{x}\right)$ with the (a) left and (b) right bounds of interval constraint mechanical performance index

Supposing that the value of interval closeness coefficient cc_i^RR(x) continuously increases from 0 to 1 when ${g}_i^R\left(\boldsymbol{x}\right)$ is approaching ${b}_i^R$ under the condition that ${g}_i^R\left(\boldsymbol{x}\right)\ge {b}_i^L$ and there is cc_i^RR(x) ≡ 1 when ${g}_i^R\left(\boldsymbol{x}\right)\ge {b}_i^R$, see Fig. 4 for illustration, the formula for calculating cc_i^RR(x) can be constructed as (4). It is obvious that there is cc_i^RR(x) ≡ 0 for the relative positional relationship between g_i(x, U) and B_i shown in Fig. 1(a) and cc_i^RR(x) ≡ 1 for the cases shown in Fig. 1(c₁), (d), (e).

$$ c{c_i}^{RR}\left(\boldsymbol{x}\right)=\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^L}{b_i^R-{b}_i^L+\mid {b}_i^R-{g}_i^R\left(\boldsymbol{x}\right)\mid}\right). $$

(4)

Fig. 4

Variation of $c{c}_i^{RR}\left(\boldsymbol{x}\right)$ with the right bound of interval constraint mechanical performance index

Supposing that the value of interval closeness coefficient cc_i^LR(x) continuously increases from 0 to 1 when ${g}_i^L\left(\boldsymbol{x}\right)$ is approaching ${b}_i^R$ under the condition that ${g}_i^R\left(\boldsymbol{x}\right)\ge {b}_i^R$ (namely, ${g}_i^L\left(\boldsymbol{x}\right)\ge {b}_i^R-{g}_i^W\left(\boldsymbol{x}\right)$) and there is cc_i^LR(x) ≡ 1 when ${g}_i^L\left(\boldsymbol{x}\right)\ge {b}_i^R$ (namely, ${g}_i^R\left(\boldsymbol{x}\right)\ge {b}_i^R+{g}_i^W\left(\boldsymbol{x}\right)$), see Fig. 5 for illustration, the formula for calculating cc_i^LR(x) can be constructed as (5). It is obvious that there is cc_i^LR(x) ≡ 0 for the relative positional relationships between g_i(x, U) and B_i shown in Fig. 1(a), (b), (c₂) and cc_i^LR(x) ≡ 1 for the case shown in Fig. 1(e).

$$ c{c_i}^{LR}\left(\boldsymbol{x}\right)=\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^R}{g_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)+\mid {b}_i^R-{g}_i^L\left(\boldsymbol{x}\right)\mid}\right). $$

(5)

Fig. 5

Variation of cc_i^LR(x) with the (a) left and (b) right bounds of interval constraint mechanical performance index

For the better understanding of interval closeness coefficients, the variation curves of cc_i^RL(x), cc_i^LL(x), cc_i^RR(x), and cc_i^LR(x) with the right bound of interval constraint mechanical performance index are simultaneously illustrated in Fig. 6, where Fig. 6a corresponds to the case when ${g}_i^W\left(\boldsymbol{x}\right)<{b}_i^W$ while Fig. 6b corresponds to the case when ${g}_i^W\left(\boldsymbol{x}\right)>{b}_i^W$. It is worth noting that the variation curves of interval closeness coefficients cc_i^LL(x) and cc_i^RR(x) partially overlap with each other when ${b}_i^L\le {g}_i^R\left(\boldsymbol{x}\right)\le {b}_i^R$ for both cases shown in Figs. 6a, b. Actually, the relative width of the interval constraint mechanical performance index g_i(x, U) with regard to its corresponding given interval constant B_i is also an important factor reflecting their relative positional relationship. The overlap ratio between the variation curves of interval closeness coefficients cc_i^LL(x) and cc_i^RR(x) reflects the closeness of interval widths ${g}_i^W\left(\boldsymbol{x}\right)$ and ${b}_i^W$. The larger overlap ratio between the variation curves of cc_i^LL(x) and cc_i^RR(x) indicates the closer value of ${g}_i^W\left(\boldsymbol{x}\right)$ with regard to that of ${b}_i^W$. And it is obvious that the variation curves of cc_i^LL(x) and cc_i^RR(x) will completely overlap when ${g}_i^W\left(\boldsymbol{x}\right)={b}_i^W$.

Fig. 6

Variation curves of different interval closeness coefficients with ${g}_i^R\left(\boldsymbol{x}\right)$: (a) ${g}_i^W\left(\boldsymbol{x}\right)<{b}_i^W$; (b) ${g}_i^W\left(\boldsymbol{x}\right)>{b}_i^W$

4 3D violation vectors of interval constraints

In this section, the concept of 3D violation vector of an interval constraint is proposed, which is constructed based on three interval closeness coefficients between the interval boundaries of the constraint mechanical performance index and those of its corresponding given interval constant. In particular, the formulae for calculating the 3D violation vectors of interval constraints in the cases of G_i(x) ≤ B_i and G_i(x) ≥ B_i are derived, including the special cases when G_i(x) and B_i degenerate into real numbers.

4.1 For interval constraint G _i(x) ≤ B _i

As is seen from Figs. 1 and 6, the interval constraint G_i(x) ≤ B_i is fully satisfied when cc_i^RL(x) < 1 and cc_i^LL(x) = cc_i^RR(x) = cc_i^LR(x) = 0, and it will be violated only when cc_i^RL(x) = 1. Considering that the larger values of interval closeness coefficients cc_i^LL(x), cc_i^RR(x), cc_i^LR(x) correspond to the greater violation degree of constraint G_i(x) ≤ B_i when cc_i^RL(x) = 1, the violation degree of interval constraint G_i(x) ≤ B_i can be measured by the following 3D violation vector:

$$ {\displaystyle \begin{array}{l}{\mathbf{v}}_i\left(\boldsymbol{x}\right)=\left({v}_{1i}\left(\boldsymbol{x}\right),{v}_{2i}\left(\boldsymbol{x}\right),{v}_{3i}\left(\boldsymbol{x}\right)\right),\\ {}\mathrm{where}\kern0.5em {v}_{1i}\left(\boldsymbol{x}\right)=c{c_i}^{LL}\left(\boldsymbol{x}\right)=\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^L}{g_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)+\mid {b}_i^L-{g}_i^L\left(\boldsymbol{x}\right)\mid}\right);\\ {}\kern2.75em {v}_{2i}\left(\boldsymbol{x}\right)=c{c_i}^{RR}\left(\boldsymbol{x}\right)=\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^L}{b_i^R-{b}_i^L+\mid {b}_i^R-{g}_i^R\left(\boldsymbol{x}\right)\mid}\right);\\ {}\kern2.75em {v}_{3i}\left(\boldsymbol{x}\right)=c{c_i}^{LR}\left(\boldsymbol{x}\right)=\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^R}{g_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)+\mid {b}_i^R-{g}_i^L\left(\boldsymbol{x}\right)\mid}\right).\end{array}} $$

(6)

In engineering practice, the constraint mechanical performance index of an uncertain structure may be independent of uncertain parameters and thus its value may degenerate into a real number while the interval constant B_i may also degenerate into a real number. In these cases, the 3D violation vector of an interval constraint cannot be calculated by (6) because some denominators in the fractional expressions for its vector components may be zero.

To avoid the occurrence of zero denominators in the formulation for calculating the 3D violation vector of an interval constraint, the following rules are proposed:

• (a) There is v_1i(x) = cc_i^LL(x) = 0 when ${g}_i^L\left(\boldsymbol{x}\right)={g}_i^R\left(\boldsymbol{x}\right)={b}_i^L$.

• (b) There is v_2i(x) = cc_i^RR(x) = 0 when ${b}_i^L={b}_i^R={g}_i^R\left(\boldsymbol{x}\right)$.

• (c) There is v_3i(x) = cc_i^LR(x) = 0 when ${g}_i^L\left(\boldsymbol{x}\right)={g}_i^R\left(\boldsymbol{x}\right)={b}_i^R$.

Consequently, the 3D violation vector of any constraint in the form of G_i(x) ≤ B_i can be calculated by the unified formula in (7).

$$ {\displaystyle \begin{array}{l}{\mathbf{v}}_i\left(\boldsymbol{x}\right)=\left({v}_{1i}\left(\boldsymbol{x}\right),{v}_{2i}\left(\boldsymbol{x}\right),{v}_{3i}\left(\boldsymbol{x}\right)\right),\\ {}\mathrm{where}\kern0.5em {v}_{1i}\left(\boldsymbol{x}\right)=c{c_i}^{LL}\left(\boldsymbol{x}\right)=\Big\{\begin{array}{c}0,\kern0.5em \mathrm{when} \operatorname {sign}\left(|{g}_i^L\left(\boldsymbol{x}\right)-{g}_i^R\left(\boldsymbol{x}\right)|+|{g}_i^L\left(\boldsymbol{x}\right)-{b}_i^L|\right)=0;\kern0.75em \\ {}\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^L}{g_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)+\mid {b}_i^L-{g}_i^L\left(\boldsymbol{x}\right)\mid}\right),\kern0.75em \mathrm{otherwise}.\end{array}\\ {}\kern2.75em {v}_{2i}\left(\boldsymbol{x}\right)=c{c_i}^{RR}\left(\boldsymbol{x}\right)=\Big\{\begin{array}{l}0,\kern0.75em \mathrm{when} \operatorname {sign}\left(|{b}_i^L-{b}_i^R|+|{g}_i^R\left(\boldsymbol{x}\right)-{b}_i^R|\right)=0;\\ {}\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^L}{b_i^R-{b}_i^L+\mid {b}_i^R-{g}_i^R\left(\boldsymbol{x}\right)\mid}\right),\mathrm{otherwise}.\end{array}\\ {}\kern2.75em {v}_{3i}\left(\boldsymbol{x}\right)=c{c_i}^{LR}\left(\boldsymbol{x}\right)=\Big\{\begin{array}{l}0,\mathrm{when} \operatorname {sign}\left(|{g}_i^L\left(\boldsymbol{x}\right)-{g}_i^R\left(\boldsymbol{x}\right)|+|{g}_i^L\left(\boldsymbol{x}\right)-{b}_i^R|\right)=0;\\ {}\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^R}{g_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)+\mid {b}_i^R-{g}_i^L\left(\boldsymbol{x}\right)\mid}\right),\mathrm{otherwise}.\end{array}\end{array}} $$

(7)

4.2 For interval constraint G _i(x) ≥ B _i

As is seen from Figs. 1 and 6, the constraint G_i(x) ≥ B_i is completely violated when cc_i^RL(x) < 1 and cc_i^LL(x) = cc_i^RR(x) = cc_i^LR(x) = 0, and the violation degree of constraint G_i(x) ≥ B_i gradually decreases with the increase of cc_i^LL(x), cc_i^RR(x), cc_i^LR(x) when cc_i^RL(x) = 1 until the constraint G_i(x) ≥ B_i is fully satisfied when cc_i^LR(x) = 1. That is, the values of interval closeness coefficients cc_i^LL(x), cc_i^RR(x), cc_i^LR(x) reversely reflect the violation degree of interval constraint G_i(x) ≥ B_i.

Considering that every interval closeness coefficient has a value between 0 and 1 and that both the interval constraint mechanical performance index G_i(x) and its corresponding given interval constant B_i may degenerate into real numbers, the 3D violation vector of constraint G_i(x) ≥ B_i can be calculated by the following:

$$ {\displaystyle \begin{array}{l}{\mathbf{v}}_i\left(\boldsymbol{x}\right)=\left({v}_{1i}\left(\boldsymbol{x}\right),{v}_{2i}\left(\boldsymbol{x}\right),{v}_{3i}\left(\boldsymbol{x}\right)\right),\\ {}\mathrm{where}\kern0.5em {v}_{1i}\left(\boldsymbol{x}\right)=1-c{c_i}^{LL}\left(\boldsymbol{x}\right)=\Big\{\begin{array}{c}1,\kern0.5em \mathrm{when} \operatorname {sign}\left(|{g}_i^L\left(\boldsymbol{x}\right)-{g}_i^R\left(\boldsymbol{x}\right)|+|{g}_i^L\left(\boldsymbol{x}\right)-{b}_i^L|\right)=0;\kern0.75em \\ {}1-\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^L}{g_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)+\mid {b}_i^L-{g}_i^L\left(\boldsymbol{x}\right)\mid}\right),\kern0.75em \mathrm{otherwise}.\end{array}\\ {}\kern2.75em {v}_{2i}\left(\boldsymbol{x}\right)=1-c{c_i}^{RR}\left(\boldsymbol{x}\right)=\Big\{\begin{array}{l}1,\kern0.75em \mathrm{when} \operatorname {sign}\left(|{b}_i^L-{b}_i^R|+|{g}_i^R\left(\boldsymbol{x}\right)-{b}_i^R|\right)=0;\\ {}1-\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^L}{b_i^R-{b}_i^L+\mid {b}_i^R-{g}_i^R\left(\boldsymbol{x}\right)\mid}\right),\mathrm{otherwise}.\end{array}\\ {}\kern2.75em {v}_{3i}\left(\boldsymbol{x}\right)=1-c{c_i}^{LR}\left(\boldsymbol{x}\right)=\Big\{\begin{array}{l}1,\mathrm{when} \operatorname {sign}\left(|{g}_i^L\left(\boldsymbol{x}\right)-{g}_i^R\left(\boldsymbol{x}\right)|+|{g}_i^L\left(\boldsymbol{x}\right)-{b}_i^R|\right)=0;\\ {}1-\max \left(0,\frac{g_i^R\left(\boldsymbol{x}\right)-{b}_i^R}{g_i^R\left(\boldsymbol{x}\right)-{g}_i^L\left(\boldsymbol{x}\right)+\mid {b}_i^R-{g}_i^L\left(\boldsymbol{x}\right)\mid}\right),\mathrm{otherwise}.\end{array}\end{array}} $$

(8)

The variation curves of v_1i(x), v_2i(x), v_3i(x) for interval constraint G_i(x) ≥ B_i with the right bound of constraint mechanical performance index are illustrated in Fig. 7, where Fig. 7(a) corresponds to the case when ${g}_i^W\left(\boldsymbol{x}\right)<{b}_i^W$ while Fig. 7(b) corresponds to the case when ${g}_i^W\left(\boldsymbol{x}\right)>{b}_i^W$. It is obvious that the variation curves of v_1i(x) and v_2i(x) will completely overlap when ${g}_i^W\left(\boldsymbol{x}\right)={b}_i^W$.

Fig. 7

Variation curves of the 3D violation vector’s components with ${g}_i^R\left(\boldsymbol{x}\right)$ for constraint G_i(x) ≥ B_i : (a) ${g}_i^W\left(\boldsymbol{x}\right)<{b}_i^W$; (b) ${g}_i^W\left(\boldsymbol{x}\right)>{b}_i^W$

5 Direct interval optimization algorithm considering global robustness

In this section, the proposed direct interval optimization algorithm with the consideration of global robustness is presented. In the first part, the preferential guidelines considering the global robustness of all the mechanical performance indices in the robust optimization model of an uncertain structure are put forward. Subsequently, the direct interval robust optimization algorithm integrating Kriging technique and nested GA is proposed in the second part. And finally, a numerical example is utilized to demonstrate the validity of the proposed algorithm in the third part.

5.1 Preferential guidelines considering global robustness

After the 3D violation vectors of all the interval constraints G_i(x) ≤ (≥)B_i(i = 1, 2, ⋯, l) in the robust optimization model in (1) have been calculated by (7) and (8), the total 3D violation vector of all the interval constraints corresponding to design vector x can be obtained by the following:

$$ {\mathbf{v}}_{\mathrm{T}}\left(\boldsymbol{x}\right)=\sum \limits_{i=1}^l{\mathbf{v}}_i\left(\boldsymbol{x}\right)=\left(\sum \limits_{i=1}^l{v}_{1i}\left(\boldsymbol{x}\right),\sum \limits_{i=1}^l{v}_{2i}\left(\boldsymbol{x}\right),\sum \limits_{i=1}^l{v}_{3i}\left(\boldsymbol{x}\right)\right). $$

(9)

Then design vector x is strictly feasible when v_T(x) = (0, 0, 0) and it is infeasible when v_T(x) > (0, 0, 0). As can be seen from (7) and (8) for calculating the 3D violation vectors of interval constraints G_i(x) ≤ B_i and G_i(x) ≥ B_i, every component of vector v_T(x) is nonnegative. Thus, the total 3D violation vectors corresponding to different design vectors can be simply compared by their norms. The interval constraints in (1) are completely violated when v_T(x) = (l, l, l).

The global robustness of an uncertain structure requires not only the strict feasibility of its constraint mechanical performance indices but also the optimal robustness of its objective mechanical performance index. Therefore, the following constraint first objective next preferential guidelines are proposed for directly sorting various design vectors of an uncertain structure.

Firstly, a design vector that is strictly feasible is always superior to the one that is infeasible. Namely, design vector x₁ is always superior to design vector x₂ when v_T(x₁) = (0, 0, 0) and v_T(x₂) > (0, 0, 0).

Secondly, the strictly feasible design vectors are sorted according to their nominal distances based on average scaling. The nominal distance based on average scaling corresponding to design vector x can be calculated by

$$ D\left(\boldsymbol{x}\right)=\sqrt{{\left({f}^C\left(\boldsymbol{x}\right)/\overline{f^C\left(\boldsymbol{x}\right)}\right)}^2+{\left({f}^W\left(\boldsymbol{x}\right)/\overline{f^W\left(\boldsymbol{x}\right)}\right)}^2}, $$

(10)

where $\overline{f^C\left(\boldsymbol{x}\right)}=\sum \limits_{i=1}^{n_1}{f}^C\left({\boldsymbol{x}}_i\right)/{n}_1$ and $\overline{f^W\left(\boldsymbol{x}\right)}=\sum \limits_{i=1}^{n_1}{f}^W\left({\boldsymbol{x}}_i\right)/{n}_1$, n₁ is the number of all the strictly feasible design vectors. The smaller nominal distance D(x) indicates the better strictly feasible design vector x.

Thirdly, the infeasible design vectors are ranked according to their corresponding norms of the total 3D violation vectors of all interval constraints, which can be calculated by

$$ \mid {\mathbf{v}}_{\mathrm{T}}\left(\boldsymbol{x}\right)\mid =\sqrt{{\left(\sum \limits_{i=1}^l{v}_{1i}\left(\boldsymbol{x}\right)\right)}^2+{\left(\sum \limits_{i=1}^l{v}_{2i}\left(\boldsymbol{x}\right)\right)}^2+{\left(\sum \limits_{i=1}^l{v}_{3i}\left(\boldsymbol{x}\right)\right)}^2}. $$

(11)

It is obvious that the larger norm ∣v_T(x)∣ indicates the worse infeasible design vector x.

5.2 Direct optimization algorithm integrating Kriging technique and nested GA

In order to directly solve the interval robust optimization model formulated in (1), an integrated optimization algorithm is proposed to realize the direct ranking of design vectors according to the preferential guidelines proposed in Sect. 5.1 based on Kriging technique and nested GA. Kriging technique is introduced to substitute the finite element analysis (FEA) to efficiently compute the mechanical performance indices of an uncertain structure corresponding to the given design variables and interval parameters. A total of l + 1 Kriging models are constructed based on the adaptive resample technology (Cheng et al. 2015) for computing the mechanical performance indices in the objective and constraint functions in (1). For a certain design vector x, a total of 2(l + 1) number of inner layer GAs are implemented in parallel for calculating the left and right bounds of the mechanical performance indices in the objective and constraint functions. The individuals of every inner layer GA correspond to different interval parameter vectors. The maximum iteration number acts as the stop criterion for every inner layer GA. The outer layer GA realizes the direct ranking of various design vectors according to the constraint first objective next preferential guidelines proposed in Sect. 5.1, the individuals of which correspond to different design vectors. Specifically, the individual corresponding to design vector x_i is assigned a rank number R(x_i) ∈ {1, 2, ..., R_max}, where R_max is the maximum rank number of all individuals. The individual corresponding to the strictly feasible design vector with the smallest nominal distance calculated by (10) is assigned the rank number 1 while the individual corresponding to the infeasible design vector with the largest norm of 3D violation vectors calculated by (11) is assigned the maximum rank number R_max. As a result, unlike the penalty-based approaches for constructing fitness functions of GA (An et al. 2015; Chen et al. 2013; Chen et al. 2017; Liu et al. 2012), the fitness values of all the individuals in the outer layer GA can be simply calculated by Fit(x_i) = 1/R(x_i).

The flowchart of the proposed direct interval optimization algorithm considering the global robustness of all the mechanical performance indices of uncertain structures is shown in Fig. 8, the implementation of which includes five steps.

Fig. 8

Flowchart of the proposed direct interval optimization algorithm considering global robustness

Algorithm: Direct interval robust optimization for uncertain structures

• Step 1. Construct the interval robust optimization model of an uncertain structure. With the uncertain factors described as interval variables, the mechanical performance indices of the uncertain structure are described as the functions of both the design and interval variables. The center and width of the most important mechanical performance index are described as the objective functions while the requirements of the other mechanical performance indices are described as the constraint functions.

• Step 2. Construct the Kriging models for calculating the mechanical performance indices of the uncertain structure based on Latin hypercube sampling (LHS) and adaptive resample technology. As far as the mechanical performance index influenced by n-dimensional design vector x and m-dimensional interval vector U such as f(x, U) and g_i(x, U) in (1) is concerned, the sample points for constructing Kriging model should be generated by LHS in the (n + m)-dimensional space determined by n design variables and m interval variables. The construction of every Kriging model is an iterative process until the achievement of the desired local and global precision evaluated by multiple correlation coefficient R² and relative maximum absolute error (RMAE) respectively.

• Step 3. Initialize the GA parameters for nested optimization, including the population sizes, maximum iteration numbers, crossover and mutation probabilities of the inner and outer layer GAs, and the convergent threshold of the outer layer GA. Set the iteration number of the outer layer GA as 1 and generate the first population of the outer layer GA.

• Step 4. Sort the individuals in the current population of outer layer GA according to the preferential guidelines proposed in Sect. 5.1 and calculate their fitness values, during the process of which the inner layer GAs integrated with Kriging models constructed in step 2 are implemented in parallel for computing the interval bounds of the mechanical performance indices in the objective and constraint functions. Specifically, the total 3D violation vectors of all interval constraints corresponding to all the individuals of the outer layer GA are calculated based on their interval closeness coefficients cc_i^LL(x), cc_i^RR(x), cc_i^LR(x) utilizing (7), (8), and (9). Then, all the individuals of the outer layer GA are classified into the strictly feasible and infeasible ones. And finally, all the individuals of the outer layer GA are sorted according to the constraint first objective next preferential guidelines considering global robustness.

• Step 5. Output the design vector with the largest fitness value as the optimal solution once the convergent threshold or maximum iteration number of the outer layer GA is reached. Otherwise, increase the iteration number of the outer layer GA by 1 and return to step 4.

5.3 Verification of the proposed optimization algorithm by a numerical example

The interval robust optimization model in (12) is utilized as a numerical example to demonstrate the validity of the proposed robust optimization algorithm. A detailed comparison analysis of the results obtained by the proposed algorithm, the algorithm based on normalized violation degree of interval constraint (NVDIC) (which is named as the NVDIC-based algorithm hereinafter for concise sake) (Cheng et al. 2017), and the indirect algorithm (Li et al. 2013) is presented to demonstrate the capability and computational efficiency of the proposed algorithm in achieving the global robustness of all the objective and constraint mechanical performance indices at the optimal solution.

$$ {\displaystyle \begin{array}{l}\underset{\boldsymbol{x}}{\min}\left\{{f}^C\left(\boldsymbol{x}\right),{f}^W\left(\boldsymbol{x}\right)\right\}=\underset{\boldsymbol{x}}{\min}\left\{\left({f}^R\left(\boldsymbol{x}\right)+{f}^L\left(\boldsymbol{x}\right)\right)/2,{f}^R\left(\boldsymbol{x}\right)-{f}^L\left(\boldsymbol{x}\right)\right\}\\ {}\mathrm{s}.\mathrm{t}.\kern1.5em {G}_1\left(\boldsymbol{x}\right)={g}_1\left(\boldsymbol{x},\boldsymbol{U}\right)={U}_1{\left({x}_1-1\right)}^2-{U}_2^2{x}_2+{U}_3^2{x}_3\ge \left[7.0,8.0\right];\\ {}{G}_2\left(\boldsymbol{x}\right)={g}_2\left(\boldsymbol{x},\boldsymbol{U}\right)={U}_1^2{x}_1+{U}_2{\left({x}_2-1\right)}^2+{U}_3^2{x}_3\ge \left[9.0,12.0\right].\\ {}\mathrm{where}\kern0.75em {f}^R\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\max }f\left(\boldsymbol{x},\boldsymbol{U}\right),{f}^L\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\min }f\left(\boldsymbol{x},\boldsymbol{U}\right);\\ {}\kern3em f\left(\boldsymbol{x},\boldsymbol{U}\right)={U}_1{x}_1^2-{U}_2{\left({x}_2-2\right)}^2+{U}_3^2{\left({x}_3-1\right)}^2;\\ {}{x}_1\in \left[2.0,12.0\right],{x}_2\in \left[2.0,12.0\right],{x}_3\in \left[2.0,12.0\right];\\ {}{U}_1=\left[0.9,1.1\right],{U}_2=\left[0.9,1.1\right],{U}_3=\left[0.9,1.1\right].\end{array}} $$

(12)

The interval robust optimization model in (12) is solved by different algorithms with the same GA parameters listed in Table 1. Besides the maximum iteration number given as the stop criterion, the outer layer GA evolution is terminated when the absolute difference of f^C(x) between the optimal solution and the average of the current population is less than 10⁻³. It is notable that no Kriging model needs to be constructed here because all the objective and constraint functions are explicit. Moreover, the interval robust optimization model in (12) has to be transformed into a deterministic one at first so as to be solved by the indirect algorithm. During the model transformation process for (12), the weighting factors of f^C(x) and f^W(x) are prescribed as 0.5 with their corresponding normalization factors settled as 3.0 and 0.6 respectively while the satisfactory degrees for both constraints are prescribed as 1 with the same penalty factor of 200,000.

Table 1 GA parameters for the numerical example in (12)

Table 2 summarizes the optimization results of the numerical example obtained by the proposed, NVDIC-based, and indirect algorithms. As is seen from Table 2, the proposed algorithm is the most efficient since it can locate the optimal solution with the fewest outer layer GA iterations. The second constraint function g₂(x, U) ≥ [9.0, 12.0] is always satisfied at the optimal solutions obtained by three algorithms, but the first constraint function g₁(x, U) ≥ [7.0, 8.0] may be violated at the optimal solution x^∗ = (4.51, 6.80, 2.00) obtained by the NVDIC-based algorithm while it is fully satisfied at the optimal solution x^o = (5.30, 7.46, 2.29) obtained by the proposed algorithm and x^I = (5.60, 10.93, 2.67) obtained by the indirect algorithm. Specifically, the optimal solution x^∗ obtained by the NVDIC-based algorithm is not strictly feasible because the interval g₁(x^∗, U) = [4.51, 10.50] partially overlaps the given interval constant [7.0, 8.0] and there is v₁(x^∗) > (0, 0, 0) according to (8), although the first constraint in (12) is regarded as feasible at x^∗ according to the definition of NVDIC based on the “center first width next” interval order relation in the NVDIC-based algorithm since there is ${g}_1^C\left({\boldsymbol{x}}^{\ast}\right)=7.51>7.5$. Therefore, the proposed algorithm can locate a strictly feasible solution to the numerical example while the NVDIC-based one cannot. Such an improvement benefits from the preferential guidelines considering the global robustness of all the objective and constraint mechanical performance indices proposed in Sect. 5.1 based on the precise determination of the violation degree of an interval constraint and the precise description of the relative positional relationship between an interval constraint mechanical performance index and its corresponding given interval constant with the introduction of the new concept of interval closeness coefficient. Both the optimal solutions x^o and x^I obtained by the proposed and indirect algorithms are strictly feasible for all constraints, but f^W(x^o) is much smaller than f^W(x^I), meaning that the proposed algorithm can achieve the more robust solution than the indirect one. To sum up, the proposed algorithm is the most efficient which can locate the most robust optimal solution to the numerical example in (12) among three algorithms.

Table 2 The optimization results of the numerical example obtained by different algorithms

6 Engineering example: robust optimization of the upper beam in a high-speed press

To demonstrate the feasibility and effectiveness of the proposed interval robust optimization approach in solving realistic engineering problems, the robust optimization of the upper beam in a high-speed press is thoroughly investigated in this section. The interval robust optimization model of the upper beam is constructed at first according to its performance requirements. Subsequently, the Kriging models for calculating the mechanical performance indices of the upper beam in the robust optimization model are constructed. Then, the robust optimization model of the upper beam is solved by the proposed, NVDIC-based, and indirect approaches based on the Kriging models and nested GA, the optimization results of which are compared and analyzed in detail.

6.1 Mathematical modeling of the interval robust optimization problem

High-speed press is widely applied in instrument, automotive, aerospace industries due to its capability of continuously and automatically punching precision parts such as motor cores at a high speed, see Fig. 9a for illustration. The upper beam in Figs. 9b, c is one of the most important components of the high-speed press, the mechanical performance indices of which greatly influence the punching precision of the machine. Meanwhile, the variations of material properties are inevitable for the upper beam, which will lead to the fluctuations of its mechanical performance indices. Therefore, it is necessary to optimize the geometrical parameters of the upper beam to improve its mechanical performance indices and robustness against uncertainties.

Fig. 9

The upper beam of a high-speed press. a The high-speed press in workplace. b One-half solid model of the upper beam. c Cross section of the upper beam

The geometrical parameters h₁, h₂, l₁, l₂, l₃ in the cross section of the upper beam in Fig. 9c are chosen as the design variables for improving the mechanical performance indices of the upper beam. The uncertain material density ρ and Poisson’s ratio ν of the upper beam are described as interval variables due to the insufficient information of uncertainties. The center and width of the maximum deformation are described as the objective functions considering that the stiffness reversely reflected by the maximum deformation is the most important mechanical performance index of the upper beam. The maximum allowable weight and maximum equivalent stress of the upper beam are described as the constraint functions to avoid the ponderous and risky design. Therefore, the interval robust optimization model of the upper beam can be constructed as

$$ {\displaystyle \begin{array}{l}\underset{\boldsymbol{x}}{\min}\left\{{d}^C\left(\boldsymbol{x}\right),{d}^W\left(\boldsymbol{x}\right)\right\}=\underset{\boldsymbol{x}}{\min}\left\{\left({d}^R\left(\boldsymbol{x}\right)+{d}^L\left(\boldsymbol{x}\right)\right)/2,{d}^R\left(\boldsymbol{x}\right)-{d}^L\left(\boldsymbol{x}\right)\right\},\\ {}\mathrm{s}.\mathrm{t}.\kern1.5em w\left(\boldsymbol{x},{U}_1\right)=\left[{w}^L\left(\boldsymbol{x}\right),{w}^R\left(\boldsymbol{x}\right)\right]\le \left[5170,5230\right]\mathrm{kg};\\ {}\kern1.98em \delta \left(\boldsymbol{x},\boldsymbol{U}\right)=\left[{\delta}^L\left(\boldsymbol{x}\right),{\delta}^R\left(\boldsymbol{x}\right)\right]\le \left[40,45\right]\mathrm{MPa}.\\ {}\mathrm{where}\kern0.5em {d}^R\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\max }d\left(\boldsymbol{x},\boldsymbol{U}\right),{d}^L\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\min }d\left(\boldsymbol{x},\boldsymbol{U}\right);\\ {}\kern2.75em {w}^R\left(\boldsymbol{x}\right)=\underset{U_1}{\max }w\left(\boldsymbol{x},{U}_1\right),{w}^L\left(\boldsymbol{x}\right)=\underset{U_1}{\min }w\left(\boldsymbol{x},{U}_1\right);\\ {}\kern2.75em {\delta}^R\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\max}\delta \left(\boldsymbol{x},\boldsymbol{U}\right),{\delta}^L\left(\boldsymbol{x}\right)=\underset{\boldsymbol{U}}{\min}\delta \left(\boldsymbol{x},\boldsymbol{U}\right).\\ {}\kern2.75em \boldsymbol{x}=\left({h}_1,{h}_2,{l}_1,{l}_2,{l}_3\right),\boldsymbol{U}=\left({U}_1,{U}_2\right)=\left(\rho, \upsilon \right);\\ {}\kern1.98em 210\mathrm{mm}\le {h}_1\le 250\mathrm{mm},250\mathrm{mm}\le {h}_2\le 300\mathrm{mm},\\ {}\kern1.98em 80\mathrm{mm}\le {l}_1\le 120\mathrm{mm},25\mathrm{mm}\le {l}_2\le 55\mathrm{mm},330\mathrm{mm}\le {l}_3\le 390\mathrm{mm};\\ {}\kern2.11em {U}_1=\rho =\left[7200,7400\right]\mathrm{kg}\cdot {\mathrm{m}}^{-3},{U}_2=\upsilon =\left[0.27,0.33\right].\end{array}} $$

(13)

where x is the design vector while U is the interval uncertain vector; d(x, U) is the maximum deformation of the upper beam; d^C(x) and d^W(x) are the center and width of d(x, U) while d^L(x) and d^R(x) are the left and right bounds of d(x, U); w(x, U₁) and δ(x, U) are the weight and maximum equivalent stress of the upper beam while w^L(x), w^R(x), δ^L(x), and δ^R(x) are their left and right bounds respectively.

6.2 Construction of Kriging models for computing mechanical performance indices

In order to efficiently solve the interval robust optimization model of the upper beam in (13), the Kriging models for computing the maximum deformation d(x, U), weight w(x, U₁), and maximum equivalent stress δ(x, U) are constructed based on the adaptive resample technology (Cheng et al. 2015). All the sample points involved in the construction of Kriging models are generated by LHS. The maximum deformation, weight, and maximum equivalent stress of the upper beam at the sample points are computed by FEA. Figure 10 illustrates the loads and constraints of the one-half upper beam, the mesh model of which comprises 5066 Solid187 elements and 9908 nodes.

Fig. 10

Loads and constraints of the one-half upper beam

The desired global and local precision of all Kriging models are prescribed as 0.95 and 0.05 respectively. The initial Kriging models are constructed by 28 sample points. Ten test points are utilized to verify the global precision of Krigings, among which those relatively far away from the previous sample points are added into the sample point set for generating new Krigings when multiple correlation coefficient R² ≤ 0.95. Three resample points within the maximum hypercube centered by the sample point with maximum RMAE are added into the sample point set for generating new Krigings when RMAE ≥ 0.05. Table 3 lists the statistics of the Kriging models for calculating d(x, U), w(x, U₁), and δ(x, U), which demonstrate that the desirable global and local precision can be achieved with 60 sample points.

Table 3 Statistics of the Kriging models for calculating the upper beam’s mechanical performance indices

6.3 Optimization results obtained by the proposed approach

Based on the Kriging models constructed in Sect. 6.2, the interval robust optimization model in (13) is solved by the proposed approach with the nested GA parameters listed in Table 4. In addition to the stop criterion of maximum iteration number, the outer layer GA evolution is terminated when the absolute difference of the objective function d^C(x) between the optimal solution and the average of the current population is less than 10⁻⁴ mm.

Table 4 Nested GA parameters for solving the interval robust optimization model of the upper beam

The convergent curves at the optimal solution to (13) obtained by the proposed approach are shown in Fig. 11. Specifically, the outer layer GA reaches the convergent threshold after 25 iterations and the optimal design vector is obtained as x^o = (213.74, 250.00, 80.61, 27.90, 370.16), the corresponding objective and constraint performance indices at which are d^C(x^o) = 0.1190, d^W(x^o) = 0.0040, w(x^o, U₁) = [4999.34, 5170.00], and δ(x^o, U) = [17.93, 40.00] respectively. It is obvious that both constraints in (13) are fully satisfied at x^o.

Fig. 11

Convergent curves of the mechanical performance indices obtained by the proposed approach. a Convergent curves of maximum deformation. b Convergent curves of weight. c Convergent curves of maximum equivalent stress

To analyze the computational performance of the proposed algorithm, 50 independent runs are conducted by varying the population sizes and maximum iteration numbers of the inner and outer layer GAs. The experimental results demonstrate that the maximum iteration numbers of both inner and outer layer GAs have few influences on the optimization results when they are greater than 100. Moreover, the larger population sizes of the inner and outer layer GAs usually produce the smaller fluctuations of the objective value at the optimal point. The fluctuation of the objective value at the optimal point is less than 1% when the population sizes of both inner and outer layer GAs are larger than 150. Therefore, it is suggested to apply the large population sizes as listed in Table 4 for the engineering example of the upper beam.

6.4 Comparison with other approaches

With the same GA parameters and convergent threshold as those utilized in the proposed approach, the interval robust optimization model in (13) is also solved by the NVDIC-based method. As can be observed from the convergent curves of the mechanical performance indices in Fig. 12, the objective values of the optimal solution converge at the 50th generation of the outer layer GA and the optimal solution is obtained as x^∗ = (255.01, 250.36, 107.14, 49.41, 349.97), the corresponding objective values at which are d^C(x^∗) = 0.1144, d^W(x^∗) = 0.0040.

Fig. 12

Convergent curves of the mechanical performance indices obtained by the NVDIC-based approach. a Convergent curves of maximum deformation. b Convergent curves of weight. c Convergent curves of maximum equivalent stress.

To solve the interval robust optimization model in (13) by the indirect approach, the interval model is firstly transformed into a deterministic one with the model transformation parameters prescribed as follows: both the weighting factors of f^C(x) and f^W(x) are 0.5 while their normalization factors are 0.1 and 0.001 respectively; the satisfactory degrees for both constraints are 1 while the penalty factors of both constraints are 200,000. With the GA parameters and convergent threshold prescribed as those utilized in the proposed approach, the objective values of the optimal solution converge at the 32nd generation of the outer layer GA, see Fig. 13 for illustration. The optimal solution is obtained as x^I = (210.00, 250.36, 107.14, 49.41, 349.97), the corresponding objective values at which are d^C(x^I) = 0.1160 and d^W(x^I) = 0.0060.

Fig. 13

Convergent curves of mechanical performance indices obtained by the indirect approach. a Convergent curves of maximum deformation. b Convergent curves of weight. c Convergent curves of maximum equivalent stress

Table 5 provides a comparison of the optimization results obtained by the proposed, NVDIC-based, and indirect approaches, the second column of which demonstrates that the proposed approach can locate the optimal design vector most efficiently. As evidently illustrated in Table 5, the interval widths of the maximum deformations corresponding to the optimal solutions obtained by both the proposed and NVDIC-based approaches are 0.0040, which are smaller than that of the optimal solution obtained by the indirect approach. That is, the proposed and NVDIC-based approaches can locate the optimal solutions of more robust objective performance index than the indirect one. However, the constraints on the weight and maximum equivalent stress at the optimal solution obtained by the NVDIC-based approach may be violated since their varying intervals under uncertain material properties are [5111.58, 5288.37] kg and [28.58, 50.62] MPa respectively, which partially overlap with their corresponding interval constants (namely, [5170, 5230] kg and [40, 45] MPa) prescribed in constraints. Although the optimal solution x^∗ = (255.01, 250.36, 107.14, 49.41, 349.97) is regarded as feasible according to the center first width next interval order relation in the NVDIC-based approach since there are ${w}_1^C\left({\boldsymbol{x}}^{\ast}\right)=5199.98\mathrm{kg}\le 5200\mathrm{kg}$ and ${\delta}_1^C\left({\boldsymbol{x}}^{\ast}\right)=39.6\mathrm{MPa}\le 42.5\mathrm{MPa}$, it is not strictly feasible according to the preferential guidelines in Sect. 5.1 since the 3D violation vectors corresponding to both constraints in (13) are nonzero. That is, the proposed approach can achieve the robust optimal solution with strictly feasible constraint mechanical performance indices while the NVDIC-based approach cannot ensure the strict feasibility of interval constraints at the optimal solution. Consequently, the optimal solution obtained by the proposed approach is the most robust considering both the objective and constraint mechanical performance indices of the upper beam, demonstrating the validity and applicability of the proposed interval robust optimization approach in engineering.

Table 5 Comparison of the optimization results of the upper beam obtained by different approaches

7 Conclusions

A direct interval robust optimization approach was proposed in this paper to achieve the robust optimal design vectors for engineering structures with interval uncertainties. The new concept of interval closeness coefficient was proposed to describe the relative positional relationship between the interval boundaries of interval constraint mechanical performance index and its corresponding given interval constant. Explicit formulas for calculating the four interval closeness coefficients between the boundaries of an interval constraint mechanical performance index and its corresponding given interval constant were presented, and subsequently, the 3D violation vectors of different interval constraints in the robust optimization model could be calculated for evaluating the feasibility robustness of a design vector. The preferential guidelines considering the global robustness of all the mechanical performance indices were proposed for directly ranking various design vectors of an uncertain structure, which was realized by an algorithm integrating Kriging technique and nested GA.

The optimization results of the numerical example demonstrated that the proposed direct interval robust optimization approach performed better than the NVDIC-based one in ensuring the strict feasibility of the optimal solution and that it could achieve the optimal solution with more robust objective performance than the indirect approach besides the advantage of avoiding the complicated model transformation process. The engineering example of the upper beam in a high-speed press with interval material density and Poisson’s ratio demonstrated the applicability and effectiveness of the proposed approach in the robust optimization of practically motivated engineering structures.