1 Introduction

Uncertainty is ever-present in both the design and management phases of engineered systems. Decades of research and development in reliability engineering, design under uncertainty, statistical model calibration and validation, and other areas have emphasized the importance and value of consideration of uncertainties (Yao et al. 2011; Lee et al. 2018; Romero 2010; Lopez and Sarigul-Klijn 2010). Uncertainty characterization, also called uncertainty modeling, is the science of quantitative characterization of uncertainties in engineering applications (Agarwal et al. 2004; Helton et al. 2006; Ghanem et al. 2008). One of the main activities in uncertainty characterization is to characterize uncertainty in data. Uncertainty in data means that the true value of a quantity of interest is unknown.

In general, uncertainty in data is characterized or quantified by a probability distribution (e.g., a probability density function (PDF)), which is assigned based upon the information (e.g., expert experience) or evidence (e.g., observed data) about the likelihood of what the true value might be (Lin et al. 2014; Soundappan et al. 2004; Guo and Du 2007). The ways of characterizing the uncertainty in data are broadly classified as parametric or nonparametric methods (McFarland and Mahadevan 2008; Cho et al. 2016). Parametric methods consist of two procedures. First, the parametric method assumes a certain type of parameterized probability distribution for the given data. Then, statistical parameters of the assumed probability distribution are estimated. Often, expert knowledge is used when assuming a type of probability distribution. However, due to a lack of knowledge, an incorrect assumption about the type of probability distribution may be made, causing an erroneous result. On the other hand, nonparametric methods do not specify a certain type of probability distribution. Instead, the probability distribution is determined directly from the data. Histograms or kernel density estimations are popular examples of nonparametric methods (Cho et al. 2016; McFarland and Mahadevan 2008). Though nonparametric methods make fewer assumptions and have more flexibility than parametric methods, a probability distribution characterized by a nonparametric method can be highly biased to the given data; thus, it may not be suitable in situations where limited data is available. To reflect situations found in real-world applications, where only limited data might be available, this research proposes a parametric method to characterize uncertainty in the data.

The true value of a quantity of interest is usually estimated by measurement or observation data. To improve the estimate of the true value of interest, repeated measurements in the same experimental conditions are often conducted. These multiple measurements are said to display various sources of uncertainty, such as variability due to physical uncertainties or measurement errors. Variability refers to the multiple values that result from physical uncertainties, such as manufacturing tolerances, different experimental settings, and other issues (Jung et al. 2016; Karniadakis and Glimm 2006; Jung et al. 2015). For example, measurements of the deflection at the tip of a cantilever beam vary due to geometric differences (e.g., height, length, and width of the cantilever beam) or material differences (e.g., heterogeneous elastic modulus of the cantilever beam) of each cantilever beam. Most existing works in uncertainty characterization are focused on how to quantify the variability in a quantity of interest through a probability distribution, with a limited amount of observed data; in these prior studies, the measurement errors are ignored.

Measurement errors, or observational errors, refer to the difference between the measured values of a quantity and its true value (Easterling 2001; Wilson and Smith 2013). Carrying out a perfect, error-free experiment is impossible. Whether its degree is large or small, a measured value always includes measurement error. The factors contributing to measurement errors are open-ended. In general, most prior studies have been conducted with a focus on eliminating sources of measurement error, for example, making effort to maintain the same experimental conditions, continuous calibrations of measurement instruments, or using expensive instruments to minimize random errors in the measured values. In many cases, however, it may not be possible to invest large expenses in experiments. Even when funding is available, results from expensive equipment still can contain measurement errors.

Most existing works in uncertainty characterization are focused on how to quantify the variability in a quantity of interest through a probability distribution, with a limited amount of observed data while measurement errors are ignored.

Previous studies have attempted to characterize the uncertainty, especially by the sources of physical uncertainties while eliminating the measurement errors or considering them independently, using various estimation methods. Estimation methods are broadly classified into likelihood and Bayesian methods. As an example of using likelihood methods, Raudenbush et al. describes the maximum likelihood method with the Laplace approximation (Raudenbush et al. 2000). Also, the expectation-maximization algorithm is a widely used likelihood method for parameter estimation (McLachlan and Krishnan 2007). Meanwhile, the Bayesian method infers the target parameters by calculating the posterior distribution. Since the direct evaluation of the posterior is not easy, various approximation methods are developed. Blei et al. reviewed the variational approximation method that finds the closest distribution to the target from the defined family of distributions (Blei et al. 2017). Sampling-based method such as the Markov chain Monte Carlo simulation is also well-known approximation for the Bayesian approach (Doucet et al. 2015). Although many estimation techniques are available for various cases, most of them assume that the variabilities by the sources of physical uncertainties and measurement errors are independent when they formulate the likelihood function or the Bayesian posterior, which is not always the case.

This study proposes a method to characterize the uncertainty of observation data in the presence of systematic and random measurement errors, which are considered as dependent to the observed data. The proposed method develops a probability distribution able to characterize the variability that arises due to physical uncertainties in the observed data. Meanwhile, the uncertainties that arise due to measurement errors are also characterized using probability distributions, which are dependent to the observed data. Statistical parameters of each probability distribution are estimated using the maximum likelihood method. As a case study for the proposed method, a cantilever beam problem posed by Sandia National Laboratories is introduced that includes an observational data set suitable for characterization with a probability distribution (Romero et al. 2017; Romero and Weirs 2018; Kim et al. 2018). The case study aims at characterizing the uncertainty in the observed deflection at the tip of a cantilever beam by using the proposed method. In this study, the uncertainties that arise from the systematic and random measurement errors are assumed to follow a uniform distribution (or an interval) and a normal distribution, respectively.

The remainder of this paper is organized as follows. Section 2 provides an overview of measurement errors through a simple introduction of the cantilever beam problem proposed by Sandia National Laboratories. Section 3 explains how the maximum likelihood method is adopted to estimate statistical parameters of each probability distribution and to explain the variability that arises from physical uncertainty sources and two measurement errors. In Section 4, the uncertainties in the observed data of the tip deflection are characterized by the proposed method, and a discussion of the results is provided. Finally, the paper’s conclusions and suggestions for future work are provided in Section 5.

2 Measurement errors observed in engineering problems

Section 2 introduces the research topics of this study. Section 2.1 explains measurement errors, which include systematic and random measurement errors. To help the reader understand measurement errors in observed data, a brief discussion on uncertainty and variability is included. Section 2.2 introduces the cantilever beam problem posed by Sandia National Laboratories, which is used as a case study in this research. The case study aims to apply the proposed technique to characterize the uncertainty in the observed data at the tip deflection of a cantilever beam.

2.1 Overview of measurement errors

Before discussing measurement errors in earnest, the terminology used to describe uncertainty and variability should be clarified. When it is said that there is “uncertainty” in a quantity, it means we do not know the value of the quantity with certainty. To estimate an unknown value of a quantity of interest, experiments are established to obtain observed or measured data. In observed data, “variability” exists due to various factors, including physical uncertainties and measurement errors (Zhang and Mahadevan 2000). The physical uncertainty is due to the natural inherent uncertainty in the material and geometric properties (e.g., inherent uncertainty in the elastic modulus and manufacturing tolerances). In general, physical uncertainty is considered aleatory uncertainty, which means irreducible uncertainty. In this case, the goal is to quantify the uncertainty well using a probability distribution in the uncertainty characterization process. However, one challenge in accurately characterizing the physical uncertainty is the existence of statistical uncertainty and measurement errors. In general, statistical uncertainty is caused by a limited amount of observed data. Most prior studies have focused on dealing with statistical uncertainty; however, measurement errors are often neglected or assumed to be absent. Methods for dealing with statistical uncertainty in uncertainty characterization are beyond the scope of this paper. This paper focuses on how to deal with measurement errors in the process of uncertainty characterization.

Measurement errors, or observational errors, are the cause of the difference between measured values of a quantity and its true value. (Here, the true value denotes the variability in a quantity that results only from the abovementioned physical uncertainty sources.) Measurement errors can be categorized into two types: (1) systematic measurement error and (2) random measurement error (Easterling 2001; Ferson and Ginzburg 1996; Liang and Mahadevan 2011; Ling and Mahadevan 2013). Systematic measurement error, also known as measurement bias, is introduced by inaccuracy factors that occur during the observation or measurement process. For example, when a particular sensor is used in all the replicate tests, or when all the replicate tests are conducted in a certain experimental setting (e.g., a higher temperature than a normal condition), then all measurements may have a similar biased error. On the other hand, random measurement error is caused by poor precision factors. Human errors, like fluctuations in the experimenter’s interpretation of the instrumental readings, are one example. As another example, measurements may be gathered from a sensor that is picked randomly from a population of sensors; in this case, multiple measurements may have inaccuracy that is described by a distribution of error. The major difference between the two types of measurement errors is that a particular source of a systematic measurement error will affect all the replicate measurements in the same way. In contrast, a source of random measurement error will randomly affect the measurements. Generally, for this reason, the uncertainties that arise due to systematic measurement errors and random measurement errors are characterized by a uniform distribution and a normal distribution, respectively.

Figure 1 helps to describe systematic and random measurement errors. Each data set of the green-, blue-, and red-shaded part in Fig. 1 denotes ten repeated experiments. In Fig. 1a, the data in the upper part (the green-shaded part) describe the true variability or the value of the quantity of interest. If there is no measurement error in the experiments while the inherent uncertainties exist, the observed data should appear like the data in the upper part of Fig. 1a. The green probability distribution of the right-hand side exhibits the mother population of the quantity of interest; this can be quantified or characterized after a perfect uncertainty characterization process. On the other hand, the sample data in the lower part (the blue-shaded part) of Fig. 1a describe that each datum is biased due to systematic error. Note that each datum has not been biased with the same magnitude of error—this is an important clarification. In Fig. 1b, the data (the red-shaded part) describe the observations that result from a situation with both systematic and random errors. For example, in the third observation from the left, the datum (the upper red point) is observed slightly deviated from the datum (the lower blue point) that exhibits only systematic error. (Note that random measurement error does not affect the average, only the variability around the average.) In the presence of systematic and random measurement errors, the observed data will be like the data shown in Fig. 1b. The goal of this research is to characterize the variability in the true value (the green probability distribution in Fig. 1a) by using the observed data and subtracting the systematic and random measurement errors.

Fig. 1
figure 1

Illustration of measurement errors: Observed data with systematic measurement error (a) and with systematic and random measurement errors (b)

Full size image

Figure 2 explains the probability density functions of systematic and random measurement errors. This paper follows the way of characterizing the measurement errors that is described in the document provided by Sandia Laboratories (Romero et al. 2017). First, systematic measurement errors, which bias the measurement from the true value, emerge from a source of measurement error that is effectively the same in all the replicate tests. This is described by a uniform distribution defined by a lower bound and an upper bound (Fig. 2a). One of the two bounds is set to “0,” which means there is no bias from the true value. The other bound denotes the maximum amount of bias α, relative to the measured value (x). For a negative systematic error (Fig. 2a, a negative systematic error biases the true value to a smaller measured value), the upper bound is set to “0” and the lower bound is set to − α relative to the measured value (x), and vice versa for a positive systematic error ([0, αx]). Second, random measurement errors are characterized to follow normal distributions due to the multiple sources of random errors (central limit theorem). Random measurement error, which follows the normal distribution with “0” mean and βx standard deviation, is added to the value biased by the systematic measurement error. Note that the random measurement error can cause either an increase or a decrease of the true value.

Fig. 2
figure 2

Probability density function of measurement errors: a Systematic measurement error and b random measurement error

Full size image

Figure 3 describes the PDFs of the true value with measurement errors (x + e). First, the gray-shaded PDFs (p(x)) in the upper part of Fig. 3 denote the PDF of the true value (x) without any measurement error. The proposed method aims to obtain p(x). Suppose that x1 and x2 are arbitrarily sampled from p(x). Depending on the randomly sampled values (x1 and x2), the PDFs of e are defined using the method explained in Fig. 2 (p(esys|x), p(eran|x)). Then, the PDFs of the true value with two measurement errors (x + esys, x + eran) are formulated as the bottom parts of Fig. 3a, b, respectively. In Fig. 3a, two uniform distributions are defined by the lower bounds (x1 − αx1, x2 − αx2) and upper bounds (x1, x2) for two samples x1 and x2. This explains that an observation x1 with systematic measurement error can be observed from the left blue-shaded uniform distribution. Therefore, an uncertainty characterization process is required to eliminate the biased effect from the systematic measurement error to obtain the gray-shaded true population p(x). In Fig. 3b, two normal distributions are defined by means (x1, x2) and standard deviations (β1x1, β2x2) for two samples, x1 and x2. An observation x1 with a random measurement error can be observed from the left red-shaded uniform distribution. Therefore, an uncertainty characterization process is required to eliminate the random effect that arises from random measurement error to obtain the gray-shaded true population p(x). For a case where both systematic and random measurement errors exist, p(x + e|x) can be defined by integrating esys and eran into e.

Fig. 3
figure 3

Probability density function (PDF) of the true value (x) of the quantity of interest, with measurement errors (e): a PDF of x and systematic error (esys) and b PDF of x and random error (eran)

Full size image

2.2 Engineering application: cantilever beam problem

In 2017, Sandia National Laboratories posed a cantilever beam problem for dealing with uncertainties in model calibration, model validation, risk assessment, and safe design (Romero et al. 2017). Proper uncertainty characterization of measurements is crucial for addressing those engineering applications. For this reason, characterizing the uncertainties in measurement of a system response is presented as one fundamental task among various specific questions and tasks posed in the problem. Analysts are asked to characterize the uncertainty in the provided measurement data of the system response or the output. As a case study, this paper adopts this uncertainty characterization problem posed by Sandia National Laboratories.

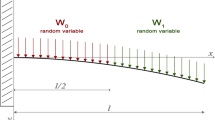
The subject of the problem is a cantilever beam horizontally protruding from a rigid, unyielding vertical wall (Fig. 4). As the quantity of interest is a system response, the problem seeks to define the cantilever beam’s deflection (x) at the free end of the beam when a vertical downward loading (P = P0) is applied at the same point. For repeated measurements, samples are randomly selected from a population of rectangular cantilever beams, of which the geometric (length (L), height (H), and width (W)) and material properties vary among the population. In particular, the material properties examine the elastic modulus. In the problem, it is tentatively assumed that the beam is made of a homogeneous isotropic material, which denotes that the same value of the elastic modulus can be attributed to the beam’s deflection through the entire beam. (Note that there is no dependency or statistical correlation among the geometric and material properties.) Due to somewhat large variations in the geometric and material properties, the randomly selected beam shows the variability in the observed system response (D).

Fig. 4
figure 4

Scheme of the deflection at the tip of a cantilever beam (Romero et al. 2017)

Full size image

In the problem, the observed data (D) are further subject to two measurement errors that arise during the pickup and usage of a measuring sensor. Here, a measuring sensor is randomly picked from a population of sensors, and the selected sensor is repeatedly used for a set of data. When the chosen sensor has biased accuracy described by a distribution or range of error, then all the measurements of each set produced from that sensor may have similar biased error; this is called systematic measurement error. Meanwhile, random measurement errors may exist both inside the set of data and across the sets of data. For example, detachment of the chosen sensor for reuse in four different beams may cause random measurement errors through the entire data in a set. Also, the chosen sensor for each set of data can have random measurement errors, since they are randomly picked up from a sensor population where variability in accuracy may exist.

Section 4 presents the estimated results of the probability density functions for the variability and two measurement errors in observed deflections (D). For the data (D) of the beam’s deflection, the authors intentionally generated sample data. The details are summarized in Section 4. In the next section, the proposed method for characterizing uncertainties in the presence of measurement errors is described.

3 Proposed methods: uncertainty characterization by maximum likelihood estimation

Section 3 introduces the method proposed in the research described in this paper. Section 3.1 explains the overall scheme to characterize uncertainties in the observed data using the proposed method. Section 3.2 summarizes the mathematical formulation of the maximum likelihood estimation. Section 3.3 provides a discussion on the estimation error due to a Gaussian assumption in this study.

3.1 Scheme of uncertainty characterization under measurement errors

The goal of this research is to estimate the statistical parameters of the probability distribution (p(x)) that describes the variability and uncertainties in the deflection (x) at the tip of a cantilever beam using the observed data set (D). The observed data (D = {d1, …, dN}) denote a set of datum (di). The method of maximum likelihood estimates the values of the statistical parameters that maximize the likelihood function, given the observations. The overall steps for the proposed method are outlined in Table 1. Table 1 involves detailed mathematical formulation before the likelihood function is formulated. Later, Section 3.2 explains the detailed mathematical formulation of estimating the unknown statistical parameter by maximizing the likelihood function. For simplicity in notation, the random variable of the probability distribution p(x) can be understood as x by its value. For example, p(x) is not distinguished by the subscript x, as in px(x), unless it is necessary. For example, p(x) is a probability distribution for the random variable x, but py(x) is the probability distribution for the random variable y.

Table 1 Steps for uncertainty characterization by maximum likelihood estimation
Full size table

First, step 1 explains how the observed data include the true variability and the two measurement errors (1). In step 2, a Gaussian distribution is assumed for describing the true variability of experimental observations. With the Gaussian assumption, the mean (μx) and standard deviation (σx) become unknown parameters to be estimated (2). This paper concludes by introducing only the Gaussian case. However, when using a parametric approach, it should be noted that wrong assumption on the type of probability distribution may cause estimation error. Further discussion on the estimation error is provided in Section 3.3. In step 3, based on the information given in Section 2.2, a uniform and a normal distribution is formulated for the probability distributions of the systematic and random measurement errors, respectively. Then, the probability distribution of the integrated measurement error (e) can be formulated as shown in (6). In (7) of step 4, the probability distributions of the observed deflection datum (d) and the integrated error (e) become equal when the given x is considered a constant value. Finally, the marginal distribution of the observed deflection (d) is formulated as (8). The following section presents how to develop the likelihood function and how to find the values of the unknown parameters that maximize the likelihood function.

3.2 Mathematical formulation of the maximum likelihood estimation

Using (8), the likelihood function (L) for the given data set (D = {d1, …, dN}) can be formulated as

$$ L(D)=\prod \limits_{i=1}^Np\left({d}_i\right)=\prod \limits_n\int p\left({d}_n|x\right)p(x)\mathrm{dx} $$
(9)

Since the true deflection (x) is assumed to follow a Gaussian distribution, as shown in (2), (9) is reformulated into

$$ L\left(D|\mu, \sigma \right)=\prod \limits_n\int p\left({d}_n|x\right)N\left({\mu}_x,{\sigma}_x\right)\mathrm{dx} $$
(10)

Using the logarithm, the log-likelihood function can be formulated as

$$ \ln \left(L\left(D|\mu, \sigma \right)\right)=\sum \limits_n\ln \left(\int p\left({d}_n|x\right)N\left({\mu}_x,{\sigma}_x\right)\mathrm{dx}\right) $$
(11)

By computing derivatives of (11) with respect to μx and σx, and equating to zero, respectively, μx and σx2 are obtained as

$$ {\mu}_x=\frac{1}{N}\sum \limits_N\frac{\int_{-\infty}^{\infty}\mathrm{xp}\left({d}_n|x\right)N\left({\mu}_x,{\sigma}_x\right)\mathrm{dx}}{\int_{-\infty}^{\infty }p\left({d}_n|x\right)N\left({\mu}_x,{\sigma}_x\right)\mathrm{dx}} $$
(12)
$$ {\sigma}_x^2=\frac{1}{N}\sum \limits_N\frac{\int_{-\infty}^{\infty }{\left(x-{\mu}_x\right)}^2p\left({d}_n|x\right)N\left({\mu}_x,{\sigma}_x\right)\mathrm{dx}}{\int_{-\infty}^{\infty }p\left({d}_n|x\right)N\left({\mu}_x,{\sigma}_x\right)\mathrm{dx}} $$
(13)

By substituting (2) and (7) into N (μx, σx) and p (dn|x), respectively, in (12) and (13), the estimate of μx and σx2 can be obtained. Note that μx and σx should be obtained by iterative updates, since (12) and (13) are not explicit equations about μx and σx.

3.3 Discussion on estimation error by the Gaussian assumption

In this study, the type of distribution for a quantity (x) in interest is assumed to follow a Gaussian distribution. However, when the true type is the non-Gaussian distribution, the estimation error (e(x)) due to the incorrect assumption on the distribution type is as follows:

$$ {\displaystyle \begin{array}{c}e(x)=p\left(x|\boldsymbol{\uptheta} \right)-N\left(x|\mu, \sigma \right)\\ {} Subject\kern0.17em to\;E\left[x\right]=\mu\;and\; Var\left[x\right]={\sigma}^2\end{array}} $$
(14)

where θ is the parameter vector of the true distribution. (14) implies that the estimation error (e(x)) between the incorrectly assumed distribution and true type of distribution may exist; the estimated mean (μ) and variance (σ2) will be identical. Hence, if the true distribution is not much biased and unimodal, the estimation error will be small. In contrast, if the true type of probability distribution for x is multimodal and highly biased, the Gaussian assumption might be irrelevant.

Calculation of the estimation error (e(x)) in (14) is not available since the true type of probability distribution is unknown for real problems. However, if the type of the true probability distribution happens to be known later, the estimation error (e(x)) and even the true distribution can be readily obtained for some cases by transforming the estimated mean and variance from the proposed method. For example, if the log-normal distribution is known to be the true type of a probability distribution for x, the estimation error (e(x)) can be expressed as

$$ {\displaystyle \begin{array}{c}e(x)=\mathrm{Log}\left(x|m,v\right)-N\left(x|\mu, \sigma \right)\\ {} Subject\kern0.17em to\;E\left[x\right]=\mu\;and\; Var\left[x\right]={\sigma}^2\end{array}} $$
(15)

where the estimated mean (μ) and variance (σ2) are the same as those of the log-normal distribution. The transformation of the mean and variance to m and v, the parameters for the log-normal distribution, gives the accurate estimation for the true distribution. The transformation from the mean (μ) and variance (σ2) to statistical parameters of a log-normal distribution refers:

$$ {\displaystyle \begin{array}{c}m=\exp \left(\mu +\frac{\sigma^2}{2}\right)\\ {}v=\left(\exp \left({\sigma}^2\right)-1\right)\exp \left(2\mu +{\sigma}^2\right)\end{array}} $$
(16)

Meanwhile, there is a case that the mean (μ) and variance (σ2) cannot be uniquely transformed to the statistical parameters of the true type of probability distribution. In this case, by substituting p(x) in (9) to the form of the true distribution, the mathematical derivations from step 2 to (13) in Section 3.2 can be re-derived.

In summary, for avoiding the estimation error, it is important to identify the true type of probability distribution for a quantity in interest. However, it is difficult to realize the true type of probability distribution for real-application problems. When the number of given data is sufficient, the methods such as goodness-of-fit test are available. Therefore, at first, it is recommended to use the Gaussian assumption, and after to modify the assumed type of probability distribution to appropriate one as the sufficient number of data is provided.

4 Results: estimating statistical parameters

To check the effectiveness of the proposed method introduced in the previous section, a case study is formulated based upon the cantilever beam problem posed by Sandia National Laboratories. The true mean and standard deviation of a beam’s deflection (x) are set to “0.1631” and “0.0153,” respectively. (The unit for the deflection is omitted since it does not matter in developing the discussion.) The method of moments without considering the measurement errors in the observed data is devised to check the effect by the proposed method. Two sub-cases are formulated to check whether the proposed method well estimates the true mean and standard deviation of the beam’s deflection: (1) large systematic measurement error case and (2) large random measurement error case.

Case 1: large systematic measurement error case

To generate the observed data (D), including the two measurement errors, the maximum amounts of bias α for systematic measurement error and βx standard deviation for random measurement are provided as “− 0.1” (a large negative systematic error) and “0.02x” (a small random error), respectively (refer to (3) and (4)). Increasing numbers (N = {3, 4, 5, 10, 25, 50}) of the observed data are sampled to examine the statistical uncertainty that is due to a lack of data.

Figure 5 represents the estimated probability distributions with N = {4, 25, 50} numbers of data. The red probability distribution refers the true probability distribution of the observed beam’s deflection without measurement errors. The blue and blue-dotted probability distribution is estimated by the proposed method and the method of moments without considering the measurement errors, respectively. The observed data shown in Fig. 5 are data including the measurement errors. For large number of data (N = 25, 50), Fig. 5b, c shows that the proposed method estimates the probability distribution closer to the true one. On the other hand, for small numbers of data (N = 4), the method of moments estimates closer to true Fig. 5a). This is because of the randomness in generated observed data. Therefore, 30 iterative studies are conducted for each number of sampled data. Figure 6 represents the estimated mean (μx) and standard deviation (σx) using repeatedly sampled (observed) deflection data. Each blue dot denotes an estimation with N numbers of sampled data. The upper parts (Fig. 6a, c) show the estimated results by the method of moments without considering measurement errors; the lower figures (Fig. 6b, d) show the estimated results using the proposed method. In common for all figures in Fig. 6, as the amount of observed data increases, the variations of the estimated results get narrower; this is because the larger amount of data alleviates the degree of statistical uncertainty that is present due to a lack of data. By comparing Fig. 6a, b, it can be confirmed that the proposed method restores the biased results that are seen from the results found without the proposed method. However, by comparing Fig. 6b, d, the estimated standard deviation using the proposed method shows no significant effect due to small degree of random measurement error in observed data. Thus, it cannot be confirmed whether the proposed method inadequately estimates the unknown parameters or not. In case 2, uncertainty characterization is performed for the observed data with a large random measurement error.

Fig. 5
figure 5

Estimated probability distributions with the number of data, N: aN = 4, bN = 25, and cN = 50

Full size image
Fig. 6
figure 6

Case 1: estimated mean (μx) and standard deviation (σx) with increasing numbers (N) of observations (3/4/5/10/25/50) (a–d)

Full size image

Case 2: large random measurement error case

To generate the observed data (D), including the two measurement errors, the maximum amounts of bias α for systematic measurement error and βx standard deviation for random measurement are provided as “− 0.05” (a small negative systematic error) and “0.1x” (a large random error), respectively. Increasing numbers (N = {3, 4, 5, 10, 25, 50}) of data are sampled to examine the statistical uncertainty that is due to a lack of data. For each number of sampled data, 30 iterative studies are conducted for checking the inaccuracy due to the randomness in generated observed data. To check the effectiveness of the proposed method, the method of moments is devised without considering the measurement errors in the observed data.

Figure 7 represents the estimated mean (μx) and standard deviation (σx) using observed (sampled) deflection data. The upper parts (Fig. 7a, c) show the estimated results without the proposed method; the lower figures (Fig. 7b, d) show the estimated results using the proposed method. In common with case 2, as the amount of observed data increases, the variations of the estimated results get narrower; this is because the larger amount of data alleviates the degree of statistical uncertainty that is present due to a lack of data. Figure 7c shows that the larger degree of random measurement error results in larger estimations of standard deviation. On the other hand, Fig. 7d shows that the proposed method adequately estimates the standard deviation by eliminating the effect by random measurement error.

Fig. 7
figure 7

Case 2: estimated mean (μx) and standard deviation (σx) with increasing numbers (N) of observations (3/4/5/10/25/50) (a–d)

Full size image

5 Summary and concluding remarks

This paper proposed a method for uncertainty characterization that includes consideration of measurement errors. Maximum likelihood estimation was utilized to estimate the unknown statistical parameters of the probability density function. Before that, the likelihood function was formulated, based on assumptions about the type of probability distributions applicable to the observed data, which include the variability, systematic measurement error, and random measurement error. The proposed method was adopted for a case study. In the case study, the proposed method produced accurate estimations when measurement errors existed in the observations. Accurate characterization of uncertainty in the data through the use of the proposed method will be helpful for various engineering problems that require consideration of uncertainty, especially when it is doubtful if the observations have measurement errors.

To expand the use of the proposed method, it will be challenging to determine the value of statistical parameters for the probability distribution of the systematic and random measurement errors. For example, in this study, the maximum amounts of bias α for systematic measurement error and βx standard deviation for random measurement are considered given information. However, information about those parameters may not available in real-world applications.

This paper follows the method for characterizing the measurement errors that is outlined in a document provided by Sandia Laboratories; specifically, the systematic and random measurement errors are assumed to follow a uniform distribution and a normal distribution, respectively. However, the proposed method also can be used in cases where different assumptions about the type of the measurement errors’ probability distributions are made. If the type of probability distribution of the measurement errors is modified, the mathematical formulations in Section 3 would need to be reformulated. However, the general scheme of the proposed method would remain: (1) assume certain types of probability distributions for the measurement errors, (2) formulate probability distributions of the measurement errors, (3) formulate the likelihood function about the given observed data, and (4) obtain the optimal value of the statistical parameters of the assumed probability distributions.