L-moments-based uncertainty quantification for scarce samples including extremes

Abstract

Sampling-based uncertainty quantification demands large data. Hence, when the available sample is scarce, it is customary to assume a distribution and estimate its moments from scarce data, to characterize the uncertainties. Nonetheless, inaccurate assumption about the distribution leads to flawed decisions. In addition, extremes, if present in the scarce data, are prone to be classified as outliers and neglected which leads to wrong estimation of the moments. Therefore, it is desirable to develop a method that is (i) distribution independent or allows distribution identification with scarce samples and (ii) accounts for the extremes in data and yet be insensitive or less sensitive to moments estimation. We propose using L-moments to develop a distribution-independent, robust moment estimation approach to characterize the uncertainty and propagate it through the system model. L-moment ratio diagram that uses higher order L-moments is adopted to choose the appropriate distribution, for uncertainty quantification. This allows for better characterization of the output distribution and the probabilistic estimates obtained using L-moments are found to be less sensitive to the extremes in the data, compared to the results obtained from the conventional moments approach. The efficacy of the proposed approach is demonstrated on conventional distributions covering all types of tails and several engineering examples. Engineering examples include a sheet metal manufacturing process, 7 variable speed reducer, and probabilistic fatigue life estimation.

1 Introduction

In structural design, uncertainties in the system inputs are considered the root cause of poor product performance and this leads to variation in the system output responses. These uncertainties typically occur in material properties, manufacturing parameters, externally applied forces, etc. (Jin et al. 2003; Lee et al. 2009; Ramu and Arul 2016; Voinov et al. 2016; Lee et al. 2019). Irrespective of the variability in the input, a designer wishes to achieve a system response that satisfies the design objectives, preferably with less variability (Ramu et al. 2017). It is a common statistical practice to quantify uncertainties by conventional moments (C-moments), mean (μ), and variance (σ²) (Hosking 1990). Higher order C-moments such as skewness (γ₁) and kurtosis (α₄) are also used to describe the system outputs more precisely (Mekid and Vaja 2008; Anderson and Mattson 2012). In order to design under uncertainty, it is important to quantify uncertainties of system output which is the result of uncertain inputs propagated through the system. This is referred to as uncertainty propagation (Mekid and Vaja 2008; Lee and Chen 2009; Anderson and Mattson 2012; Jayaraman et al. 2018; Liu et al. 2019). Sometimes, input distributions are known and moments are computed to be propagated through the system model to obtain statistics of output response. When moments of distributions are used for propagation, it is imperative to compute higher order moments accurately (Lee and Chen 2009).

Most engineering applications have scarce data and description of the uncertainties associated with the input variables is usually not available readily (Ramu and Arul 2016). One way of quantifying this uncertainty is to use nonparametric methods such as histogram, kernel density estimation (KDE) techniques, and interval analysis (Lee et al. 2019). Though histogram is a nonparametric density estimation approach, it is less robust and the challenge lies in choosing the bin size. Changing the bin size leads to different inference from the data (Rudemo 1982; Silverman 1986; Lee et al. 2019). In KDE, the smoothing of the density curve is controlled by bandwidth and selecting the right bandwidth is a major challenge (Hall et al. 1991; Kang et al. 2018). Often, higher bandwidth leads to over-smoothing and lower bandwidth leads to under-smoothing of the density curve (Lee et al. 2019). Bandwidth selection for heavy tailed distributions is relatively difficult (Buch-Larsen et al. 2005). Integrated squared error, mean integrated squared error, and least squares cross validation error are used to choose the optimal bandwidth (Silverman 1986; Hall et al. 1991; Shirahata and Is 1992; Turlach 1993). These error metrics are more sensitive to the extremes present in the small data and suffer from sampling variability (Silverman 1986; Park and Marron 1990; Hall et al. 1991). Sometimes KDE can represent a very irregular shape of distribution for small data (Kang et al. 2018). Interval analysis is also used to represent the uncertainty as an interval or variable that has lower and upper bound. Fuzzy set theory and evidence theory are generally used to estimate the interval. Major drawback of this approach is that it requires interval arithmetic for statistical model comparison and validation (Rokne 2001; Gao et al. 2010; Lee et al. 2019). Though nonparametric methods are robust, they require sufficient data for accurate modelling (Lee et al. 2019). When the interest is in extreme probabilities, tail modeling techniques are also used to quantify the uncertainties. These techniques approximate the tail portion of the cumulative density function (CDF) using limited samples. However, the tail itself is highly volatile and very sensitive to number of data points (Ramu P 2013; Acar and Ramu 2014). These techniques are usually suitable for low probabilities and not to model the entire probability space, which is the general interest in uncertainty quantification.

A widely used parametric approach is the Pearson system which is based on the hypothesis that higher order moments provide a good representation of PDF. However, researchers (Hosking 1990) observe that there is lack of clarity on what information does the higher order moments impart, on the shape of the distribution. Also, moments computed from scarce data can be markedly different from those of the probability distribution from which the sample was drawn. The choice of underlying probabilistic distribution plays a very crucial role. When the choice is influenced by scarce samples, it is likely to have errors, which when propagated through the model result in amplified errors in the system output. In addition, the scarce samples might also include extremes, which will only worsen the errors. In scarce data, extremes have large influence on the moments estimation (Moon et al. 2020). C-moments are sensitive to extremes present in the data leading to large variation in the computed moments. Extremes can sometimes be classified as outliers and excluded from the statistical study (Jayaraman et al. 2018; Jayaraman and Ramu 2019). This again will lead to large error between computed moments and actual moments. Since the available data itself is scarce, excluding one or a few data points leads to significant information loss. Therefore, it is desirable to develop an approach that can:

(i) Identify appropriate probabilistic distribution with scarce data.

(ii) Estimate moments accurately from scarce data with possible extremes. This translates to the estimation technique being less or insensitive to the extremes.

To overcome the hurdle of computing robust moments while accounting for extreme realizations, researchers recommend using linear moments (L-moments) which uses linear combinations of order statistics. L-moments are known to be robust and less sensitive to extremes or outliers in the scarce samples. In addition, L-moments are less subject to bias in estimation and their approximations on the asymptotic normal distribution are better, when the samples are finite (Sillitto1969; David 1981; Hosking 1989, 1990, 1992; Gubareva and Gartsman 2010). L-moments are widely used in various applications in hydrology, water resource applications, and regional frequency analysis (Hosking and Wallis 1997; Sankarasubramanian and Srinivasan 1999; Adamowski 2000; Kumar and Chatterjee 2005; Atiem and Harmancioǧlu 2006). L-moment approach is preferable for insufficient or lesser data in flood or rainfall analysis (Smithers and Schulze 2001; Haddad et al. 2011). L-moments are used to identify the probability distribution of the censored data in the fields of environmental quality and quantity monitoring (Zafirakou-Koulouris et al. 1998; Sankarasubramanian and Srinivasan 1999; Elamir and Seheult 2004). In reliability analysis, L-moments are used to analyze and characterize the life time data (Nair and Vineshkumar 2010). Based on the discussions presented above, the use of L-moments in the context of design with scarce samples that might include extremes is not available. Hence, the authors propose a framework using L-moments to quantify and propagate uncertainties in an optimization framework, when the available data is scarce and could include potential extremes.

To this end, the purpose of this study is to identify the PDF of response, with scarce samples and in the presence of extremes. We propose using L-moment ratio to identify the PDF. The identified PDF is compared to the exact PDF using the Jensen-Shannon divergence. This comparison is only to validate the proposed approach, because in reality, one will not have the information about the exact PDF. Higher order L-moments are used to compute the L-moment ratios such as L-skewness (τ₃) and L-kurtosis (τ₄). We compare L-moment estimates against C-moment estimates and their effects on identifying the underlying distribution using L-moment ratio and the Pearson system, respectively. The novelty lies in aspects such as the following: (i) comprehensive understanding of performance of L-moments on different types of tails when the data is scarce and with potential extremes; (ii) combining scarce data, extremes, and L-moments in a design context; (iii) using L-moments to quantify the uncertainty and propagate it in a design framework, while implementing on real-life engineering examples. The proposed approach is demonstrated on a suite of distributions that cover all type of tails and several engineering examples.

The rest of the paper is organized as follows: In Section 2, it is explained how the PDFs are identified using the Pearson system and L-moment ratio diagram. Investigation strategy of the proposed approach and the comparison of obtained PDFs with the exact PDF using the Jensen-Shannon divergence and how extremes are generated and incorporated in the data is discussed in Section 3. Demonstration of the proposed approach on a suite of statistical distributions and engineering examples is carried out in Section 4 followed by conclusions in Section 5.

2 C-moments and L-moments

In this study, we focus on scarce data that might include extremes. The goal is to identify the underlying PDF and use its moments for characterising uncertainties. The two approaches that we compare here (C- and L- moment approaches) compute the moments and identify the respective PDFs using the Pearson system and L-moment ratio diagram, respectively. The specific objective is to compare the performance of the approaches in the presence of extremes. The process of investigation is presented in Fig. 1 and the elements of Fig. 1 are discussed below.

Fig. 1

Generalized distribution identification procedure

2.1 Identification of distribution using C-moments and Pearson system

The Pearson system (Pearson 1916) is a method of choosing appropriate distribution from a set of distributions called the Pearson distribution, based on first four C-moments of the system response. The Pearson distribution contains several distributions such as beta, normal, and gamma. Each PDF in the Pearson distribution satisfies the generalized differential equation, in (1) (Kenney and Keeping 1947; Craig 1991; Weisstein et al. 2004).

$$ \frac{dy}{dx}=\frac{y(m-x)}{a_{0}+a_{1}x+a_{2}x^{2}} $$

(1)

where y is the PDF, a₀,a₁,a₂, and m are the parameters expressed in terms of C-moments of the system, in (2).

$$ \begin{array}{ll} a_{0} &= \frac{2+\delta}{2(1+2\delta)}\\ a_{1} &= -m = \frac{\gamma_{1}}{2(1+2\delta)}\\ a_{2} &= \frac{\delta}{2(1+2\delta)} \end{array} $$

(2)

where $\delta =\frac {2\alpha _{4}-3{\gamma _{1}^{2}}-6}{\gamma _{1}+3}$, γ₁ is the skewness, and α₄ is the kurtosis of the data.

The roots c₁, c₂ and the coefficients of a₀ + a₁x + a₂x² provide information that can be used to classify the distributions. Few possible types of distribution are (i) a₁ = a₂ = 0,a₀ > 0: normal distribution, (ii) ${a_{1}}^{2}/4{a_{0}}{a_{2}}<0,c_{1} \leq {x} \leq c_{2}$: beta distribution (iii) ${a_{1}}^{2}/4{a_{0}}{a_{2}}=0,{a_{2}}>0,-\infty <x< \infty$: Student’s t-distribution, etc. The solution of (1) needs to satisfy the following conditions:

i. the distribution curve should vanish at the ends of the range, i.e., as $y\rightarrow 0, dy/dx \rightarrow 0$

ii. when $x=m , dy/dx \rightarrow 0$

In this study, the Pearson system is adopted to identify the distribution using C-moments computed from the scarce samples.

2.2 L-moments

L-moments (Hosking 1989; 1990; 1992; Hosking and Wallis 1997; Hosking 2006) are expectations of certain linear combinations of order statistics. These combinations provide information about location, scale, and shape of the distribution from which the samples are drawn. Since L-moments are linear functions of the data, they suffer less from the effects of sampling variability and are reported to be robust in the presence of extremes. L-moments which are modifications of probability weighted moments (PWM) can be used to define the shape of the probability distribution (Greenwood et al. 1979). PWM (β_r) (Hosking and Wallis 1997) for a probability distribution with cumulative density function, F and quantile function, x(F) is given by $\beta _{r}={{\int \limits }_{0}^{1}}x(F)F^{r}dF$. The population L-moment is

$$ \begin{array}{ll} \lambda_{r+1}={\sum}_{k=0}^{r}p_{r,k}^{*}\beta_{k},r=0,1,\dots,n-1; \end{array} $$

(3)

where λ is the population L-moment, $p^{*}_{r,k}$ is

$(-1)^{r-k}\binom {r}{k}\binom {r+k}{k}$, n is the sample size.

Equation (3) can be rewritten in terms of the expectations of order statistics of a random variable, X, as

$$ \begin{aligned} \lambda_{r}&=\frac{1}{r}\sum\limits_{k=0}^{r-1}(-1)^{k}\binom{r-1}{k}E(X_{r-k:r}),\\r&=1,2,\dots,n; \end{aligned} $$

(4)

where E(.) is the expectation value. The first four L-moments are given in terms of PWMs derived from (3), and presented in (5)

$$ \begin{array}{ll} \lambda_{1_{r=0}}&=\beta_{0},\\ \lambda_{2_{r=1}}&=2\beta_{1}-\beta_{0},\\ \lambda_{3_{r=2}}&=6\beta_{2}-6\beta_{1}+\beta_{0},\\ \lambda_{4_{r=3}}&=20\beta_{3}-30\beta_{2}+12\beta_{1}-\beta_{0} \end{array} $$

(5)

In practice, L-moments are estimated from the ordered sample, $x_{1:n}\leq x_{2:n}\leq \dots \leq x_{n:n}$. The sample PWM, b_r is presented in (6).

$$ \begin{aligned} b_{r} &= \frac{1}{n} \sum\limits_{j=r+1}^{n}\frac{(j-1)(j-2)\dots(j-r)}{(n-1)(n-2){\dots} (n-r)} x_{j:n},\\r&=0,1,2,\dots,n-1; \end{aligned} $$

(6)

The general form of sample L-moment (l) in terms of sample PWM is

$$ l_{r+1}=\sum\limits_{k=0}^{r}p_{r,k}^{*}b_{k},r=0,1,2,\dots,n-1; $$

(7)

The first sample L-moment (l₁) is the sample mean, a measure of location. The dispersion measure of the sample is provided by the second L-moment (l₂), a scalar multiple of Gini’s mean difference statistic (Hosking 1990; Ceriani and Verme 2012). Sample L-moment ratios (t_r) are obtained by dividing the higher order sample L-moments by the dispersion measure (l₂), t_r = l_r/l₂. These are dimensionless quantities, independent of the units of measurement data. The L-moment analogue of the coefficient of variation (σ/μ), is L-coefficient of variance, $\tau _{_{L-CV}} =\lambda _{2}/\lambda _{1}$ and it varies as $0\leq \tau _{_{L-CV}} <1$ (Hosking 1990; Hosking and Wallis 1997).

2.3 Identification of distribution using L–moment ratio

Similar to conventional moments, L-moments are used to summarize the characteristics of the sample data. Many researchers (Hosking 1990; Hosking and Wallis 1997; Zafirakou-Koulouris et al. 1998; Adamowski 2000; Kumar and Chatterjee 2005) have used L-moment ratio diagram to describe the PDF. L-moment ratio diagram shown in Fig. 2, is a plot of L-skewness vs L-kurtosis of standard distributions such as uniform, normal, exponential, log-normal, logistic, gumbel, generalized extreme value (GEV), generalized pareto (GP) and gamma. It is useful to provide simple explicit expressions for τ₄ (L-kurtosis) in terms of τ₃ (L-skewness) for some widely used three-parameter distributions of probability such as lognormal, gamma, GEV and GP (Hosking and Wallis 1997). The L-moment ratio of two-parameter distributions is shown in Fig. 2 as single dots and mentioned in Table 1. Polynomial approximations of the form $\tau _{4} = A_{0}+A_{1}\tau _{3}+A_{2}{\tau _{3}^{2}}+\dots +A_{8}{\tau _{3}^{8}}$, have also been obtained and the coefficients are provided in Hosking and Wallis (1997). Overall bound is the lower bound on L-moment ratios of the all distributions obtained while satisfying the constraints, λ₂ ≥ 0, − 1 < τ₃ < 1 and $\frac {1}{4}(5{\tau _{3}^{2}}-1)\leq \tau _{4} < 1$.

Fig. 2

L-moment ratio diagram (Hosking 1990)

Table 1 L-moment ratio of distributions

The approximations yield values of τ₄ for a given τ₃, are accurate within 0.0005 provided that the range of τ₃ is − 0.9 to 0.9. For GEV distribution, an accuracy of 0.0005 is achieved only if the range of τ₃ is − 0.6 to 0.9 (Hosking and Wallis 1997).

L-moment ratio diagram permits a visual indication of which distribution maybe a good fit to the data. L-moment ratios t₃ and t₄, computed from sample can be plotted in the L-moment ratio diagram to see which distribution is the closest. It is to be noted that our interest in the current work lies in computing the probabilities correctly rather than identifying the true parent distribution. Hence, we select distribution that is closest to the sample L-moment ratio plotted in Fig. 2. To understand the performance of the proposed approach, we compare the distribution identified through t₃ and t₄, to the actual distribution. In order to select a suitable distribution from L-moment ratio diagram, euclidean norm in (8) is used for the distributions that are represented as points.

$$ {\left\lVert{Ed_{i}}\right\rVert}_{2} = \sqrt{({\tau_{4}^{i}}-t_{4})^{2}+({\tau_{3}^{i}}-t_{3})^{2}} $$

(8)

where ${\left \lVert {Ed_{i}}\right \rVert }_{2}$ is the euclidean norm, i is the i th distribution in the L-moment ratio diagram, (.)₄ is the L-kurtosis, (.)₃ is the L-skewness, τ_r is the population L-moment ratio, and t_r is the sample L-moment ratio. t₃ and t₄ are computed from available scarce data. For the distributions that are represented as curves in L-ratio diagram, the distance of the (t₃,t₄) from the respective curve is computed as the value of the curve evaluated at (t₃,t₄). The distribution with the least distance is chosen as the best possible distribution. The algorithm for the best distribution selection is provided in Appendix Appendix. Once the PDF is chosen from the L-moment ratio diagram, the Jensen-Shannon divergence is used to compare the predicted PDF to the actual PDF.

3 Investigation strategy

The hypothesis in the current work is that L-moments are robust compared to C-moments, from an estimation perspective and L-moments provide a better characterization of the response PDF. We are interested in investigating this for scarce samples (small sample size), especially in the presence of extremes. We thus proceed as follows, for scarce samples, PDFs are obtained using C- and L-moment approaches and compared with the actual population PDF. Extremes are then introduced in the scarce samples and the PDFs are recomputed to be compared with the actual population PDF. Sample sizes considered in this study are 10, 25, 50, and 100. The Jensen-Shannon divergence is used as a comparison metric. The process is repeated 100 times to account for sampling variability.

3.1 Jensen-Shannon divergence

The Jensen-Shannon divergence (D_JS) is a widely used distance measure, to study the similarity between finite number of probability distributions (Melville et al. 2005). D_JS can be understood as symmetrized extension of Kullback-Leibler divergence (D_KL) with finite bounds. Sometimes, D_JS is also called as the smooth version of D_KL. D_KL is also a similarity measure between two probability distributions but unbounded. D_JS is presented in (9)

$$ D_{JS}(P||Q) =\frac{1}{2} D_{KL}(P||M)+\frac{1}{2} D_{KL}(Q||M)\\ $$

(9)

where $M = \frac {1}{2} {(P+Q)}$,

$D_{KL}(P||M) = {\sum }_{x\epsilon X}P(x) \log _{2} \left (\frac {P(x)}{M(x)}\right )$, P is probability of actual distribution and Q is probability of distribution to be compared with P. D_JS is bounded between 0 and 1, given that D_JS uses base 2 logarithm. D_JS = 0 represents identical distributions.

3.2 Incorporation of extremes

Extreme event or extremes are rare events which have very less probability to occur but cannot be ignored as an outlier (Abarbanel et al. 1992; Moustapha and Sudret 2019). The impact of extremes is crucial in many areas of application, such as environmental disasters (flood, climate change, forest fire, etc.), finance (risk analysis, insurance losses), engineering (structural, traffic analysis), and biomedical (side effects of drugs) (Abarbanel et al. 1992; Alvarado et al. 1998; Davison and Huser 2015). In real-life scenarios or in any engineering application, often only small samples are available to perform the analysis. These samples need not necessarily come as a result of design of experiment (DoE). Sometimes, the small sample might include extremes and are prone to be classified as outliers (erroneous data). But extremes (belonging to the parent distribution) cannot be excluded from the data set. In small sample, omitting data will lead to significant information loss. Hence, data points, which are significantly different from other samples or has less probability, need to be accounted in data analysis. To understand the effect of extremes and the performance of proposed approach, we deliberately introduce extremes in the scarce data, for the examples discussed. 10⁶ samples from the parent distribution are generated and the maximum value is considered as extreme. This extreme is then incorporated into the scarce samples.

4 Results and discussion

In this section, we demonstrate the proposed approach on (i) a suite of distributions that covers all type of tails, (ii) uncertainty quantification of sheet metal manufacturing process, (iii) design of speed reducer, and (iv) probabilistic fatigue life assessment. The study on the performance of proposed approach on different types of tail provides a comprehensive perspective on the superiority of the approach on data from any type of distribution. Section 4.2.1 discusses the proposed approach on a single variable problem where uncertainty quantification and propagation are also discussed. Section 4.2.2 discusses the proposed approach on large dimension example. Section 4.2.3 contains real-life data on which the proposed approach is demonstrated, to arrive at critical decisions.

4.1 Statistical distributions

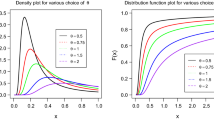
The tails of any probabilistic distribution can be approximated by a generalized pareto distribution (GPD). ψ, the scale and ξ, the shape parameters characterize the GPD (Ramu et al. 2010). ξ plays a significant role in quantifying the weight of the tail or tail heaviness. Probability distributions can be classified as light (ξ < 0), medium (ξ = 0), and heavy tail (ξ > 0) distributions based on the tail heaviness. Detailed description of ξ and the relation with tail heaviness of the probability distributions is discussed in the Appendix. Since it is impractical to test the approach on all possible distributions, we classify the distributions based on tail heaviness and demonstrate the superiority of the method on all possible types of tails. The distributions, their shape (ξ), and size parameters are mentioned in Table 2. The PDF and CDF of the distributions listed in Table 2 are presented in Fig. 3a and b respectively. Here, we study the effect of extremes in scarce data on identifying the PDFs using samples of sizes 10, 25, 50, and 100.

Fig. 3

PDF, CDF, and GPD of distributions. (a) PDF of distributions (b) CDF of distributions (c) GP t for selected distributions

Table 2 Details of distributions

Samples for all the distributions listed in Table 2 are generated and the corresponding C- and L-moments are computed. With the help of the Pearson system and L-moment ratio diagram, PDFs are predicted. The predicted PDFs are compared to the parent PDF using D_JS. In the sample data, an extreme is inserted to study its effect and the PDFs are repredicted with the extreme and compared. This process is repeated 100 times. Figure 4 presents the performance of the proposed approach compared to C-moment approach for light tail. The figure is separated into four columns, representing different sample sizes. In each column, first two boxes are the results for sample with extremes (ex: sample size 11) and the rest of the two boxes are the results of sample with extremes removed (ex: sample size 10). From Fig. 4, it can be observed that the L-moment approach while considering the extreme has minimum D_JS compared to its C-moment counterpart. This implies that L-moment approach is robust to extremes. When the sample size increased, the variability in D_JS decreased as expected. However, with samples as scarce as 10 or 25, L-moments certainly works far better while including extremes. The values corresponding to median and quartiles are listed in the Appendix, for the interested reader. For a sample size of 10, the median values of D_JS based on L-moment approach is lesser than the C-moment approach. This clearly shows that PDF identification using L-moment approach works better. The interquartile range is lesser for L-moment approach, implying they perform better under the sampling variability. For larger sample size, the interquartile range is less for L-moment approach compared to C-moment approach. This indicates that L-moment approach works well when sample size are increased. The results for medium tail are presented in Fig. 5. The performance of L-moment approach is similar to that of in the light tail distribution. However, the effect of extreme in C-moment is large, even in a sample of size 100. The results of heavy tail I and heavy tail II are presented in Figs. 6 and 7 respectively. In heavy tail II case, there is large difference in the performance of C-moment and L-moment approach, even for samples as large as 100. The L-moment approach performance is similar to the other distribution types establishing the fact that L-moments perform better in terms of identifying the distribution in scarce data that includes extreme. Though L-moment approach works better compared to its C-counterpart, the difference is marginal between L-moment with and without the extremes. For heavy tail II, it can be seen that L-moment with extremes performs the best, in terms of variability. Hence using L-moment instead of C-moment approach is necessarily a better choice but within L-moments, whether to leave out the extreme or not might depend on tail heaviness. Nevertheless, it is important to note that one does not possess the information on tail heaviness with scarce data and one does not loose much by considering the extremes while using the L-moments. Information about quartile values for all distributions are presented in Appendix. Effects of two extremes (instead of 1 discussed above) in the scarce samples are also studied and the corresponding PDF comparison results are presented in the Appendix. The results indicate that PDF identified using L-moment ratio diagram has less D_JS, strengthening our earlier conclusion on the performance of L-moment approach.

Fig. 4

JS divergence for light tail

Fig. 5

JS divergence for medium tail

Fig. 6

JS divergence for heavy tail I

Fig. 7

JS divergence for heavy tail II

4.2 Engineering examples

In this section, we discuss three engineering examples to demonstrate the proposed approach.

4.2.1 A flat rolling process: sheet metal manufacturing

Flat rolling process is used to manufacture metal sheets or plates. In this process, the metal is fed between the working rolls or rollers and the distance between the rolls is used to obtain the desired thickness of the metal sheet. The material is pulled by the rollers and eventually results in elongation with reduced thickness. The uncertainty in friction between rollers and the material affects the outcome of the manufacturing process. The process illustrated in Fig. 8 can be performed either below (cold rolling) or above (hot rolling) the material temperature.

Fig. 8

Flat rolling metal sheet manufacturing process

The aim of this process is to minimize the number of passes required to achieve final plate thickness (Anderson and Mattson 2012). The total deformation possible in a single pass depends on the friction between the rollers and the material at the interface. Factors such as rolling speed (V ), material properties, surface finish of the rollers cause friction, and lubricants are used to control friction during the process. Maximum change in thickness that can be achieved in a single pass, ΔH is presented in (10)

$$ {\varDelta}{H}={\mu_{f}^{2}}R $$

(10)

where μ_f is the friction coefficient between the working rollers and the sheet metal, and R is the radius of rollers. In this example, we treat μ_f as random variable that follows a generalized pareto distribution (GPD). The GPD of μ_f is depicted in Fig. 9 and the parameters are location, μ = 0.282, scale, σ = 0.103, and shape, ξ = − 0.325. We consider R = 40.6 cm.

Fig. 9

Distribution of coefficient of friction

We intend to study the effect of extremes in uncertainty quantification and propagation in this example. For uncertainty quantification, we pretend that the distribution of μ_f is not known and only scarce samples are available. Using scarce samples of μ_f, we compute ΔH and its distribution is predicted using the C- and L-moment approach. This process is repeated 100 times to account for sampling variability. One out of the 100 repetition is presented in Fig. 10 for illustration purpose. The PDFs obtained for various sample sizes in the presence of extremes based on L-moment ratio diagram and Pearson system approaches are presented in Fig. 10. The plots clearly indicate the superiority of the L-moment approach and in obtaining approximations closest to the exact PDF. D_JS results are presented in Fig. 11. As observed in earlier examples, L-moment approach is superior in identifying the distributions compared to C-moment approach. For uncertainty propagation, we predict the distribution of μ_f using limited samples and draw 10⁶ samples from the predicted distribution, propagate it through (10), and compute the corresponding ΔH. In this example, we know the explicit expression of the system to propagate the uncertainties. When the expression is not known, implicit metamodels or response surfaces can be constructed and uncertainties can be propagated through them.

Fig. 10

PDFs of maximum change in thickness, ΔH. (a) 10 samples (b) 25 samples (c) 50 samples (d) 100 samples (e) 10,000 samples

Fig. 11

JS divergence - uncertainty quantification of ΔH of flat rolling sheet metal manufacturing process

Finally, the PDF of ΔH is obtained from this 10⁶ samples and compared against the original PDF. D_JS of L-moment approach shows a trend similar to previous examples and is presented in Fig. 12. Similarly, effects of two extremes present in the scarce data are studied. The results presented in the Appendix indicate the superiority of the L-moment approach.

Fig. 12

JS divergence - uncertainty propagation of ΔH of flat rolling sheet metal manufacturing process

4.2.2 Design of speed reducer with 7 variables

Speed reducers are used in industrial and domestic machinery to safely and efficiently reduce speed of the electric motors. It is also an integral part of gearbox of a mechanical system. Speed reducer adjusts the motor speed to ensure that a machine operates correctly (Lin et al. 2013; Shi et al. 2013; Chatterjee et al. 2017). Figure 13 presents the variables of the speed reducer which are face width (x₁), module of teeth (x₂), number of teeth on pinion (x₃), length of first shaft between bearings (x₄), length of second shaft between bearings (x₅), diameter of first shaft (x₆), and diameter of second shaft (x₇). The aim is to minimize the total weight of the speed reducer which is computed as presented in (11). In the speed reducer design, all the design variables are considered to follow a normal distribution. The description of all variables are mentioned in Table 3 and coefficient of variation (CoV) is 10%.

$$ \begin{aligned} W & = 0.7854x_{1}{x_{2}^{2}}\times(3.3333{x_{3}^{2}} \\ & \quad+14.9334x_{3} -43.0934) \\ & \quad-1.508x_{1}({x_{6}^{2}}+{x_{7}^{2}}) +7.4777({x_{6}^{3}}+{x_{7}^{3}})\\ & \quad+0.7854(x_{4}{x_{6}^{2}}+x_{5}{x_{7}^{2}}) \end{aligned} $$

(11)

Fig. 13

Speed reducer design

Table 3 Description of random variables

In this example, different number of extremes are incorporated at a time. The variables in which the extreme is generated is randomly picked. That is, when only 1 extreme is added, it is randomly added to one of the 7 variables. Similarly, extremes are added to 3 variables at a time, 5 variables at a time, and all the random variables at a time. Figure 14 presents the results of distribution obtained using C- and L-moments for extremes added to one random variable. It indicates that results obtained using L-moments are better compared to C-moments for all sample sizes. Within L-moments, the median and variability of D_JS are less when the extremes are considered. For the other cases presented in Figs. 15, 16, and 17, similar observations are made. In all cases, L-moment approach is robust to the presence of outliers. The median and variability of D_JS in L-moment approach is less than the median and variability of D_JS in C-moment counterpart, for all the cases. Within, the L-moment approach, sometimes the sample with extremes perform better than the sample without extremes. In particular, the difference between the L- and C-moment approaches are large when extremes are considered and included in more variables. The results of two extremes in the scarce data are presented in the Appendix and it is clear that L-moment approach works better than C-moment for all the cases.

Fig. 14

JS divergence - extreme at 1 variable at a time

Fig. 15

JS divergence - extreme at 3 variables at a time

Fig. 16

JS divergence - extreme at 5 variables at a time

Fig. 17

JS divergence - extreme at 7 variables at a time

In the examples discussed above, we have the prior knowledge of the exact PDF to evaluate the performance of the two approaches. However, in reality, one cannot estimate the D_JS. Nevertheless, it is established that the L-moment approach does better or as good as the C-moment approach because of the linear combination of order statistics as against the moment computation in classical approach. The variability in the estimate could be computed using approaches such as bootstrap.

4.2.3 Probabilistic fatigue life assessment

The stress-life (S-N) curve is used to describe fatigue life and it is experimentally measured but usually dispersed in the life axis. Hence, it is preferable to probabilistically measure the fatigue life. Often probabilistic stress-life (P-S-N) curve is used to characterize the uncertainty in the fatigue life. P-S-N curve can be interpreted as a family of S-N curves in which each curve reflect a different % of survival of specimens. Researchers usually model the dispersion by a log-normal distribution (Hu et al. 2014; Ramu and Arul 2016).

In the current work, P-S-N for ultra-high cycle fatigue (UHCF) vibration tests are derived from scarce samples (fewer experiment data) of screws of strength class 8.8. The experimental data for different load cases 2.5 kN, 4 kN, and 7 kN are provided in Schäfer (2008) and the experimental data size of the three load cases are 101, 500, and 103 respectively. In Schäfer (2008), experimental data is assumed to follow normal distribution but as per the Bayesian inference criterion (BIC) and Akaike information criterion (AIC), the experimental data does follow a lognormal distribution. Hence, assuming a distribution a priori might lead to erroneous results. Here, we pretend that only scarce samples are available and are interested in finding the different percentiles.

Sample sizes used in this study are 10, 15, 20, and 25. Samples are randomly drawn from the experimental data and the detailed sample selection process is mentioned in the Appendix. The maximum value in the experimental data is considered as extreme for each load case. Probabilistic distributions are identified from C- and L-moment approaches and the survival percentiles of 90 and 95 of sample S-N are computed. Survival % obtained from scarce samples with extremes are compared with the ones obtained from the population. Error metric used in this study is ratio of sample percentile (P_S) to the population percentile (P_P), which is R_P = P_S/P_P. This process is repeated for 100 times to account for sampling variability.

Figure 18 presents the ratio of the 90th percentile obtained from the sample distribution to the parent distribution for different sample sizes. L-moment approach works well when the extremes are present in the scarce samples and gives the number of cycles value closer to the population for all the percentiles. While designing with fatigue life as a design criteria, one needs to account for the variability in the life estimates and usually require percentiles of life that depends on how critical is the application. Similar observations are obtained in 95th percentile case and the results are presented in the Appendix. Median and the confidence bounds of the all cases are provided in Appendix (25th and 75th percentile of % survival) for 90th and 95th percentiles. Predicted fatigue life from the L-moment approach is closer to the population estimate compared to the C-moment approach.

Fig. 18

Comparison of 90th survival % of sample distribution to parent distribution with different sample sizes

5 Conclusion

L-moments based approach is proposed to identify PDF and estimate probabilistic quantities, for uncertainty quantification, with scarce data and in the presence of extremes. It is found through numerical examples that L-moments are very robust to extremes, compared to C-moments, in estimating probabilistic quantities. L-moment ratio diagram is adopted to identify closest possible distribution. The identified distributions are compared to the original distribution using JS divergence. The proposed approach is demonstrated on a suite of statistical distribution covering all type of tails and three engineering examples. In all examples, L-moment approach performs better than the C-moment approach. Though the variability of the estimates cannot be obtained in real-life problems, approaches such as bootstrap can be used to obtain confidence bounds, which is scope of future work. The scope of application of the proposed approach was discussed on several engineering examples covering quantile estimation and large variable uncertainty propagation.

Appendices

Appendix 1: Distribution selection based on L-moment

Based on generalized distribution identification procedure mentioned in Fig. 1, the step-by-step distribution selection process based on L-moment ratio diagram is provided in Algorithm 1.

Appendix 2: Statistical distributions

1.1 2.1 Shape parameter and tail heaviness

Generalized pareto distribution (GPD) is used to approximate the tails of any parent distribution. ψ, the scale, and ξ, the shape, parameters characterize the GPD fit (Ramu et al. 2010). ξ plays a significant role in quantifying the weight of the tail or tail heaviness. Probability distributions can be classified as light (ξ < 0), medium (ξ = 0), and heavy tail (ξ > 0) distributions based on the tail heaviness. Let G be the performance measure which is random and u is threshold of G. The observations of G that surpass u are called, exceedance, Z in the following (12).

$$ Z = G-u $$

(12)

The conditional CDF of exceedance is modeled by GPD and denoted by $\hat {F}{_{\xi ,\psi }(Z)}$. The distribution function of (G − u) is mentioned in (13).

$$ \hat{F}{{~}_{\xi,\psi}(Z)}=\begin{cases}1-\left( 1+\frac{\xi}{\psi}Z\right)^{-\frac{1}{\xi}} & \text{if} \xi \not= 0\\1-\exp\left( -\frac{Z}{\psi}\right) & \text{if} \xi = 0\end{cases} $$

(13)

ξ for exponential distribution is approximately 0. Similarly, ξ is lesser than 0 for light tail and greater than 0 for heavy tail. Figure 19 shows different CDF of tails approximated by GPD of the selected distributions.

Fig. 19

CDF and shape parameter values of selected distribution

1.2 2.2 Results—One extreme

In Tables 4, 5, 6, and 7, the quartile (Q) values of the D_JS are presented which are obtained for different sample sizes based on the Pearson system and L-moment ratio diagram. In all cases, it can be observed that L-moment approach works better.

Table 4 Quartile values of JS divergence - light tail

Table 5 Quartile values of JS divergence - medium tail

Table 6 Quartile values of JS divergence - heavy tail I

Table 7 Quartile values of JS divergence - heavy tail II

1.3 2.3 Results—Two extremes

Two extremes are incorporated in the samples in this study. 10⁶ samples from the parent distribution are generated and the maximum value and the value at 9.9 × 10⁵ is considered as extremes in the ordered data. In Tables 8, 9, 10, and 11, and Figs. 20, 21, 22, and 23, the results are presented for two extremes case. For all the sample sizes, L-moment approach work better than the C-moment approach.

Fig. 20

JS divergence for light tail

Fig. 21

JS divergence for medium tail

Fig. 22

JS divergence for heavy tail I

Fig. 23

JS divergence for heavy tail II

Table 8 Quartile values of JS divergence - light tail

Table 9 Quartile values of JS divergence - medium tail

Table 10 Quartile values of JS divergence - heavy tail I

Table 11 Quartile values of JS divergence - heavy tail II

Appendix 3: Flat rolling metal sheet manufacturing process

1.1 3.1 Distribution selection process based on L-moment

As mentioned in Algorithm 1, the step by step distribution selection process is demonstrated for this example. In this example, coefficient of friction (μ_f) is considered as random variable and follows the distribution mentioned in Fig. 9. Sample size considered to demonstrate the distribution selection process is 100.

• 1. Samples are generated and the response, maximum change in thickness (ΔH) is computed using (10).

• 2. L-moment ratios L-skewness (t₃) and L-kurtosis (t₃) are estimated and the values are 0.3, 0.19. Estimated sample L-moment ratios are plotted in L-moment ratio diagram and shown in Fig. 24.

• 3. Shortest distance is computed for all possible distributions in the L-moment ratio diagram and presented in Table 12.

• 4. Generalized pareto distribution is considered as the best possible distribution which has less distance compared to all other distributions.

• 5. Parameters of generalized pareto distribution obtained from the sample and corresponding PDF is plotted with the actual PDF (sample size for population is 10000), presented in Fig. 25.

• 6. Distributions obtained from sample is compared with the population distribution using D_JS. The D_JS value is 0.002.

In Tables 13 and 14, the quartile (Q) values of the D_JS are presented, which are obtained for different sample sizes. L-moment approach works well in all cases compared to the C-moment approach.

Fig. 24

L-moment ratio diagram with sample L-moment ratio

Fig. 25

PDF obtained with sample size 100

Table 12 Shortest distance of all possible distributions in L-moment ratio diagram

Table 13 Quartile values of JS divergence - uncertainty quantification of ΔH of flat rolling sheet metal manufacturing process

Table 14 Quartile values of JS divergence - uncertainty propagation of ΔH of flat rolling sheet metal manufacturing process

1.2 3.2 Results—Two extremes

In this section, results of the two extremes in the scarce data are presented. The D_JS obtained for various sample size are presented in Figs. 26 and 27 and the corresponding Q values are provided in the Tables 15 and 16. Similar observations are obtained as mentioned in one extreme case.

Fig. 26

JS divergence - uncertainty quantification

Fig. 27

JS divergence - uncertainty propagation

Table 15 Quartile values of JS divergence - uncertainty quantification of ΔH of flat rolling sheet metal manufacturing process

Table 16 Quartile values of JS divergence - uncertainty propagation of ΔH of flat rolling sheet metal manufacturing process

Appendix 4: Design of speed reducer

1.1 4.1 Results—One extreme

In this section, the quartile (Q) values of the D_JS are presented for different sample sizes. The Q values clearly indicate that L-moment approach are less affected by the sampling variability and works better than C-moment approach.

1.2 4.2 Results—Two extremes

D_JS results are presented in Figs. 28, 29, 30, and 31 and the corresponding Q values are presented in Tables 21, 22, 23, and 24. The results clearly show that the superiority of the L-moment approach over C-moment approach.

Fig. 28

JS divergence - extreme at 1 variable at a time

Fig. 29

JS divergence - extreme at 3 variables at a time

Fig. 30

JS divergence - extreme at 5 variables at a time

Fig. 31

JS divergence - extreme at 7 variables at a time

Table 17 Quartile values of JS divergence - extreme at 1 variable at a time

Table 18 Quartile values of JS divergence - extreme at 3 variable at a time

Table 19 Quartile values of JS divergence - extreme at 5 variables at a time

Table 20 Quartile values of JS divergence - extreme at 7 variables at a time

Table 21 Quartile values of JS divergence - extreme at 1 variable at a time

Table 22 Quartile values of JS divergence - extreme at 3 variables at a time

Table 23 Quartile values of JS divergence - extreme at 5 variables at a time

Table 24 Quartile values of JS divergence - extreme at 7 variables at a time

Appendix 5: Probabilistic fatigue life assessment

In this section, probabilistic fatigue life assessment for different sample sizes are presented. μ + 0.5σ of fatigue life is considered the upper bound and the minimum value of ordered experimental data is considered as the lower bound for scarce sample selection. Samples are randomly drawn between the upper and lower bound of the ordered experimental data for all load cases. The survival % comparison results are presented in Fig. 32. The confidence bounds of 90th and 95th survival % are provided in Tables 25, 26, 27, and 28. In all cases, L-moments approach predicts the probability of fatigue life closer to the actual for different loading conditions.

Fig. 32

Comparison of 95th survival % of sample distribution to parent distribution with different sample sizes

Table 25 Survival % of fatigue life at different load cases and confidence bounds for sample size 10

Table 26 Survival % of fatigue life at different load cases and confidence bounds for sample size 15

Table 27 Survival % of fatigue life at different load cases and confidence bounds for sample size 20

Table 28 Survival % of fatigue life at different load cases and confidence bounds for sample size 25