Abstract
Gaussian-Process based optimization methods have become very popular in recent years for the global optimization of complex systems with high computational costs. These methods rely on the sequential construction of a statistical surrogate model, using a training set of computed objective function values, which is refined according to a prescribed infilling strategy. However, this sequential optimization procedure can stop prematurely if the objective function cannot be computed at a proposed point. Such a situation can occur when the search space encompasses design points corresponding to an unphysical configuration, an ill-posed problem, or a non-computable problem due to the limitation of numerical solvers. To avoid such a premature stop in the optimization procedure, we propose to use a classification model to learn non-computable areas and to adapt the infilling strategy accordingly. Specifically, the proposed method splits the training set into two subsets composed of computable and non-computable points. A surrogate model for the objective function is built using the training set of computable points, only, whereas a probabilistic classification model is built using the union of the computable and non-computable training sets. The classifier is then incorporated in the surrogate-based optimization procedure to avoid proposing new points in the non-computable domain while improving the classification uncertainty if needed. The method has the advantage to automatically adapt both the surrogate of the objective function and the classifier during the iterative optimization process. Therefore, non-computable areas do not need to be a priori known. The proposed method is applied to several analytical problems presenting different types of difficulty, and to the optimization of a fully nonlinear fluid-structure interaction system. The latter problem concerns the drag minimization of a flexible hydrofoil with cavitation constraints. The efficiency of the proposed method compared favorably to a reference evolutionary algorithm, except for situations where the feasible domain is a small portion of the design space.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The use of surrogate models is a classical approach to reduce the computational burden related to the optimization of complex systems (Simpson et al. 2001). Polynomial models were first used as surrogates, thanks to their ease of construction. More recently, sophisticated surrogate models such as Gaussian processes (GP) (Kleijnen 2009) or Support Vector Machines (SVM) (Vapnik 1995) have emerged. Gaussian Process (GP) modeling is a statistical method to approximate functions from a finite set of observations, possibly noisy, at arbitrary points. Using the observations, it explicitly updates the prior mean and covariance functions into their posterior counterparts, minimizing the mean-squared-error of the estimator. In the case of Gaussian observation noise, the estimator corresponds to the optimal Bayesian posterior. Contrary to alternative regression-type approaches, GP modeling does not require to prescribe explicitly a basis for the approximation space. GP surrogates have been applied to several problems such as uncertainty quantification (Marrel et al. 2009; Wang et al. 2013), binary classification (Nickisch and Rasmussen 2008), multi-levels system (Liu et al. 2016), multi-fidelity surrogate (Park et al. 2017) or clustering-based space exploration (Dong et al. 2017).
GP models have also been found especially appealing for optimization, in the framework of the Efficient Global Optimization (EGO) (Jones et al. 1998) method, because their statistical nature allows to provide both a prediction of the objective function, in terms of model mean, and an error estimate, in terms of model variance. EGO strategies have been used in several engineering applications, such as aerodynamic drag reduction of transonic wings (Liu et al. 2017), vibration reduction for rotating aircrafts (Glaz et al. 2008; 2009), optimization of FSI problems (Aghajari and Schäfer 2015) and sail trimming optimization (Sacher et al. 2017). The EGO efficiency has been demonstrated for the optimization of complex systems with costly objective function evaluations (Simpson et al. 2001).
In all these problems, a statistical criterion accounting for the Expected Improvement (EI) (Picheny et al. 2013), usually referred to as merit function, is used to select a new (or multiple (Li et al. 2016)) design point, at which the objective function should be evaluated. This new evaluation is used to improve the accuracy of the surrogate. However, in some situations, the analysis may not be possible for the newly selected design point. In the context of simulation-based optimization, such situations can be related for instance to the existence of unphysical configurations, ill-posed problems, or the lack of numerical robustness (weak convergence of the solvers, non-convergence to a steady solution, unstable computation, poor mesh quality for extreme configuration, etc). The origin of such failures is dependent on the application domain and an example will be provided below in the context of hydrodynamic design. Note that the automatic detection of non-computable points is a real issue in practical applications. Indeed, the origins of the failures can be very diverse and their detection is therefore not obvious. In some cases, the failure can be relatively easy to detect by monitoring the evolution of residuals or any variable of interest (e.g. forces). In other cases, the computational time might be a way to identify the simulations that are not converging. The use of clustering approaches (Jain et al. 1999) may also be an alternative to detect such computational failures. All these situations will be referred generically as cases of non-computable design points. The occurrence of such non-computable points is critical to sequential EGO method because it leads to a premature halt of the optimization process, due to the impossibility to update the surrogate model. A possible way to overcome this problem would be to interpolate/extrapolate the non-computable objective function values, using directly the current GP model or more sophisticated methods (Zhang et al. 2017). However, the accuracy of these values and their impact on the convergence of the optimization procedure are questionable. Moreover, such methods are not always satisfactory since we may not be interested in non-computable points that correspond to unphysical designs.
Unphysical or ill-posed situations typically arise from the definition of the design space that is too large and includes non-feasible situations. Similarly, the presence of design points that are not computable because of numerical issues should be traced back to a design space that is too rich and contains extreme situations that should not be considered as potential candidates for the optimum. Otherwise, it implies that the numerical solvers considered for the evaluation of the objective function are simply not suitable for the optimization task. However, even though the numerically critical areas of the design space may not be close to the sought optimum, the EGO eventually visit them because of the infilling strategy. A naive fix to the encounter of a non-computable point consists in associating to it a prescribed high (resp. low) value for the objective function to be minimized (resp. maximized). This avoids halting the EGO procedure and prevents the future exploration of the non-computable point neighborhood. Unfortunately, the selection of an appropriate value for the non-computable points is not a trivial task with, in practice, detrimental consequences such as a significant loss of accuracy on the whole GP model approximating the objective function and a possibly strong deterioration of the EGO convergence. Alternative remedies are a better definition of the design space, to explicitly remove design points leading to unphysical or ill-posed problems, and the improvement of the numerical robustness through, e.g., the tuning of solvers parameters. Unfortunately, depending on the situation these two tasks can be extremely cumbersome, if possible at all.
In this work, we propose to combine a classical EGO method and a classification approach in order to deal with the possible existence of non-computable design areas. In this approach, the subset of the design space corresponding to computable points is progressively determined, by the Least-Squares Support Vector Machine (LS-SVM) classification method (Suykens and Vandewalle 1999), on the basis of previously classified computable / non-computable points. The SVM classification method was first proposed in the EGO context by Basudhar et al. (2012) for the treatment of discontinuous or binary constraints. We extend this idea to the case of non-computable design areas, with the suggestion of using LS-SVM instead of SVM models. Indeed, LS-SVMs are computable at a lower cost than SVMs since the SVM formulates the classifier as a quadratic programming problem while LS-SVM deals with a set of linear equations. Specifically, each iteration step in the iterative method for solving the SVM consists of a linear system to be solved which has the same complexity as one single LS-SVM. Moreover, benchmarks in van Gestel et al. (2004) have shown that LS-SVMs are performing consistently very well in comparison with many other methods. The LS-SVM classifier provides a probability that a new point is computable. We incorporate this probabilistic information in the definition of the merit function when selecting the new design point to be analyzed. The merit function also involves a classical EI criterion, based on the GP model of the objective function constructed on the subset of computable design points. Therefore, the key advantages of the proposed method, called EGO-LS-SVM hereafter, are the following: it does not halt when a non-computable point is proposed; it does not require an explicit definition of the computable domain, but rather it constructs it; the GP model of the objective function uses only computable values and so is not polluted by arbitrary values at non-computable points. Finally, the EGO-LS-SVM method can handle optimization problems with inequality constraints and non-computable points, in a unified fashion employing the same classification strategy.
The present paper is organized as follows. The EGO-LS-SVM method is progressively introduced in Section 2, starting with the classical EGO method, presenting next the LS-SVM classification method to handle non-computable domains and inequality constraints, and finally deriving several merit functions. The efficiency of the EGO-LS-SVM method is first assessed on a series of analytical optimization problems in Section 3. A comparison with the reference evolutionary algorithm CMA-ES (Hansen 2006) is also provided. The optimization of a fully nonlinear Fluid-Structure Interaction (FSI) system involving non-computable domains is subsequently considered in Section 4. It consists in the minimization of the hydrodynamic drag of a two-dimensional flexible hydrofoil, with non-cavitation constraints, for a 5-dimensional design space defining the unloaded geometry and mechanical properties of the hydrofoil. Finally, the conclusions of the work are proposed in Section 5.
2 GP-based constrained optimization
Our objective is to estimate the solution \({\mathbf x}_{\text {opt}}\) of the following generic optimization problem
where \({\mathbf x}\) is the vector of design parameters, \({\Omega }\subset {\mathbb R}^{d}\) is the optimization domain, \(f: {\Omega } \mapsto {\mathbb R}\) the objective function and \({\mathbf Q}:{\mathbf x} \mapsto {\mathbb R}^{m}\) is the vector of (non-linear) constraints. Even in the unconstrained case, \(m = 0\), finding the global optimum of f can be very costly, in particular when its evaluation is numerically expensive. The use of surrogate models in place of f is then a classical approach to reduce the computational burden related to the optimization of complex systems (Simpson et al. 2001). In this work, we consider the use of Gaussian processes (GP) (Kleijnen 2009) which, owing to their statistical nature, provide both a prediction of the objective function and a measure of the uncertainty (variance) in the prediction. These features are appealing in optimization, as they can be used to derive rigorous optimization strategies based on the maximization of the Expected Improvement (EI) criterion. These methods are globally referred to as the Efficient Global Optimization (EGO) (Jones et al. 1998) methods. A summary of the construction of the GP model for f is provided in Section 2.1, as well as the resulting optimization strategy in the unconstrained case. The classification approach to account for constraints and non-computable subsets of points is considered in Section 2.2.
2.1 Unconstrained EGO using GP
Consider a set of n training inputs points \({\mathbf X}_{n} = \left \{{\mathbf x}_{1},\dots ,{\mathbf x}_{n}\right \}\), each associated to a noisy observation \(y_{i}\) of the objective function f. It is assumed that \(y_{i} = f({\mathbf x}_{i}) + \varepsilon _{i}\), where the \(\varepsilon _{i}\) are Gaussian measurement noises, assumed for simplicity independent and identically distributed with variance σ𝜖2. The GP construction considers that \(f({\mathbf x})\) is a realization of a zero-mean multivariate Gaussian process with covariance function \(C_{f}\). In this work, we consider the multidimensional squared exponential covariance functions defined by
where \({{\Theta }} = \{\theta _{1},\theta _{2},l_{1},l_{2},\dots ,l_{d}\}\) is a vector of hyper-parameters to be inferred from the observations. Denoting \({\mathbf C}({{\Theta }}) \in {\mathbb R}^{n\times n}\) the covariance matrix with entries \(C_{i,j} ({{\Theta }}) \doteq C_{f}({\mathbf x}_{i},{\mathbf x}_{j};{{\Theta }})\), \(~1 \le i,j\le n\), the joint Gaussian distribution of the noisy observation vector, \({\mathbf Y}_{n} =\left (y_{1},\dots ,y_{n}\right )^{\text {T}}\), and the predicted observation \(y({\mathbf x})\) is given by
In (3) we have denoted \(\kappa ({\mathbf x})\doteq C_{f}({\mathbf x},{\mathbf x};{{\Theta }})\), \({\mathbf k}({\mathbf x})\doteq \left (C_{f}({\mathbf x},{\mathbf x}_{1};{{\Theta }}) {\cdots } C_{f}({\mathbf x},{\mathbf x}_{n};{{\Theta }})\right )^{\text {T}}\) and \(\mathbf I\) the identity matrix of \({\mathbb R}^{n}\). From the conditional rules of joint Gaussian distributions (Rasmussen and Williams 2006), the best prediction \(\widehat {f}({\mathbf x})\) of \(f({\mathbf x})\), i.e. the mean of y, and the prediction variance \(\hat {\sigma }^{2}_{f}({\mathbf x})\) are given by
The hyper-parameters \({{\Theta }}\) and noise variance \({\sigma _{\epsilon }}^{2}\) can be determined by maximizing the log-marginal likelihood (Rasmussen and Williams 2006) using the “Covariance Matrix Adaptation Evolution Strategies” (CMA-ES) algorithm (Hansen 2006). This powerful evolutionary based optimizer is an improvement of the original \((\mu /\rho {+ \atop ,} \lambda )\)-ES variants (Hansen et al. 2015), thanks to the covariance matrix adaptation property. Indeed, the CMA-ES allows generations of new individuals that are possibly not distributed along the principal axis of the covariance matrix. In the present work, we apply this evolutionary algorithm by using the recommended parameters values (step-size \(\sigma = 0.5\), population size \(\lambda = 4 + \lfloor 3 \log d \rfloor \), number of parents for recombination \(\mu = \frac {\lambda }{2}\), etc.) of Hansen (2006). A complete tutorial of the CMA-ES algorithm, including a source code and best uses, is available in Hansen (2016). More details on GP meta-models can also be found in Rasmussen and Williams (2006).
Let \(\hat {{\mathbf x}}_{n}\) be the optimum of \(\widehat {f}({\mathbf x})\). It is expected that \(\hat {{\mathbf x}}_{n} \approx {\mathbf x}_{\text {opt}}\) if the approximation error \(\widehat {f}-f\) is small enough. The advantage of minimizing \(\widehat {f}\) instead of f is that GP models are usually inexpensive to evaluate compared to the original objective function. To control the error in the approximation, one proceeds sequentially by adding progressively new points in the area of interest. A deterministic optimization procedure would choose the next point \({\mathbf x}_{n + 1}\) as the optimal point of \(\widehat {f}\). However, the GP model provides probabilistic information that can be exploited to propose more robust strategies based on merit functions, which combine the prediction and its variance. In this work, we use the Augmented Expected Improvement (AEI) merit function (Huang et al. 2006), which estimates the expected progress in the cost, taking into account the noise in the observed values and the prediction variance:
where the Expected Improvement \(EI({\mathbf x})\) is defined by
with \({\Phi }\) and \(\phi \) the cumulative and density functions of the standard Gaussian distribution, and \({\mathbf x}_{*,n} \in {\mathbf X}_{n}\) is the current effective best solution (see Huang et al. (2006)). The optimum \({\mathbf x}_{n + 1}\) of the AEI is added to \({\mathbf X}_{n}\), and f is evaluated at the new point providing \(y_{n + 1}\). Setting \(n \leftarrow n + 1\), a new iteration can start updating the GP model. Overall, each iteration requires one computation of the cost and the resolution of two optimization problems: a first one for the hyper-parameters of the GP model, and a second one to find the AEI optimum. The iterations of the GP-based optimization problem are continued until a stopping criterion is satisfied or the resources allocated to the optimization have been exhausted. Obviously, if f is not computable for the proposed \({\mathbf x}_{n + 1}\), the optimization process is stopped prematurely, because \({\mathbf x}_{n + 1}\) and \(y_{n + 1}\) cannot be added to \({\mathbf X}_{n}\) and \({\mathbf Y}_{n}\).
2.2 Classification method
As underlined in the introduction, the proposed approach based on a classification method is closely related to the handling of inequality constraints in the optimization problem (1). Indeed, the non-computable simulations are usually located in some specific regions of the design space. Therefore, the presence of non-computable points can be managed as inequality constraints if these regions of failures can be identified thanks to a probabilistic formulation. In this framework, a failure probability would be used within the optimization process to avoid the non-computable simulations.
EGO methods with inequality constraints were considered by Schonlau (1997). The key idea followed in this reference is to rely on m additional surrogates to estimate the constraints \(Q_{i}({\mathbf x})\). For Gaussian Process models, one can easily determine the probability \(P_{i}(Q_{i}\ge 0|{\mathbf x})\) that the constraint \(Q_{i}\) is satisfied at \({\mathbf x}\). Assuming the independence of the constraints probability, the consolidated probability \(P({\mathbf Q} \ge {\mathbf 0} | {\mathbf x}) = {\Pi }_{i = 1}^{m} P_{i}(Q_{i}\ge 0|{\mathbf x})\) is obtained. This probability is used to modify the unconstrained AEI criterion and favor regions feasible with a probability:
Although effective in many problems, this GP modeling of the constraints faces several limits. First, its computational cost increases with the number m of constraints and can be an issue for problems with large m. Second, the approximation by GP models assumes a sufficient smoothness of the \(Q_{i}\). This rules out the case of binary constraints (feasible/infeasible). Another situation, non-amenable to the GP approximations of the constraints, is when the search domain \({\Omega }\) possesses a sub-domain  over which f is non-computable, i.e. undefined, but there is no explicit expression or a priori knowledge of this sub-domain. As a result,
over which f is non-computable, i.e. undefined, but there is no explicit expression or a priori knowledge of this sub-domain. As a result,  cannot be expressed in terms of inequality constraints.
cannot be expressed in terms of inequality constraints.
Classification methods recently proposed by Basudhar et al. (2012) are better suited to deal with discontinuous and binary constraints in GP-based optimization procedures. Therefore, we aim at using this approach to define a unique framework to deal with inequality constraints and non-explicit feasible domain definition in presence of a non-computable domain  . In essence, classification is based on the reformulation of problem (1) into the unconstrained form
. In essence, classification is based on the reformulation of problem (1) into the unconstrained form

where \({\Omega }_{{\mathbf Q}} := \{ {\mathbf x} \in {\Omega }, Q_{i = 1,\dots ,m}({\mathbf x}) \ge 0 \}\) is the subset of \({\Omega }\) satisfying the inequality constraints. As the admissible set \({\Omega }_{\text {adm}}\) has no explicit form, in general, we rely on a binary classifier with two classes \(C^{+}\) and \(C^{-}\) over \({\Omega }\), corresponding to the admissible (x satisfies all constraints and \(f({\mathbf x})\) is computable) and non-admissible (x does not satisfy all constraints or \(f({\mathbf x})\) is not computable) domains respectively. To construct this classifier, each \({\mathbf x}_{i}\) of \({\mathbf X}_{n}\) is equipped with a value \(z_{i}=\pm 1\) depending on its membership \(C^{\pm }\). To predict the class of a new point \({\mathbf x}\) we introduce a classification function \(h:{\mathbf x} \in {\Omega } \rightarrow {\mathbb R}\), such that \(z({\mathbf x}) = \text {sign} h({\mathbf x})\). A Least-Squares Support Vector Machine (LS-SVM) (Suykens and Vandewalle 1999) is used to construct h. The LS-SVM method extends the original Support Vector Machine (SVM) classifier (Vapnik 1995) to quadratic penalization, resulting in a linear (but non-sparse) system to be solved (see below). Further details and discussion on SVM and LS-SVM methods can be found in Cawley (2006).
The LS-SVM method (Suykens and Vandewalle 1999) is a linear classifier, for \(C^{+}\) and \(C^{-}\), in a feature space induced by the transformation \({\boldsymbol \phi } : {\Omega } \rightarrow {\mathcal F}\):
Here, \({\mathbf w}\) and \({\boldsymbol \phi }({\mathbf x})\) are the weights and features vectors, while \(b \in {\mathbb R}\) is a constant. The feature space \({\mathcal F}\) is generated by a reproducing kernel \(r : {\Omega } \times {\Omega } \rightarrow {\mathbb R}\) representing the inner product between images in \({\mathcal F}\) of vectors: \(r({\mathbf x},{\mathbf x}^{\prime }) = {\boldsymbol \phi }({\mathbf x})\cdot {\boldsymbol \phi }({\mathbf x}^{\prime })\). We use the classical Gaussian kernel,
with scale factor \(\lambda \in {\mathbb R}\) to be adjusted. The LS-SVM parameters \(({\mathbf w},b)\) satisfy the primal constrained optimization problem
with trade-off parameter \(\gamma \in {\mathbb R}^{+}\) (to be fixed) and relaxation variables \(e_{i}\) allowing for miss-classification. The Lagrangian of this optimal problem is
where the \(\alpha _{i} \in {\mathbb R}\) are the Lagrange multipliers of the constraints. Denoting \({\mathbf Z}_n = (z_{1} {\cdots } z_{n})^{\text {T}}\), the optimality conditions of the Lagrangian (15)
are used to derive a linear system for the dual model parameters b and \({\boldsymbol \alpha }_n = (\alpha _{1}\cdots \alpha _{n})^{\text {T}}\),
where \({\mathbf R} \in {\mathbb R}^{n\times n}\) is the kernel matrix with \(R_{i,j}=r({\mathbf x}_{i},{\mathbf x}_{j})\). This system is solved via a Cholesky factorization (Cawley 2006), and h in (11) is expressed in terms of dual model parameters to obtain
The LS-SVM classifier depends on two parameters, \(\gamma \) and \(\lambda \), to be determined when solving (16). This step is called model selection and it is usually performed with cross-validation approaches (Stone 1974). The most common method is the k-fold cross-validation, in which the training set is split into k disjoint subsets. Then, the LS-SVM model is sequentially trained on \(k-1\) subsets and the remaining subset is used to evaluate the classification efficiency by computing the error rate. The global k-fold estimate of the error rate is the average of the k error rates. The extreme case where \(k=n\) is called the Leave-One-Out (LOO) cross-validation and it allows an almost unbiased estimate of the error rate (Vapnik and Vapnik 1998). Unfortunately, the LOO computation is too expensive to be applied on common training sets. However, in the specific case of LS-SVM classifiers, it was shown (Cawley and Talbot 2003, 2004, 2007) that exact LOO can be performed in only \(\mathcal {O}(n)\) operations. In this work, we rely on this efficient LOO procedure to determine \(\gamma \) and \(\lambda \) that minimize the Predicted Residual Sum-of-Squares (PRESS) criterion (Allen 1974),
where \(\widehat {z_{i}}^{(-i)}\) is the predicted output \(z({\mathbf x}_{i})\) of the LS-SVM, when the i-th training point \(({\mathbf x}_{i},z_{i})\) is disregarded from the construction of the classifier. A simple expression for the predicted residuals is proposed in Cawley and Talbot (2007),
where the \(D_{ii}^{-1}\) are the diagonal entries of the inverse of \({\mathbf D}\), the matrix of system (16). An explicit expression is also provided in Cawley and Talbot (2007) to compute \(D_{ii}^{-1}\) during the factorization of \({\mathbf D}\). The minimization of the PRESS (18) for \(\lambda \) and \(\gamma \) is performed with the CMA-ES algorithm (Hansen 2006) in all the examples presented below.
The LS-SVM binary classifier is finally extended to a probabilistic classification, relating h in (17) to the probability of the class \(C^{+}\), denoted \(P(C^{+}|{\mathbf x})\). A comparison of several probability models for the LS-SVM classification is provided in Van Calster et al. (2007). We use the sigmoid function (Platt 1999) and expressing the probability of \(C^{+}\) as
The parameters A and B of the sigmoid are determined by minimizing the probability of misclassification, see Platt (1999) and Lin et al. (2007). In practice, the probability P goes to 1 (resp. 0) as the classifier is certain that \({\mathbf x}\in {\Omega }_{\text {adm}}\) and belongs to \(C^{+}\) (x∉Ωadm and belongs to \(C^{-}\)), while a value of \(P = 1/2\) denotes a complete uncertainty in the classification. This can occur when \({\mathbf x}\) is far from any observations in \({\mathbf X}_{n}\) or close to the interface between the two classes.
2.3 EGO-LS-SVM method
2.3.1 Extended merit functions
We now return to the optimization problem and introduce the EGO-based method that we call EGO-LS-SVM for it is based on the LS-SVM classifier. The EGO-LS-SVM method uses the probability \(P \left (C^{+} | {\mathbf x} \right )\) to derive a merit function from the AEI, in order to select a new point \({\mathbf x}_{n + 1}\in {\Omega }\). Following (Schonlau 1997; Basudhar et al. 2012), the selected point should present high expected improvement (relatively to another point) of the objective function value and a high probability of belonging to \({\Omega }_{\text {adm}}\). These considerations lead us to propose the following sequential infilling strategy, selecting alternatively one of the following definitions for \({\mathbf x}_{n + 1}\) in the EGO-LS-SVM method:
The first definition in (21) corresponds to the extension of the AEI favoring points with high chance of feasibility. The second expression (22) maximizes the original AEI definition by enforcing a minimal probability \(\rho \) of feasibility; we use \(\rho = 0.5\) in all subsequent computations. In (23), the predicted objective function is directly minimized over the approximated feasible domain defined by \(\{{\mathbf x} \in {\Omega }, P(C^{+}|{\mathbf x}) > \rho )\}\). Finally (24) combines the two classes probabilities to favor areas where the classification is the most uncertain (\(P \sim 0.5\)), to improve the exploration along the estimated feasible domain boundaries.
Finally the new points \({\mathbf x}_{n + 1}\) are determined using CMA-ES algorithms without (Hansen 2006) or with constraints (Arnold and Hansen 2012), depending on the considered definition. Whence the new point has been selected, the constraints \(Q_{i}\) and the objective function f are evaluated at the selected point. If  , that is \(f({\mathbf x}_{n + 1})\) is computable we add \(f({\mathbf x}_{n + 1})\) to the training set and update the GP model of f. Otherwise the new point is simply considered as a missing data and disregarded in the subsequent constructions of the GP model of f. In any cases, we set \(z_{n + 1}=+ 1\) if \(f({\mathbf x}_{n + 1})\) is computable and \({\mathbf Q}({\mathbf x}_{n + 1})\le 0\), and \(z_{n + 1}=-1\) otherwise. Therefore, the GP model of f and the LS-SVM classification may involve different numbers of observations if some of them fall in
, that is \(f({\mathbf x}_{n + 1})\) is computable we add \(f({\mathbf x}_{n + 1})\) to the training set and update the GP model of f. Otherwise the new point is simply considered as a missing data and disregarded in the subsequent constructions of the GP model of f. In any cases, we set \(z_{n + 1}=+ 1\) if \(f({\mathbf x}_{n + 1})\) is computable and \({\mathbf Q}({\mathbf x}_{n + 1})\le 0\), and \(z_{n + 1}=-1\) otherwise. Therefore, the GP model of f and the LS-SVM classification may involve different numbers of observations if some of them fall in  . Note that if
. Note that if  , we have \(\hat {f}_{n + 1} = \widehat {f}\), but because of the update of \(P(C^{+}|{\mathbf x})\) we shall have in general \({\mathbf x}_{n + 2} \neq {\mathbf x}_{n + 1}\). Consequently, the EGO-LS-SVM method will improve the estimation of \({\Omega }_{\text {adm}}\) till it proposes a new point \({\mathbf x}_{n + 1} \in {\Omega }_{\text {adm}}\) to update \(\widehat {f}\).
, we have \(\hat {f}_{n + 1} = \widehat {f}\), but because of the update of \(P(C^{+}|{\mathbf x})\) we shall have in general \({\mathbf x}_{n + 2} \neq {\mathbf x}_{n + 1}\). Consequently, the EGO-LS-SVM method will improve the estimation of \({\Omega }_{\text {adm}}\) till it proposes a new point \({\mathbf x}_{n + 1} \in {\Omega }_{\text {adm}}\) to update \(\widehat {f}\).
Compare to the similar classification based approach proposed in Basudhar et al. (2012), we remark that our approach is based on the original sigmoid probability in (34) such that \(P(C^{+}|{\mathbf x})\) remains differentiable, facilitating the search of \({\mathbf x}_{n + 1}\). Second, a single point is added and have to be evaluated per EGO iteration, where the approach in Basudhar et al. (2012) enriches the training set with \(d + 1\) new points at each iteration. The computational cost to perform these \(d + 1\) evaluations of f is expected to be too important in many application and is not necessary for the LS-SVM classification procedure. This is demonstrated on a numerical example later, in Section 3.5, where we discuss further the differences and respective efficiencies of the method of Basudhar et al. (2012) and our.
The work-flow of one iteration step of the EGO-LS-SVM method is summarized in the Algorithm 1 below. In the full optimization process, the Algorithm 1 is called iteratively until a convergence is reached or a maximum workload has been reached. The lines 1 and 2 correspond to the GP surrogate construction of the objective function f. This allows computing the mean and variance predictions given in (4) and (5). Lines 3 to 5 concern the LS-SVM classification model with the classification probability in (20) as output. To do this, a first optimization problem is solved for the parameters \((\gamma ,\lambda )\) (line 3). Then, the system (16) is solved, at line 4, to determine \(({\boldsymbol \alpha }_n,b)\) in (17). Finally, the coefficients A and B in (20) are computed by Newton’s method (Lin et al. 2007). To the end, the new point \({\mathbf x}_{n + 1}\) is determined at line 6 by solving a last optimization problem for one of the merit functions in (21)–(24).

2.3.2 Convergence assessment
In the following sections, we are assessing and comparing the efficiency of the proposed EGO-LS-SVM method on several problems. To this end, we need to monitor the convergence of the sequence of optimization iteration. The convergence can be characterized in different ways. For instance one may report the best point in the training set, \({\mathbf x}_{\text {best}}\in {\mathbf X}_{n}\), corresponding to the smallest objective function value \(f_{\text {best}} \doteq f({\mathbf x}_{\text {best}})\). Note that \(f_{\text {best}}\) is an upper bound of the true optimal value, and that \(f_{\text {best}}\) can only improve as the optimization iterations proceeds. Alternatively, in the analytical tests presented in the next section, where the objective function is easily evaluated, one can determine at each iteration the approximated optimal point \({\mathbf x}^{*}_{\text {opt}}\) and objective function value \(f_{\text {opt}}^{*} \doteq f({\mathbf x}_{\text {opt}}^{*})\) associated to the current state of knowledge of f and computable domain \(P(C^{+}|{\mathbf x})\). Specifically, one can solve for \({\mathbf x}_{\text {opt}}^{*}\) the following constrained optimization problem
and subsequently evaluate \(f_{\text {opt}}^{*} = f({\mathbf x}_{\text {opt}}^{*})\). It is noted, however, that \({\mathbf x}_{\text {opt}}^{*}\) may not be a computable point since the classifier may have a non-zero misclassification rate. Further, when the exact solution of the optimization problem is known, one can report the distance to current estimate \({\mathbf x}^{*}_{\text {opt}}\) to the optimum true optimum \({\mathbf x}_{\text {opt}}\), in terms of Euclidian distance \(\|{\mathbf x}_{\text {opt}}-{\mathbf x}_{\text {opt}}^{*}\|\) or objective function values \(f({\mathbf x}^{*}_{\text {opt}})-f({\mathbf x}_{\text {opt}})\ge 0\).
2.3.3 Illustration of the infilling strategy
Before applying the EGO-LS-SVM method to generic problems, we first illustrate the properties of the different merit functions in the criteria (21)–(24), and the benefit of applying them in a sequential fashion. To this end, we consider the one-dimensional domain \({\Omega }=\left [0,1\right ]\) and the Ricker Wavelet objective function \(f(x)=\left (1-2 \pi ^{2} x^{2} \right ) \exp \left (- \pi ^{2} x^{2} \right )\). We define the set of non-computable points through

where \(x_{\min } = \frac {\sqrt {3/2}}{\pi }\) is the minimum of f in \({\Omega }\). Letting  , the optimization problem becomes
, the optimization problem becomes
The optimum of (27) is found on the boundary of \({\Omega }_{\text {adm}}\) at \(x_{\text {opt}} = x_{\min } + 0.2\). We solve this problem for several infilling strategies, with an initial sample set with size \({n_{\text {LHS}}} = 10\). observations, and fix the maximum number of calls to f to \({N_{\mathrm {f}}} = 50\) (thus 40 optimization iterations are performed). Figure 1 compares the distances to the optimum as a function of \({N_{\mathrm {f}}}\) for the sequential use of all the merit functions (21)–(24), or using systematically only one of them. It is seen that using only (21) (pink curve) or (24) (black curve) to drive the procedure does not yield satisfactory results on this example. In contrast, using (22) alone (blue curve) or (23) alone (green curve) yields a convergence similar to that obtained using the four merit functions sequentially (red curve). These behaviors can be explained on this simple problem: because the criteria (22) and (23) produce points closer to the boundary than the unconstrained merit functions in (21) and (24), they are more efficient to recover an optimum located on the boundary. Nevertheless, using sequentially all the merit functions (21)–(24) does not impact negatively the convergence. We thus advise for the alternative use of all the four merit functions in a sequential infilling strategy. This setting favors both the exploration of promising areas (with large AEI) of the design space and of the most uncertain boundaries of the computable domain (\(P \sim 0.5\)).
Finally, we report in Fig. 2 the convergence of EGO-LS-SVM when using the merit functions (22) alone (left plot), or (23) alone (right plot), and for different values of the threshold probability \(\rho = 0.2\), 0.5 and 0.8. Again, the curves depict the distance to the optimum as a function of the total number \({N_{\mathrm {f}}}\) of calls to f. These plots show that the value of \(\rho \) seems to have a moderate effect on the convergence in the present example. In addition, using \(\rho = 0.5\) appears to be the best choice for the two merit functions. This value will be considered as the default value in the following experiments.
Convergence with the number of calls Nf of the distance to optimum, \(\|{\mathbf x}_{\text {opt}}-{\mathbf x}_{\text {opt}}^{*}\|\), for the infilling strategy based on single merit function (22) (left) or (23) (right), and for different threshold probabilities ρ. Values are only reported for computable optimum \({\mathbf x}_{\text {opt}}^{*}\) solution of (25). Case of problem (27)
3 Analytical test problems
In this section, we illustrate the accuracy and the computational efficiency of the EGO-LS-SVM approach by solving few optimization problems defined analytically. We consider problems with objective functions that are not computable over a subset  of the full design space \({\Omega }\). The classification approach is used to estimate the admissible (i.e. computable) domain
of the full design space \({\Omega }\). The classification approach is used to estimate the admissible (i.e. computable) domain  , and the GP model of f is constructed using only evaluations at points proposed in Ωadm. For reference and comparison purposes, we rely on the evolutionary algorithm CMA-ES (Hansen 2006) to solve the different problems, employing a high penalization value \(f({\mathbf x}) = f_{\infty }\) for the individual \({\mathbf x} \notin {\Omega }_{\text {adm}}\). This penalization \(f_{\infty }\) and other parameters of the CMA-ES method (population size, cross-over parameter…) are carefully set for each optimization problem, following the recommendations (Hansen 2006).
, and the GP model of f is constructed using only evaluations at points proposed in Ωadm. For reference and comparison purposes, we rely on the evolutionary algorithm CMA-ES (Hansen 2006) to solve the different problems, employing a high penalization value \(f({\mathbf x}) = f_{\infty }\) for the individual \({\mathbf x} \notin {\Omega }_{\text {adm}}\). This penalization \(f_{\infty }\) and other parameters of the CMA-ES method (population size, cross-over parameter…) are carefully set for each optimization problem, following the recommendations (Hansen 2006).
The selected test problems are presented in the following. A simple two-dimensional illustrative example is firstly proposed in Section 3.1; a multi-dimensional optimization problem is considered in Section 3.2, which includes optimizations in increasing dimensions and calculations with different initial sample set sizes; Section 3.3 investigate the behavior of the EGO-LS-SVM method in the case of a multi-dimensional optimization problem with complex domain  corresponding to a large portion of \({\Omega }\) (case of an over-constrained problem); Section 3.4 proposes the minimization of a problem where the domain \({\Omega }_{\text {adm}}\) and objective function f are defined probabilistically; finally Section 3.5 concerns the efficiency comparison of the original SVM based approach (Basudhar et al. 2012) to our new EGO-LS-SVM method.
corresponding to a large portion of \({\Omega }\) (case of an over-constrained problem); Section 3.4 proposes the minimization of a problem where the domain \({\Omega }_{\text {adm}}\) and objective function f are defined probabilistically; finally Section 3.5 concerns the efficiency comparison of the original SVM based approach (Basudhar et al. 2012) to our new EGO-LS-SVM method.
3.1 Two-dimensional illustrative example
We consider the two-dimensional domain \({\Omega } = [0,4]^{2}\) and the simple convex objective function \(f({\mathbf x}) = {x_{1}^{2}} + {x_{2}^{2}}\). We define the set of non-computable points through

where \(c_{1}({\mathbf x}) = 0.25{x_{1}^{2}} + 0.75{x_{2}^{2}} -1\) and \(c_{2}({\mathbf x}) = 0.75{x_{1}^{2}} + 0.25{x_{2}^{2}} -1\). Letting  , the optimization problem becomes
, the optimization problem becomes
The exact optimum of the problem is found to be on the boundary of \({\Omega }_{\text {adm}}\) at \({\mathbf x}_{\text {opt}} = (1,1)\).
The EGO-LS-SVM algorithm is initialized using a Latin Hypercube Sampling (LHS) set of 15 points drawn randomly in \({\Omega }\). The optimization iterations are repeated till the AEI merit function reaches a value less than \(10^{-3}\). In the CMA-ES method, the optimization is carried-out until the estimated optimum is in \({\Omega }_{\text {adm}}\) with a value of f less than the EGO-LS-SVM solution. As mentioned before, a large penalization \(f_{\infty }= 100\) is applied to points not belonging to \({\Omega }_{\text {adm}}\) in the CMA-ES algorithm.
Figure 3 shows the convergence of the error (red squares and blue triangles, left axis) with the cumulated number of calls to (attempts to evaluate) f, denoted \({N_{\mathrm {f}}}\). Note that \({N_{\mathrm {f}}}\) is also accounting for calls to f with \({\mathbf x}\notin {\Omega }_{\text {adm}}\). The error on the solution is defined as the Euclidian distance between the current estimate \(\hat {{\mathbf x}}_{\text {opt}}\) of the optimum and the exact one, \({\mathbf x}_{\text {opt}}\). For the EGO-LS-SVM method, \(\hat {{\mathbf x}}_{\text {opt}}\) is the solution of (29) where f is substituted with its GP model. For the CMA-ES approach, the distance to the exact optimum of each member of the population in \({\Omega }_{\text {adm}}\) is reported. The number \({N_{\text {adm}}}\) of computable calls to f is also reported for both methods, using red and blue lines (right axis) in the same Figure. The EGO-LS-SVM (squares and red line) terminated at \({N_{\mathrm {f}}} = 142\), with a number of computable calls equal to 91, such that roughly 50 points have been proposed in the non-feasible region  . The evolutionary method needs 599 calls to f before it finds a better optimum than the EGO-LS-SVM one, among which 401 were for computable points. This result shows that, in this example, the EGO-LS-SVM method is able to properly estimate the feasible domain \({\Omega }_{\text {adm}}\) in the neighborhood of the optimum, and converges to this optimum at a significantly faster rate than the CMA-ES approach.
. The evolutionary method needs 599 calls to f before it finds a better optimum than the EGO-LS-SVM one, among which 401 were for computable points. This result shows that, in this example, the EGO-LS-SVM method is able to properly estimate the feasible domain \({\Omega }_{\text {adm}}\) in the neighborhood of the optimum, and converges to this optimum at a significantly faster rate than the CMA-ES approach.
Distance to the optimum (\(\|{\mathbf x}_{\text {opt}}-{\mathbf x}_{\text {opt}}^{*}\|\)) and cumulated number of computable calls to f (Nadm) as functions of the total number of calls Nf and for the EGO-LS-SVM and CMA-ES optimization procedures. Distance is reported only for computable \({\mathbf x}_{\text {opt}}^{*}\) solution of (25). Case of problem (29)
To better appreciate the effectiveness of the classification approach, contours of \(P (C^{+}|{\mathbf x})\) are reported in Fig. 4 at \({N_{\mathrm {f}}}= 50\) and 100. Also shown in the plots are the iso-value corresponding to \(P(C^{+}|{\mathbf x})= 0.5\) (dashed white line), proposed computable points (white squares) and non-computable points (black triangles). After 50 calls to f, the classification has well discovered \({\Omega }_{\text {adm}}\) and the level \(P(C^{+}|{\mathbf x})= 0.5\) is not far from the actual boundary of \({\Omega }_{\text {adm}}\). After 100 calls to f, a large fraction of the proposed points are concentrated around the optimum and the contour \(P(C^{+}|{\mathbf x})= 0.5\) is not following anymore the boundary of \({\Omega }_{\text {adm}}\), except in the immediate neighbor of the optimum. Farther from the optimum in areas less explored, the classification probability quickly returns to \(P(C^{+}|{\mathbf x})\approx 0.5\) as we move away from observed points. This behavior is due to the classification parameters \(\lambda \) and \(\gamma \) (see Section 2.2) that are adjusted to capture the steep transition in P(C+|x) at the interface between \({\Omega }_{\text {adm}}\) and  , where the optimum point \({\mathbf x}_{\text {opt}}\) is located. This behavior is desirable because it allows considering the exploration of areas that were initially classified as unfeasible with high probability if they exhibit large merit function AEI. Indeed, the plot also reveals several calls to f for points in
, where the optimum point \({\mathbf x}_{\text {opt}}\) is located. This behavior is desirable because it allows considering the exploration of areas that were initially classified as unfeasible with high probability if they exhibit large merit function AEI. Indeed, the plot also reveals several calls to f for points in  , far from the optimum, that confirm non-feasibility and balance large merit function values (recall that the unconstrained optimum is at the origin).
, far from the optimum, that confirm non-feasibility and balance large merit function values (recall that the unconstrained optimum is at the origin).
Contours of the classification probability P(C+|x) after 50 and 100 calls. Case of problem (29)
3.2 Higher dimensional problems
3.2.1 Influence of dimensionality
To investigate the behavior of the EGO-LS-SVM method as the dimensionality of the search space \({\Omega }\) is increasing, we propose the following problem where no function value is provided for points not belonging to the feasible domain. Let \(d>1\) be the dimensionality of \({\Omega }:=[-1,1]^{d}\). We denote \(B_{d}\) the hypersphere center on \({\mathbf x}_{c}=(0.1 {\cdots } 0.1)\) with radius \(R_{d} = \sqrt {0.05(d-1)}\) and set  . The optimization problem is then defined by
. The optimization problem is then defined by
As for the previous problem, the optimal solution is found on the boundary of  . The initialization of the EGO-LS-SVM method uses LHS set having increasing size with d. Specifically the tests shown below correspond to \(d = 2\), 5, 10 and 20 and respective LHS sizes \(n_{\text {LHS}} = 15\), 40, 100 and 200. The stopping criteria for the EGO-LS-SVM and CMA-ES methods are identical to the previous one in Section 3.1.
. The initialization of the EGO-LS-SVM method uses LHS set having increasing size with d. Specifically the tests shown below correspond to \(d = 2\), 5, 10 and 20 and respective LHS sizes \(n_{\text {LHS}} = 15\), 40, 100 and 200. The stopping criteria for the EGO-LS-SVM and CMA-ES methods are identical to the previous one in Section 3.1.
Figure 5 shows the convergences for the different dimensionality d tested. The plot shows the sequence of values \(f({\mathbf x})\) at computable proposed points \({\mathbf x}\) as a function of \({N_{\mathrm {f}}}\). The evolutions of the cumulated number of computable calls \({N_{\text {adm}}}\) are also reported.
Sequence of computable values of f(xn) and cumulated number of computable calls Nadm as functions of Nf and for the EGO-LS-SVM and CMA-ES optimization procedures. Case of problem (30) with different dimensionality d as indicated
For all the dimensionality d tested, the CMA-ES method needs more function calls than the EGO-LS-SVM method and the ratio of numbers of calls increases with d. In other words, the efficiency of the EGO-LS-SVM method relatively to the CMA-ES method is increasing with d. It is remarked that for the same number of calls to f, the CMA-ES is proposing more points in Ωadm than the EGO-LS-SVM method, but the latter is more effective at proposing points with low f value. For the EGO-LS-SVM method, we also note the presence of distinct branches of function values. These branches reflect the competing trends involved in the selection of the new optimum candidates \({\mathbf x}_{n + 1}\), because of the alternated use of conservative or aggressive strategies specified by (23) and (24).
3.2.2 Influence of initial sample set size
This section aims at assessing the impact of the initial sample set size on the convergence of the optimization procedure. Indeed, the initial design of experiments can be crucial in the optimization process and may significantly affect the EGO procedure. To study the robustness of the EGO-LS-SVM method, we solve the problem (30), with \(d = 5\) and three different initial sample set sizes: \(n_{\text {LHS}}= 10\), 50 and 100. For these three cases, we perform 300 EGO iterations.
Figure 6 shows the convergences for the different sample set sizes \(n_{\text {LHS}}\). The plot shows the sequence of objective function values f at computable points as a function of \({N_{\mathrm {f}}}\) (also counting the initial sample set generation). We see that for the \(n_{\text {LHS}}= 50\) and 100 cases the algorithm immediately proposed new points that improve the function values of f and accordingly converge quickly within \(\approx 200\) iterations. The case of only \(n_{\text {LHS}}= 10\) initial samples exhibits a very different behavior with an initial exploration phase with selected points having high objective function values, up to \({N_{\mathrm {f}}}\approx 150\). after which the optimization quickly converges. Overall, the convergence requires slightly more iterations for \(n_{\text {LHS}}= 10\) than for the larger initial sample sets. Nevertheless, this example highlights the robustness of the EGO-LS-SVM method since the procedure converges to the optimum even when a coarse initial sample set (10 points in 5 dimension) is employed.
Sequences of optimum computable values of fopt, as a function of Nf, for different initial sample set sizes nLHS. Case of problem (30) with d = 5
3.3 Over-constrained problem
The following problem is designed to illustrate the limits of the EGO-LS-SVM method in the case where the feasible domain \({\Omega }_{\text {adm}}\) is hard to learn and explore, because of a complex structure. This problem which was proposed in Tenne and Goh (2010) is then said over-constrained. The domain \({\Omega }_{\text {adm}}\) is here define as a subset of Ω = [− 10,10]d, for \(d = 7\), through
where
The optimization problem finally writes as
The global optimum is located at
As before, only the proposed points in \({\Omega }_{\text {adm}}\) are evaluated and used to approximate f, while the classification proceeds with all the points, computable or not. Therefore, a large LHS set of 800 points drawn uniformly in \({\Omega }\) is needed to ensure that the initial GP model of f uses sufficiently many points. In the experiment presented below, only 7 of the 800 LHS points were drawn in \({\Omega }_{\text {adm}}\), a low fraction illustrating the complexity of the constrained problem.
Figure 7 shows the evolution of the Euclidian distances to the exact optimum, \(\|{\mathbf x}_{\text {opt}} - \hat {{\mathbf x}}_{\text {opt}}\|_{2}\) as a function of \({N_{\mathrm {f}}}\). The EGO-LS-SVM method progresses during the first 500 calls to f (EGO iterations), but subsequently stalls. Note that when the optimization procedure is halted, only 187 evaluations have been generated for a total of 3541 calls to f. The low ratio of computable proposed points \({\mathbf x}_{n}\) indicated that for this example the EGO-LS-SVM method is not able to properly learn the domain \({\Omega }_{\text {adm}}\). On the contrary, the CMA-ES method performs satisfactorily on this problem and appears to be much more robust against the complexity of \({\Omega }_{\text {adm}}\). Nevertheless, it should be underlined that this problem corresponds to an extreme situation where the objective function is not computable over most of the search domain \({\Omega }\).
Distance to the optimum \(\|{\mathbf x}_{\text {opt}}-{\mathbf x}_{\text {opt}}^{*}\|\) and cumulated number of computable calls to f Nadm as functions of Nf and for the EGO-LS-SVM and CMA-ES optimization procedures. Case of problem (32)
3.4 Problem with random computable domain
To complete the series of tests on analytically defined problems, we propose a problem for which the domain of non-computable function  and the objective function are defined randomly. We set \({\Omega }=[-5,5]^{2}\) and generate randomly
and the objective function are defined randomly. We set \({\Omega }=[-5,5]^{2}\) and generate randomly  using the following procedure. We first generate randomly 100 points \({\mathbf x}^{c}_{l = 1,\cdots ,100} \in {\Omega }\). Then, for each point \({{\mathbf x}^{c}_{l}}\) we decide with a probability
using the following procedure. We first generate randomly 100 points \({\mathbf x}^{c}_{l = 1,\cdots ,100} \in {\Omega }\). Then, for each point \({{\mathbf x}^{c}_{l}}\) we decide with a probability  if f is non-computable in the neighborhood \(\|{\mathbf x} - {{\mathbf x}^{c}_{l}}\|_{2} \le 1\). We then define
if f is non-computable in the neighborhood \(\|{\mathbf x} - {{\mathbf x}^{c}_{l}}\|_{2} \le 1\). We then define  as the intersection of \({\Omega }\) with the non-computable neighborhoods. For this construction, the probability
as the intersection of \({\Omega }\) with the non-computable neighborhoods. For this construction, the probability  that f is not computable at a given \({\mathbf x}\in {\Omega }\) is approximated from the cumulative distribution function of the binomial law
that f is not computable at a given \({\mathbf x}\in {\Omega }\) is approximated from the cumulative distribution function of the binomial law  , where \(|{\Omega }|\) is the volume of Ω. Figure 8 presents two random realizations of
, where \(|{\Omega }|\) is the volume of Ω. Figure 8 presents two random realizations of  (gray areas) for a probability
(gray areas) for a probability  and \(61\%\) in the left and right plot respectively.
and \(61\%\) in the left and right plot respectively.
The optimization problem is finally defined as

where the solution \({\mathbf x}_{\text {opt}}\) is drawn at random in  . In the computations, the EGO-LS-SVM method is initialized with an LHS set of \({n_{\text {LHS}}}= 10\) points in \({\Omega }\) and the optimization procedure is stopped at \({N_{\mathrm {f}}} = 50\).
. In the computations, the EGO-LS-SVM method is initialized with an LHS set of \({n_{\text {LHS}}}= 10\) points in \({\Omega }\) and the optimization procedure is stopped at \({N_{\mathrm {f}}} = 50\).
We solve the optimization problem (3.4) for several probabilities  . For every value of
. For every value of  several realizations of
several realizations of  and \({\mathbf x}_{\text {opt}}\) are generated to estimate statistics of the solution. Figure 9 shows the convergence of the optimization procedure with \({N_{\mathrm {f}}}\) (optimization iteration) and for increasing values of
and \({\mathbf x}_{\text {opt}}\) are generated to estimate statistics of the solution. Figure 9 shows the convergence of the optimization procedure with \({N_{\mathrm {f}}}\) (optimization iteration) and for increasing values of  . Figure 9a–c correspond to increasing values of
. Figure 9a–c correspond to increasing values of  and reports the median (blue line) and first and third quartiles (red lines) of the distance to the optimum. Figure 9d compares the convergence of the median distance to the optimum, for several values of
and reports the median (blue line) and first and third quartiles (red lines) of the distance to the optimum. Figure 9d compares the convergence of the median distance to the optimum, for several values of  . The plots show that as
. The plots show that as  increases from 0, the convergence of the median and first quartile is only mildly affected. In contrast, the third quartile is significantly impacted, with an \(O(1)\) distance to the optimum when
increases from 0, the convergence of the median and first quartile is only mildly affected. In contrast, the third quartile is significantly impacted, with an \(O(1)\) distance to the optimum when  . This behavior indicates that the EGO-LS-SVM method is quite robust and successful in finding the optimum, except when
. This behavior indicates that the EGO-LS-SVM method is quite robust and successful in finding the optimum, except when  becomes too large with computable domains \({\Omega }_{\text {adm}}\) with a low ratio of \(|{\Omega }_{\text {adm}}|/|{\Omega }|\) and complicated structures. In these situations, the EGO-LS-SVM method is not making progress and becomes inefficient at proposing new points \(\in {\Omega }_{\text {adm}}\) to improve the model of f. As a result, the approach is either successful or completely failing, with a significantly skewed distribution of the distance to the optimum as evidenced by the distance between the first and third quartiles to the median. However, the results reported in Fig. 9d show that the EGO-LS-SVM method is quite robust since for probabilities as high as
becomes too large with computable domains \({\Omega }_{\text {adm}}\) with a low ratio of \(|{\Omega }_{\text {adm}}|/|{\Omega }|\) and complicated structures. In these situations, the EGO-LS-SVM method is not making progress and becomes inefficient at proposing new points \(\in {\Omega }_{\text {adm}}\) to improve the model of f. As a result, the approach is either successful or completely failing, with a significantly skewed distribution of the distance to the optimum as evidenced by the distance between the first and third quartiles to the median. However, the results reported in Fig. 9d show that the EGO-LS-SVM method is quite robust since for probabilities as high as  the approach is still converging for at least half of the generated problems.
the approach is still converging for at least half of the generated problems.
3.5 Comparison with EGO-SVM(d+ 1)
A classification approach was proposed in Basudhar et al. (2012) for the treatment of constraints, and it can be adapted to the case of non-computable domains. This section aims at contrasting this approach with ours, and at highlighting the improved efficiency of our approach.
As mentioned before, the method proposed in Basudhar et al. (2012) uses a classifier to predict the feasibility of new points (i.e. whether constraints are satisfied), and so can be used in the same way to predict if f is computable. Compared to our approach, the method in Basudhar et al. (2012) differs on four main points. First, it uses an SVM method to determine the classification function \(h({\mathbf x})\), in a polynomial space, where we use an LS-SVM method in general Reproducing Kernel Hilbert spaces. The LS-SVM has thus generally better approximation properties when the SVM method selects a subset of points to construct h with possibly a reduced computational cost. Second, using a reduced training set in SVM calls for a correction of the classification probability to ensure that disregarded training samples are correctly classified. In Basudhar et al. (2012) the following correction of the sigmoid function (20) was considered,
where \(d^{+}({\mathbf x})\) (resp. \(d^{-}({\mathbf x})\)) is the distances of \({\mathbf x}\) to the closest point in the training set belonging to \(C^{+}\) (resp. \(C^{-}\)), and \(\delta = 10^{-10}\) is used to avoid numerical overflows. This modification is introduced to account for the fact that the class of the training samples is exactly known. Third, the method in Basudhar et al. (2012) considers a single merit function based on the expected improvement (EI). Forth and finally, the infilling strategy in Basudhar et al. (2012) adds not only the point \({\mathbf x}_{n + 1}\) classified in \(C^{+}\) and maximizing the EI but also d additional new points in its neighborhood to maintain the isotropy of the training set (a requirement made necessary by the corrected probability in (34)). In contrast, our approach uses the simpler and smoother sigmoid function, alternates between the criteria in (21)–(24) to accommodate different situations and enrich the training set by a single element at each iteration of the iterative procedure. As subtle as they may appear, these differences greatly impact the efficiency of the optimization procedures.
To distinguish between the impacts of the classifier construction methods and of the infilling strategies (classification probability, selection criteria for \({\mathbf x}_{n}\)), we considered the following methods:
-
EGO-LS-SVM : the approach proposed in this paper, with LS-SVM construction of the classification function \(h({\mathbf x})\), sigmoid classification probability definition, sequential selection using criteria (21)–(24).
-
EGO-SVM(d+ 1) : the approach proposed (Basudhar et al. 2012), with SVM construction of \(h({\mathbf x})\), modified sigmoid classification probability definition in (34), EI-only selection criteria and d-points neighborhood exploration.
-
EGO-SVM : the same as EGO-LS-SVM but with a SVM construction of \(h({\mathbf x})\).
-
EGO-LS-SVM(d+ 1) : the same as EGO-SVM(d+ 1) but with a LS-SVM construction of \(h({\mathbf x})\).
These methods are tested on problem (30), fixing \(d = 5\). The results of these experiments are summarized in Fig. 10. Note that the SVM and LS-SVM methods both use kernel-based constructions. The plots report the sequence of computable function values \(f({\mathbf x}_{n})\) as a function of the number of function calls \({N_{\mathrm {f}}}\). In the case of the EGO-SVM(d+ 1) and EGO-LS-SVM(d+ 1), the function values are reported only for the newly selected point \({\mathbf x}_{n + 1}\), if computable, and not for its d additional companion points. In addition, the convergence of the best feasible function value \(f_{\text {best}}\) is reported, using lines, and considers all evaluations of f (including the eventual d additional points).
Figure 10a compares the LS-SVM methods for an initial sample set with \({n_{\text {LHS}}}= 10\) points. It is seen that our approach EGO-LS-SVM explores the design space during about 100 function calls and converges to the computable optimum in about 250 calls. In contrast, the EGO-LS-SVM(d+ 1) method that uses the probability function and infilling strategy of Basudhar et al. (2012) is seen to have not converged even after 1,800 function evaluations, being unable to focus on the correct area. Figure 10b shows the case of the SVM methods using again \({n_{\text {LHS}}}= 10\) samples. The plot shows that the EGO-SVM method converges essentially as fast as for our proposed EGO-LS-SVM, albeit with a somehow longer exploration phase, as one would have expected for using the SVM in place of the LS-SVM model. For the EGO-SVM(d+ 1) method, corresponding to the original method proposed in Basudhar et al. (2012), we observe that it is now converging too, but it requires a few times more function evaluations to achieve a comparable best value \(f_{\text {best}}\) compared to our infilling strategy. This result highlights the computational overhead due to the need of adding d additional points to maintain the isotropy of the sample points. Figure 10c (resp. Fig. 10d) corresponds to the same methods as in Fig. 10a (resp. Fig. 10b) but now using an initial sample set with \({n_{\text {LHS}}}= 100\) points. It shows that our infilling method does not improve significantly when increasing \({n_{\text {LHS}}}\), or conversely demonstrating once more the robustness and interest of alternating between merit criteria.
Sequence of computable objective function values f(xn) (symbols) and convergence of the best value fbest (lines) as functions of the total number of calls Nf for different classifiers constructions, infilling strategies and initial sample set sizes. Case of problem (30) with d = 5
We finally remark that the construction of the SVM classifier is much more time consuming than the LS-SVM one, in the presented experiments using a kernel-based approach. This can be appreciated from the computational times reported Table 1 for different training set sizes. The differences in the computational times are mainly due to model selection step in the SVM classifier, which involves the resolution of a quadratic problem (using an SMO method (Platt 1999)). The higher computational cost of the SVM classifier construction further pleads for using the LS-SVM.
4 Application to flexible hydrofoil optimization
4.1 Optimization problem and solvers
We now apply the EGO-LS-SVM on a realistic problem corresponding to the optimization of a flexible hydrofoil. The objective of the optimization is to minimize the hydrofoil drag force at selected conditions (forward speed and lifting force) while ensuring non-cavitating flows. The complete description of the optimization problem and the hydrodynamical analysis of the optimized hydrofoil are not provided in this paper, which focuses on the method; interested readers can refer to Sacher et al. (2017). The original optimization problem proposed in Sacher et al. (2017) involved 11 design variables describing the shape and elastic characteristics of the foil flexible trailing edge, as schematically illustrated in Fig. 11. In the present work, the number of design variables is reduced to 5 in order to maintain reasonable computational times and to allow extensive comparisons of the optimization methods. Among the retained optimization variables, 4 concern the trailing edge camber geometry at rest (\(\mathrm {p}_{1,\dots ,4}\)), while the last one modifies the Young modulus \(\mathrm {E}_{\text {Beam}}\) of the flexible part. We set \({\Omega }=[-0.1,1.5]\times [-0.5,0.2]\times [-0.3,0.5]\times [-0.3,0.3]\times [0.1,1.2]\).
As mentioned before, the optimization concerns the minimization, for 4 conditions, of the hydrofoil drag coefficients \(\mathrm {C}_{\mathrm {D}_{i = 1,\dots ,4}}\). Each condition corresponds to a prescribed forward speed and hydrodynamic lift force developed by the hydrofoil. The optimization problem is written as
where the \(w_{i}>0\) are prescribed weighting coefficients fixing the relative importance of the 4 conditions. Constrains \(Q_{i}({\mathbf x})\) are introduced to prevent the cavitation of the flow for 4 other conditions. The admissible and computable domain is then defined as the intersection of the set of design points \({\mathbf x}\) satisfying the cavitation constraints, with  the set of \({\mathbf x}\) having computable function f:
the set of \({\mathbf x}\) having computable function f:

Indeed, parts of the search domain \({\Omega }\) corresponds to non-computable points, because of the lack of robustness of the simulation tool. As an example, Fig. 12 shows a hydrofoil corresponding to a non-computable point of the search space, at which the flow solver is not able to determine the hydrodynamic forces. Although it may be possible to finely tune the solvers to improve their robustness, automating the tuning process can be a difficult task. In addition, these non-computable configurations often correspond to uninteresting or even unphysical design points, such that the direct classification of these non-computable areas has been found very effective.
The explicit constraints \(Q_{i}\) are expressed as
where \(\rho \) is the fluid density, \(p_{v}\) the saturated vapor pressure, \(\mathrm {C}_{\mathrm {P}_{i}}\) the minimal pressure coefficient, \(\lambda _{i}\) the cavitation number, and \(U_{i}\) and \(\bar p_{i}\) are the reference velocity and pressure for the i-th condition. The minimum of the pressure coefficient is defined by \(\mathrm {C}_{\mathrm {P}_{i}}({\mathbf x}) := \frac {p_{i}^{-}({\mathbf x}) - \bar p_{i}}{0.5 \rho {U_{i}^{2}}}\), where \(p_{i}^{-}\) is the lowest pressure over the hydrofoil surface. The condition \(Q_{i} \le 0\) expresses the constraint that the minimum of the pressure around the hydrofoil should remain higher than the vapor pressure: \(p_{i}^{-} ({\mathbf x}) \ge p_{v}\).
Given a value \({\mathbf x}\) of the design variable, the evaluation of the objective function f and the constraints \(Q_{i}\) requires the resolution of 8 nonlinear fluid-structure interaction problems. For the flow, we rely on a static vortex lattice method with viscous boundary layer equations, using the solver XFOIL (Drela 1989; Morgado et al. 2016), while a nonlinear elasticity solver (Durand et al. 2014) is used for the elastic deformations of the foil (Durand et al. 2014), modeling the elastic trailing edge with 2D Linear Strain Triangles (LST) (Pedersen 1973) and Timoshenko beam elements (see Fig. 11a). The nonlinear equilibrium FSI solutions are computed by a Newton method with Aitken relaxation. We mention that the conditions call for the enforcement of a prescribed lift force. This is achieved in XFOIL by adjusting the Angle of Attack (AoA) of the hydrofoil.
4.2 Optimization results
In the following, we consider two EGO approaches to handle the constraints related to the cavitation. First, the proposed EGO-LS-SVM method is used to estimate directly \({\Omega }_{\text {adm}}\) from the classification of previous points \({\mathbf x}\). In other words, the LS-SVM method is employed to predict both the satisfaction of the constraints \(Q_{i}({\mathbf x}) \le 0\) and the computability of future points. For the second method, the LS-SVM classification is used only to predict the computability, while the functionals \(Q_{i}\) of the cavitation constraints are approximated by individual GP models following the EGO method presented in Schonlau (1997). We call this second approach the EGO-GPC. These two approaches are also compared to the reference CMA-ES algorithm (Hansen 2006) with a penalty value \(f_{\infty }= 100\) for the non-computable points. In all computations, the two EGO methods are initialized using an LHS set of size 100. For this example, the EGO optimizations are continued until a maximum computational budget of 36 hours is exhausted. Both the resolutions of the non-linear FSI problems, the construction of the GP models and the search for the maximizer of the AEI criteria are included in the computational time. Note that on a classical workstation computer it takes approximatively \(T_{f}= 75\)s to decide the admissibility of a point and evaluate f at a given computable \({\mathbf x}\), solving the FSI problems corresponding to the prescribed 8 conditions.
Figure 13 shows the evolution of the successive values of f with the number of calls to f. It is seen that the EGO-LS-SVM and EGO-GPC methods require a significantly lower number of function evaluations than CMA-ES to reach the optimum neighborhood. Specifically, the CMA-ES optimization needs 1615 function evaluations, that is, twice as much, to eventually produce a better point than the EGO-LS-SVM optimum (stopped after 36h of computations). The two EGO methods have similar behavior, although the sequence of computed values of f produced the EGO-GPC method is slightly more dispersed than for the EGO-LS-SVM method. This difference can be explained by the additional evaluations needed to construct the GP models of the constraints in the EGO-GPC method.
Sequence of computable function values f(xn) as a function of the number of calls Nf for the EGO-LS-SVM, EGO-GPC and CMA-ES methods. Case of problem (35)
If the two EGO methods behave similarly in term of the convergence with the number of calls to f, they do present significant differences in terms of computational times. This can be appreciated from the plots of Fig. 14. Figure 14a reports the cumulated computational times of the EGO-LS-SVM and EGO-GPC methods as functions of the optimization iteration. The computational times are split into the time dedicated to the FSI problems resolution, called FSI time, and the construction of the GP models and search of maximizer of the extended AEI, called EGO time. It is seen from the graph that the EGO time is dominant for the two approaches and increases with the iteration index at a polynomial rate \(r \gtrsim 2\), because of the increasing size of the GP models construction. Furthermore, the EGO time of the EGO-GPC method is significantly higher than that of the EGO-LS-SVM method, as one may have expected since more GP processes must be estimated. In contrast to the EGO time, the computational times spent on the FSI problems increase roughly at a linear rate, with the EGO-LS-SVM FSI time being half of the EGO-GPC FSI time. A closer inspection of the results reveals that, when the computational budget of 36 hours is reached, the EGO-GPC method called for 312 evaluations of f, including 8 non-computable points, while EGO-LS-SVM made up to 554 calls to f, among which 294 violated the constraints and 5 were not computable. These numbers explain the lower FSI time of the EGO-LS-SVM method, compared to the EGO-GPC method. Indeed, the full classification approach of the EGO-LS-SVM method allows for significant computational savings because once the constraint on cavitation for a certain condition has been found to be non-satisfied, there is no need to solve the remaining FSI problems for the other conditions and to compute f. For the EGO-GPC method, on the contrary, one must solve systematically all the FSI problems for the whole set of 8 (constraints and objective) conditions to improve the GP models of all the \(Q_{i}\) and f. To further illustrate this point, we compare in Fig. 14b the current best value of f observed, denoted \(\min \left (f\right )\), as a function of the computational time, for the two EGO methods. The EGO-LS-SVM method is seen to be more efficient as it gives a better optimum than the EGO-GPC approach. Moreover, the convergence rate seems faster for the EGO-LS-SVM method: an excellent minimum within less than 0.1% of the terminal value of f is obtained in just 4 hours when for the GP method a comparable point is obtained after 17 hours. These differences are consistent with the fact that the number of EGO-LS-SVM iterations performed in a given computational time is essentially twice that of the EGO-GPC: although it is proposing a significant fraction of non-feasible points, the EGO-LS-SVM method better explores the design space and takes advantage of a cheaper evaluation cost for non-feasible points.
Left: comparison of the computational times of the EGO-LS-SVM and EGO-GPC methods, splitting the FSI solves (FSI time) and the GP models construction and AEI exploration (EGO time) contributions. Right: convergence of the computable fbest value with the total computational time. Case of problem (35)
Nevertheless, it should be noted that the CMA-ES algorithm can be computationally cheaper than the EGO methods, depending on the computational budget and the problem considered. For instance, Fig. 15a shows the best admissible (and computable) value of f obtained as a function of the computational time for the two EGO methods and the CMA-ES procedure. It is seen that in the case of the hydrofoil optimization with the numerical models considered here, the CMA-ES always outperforms EGO-GPC, except for a point around 17 hours of computational time. Compared to the EGO-LS-SVM, the CMA-ES is significantly less efficient at the beginning of the optimization procedure but eventually do better as the computational time increases, with a better point found by the evolutionary approach after \(\approx 26\) hours of calculation. Obviously, these results are for a single realization of the optimization procedures that are random in essence (through the selection / re-sampling of the population in CMA-ES and initial LHS sample in the EGO methods). A complete comparison should consider averages over multiple realizations, but the results reported in Fig. 15a are representative of the relative behavior of the different methods. However, these relative efficiencies are highly dependent on the problem and the numerical model involved. In the present case, the important fraction of the computational time dedicated to the GP models construction is detrimental to the relative performance of the EGO methods. To illustrate this, we can estimate the computational times that would result if the resolution of the FSI problems were much more demanding, so the EGO times become relatively less significant. This is made in Fig. 15b where we have considered the case of an evaluation of f requiring 30 minutes of computational time, instead of 75 seconds. In this situation, the CMA-ES optimization would need roughly 525 hours to find a better point than the one obtained in just 125 hours by the EGO-LS-SVM. Even the EGO-GPC method would become more competitive than the CMA-ES strategy for \(T_{f}\) large enough. In conclusion, the EGO-based methods are most suited to the case of costly models.
Evolution of the best computable objective function value fbest with the total computational time for the EGO-LS-SVM, EGO-GPC and CMA-ES methods and considering different evaluation times Tf. The sequence of computable function values f(xn) are also reported. Case of problem (35)
5 Conclusion
In this work, we have proposed the use of a classification approach in EGO procedures to deal with the existence of non-computable design points and inequality constraints. The key idea of the approach is to define the admissible sub-domain of the original design space consisting of points being computable and satisfying the problem constraints. The method, named EGO-LS-SVM, relies on an LS-SVM classifier to predict the admissibility of points in the global search domain. The LS-SVM classifier composes a Gaussian process model with a sigmoid function, leading to an admissibility probability. It is trained on the set of previously classified points. We combine the probabilistic characterization of the admissibility with the classical Augmented Expected Improvement (AEI) statistical criterion, to propose several merit functions for the selection of the next EGO point. These merit functions induce conservative or on the contrary aggressive strategies, with respect to admissibility when exploring the design space. In fact, we recommend to actually alternate between the merit functions to yield a robust but effective sequential infilling strategy, ensuring the intensive exploration of promising areas of the search domain and the boundaries of the admissible domain.
The EGO-LS-SVM method has been tested on several analytical problems presenting different types of difficulties. These tests have validated the method and revealed its robustness with respect to the number of design variables. In fact, it is shown that compared to standard evolutionary algorithms (CMA-ES) the relative efficiency of EGO-LS-SVM is increasing with the number of parameters in the range tested. However, the EGO-LS-SVM method can be challenged in extreme situations where the admissible domain consists of a small portion of the global design set with complex geometry. For these situations, the EGO-LS-SVM may not have found admissible points, stalling the convergence.
Finally, the method was tested on the constrained optimization of a fully nonlinear numerical fluid-structure interaction system. Here we aimed at minimizing the drag of a flexible hydrofoil in several operating conditions, with constraints related to the cavitation. On this example, the EGO-LS-SVM method has been compared with the CMA-ES and EGO methods with GP models of the constraints. This example highlighted the interest of using EGO-based methods compared to the CMA-ES on these complex problems, and the advantages of treating the constraints and computable domain in a unified approach to the EGO-LS-SVM method.
Future works should focus on the current limits of the EGO-LS-SVM method. In particular, the initialization procedure must be improved in the situation where the computable domain is small compared to the whole search domain. One possible route in this direction could be to initiate the optimization with an evolutionary method, and subsequently switch to EGO-LS-SVM when sufficiently many points have been found in the admissible domain. Also, when the absolute probabilities of \(C^{\pm }\) are much unbalanced (small or large computable domain, compared to the search domain) the use of a Weighted-SVM approach (Yang et al. 2005) could help achieving better classification performances, in particular during the initial optimization iterations.
References
Simpson T, Poplinski J, Koch NP, Allen J (2001) Metamodels for computer-based engineering design: survey and recommendations. Eng Comput 17(2):129–150
Kleijnen JP (2009) Kriging metamodeling in simulation: a review. Eur J Oper Res 192(3):707–716
Vapnik V (1995) The nature of statistical learning theory. Springer, New York
Marrel A, Iooss B, Laurent B, Roustant O (2009) Calculations of sobol indices for the gaussian process metamodel. Reliab Eng Syst Saf 94(3):742–751
Wang P, Lu Z, Tang Z (2013) An application of the kriging method in global sensitivity analysis with parameter uncertainty. Appl Math Model 37(9):6543–6555
Nickisch H, Rasmussen CE (2008) Approximations for binary gaussian process classification. J Mach Learn Res 9:2035–2078
Liu Y, Shi Y, Zhou Q, Xiu R (2016) A sequential sampling strategy to improve the global fidelity of metamodels in multi-level system design. Struct Multidiscip Optim 53(6):1295–1313
Park C, Haftka RT, Kim NH (2017) Remarks on multi-fidelity surrogates. Struct Multidiscip Optim 55 (3):1029–1050
Dong H, Song B, Wang P, Dong Z (2017) Surrogate-based optimization with clustering-based space exploration for expensive multimodal problems. Struct Multidisc Optim 57(4):1553– 1577
Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive Black-Box functions. J Glob Optim 13(4):455– 492
Liu J, Song WP, Han ZH, Zhang Y (2017) Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models. Struct Multidiscip Optim 55(3):925–943
Glaz B, Friedmann PP, Liu L (2008) Surrogate based optimization of helicopter rotor blades for vibration reduction in forward flight. Struct Multidiscip Optim 35(4):341–363
Glaz B, Friedmann PP, Liu L (2009) Helicopter vibration reduction throughout the entire flight envelope using surrogate-based optimization. J Amer Helicopter Soc 54(1):12007
Aghajari N, Schäfer M (2015) Efficient shape optimization for fluid–structure interaction problems. J Fluids Struct 57:298–313
Sacher M, Hauville F, Duvigneau R, Maître OL, Aubin N, Durand M (2017) Efficient optimization procedure in non-linear fluid-structure interaction problem: application to mainsail trimming in upwind conditions. J Fluids Struct 69:209–231
Picheny V, Wagner T, Ginsbourger D (2013) A benchmark of kriging-based infill criteria for noisy optimization. Struct Multidiscip Optim 48(3):607–626
Li Z, Ruan S, Gu J, Wang X, Shen C (2016) Investigation on parallel algorithms in efficient global optimization based on multiple points infill criterion and domain decomposition. Struct Multidiscip Optim 54 (4):747–773
Jain AK, Murty MN, Flynn PJ (1999) Data clustering: a review. ACM computing surveys (CSUR) 31 (3):264–323
Zhang Y, Park C, Kim NH, Haftka RT (2017) Function prediction at one inaccessible point using converging lines. J Mech Des 139(5):051402
Suykens J, Vandewalle J (1999) Least squares support vector machine classifiers. Neural Process Lett 9 (3):293–300
Basudhar A, Dribusch C, Lacaze S, Missoum S (2012) Constrained efficient global optimization with support vector machines. Struct Multidiscip Optim 46(2):201–221
van Gestel T, Suykens JA, Baesens B, Viaene S, Vanthienen J, Dedene G, de Moor B, Vandewalle J (2004) Benchmarking least squares support vector machine classifiers. Mach Learn 54(1):5–32
Hansen N (2006) The CMA Evolution Strategy: a comparing review. In: Towards a new evolutionary computation. Springer, pp 75–102
Rasmussen CE, Williams CKI (2006) Gaussian processes for machine learning. MIT Press, Cambridge
Hansen N, Arnold DV, Auger A (2015) Evolution strategies. In: Springer handbook of computational intelligence. Springer, pp 871–898
Hansen N (2016) The cma evolution strategy: a tutorial. arXiv:1604.00772
Huang D, Allen TT, Notz WI, Zheng N (2006) Global optimization of stochastic Black-Box systems via sequential kriging meta-models. J Global Optim 34(3):441–466
Schonlau M (1997) Computer Experiments and Global Optimization. PhD thesis, University of Waterloo, Waterloo, Ont., Canada, Canada. AAINQ22234
Cawley GC (2006) Leave-one-out cross-validation based model selection criteria for weighted ls-svms. In: 2006 IEEE international joint conference on neural network proceedings. IEEE, pp 1661–1668
Stone M (1974) Cross-validatory choice and assessment of statistical predictions. J R Stat Soc Ser B Methodol 36(2):111–147
Vapnik VN, Vapnik V (1998) Statistical learning theory, vol 1. Wiley, New York
Cawley GC, Talbot NL (2003) Efficient leave-one-out cross-validation of kernel fisher discriminant classifiers. Pattern Recogn 36(11):2585–2592
Cawley GC, Talbot NL (2004) Fast exact leave-one-out cross-validation of sparse least-squares support vector machines. Neural Netw 17(10):1467–1475
Cawley GC, Talbot NL (2007) Preventing over-fitting during model selection via bayesian regularisation of the hyper-parameters. J Mach Learn Res 8:841–861
Allen DM (1974) The relationship between variable selection and data augmentation and a method for prediction. Technometrics 16(1):125–127
Van Calster B, Luts J, Suykens JAK, Condous G, Bourne T, Timmerman D, Van Huffel S (2007) Comparing methods for multi-class probabilities in medical decision making using LS-SVMs and kernel logistic regression. In: Artificial neural networks – ICANN 2007: 17th international conference, Porto, Portugal, September 9-13, 2007, Proceedings, part II. Springer, Berlin, pp 139–148
Platt JC (1999) Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Advan Large Margin Classifiers 10(3):61–74
Lin HT, Lin CJ, Weng RC (2007) A note on platt’s probabilistic outputs for support vector machines. Mach Learn 68(3):267– 276
Arnold DV, Hansen N (2012) A (1 + 1)-CMA-ES for constrained optimisation. In: Soule T, Moore JH (eds) GECCO, Philadelphia, United States, ACM. ACM Press, pp 297–304
Tenne Y, Goh C (2010) Computational intelligence in expensive optimization problems. Adaptation, learning, and optimization. Springer, Berlin
Platt JC Schölkopf B, Burges CJC, Smola AJ (eds) (1999) Fast training of support vector machines using sequential minimal optimization. MIT Press, Cambridge
Sacher M, Durand M, Berrini E, Hauville F, Duvigneau R, Le Maître O, Astolfi JA (2017) Flexible hydrofoil optimization for the 35th america’s cup with constrained ego method. In: International Conference on Innovation in High Performance Sailing Yachts, Innov’Sail, pp 193–205
Drela M (1989) XFOIL: an analysis and design system for low Reynolds number airfoils. Springer, Berlin, pp 1–12
Morgado J, Vizinho R, Silvestre M, Ps̈coa J (2016) {XFOIL} vs {CFD} performance predictions for high lift low reynolds number airfoils. Aerosp Sci Technol 52:207–214
Durand M, Leroyer A, Lothodé C, Hauville F, Visonneau M, Floch R, Guillaume L (2014) FSI Investigation on stability of downwind sails with an automatic dynamic trimming. Ocean Eng 90:129–139
Pedersen P (1973) Some properties of linear strain triangles and optimal finite element models. Int J Numer Methods Eng 7(4):415–429
Yang X, Song Q, Cao A (2005) Weighted support vector machine for data classification. In: Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, vol 2, pp 859–864
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Raphael Haftka
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Sacher, M., Duvigneau, R., Le Maître, O. et al. A classification approach to efficient global optimization in presence of non-computable domains. Struct Multidisc Optim 58, 1537–1557 (2018). https://doi.org/10.1007/s00158-018-1981-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-018-1981-8



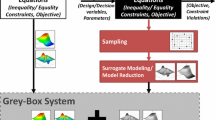
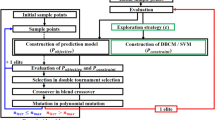








 (gray circles) for probabilities
(gray circles) for probabilities  and 0.61. Also shown are color contours of f
and 0.61. Also shown are color contours of f 






