1 Introduction

Design optimization techniques have already been used in actual designs such as a winglet shape design of Mitsubishi Regional Jet (Takenaka et al. 2008) and a nose shape design of the Bullet Train 700 series (Igarashi 2008). Recently, major optimization targets have been changed to more complicated ones such as discontinuous optimization problem, robust optimization problem, high dimensional optimization problem and so on. Such complicated optimization problems often appear in topology design optimizations due to the complexity of its topology/shape expressions. The topology optimization is a design approach to obtain an optimal layout including the changes of size, shape and topology. In the aircraft design, for example, the topology optimization can determine not only the optimal size and shape of aircraft, but also the number of blades, fuselages, engines and so on. By applying the topology optimization instead of the conventional shape optimization, it is possible to explore innovative optimal design configurations that exceed the designer’s idea/experience.

The optimization methods in numerical simulation fields can be roughly divided into two groups, invasive and noninvasive types. The noninvasive optimization methods include evolutionary strategies such as genetic algorithms (GA) and differential evolution. These methods have the feature to explore global optimal solutions even with complicated objective functions. As one of famous noninvasive approaches for high dimensional functions, there is an intense stochastic search method which is based on evaluation and optimization of a hypercube and is called the hypercube optimization (HO) algorithm (Rahib and Mustafa 2015). The hypercube is used to describe searching areas, and the algorithm can explore a global optimal solution by mimicking the behavior of a dove discovering new areas for food in natural life. The HO algorithm was executed in optimization problems with 1000, 5000 and 10,000 dimensions, and then it was demonstrated that the algorithm was a potential candidate for optimization of both low and high dimensional functions. However, required numbers of functional evaluations were from 500,000 to 50 million. The invasive optimization method often includes adjoint-based approach. In the adjoint approach, the gradient of the objective function with respect to all design variables can be obtained at once by solving the adjoint equation, and optimal solutions are explored by using gradient based optimization methods. It has the feature to be able to explore a local optimal solution even in high dimensional optimization problems. Therefore, the topology design optimization is generally executed with the adjoint approach (Fujii et al. 2000; Lars et al. 2002) since the topology design optimization requires an enormous number of design variables in order to express various topologies/shapes. In Fujii et al. (2000), an effective gradient-based method for the topology optimization of 3D structures has been presented. A flat cantilever beam problem of 32,000 dimensions, MBB beam problem of 60,000 dimensions, and 3D beam design problem of 144,000 dimensions were solved by the adjoint-based optimization approach. However, the adjoint approach requires to develop the program code to solve the adjoint equation and is not possible to search global optimal solutions. In addition, the adjoint approach cannot set integer/binary type constraints such as the acceptable number of objects. To tackle these issues, there is an example of topology design optimization using evolutionary algorithms (Payot et al. 2017). Payot et al. applied an R-snake method to the topology design optimization as a topology expression method, and then the topology design optimization was conducted in supersonic flow conditions using a differential evolutional optimization method. As a result, the topology optimization revealed optimum profiles that have both features of the Busemann biplane and conventional single body optimal airfoils. However, there is a problem in terms of optimization costs since the differential evolutional optimization approach was directly used in this research. In the topology design optimization in the field of aerodynamics, flow simulations are generally used to evaluate the objective function whose computational cost is not trivial. Therefore, it is necessary to reduce the number of evaluations of aerodynamic objective functions.

To realize efficient global topology design optimization at supersonic flow conditions, it is necessary to efficiently solve three challenging optimization problems, i.e. discontinuous optimization problem, optimization problem with infeasible regions and high dimensional optimization problem. With respect to the discontinuous optimization problem, the objective functions have discontinuities due to shock waves that have to be treated in optimization problems. With respect to the optimization problem with infeasible regions, the generation of large shock waves yields large infeasible regions of design space. In addition, the negative thickness of airfoil occurs depending on the definition of the ranges of design variables, and then the negative thickness of airfoil leads to an infinite loop in the optimization process by iteratively selecting a same additional sample point in the infeasible regions. In our previous research, an efficient global optimization method for discontinuous optimization problems with infeasible regions using classification method (EGODISC) (Ban and Yamazaki 2019) has been developed to efficiently solve discontinuous optimization problems as well as optimization problems with large infeasible regions by using machine learning technologies. By developing the EGODISC algorithm, an efficient global optimization could be executed without the infinite loop in the optimization process. However, it is still necessary to develop an efficient optimization approach for high-dimensional optimization problems since the topology design optimization generally has an enormous number of design variables in order to express various topologies/shapes.

There are several efficient optimization methods to solve the complicated optimization problems by using noninvasive approaches and machine learning techniques. For example, there is an optimization method using the Bayesian approach such as Gaussian process (Kriging) (Jones et al. 1998). The Bayesian optimization method has already been applied to a design optimization problem of supersonic transport, and it could obtain design knowledge of a twin-body/biplane-wing configuration (Ban et al. 2016, 2018). Although the Bayesian optimization isn’t a state-of-the-art algorithm, it is still often utilized in many research fields. In addition, several advanced approaches using multi fidelity information have also been proposed (Han and Görtz 2012; Yamazaki and Mavriplis 2013). In the Bayesian optimization approaches, however, the Gaussian process is used to construct a response surface model, and it takes large calculation cost to solve inverse matrices whose calculation cost is proportional to the cube of the number of sample points. In addition, it is necessary to optimize hyperparameters in the Bayesian optimization, and a gradient-based optimization method or GA is generally used for the optimization of the hyperparameters. Therefore, although the Bayesian optimization method enables to reduce the number of evaluations of objective functions (number of sample points), it requires huge construction costs of the response surface model especially with larger number of sample points. Since the number of sample points tend to become larger in higher dimensional optimization problems to explore higher dimensional design space, it is difficult to utilize the Bayesian method in high dimensional optimization problems. In addition, the prediction accuracy of the Gaussian process regression decreases at the high dimensional optimization problems and it was indicated that the upper limit of the dimensionality of the design variables space to efficiently obtain global optimal solutions was about 10 (Ziyu et al. 2013). There are several other methods to efficiently solve the high-dimensional optimization problems, such as GPEME and KPLS. The Gaussian Process surrogate model assisted Evolutionary algorithm for Medium-scale computationally Expensive optimization problems (GPEME) uses dimension reduction machine learning techniques for tackling the “curse of dimensionality”. In GPEME, the Sammon mapping is introduced to transform the design variables space to take advantage of the Gaussian process surrogate modeling in a low-dimensional space (Liu et al. 2014). However, since the dimension reduction method may lose some neighborhood information of the training data points in the original space, it is difficult to obtain comparable results with the direct Bayesian optimization. Another optimization method for the high-dimensional optimization problems has been proposed as the Kriging model with the Partial Least Squares technique to obtain a fast predictor (KPLS). The combination of Kriging and Partial Least Square (PLS) is abbreviated KPLS and allows us to build a fast Kriging model because it requires fewer hyper-parameters in its covariance function. The KPLS method is used for many academic and industrial verifications, and promising results have been obtained for problems with up to 100 dimensions (Bouhlel et al. 2016). However, it was also shown in (Bouhlel et al. 2016) that the KPLS has lower prediction accuracy than the Gaussian process (Kriging) model with a lot of sample points, which is not adequate to use in high dimensional optimization problems. As a state-of-the-art algorithm in the optimization, the reinforcement learning has been proposed (Volodymyr et al. 2016) to achieve the balance of “exploration at unknown region” and “utilization of prediction” that are similar principles to the Bayesian optimization. The reinforcement learning is a method to select actions by maximizing the assessment from environments such as recognitions, judgements and actions, and then it is used for the controls of complex systems such as automatic driving, game AI and robot. On the other hand, since the reinforcement learning needs an enormous number of iterations (Volodymyr et al. 2016), it is considered not to be appropriate for the design optimization problems discussed in this research.

Furthermore, there are several efficient optimization methods by combining the above-mentioned approaches such as gradient-enhanced Kriging and DynDGA. The gradient-enhanced Kriging method (Mohamed and Joaquim 2019; Rumpfkeil et al. 2011; Han et al. 2017) utilizes the gradient of the objective function with respect to all design variables obtained by solving the adjoint equation and more accurate surrogate models can be constructed. This approach can reduce the number of optimization iterations thanks to the accurate surrogate model. However, this approach still has an issue of the invasive optimization approach. A distributed genetic algorithm that divides and merges individuals dynamically (DynDGA) (Sugimoto et al. 2019) utilizes both of simulation and Kriging estimation to reduce the number of simulations for GA. In this approach, the number of simulation calls reduces to approximately 63% while maintaining the performance. However, this approach still has an issue of the Kriging method for the high dimensions.

In summary, the conventional approaches to solve the high dimensional optimization problems can be classified into five types even though the state-of-the-art algorithms. The first is to use the HO algorithm or evolutionary algorithms as GA by evaluating an enormous number of objective functions. The second is the gradient-based optimization using the adjoint sensitivity analysis whose solution is considered to be a local optimum. The third is to use the Bayesian optimization despite its difficulties. The fourth is to introduce some dimension reduction methods despite loss of neighborhood information of the training data points. The fifth is to combine the above-mentioned approaches. Our proposed approach is completely different from the five conventional approaches. A novel optimization method is developed using machine learning technologies to efficiently solve the high dimensional optimization problems without Gaussian process. The present paper is organized as follows. The optimization methods and performance evaluation methods used in this research are concisely described in Sect. 2. Then, several surrogate models used in this research are concisely introduced and construction/utilization costs of them are compared in Sect. 3. And then, optimization results obtained by the conventional Bayesian/GA approaches and the developed approach are compared/discussed in Sect. 4. Finally, concluding remarks are provided in Sect. 5.

2 Optimization and evaluation methods

2.1 Bayesian optimization

2.1.1 Algorithm of Bayesian optimization

Several surrogate model-based optimization methods have been proposed to efficiently explore global optimal solutions on blackbox functions such as the Bayesian approaches (Jones et al. 1998; Yamazaki and Mavriplis 2013; Forrester et al. 2008; Williams and Carl 1996) (Kriging response surface model-based approaches). The Gaussian process regression is used to construct a prediction model for mean and standard deviation values at unknown locations in design variables space, and then GA is used to explore promising locations in the design variables space in the general Bayesian optimization approach. The expected improvement (EI) is calculated from the mean and standard deviation values to achieve the balance of “exploration at unknown region (with larger standard deviation values)” and “utilization of prediction by response surface model (with lower mean values)”, and an additional point is selected at the maximum location of the EI value.

2.1.2 Gaussian process regression

The Gaussian process regression was introduced in Williams and Carl (1996) and Rasmussen and Williams (2006). The regression problem is considered for an unknown blackbox function giving the input/output relationship when the observation values \(\varvec{y} = \left\{ {y_{1} ,y_{2} , \ldots ,y_{n} } \right\}\) and the input values \(\varvec{x} = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}\) are given. Mean \(\mu_{{y^{*} |\varvec{y}}}\) and variance \(\varSigma_{{y^{*} |\varvec{y}}}\) of the posterior distribution of Gaussian distribution are expressed by the following equations.

$$\begin{array}{*{20}c} {\mu_{{y^{*} |\varvec{y}}} = \varvec{k}^{T} \varvec{C}^{ - 1} \varvec{y} = \mu ,} & {\varSigma_{{y^{*} |\varvec{y}}} = c - \varvec{k}^{T} \varvec{C}^{ - 1} \varvec{k}} \\ \end{array} = \sigma^{2}$$
(2.1.2.1)
$$\begin{array}{*{20}c} {c = k\left( {x^{*} ,x^{*} } \right),} & {\varvec{k} = \left[ {k\left( {x_{1} ,x^{*} } \right) k\left( {x_{2} ,x^{*} } \right) \cdots k\left( {x_{n} ,x^{*} } \right)} \right]^{T} } \\ \end{array}$$
(2.1.2.2)

where \(\varvec{C}\) is a gram matrix having \(\varvec{C}_{i,j} = k\left( {x_{i} ,x_{j} } \right)\) as an element, and \(k\left( {x_{i} ,x_{j} } \right)\) is referred to as a kernel function, and then the following ARD Matern 5/2 kernel is used in this research.

$$\begin{aligned} k\left( {x_{i} ,x_{j} } \right) & = \theta_{0} \left( {1 + \sqrt {5r^{2} \left( {x_{i} ,x_{j} } \right)} + \frac{5}{3}r^{2} \left( {x_{i} ,x_{j} } \right)} \right)e^{{ - \sqrt {5r^{2} \left( {x_{i} ,x_{j} } \right)} }} \\ r^{2} \left( {x_{i} ,x_{j} } \right) & = \mathop \sum \limits_{d = 1}^{D} \left( {x_{i,d} - x_{j,d} } \right)^{2} /\theta_{d}^{2} \\ \end{aligned}$$
(2.1.2.3)

where \(D\) represents the number of design variables.

2.1.3 Genetic algorithm

GA is one of the metaheuristic methods inspired by the process of natural selection such as selection, crossover and mutation. GA simulates the selection of the individuals by considering the relationship between the applicability to the environment and the probability to survive (Selection). Then, it simulates the natural evolution of the individuals by generating child individuals from the selected parental individuals (Crossover). In addition, it maintains the diversity of the population by altering a part of the genes of the child individuals (Mutation). In this research, a tournament selection, the blend cross over (BLX-α) (Eshleman and Schaffer 1993), and a polynomial mutation (Deb and Deb 2014) are used as the selection, crossover, and mutation methods.

2.2 Efficient global optimization method via clustering/classification methods and exploration strategy, EGOCCS

In the conventional Bayesian optimization, the Gaussian process regression is used to construct a response surface model, and it takes large calculation cost to solve inverse matrices whose size is n × n (n: number of sample points) since the calculation cost is proportional to the cube of the number of sample points. In addition, it is necessary to optimize hyperparameters in the Bayesian optimization [\(\theta_{i}\) in Eq. (2.1.2.3)], and a gradient-based optimization method or GA is generally used for the optimization of the hyperparameters. Therefore, since the Bayesian optimization requires huge construction cost for the response surface model and the prediction accuracy of the Gaussian process regression decreases at high dimensional optimization problems, it is difficult to utilize for high dimensional optimization problems. To tackle these problems, a novel efficient global optimization method without using probabilistic values as the standard deviation given in the Gaussian process is proposed, and then its construction cost is also reduced to efficiently obtain global optimal solutions in the high dimensional design variables space. In the proposed method, optimization problems are solved only with predicted functional values without the uncertain metrics of the surrogate model (standard deviation) which is used for calculating EI value in the conventional Bayesian optimization approach. Therefore, the proposed approach will bring higher compatibility with arbitrary response surface models such as radial basis function interpolation, inverse distance weighting, neural network regression, support vector regression, random forest regression and so on. For example, the inverse distance weighting can be used when the optimization cost is necessary to be reduced, and the neural network can be used when big data (a very large number of design variables) has to be taken into consideration in the optimization.

2.2.1 Algorithm of EGOCCS

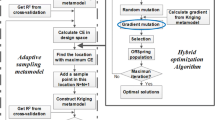
The flowchart of efficient global optimization method via clustering/classification methods and exploration strategy (EGOCCS) is shown in Fig. 1, and an outline diagram of EGOCCS is shown in Fig. 2. In this algorithm, firstly, initial sample points are generated in the design variables space by the Latin hypercube sampling method (Fig. 2a). Then, generation of computation grids and evaluation of objective function are carried out for the models corresponding to the initial sample points (Fig. 2b). And then, the response surface model is constructed based on the objective function values (Fig. 2c). Sparse regions of sample points are considered as the candidates to generate an additional sample point and are defined by using the machine learning methods of the density-based clustering method (DBCM) (Fig. 2d) and support vector machine classification method (SVM) (Fig. 2e). By generating additional samples in the sparse regions, bias/concentration of the distributions of sample points can be reduced. The DBCM is a method to group sample points using a distance parameter \({\varepsilon }\), and it is used to make a group of sample points in which the current optimal solution belongs in. The SVM is a method to classify the design variables space, and it is used to classify the design variables space into two groups, one of which is the group obtained by the DBCM. The SVM has a feature to create a separating hyperplane by maximizing a margin between two groups. It means that the separating hyperplane represents the sparsest region of sample points between two groups. In other words, it is possible to efficiently generate additional sample points considering the predicted value of the objective function as well as the separating hyperplane. In this research, GA is used to search an additional sample point where the predicted objective function value is the lowest on the separating hyperplane (sparse region of sample points) (Fig. 2f).

Fig. 1
figure 1

Flowchart of EGOCCS

Full size image
Fig. 2
figure 2

Outline of EGOCCS

Full size image

2.2.2 Density-based clustering method (DBCM)

Density-based clustering method (DBCM) is used to classify input datasets into two groups via unsupervised learning. This method is similar to the density-based spatial clustering of applications with noise (DBSCAN) (Ester et al. 1996), and it is possible to classify sample points into two groups based on the distance between points. The outline of this algorithm is summarized in Fig. 3. In this algorithm, firstly, a starting point \(P_{s}\) and a reference distance \({\varepsilon }\) are defined as a criterion of the clustering (Fig. 3a, b). The starting point corresponds to the current optimal sample point in this research. Then, sample points within the reference distance \({{\varepsilon }}\) are classified into the group same with the starting point (Fig. 3c), and then other sample points are checked again whether they are within the reference distance \({\varepsilon }\) from the sample points of the group (Fig. 3d). By iteratively performing this process until there are no more points to add (Fig. 3e–g), finally, the sample points can be divided into two groups whether the starting point belongs in or not (Fig. 3h). The reference distance \({\varepsilon }\) can be changed at each iteration as an exploration strategy explained in Sect. 2.2.4.

Fig. 3
figure 3

Outline of density-based clustering method

Full size image

2.2.3 Support vector machine classification method (SVM)

The support vector machine (SVM) is one of the two-classes classification methods proposed by Corinna and Vapnik (Corinna and Vladimir 1995) and one of the popular machine learning algorithms (Alex and Bernhard 2004). It is possible to obtain the optimal separating hyperplane even in the nonlinear data by mapping the data to a high dimensional space by using a kernel method. In addition, SVM separates the two-classes data with the idea of the maximum-margin hyperplane, and it is known to have high accuracy to predict for unknown data. The characteristic of the maximum-margin is important for EGOCCS algorithm.

2.2.4 Exploration strategy in EGOCCS

Consideration of “exploration at unknown regions” and “utilization of predictions by response surface models” with a proper balance is required in efficient global optimizations. With respect to the “exploration at unknown regions”, the idea of Bayes is to generate an additional sample point at the maximum standard deviation location on the probabilistic prediction model in the design variables space. The idea of EGOCCS is to generate an additional sample point at the sparsest region in the design variables space. Of course, it is difficult to obtain exact global optimal solutions when only the “exploration at unknown regions” is considered to obtain additional sample points, so that the “utilization of predictions by response surface models” should be considered to explore better solutions. In the minimization problem, the idea of Bayes is to generate an additional sample point at the minimum mean location on the probabilistic prediction model in the design variables space. The idea of EGOCCS is similar with that, to generate an additional sample point at the minimum location on the prediction model in the design variables space. However, it is difficult to obtain global optimal solutions by falling into local optimal solutions when only the “utilization of predictions by response surface models” is considered to obtain additional sample points. Therefore, the balance between them is important for the efficient global optimization. This can be achieved by using EI value in the Bayesian optimization, while this can be considered by using following strategy in EGOCCS.

The exploration strategy of GA is modeled into the EGOCCS algorithm as “exploration at unknown region” and “utilization of predictions by response surface models”. In the optimization process of GA, individuals are widely distributed in the design variables space at the initial stage of the optimization, and then the distribution becomes narrower with the advancement of generations and converges to global optimal solutions. In other words, the proper balance between “exploration at unknown regions” and “utilization of predictions by response surface models” can be expressed by modeling the exploring strategy of GA. It is modeled by using the parameter of \({\varepsilon }\) used in DBCM which determines the details of exploration. \({\varepsilon }\) should be set to a large value at the initial stage of the optimization for the “exploration at unknown regions”, and then it decreases with the advancement of optimizations for the exploration around the current optimal solution, in other words for the “utilization of predictions by response surface models”.

In this research, the DBCM is used to classify input datasets into two groups, and then the SVM is used to obtain a separating hyperplane by maximizing a margin between the two groups. It is possible to efficiently determine the location of an additional sample point by minimizing the predicted objective function value on the separating hyperplane. In the EGOCCS, it is necessary to set an appropriate value of \({\varepsilon }\) to carry out an efficient iterative process of optimization. The balance of “exploration at unknown regions” and “utilization of predictions by response surface models”, in other words the balance between global/local search is modeled as follows by changing the parameter \({\varepsilon }\). Examples of the exploration strategy in this research are summarized in Fig. 4, and typical parameters settings of this method are summarized in Table 1. Figure 4a is the general settings of \({\varepsilon }\) among the total number of sub iterations (\(t_{max}\)) whose value is set to 200. The value of \({\varepsilon }\) is represented as follows:

$$\varepsilon = F\left( {mut\left( {r,f\left( {t_{i} } \right)} \right)} \right)$$
(2.2.4.1)

where \(t_{i}\) and \(r\) are respectively the integer number of sub iterations between 1 to \(t_{max}\) and random real number between 0 to 1. The values of \(t_{i}\) and \(r\) change in each sub iteration. In Fig. 4a, \(\bar{\varepsilon }\) indicates the value of \({\varepsilon }\) with \(r = 0.5\). \(f\left( {t_{i} } \right)\) represents a monotonically decreasing function with increasing of the sub iteration as following equation.

$$f\left( {t_{i} } \right) = 1 - \frac{{t_{i} }}{{t_{max} }}$$
(2.2.4.2)
Fig. 4
figure 4

Variable definition of reference distance \(\varepsilon\)

Full size image
Table 1 Parameters settings for exploration strategy of EGOCCS
Full size table

\(mut\left( {r,p} \right)\) is defined as the same formulation with the polynomial mutation of the GA (Deb and Deb 2014), and it models the mutation of the GA as following equation.

$$mut\left( {r,p} \right) = p + \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {2r + \left( {1 - 2r} \right)\left( {1 - p} \right)^{\eta + 1} } \right)^{{\frac{1}{\eta + 1}}} - 1} & {if\; r \le 0.5} \\ \end{array} } \\ {\begin{array}{*{20}c} {1 - \left( {2\left( {1 - r} \right) + \left( {2r - 1} \right)p^{\eta + 1} } \right)^{{\frac{1}{\eta + 1}}} } & {if\; r > 0.5} \\ \end{array} } \\ \end{array} } \right.$$
(2.2.4.3)

The value of \(mut\left( {r,p} \right)\) is given between 0 to 1. The probabilistic distribution of the polynomial mutation can be adjusted by the additional parameter of \(\eta\) in which smaller \(\eta\) leads to lower probability of \(p\), while larger \(\eta\) leads to higher probability of \(p\). In other words, smaller \(\eta\) should be adopted when global search is necessary to focus as well as larger \(\eta\) should be adopted when local search is necessary to focus. In this research, \(\eta\) is set to 100 to aim to obtain exact optimal solutions. The example of the polynomial mutation is summarized in Fig. 5, in which the histogram is calculated from 1000 samples generated at even intervals between 0 and 1. \(F\left( x \right)\) is defined as follows which determines the reference distance \({\varepsilon }\).

$$F\left( x \right) = 10^{{\left( {\log_{10} \varepsilon_{min} + x\left( {\log_{10} \varepsilon_{max} - \log_{10} \varepsilon_{min} } \right)} \right)}}$$
(2.2.4.4)

where \(\varepsilon_{min}\) and \(\varepsilon_{max}\) are respectively the user-specified minimum and maximum values of \(\varepsilon\). In this equation, since the value of \(x\) is mainly decided by the iteration number \(t_{i}\) as seen in Eq. (2.2.4.2) and the value is fluctuated by the effect of \(r\) and \(\eta\) as shown in Fig. 6 and Eq. (2.2.4.3), \(F\left( x \right)\) decreases exponentially with decreasing of \(x\) as well as increasing of the iteration number \(t_{i}\). In the actual optimization process on the EGOCCS algorithm, since it is difficult to set an appropriate number of the optimization iterations beforehand, the total number of iterations is divided into several sets of the sub iterations as shown in Fig. 4b in which the total number of iterations is set to 1000 while the total number of sub iterations is set to 200.

Fig. 5
figure 5

Histogram of polynomial mutation

Full size image
Fig. 6
figure 6

Variation tendency of reference distance \(\varepsilon\)

Full size image

The example of the global optimization by the EGOCCS is summarized in Figs. 7 and 8. Two dimensional Rosenbrock function is used as an analytic function to be minimized. When the relationship between the design variables (x and y coordinates) and output (color) is given at several locations as the white filled points in Figs. 7a-1 and 8a-1, functional values at arbitrary locations on the design variables space can be predicted by any interpolation (response surface) methods as shown in Figs. 7a-1 and 8a-1. In this example, the Gaussian process regression is used to construct the prediction model. Figures 7a-2 and 8a-2 indicate the distance to the separating hyperplane which is created by maximizing a margin between two groups of black filled points and the other (white filled) points in Figs. 7a-2 and 8a-2. An additional sample point is generated at the position where the predicted objective function value is the lowest on the separating hyperplane (red filled point). In the example of Fig. 7, the reference distance \(\varepsilon\) is fixed to 0.2 and the maximum number of iterations \(t_{max}\) is set to 10. In the example of Fig. 8, the reference distance \(\varepsilon\) is decreased monotonically from 0.2 to 0.1 and the maximum number of (sub) iterations \(t_{max}\) is set to 10. It is confirmed that the additional sample points in Fig. 7j-1 are widely distributed on lower objective function regions while the additional sample points in Fig. 8j-1 are widely/effectively distributed on lower objective function regions. In other words, the decreasing of the reference distance \(\varepsilon\) in the optimization process leads to smaller numbers of sample points in the group including the current optimal solution (black points), which results in that additional sample points are efficiently generated around the current optimal solution as a function of local search.

Fig. 7
figure 7

Optimization process of EGOCCS-GPs approach with fixed \({{\varepsilon }}\)

Full size image
Fig. 8
figure 8

Optimization process of EGOCCS-GPs approach with decreasing \({{\varepsilon }}\)

Full size image

2.3 Computational fluid dynamics analysis method

An inhouse Computational Fluid Dynamics (CFD) code using a gridless method is used to evaluate aerodynamic objective functions in present optimization problems. In the gridless method (Ma et al. 2008; Suga and Yamazaki 2015), computational points are distributed in the calculation domain and a spatial differential term of a physical quantity around the computational point is approximated by a least squares method. Therefore, this method is unnecessary to construct the grid connectivity information and can analyze flow fields around complicated shapes. Two-dimensional inviscid compressible Euler equations are solved by the gridless method. The Euler equations express the conservation law of mass, momentum and energy in inviscid and compressible fluids. The two-dimensional Euler equations are expressed as follows.

$$\begin{array}{*{20}c} {\frac{{\partial {\mathbf{W}}}}{{\partial {\text{t}}}} + \frac{{\partial {\mathbf{E}}}}{{\partial {\text{x}}}} + \frac{{\partial {\mathbf{F}}}}{{\partial {\text{y}}}} = 0} \\ {{\mathbf{W}} = \left[ {\begin{array}{*{20}c} \rho \\ {\rho u} \\ {\begin{array}{*{20}c} {\rho v} \\ e \\ \end{array} } \\ \end{array} } \right], {\mathbf{E}} = \left[ {\begin{array}{*{20}c} {\rho u} \\ {\rho u^{2} + p} \\ {\begin{array}{*{20}c} {\rho uv} \\ {u\left( {e + p} \right)} \\ \end{array} } \\ \end{array} } \right],{\mathbf{F}} = \left[ {\begin{array}{*{20}c} {\rho v} \\ {\rho uv} \\ {\begin{array}{*{20}c} {\rho v^{2} + p} \\ {v\left( {e + p} \right)} \\ \end{array} } \\ \end{array} } \right]} \\ {e = \frac{p}{\gamma - 1} + \frac{1}{2}\rho \left( {u^{2} + v^{2} } \right)} \\ \end{array}$$
(2.3.1)

where \({\mathbf{W}}\) represents the vector of conservative variables, and \({\mathbf{E}}\) and \({\mathbf{F}}\) represent flux vectors. \(\rho\), \(u\), \(v\), \(p\), \(e\) respectively represent fluid density, velocity components in X/Y directions, pressure and total energy per unit volume. The specific heat ratio \(\gamma\) of the ideal gas is set to 1.4.

3 Comparison of regression methods

The EGOCCS algorithm has higher compatibility with any kind of surrogate models such as radial basis function interpolation, inverse distance weighting, neural network regression, support vector regression, random forest regression and so on. In this research, Gaussian process regression, radial basis function, and inverse distance weighting are considered. In this section, these methods are concisely introduced and then construction and utilization costs of them are compared.

3.1 Inverse distance weighting (IDW)

Inverse distance weighting (IDW) is a method to predict functional values at unknown points with a weighted average of the information of known sample points (Shepard 1968). The interpolated function is expressed as following equations.

$$f\left( \varvec{x} \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\mathop \sum \nolimits_{i = 1}^{n} w_{i} \left( \varvec{x} \right)y_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} w_{i} \left( \varvec{x} \right)}},} \hfill & {{\text{if}}\; d\left( {\varvec{x},\varvec{x}_{\varvec{i}} } \right) \ne 0 \;{\text{for}}\; \forall \,_{i} } \hfill \\ {y_{i} ,} \hfill & {{\text{if}}\; d\left( {\varvec{x},\varvec{x}_{\varvec{i}} } \right) = 0} \hfill \\ \end{array} } \right.$$
(3.1.1)
$$w_{i} \left( \varvec{x} \right) = \frac{1}{{d\left( {\varvec{x},\varvec{x}_{\varvec{i}} } \right)^{P} }}$$
(3.1.2)

where \(d\) is the distance from the known sample point \(\varvec{x}_{\varvec{i}}\) to the unknown point \(\varvec{x}\) and the power parameter \(P\) is set to 2 in this research. \(n\) and \(y_{i}\) are the total number of known sample points used in the interpolation and the output functional values of the known sample points \(\varvec{x}_{\varvec{i}}\). Since IDW has a feature that there is almost no construction cost of the surrogate model, it is expected that the optimization cost will be dramatically reduced in high dimensional problems by using the IDW as the prediction model of EGOCCS.

3.2 Radial basis function interpolation (RBF)

Radial basis function interpolation is one of the methods to predict functional values at unknown points (Press et al. 2007). The interpolated function can be expressed as following equation by using known output data \(y_{i}\) and input data \(\varvec{x}_{i}\) \(\left\{ {i = 1,2, \ldots ,n} \right\}\).

$$f\left( \varvec{x} \right) = \mathop \sum \limits_{i = 1}^{n} \omega_{i} \phi \left( {\left\| {\varvec{x} - \varvec{x}_{i} } \right\|} \right)$$
(3.2.1)

where the approximating function \(f\left( \varvec{x} \right)\) is represented as the sum of \(n\) radial basis functions, each associated with the center point \(\varvec{x}_{i}\), and weighted by an appropriate coefficient \(\omega_{i}\). \(\phi\) is a kernel function, and there are various kernel functions as follows.

$$r = \left\| {\varvec{x} - \varvec{x}_{i} } \right\|$$
(3.2.2)
$$\begin{aligned} & \phi_{multiquadric} = \sqrt {\left( {\frac{r}{\beta }} \right)^{2} + 1} ,\quad \phi_{inverse\, multiquadric} = \frac{1.0}{{\sqrt {\left( {\frac{r}{\beta }} \right)^{2} + 1} }} \\ & \phi_{gaussian} = e^{{ - \left( {\frac{r}{\beta }} \right)^{2} + 1}} ,\quad \phi_{linear} = r \\ \end{aligned}$$
(3.2.3)

where \(\beta\) is a hyperparameter and it is generally determined by cross-validation approaches. In this research, since the optimization cost reduction is one of the aims of EGOCCS, the linear kernel \(\phi_{linear}\) is used as the kernel function. There is no hyperparameter in the linear kernel. The weights \(\omega_{i}\) can be estimated as follows.

$$\begin{aligned}& {\varvec{y} = {{\Upphi }}\varvec{\omega}} \\& \varvec{y} = \left[ \begin{array}{*{20}c} {y_{1} } & \ldots & {y_{n} }\end{array}\right]^{T} , & {{{\Upphi }} = \left[ {\begin{array}{*{20}c} {\phi_{1,1} } & \cdots & {\phi_{1,n} } \\ \vdots & \ddots & \vdots \\ {\phi_{n,1} } & \cdots & {\phi_{n,n} } \\ \end{array} } \right]} \\ \end{aligned}$$
(3.2.4)
$$\varvec{\omega}= {{\Upphi }}^{ - 1} \varvec{y}$$
(3.2.5)

3.3 Calculation times of various regression methods

In the RBF, the calculation cost for the inverse matrix for n \(\times\) n is also expensive which is proportional to the cube of the number of sample points. However, since the hyperparameters are not included in the linear kernel \(\phi_{linear}\) contrary to the Gaussian process regression and the calculation of the inverse matrix is only once, it can dramatically reduce the construction cost of the surrogate model. For example, comparing with the Gaussian process regression in which the hyperparameters are optimized by GA with 100 population and 100 generation, the construction cost of the RBF becomes \(1/10000\).

The construction cost and utilization cost of the Gaussian process regression, RBF, and IDW are compared using the Rosenbrock analytic function as shown in Fig. 7. The Rosenbrock analytic function is expressed as follows.

$$f\left( \varvec{x} \right) = \mathop \sum \limits_{i = 1}^{{n_{d} - 1}} \left[ {100\left( {x_{i + 1}^{{\prime }} - x_{i}^{{{\prime }2}} } \right)^{2} + \left( {1 - x_{i}^{{\prime }} } \right)^{2} } \right],\quad x_{i}^{{\prime }} = - 2.048 + 4.096x_{i} ,\quad 0 \le x_{i} \le 1$$
(3.3.1)

In Fig. 9, the horizontal axis indicates the number of sample points to construct a surrogate model, and the vertical axis indicates the construction time for the surrogate model and utilization time for 40,000 predictions which corresponds to the execution of GA with 200 populations and 200 generations. All simulations were processed in a Processor Intel(R) Xeon(R) CPU E7-8867 v3 @ 2.50 GHz. The hyperparameters of the Gaussian process regression are optimized by a gradient-based optimization method in which optimization is executed with the scaled conjugate gradients (SCG) method of 500 iterations. The calculation times are investigated at various dimensions (\(n_{d}\)) of 2, 4, 8, 16, 32, 64, 128, and the color lines are averaged values of 10 times trials. It is confirmed that the construction time is increased with larger numbers of sample points and with larger numbers of dimensions in the Gaussian process regression and RBF, and it is also confirmed that the construction cost of RBF is much smaller than the Gaussian process regression whose ratio is about 1/1000. Therefore, the adoption of the RBF interpolation can reduce the construction cost. It is also confirmed that IDW has the lowest construction/prediction costs among the three surrogate model approaches.

Fig. 9
figure 9

Construction and prediction costs of representative surrogate models

Full size image

4 Results and discussion

Two optimization problems are solved to verify the usefulness of the developed method of EGOCCS. First optimization is executed to demonstrate the validity of the EGOCCS in 2, 10, 40, 80, 160-dimensional analytic function problems within a limited number of functional evaluations. Second optimization is executed to examine the effect of the EGOCCS in 2, 10, 40, 80 dimensional aerodynamic shape optimization problems of a biconvex airfoil, and to demonstrate the applicability of the EGOCCS to more realistic optimization problems than Sect. 4.1.

4.1 Optimization of various analytic functions

In order to verify the usefulness of the EGOCCS, optimization problems of various analytic functions are solved by both of the conventional Bayesian optimization and the developed algorithm of EGOCCS. The analytic functions are Sumsquares function (Eq. 4.1.1), Quadric function (Eq. 4.1.2), Schwefel function (Eq. 4.1.3), Ackley function (Eq. 4.1.4), Rosenbrock function (Eq. 4.1.5), and Levy function (Eq. 4.1.6), and the two-dimensional analytical functions are visualized in Fig. 10. The Sumsquares/Quadric functions are concave analytic functions, the Schewefel function is a discontinuous analytic function, the Ackley function is a multi-modal function, and the Rosenbrock/Levy functions are complex functions (Crina and Ajith 2009). The geometric mean of 10 optimization histories are summarized in Figs. 11, 12, 13, 14 and 15. The optimization conditions of the 40, 80 160-dimensional variables space are almost same with that of the 10-dimensional variables space excepting the number of initial sample points (20 → 80, 160, 320).

Fig. 10
figure 10

Analytic functions in two-dimensional design variables space

Full size image
Fig. 11
figure 11

Optimization histories of various function problems in 2-dimensional variable space

Full size image
Fig. 12
figure 12

Optimization histories of various function problems in 10-dimensional variable space

Full size image
Fig. 13
figure 13

Optimization histories of various function problems in 40-dimensional variable space

Full size image
Fig. 14
figure 14

Optimization histories of various function problems in 80-dimensional variable space

Full size image
Fig. 15
figure 15

Optimization histories of various function problems in 160-dimensional variable space

Full size image

Firstly, the optimizations of the analytic functions are solved in the 2-dimensional variables space. Each optimization problem was solved 10 times by the Bayesian approach and EGOCCS with three different strategies of Coarse, Middle, Fine as shown in Table 1. The type of the surrogate model used in EGOCCS is the Gaussian process regression to examine the pure effect of the difference between the algorithms. The number of initial sample points is 8, and then 200 additional sample points are evaluated. In higher dimensional optimization problems, initial surrogate models are necessary to be accurate for efficient optimizations and the number of initial sample points becomes larger. Then, the number of additional sample points is desired to be smaller to reduce the construction cost of surrogate models in the optimization. In many global optimization problems motivated by engineering applications, the number of function evaluations is severely limited by time or cost (Julien et al. 2009). In this research, the number of additional functional evaluations is limited to 200. The setting of major parameters of GA is the mutation rate of 0.1, population size of 100 and number of generations of 50. In the optimization history of Fig. 11, the horizontal axis represents the number of optimization iterations, and the vertical axis represents the objective function to be minimized. The black line is the optimization history of the Bayesian approach, and the red, blue and green lines are respectively the optimization histories of the EGOCCS approach with the strategies of Coarse, Middle and Fine. It is confirmed that EGOCCS-Fine can explore better optimal solutions in the Sumsqares, Quadric, Schwefel, Ackley and Levy functions compared with the EGOCCS-Middle and EGOCCS-Coarse, while the EGOCCS-Fine cannot reach exact optimal solutions in the Rosenbrock function. This result indicates the tradeoff relationship between local/global searches, and the Fine-strategy can reach exact optimal solutions while that is sometimes difficult to reach the vicinity of the global optimal solution. On the other hand, the Coarse-strategy can reach the vicinity of the global optimal solution while that is difficult to reach the exact optimal solutions. It is also confirmed that EGOCCS-Middle can obtain better solutions in all analytic functions compared with the conventional Bayesian optimization, which indicates that the EGOCCS has the ability to explore better solutions in various optimization problems.

Secondly, in the 10-dimensional variables space. According to another report (Ziyu et al. 2013), the 10-dimensiuonal variables space is almost the upper limit of the Bayesian approach to explore exact global optimal solutions. Each optimization problem was solved 10 times by the Bayesian optimization and EGOCCS with three different surrogate models of Gaussian process regression (GPs), radial basis function interpolation (RBF), and inverse distance weighting (IDW). The exploring strategy is set to \(\varepsilon_{min} = 1.0 \times 10^{ - 3} \times \sqrt {n_{d} }\) and \(\varepsilon_{max} = 2.0 \times 10^{ - 1} \times \sqrt {n_{d} }\) as seen in Fig. 4 and Table 1. The number of initial sample points is 20, and then 200 additional sample points are evaluated. The setting of major parameters of GA is the mutation rate of 0.1, population size of 200 and number of generations of 200. In the optimization history of Fig. 12, the black line is the optimization history of the Bayesian approach, and the red, blue and green lines are respectively optimization histories of the EGOCCS with GPs, RBF and IDW. It is confirmed that EGOCCS-GPs can obtain better solutions in all cases compared with the conventional Bayesian optimization, which indicates that the EGOCCS algorithm has ability to explore better solutions in various optimization problems in this strategy and also in 10-dimensional variables space. However, since the EGOCCS-GPs uses the Gaussian process regression for the surrogate model, the optimization cost is not reduced compared with the conventional Bayesian optimization. It is also confirmed that the EGOCCS-RBF can obtain better solutions in the Schwefel, Ackley and Levy functions compared with the Bayesian optimization. The EGOCCS-IDW can obtain the best solution in the Schwefel, Rosenbrock and Levy functions. These results indicate that the EGOCCS algorithm has the ability to obtain better solutions while reducing the construction cost for the surrogate model in several function cases. In the 10-dimensional variables space, it is considered that the EGOCCS-GPs is the most appropriate to obtain global optimal solutions since optimization problems in the 10-dimensional variables space don’t require much cost for the construction and the EGOCCS-GPs has the ability to obtain better solutions in various optimization problems compared with the conventional Bayesian optimization.

Thirdly, in the 40-dimensional variables space. It is considered that the optimization in the 40-dimensional variables space is difficult to obtain the global optimal solutions with the Bayesian approach. It is confirmed from Fig. 13 that the EGOCCS-RBF can obtain better solutions in the Quadric, Schwefel, Ackley, Rosenbrock and Levy functions compared with the Bayesian optimization while it cannot obtain better solution in the Sumsquares function. Since the Sumsquares function is the simplest function and the Gaussian process regression can easily fit the exact functional shape, the Bayesian optimization can explore better solutions compared with the EGOCCS. It is also confirmed that the EGOCCS-IDW can obtain the best solutions in the Quadric and Schwefel, while it falls into local optimal solutions in the other functions. Since IDW is the simplest prediction method only using the neighboring sample points information, the prediction accuracy should be lower than the other response surface models so that the optimization falls into local optimal solutions in the analytic functions. In the 40-dimensional variables space, it is considered that the EGOCCS-RBF is the most appropriate to obtain the global optimal solution robustly since the EGOCCS-RBF can obtain better solutions in the various analytic functions and can dramatically reduce the optimization cost.

Fourthly, in the 80-dimensional variables space. It is considered that to obtain global optimal solutions in the 80-dimensional variables space with the Bayesian optimization is impossible. It is confirmed from Fig. 14 that the EGOCCS-RBF can obtain the best solutions in all analytic functions. Therefore, it is considered that the EGOCCS-RBF is the most appropriate to obtain better solutions in the 80-dimensional variables space.

Fifthly, in the 160-dimensional variables space. It is considered that to obtain global optimal solutions in the 160-dimensional variables space with the Bayesian optimization is impossible. The optimization in the Schwefel function cannot be executed since the function value exceeds the maximum number of considerable digits. It is confirmed from Fig. 15 that the EGOCCS-RBF can obtain the best solutions in all analytic functions. However, it is also confirmed that the update of optimal solutions seldom occurs in the optimization process and then the obtained solutions by the EGOCCS-RBF are not at the vicinities of exact global optimal solutions. Therefore, it is considered that the EGOCCS-RBF should be used in the optimization problems whose number of design variables is less than 160, in which the update of optimal solutions continuously occurs in the optimization process. It can be expected that the EGOCCS-RBF can finally obtain exact optimal solutions by iteratively performing the sub iterations as Fig. 4b.

For more quantitative comparison, gradient-based optimizations were executed from the optimal solutions obtained by the Bayesian/EGOCCS in the cases of the Ackley and Levy functions that are multimodal functions. The conjugate gradient algorithm was used as the gradient-based optimization algorithm (Hestenes and Stiefel 1952). When the final objective function value was less than 10−5, it was considered as reaching the global optimal solution. In Table 2, the numbers of cases reaching the global optimal solution (among 10 trials) were summarized. It was confirmed that most optimal solutions of the EGOCCS-RBF reached the global optimal solutions in 10, 40 and 80 design variables in the Ackley function while that of the Bayesian optimization falls into local optimal solutions. This means that the EGOCCS could reach the vicinities of the global optimal solutions within the limited number of functional evaluations. In other words, the EGOCCS would be utilized as the preprocess for the local search using the gradient-based optimization. It was confirmed that most optimal solutions of the Levy function couldn’t reach the global optimal solutions. It is considered that the Levy function is too complex to reach the vicinities of the global optimal solutions within the limited number of functional evaluations. The optimization costs with various number of design variables are summarized in Fig. 16. The horizontal axis represents the number of dimensions, and the vertical axis represents the computational time required in each optimization algorithm. The computational time is calculated by averaging 60 times optimizations (6 analytic function × 10 times optimizations). It is confirmed that the EGOCCS-GPs has higher computational cost compared with the Bayesian optimization due to additional computational cost for SVM classifier. It is also confirmed that the EGOCCS-RBF and EGOCCS-IDW have lower costs than the Bayesian optimization due to the cost reduction in the construction of surrogate models. It can be confirmed that the developed EGOCCS algorithm can obtain better optimal solutions inexpensively than the conventional Bayesian optimization in the high dimensional design variables space.

Table 2 Number of cases reaching the global optimal solutions
Full size table
Fig. 16
figure 16

Optimization costs with various numbers of dimensions

Full size image

  • Sumsquares function

    $$\begin{aligned} &f\left( \varvec{x} \right) = \mathop \sum \limits_{i = 1}^{{n_{d} }} \left[ {ix_{i}^{{\prime}{2}} } \right] \\ & x_{i}^{\prime} = - 10 + 20x_{i}, \quad {0 \le x_{i} \le 1,} \quad f_{min} = f\left( \varvec{x} \right) = f\left( {0.5,0.5, \ldots 0.5} \right) = 0 \\ \end{aligned}$$
    (4.1.1)

  • Quadric function

    $$\begin{aligned} & f\left( \varvec{x} \right) = \mathop \sum \limits_{i = 1}^{{n_{d} }} \left( {\mathop \sum \limits_{j = 1}^{i} x_{j}^{{\prime }} } \right)^{2} \\ & x_{i}^{{\prime }} = - 10 + 20x_{i} ,\quad 0 \le x_{i} \le 1,\quad f_{min} = f\left( \varvec{x} \right) = f\left( {0.5,0.5, \ldots 0.5} \right) = 0 \\ \end{aligned}$$
    (4.1.2)

  • Schwefel function

    $$\begin{aligned} & f\left( \varvec{x} \right) = \mathop \sum \limits_{i = 1}^{{n_{d} }} \left| {x_{i}^{{\prime }} } \right| + \mathop \prod \limits_{i = 1}^{{n_{d} }} \left| {x_{i}^{{\prime }} } \right| \\ & x_{i}^{{\prime }} = - 10 + 20x_{i} ,\quad 0 \le x_{i} \le 1,\quad f_{min} = f\left( \varvec{x} \right) = f\left( {0.5,0.5, \ldots 0.5} \right) = 0 \\ \end{aligned}$$
    (4.1.3)

  • Ackley function

    $$\begin{aligned} & f\left( \varvec{x} \right) = 20 + e - 20e^{{ - 0.2\sqrt {\frac{1}{{n_{d} }}\mathop \sum \limits_{i = 1}^{{n_{d} }} x_{i}^{{{\prime 2}}} } }} - e^{{\frac{1}{{n_{d} }}\mathop \sum \limits_{i = 1}^{{n_{d} }} \cos \left( {2\pi x_{i}^{{\prime }} } \right)}} \\ & x_{i}^{{\prime }} = - 10 + 20x_{i} ,\quad 0 \le x_{i} \le 1,\quad f_{min} = f\left( \varvec{x} \right) = f\left( {0.5,0.5, \ldots 0.5} \right) = 0 \\ \end{aligned}$$
    (4.1.4)

  • Rosenbrock function

    $$\begin{aligned} & f\left( \varvec{x} \right) = \mathop \sum \limits_{i = 1}^{{n_{d} - 1}} \left[ {100\left( {x_{i + 1}^{{\prime }} - x_{i}^{{{\prime }2}} } \right)^{2} + \left( {1 - x_{i}^{{\prime }} } \right)^{2} } \right] \\ & x_{i}^{{\prime }} = - 2.048 + 4.096x_{i} ,\quad 0 \le x_{i} \le 1 \\ & f_{min} = f\left( \varvec{x} \right) = f\left( {3.048/4.096,3.048/4.096, \ldots 3.048/4.096} \right) = 0 \\ \end{aligned}$$
    (4.1.5)

  • Levy function

    $$\begin{aligned} & f\left( \varvec{x} \right) = \sin^{2} \left( {\pi y_{1} } \right) + \mathop \sum \limits_{i = 1}^{{n_{d} - 1}} \left( {y_{i} - 1} \right)^{2} \left( {1 + 10\sin^{2} \left( {\pi y_{i} + 1} \right)} \right) + \left( {y_{{n_{d} }} - 1} \right)^{2} \left( {1 + \sin^{2} \left( {2\pi x_{{n_{d} }}^{{\prime }} } \right)} \right) \\ & x_{i}^{{\prime }} = - 10 + 20x_{i} ,\quad y_{i} = 1 + \frac{{x_{{n_{d} }}^{{\prime }} - 1}}{4},\quad 0 \le x_{i} \le 1,\quad f_{min} = f\left( \varvec{x} \right) = f\left( {\frac{11}{20},\frac{11}{20}, \ldots \frac{11}{20}} \right) = 0 \\ \end{aligned}$$
    (4.1.6)

4.2 High dimensional aerodynamic shape optimization problem of biconvex airfoil

Since the performance of the EGOCCS has been validated in 4.1 with the various analytic function problems by comparing with the conventional Bayesian approach, high dimensional aerodynamic shape optimization problems in two-dimensional supersonic flow field are solved in this section to demonstrate the applicability of the EGOCCS to more realistic optimization problems. The baseline airfoil is set to a biconvex airfoil (Fig. 17a, c, black line). New airfoil shapes are given as symmetrical airfoils, and the shape of the one side surface is modified by 2, 10, 40, 80 Hicks-Henne bump functions arranged in even intervals (Fig. 17b). A Hicks-Henne bump function is expressed as following equation.

$$\begin{aligned} & h_{i} \left( x \right) = h_{max} \left( {x_{bump,i} } \right) \times \sin^{3} \left( {\pi \left( {1 - x} \right)^{{\frac{{\log \left( {x_{bump,i} } \right)}}{{\log \left( {0.5} \right)}}}} } \right) \\ & h_{max} \left( {x_{bump,i} } \right) = 0.1 \times tc\left( {x_{bump,i} } \right) \times dv_{i} \\ \end{aligned}$$
(4.2.1)

where \(x_{bump}\) and \(tc\) are the bump apex position and the thickness of the biconvex airfoil at \(x_{bump}\). \(h_{max}\) indicates the maximum height of the bump, and it can be adjusted by the design variable \(dv_{i}\). The displacement of a new airfoil at a location x is expressed by a summation of 2, 10, 40, 80 bump functions as following equation.

$$\Delta y\left( x \right) = \mathop \sum \limits_{i = 1}^{{n_{d} }} h_{i} \left( x \right),\quad 0 < x < 1,\quad 0 < dv_{i} < 1$$
(4.2.2)

A new airfoil is created by adding the displacement (Fig. 17c, blue line) on the baseline biconvex airfoil (Fig. 17c, red line), and then the y-coordinate of the new airfoil is rescaled to keep a constant airfoil area (Fig. 17c, green line). The negative thickness of airfoil never occurs with this definition of design variables. In this problem, the drag coefficient of airfoil is minimized. The aerodynamic performance is evaluated at the freestream Mach number of 1.7 and angle of attack of 0 degree by using inviscid CFD computations. This optimization problem is solved three times with different sets of initial sample points at all conditions of the number of design variables. The numbers of initial sample points are set to 8 at \(n_{d} = 2\) and 200 at the other cases. New sample points are iteratively added 200 times within a set of sub iterations. Table 3 shows the objective function values of the obtained optimal solutions, and Fig. 18 shows the average of the three times optimization histories. The dotted lines indicate the results using the GA directly to the 10, 40 and 80 design variables problems, that were also executed for comparison purposes. The setting of major parameters of GA is the mutation rate of 0.1, population size of 200 and 3, 5 and 7 generations that correspond to the same numbers of functional evaluations with the EGOCCS cases. It is confirmed that the EGOCCS algorithm can obtain lower drag coefficient values than the GA in all cases. This result can emphasize the superiority of the developed EGOCCS algorithm over the conventional approach. Since the three optimizations by EGOCCS with different sets of initial sample points give almost same objective function values in all numbers of design variables, it could be confirmed that the developed EGOCCS algorithm worked robustly even in 80 dimensional design variables space. Figures 19 and 20 show the shapes and pressure visualizations around optimal designs obtained by the EGOCCS algorithm. With respect to the optimal designs, it was demonstrated that the theoretical optimal shape with minimum pressure drag has a blunt trailing edge (Chapman 1951; Klunker and Harder 1952). In addition, an optimal profile is shown in Payot et al. (2017) at the freestream Mach number of 2.0 (1.7 in this research) and angle of attack of 0 degree, and the optimal profile also has the blunt trailing edge. Therefore, it is considered that the obtained optimal designs have thicker trailing edge shapes to express the blunt trailing edge within the given degree of freedom. Larger numbers of design variables enable to express the airfoil shape in more detail, and then the optimal airfoil should have better performance than that obtained with smaller numbers of design variables. It is confirmed from Figs. 18, 19 and 20 that the optimal designs with larger numbers of design variables have thinner leading edge and thicker trailing edge, and the static pressure around the leading edge becomes lower, and then the objective function value becomes lower. Since better solutions were obtained with larger numbers of design variables (with more degree of freedom) monotonically, it was confirmed that the EGOCCS algorithm could be appropriately used in the present high-dimensional aerodynamic shape optimization problems without to be caught in local optimal solutions.

Fig. 17
figure 17

Example of shape modification

Full size image
Table 3 Objective function values of optimal solutions at every 200 iteration
Full size table
Fig. 18
figure 18

Optimization histories in various numbers of design variables

Full size image
Fig. 19
figure 19

Shapes of optimal solutions obtained by EGOCCS

Full size image
Fig. 20
figure 20

Pressure visualizations around optimal solutions obtained by EGOCCS

Full size image

5 Concluding remarks

In this research, an efficient global optimization method via clustering/classification methods and exploration strategy (EGOCCS) has been developed to efficiently solve high-dimensional optimization problems. The conventional Bayesian optimization method takes a huge calculation cost to construct a response surface model, and the accuracy of that decreases at high-dimensional cases. To tackle these issues, a novel efficient global optimization method without using probabilistic values as standard deviation obtained in the Gaussian process was proposed and aimed to reduce the construction cost of the response surface model and to efficiently obtain global optimal solutions in high-dimensional optimization problems. The developed algorithm has achieved better performance than conventional approaches by using the machine learning methods of a density-based clustering method and a support vector machine classification method.

Two optimization problems were solved to verify the usefulness of the developed method of EGOCCS. First optimization was executed to demonstrate the validity of the EGOCCS in 2, 10, 40, 80, 160-dimensional analytic function problems that were solved by both of the Bayesian optimization and the EGOCCS. In the 2-dimensional analytic functions, the EGOCCS could obtain better solutions in all analytic functions compared with the conventional Bayesian approach by adopting an appropriate exploration strategy. In the 10-dimensional analytic functions, the EGOCCS on the Gaussian process regression had the ability to obtain better solutions in many problems compared with the conventional Bayesian optimization. In the 40, 80 and 160-dimensional analytic functions, the EGOCCS with the radial basis function interpolation was the most appropriate to obtain better optimal solutions. In addition, it was also confirmed that the EGOCCS with the radial basis function interpolation and inverse distance weighting could execute with much lower computational costs than the Bayesian optimization. Second optimization was executed to examine the effect of the EGOCCS in 2, 10, 40, 80-dimensional aerodynamic shape optimization problems of a biconvex airfoil. The biconvex airfoil was deformed by 2, 10, 40, 80 Hicks-Henne bump functions, to minimize its drag coefficient at the freestream Mach number of 1.7 and angle of attack of 0 degree. Larger numbers of design variables could express optimal airfoil shapes in more detail, and then the optimal airfoils had better objective function values compared with that with smaller numbers of design variables. Since better solutions were obtained with larger numbers of design variables (with more degree of freedom) monotonically, it was confirmed that the EGOCCS algorithm could be appropriately used in the present high-dimensional aerodynamic shape optimization problems without to be caught in local optimal solutions.

The proposed EGOCCS algorithm brings higher compatibility with other response surface models such as neural network regression, support vector regression, random forest regression and so on. For example, the neural network can be used when a very large number of design variables has to be taken into consideration. The compatibility with the other response surface models will be examined as future work. In addition, since the EGOCCS has been developed as noninvasive approaches, it can be applied to optimization problems of other disciplines. It is necessary to efficiently solve three challenging optimization problems that are discontinuous optimization problem, optimization problem with infeasible regions and high dimensional optimization problem, to realize efficient global topology optimizations in supersonic flow conditions. By using the developed EGODISC (Ban and Yamazaki 2019) and EGOCCS algorithms, an efficient global optimization method for the three challenging optimization problems can be constructed. Therefore, the topology optimization in supersonic flow conditions will be carried out as our future works.