Structural optimization oriented time-dependent reliability methodology under static and dynamic uncertainties

Abstract

Uncertainty with characteristics of time-dependency, multi-sources and small-samples extensively exists in the whole process of structural design. Associated with frequent occurrences of material aging, load varying, damage accumulating, traditional reliability-based design optimization (RBDO) approaches by combination of the static assumption and the probability theory will be no longer applicable when dealing with the design problems for lifecycle structural models. In view of this, a new non-probabilistic time-dependent RBDO method under the mixture of time-invariant and time-variant uncertainties is investigated in this paper. Enlightened by the first-passage concept, the hybrid reliability index is firstly defined, and its solution implementation relies on the technologies of regulation and the interval mathematics. In order to guarantee the stability and efficiency of the optimization procedure, the improved ant colony algorithm (ACA) is then introduced. Moreover, by comparisons of the models of the safety factor-based design as well as the instantaneous RBDO design, the physical means of the proposed optimization policy are further discussed. Two numerical examples are eventually presented to demonstrate the validity and reasonability of the developed methodology.

1 Introduction

Owing to the multi-source uncertainties in engineering problems, such as the material dispersion, the load deviation, the measurement error, the criterion fuzziness and so forth, quantifying and controlling their effects on the structural responses is of great importance to ensure the product quality (Frangopol et al. 1997; Wang et al. 2014a; Liu et al. 2017). Structural optimization with reliability constraints or optimal reliability-oriented structural design has been subject of research, and large amounts of academic achievements have been published in the past decades (for example, see (Frangopol et al. 1997; Ditlevsen and Madsen 1996; Kharmanda et al. 2004; Nikolaidis and Burdisso 1988; Aoues and Chateauneuf 2010) for typical approaches). Nevertheless, most of the current RBDO methods have the following two main shortages: (1) general treatments in reliability analysis assume probability distributions of all the uncertain parameters, but regardless of that the variation bounds can be only determined in many practical applications with limited information; (2) for dynamic issues, existing optimization ideas are commonly based on the quasi-static hypothesis, which, while may lead to uncontrolled errors when conducting the reliability assessment. How to overcome such deficiencies and whereby improve the confidence of the RBDO results has stood in the spotlight of research fields by academic and engineering society recently.

With regard to the first shortage, several attempts have been made to apply non-probabilistic models for RBDO via limited uncertainty samples. In the 1990s, Ben-Haim (Ben-Haim 1994) first proposed the concept of structural reliability based on the convexity theory and then applied it into the optimal solution. Almost simultaneously, Elishakoff (Elishakoff et al. 1994) gave the definition of a non-probabilistic safety measure deduced from interval analysis, and further carried out the optimization by fusing the non-probabilistic reliability index. Qiu et al. (Qiu and Elishakoff 2001; Qiu et al. 2013) established the interval RBDO model derived from the volume-ratio idea, and take the lead in application of aerospace structures. Kan et al. (Kang and Luo 2009; Kang et al. 2011) investigated the solution strategy of RBDO for structures exhibiting grouped uncertain-but-bounded variations, and also conducted a convex reliability-based topology optimization (RBTO) method for the design of continuum structures undergoing large deformations. Jiang et al. (Jiang et al. 2010; Jiang et al. 2011) developed the non-probabilistic RBDO methods for dealing with the complicated engineering problems of the nonlinearity, multi-dimensions, and nestification. Besides, some exploratory works had been also carried out in aspects of the studies on hybrid RBDO (Du et al. 2005; Luo et al. 2011; Ge et al. 2008) as well as the compatibility with safety factor based design (Wang et al. 2016a; Li et al. 2016; Yi et al. 2016; Yang and Lu 2017) in recent several years.

Considering that the effects of samples-dependent and time-varying cannot be ignored in engineering, a large number of researches have been carried out. Since the definition of time-dependent reliability was explained by Kameda in 1975, a new attempt has been made by Kuschel (Kuschel 2000; Kuschel and Rackwitz 2000), where the structural reliability was determined by the first passage theory and applied to structural reliability optimization. In order to determine the optimal design and preventive maintenance, one methodology based on time-dependent reliability was proposed by Singh (Hu and Du 2014) for multi-response systems. Youn et al. (Yoon et al. 2013) advanced a time-dependent resilient-driven system design (RDSD) framework and the method was accounted for with a wind turbine system design problem. Wang (Wang and Wang 2012) presented an efficient nested extreme response surface (NERS) approach to carry out time-dependent reliability analysis. Du et al. (Hu 2014; Zhang et al. 2011; Hu and Du 2015) applied the method of time-dependent reliability to the mechanical optimization design and created the design model of time-dependent reliability. Subsequently, he presented the sequential optimization and reliability analysis (SORA) method to largely improve the computational efficiency. Wang et al. (Wang et al. 2013) gave a time-dependent RBDO method considering both the time-dependent kinematic reliability and the time-dependent structural reliability as constrains. Furthermore, several researches about the time-dependent RBDO (Singh et al. 2010; Spence and Gioffrè 2011; Wang et al. 2011a) as well as the instantaneous design (Chun et al. 2015; Xu et al. 2016; Kayedpour et al. 2016; Babykina et al. 2016) were also conducted.

As stated above, although the current methods of RBDO have achieved many excellent developments, most of these work were only concentrated on non-probabilistic reliability designs based on static simplification (Wang et al. 2015; Wang et al. 2016b) or time-dependent reliability designs based on random theory (Wang et al. 2016a; Wang et al. 2016c). For example, Wei (Wei and Li 2011) put forward the computational method with non-probabilistic time-dependent reliability index based on residual strength degradation interval model. Jiang et al. (Zhang et al. 2015; Jiang et al. 2014) combined the PHI2 and first-passage probability to solve the time-varying issue with interval distributed parameters, where the non-probabilistic convex process model was explained to tackle the problems of time-varying safety assessment. Sickert (Sickert et al. 2005) presented a new safety concept considering time-dependent data uncertainty of fuzzy random types and the fuzzy Monte Carlo simulation (FMCS) method was applied in the process of the fuzzy failure probability optimization. However, the essence of these researches was still based on probabilistic solving ideas.

It should be also noted that the cross-coupling effects of multi-source uncertainties are always existent extensively in practical engineering applications. Besides, probability distributions of uncertainties are difficult or limited to be known and time-varying effects are significant, which should be considered. As a result, mixture problems of non-probabilistic static and dynamic uncertainties analysis are worth developing.

This paper aims at developing an efficient optimization framework with a hybrid time-dependent reliability measurement. Firstly, with the help of the interval mathematics and the interval process model, the static and dynamic uncertainty parameters are quantified. Enlightened by the first-passage approach in random process theory, the hybrid time-dependent reliability index for structures with multi-source uncertainties is then established. In order to acquire better properties of accuracy as well as efficiency in convergence, the improved ant colony algorithm (ACA) is also involved for the presented optimization issues. Moreover, for comparison’s purpose, the classical RBDO policies based on the time-invariant reliability as well as the safety factor are discussed from the theoretical aspects. Two engineering examples eventually demonstrate the usage and the rationality of the method in this study.

The remainder of this paper is organized as follows. After this introduction, the hybrid time-dependent reliability analysis is firstly reviewed in Section 2. Section 3 then discusses the optimization details integrating the reliability constraint and the solution algorithm. Furthermore, Section 4 compares the applicability between the present hybrid RBDO and other two main optimization models. Some numerical examples are given in Section 5, followed by some conclusions in section 6.

2 The time-dependent reliability assessment under mixture of interval variables and processes

In this section, the time-dependent reliability analysis with consideration of non-probabilistic static and dynamic uncertainties is presented. The general concepts of the first-passage theory are firstly reviewed, and the mathematical expressions of the out-crossing possibility as well as the hybrid reliability measurement are then discussed. According to the definitions of the uncertainty characteristics for the limit state, the interval process interference model is further established. At the end of this section, how to perform the solving process of the defined time-dependent reliability index is specifically expanded.

2.1 Overview of the classical first-passage approach when tracking with the time-varying uncertainty issues

For static reliability analysis, the failure probability and reliability can be defined as

$$ {P}_f=\Pr \left\{G\left(\mathbf{X},\mathbf{d}\right)\le 0\right\}=\int \dots \underset{G\left(\mathbf{X},\mathbf{d}\right)\le 0}{\int }{f}_X\left(\mathbf{X}\right)d\mathbf{X}\kern0.50em \mathrm{and}\kern0.5em {R}_s=1-{P}_f $$

(1)

where X represents n ₁-dimensional random input variables with a joint probability density function (PDF) f _X (X), the vector d stands for design parameters, G(X, d) is the limit state.

Once time-variant characteristics are taken into account, let us denote by Y(t) the set of the random processes {Y _j (t), j = 1, 2, …, n ₂}^T describing the time-varying uncertainty in mechanical applications under consideration, and the limit-state function is then rewritten as G(t, X, Y(t), d). Thus, the time-dependent reliability R _s (t _l ) may provide the probability that a product works properly after it has been in operation for a specific period of time interval [0, t _l ], namely,

$$ {R}_s\left({t}_l\right)=1-{P}_f\left({t}_l\right)=\Pr \left\{\forall t\in \left[0,{t}_l\right],G\left(t,\mathbf{X},\mathbf{Y}(t),\mathbf{d}\right)>0\right\} $$

(2)

where P _f (t _l ) means the probability of failure during the integral lifecycle.

Generally, the solution for (2) is extremely difficult as it requires quite complicated operation of the multidimensional integration of random variables and processes over time. It typically defines that the failure judgement relies on the appearance of any crossing of the response processes out of the safety domain G(t, X, Y(t), d) > 0 at each instant time t. Hence, (2) also reads

$$ {\displaystyle \begin{array}{l}{P}_f\left({t}_l\right)=\Pr \left\{\left(G\left(0,\mathbf{X},\mathbf{Y}(0),\mathbf{d}\right)\le 0\right)\cup \left(N\left(0,{t}_l\right)>0\right)\right\}\\ {}\approx {P}_f(0)+E\left[N\left(0,{t}_l\right)\right]\approx {P}_f(0)+{\int}_0^{t_l}\nu (t) dt\end{array}} $$

(3)

where P _f (0) represents the instantaneous probability of failure when t = 0, E[N(0, t _l )] denotes the mean number of the crossings, the our-crossing rate ν(t), as the critical point for solving (3), is further defined by

$$ \nu (t)=\underset{\varDelta t\to 0}{\lim}\frac{\Pr \left\{A\cap B\right\}}{\varDelta t}\Rightarrow \left\{\begin{array}{l} Event\ A:G\left(t,\mathbf{X},\mathbf{Y}(t),\mathbf{d}\right)>0\\ {} Event\ B:G\left(t+\varDelta t,\mathbf{X},\mathbf{Y}\left(t+\varDelta t\right),\mathbf{d}\right)\le 0\end{array}\right. $$

(4)

where Δt means the time increment. Introducing the finite-difference method and the repartition of the binormal law Φ ₂, the our-crossing rate follows

$$ \nu (t)\approx \frac{\varPhi_2\left(\beta (t),-\beta \left(t+\varDelta t\right),\rho \Big(t,t+\varDelta t\Big)\right)}{\varDelta t} $$

(5)

where β(t) and β(t + Δt) are respectively the reliability index of fixed time t and t + Δt, ρ(t, t + Δt) is the correlation coefficient between the two events A and B. The time increment Δt has to be selected properly (under the sufficiently small level).

It should be pointed out that the single-upcrossing rate method as previously noted may result in large error (assuming that the events that the response upcrosses the failure threshold are completely independent from each other) in reliability analysis due to the Poisson assumption when the failure threshold is low (Rice 1944; Madsen and Krenk 1984). Under this case, the joint-upcrossing rate method, which aims to release the Poisson assumption by considering the correlations between the limit-state function at two time instants, has been explored by Ref. (Song and Kiureghian 2006; Hu et al. 2013; Hu and Du 2013).

2.2 Out-crossing failure mechanism in application to non-probabilistic reliability analysis

Under the limitation of insufficient samples of time-invariant and time-variant uncertainties, the classical probability theory is infeasible. Assume that X ∈ X ^I is the vector containing n ₁ independent interval variables, and $\mathbf{Y}(t)\in {\mathbf{Y}}^{\mathbf{I}}(t)={\left\{{Y}_j^I(t),j=1,2,\dots, {n}_2\right\}}^T$ means the interval process vector with auto-correlation ρ _Y (t ₁, t ₂) = {ρ _j (t ₁, t ₂), j = 1, 2, …, n ₂}^T as well as cross-correlation ${\boldsymbol{\uprho}}_{{\mathbf{Y}}_{\mathbf{j1}}{\mathbf{Y}}_{\mathbf{j2}}}\left({t}_1,{t}_2\right)={\left\{{\rho}_{j_1{j}_2}\left({t}_1,{t}_2\right),{j}_1,{j}_2=1,2,\dots, {n}_2\wedge {j}_1\ne {j}_2\right\}}^T$. Herein, it stresses that all characteristic parameters for quantification of static and dynamic uncertainties, particularly the autocorrelation information of an interval process Y _j (t) should be determined by real test curves. Appendix A introduces an optimization strategy based on the smallest parametric set to tackle this correlation issue.

Hence, the hybrid time-dependent reliability can be respectively expressed as

$$ {\displaystyle \begin{array}{l}{R}_s^{hybrid}\left({t}_l\right)=1-{P}_f^{hybrid}\left({t}_l\right)\\ {}=1- Pos\left\{\exists t\in \left[0,{t}_l\right],G\left(t,\mathbf{X},\mathbf{Y}(t),\mathbf{d}\right)\le 0\right\}\\ {}=1- Pos\left\{\left(G\left(0,\mathbf{X},\mathbf{Y}(0),\mathbf{d}\right)\le 0\right)\cup \left(N\left(0,{t}_l\right)>0\right)\right\}\\ {}\approx 1- Pos(0)-\sum \limits_{k=1}^{k\varDelta t={t}_l} Pos\left\{{A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right\}\\ {}\approx 1- Pos(0)-\sum \limits_{k=1}^{k\varDelta t={t}_l} Pos\left\{G\left( k\varDelta t,\mathbf{X},\mathbf{Y}\left( k\varDelta t\right),\mathbf{d}\right)>0\cap G\left(\left(k+1\right)\varDelta t,\mathbf{X},\mathbf{Y}\left(\left(k+1\right)\varDelta t\right),\mathbf{d}\right)\le 0\right\}\end{array}} $$

(6)

where ${P}_f^{hybrid}\left({t}_l\right)$ denotes the failure possibility with mixed uncertainties, Pos(⋅) stands for the possibility of an event. Apparently, the key of the solution for (6) is to calculate $Pos\left\{{A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right\}$, which depends on the properties of the process G(t, X, Y(t), d). For ease of understanding, several characteristic quantities are defined in advance. The following linear case is taken into account that

$$ G\left(t,\mathbf{X},\mathbf{Y}(t),\mathbf{d}\right)=f\left(t,\mathbf{d}\right)+\mathbf{a}\left(\mathbf{d}\right)\mathbf{X}+\mathbf{b}\left(t,\mathbf{d}\right)\mathbf{Y}(t) $$

(7)

where f(t, d) is a deterministic function, a(d) = {a _i (d), i = 1, 2, …, n ₁} and b(t, d) = {b _j (t, d), j = 1, 2, …, n ₂} are respectively coefficient vectors. Thus, the mean value function as well as the radius function can be obtained by

$$ {\displaystyle \begin{array}{l}{G}^c\left(t,\mathbf{X},\mathbf{Y}(t),\mathbf{d}\right)=f\left(t,\mathbf{d}\right)+\mathbf{a}\left(\mathbf{d}\right)\cdot {\mathbf{X}}^{\mathbf{c}}+\mathbf{b}\left(t,\mathbf{d}\right)\cdot {\mathbf{Y}}^{\mathbf{c}}(t)\\ {}=f\left(t,\mathbf{d}\right)+\sum \limits_{i=1}^{n_1}{a}_i\left(\mathbf{d}\right)\cdot {X}_i^c+\sum \limits_{j=1}^{n_2}{b}_j\left(t,\mathbf{d}\right)\cdot {Y}_j^c(t)\end{array}} $$

(8)

and

$$ {\displaystyle \begin{array}{l}{G}^r\left(t,\mathbf{X},\mathbf{Y}(t),\mathbf{d}\right)\\ {}=\left|\mathbf{a}\left(\mathbf{d}\right)\right|\cdot {\mathbf{X}}^{\mathbf{r}}+\sqrt{\mathbf{b}{\left(t,\mathbf{d}\right)}^2\cdot {\left({\mathbf{Y}}^{\mathbf{r}}(t)\right)}^2+\sum \limits_{j_1=1}^{n_2}\sum \limits_{\begin{array}{c}\hfill {j}_2=1\hfill \\ {}\hfill {j}_1\ne {j}_2\hfill \end{array}}^{n_2}{\rho}_{j_1{j}_2}\left(t,t\right)\cdot {b}_{j_1}\left(t,\mathbf{d}\right)\cdot {b}_{j_2}\left(t,\mathbf{d}\right)\cdot {Y}_{j_1}^r(t)\cdot {Y}_{j_2}^r(t)}\end{array}} $$

(9)

where X ^c, Y ^c(t), X ^r, and Y ^r(t) respectively denote the mean value and the radius vectors of X and Y(t).

As shown previously, the uncertainty properties of the limit state can be embodied by (8) and (9) if the instant time t is fixed. For any two different times t ₁ and t ₂, however, the correlativity between G(t ₁) and G(t ₂) should be further deduced by

$$ {\displaystyle \begin{array}{l}{Cov}_G\left({t}_1,{t}_2\right)=\sum \limits_{i=1}^{n_1}{a}_i{\left(\mathbf{d}\right)}^2\cdot {\left({X}_i^r\right)}^2+\sum \limits_{j=1}^{n_2}{\rho}_j\left({t}_1,{t}_2\right)\cdot {b}_j\left({t}_1,\mathbf{d}\right)\cdot {b}_j\left({t}_2,\mathbf{d}\right)\cdot {Y}_j^r\left({t}_1\right)\cdot {Y}_j^r\left({t}_2\right)\\ {}+\sum \limits_{j_1=1}^{n_2}\sum \limits_{\begin{array}{c}\hfill {j}_2=1\hfill \\ {}\hfill {j}_1\ne {j}_2\hfill \end{array}}^{n_2}{\rho}_{j_1{j}_2}\left({t}_1,{t}_2\right)\cdot {b}_{j_1}\left({t}_1,\mathbf{d}\right)\cdot {b}_{j_2}\left({t}_2,\mathbf{d}\right)\cdot {Y}_{j_1}^r\left({t}_1\right)\cdot {Y}_{j_2}^r\left({t}_2\right)\end{array}} $$

(10)

where Cov _G (t ₁, t ₂) is called as the covariance function. Then, we also define the correlation coefficient function as ${\rho}_G\left({t}_1,{t}_2\right)=\frac{Cov_G\left({t}_1,{t}_2\right)}{G^r\left({t}_1,\mathbf{X},\mathbf{Y}\left({t}_1\right),\mathbf{d}\right){G}^r\left({t}_2,\mathbf{X},\mathbf{Y}\left({t}_2\right),\mathbf{d}\right)}$.

As noted, the characteristics of the limit state with both static and dynamic uncertainties are determined directly. Once the complete cognition for G(t, X, Y(t), d) is realized, the possibility of the out-crossing event can be solved with the help of the interval process interference theory as well as the volume ratio conception. For details, see the next section.

2.3 Solution strategy for the hybrid time-dependent reliability measurement

In order to analytically solve $Pos\left\{{A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right\}$, the feasible region between the limit states of G(kΔt, X, Y(kΔt), d) and G((k + 1)Δt, X, Y((k + 1)Δt), d) must be described geometrically. By normalization treatment, namely,

$$ {\displaystyle \begin{array}{l}G\left( k\varDelta t,\mathbf{X},\mathbf{Y}\left( k\varDelta t\right),\mathbf{d}\right)={G}^c\left( k\varDelta t,\mathbf{X},\mathbf{Y}\left( k\varDelta t\right),\mathbf{d}\right)+{G}^r\left( k\varDelta t,\mathbf{X},\mathbf{Y}\left( k\varDelta t\right),\mathbf{d}\right){\xi}_1\\ {}G\left(\left(k+1\right)\varDelta t,\mathbf{X},\mathbf{Y}\left(\left(k+1\right)\varDelta t\right),\mathbf{d}\right)\\ {}={G}^c\left(\left(k+1\right)\varDelta t,\mathbf{X},\mathbf{Y}\left(\left(k+1\right)\varDelta t\right),\mathbf{d}\right)+{G}^r\left(\left(k+1\right)\varDelta t,\mathbf{X},\mathbf{Y}\left(\left(k+1\right)\varDelta t\right),\mathbf{d}\right){\xi}_2\end{array}} $$

(11)

a rotary rectangular domain (as illustrated in Figs. 1 and 2) is formed corresponding to specific value of ρ _G (t, t + Δt), in which ones obtain

$$ {L}_1=\sqrt{2}\left(1-{\rho}_G\left(t,t+\varDelta t\right)\right)\kern0.5em \mathrm{and}\kern0.5em {L}_2=2\sqrt{2}-{L}_1=\sqrt{2}\left(1+{\rho}_G\left(t,t+\varDelta t\right)\right) $$

(12)

where L ₁ and L ₂ are respectively the length of the two sides (L ₁ ≤ L ₂). Combined with the operations of the coordinate transformation, the geometrical limitations subjected to the events A and B are redefined as

$$ {\displaystyle \begin{array}{l}G\left( k\varDelta t,\mathbf{X},\mathbf{Y}\left( k\varDelta t\right),\mathbf{d}\right)>0\Rightarrow {\xi}_1>-\frac{G^c\left( k\varDelta t,\mathbf{X},\mathbf{Y}\left( k\varDelta t\right),\mathbf{d}\right)}{G^r\left( k\varDelta t,\mathbf{X},\mathbf{Y}\left( k\varDelta t\right),\mathbf{d}\right)}\\ {}G\left(\left(k+1\right)\varDelta t,\mathbf{X},\mathbf{Y}\left(\left(k+1\right)\varDelta t\right),\mathbf{d}\right)\le 0\Rightarrow {\xi}_2\le -\frac{G^c\left(\left(k+1\right)\varDelta t,\mathbf{X},\mathbf{Y}\left(\left(k+1\right)\varDelta t\right),\mathbf{d}\right)}{G^r\left(\left(k+1\right)\varDelta t,\mathbf{X},\mathbf{Y}\left(\left(k+1\right)\varDelta t\right),\mathbf{d}\right)}\end{array}} $$

(13)

Fig. 1

The optimization-based strategy for determination of the smallest rotary rectangle

Fig. 2

Effect of the auto-covariance function on determination of the rectangular domain between Ψ ₁ and Ψ ₂

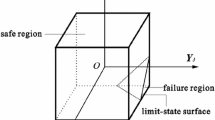
In this way, the interval process interference model for judging out-crossing failure mechanism within the small time range [kΔt, (k + 1)Δt] can be constructed and be further illustrated in Fig. 3, in which the interference region with a shaded sign reflects the range of the passage occurrence, and the rotary rectangle represents the feasible domain for quantifying the uncertainties of G. Enlightened by the volume ration idea in non-probabilistic time-independent reliability theory, the possibility $Pos\left\{{A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right\}$ can be reformed by

$$ {\displaystyle \begin{array}{l} Pos\left\{{A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right\}= Pos\left\{G\left( k\varDelta t,\mathbf{X},\mathbf{Y}\left( k\varDelta t\right),\mathbf{d}\right)>0\cap G\left(\left(k+1\right)\varDelta t,\mathbf{X},\mathbf{Y}\left(\left(k+1\right)\varDelta t\right),\mathbf{d}\right)\le 0\right\}\\ {}=\frac{A_{interference\left({A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right)}}{A_{total}}=\frac{A_{interference\left({A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right)}}{L_1{L}_2}=\frac{A_{interference\left({A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right)}}{2\left(1-{\rho}_G\Big( i\varDelta t,\left(i+1\right)\varDelta t\Big){}^2\right)}\end{array}} $$

(14)

where ${A}_{interference\left({A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right)}$ and A _total are respectively the areas of the shaded region and the total region. Substitution of (14) into (6) yields

$$ {R}_s^{hybrid}\left({t}_l\right)=1-{P}_f^{hybrid}\left({t}_l\right)\approx 1- Pos(0)-\sum_{k=1}^{k\varDelta t={t}_l}\frac{A_{interference\left({A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right)}}{A_{total}} $$

(15)

Fig. 3

Variant cases of the correlation coefficient function ρ _G (t, t + Δt) with respect to different geometric feasible regions

It is obvious that with changing values of k, the uncertainty properties of G(kΔt) and G((k + 1)Δt) will be different as well, so that various cases of the interference conditions between the feasible region of limit states and the geometric bounds for describing out-crossing event will be confronted. That is to say, the areas ${A}_{interference\left({A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right)}$ and A _total are the functions of counting index k, particularly that the former one is a piecewise function in essence. Therefore, according to (15), we should traverse each small time interval [kΔt, (k + 1)Δt] from the whole life cycle t _l , and an overlaying operation for all discrete cases of $Pos\left\{{A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right\}$ must to be conducted to ultimately achieve the explicit calculation for the hybrid reliability measurement ${R}_s^{hybrid}\left({t}_l\right)$. The above contents can be more clearly embodied in Fig. 4.

Fig. 4

Procedure for the hybrid time-dependent reliability analysis

2.4 Discussions on the relationship between possibility and probability

• (a). Concept interpretation: As is known to all, the model of “probability”, which originates from the statistics and large number theorem, is generally used to describe the randomness of an independent and repeatable event. In terms of the reliability analysis, probability solutions in (1)–(5) must resort to probability distribution functions (PDFs) or higher moment information to estimate structural safety/failure levels. By contrast, the concept of “possibility”, which derives from the interval mathematics and convex model theory, will always be suitable for representation of the confidence degree of an event occurrence under unknown-but-bounded (UBB) uncertainties. As per the time-dependent reliability evaluation cited in (6) and (15), the bounds rules and the autocorrelation information of interval processes are needed, and the equal possibility hypothesis should be employed. Table 1 compares and analyzes their relationship in details.

• (b). Difference analysis in reliability assessment: As mentioned above, the measures of “probability” and “possibility” have their own applicable conditions. With regard to the time-dependent reliability issue, there are striking differences between the possibility quantity cited in (15) and the probability one defined in (2)–(3), which is mainly behaved in: (1) terms of initial failure P _f (0) and Pos(0) are respectively determined by techniques of the probability density evolution and the set-interference theory (our previous work in Ref. (Wang et al. 2016a; Wang et al. 2011b; Wang et al. 2014b) have discussed the details); (2) for out-crossing rates ν(t), the probability definition is on the basis of the binormal law and system reliability framework, whereas the possibility solution is achieved by combination of the non-probabilistic interval process model and the equal possibility hypothesis.

Table 1 Relationship between probability and possibility in dealing with uncertainty issues

It may be confused that the volume-ratio principle in (15) seems the case of the probability measure under uniform distribution assumption, so that both probability and possibility ideas appear in the same equation. In fact, the above two reliability methodology have significant differences: for one thing, the treatments of uncertainty analysis, containing the characterization of uncertainty sources as well as the cumulative evolution of uncertainty responses are entirely different; for another, the physical meaning of the time-dependency feature ρ _G (t, t + Δt) is also inequable, and the definition in interval process model may further give the geometric mapping relation corresponding to the feasible region of G(t) and G(t + Δt), which the probabilistic one may not determine.

To sum up, the developed reliability index in (15) is a possibility quantity in essence. Incorporating this safety measure (considering the static and dynamic uncertainties simultaneously) into the following procedure of structural optimization will be a major contribution in this study.

3 Design optimization incorporating the proposed hybrid time-dependent reliability constraints

3.1 Optimization problem formulation

It’s well known that the ultimate aim of structural analysis for a real mechanical system is not just to achieve the safety assessment but for the precise design. The essence of optimization is to seek the best designs that satisfy certain structural behavior requirements. Generally, a typical optimization problem can be mathematically formulated as

$$ {\displaystyle \begin{array}{l} find:\\ {}\min \kern1em f\left(\mathbf{d}\right)\\ {}s.t.\kern1.25em {g}_{i^{\ast }}\left(\mathbf{d}\right)\le 0,\kern0.75em {i}^{\ast }=1,2,\dots, {l}_1\\ {}\kern2.25em \mathbf{d}\in {\varOmega}_{\mathbf{d}}^m\end{array}} $$

(16)

where d is the aforementioned m-dimensional design parameters enclosed by the region ${\varOmega}_{\mathbf{d}}^m$, f(d) is the objective function to be minimized, ${g}_{i^{\ast }}$ represents the i ^∗-th constraint function generally related to the structural responses, and l ₁ means the number of constraints.

However, due to the comprehensive effects of uncertainty factors on functions f and g, the deterministic design complied with (16) may lead to an invalid solution in engineering applications. Associated with the ever-growing demands in structural integrity design via limited sample information, the technique of RBDO is emerged as the times require, and its optimal formulation under non-probabilistic reliability measurement can be expressed as

$$ {\displaystyle \begin{array}{l} find:\mathbf{d}\\ {}\min \kern1em f\left(\mathbf{d},{\mathbf{X}}^{\mathbf{c}}\right)\\ {}s.t.\kern1.25em {g}_{i^{\ast }}\left(\mathbf{d},{\mathbf{X}}^{\mathbf{c}}\right)\le 0,\kern0.75em {i}^{\ast }=1,2,\dots, {l}_1\\ {}\kern2.25em {R}_{s,{j}^{\ast }}\left(\mathbf{d},\mathbf{X}\right)\ge {R}_{j^{\ast}}^{criteria},\kern0.75em {j}^{\ast }=1,2,\dots, {l}_2\\ {}\kern2.25em \mathbf{d}\in {\varOmega}_{\mathbf{d}}^m,\mathbf{X}\in {\mathbf{X}}^{\mathbf{I}}\end{array}} $$

(17)

where ${R}_{s,{j}^{\ast }}\left(\mathbf{d},\mathbf{X}\right)$ represents the j ^∗-th non-probabilistic time-independent reliability index, which should be higher than the allowable value ${R}_{j^{\ast}}^{criteria}$. Even though the optimization methodology as stated above has been well demonstrated and gradually adopted in practice, the pure static simplifying assumption still remain the challenges and limitations for applications in dynamic engineering. In our study, the hybrid reliability measurements under both time-invariant and time-variant uncertainties are considered as the constraints of design formulation, namely, the main concept of our design is to pursue the minimum for several performance indexes such as the structural weight or energy consumption on the premise of safety with the whole device life. Integrated with the discussions cited in section 2, the optimization formulation becomes

$$ {\displaystyle \begin{array}{l} find:\mathbf{d}\\ {}\min \kern1em f\left({t}_l,{\mathbf{X}}^{\mathbf{c}},{\mathbf{Y}}^{\mathbf{c}}(t),\mathbf{d}\right)\\ {}s.t.\kern1.25em {g}_{i^{\ast }}\left(t,{\mathbf{X}}^{\mathbf{c}},{\mathbf{Y}}^{\mathbf{c}}(t),\mathbf{d}\right)\le 0,\kern0.75em {i}^{\ast }=1,2,\dots, {l}_1\\ {}\kern2.25em {R}_{s,{j}^{\ast}}^{hybrid}\left({t}_l\right)=1- Pos(0)-\sum \limits_{k=1}^{k\varDelta t={t}_l}\frac{A_{interference\left({A}_k^{\hbox{'}}\cap {B}_k^{\hbox{'}}\right)}}{A_{total}}\ge {R}_{j^{\ast}}^{criteria},\kern0.75em {j}^{\ast }=1,2,\dots, {l}_2\\ {}\kern2.25em \mathbf{d}\in {\varOmega}_{\mathbf{d}}^m\kern1em \mathbf{X}\in {\mathbf{X}}^{\mathbf{I}}={\left\{{X}_i\left|{X}_i\in \left[{X}_i^c-{X}_i^r,{X}_i^c+{X}_i^r\right]\right.,i=1,2,\dots, {n}_1\right\}}^T\\ {}\kern2.25em \mathbf{Y}(t)\in {\mathbf{Y}}^{\mathbf{I}}(t)={\left\{{Y}_j(t)\left|{Y}_j(t)\in \left[{Y}_j^c(t)-{Y}_j^r(t),{Y}_j^c(t)+{Y}_j^r(t)\right]\right.,j=1,2,\dots, {n}_2\right\}}^T\end{array}} $$

(18)

Note that with regard to any given design parameters d, the objective function f(t _l , X ^c, Y ^c(t), d) as well as each deterministic response ${g}_{i^{\ast }}\left(t,{\mathbf{X}}^{\mathbf{c}},{\mathbf{Y}}^{\mathbf{c}}(t),\mathbf{d}\right)$ will be obtained, and thus, the nominal status of the optimization framework in (18) can be easily available. Herein, directly incorporating the hybrid time-dependent reliability ${R}_{s,{j}^{\ast}}^{hybrid}\left({t}_l\right)$ into the optimal constraint aims at supplementing a more elaborate safety judgment when static and dynamic uncertainties X and Y(t) are taken into consideration, as discussed below.

Actually, with each iteration of d, the bearing capacity of the structure, i.e., the nature of the limit state ${G}_{j^{\ast }}(t)$ changes accordingly. Hence, as per the solution procedure cited in (11)–(15), the reliability measure ${R}_{s,{j}^{\ast}}^{hybrid}\left({t}_l\right)$ is also updated versus different values of d. As stated in (18), only all the reliability constraints ${R}_{s,{j}^{\ast}}^{hybrid}\left({t}_l\right)\ge {R}_{j^{\ast}}^{criteria}$ (j ^∗ = 1, 2, …, l ₂) are satisfied, the current design d ^(k) can be a feasible one; only two adjacent feasible solutions close enough (|f(d ^(k)) − f(d ^{(k − 1)})| < ε, ε denotes a small quantity), the optimal design can be gained. Obviously, from aspects of time-varying issues, e.g. factors of residual strength and stiffness degradation, assigning a relatively conservative value of the threshold ${R}_{j^{\ast}}^{criteria}$ may guarantee a higher safety level of the optimization solution, which may not be derived from the deterministic or the static reliability optimization model. For better understandings, Fig. 5 illustrates a typical one-dimensional case.

Fig. 5

Illustration for the meaning of the hybrid time-dependent RBDO via a typical one-dimensional case

It should be also indicated that the hybrid time-dependent RBDO strategy described by (18) contains two core segments: (1) the time discretization treatment for limit-state function and the possibility calculation of each passage failure event in analysis module; (2) the criterion of the iterative paths for design parameters and the robust model updating in optimization module, which mainly affect the accuracy and efficiency of the design procedure. Consequently, the choice of the optimization algorithms is significantly important subjected to the whole life cycle design for engineering structures.

3.2 The improved ant colony algorithm (ACA) based on the iterative policy

The structural optimization incorporating reliability constraints under a mixed model of non-probabilistic static and dynamic uncertainties presents a challenging subject with complicated optimal iteration. Conventional algorithms are computationally efficient in general, but often encounter two critical problems that: (1) the optimal results may be sensitive to the initial definition; (2) the differentiation calculations have to be required. To overcome the algorithmic deficiencies, several biologically evolutionary techniques have been developed. One of the most mature is the ant colony algorithm (ACA).

Compared with traditional gradient-based approaches, the ACA based on the iterative policy has remarkable global search capability which originates from the inherent positive feedback principle on one hand; on the other hand, continuous information exchange between individuals forms its essence of the distributed computation and further speeds up the evolutionary process for ant colony. The core formula of ACA is written as

$$ {\tau}_{\mathbf{uv}}\left(T+N\right)={\varPsi}_N\cdot {\tau}_{\mathbf{uv}}(T)+\sum_{w=1}^W\varDelta {\tau}_{\mathbf{uv}}^w\left(T,T+N\right) $$

(19)

where τ _uv (T + N) and τ _uv (T) are respectively the pheromones (be regarded as information broadcasted or communicated within the ant system) from design location u to v at times T + N and T, W denotes the total number of the colony, $\varDelta {\tau}_{\mathbf{uv}}^w\left(T,T+N\right)$ represents the quantity of pheromone left on the path u → v by ant w, 1 − Ψ _N means the attenuation coefficient (Ψ _N  < 1). Here, let’s introduce the preference index ${PI}_{uv}^w(T)$ as the transition possibility judgement for ant w from u to v, i.e.

$$ {PI}_{uv}^w(T)=\left\{\begin{array}{l}\frac{{\left({\tau}_{\mathbf{uv}}(T)\right)}^{\alpha}\cdot {\left({E}_{\mathbf{uv}}(T)\right)}^{\beta }}{\sum \limits_{\mathbf{s}\in {\varOmega}_{\mathbf{d}}^m}{\left({\tau}_{\mathbf{us}}(T)\right)}^{\alpha}\cdot {E}_{\mathbf{us}}(T)}\kern1.25em \mathbf{v}\in {\varOmega}_{\mathbf{d}}^m\\ {}0\kern1.25em otherwise\end{array}\right. $$

(20)

where ${PI}_{uv}^w(T)$ determine the tendency of the population evolution, E _uv (T) stands for the heuristic information, α and β indeed reflect the relative importance between pheromone accumulation and heuristic degree in route choice for ant colony updation.

Although the ACA as mentioned before have advantages for better robustness and efficiency when tackling with conventional optimization issues, for the proposed RBDO problems with multi-extremum features, it still easily falling into awkward situation of local optimum precisely because the information interaction among all the ant individuals must be executed in each updating step. In response to these circumstances, an improved ACA which fuses the local-global search strategy is investigated in this section to overcome the bottleneck of convergence instability confronting with the RBDO problems under the mixture of time-invariant and time-variant uncertainties. The detailed operating procedure can be illustrated in Fig. 6, in which the choice of the search policy for every ant relies on the comparative result between the preference index ${PI}_{uv}^w(T)$ and the set threshold P ₀, i.e.

$$ {\displaystyle \begin{array}{l} if\ {PI}_{uv}^w(T)>{P}_0\to {\tau}_{\mathbf{uv}}\left(T+1\right)>{\tau}_{\mathbf{uv}}(T)\to Global search\\ {} else\to Local search\end{array}} $$

(21)

Fig. 6

Procedure for the proposed time-dependent RBDO method based on the improved ant colony algorithm (ACA)

It can be found that the improved ACA model may observably enhance the proportion of local optimization, and to a certain extent, the information sharing and exchange in global optimization is weakened.

Additionally, what needs to be particularly stressed is that any iterative algorithm has its own feasibility and limitation. The amount of uncertain information, the complexity of the structures, and the requirements of accuracy and efficiency are the core factors in appropriate choices.

3.3 Implementation of the developed RBDO methodology

In this section, the analysis and design process based on the proposed hybrid RBDO methodology will be again unscrambled, and the specific treatments are handled as following steps.

• (1) Construct the physical model extracted from practical structural problems and then determine the expression of the time-varying limit state G(t);

• (2) Establish optimal formulations (as shown in (18)) with consideration of non-probabilistic static and dynamic uncertainties, namely, provide definitions of design variables d, uncertain parameters X and Y(t), objective function f(t _l , X ^c, Y ^c(t), d), and reliability constraints ${R}_{s,{j}^{\ast}}^{hybrid}\left({t}_l\right),{j}^{\ast }=1,2,\dots, {l}_2$;

• (3) Initialize values of d to conduct structural analysis for integral service life, and further obtain the measures of hybrid reliability ${R}_{s,{j}^{\ast}}^{hybrid}\left({t}_l\right),{j}^{\ast }=1,2,\dots, {l}_2$ mathematically;

• (4) Utilize the improved ant colony algorithm (ACA) to complete the digital simulation of the structural design, from which the getting optimum relies on the level of hybrid time-dependent reliability from each iteration and the health conditions of particles in ant-cycle system;

• (5) Verification and validation of all analysis and design results.

In order to smoothly realize the optimal solution, several auxiliary means are also needed: a) uncertainty quantification analysis of static variables and dynamic processes via the limited experimental data; b) uncertainty propagation analysis based on methods of the series expansion and the finite difference; c) hybrid time-dependent reliability computation deduced by the numerical simulations; d) the RBDO accomplishment for large-scale structures through the instrumentality of the surrogate model.

4 Comparisons among the safety factor-based design, the instantaneous RBDO, and the proposed hybrid time-dependent RBDO

In fact, from the perspective of engineering applicability, one more universal design strategy (differed from the RBDO concepts) named as the safety factor-based design is widely used at present, in which the optimal formulation reads

$$ {\displaystyle \begin{array}{l} find:\mathbf{d}\\ {}\min \kern0.75em f\left(\mathbf{d},{\mathbf{X}}^{\mathbf{c}}\right)\\ {}s.t.\kern1.25em {g}_{i^{\ast }}\left(\mathbf{d},{\mathbf{X}}^{\mathbf{c}}\right)\le 0,\kern0.75em {i}^{\ast }=1,2,\dots, {l}_1\\ {}\kern2.25em {n}_{j^{\ast}}^{safe}=\frac{R_{j^{\ast}}^c\left(\mathbf{d},\mathbf{X}\right)}{S_{j^{\ast}}^c\left(\mathbf{d},\mathbf{X}\right)}\ge {n}_{j^{\ast}}^{criteria},\kern0.75em {j}^{\ast }=1,2,\dots, {l}_2\end{array}} $$

(22)

where the safety factor ${n}_{j^{\ast}}^{safe}$ is obtained by the ratio between mean values of the allowable response ${R}_{j^{\ast}}^c\left(\mathbf{d},\mathbf{X}\right)$ and the real response ${S}_{j^{\ast}}^c\left(\mathbf{d},\mathbf{X}\right)$, ${n}_{j^{\ast}}^{criteria}$ means the threshold. Apparently, once the time-varying uncertainty effects are taken into account, the safety factor is commonly turned out to be the ratio under the most dangerous moment ${n}^{safe}\to \underset{0<t\le {t}_l}{\min}\left\{{n}_{j^{\ast}}^{safe}(t)\right\}$.

However, the assignment for ${n}_{j^{\ast}}^{safe}(t)$ is essentially based on the mean value assumption so that the influences of the parametric dispersion on structural analysis and design cannot be quantitatively evaluated. Moreover, the value of ${n}_{j^{\ast}}^{criteria}$, which directly affects the final results of optimization, should not be arbitrarily assumed under various cases in engineering, especially in different uncertainty environments. With a view to breaking through the above difficulties, the instantaneous RBDO model as a means of supplementation emerges as the times require. It becomes

$$ {\displaystyle \begin{array}{l} find:\mathbf{d}\\ {}\min \kern1em f\left({t}_l,{\mathbf{X}}^{\mathbf{c}},{\mathbf{Y}}^{\mathbf{c}}(t),\mathbf{d}\right)\\ {}s.t.\kern1.25em {g}_{i^{\ast }}\left(t,{\mathbf{X}}^{\mathbf{c}},{\mathbf{Y}}^{\mathbf{c}}(t),\mathbf{d}\right)\le 0,\kern0.75em {i}^{\ast }=1,2,\dots, {l}_1\\ {}\kern2.25em \underset{0<t\le {t}_l}{\min \limits}\left\{{R}_{\boldsymbol{s},{\boldsymbol{j}}^{\ast}}^{\boldsymbol{instantaneous}}(t)\right\}=\underset{0<t\le {t}_l}{\min \limits}\left\{ Pos\left({G}_{j^{\ast }}\left(t,\mathbf{X},\mathbf{Y}(t),\mathbf{d}\right)>0\right)\right\}\ge {R}_{j^{\ast}}^{criteria},\kern0.75em {j}^{\ast }=1,2,\dots, {l}_2\end{array}} $$

(23)

where ${R}_{\boldsymbol{s},{\boldsymbol{j}}^{\ast}}^{\boldsymbol{instantaneous}}(t)$ is called as the instantaneous reliability. It is easy to understand that the quantity of ${R}_{\boldsymbol{s},{\boldsymbol{j}}^{\ast}}^{\boldsymbol{instantaneous}}(t)$ could be computed by “freezing” time in the limit state and using classical non-probabilistic static reliability method (as illustrated in Fig. 7).

Fig. 7

Schematic diagram for classical non-probabilistic static reliability method obtained by ${G}_{j^{\ast }}(t)={R}_{j^{\ast }}(t)-{S}_{j^{\ast }}(t)$

Nevertheless, compared with the hybrid time-dependent RBDO investigated in this paper, the methods of the safety factor-based design and the instantaneous RBDO both take time independence as the premise when establishing the safety constraints in optimal formulas. That being said, the latter two design policies both take structural health conditions within a fixed time (even though the period of greatest risk) as the guidance, but never judiciously consider the continuity in time series for safety estimation of existing structures. Accordingly, the validity and feasibility of these two optimization results may not be fully guaranteed embarked from the life cycle designing theory. It should be also noted that solely in mathematical terms, the value of the time-dependent ${R}_{s,{j}^{\ast}}^{hybrid}\left({t}_l\right)$ is commonly less than the instantaneous one of $\underset{0<t\le {t}_l}{\min}\left\{{R}_{\boldsymbol{s},{\boldsymbol{j}}^{\ast}}^{\boldsymbol{instantaneous}}(t)\right\}$, i.e.,

$$ {\displaystyle \begin{array}{l}{R}_{s,{j}^{\ast}}^{hybrid}\left({t}_l\right)\le \underset{0<t\le {t}_l}{\min \limits}\left\{{R}_{s,{j}^{\ast}}^{hybrid}\left(t,{t}_l\right)\right\}=\underset{0<t\le {t}_l}{\min \limits}\left\{1-{P}_{f,{j}^{\ast}}^{hybrid}\left(t,{t}_l\right)\right\}\\ {}\le 1-\underset{0<t\le {t}_l}{\max \limits}\left\{ Pos\left({G}_{j^{\ast }}\left(t,\mathbf{X},\mathbf{Y}(t),\mathbf{d}\right)\le 0\right)\right\}\le \underset{0<t\le {t}_l}{\min \limits}\left\{{R}_{\boldsymbol{s},{\boldsymbol{j}}^{\ast}}^{\boldsymbol{instantaneous}}(t)\right\}\end{array}} $$

(24)

where ${R}_{s,{j}^{\ast}}^{hybrid}\left(t,{t}_l\right)=1-{P}_{f,{j}^{\ast}}^{hybrid}\left(t,{t}_l\right)= Pos\left\{\forall \tau \in \left[t,{t}_l\right],{G}_{j^{\ast }}\left(\tau, \mathbf{X},\mathbf{Y}\left(\tau \right),\mathbf{d}\right)>0\right\}$. That is to say, the optimal results based on the presented RBDO model will be on the conservative side but more accordant with the actual situation than the ones derived from the instantaneous RBDO method. It is obvious that structural design without accurate safety checking mechanism is of no value indeed, and hence the significance of our work is self-evident in terms of the physical meaning. The following numerical examples will further demonstrate the usage and rationability of the developed design strategy aiming at the engineering practice.

5 Numerical applications

This section describes the detail of two numerical applications for demonstrating the effectiveness and validity of the proposed hybrid time-dependent RBDO technique: (1) the first example is oriented to the light weight design for a plate with initial crack, and the time-dependent reliability analysis is based on the prediction of the crack propagation life; (2) the second example is subjected to a complicated wing structure of reusable aircraft X-37B, in which the static uncertainty factors (the material characteristics) and the time-varying uncertainty effects (aerodynamic loads of the whole flight ballistic trajectory) are particularly studied. The two engineering cases are solved by three design policies as above mentioned, and their optimization results are reported and discussed in the following statements.

5.1 A finite plate structure with edge crack

As the first example, we consider a finite 20Cr2Ni4A plate (widely used in structural engineering) containing one edge crack (a ₀ = 5mm) as shown in Fig. 8. This plate is subjected to an alternating load P at distance e = 60mm from central axis. The original width and thickness of the structure are respectively W = 160mm and T = 12mm. Here, the effect of the external load is equivalent with the composition between the tensile case and the pure bending (as illustrated in Fig. 9), and the stress amplitude Δσ is given by

$$ \varDelta \sigma =\frac{P}{WT}+\frac{Pe}{6{W}^2T} $$

(25)

Fig. 8

Schematic diagram for the finite plate structure with edge crack

Fig. 9

Equivalent transformation of the external load

Associated with the loading effect of P, the initial crack are expanding consciously until reach the failure threshold. It is indeed a typical dynamic fracture mechanics problem. In accordance with the classical the Paris-Erdogan model, ones get

$$ \frac{da(N)}{dN}=C{\beta}^n{\left(\varDelta \sigma \right)}^n{\left(\pi a(N)\right)}^{\frac{n}{2}} $$

(26)

where a(N) means the crack length after N fatigue load cycles, $\frac{da(N)}{dN}$ stands for the crack growth rate, C, β and n are property parameters. As is noted in (26), the value of $\frac{da(N)}{dN}$ relies on the current scale of a(N), and the whole procedure of the crack extension has remarkable time accumulation effect. Denote by a _cr the design allowable, and the failure judgement can be clearly expressed as a(N) ≥ a _cr .

Owing to the uncertainties existed in material properties and loading conditions, C, β, P as well as a _cr are all assumed as interval variables, and a(N) is defined as an interval process. The details of the static and dynamic uncertainty characteristics are summarized in Table 2. Therefore, the hybrid time-dependent reliability ${R}_s^{hybrid}(N)$ can be measured as

$$ {R}_s^{hybrid}(N)=1- Pos\left\{\exists {N}_i\le N,G\left({N}_i\right)={a}_{cr}-a\left({N}_i,C,\beta, P,W,T\right)\le 0\right\} $$

(27)

where N _i corresponds to the discrete time of alternating load P, N = 1 × 10⁶ means the integral service life, G(N _i ) is the time-varying limit state. Thus, the following optimization formulation can be obtained as

$$ {\displaystyle \begin{array}{l} find:W,T\\ {}\min \kern0.75em A=W\cdot T\\ {}s.t.\kern1.25em {R}_s^{hybrid}\left(N,C,\beta, P,{a}_{cr},a\left({N}_i\right),W,T\right)\ge {R}^{cr iteria}\end{array}} $$

(28)

in which W and T are treated as basic design variables, the section area A is considered as the optimal objective function (weight loss as the goal), different allowable values of reliability constraints are R ^criteria = 0.9, 0.99, 0.999. Figure 10 shows the iterative procedures of the objective function, and the ultimate optimal results are listed in Table 3. For comparison’s purpose, the instantaneous RBDO design and the safety factor-based design are further carried out under the case of R ^criteria = 0.999. Corresponding details are illustrated in Fig. 11, Tables 4 and 5.

Table 2 Parametric characteristics of the plate structure

Fig. 10

Iteration of objective function given by the hybrid time-dependent RBDO with different values of R ^criteria

Table 3 Optimal results obtained by the hybrid time-dependent RBDO strategy

Fig. 11

Comparisons of the three optimization models under given design allowable value R ^criteria = 0.999

Table 4 Optimal results obtained by different design schemes

Table 5 Computational efforts of different design optimization models

From the results in Figs. 10 and 11, Tables 3, 4 and 5, the following points can be summarized:

• (1) Compared with the original design, better weight loss effects can be obtained for the plate structure based on the hybrid time-dependent RBDO strategy (the reduction effect may reach about 20%), as expected. In other words, our work can effectively reduce the redundancy of the initial scheme.

• (2) The optimal value of section area A given by the presented model increases as R ^criteria increases. A more rigorous requirement of time-varying safety (R ^criteria : 0.9 → 0.999) inevitably leads to a lower economic result (${A}_{R_s^{hybrid}(N)}^{optimial}:1529.85\ {mm}^2\to 1564.20\ {mm}^2$).

• (3) As is manifested in Fig. 11 and Table 4, even though the iterative processes are slightly different, there have nearly the same optimums for objective function from the instantaneous RBDO model and the safety factor-based model, that means the theoretical compatibility can be verified by the numerical results.

• (4) Table 5 indicates that different scales of computational efforts are required by three optimization models. Herein, the developed time-dependent approach needs the largest, the instantaneous one the second, and the safety-factor model requires smallest (28.9212 secs → 55.296 secs).

• (5) Last and the most important, the main innovation of this study lies in that is to take full account of the static and dynamic uncertainty issues (particularly the time-varying dependency) of the RBDO design. By the contrast of the three optimization policies, it is not difficult to understand that our work can improve the safety performance under cyclic loading conditions much more obviously (${R}_s^{hybrid}(N):0.9648\to 0.9992$) and only a quite small price of structural weight may be sacrificed (the addition of A ^optimal is about 15 mm ²). Therefore, in the perspective of maintenance cost, the design results obtained by the hybrid time-dependent RBDO method are more useful and more consistent with the reality.

Apparently, considering that the crack growth problem in this example is indeed a monotonic one over time, results of the reliability analysis given by either the instantaneous model or the hybrid time-dependent model mainly relies on the ultimate response conditions near N = 1 × 10⁶. Under such circumstances, the analysis process can be simplified but the time-dependency effect is not obvious owing to the single-crossing essence. For better embody the effectiveness of the proposed methodology, a more complicated case with response oscillation (multi-crossing) characteristics should be further explored.

5.2 A complex wing structure of reusable aircraft X-37B

The hypersonic wing structure, as a core part of reusable vehicle, must meet high-level safety requirements during integral flight ballistic trajectory, and its stress and deformation conditions in harsh service environment are always the major concerns in structural design. In this example, the wing structure is based on X-37B (as illustrated in Fig. 12), and it is consist of aluminum alloy skin, titanium alloy ribs and beams, composite honeycomb sandwiches. The region which connects to fuselage is imposed by fixed constraints, and the aerodynamic loads determined by engineering algorithms act on each node of skin surface.

Fig. 12

Schematic diagram for the complex hypersonic wing structure (X-37B)

For the complexity of the X-37B system, the influences of the static and the dynamic uncertainty factors on mechanical behaviors are extremely apparent. In this case, assuming that structural parameters of alloy materials (E _Al , μ _Al , E _Ti , μ _Ti ) are interval variables and the atmosphere pressure p _atm (t) (the key point for solution of aerodynamic loads) is interval process (as listed in Table 6), the developed hybrid time-dependent RBDO model based on the strength and stiffness criterions (${G}_1(t)=250 MPa-\underset{i=1,2,\dots }{\max}\left|{stress}_i(t)\right|$ and ${G}_2(t)=150 mm-\underset{i=1,2,\dots }{\max}\left|{disp}_i(t)\right|$) can be constructed in which structural mass M _t is deemed to be the optimization objective, the thickness of skin T _s as well as the width of ribs and beams (W _r and W _b ) are taken as design variables, i.e.

$$ {\displaystyle \begin{array}{l} find:{T}_s,{W}_r,{W}_b\\ {}\min \kern0.75em {M}_t\left({T}_s,{W}_r,{W}_b\right)\\ {}s.t.\kern1.25em {R}_{s, stress}^{hybrid}\left({t}_l,{E}_{Al},{\mu}_{Al},{E}_{Ti},{\mu}_{Ti},{p}_{atm}(t),{T}_s,{W}_r,{W}_b\right)\ge {R}_1^{criteria}\\ {}\kern2.5em {R}_{s, disp}^{hybrid}\left({t}_l,{E}_{Al},{\mu}_{Al},{E}_{Ti},{\mu}_{Ti},{p}_{atm}(t),{T}_s,{W}_r,{W}_b\right)\ge {R}_2^{criteria}\end{array}} $$

(29)

Table 6 Properties of the time-invariant and time-variant uncertainties for the hypersonic wing structure

With given ${R}_1^{criteria}={R}_2^{criteria}=0.999$, the optimization procedures from (29) as well as the other two provided design policies can be achieved by combinations of multiple software modules (as shown in Fig. 13), and their optimal results are further summarized in Table 7. Figure 14 shows the iterative histories of M _t . It can be indicated that: for one thing, the proposed optimization technology still has excellent ability in fast solution and robust convergence when dealing with the life cycle design for large-scale complicated structures (only 46 iteration steps to converge); for another, owing to that the more reasonable treatments for quantification and estimation of the static and dynamic uncertainties are involved into structural design procedure (as listed in Table 6), more reliable optimization results can be obtained in this paper (the weight loss ratio achieves about 8.6%), and to a certain extent, the safety risk originating from the scheme defects may be reduced or even avoided in practical engineering (${R}_{s, stress}^{hybrid}\left({t}_l\right)=0.9993$ and ${R}_{s, disp}^{hybrid}\left({t}_l\right)=0.9992$).

Fig. 13

Procedure for the proposed hybrid time-dependent RBDO of the wing structure

Table 7 Optimal results obtained by different design schemes

Fig. 14

Comparisons of the three optimization models under given design allowable values ${R}_1^{criteria}={R}_2^{criteria}=0.999$

Compared with the first example, the time-dependency influences originating from high maneuverability settings in trajectory control are more pronounced, so that the peak responses (displacement and stress) may recur during the whole service cycle. In this case, the superiority of the proposed method, which reflects in fine safety evaluation, will be more prominent. Of course, it is undeniable that with respect to this complex wing structure, the hybrid time-dependent RBDO method requires higher resource consumption of computation (over 36 h worked by multicore servers, as summarized in Table 8). That is to say, in practical engineering, we must keep a good balance between the efficiency and precision when dealing with large-scale optimization problems.

Table 8 Computational efforts of different design optimization models

6 Conclusions

Due to the particular advantage of uncertainty management in structural design, more academic researches and engineering applications have paid attention to the RBDO strategies in recent decades. However, the reliability constraints in most of the current models are usually static without accounting for product lifecycle issues. Additionally, considering that the sample limitation of time-varying uncertainty in practical engineering, some other approaches based on the random process theory may also no longer be feasible.

In view of the above-mentioned facts, a new non-probabilistic time-dependent RBDO method under the mixture of static and dynamic uncertainties is proposed by combination of the interval mathematics and intelligent optimization algorithms. By virtue of the first-passage ideas, the reliability analytic model corresponding to the mixed uncertainties of interval variables and processes is firstly established, and the improved ant colony algorithm is then employed to the optimization procedure to ensure the iterative efficiency and convergence. Furthermore, by introducing the general concepts of the safety factor-based design, the instantaneous RBDO design, the compatibility analysis among these three optimization policies is further discussed. To several specific problems, the given hybrid time-dependent RBDO model can accomplish the optimization more effectively in case of the safety requirement, which may provide reliable theoretical support for engineering practice.

The main innovation points and academic contributions are: (1) a novel index of structural reliability under the mixture of non-probabilistic time-invariant and time-variant uncertainties is defined and solved mathematically; (2) by improving the traditional ACA, a feasible technique of hybrid time-dependent RBDO is conducted and verified by complex engineering cases; (3) the compatibility among the presented hybrid time-dependent RBDO model, the instantaneous RBDO model and the safety factor-based model is further demonstrated.

It must be stressed that the purpose of the paper is not to suggest a replacement of the current technologies of RBDO theory, but may be a viable alternative. Furthermore, the hybrid time-dependent reliability analysis applying to structural design optimization in complex system is still in its preliminary stage, and some important issues remain unsolved, such as the difficulties in dealing with the sensitivity analysis for multi-source time-variant uncertainties, the time-dependent reliability evaluation with joint-upcrossing rates, and the multi-objective RBDO design issues, etc. The relative studies will be developed in our future work.

Appendix A

• (a) Firstly, the common approach for determination of the smallest parametric set (i.e., one hyper-rectangular ‘box’ in essence) containing multi-dimensional sample data is discussed. In consideration of the case that the uncertain parameters α _l (l = 1, 2, …, s) constitute an s-dimensional parametric space, and we have limited information corresponding to these parameters, manifested by a set containing S sample points, namely, ${\alpha}_l^{(S)}=\left\{{a}_l(1),{\alpha}_l(2),\dots, {\alpha}_l(S)\right\}$. Thus, the expression of the transformation matrix reads

$$ \mathbf{T}\left(\boldsymbol{\uptheta} \right)=\left({\boldsymbol{\updelta}}_1,{\boldsymbol{\updelta}}_2,\cdots, {\boldsymbol{\updelta}}_{\mathbf{s}}\right) $$

(30)

where θ = (θ _l ) (l = 1, 2, …, s − 1) denotes the vector of rotation angles related to the original coordinate space, and

$$ {\boldsymbol{\updelta}}_{\mathbf{l}}=\left\{\begin{array}{c}\hfill {\mathbf{0}}_{\mathbf{l}-2}\hfill \\ {}\hfill {\tilde{\boldsymbol{\updelta}}}_{\mathbf{l}}\hfill \end{array}\right\} $$

(31)

where 0 _l − 2 means a column vector with l − 2 zero items, ${\tilde{\boldsymbol{\updelta}}}_{\mathbf{l}}$ is deduced by

$$ {\tilde{\boldsymbol{\updelta}}}_{\mathbf{l}}=\left(\begin{array}{c}\hfill -\sin {\theta}_{l-1}\hfill \\ {}\hfill \cos {\theta}_{l-1}\cos {\theta}_l\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill \cos {\theta}_{l-1}\sin {\theta}_l\cdots \sin {\theta}_{s-2}\cos {\theta}_{s-1}\hfill \\ {}\hfill \cos {\theta}_{l-1}\sin {\theta}_l\cdots \sin {\theta}_{s-2}\sin {\theta}_{s-1}\hfill \end{array}\right) $$

(32)

By utilizing of the transformation matrix T(θ), each point of the original sample set ${\alpha}_l^{(S)}$ will be modified and be further rewritten as ${\beta}_l^{(S)}$ (from α-space to β-space). In order to determine the smallest interval set to envelope full samples, the boundary laws of the s-dimensional ‘box’ should be examined by

$$ \left|\boldsymbol{\upbeta} -{\boldsymbol{\upbeta}}^{\mathbf{c}}\right|\le {\boldsymbol{\upbeta}}^{\mathbf{r}} $$

(33)

where the center vector ${\boldsymbol{\upbeta}}^{\mathbf{c}}={\left({\beta}_1^c,{\beta}_2^c,\cdots, {\beta}_s^c\right)}^T$ and the semi-axis vector ${\boldsymbol{\upbeta}}^{\mathbf{r}}={\left({\beta}_1^r,{\beta}_2^r,\cdots, {\beta}_s^r\right)}^T$. The components ${\beta}_l^c$ and ${\beta}_l^r$ are given by

$$ {\beta}_l^c=\frac{1}{2}\left(\underset{S}{\max}\left({\beta}_l^{(S)}\right)+\underset{S}{\min}\left({\beta}_l^{(S)}\right)\right)\kern0.5em \mathrm{and}\kern0.5em {\beta}_l^r=\frac{1}{2}\left(\underset{S}{\max}\left({\beta}_l^{(S)}\right)-\underset{S}{\min}\left({\beta}_l^{(S)}\right)\right) $$

(34)

Accordingly, the hyper-volume of the ‘box’ as enclosed in (33) is obtained by

$$ {V}_{hyper}=\prod_{l=1}^s{\left(2{\beta}_l^r\right)}^s $$

(35)

which is a function of the rotation angles θ _l . Consequently, it can be defined that the best interval set or the hyper-rectangle among all possible boxes is the one which contains all given sample points and processes the minimum volume, i.e.,

$$ {V}_{hyper}^{\ast }=\underset{{\boldsymbol{\uptheta}}^{\ast}}{\min }{V}_{hyper}\left({\theta}_1,{\theta}_2,\dots, {\theta}_{s-1}\right) $$

(36)

Certainly, once the minimum ${V}_{hyper}^{\ast }$ is gained, the optimal design parameters ${\theta}_l^{\ast }$ may actually reflect the correlationship between the uncertain variables α _l and α _l + 1.

• (b) In terms of a specific interval process Y _j (t), the correlation properties between Y _j (t ₁) and Y _j (t ₂) with any instant times t ₁ and t ₂ are what we really concerned. Hence, the above optimization procedure can be simplified and be executed by following steps:

• i) Collect all the sample curves ${y}_j^{(S)}(t)=\left\{{y}_j\left(t,1\right),{y}_j\Big(t,2\Big),\dots, {y}_j\Big(t,S\Big)\right\}$ and conduct the time-discretization operation with small increment Δt as

$$ {y}_j^{(S)}\left({t}_1\right)=\left\{{y}_j\left({t}_1,1\right),{y}_j\Big({t}_1,2\Big),\dots, {y}_j\Big({t}_1,S\Big)\right\} $$

(37)

and

$$ {y}_j^{(S)}\left({t}_2\right)=\left\{{y}_j\left({t}_2,1\right),{y}_j\Big({t}_2,2\Big),\dots, {y}_j\Big({t}_2,S\Big)\right\} $$

(38)

where t ₁ = j ₁ Δt and t ₂ = j ₂ Δt (j ₁, j ₂ = 1, 2, …).

• ii) Construct a two-dimensional sample space (Y _j (t ₁)-Y _j (t ₂)) originating from (37) and (38), and accomplish the aforementioned optimization solution to get the smallest rotary rectangular domain (as illustrated in Fig. 1), with rotation angel ${\theta}_j^{\ast}\left({t}_1,{t}_2\right)$ and the two semi-axes ${\beta}_j^r\left({t}_1\right)$ and ${\beta}_j^r\left({t}_2\right)$.

• iii) By virtue of the characteristic parameters of the smallest interval set, the covariance function ${Cov}_{Y_j}\left({t}_1,{t}_2\right)$ can be given by

$$ {Cov}_{Y_j}\left({t}_1,{t}_2\right)=\frac{{\left({\beta}_j^r\left({t}_1\right)\right)}^2-{\left({\beta}_j^r\left({t}_2\right)\right)}^2}{3}\cdot \sin {\theta}_j^{\ast}\left({t}_1,{t}_2\right)\cdot \cos {\theta}_j^{\ast}\left({t}_1,{t}_2\right) $$

(39)

Then, the auto-correlation coefficient function ρ _j (t ₁, t ₂) arrives at

$$ {\rho}_j\left({t}_1,{t}_2\right)=\frac{Cov_{Y_j}\left({t}_1,{t}_2\right)}{Y_j^r\left({t}_1\right)\cdot {Y}_j^r\left({t}_2\right)} $$

(40)

• iv) By traversing all values of counting indexes j ₁ and j ₂, properties of autocorrelation of the interval process vector Y _j (t) can be eventually confirmed.