1 Introduction

Like for most of the areas in structural mechanics, optimization for car body development and especially for crashworthiness can be categorized into size, shape, and topology optimization, e.g., Bendsøe and Sigmund (2003). In addition, material or concept optimization may be considered (Volz 2011). Size optimization is often embedded into a multi-disciplinary scheme (e.g., Duddeck 2008) and used in the late design stages. Approaches for shape optimization can be divided into morphing techniques, where the finite element (FE) mesh is moved to realize changes in shape, and approaches using re-meshing techniques and explicit or implicit parameterizations, see Duddeck and Zimmer (2013). This is discussed in detail in Rayamajhi et al. (2014). Topology optimization for crashworthiness is used mainly in the early design phases where the best structural concept has to be identified. It is either applied on the complete vehicle level or on component level, see the state-of-the-art overview in the next section. The optimization objectives for these levels are either approximated or ideally derived via system engineering (V-model approach) as discussed in Fender et al. (2014) and Zimmermann et al. (2012).

Fig. 1
figure 1

Full vehicle simulation model for the front end (Volz 2011)

Full size image

To illustrate the different tasks for topology optimization, first a full vehicle case is regarded as shown in Fig. 1 studied by Volz (2011). The relevant structural skeleton establishes the load paths for the different crash load cases (here EuroNCAP, see www.euroncap.com). One way to derive this principle structure, is to define the design space according to the package definition respecting the volumes of the non-structural components like engine, wheels, etc. This can then be filled by so-called voxels, which are regular three-dimensional finite elements as shown in Fig. 2. Due to the optimization process based on successive deletion of voxels, a zigzag structure is obtained which may inspire the principle location of structural beams to obtain an optimal energy absorption. Beside the smoothening issue, one of the main questions is if an optimization of a volume structure leads to optimal car body designs made from thin-walled components. Figure 3 shows the result for volume elements in comparison to a standard car body design based on thin-walled structures. The mechanics of energy absorption are totally different for volume material. Hence, it is desirable to look for an alternative approach.

Fig. 2
figure 2

Voxel-based topology optimization for crash (Volz 2011)

Full size image
Fig. 3
figure 3

Voxel result and standard thin-walled structure (Volz 2011)

Full size image

In addition, it is important for this type of topology optimization to distinguish between topology optimization for

  • Structural areas that should absorb energy by highly non-linear deformations and

  • Structural areas that should not deform intensively to assure survival space of the occupants.

As can be seen in the literature survey (Section 2), this is often neglected in approaches published on topology optimization for crashworthiness – the two areas should have different objectives, either high energy absorption by large deformations and failure or high resistance forces avoiding intrusions for the safety cell. The latter, because of the lack of large deformations, resembles roughly a standard topology optimization based on linear elastic approaches. A result obtained by equivalent static loads (ESL) is shown in Fig. 4.

Fig. 4
figure 4

Optimized topology (red) for the safety cell via ESL in comparison to reference structure (blue) (Volz and Duddeck 2012)

Full size image

A slightly different task for topology optimization is related to the identification of optimal cross-sectional layouts, rib design, or in general optimal reinforcements. Here, the main load path is defined but the structures, and components along theses paths can be varied according to their local topologies. An example is shown in Fig. 5 where the optimization should determine the best cross-section for the extrusion beam (sill). Again, the optimization approach for the requirement of integrity of the safety cell should be different to cases where high energy absorption is required.

Fig. 5
figure 5

Top: Example for a local topology optimization task; bottom: example of derived topology for the cross-section of a sill in a pole side impact (Walser 2013)

Full size image

For both types of topology problems, the full vehicle and the local reinforcement case, it is essential to realize an approach, which is respecting the special characteristics of thin-walled structures. Most parts of current car body structures are made of these types taking advantage of the special energy absorption behavior. A typical energy absorption of a thin-walled beam structure is shown in Fig. 6. The cylindrical aluminum tube in this study shows two alternative modes both with good energy absorption characteristics. The progressive folding is characterized by the oscillating force-displacement diagrams shown at the bottom of this figure.

Fig. 6
figure 6

Force-displacement curves for aluminum tubes (Marsolek 2002)

Full size image

This performance is normally desirable, i.e., the structure performs optimally with respect to crashworthiness criteria. It should be noted here, that the collapse due to plastic deformations and eventually fracturing does not correspond to a homogeneous distribution of the deformation energy. Indeed, the main deformation energy is concentrated at local plastic hinge lines while the material in between takes only a minor part of the total deformation energy. Hence, the optimization criterion for crash topology optimization has to be defined carefully.

To summarize, topology optimization of thin-walled structures with respect to crashworthiness requires a method based on

  • a modeling, which is truly based on shell elements capturing the typical behavior of thin-walled structures,

  • a definition of an objective allowing non-homogenous energy densities,

  • a distinction between optimization for high energy absorption or for high resistance against intrusion, and

  • an optimization using non-linear crash simulations for the high energy absorption case taking into account that structures support dynamic loads differently than static loads.

The last point is necessary because first studies have shown that the topological results depend on the load velocities of the impact, see Patel (2007) and Patel et al. (2009).

2 State of the art in crash topology optimization

In the past few years, several studies have been published on topology optimization for crash, e.g., Chuang and Yang (2012), Forsberg and Nilsson (2007), Fredricson (2004), Pedersen (2003), Torstenfelt and Klarbring (2007), and Volz (2011). They can be roughly grouped into (i) methods using equivalent static loads, (ii) ground structure and permutative approaches, (iii) bubble and graph/heuristic-based techniques, and finally (iv) approaches based on hybrid cellular automata. The main contributions are summarized and discussed briefly in this section.

2.1 Equivalent static loads approaches (ESL)

Some of the earliest approaches for crash topology optimization are based on the definition of static loads representing roughly the dynamic impact, e.g., Cavazzuti et al. (2011) and Christensen et al. (2012). These loads do not vary in time and are applied over a certain area of the vehicle model where the design space is filled with voxels as shown in Section 1. Because the load definition is coarse and covers a wider area of the car body, this approach is named here global ESL method. To identify the best concepts, linear elastic simulations and corresponding standard topology optimization methods for linear elastic problems are used (see Bendsøe and Sigmund 2003). Each crash case is considered independently and the topology optimization is based on a multi-load case approach (e.g., Fig. 7). Because the dynamic effects cannot be captured here, this approach is only appropriate for safety cell design and not for the energy absorbing areas. A homogeneous energy density as objective leads to strong structures protecting the occupants but it does not lead to optimal structures for high energy absorption.

Fig. 7
figure 7

Global ESL approach for several crash load cases (Christensen et al. 2012)

Full size image

Volz improved this approach by considering different load sets for a single crash case, which vary in time and location, Volz (2011) and Volz and Duddeck (2012). The ESL are derived by general energy considerations, which are based on free crush length and mean force estimates in the energy absorbing areas. Hence, this approach captures better the dynamic characteristic and the requirement for energy absorption.

An alternative way to use ESL is based on an initial non-linear crash simulation where the non-linear displacement is multiplied with the linear stiffness matrix for a certain set of times to create the nodal ESL (or local ESL), for more details see Park (2011). The optimization is then realized by a double loop approach where the inner loop uses the ESL to optimize the linear and static FEM problem and the ESL are updated after the inner optimization is finished by a new non-linear computation based on the optimal design variables obtained in the inner loop. Crash simulation is normally based on the deforming geometry, i.e., it is questionable if the undeformed stiffness matrix used in this approach is the appropriate choice. Furthermore, it is assumed here that the linear optimizations (inner loop) point in the direction of the non-linear optimum. This might be only justifiable for problems with small non-linearities. Due to the nodal character of the ESL, topology optimization approaches with element deletion need special attention. Nevertheless, first applications were promising, e.g., Erhart et al. (2012) and Walser (2013) using an implementation in GENESIS and LS-DYNA (Vanderplaats Research and Development, Inc. 2012; Livermore Software Technology Corporation 2006).

2.2 Ground structure approach (GSA)

In the Ground Structure Approach (GSA), the design space is filled with elementary macro-elements (often beams) with a simplified crash behavior. Different methods to remove and/or modify these macro-elements to reach an optimum design are used, e.g., Fredricson (2004), Pedersen (2003), and Torstenfelt and Klarbring (2007). The latter proposed a property-based model (PBM) where the crash model consists of beams and joints, which can then be optimized (Fig. 8).

Fig. 8
figure 8

PBM model as ground structure (Torstenfelt and Klarbring 2007)

Full size image

The advantage is that non-linear crash simulations can be used without high numerical effort. Because the ground structures are limited in their variability, the quality of the results depends on the initial choice of ground structures.

2.3 Bubble and graph/heuristic-based approach

Earlier work by the research group of Schumacher investigated an approach where holes are introduced successively into a structure and optimized with respect to location and shape, Schumacher (2005). These ideas were then transferred to a graph-based method where heuristic rules are taken to decide on topological changes, Ortmann and Schumacher (2013). This method was also partially integrated into the German research project summarized in Walser (2013). Applications published here focus on the second topology optimization category mentioned above, optimization of reinforcement layouts as shown in Fig. 9.

Fig. 9
figure 9

Graph and heuristic based approach (Ortmann and Schumacher 2013)

Full size image

2.4 Hybrid cellular automata approach (HCA)

The last category of crash topology optimization methods is using cellular automata where the domain is represented by a grid of cells, each characterized by a finite number of possible states and evolving depending on the state of their neighbors. Hybrid Cellular Automata (HCA) consider additional global information of the design space within the update rules, e.g., Penninger et al. (2010). Adaptations to crashworthiness design are presented in Mozumder (2010) and Patel (2007). Like the ESL method, the HCA uses a space filling with 3D voxels, which cannot represent well the energy absorption modes of thin-walled structures. In contrast to ESL, non-linear FE methods (explicit) can be used. Problematic is the optimality criterion. The original papers proposed to homogenize the internal energy, which is not appropriate for thin-walled structures manufactured in metal in cases where energy absorption is the objective. The approach might work well for the other case where intrusion should be avoided and integrity of the safety cell assured. Results were also published in Walser (2013) based on an implementation in the framework of LS-DYNA (LS-TaSC), see Livermore Software Technology Corporation (2011).

To summarize, all these approaches have their advantages and drawbacks. To overcome the difficulties related to the HCA, a new approach is presented here, which changes (i) the space filling and (ii) the optimality criterion. As space filling, a ground structure approach is chosen where larger walls consisting of several shell elements are used, i.e., thin-walled macro-structures are used and not voxels. This enables to modify also the optimality criterion; because homogeneity of energy density is only required for the larger macro-structures, local buckling, folding etc. are now achievable. Hence we believe that this method offers improved capabilities for topology optimization of crash problems. The work presented here is based on the PhD thesis of the second author at Queen Mary University of London, (Hunkeler 2013).

3 HCA for thin-walled structures (HCATWS)

3.1 Main algorithm

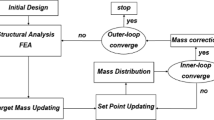
As discussed in Section 2, the existing methods for crash topology optimization are not sufficient for cases where thin-walled structures have to be derived in high energy absorption zones. An approach without using 3D voxels and with an ability to allow for localized plastic zones (plastic hinge lines) is required. Hence, we propose here a new method (see Fig. 10) combining the ground structure approach using thin walls with the HCA method and a modified objective (i.e., a non-homogeneous deformation energy for each wall).

Fig. 10
figure 10

Scheme for the HCA for thin-walled structures (Hunkeler 2013)

Full size image

The algorithm is inspired by the work of Patel and Mozumder on HCA based on 3D voxels (Mozumder 2010; Patel 2007). It consists of an outer loop where non-linear crash simulations are performed to evaluate the crash constraints and the deformation energy of the components (here thin walls). The latter is then used in the inner loop together with the mass fraction objective for this optimization step. In this inner loop, the elements (i.e., the walls taken as cells) are adapted to reach the mass fraction objective using cellular automata rules. It should be noted here that in contrast to Mozumder (2010) and Patel (2007), the cells for the HCA approach are not small 3D voxel elements but walls, i.e., larger components of the ground structure consisting of a high number of shell elements. This has two advantages: Firstly, local plastic hinge lines can occur leading to optimal folding patterns allowing inhomogeneous energy distribution inside of a single wall. Secondly, the walls consist of thin walls defined with standard shell elements. No smoothening of a voxel outcome is necessary. In this inner loop, the thickness of each wall is modified until the mass fraction objective of optimization step k is reached. Back in the outer loop, the optimization is continued as long as global convergence is not achieved. Before the next crash simulation is performed, the geometry is updated considering the changed wall thicknesses from the inner loop. In case that the wall thickness lies below a threshold, the wall is deleted; if previously deleted walls are above the threshold they are re-introduced. To realize this geometrical handling, the software SFE CONCEPT is used, which allows parametric modeling based on a unique implicit parameterization, e.g., Duddeck and Zimmer (2013) and SFE GmbH (2009). The connectivity between the walls is assured by this approach. The changes are performed in the SFE CONCEPT model and a FE model is generated (here without re-meshing of the walls).

The approach outlined here is discussed more in detail in the following sections; especially, the chosen ground structure (i.e., the space filling and the neighborhood definition) is discussed considering applications for 2D and 3D optimization problems. In addition, the chosen routine for setpoint update within the inner loop to achieve the mass fraction objective is presented, which allows a more detailed understanding of the procedure. For further algorithmic details, the PhD thesis of the second author should be consulted (Hunkeler 2013).

3.2 Space filling with thin walls and neighborhoods

To adapt to the traditional HCA where the update rule requires equally sized cells, a regular grid is chosen for space filling. For the 2D case, e.g., for topology optimization of ribs and reinforcements or for cross-sections of extrusion beams, the design space is filled by an orthogonal wall grid while for 3D cases, a cubic honeycomb is defined, see Fig. 11. The number of cells must be chosen carefully; the size of the cells must be big enough to allow folding deformation and to account for eventual manufacturing aspects. The last image on the right of Fig. 11 shows the FE mesh to illustrate that one cell consists of a high number of shell elements such that inside of the cell plastic folding is possible with inhomogeneous energy density.

Fig. 11
figure 11

Space filling for 2D and 3D problems (Hunkeler 2013)

Full size image

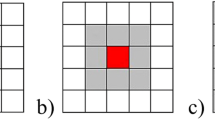
HCA are based on an evaluation of the cells (here walls) with respect to their neighbors. Hence a topological neighborhood also needs to be defined as shown in Fig. 12.

Fig. 12
figure 12

Neighborhood definitions for the 3D case (Hunkeler 2013)

Full size image

3.3 Mass fraction objectives and IED setpoint

The update rules for the cells use the output values of a given cell and its neighboring cells. Here, the internal energy density (IED), \(U_{i}^{(k)}\), of each cell or wall is used. In the outer loop (see Fig. 10), the mass fraction objective (i.e., mass objective divided by reference mass) for the inner loop has to be defined. It is derived by taking the maximum of a pre-defined minimal value \(M_{f,\min }\) and the mass fraction of the prior iteration (k−1) plus the mass increment for this iteration step \({\Delta } M_{f}^{(k)}\).

$$\begin{array}{@{}rcl@{}} M_{f}^{(k)}&=&\max\left( M_{f,\min},M_{f}^{(k-1)}+{\Delta} M_{f}^{(k)}\right); \\ {\Delta} M_{f}^{(k)} &=& \min \left( {\Delta} M_{f,\max}^{(k)}, \max (-{\Delta} M_{f,\max}^{(k)}, \lambda_{\Delta M_{f}}^{(k)}\varepsilon_{d}^{(k)})\right) \end{array} $$
(1)

Here \(\lambda _{\Delta M_{f}}^{(k)}\) denotes the current mass fraction change modulation factor, which is defined in Hunkeler (2013). It balances the speed of correction between the mass fraction and the design constraint error \(\varepsilon _{d}^{(k)}\). The latter is related to the maximum permissible displacement, \(d_{\max }\), and the displacement output in iteration k, \(d_{\text {out}}^{(k)}\), via (2). Here, this displacement is taken as the movement of the rigid impactor in axial direction. Alternative global design constraints can be implemented in a similar manner.

$$ \varepsilon_{d}^{(k)}=\frac{ d_{\text{out}}^{(k)} - d_{\max}} {d_{\max}}. $$
(2)

The permissible change of mass fraction, \( {\Delta } M_{f,\max }^{(k)}\), decreases with the iteration number. The mass fraction objective, \(M_{f}^{(k)}\), is then realized iteratively in the inner loop. For this, an IED setpoint, S ∗(j,k), has to be initialized and further updated using (3).

$$ S^{*(j,k)} =\min\left( S^{*}_{\max},\max\left( S^{*}_{\min},S^{*(j-1,k)} \frac{M^{(j-1)}}{M_{f}^{(k)}}\right)\right) $$
(3)

\(S^{*}_{\min } S^{*}_{\max }\) are the IED setpoint limits, and M (j−1) is the mass fraction derived from the thickness updates of step (j−1) in the inner loop.

3.4 Cell update rule

Inspired by Bochenek and Tajs-Zielinska (2010) and Patel (2007), the update rule of the cells (i.e., of the wall thicknesses) uses separate contributions from each neighbor cell and accounts for the discrepancies between the setpoint and the IED levels of each neighbor. The thickness change, \(\delta t_{i}^{(j,k)}\), for cell i is defined by the following equations

$$\begin{array}{@{}rcl@{}} \delta t_{i}^{(j,k)} &=& \min\left( \delta t_{\max},\max\left( -\delta t_{\max}, \sum\limits_{q=0}^{n_{i}} \alpha_{q}^{(j,k)} \right)\right);\\ \alpha_{q}^{(j,k)} &=& \sum\limits_{u=1}^{c_{q}} \zeta \, \chi_{P_{u}}(U_{q}^{(k)}) - \sum\limits_{u=1}^{c_{q}} \zeta \, \chi_{M_{u}}(U_{q}^{(k)}). \end{array} $$
(4)

\(\alpha _{q}^{(j,k)}\) is the contribution of neighboring cell q; here a hybrid approach is introduced, which does not only consider the contributions of the neighboring cells, but also accounts for the discrepancy between the setpoint and the cells’ IED levels. ζ is an increment parameter which modulates the thickness changes depending on the mass fraction change of the current iteration. χ (.) is the indicator function filtering the contributions of the neighboring cells. P u represents the discrepancies above the setpoint S ∗(j,k) and M u those below. \(\delta t_{\max }\) is the maximum thickness variation allowed per iteration. For further details, see Hunkeler (2013). It should be noted here, that oscillations of the algorithm need to be avoided; hence a regularization is employed here by replacing the IED of cell i at iteration k, \(U_{i}^{(k)}\), by a weighted sum of the three previous iterations:

$$ \tilde U_{i}^{(k)} = \frac{1}{2} U_{i}^{(k)} + \frac{1}{3} U_{i}^{(k-1)} + \frac{1}{6} U_{i}^{(k-2)}. $$
(5)

4 Topology optimization of thin-walled beams under axial impact via the HCATWS

4.1 Load case I – axial impact, d max=75mm

The response of simple metallic tubes to axial impacts is widely studied in literature, e.g., Abramowicz (2003), and hence this case is well suited for validation. Interior reinforcements can improve the energy absorption, e.g., Alavi Nia and Parsapour (2013); therefore, a multi-cell rectangular tube (length L=400 mm) is regarded here where the outer frame (cross-section A=80×100 mm2, thickness t=1.5 mm) is not changed and only the interior topology is optimized. A regular grid of reinforcement walls is chosen as initial geometry, see Fig. 13. Due to the manufacturing by extrusion, this is a 2D topology case. The walls have a width of 20 mm and a length of 400 mm which generates a total of 31 walls (10 independent design parameters due to symmetry conditions). The initial interior wall thickness is t init=0.5 mm. The beam is impacted on one end by a rigid wall perpendicular to its longitudinal direction, and fixed on the other end. The rigid wall has a mass of m=500 kg and an initial speed of v=5 m/s. The impact is simulated for a duration of 25 ms. The displacement of the impactor over this duration is taken as constraint. The beam is made of an aluminum extrusion (Young’s modulus E=70 GPa, mass density ρ=2.7 t/m3, Poisson ratio ν=0.33 and yield strength σ y =180 MPa). Hardening is represented by a piecewise linear stress-strain curve as defined in Table 1.

Fig. 13
figure 13

Rectangular beam under axial impact – load case I and initial space filling (Hunkeler 2013)

Full size image
Table 1 Piecewise linear isotropic hardening of the extrusion beam (aluminum) defined by effective plastic strain \(\varepsilon ^{p}_{\text {eff}}\) [–] and corresponding stress σ [MPa] (Hunkeler 2013)
Full size table

For optimization, the displacement constraint is chosen as \(d_{\max } = 75\,\text {mm}\), which is 32% less than the value obtained for the empty cross-section (mass 583 g). The von Neumann neighborhood (Fig. 12) and the hybrid update rule (Section 3.4) are chosen for the HCATWS. The best design is found after 34 iterations (i.e., after only 34 non-linear crash simulations) with a mass of 865 g and maximal displacement of 74.24 mm. Fig. 14 gives the evolution from the initial to the optimal geometry showing that mainly the corners are reinforced. This was expected as prior studies without optimization have indicated the superior behavior of comparable structures (Alavi Nia and Parsapour 2013; Kim 2002). The corresponding graphs for force-displacement and for the evolution of the displacement constraint and the objective are given in Fig. 15.

Fig. 14
figure 14

Topology evolution for case I (HCATWS)

Full size image
Fig. 15
figure 15

Optimization results for case I: force-displacement curves for the initial design and the two optima (HCATWS and LS-OPT) and evolution of the mass objective and displacement constraint for the HCATWS

Full size image

The force-displacement relation improved reducing the difference between peak and average force (the peak force, which is only monitored in this optimization, is related to the deceleration, which should not be too high). The strong increase in mass (the objective) at the beginning of the optimization (iteration 5) is due to the initial violation of the constraint.

To assess optimality of the results, an alternative approach is regarded (only possible without extensive computations due to the relatively low number of design parameters). A sizing optimization is solved with a commercial optimizer LS-OPT (Livermore Software Technology Corporation 2012) and an iterative response surface method (RSM) using radial basis functions. Starting from a complete set of walls, the wall thicknesses are modified and eventually deleted when they become smaller than 0.4 mm. The maximum number of iterations is set to 15 to keep the total number of crash simulations under 300 (17 simulations per iteration). The best design was found at iteration 11 (i.e., 187 non-linear crash simulations) with a mass of 863 g and a final displacement of 74.7 mm, both very comparable to the results from the HCATWS. Note that the number of non-linear crash simulations is much higher than for the HCATWS. As the references mentioned above, this validation confirms the principle topology identified by the HCATWS: the corners are reinforced again, Fig. 16.

Fig. 16
figure 16

Best cross-section obtained by standard size optimization for case I (LS-OPT) and the folding pattern at the end of the simulation (Hunkeler 2013)

Full size image

The results for the design variables, i.e., the wall thicknesses are given in Table 2. They differ slightly, which may indicate that there exist several comparable nearly optimal designs.

Table 2 Optimal thicknesses for case I (\(d_{\max }=75\) mm)
Full size table

4.2 Load case II – axial impact, d max=50mm

Considering a more demanding displacement constraint (\(d_{\max }=50\text {mm}\)), we obtain a comparable cross-section topology where mainly the wall thicknesses are increased while the topology is nearly similar. Some additional walls on the outer rectangular box are required. The HCATWS (61 iterations, i.e., 61 non-linear simulations) leads to a beam with a mass of 1.107 kg and a maximum displacement of 50.0 mm. The same case optimized by LS-OPT finishes with m=1.098 kg and \(d_{\max }=47\,\text {mm}\). Both have comparable cross-sectional topologies as shown in Fig. 17. The thicknesses are given in Table 3. In contrast to case I, the topology results do not match totally. This is due to the fact, that the optimization problem regarded here is multimodal. Hence, the optima are local optima and it is possible to find several different cross-sections with comparable performance. This needs further investigations especially with respect to additional constraints (e.g., a limitation of the peak force). As already mentioned above, all results show a reinforcement of the corners, which means that the coupling of the different walls via the external rectangular box is important.

Fig. 17
figure 17

Best cross-sections for load case II

Full size image
Table 3 Thicknesses in [mm] for case II (\(d_{\max }=50\) mm)
Full size table

The results for the axial impact (case I and II) are summarized in Tables 4 and 5. The higher number of iterations in case II is due to the higher constraint. Again, it can be seen that the HCATWS is much more efficient requiring much less non-linear crash simulations. The force-displacement graph and the evolution of the constraint and objective are given in Fig. 18.

Fig. 18
figure 18

Optimization results for case II: force-displacement curves for the initial design and the two optima (HCATWS and RSM) and evolution of the mass objective and displacement constraint for the HCATWS

Full size image
Table 4 Results for case I (\(d_{\max }=75\) mm)
Full size table
Table 5 Results for case II (\(d_{\max }=50\) mm)
Full size table

4.3 Load case III – oblique impact, d max=80mm

As third example, an oblique impact is regarded, i.e., the rigid wall impacting the structure is slightly rotated around x- and y-directions by 5.7∘ (see Fig. 19). This angle is chosen empirically to avoid global buckling (regarded as infeasible) of the empty cross-section; this means a higher angle leads to a high number of infeasible designs. The symmetry condition is discarded; we have hence 31 independent wall parameters (which makes a RSM approach more or less unaffordable). The empty cross-section shows a maximum displacement of 113.2 mm. Hence \(d_{\max }=80\text {mm}\) is chosen as displacement constraint for the optimization. The evolution of the HCATWS optimization is shown in Fig. 20. The best design (iteration 52) has a mass of 892 g and a maximum displacement of 79.9 mm.

Fig. 19
figure 19

Rectangular beam under oblique impact (Hunkeler 2013)

Full size image
Fig. 20
figure 20

Topology evolution for case III (HCATWS)

Full size image

The corresponding result with LS-OPT is shown in Fig. 21, which was obtained via the same RSM method but with a higher number of simulations (in total 1000 non-linear crash simulations) due to the higher number of design variables in this case (no symmetry conditions).

Fig. 21
figure 21

Best design for case III (LS-OPT)

Full size image

Note that only the corner impacted last by the wall is not reinforced. At this corner a fold appears near the constrained end of the beam (see right part of Fig. 21). This is a consequence of the other corners being stiffer. Here an undesirable global buckling might be initiated. Robustness should be included into the optimization, see for example (Hunkeler et al. 2013). The results for HCATWS and LS-OPT are given in Table 6. Note here that the peak forces not considered in the optimizations differ strongly. This means that there is a high potential to identify special cross-sectional topologies which show advantageous low peak forces. This is currently under investigation by the authors and will be published in a separate paper. The paper at-hand addresses the new HCA method and not so much physical phenomena. Compare also the corresponding force-displacement curves (Fig. 22, top).

Fig. 22
figure 22

Optimization results for case III: force-displacement curves for the initial design and the two optima (HCATWS and RSM) and evolution of the mass objective and displacement constraint for the HCATWS

Full size image
Table 6 Results for case III (\(d_{\max }=80\) mm)
Full size table

The results for the design variables for both optimizations are finally given in Fig. 23. It can be seen that the design variables differ. Nevertheless, the response parameters regarded in the optimizations (mass and displacement constraint) are very similar (Table 6).

Fig. 23
figure 23

Results for case III: thicknesses in [mm]

Full size image

5 Conclusions

As shown by the examples discussed in the previous section, the proposed method is able to derive optimal topologies for thin-walled structures for crashworthiness. The evaluations are based on fully non-linear crash simulations (explicit FEM). The geometries are realized with standard shell elements used for crash analysis; no 3D voxels are used, which would first require smoothening in a post-processing and second which cannot represent the typical behavior of thin-walled structures in crash (folding mechanisms based on the formation of plastic hinge lines). In addition, the problem of the original HCA, see Mozumder (2010) and Patel (2007), that the objective leads to homogeneous energy density in all voxel elements does not occur here. Hence the authors believe that this method has a high potential to overcome some of the existing problems encountered in crash topology optimization. Further applications were already studied in the PhD thesis of the second author (Hunkeler 2013) and will be extended and published in the near future, see also Hunkeler et al. (2013). In addition, different space filling schemes have to be studied. First attempts on including diagonal wall elements are encouraging. The obtained differences in designs originating just from a small change in impact angle also illustrate the necessity to include robustness into the studies, e.g., Hunkeler et al. (2013) and Rayamajhi (2014).