Robust optimization with convex model considering bounded constraints on performance variation

Abstract

In robust optimization, double-looped structures are often adopted where the outer loop is used to seek for the optimal design and the optimization performed in the inner loop is for the robustness assessment of the candidate solutions. However, the double-looped techniques usually will lead to a significant increase in computational efforts. Therefore, in this paper, a new robustness index is developed to handle bounded constraints on performance variation where no optimization run is required for the robustness evaluation work in the inner loop. The computation of this new index is based on the sensitivity Jacobian matrix of the system performances with respect to the uncertainties and it can quantitatively measure the maximal allowable magnitude of system variations. By introducing this index, the robust design problem can be reformulated as a deterministic optimization with robustness indices requirements. Two numerical examples are tested to show the effectiveness and efficiency of the proposed approach, whose solutions and computational efforts are compared to those from a double-looped approach proposed in previous literature.

1 Introduction

In the design of engineering structures, there are many system uncertainties inherent in the material properties, geometrical dimensions, loading conditions and so on. Since these uncertainties may cause significant variability in structural performances, they should be considered in the mathematical modeling of the structural optimization problem. Many researches have been carried out to reduce the sensitivity of a solution with respect to the system input variations, which is the so-called robust design.

Since Taguchi (1978) proposed the concept of robust design, it has been an active research topic in the past several decades and many methods have been developed (Bacarreza et al. 2015; Doltsinis et al. 2005; Guo et al. 2013; Hashimoto and Kanno 2015; Sun et al. 2014; Wu et al. 2015; Zaman et al. 2011). Two categories of uncertainty description are mainly considered in this area: one is probabilistic models and the other is non-probabilistic models, including the convex models and interval models. The probabilistic models are mostly widely used to quantify the uncertainty based on the statistic information, such as the mean and variance of the uncertainties (Doltsinis et al. 2005; Gaspar-Cunha et al. 2014; Medina and Taflanidis 2015; Venanzi 2015). However, the methods with probabilistic model need the precise data of the probability distribution of the random variables which is usually difficult to obtain (Ben-Haim and Elishakoff 1990; Ellishakoff 1995). In the application of probabilistic approach, certain assumptions of the probabilistic model may be necessary, which, as pointed out by Ellishakoff (1995), can lead to large errors in the estimation of failure probabilities.

Non-probabilistic models, as new and appealing supplements to conventional probabilistic models, have received considerable attentions since the pioneering work by Ben-Haim and Elishakoff (1990). In the convex model or interval-model-based approaches, only the bounds of the uncertain parameters are needed and they can be obtained from a small number of samples (Jiang et al. 2007, 2011). In practical engineering design problems, the bounds of the uncertain parameters can be more easily determined as compared to their precise statistical distribution (Kang and Bai 2013). Due to these advantages over the probabilistic approach, the non-probabilistic approaches have attracted growing attentions.

There have been several interval-based methods proposed for robust optimization. Zhou et al. (2012) introduced a sequential quadratic programming for robust optimization (SQP-RO) under interval uncertainties with both objective robustness and feasibility robustness. A sensitivity-region-based method was developed to get the maximum allowable variation of uncertain parameters or variables (Gunawan and Azarm 2004, 2005a, b; Li 2007). Generally, most existing robust optimization methods have the so-called double-looped structure where the robustness assessment work is performed in the inner loop through optimization procedure. This double-looped structure usually tends to decrease the computational efficiency of robust optimization significantly (Zhou and Li 2014).

For robust optimization with convex model, Kang and Bai (2013) defined a robustness measurement as the minimal distance from the origin to the limit-state surface. This is similar to the definition of non-probabilistic reliability measure (Cao and Duan 2005; Kang et al. 2011) and the design objective is to maximize the minimum one of the robustness indices. The work by Kang and Bai (2013) dealt with the robustness induced by unilateral constraints on structural performance variation, just as shown in (1):

$$ f\left(\mathbf{X},\mathbf{P}\right)=f\left(\mathbf{X},{\mathbf{P}}_0\right)+\varDelta f\le \overline{f} $$

(1)

$$ \mathbf{P}\in \boldsymbol{\Omega} $$

(2)

Then,

$$ \varDelta f\le \overline{f}-f\left(\mathbf{X},{\mathbf{P}}_0\right) $$

(3)

where X is the vector of design variables, P represents the uncertain parameters whose values can vary within the convex domain Ω and P ₀ is the vector of nominal values of P. Δf is the performance variation with respect to its nominal value and $\overline{f}$ is the prescribed upper bound for performance f. The performance could be the structural displacement, stress, weight, and so on.

In Kang and Bai’s work, (3) is used as the limit-state function and the robustness index is defined by SQP, which is still an optimization procedure.

In practical engineering, the restrictions on system performance variation under parameter uncertainties may appear in the form of bounded constraints. For example, as shown in Fig. 1, the two structures are going to be assembled at point A and B. The blue lines represent part of the deformed structure, and A ′ and B ′ are the deformed locations of A and B, respectively. The displacements of A and B in the y direction are ${d}_A={y}_{A^{\prime }}-{y}_A$ and ${d}_B={y}_{B^{\prime }}-{y}_B$, respectively. In order to ensure the accuracy of the assembly under uncertainty, the two displacements should be smaller than certain values. Obviously, these are bounded (bilateral) constraints on displacements, as shown in (4).

Fig. 1

Assembly of two structures

$$ -\overline{d}\le d\le \overline{d} $$

(4)

where $\overline{d}$ is a positive prescribed performance variation tolerance.

This constraint in (4) can be converted to a unilateral constraint by taking square of d, i.e., ${(d)}^2\le {\overline{d}}^2$. Thus, the bounded constraint on d is transformed into a unilateral constraint, just like shown in (3). In this situation, an optimization procedure is usually adopted to deal with this unilateral constraint, which will lead to a double-looped optimization problem. As far as the authors’ knowledge, when the uncertainty is modelled with convex model, there are few publications concerning the efficiency improvement for bounded restrictions on performance variation.

To overcome the issue of the low computational efficiency of double-looped robust optimization approaches, in this paper, a new robustness index for bounded restrictions on performance variation is proposed based on non-probabilistic convex model. This index can be easily computed by the sensitivity Jacobian matrix instead of an optimization procedure.

The rest of this article is arranged as follows. Section 2 presents a general formulation of robust optimization with both unilateral constraint and bounded constraint on performance variations. In section 3, the definition of the proposed robustness index for bounded restriction on performance variation is detailed. This part is the main contribution of our work. Also, the existing robustness index definition for unilateral constraints on performance variations in literature is briefly introduced. In section 4, a new robust optimization model is established with two robustness indices (i.e., the robustness indices for unilateral and bounded constraints for performance variations) constraints. Then, two truss structures are provided to demonstrate the effectiveness of the presented method in section 5. Section 6 gives a discussion about the application scope of the new method. Finally, the conclusions are given.

2 Robust optimization model with constraints on performance variations

A robust optimization with both unilateral constraints and bounded constraints on performance variation can be formulated in the following equation:

$$ \begin{array}{l}\mathrm{M}\mathrm{i}\mathrm{n}\kern0.5em {f}_{\mathrm{obj}}\left(\mathbf{X},{\mathbf{P}}_0\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1.25em {f}_i^{(u)}\left(\mathbf{X},\mathbf{P}\right)\le {\overline{f}}_i^{(u)},\kern0.75em i=1,2,\dots, k\\ {}\kern2em -\varDelta {f}_j^{*}\le {f}_j^{(b)}\left(\mathbf{X},\mathbf{P}\right)-{f}_j^{(b)}\left(\mathbf{X},{\mathbf{P}}_0\right)\le \varDelta {f}_j^{*},\kern0.5em j=1,2,\dots, q\\ {}\kern2.25em \mathbf{lb}\le \mathbf{X}\le \mathbf{u}\mathbf{b}\\ {}\kern2.25em \mathbf{P}\in \boldsymbol{\Omega} \end{array} $$

(5)

where f _obj(X, P ₀) is the objective performance. The design objective is to minimize the objective performance when the uncertainties P take their nominal values P ₀. f ^(u) and f ^(b) are the system performances involved in unilateral and bounded design constraints, respectively and the superscript u and b represent unilateral and bounded, respectively. The robustness represented by ${f}_i^{(u)}\left(\mathbf{X},\mathbf{P}\right)\le {\overline{f}}_i^{(u)}$, i = 1, 2, …, k can be called robustness for the unilateral constraint on performance variation (RUC) and ${\overline{f}}_i^{(u)}$ is the prescribed upper bound of the ith performance involved in unilateral constraint. The robustness of − Δf ^* _j  ≤ f ^(b) _j (X, P) − f ^(b) _j (X, P ₀) ≤ Δf ^* _j , j = 1, 2, …, q is for bounded constraint on performance variation (RBC) and Δf ^* _j  > 0 is the upper bound of the variation for the jth performance involved in bounded constraint, i.e., the performance tolerance.

3 Definition of the indices of RBC and RUC

In this section, the concept of convex model for uncertainties is presented and the definitions of the indices of RBC and RUC are shown. The indices are used to quantitatively measure the maximum allowable magnitude of the system variations. By defining the robustness indices, the robust design problem can be transformed into a deterministic optimization which can be solved easily with existing optimization algorithms.

3.1 Convex model of uncertainties

Assume that there exist n uncertain-but-bounded parameters P _i , i = 1, 2, …, n which constitute a n dimensional parameter space P ^T = {P ₁, P ₂, …, P _n }.P ^c = {P ^c₁ , P ^c₂ , …, P ^c _n } is the midpoints set in which P ^c _i is the nominal value of the ith uncertain parameter. Assuming that the uncertainty of P falls into a multidimensional ellipsoid, the uncertainty set Ω _p in p space can be given (Ben-Haim and Elishakoff 1990) as

$$ \mathbf{P}\in {\varOmega}_{\mathrm{p}}=\left\{\left.\mathbf{P}\right|{\left(\mathbf{P}-{\mathbf{P}}^{\mathrm{c}}\right)}^T\mathbf{W}\left(\mathbf{P}-{\mathbf{P}}^{\mathrm{c}}\right)\le 1\right\} $$

(6)

where W is a real symmetric positive definite matrix known as the characteristic matrix of the convex model and defines the principal axes of the ellipsoid.

In practical applications, the uncertainty of parameters often arise from different sources, and then they may in different orders of magnitude. To overcome this problem and whereby ensure the numerical precision, the uncertain parameters P (p space) can be transformed into a set of regularized variables U (u space)

$$ {U}_l=\frac{P_l-{P}_l^{\mathrm{c}}}{P_l^{\mathrm{c}}},\kern0.5em l=1,2,\dots, n $$

(7)

Then,

$$ \mathbf{U}=\mathbf{Q}\left(\mathbf{P}-{\mathbf{P}}^{\mathrm{c}}\right) $$

(8)

where Q = diag(1/P ^c₁ , 1/P ^c₂ , …, 1/P ^c _n ).

Based on the linear transformation in (8), Ω _p can be changed into another convex set Ω _u in the u space

$$ \mathbf{U}\in {\varOmega}_u=\left\{\left.\mathbf{U}\right|{\mathbf{U}}^T{\mathbf{W}}_u\mathbf{U}\le 1\right\} $$

(9)

where W _u denotes the characteristic matrix of the convex model in the u space.

Then the eigenvalue decomposition is utilized for the matrix W _u

$$ {\boldsymbol{\Phi}}^T{\mathbf{W}}_u\boldsymbol{\Phi} =\boldsymbol{\Lambda}, \kern0.5em {\boldsymbol{\Phi}}^T\boldsymbol{\Phi} =\mathbf{I} $$

(10)

where Φ is an orthogonal matrix formed by the normalized eigenvectors and Λ is a diagonal matrix consisting of the eigenvalues of W _u . I is an identity matrix. Then another linear transformation is introduced as

$$ \boldsymbol{\updelta} ={\boldsymbol{\Lambda}}^{1/2}\boldsymbol{\Phi} \mathbf{U} $$

(11)

Ω _u can be transformed into the δ space

$$ \boldsymbol{\updelta} \in {\varOmega}_{\delta }=\left\{\left.\boldsymbol{\updelta} \right|{\boldsymbol{\updelta}}^T\boldsymbol{\updelta} \le 1\right\} $$

(12)

By means of these two linear transformations in (7) and (11), a multiple sphere with a unit radius can be obtained in δ space. The definitions of the indices of RUC and RBC in the following sections are both performed in this δ space.

3.2 Index of RUC

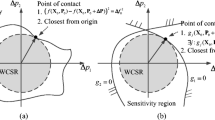
In this paper, the index of RUC ξ is obtained from the work of Kang and Bai (2013), which is shown in (13). The procedure is carried out in the δ space which has been mentioned in the previous section. It should be noted that this sub-optimization is performed when the design variables X of design problem (5) are at their nominal values and the design variables in (13) are uncertain parameters in δ space. In Fig. 2, a two-dimensional case is shown. The index ξ _i is defined as the smallest distance from the critical curve (i.e., ${f_i}^{(u)}\left(\boldsymbol{\updelta} \right)-{\overline{f}}_i^{(u)}=0$) to the origin of δ space. The indices are used as the optimization constraints in the final robust optimization problem shown in section 4.

Fig. 2

Robustness index for a unilateral constraint (Kang and Bai 2013)

$$ \begin{array}{l}\mathrm{M}\mathrm{i}\mathrm{n}\kern0.75em {\xi}_i=\sqrt{{\boldsymbol{\updelta}}^{\mathbf{T}}\boldsymbol{\updelta}}\\ {}\mathrm{s}.\mathrm{t}.\kern1.5em {f_i}^{(u)}\left(\boldsymbol{\updelta} \right)-{\overline{f}}_i^{(u)}=0\end{array} $$

(13)

3.3 Index of RBC—the proposed approach

This section is the main contribution of our proposed method. According to the work by Zhu and Ting (2001), the performance variations caused by parameter uncertainties can be approximated by the linear expansion:

$$ \mathbf{Y}=\mathbf{J}\cdot \varDelta \mathbf{P} $$

(14)

where, $\mathbf{J}=\frac{\partial \left({f}_1^{(b)},{f}_2^{(b)},\dots, {f}_q^{(b)}\right)}{\partial \left({p}_1,{p}_2,\dots, {p}_n\right)}$ is the sensitivity Jacobian matrix evaluated at the nominal dimensions. f ^(b) _j , j = 1, 2, …, q and p _l , l = 1, 2, …, n are the performance functions and uncertain parameters, respectively. Y = (Δf ₁ ^(b), Δf ₂ ^(b), …, Δf _q ^(b))^T and Δ P = (Δp ₁, Δp ₂, …, Δp _n )^T are the variation vectors of the performance functions and uncertain parameters, respectively.

By taking a norm of the vector Y,

$$ {\left\Vert \mathbf{Y}\right\Vert}_2^2={\left(\varDelta {f}_1^{(b)}\right)}^2+{\left(\varDelta {f}_2^{(b)}\right)}^2+\cdots +{\left(\varDelta {f}_q^{(b)}\right)}^2={\mathbf{Y}}^T\mathbf{Y}=\varDelta {\mathbf{P}}^T{\mathbf{J}}^T\mathbf{J}\varDelta \mathbf{P}=\varDelta {\mathbf{P}}^T\mathbf{A}\varDelta \mathbf{P} $$

(15)

where Δ P = P − P ^c. When each performance tolerance is given as Δf ^* _j , j = 1, 2, …, q, each of the design candidates will associate with a subspace in which the system will satisfy the constraint shown in (16).

$$ {\left\Vert \mathbf{Y}\right\Vert}_2^2=\varDelta {\mathbf{P}}^T\mathbf{A}\varDelta \mathbf{P}\le {\displaystyle \sum_{j=1}^q\varDelta {f_j^{*}}^2} $$

(16)

For matrix A of the quadratic, it must be either positive or semi-positive definite. If A is positive definite, the (16) represents a n dimensional hyper-ellipsoid with a parameter ‖Y‖ ²₂ . If A is semi-positive definite, the domain which (16) represents is a hyper-cylindroid. A modified method (Zhu and Ting 2001) is used to adjust the infinite principal axes to finite lengths.

Therefore, the hyper-ellipsoid is called the feasible ellipsoid. The feasible ellipsoid represented by (16), as we can see, is the subspace where the gross performance but not necessarily every individual performance is acceptable (Zhu and Ting 2001). This method in this section aims to develop a more efficient way to handle robust bounded constraints, which may result in some constraints violations. This problem will be discussed in section 5 with numerical examples.

Transformed into the δ space, the index of RBC is defined as the length of the smallest semi principal axis of it, as shown in (17). λ _i is the length of ith semi principal axis. A 2-dimensinal robustness index is shown in Fig. 3.

Fig. 3

Proposed index of RBC in 2-dimensional

$$ \eta = \min \left\{{\lambda}_1,{\lambda}_2,\dots, {\lambda}_n\right\} $$

(17)

When η ≥ 1, all of the uncertain sphere (circle in 2-dimensional) is located in the feasible ellipsoid and when η < 1, some part of the uncertain sphere is not enclosed by the feasible ellipsoid, which may lead to a violation of restriction. The larger the η value, the more robust the design, and vice versa.

An aggregate function (Kang and Bai 2013; Luo et al. 2013; Kreisselmeier and Steinhauser 1983; Poon and Martins 2007) is used to convert the minimum operator in (17) into a smooth function which make it easier to adopt gradient-based optimization. With the aggregate function, the η is defined as

$$ \eta =-\frac{1}{\rho } \ln \left({\displaystyle \sum_{l=1}^n{e}^{-\rho {\lambda}_l}}\right) $$

(18)

where the ρ is 10 in this paper.

The relevant flowchart is shown in Fig. 4 and the explanations can be stated as:

Fig. 4

Flowchart for obtaining the index for RBC

• 1. Evaluate the derivatives ∂f _i /∂p _j , i = 1, 2, …, m, j = 1, 2, …, n.

• 2. Form the Jacobian matrix J.

• 3. Give the tolerances for performances Δf ^* _i , i = 1, 2, …, m.

• 4. Generate the feasible ellipsoid by (16)

• 5. Transfer the feasible ellipsoid into δ space. Firstly, the Δ P in (16) is transformed into u space by (8), and then second transformation in (11) is adopted. Therefore, after the two linear transformations, the feasible ellipsoid shown in (16) is transferred into δ space.

• 6. Define the index of RBC η. 1) The eigenvalue decomposition is utilized for the matrix A and the eigenvalues ω ₁, ω ₂, …, ω _n are obtained. 2) If A is semi-positive definite, the modification method by Zhu and Ting (2001) is used to adjust the infinite principal axes to finite lengths. 3) The lengths of the semi principal axis are calculated by ${\lambda}_l={\left\Vert \mathbf{Y}\right\Vert}_2/\sqrt{\omega_l},l=1,2,\dots, n$. 4) Finally, the η is defined by (18).

4 Formulation of robust optimization with the two robustness indices

In the last section, the indices for RUC and RBC are defined and then the robust design problem (5) can be reformulated as follows:

$$ \begin{array}{l}\mathrm{M}\mathrm{i}\mathrm{n}\kern1em {f}_{\mathrm{obj}}\left(\mathbf{X},{\mathbf{P}}_0\right)\\ {}\mathrm{s}.\mathrm{t}.\kern1.5em {\xi}_i\ge {\xi}_{i,t},\ i=1,2,\dots, k\ \\ {}\kern2.5em \eta \ge {\eta}_t\\ {}\kern2.5em \mathbf{P}\in \boldsymbol{\Omega} \end{array} $$

(19)

where ξ _i,t and η _t are the target indices of the ith RUC and RBC, respectively. When the values of these two kinds of indices equal 1, it implies that the designer allows no robust constraints violations. Therefore, in this paper, the levels of the robustness, i.e., the indices, are defined as requirements of the design. Several examples with different target indices are performed in the next section. It should be noted that if there are variations in some of the design variables, a subset of X belongs to P.

In (19), the index η concerns the robustness of RBC and it is defined by the proposed method in this paper. The definition of ξ is based on the work by Kang and Bai (2013) and it deals with robustness of RUC. These two indices handle different types of robustness and form a general form of robust optimization.

In this paper, the outer optimization is solved by the fmincon function of the Matlab Optimization Toolbox (2012b Release) optimization toolbox. In the inner level, the index of RUC ξ is obtained by HL-RF method, which is often used in reliability analysis (Hasofer and Lind 1974; Jiang et al. 2013; Rackwitz and Flessler 1978). The index of RBC η is acquired with the proposed algorithm. The flowchart for solving the double-looped optimization problem is shown in Fig. 5. As we can see from the figure, in each iteration of the outer optimization, the ξ and η should be calculated.

Fig. 5

Flowchart for solving the double-looped optimization problem

In order to verify the effectiveness of the proposed method for RBC, Monte Carlo simulation (MCS) is executed to compute the yield level β of solutions concerning the bounded constraints on performance variations. The yield level, i.e., the qualification rate of the structure under parameter uncertainty, represents the possibility that a qualified product occurs when the parameters are uncertain. In this circumstance, the word “qualification” means (16) is satisfied. The MCS for the yield level can be outlined as follows:

• 1. In δ space, make the n uncertain parameter as independent random variables under uniform distributions within the unit box and whereby obtain m ₁ samples. As shown in Fig. 6, all the obtained samples are uniformly distributed in an n-dimensional box.

  Fig. 6

  

  Samples for MCS for the computation of yield level

  Fig. 7

  

  A five-bar planar truss

• 2. Sequentially substitute the m ₁ samples into the unit hyper-sphere function δ ^T δ ≤ 1 and get m ₂ ones satisfying this function. Through this, we can obtain a pile of samples uniformly distributed in the n-dimensional unit hyper-sphere.

• 3. The m ₂ samples are transformed into x space, and then substitute all of them into the performance evaluation and obtain m ₃ samples satisfying the performance bounded constraint in (16).

• 4. The final yield level is β = m ₃/m ₂.

5 Numerical examples

For illustrating the validity of the proposed robust design formulation, two examples are given in this section. The first one copes with the problem with bar cross-section areas uncertainty and the second one regards the material property fluctuation. The aforementioned two kinds of robustness indices are both involved. The physical quantities are in the imperial system of units. The length unit is inch (in), the unit of elastic modulus is kilo pounds per square inch (ksi), the area unit is square inch (in²), and the force unit is kilo pounds-force (kip).

5.1 A five-bar planar truss structure design

The five-bar truss problem from Kang and Bai (2013) is tested in this paper, which is shown in Fig. 7. Uncertain cross-section areas are considered and the convex model is expressed as Ω _u  = {U|U ^T W _u U ≤ 1}, where W _u  = 100 × diag(1, 1, 1, 1, 1). The truss is subjected to a horizontal force P ₁ = 10 kip and a vertical force P ₂ = 10 kip at node 3. The design objective is to minimize the total volume of the structure while the nominal values of cross-section areas are design variables. Their lower/upper bound limits are x ^L _i  = 0.01 in², x ^U _i  = 40 in², i = 1, 2,..., 5. In this example, both the design variables and the uncertain parameters are the cross-section areas.

The horizontal and vertical displacements of node 3 are restricted by u ₃ ≤ 1.6 in and v ₃ ≤ 2.8 in, which are the unilateral constraints. Also, the bounded constraints are that the two displacement variations should be no more than 0.05 in from their nominal values, respectively.

Four cases of performance requirements and robustness index constraints are listed in Table 1. Case 1, 2 and 3 are with both RUC and RBC and Case 0 represents the optimization with only RUC. The Case 0 is carried out for comparison. A deterministic optimization is also carried out for comparison, which includes no robustness constraint but the two displacement limitations under no uncertainty.

Table 1 Optimization constraints for the five-bar truss optimization

The initial design and optimal results for the four cases are listed in Table 2. The values in bold mean that this constraint value of the optimal design reaches its boundary and it means the same in the following tables in this paper. From the optimization results the following conclusions can be drawn.

Table 2 Optimal solutions for the five-bar truss

(1) Better robustness can be achieved with larger material volume. (2) It is a direct proportional relationship between the indices of RUC ξ ₁, ξ ₂ and the index of RBC η, which means the larger the ξ, the larger the η, and vice versa. (3) In the optimal design results of the deterministic optimization and case 0, the values of η shows that the bound constraints on the displacement variations are not satisfied. (4) The RBC index η is able to represent the yield level, i.e., a larger η can guarantee a higher yield level and when η reaches 1, the yield level is 100%.

It should be noted that, η in deterministic optimization and Case 0 are the same 0.16, but the yield levels differ slightly. This is because the definition of η only concerns the smallest semi-axis length and the optimal solutions for these two designs are different in other axis lengths, which will lead to a different yield level.

The iteration histories of the optimization in case 1, 2 and 3 are shown in Fig. 8, which shows a stable convergence with a steady decrease of the structure material volume from the first iteration step.

Fig. 8

Iteration histories of the five-bar truss optimization

Table 2 has shown the effectiveness of the proposed method. In order to show the high-efficiency of the proposed algorithm, another optimization procedure is carried out based on the work by Kang and Bai (2013) as a comparison. The two bounded constraints (two displacement variations should be no more than 0.05 in from their nominal values) are transformed into unilateral constraints by square operator and therefore the optimization procedure has four indices of RUC (the other two are from u ₃ ≤ 1.6 and v ₃ ≤ 2.8). These four indices are obtained by the HL-RF method and therefore the whole design problem is a double-looped structure.

Due to the fact that the proposed method deals with the performance tolerance with norm operator which is shown in (16), and therefore it cannot be guaranteed that the optimal solutions satisfy every individual performance. In order to investigate to what extent the optimal solutions obtained by the proposed method satisfy every individual performance, a new yield level $\widehat{\beta}$ is developed by MCS. The computation of $\widehat{\beta}$ is the same as β except that the gross performance restriction is replaced by every individual performance restriction.

As shown in Table 3, the Kang’s method achieves a solution whose $\widehat{\beta}$ equals 100% with 465874 function calls while the number of function calls of Case 3 is 83395, which is only 17.9% of that of Kang and Bai’s method. The $\widehat{\beta}$ of Case 3 is 96% that is almost 100%. It can be concluded that the proposed method can produce a relatively good solution with considerably less computational time. It should also be noted that the main contribution of this paper is the development of the new index of RBC. Therefore the sensitivity information of the constraints (indices) with respect to the design variables have not been offered by the authors to the optimizer in the outer loop. This may lead to more function calls. Nevertheless, the two cases in the Table 3 are still comparative.

Table 3 Comparison of optimal solutions by Case 3 and Kang and Bai’s method for the five bar truss

5.2 A ten-bar planar truss structure design

A practical ten-bar planar truss with material property uncertainty is investigated in this example, which is shown in Fig. 9. This example is originally formulated by Kang and Bai (2013) and we slightly modified this problem by assuming a different uncertainty characteristic matrix. The structure is subjected to two vertically concentrated forces P ₁ = P ₂ = 100 kip at node 4 and 6, respectively. The total 10 bars are classified into two groups and the bars within each group have the same Young’s modulus. As shown in Fig. 9, the bars from number 1 to 6 are with an elastic modulus E ₁ whose nominal value is 10,000 ksi. The other bars are with an elastic modulus E ₂ whose nominal value is 8000 ksi. The design objective is to minimize the total volume of the structure and the nominal values of the cross-section areas are the design variables. Their lower/upper bound limits are x ^L _i  = 0.01 in², x ^U _i  = 40 in², i = 1, 2,..., 10. In this problem, the uncertain parameters P are the elastic modulus and the design variable X are cross-section areas. Therefore, from the two examples, the uncertainties can be from either design variables or parameters.

Fig. 9

A ten-bar planar truss

The vertical displacement of node 3 and node 6 are restricted by u ₃ ≤ 2.0 in and v ₆ ≤ 2.8 in respectively. Also, the acceptable performance variations of these two displacements are both 0.05 in.

The Young’s modulus E ₁ and E ₂ are uncertain parameters and the characteristic matrix of ellipsoid model is

$$ {W}_u=\left[\begin{array}{cc}\hfill 1000\hfill & \hfill 1.21\hfill \\ {}\hfill 1.21\hfill & \hfill 1210\hfill \end{array}\right] $$

(20)

The initial design and optimal results for the five cases are listed in Table 4. Obviously, the initial design satisfies all the three robustness constraints. A deterministic optimization is carried out for comparison, which includes no robustness constraints but the two displacement limitations. The results of the optimizations are listed in Table 5. The zero-valued robustness index ξ ₂ of the deterministic optimization indicates that any fluctuation around the nominal values will lead to violation of displacement requirement. The result of the robust optimization with only RUC (i.e., Case 0) can get a yield level of 75.92% and Case 4 can get a yield level of almost 100%.

Table 4 Optimization constraints for the ten-bar truss optimization

Table 5 Optimal solutions for the ten-bar truss

The results of MCS for Case 3 are given in Fig. 10. The declining ellipses in blue are the feasible ellipse and the unit-radius circle in red is uncertain sphere in 2-dimensional. From the results, we can see that no violation is observed in the whole uncertain circle, i.e., the yield level is almost 100%. The iteration histories of the optimization in case 1, 2 and 3 are shown in Fig. 11.

Fig. 10

Monte Carlo simulation results for the ten-bar robust optimization in case 3

Fig. 11

Iteration histories of the ten-bar truss optimization

In this circumstance, as shown in Table 6, the optimal solution of Case 3 achieves a $\widehat{\beta}$ of 88% with only 11% function calls compared with Kang and Bai’s method. Due to the fact that the Kang and Bai’s method handles the bounded constraints with each individual performance restriction, the $\widehat{\beta}$ it obtained is naturally 100%.

Table 6 Comparison of optimal solutions by Case 3 and Kang and Bai’s method for ten bar truss

The nominal displacements for the optimal designs of the two examples are listed in Table 7. As we can see, the displacements of optimal result of deterministic optimization reach the constraint boundary, i.e., this design cannot endure any uncertaity. The displacements of Case 1 to Case 3 are smaller than that obtained by Case 0 because Case 0 only takes RUC into account. From Case 1 to Case 3, with the increasement of requiement of index of RBC, the nominal values get smaller.

Table 7 The nominal displacements for the optimal designs of the two examples (in)

6 Discussions on the application scope of the proposed method

The application scope of the proposed method in section 3.3 is an important issue, especially when we consider it for engineering applications. Due to the fact that the assessment method is based on Jacobian matrix, which only uses the first–order derivatives, the proposed method may only be applicable in small uncertainty situation. Some investigations (Lee et al. 1999; Parkinson 1995) have found that if the component variations are less than 3–5% of the nominal dimensions, the linear relationship would hold. The uncertainty level may vary in different engineering problems and in this paper, the ten bar truss is used to demonstrate the application scope of the proposed method.

The MCS is used to compute the approximation error contour. The relative approximation error is defined as

$$ {\varepsilon}_i=\frac{f_i-\left({f}_{0,i}+{\mathbf{Y}}_i\right)}{f_i}\times 100\%,\kern0.5em i=1,2 $$

(21)

where ε _i is the ith approximation error and ε ₁ is for u ₃ and ε ₂ is for v ₆. f _i is the actual displacement and f _0,i is the nominal displacement without uncertainty. The contours and the uncertain ellipses defined by (20) are shown in Fig. 12. The readers can get such information. a) For these two displacements, when uncertainty level reaches around 12–18% (the maximal absolute deviation of two elastic modulus divided by their nominal values, respectively), the approximation errors are around 1–2%, which is considered as acceptable in practical engineering. b) The approximation errors in the uncertain ellipses adopted in the ten bar truss example are much smaller than 1%.

Fig. 12

The contours of relatively approximation error for the two displacements of the ten bar truss

Therefore, it is concluded that for truss problem, when the variations of the parameter are smaller than 18% of their nominal values, the method of section 3.3 can be employed. For other engineering problems, the parameter variation is usually far below 18%. Nevertheless, when the relation between parameters and performances is relatively nonlinear, a MCS is recommended before the adoption of the proposed method. Only several examples are required in the MCS to yield a general view of the approximation errors in the uncertainty region for the designers to see if it is acceptable in the particular engineering problem. If the approximation errors are acceptable within the uncertainty domain, then the presented method can be applied.

7 Conclusions

In this paper, a new robustness index is developed to handle bounded constraints on performance variation with convex uncertainty. The index can quantitatively measure the maximal allowable magnitude of system variations. By means of the proposed algorithm, the inner loop for the robustness evaluation of the bounded constraints of the traditional double-looped robust design problem can be replaced by a procedure without any optimization run and the robust design problem can be converted into a deterministic optimization with indices requirements. Two examples of truss structures design problem are investigated and the results show the validity of the proposed method.

Based on the numerical results, the following conclusions are drawn out.

• 1. The proposed method can directly handle the bounded constraints for performance variation in robust design without any optimization procedure. Compared with the traditional double-looped algorithm, the proposed method can achieve relatively good solutions with much less computational efforts.

• 2. In this method, the levels of the robustness, i.e., the indices, are defined as requirements of the design. This will allow the designers to decide the robustness of the system.

• 3. In the presented method, the gross performance but not necessarily every individual performance is acceptable. However, by the numerical examples, we can find that the proposed method can also obtain solutions with high possibilities that satisfy every performance tolerance.

• 4. For the uncertainty level in the two truss examples shown in this paper, the effectiveness of the proposed method has been testified. For other engineering problems with high nonlinearity, a MCS with not too many examples is recommended before the adoption of the proposed method.