Probabilistic measures for assessing appropriateness of robust design optimization solutions

Abstract

Robust design optimization (RDO) is a popular framework for addressing uncertainties in the design of engineering systems by considering different statistical measures, typically the mean and standard deviation of the system response. RDO can lead to a wide range of different candidate designs, establishing a different compromise between these competing objectives. This work introduces a new robustness measure, termed probability of dominance, for assessing the appropriateness of each candidate design. This measure is defined as the likelihood that a particular design will outperform the rival designs within a candidate set. Furthermore, a multi-stage implementation is introduced to facilitate increased versatility/confidence in the decision-making process by considering the comparison among smaller subsets within the initial larger set of candidate designs. For enhancing the robustness in these comparisons the impact of prediction errors, introduced to address potential differences between the real (i.e. as built) system and the numerical model adopted for it, is also addressed. This extends to proper modeling of the influence of the prediction error, including selection of its probability model, as well as evaluation of its impact on the probability of dominance and on the RDO formulation itself. Two illustrative examples are presented, the first considering the design of a tuned mass damper (TMD) for vibration mitigation of harmonic excitations and the second a topology optimization problem for minimum compliance. Extensive comparisons are presented in these two examples and the discussions demonstrate the power of the proposed approach for assessing the designs’ robustness.

1 Introduction

In engineering design, the performance predictions for the system under consideration may involve some level of uncertainty, stemming from the incomplete knowledge about the system itself and its excitation (Schuëller and Jensen 2008; Beck and Taflanidis 2013). Explicitly accounting for these uncertainties is exceptionally important for providing optimal configurations that exhibit a robust performance (Doltsinis 2004; Beck and Santana Gomes 2012). A probability logic approach provides a rational and consistent framework for performing this task (Jaynes 2003), employing probability models to characterize the relative plausibility of the different model parameter values. Within this setting, various formulations have been proposed for addressing the design of engineering systems under uncertainty (Schuëller and Jensen 2008; Doltsinis 2004; Beck and Santana Gomes 2012; Beyer and Sendhoff 2007), one of the more popular ones being Robust Design Optimization (RDO).

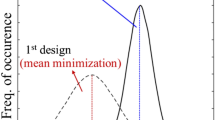
Typically, RDO is formulated (Beyer and Sendhoff 2007; Lee and Park 2001) by considering as objectives the mean value as well as the standard deviation of the performance (although different statistical measures can be also used), either within a multi-objective setting (Doltsinis 2004; Marler and Arora 2004) or, and perhaps more commonly, by formulating a single objective through the introduction of an appropriate weight between these two competing objectives (Dunning and Kim 2013; Lee and Park 2001). Different design can then be attained through this problem formulation either by varying the latter weight or by approaching the initial problem as an explicit multi-objective optimization, establishing a different compromise between the mean and standard deviation of the performance. Viewing this as a multi-objective optimization problem, these designs will lay on the region of the objective space defined as the Pareto frontier (Sawaragi et al. 1985). Frequently, this approach will provide designs that are fundamentally different in the design space, but exhibit similar robust traits (i.e. values for mean and variance). Selecting the most suitable design among the candidate set is then a challenging task, as it requires either some measure of appropriateness, or that a design stands out from the rest because of its superior performance (mean value) and robustness (standard deviation), which is, though, not the typical case as the two competing objectives usually conflict with one another.

The final design selection among the set of Pareto-optimal points, can be then viewed as the responsibility of a Decision Maker (DM) (Miettinen 1999). This selection process will typically involve the integration of additional criteria that were not part of the initial objective function formulation incorporating the DM preferences and experience. Normally, the DM preferences are explicitly quantified through adoption of a utility (or valued) function (Keeney and Raiffa 1993) which might entail some a posteriori modification of the problem objective/constraints. An interactive implementation can be also considered, with the DM providing explicit feedback during the solution phase (Reeves and Gonzalez 1989), which is though not the typical case in RDO applications, where the selection of a final design is executed after the Pareto-optimal designs have been generated (employing any desired method). A common preference function in this case (i.e., for RDO) for selecting the final design, especially when no other utility function is available and the DM cannot impose additional preferences a posteriori, is to use some metric between the Pareto-optimal points and a point of interest (Rangavajhala 2007), normally the utopia point, corresponding to the minimum mean and standard deviation treated as single-objectives for each instance (Beyer and Sendhoff 2007). This requires the definition of a proper norm (to quantify distance), and establishing a proper weighting of the two objectives for this purpose is not always straightforward.

This work introduces a new preferences measure, termed probability of dominance, and a multi-stage evaluation approach to aid the DM in assessing the appropriateness of different candidate designs within an RDO setting. This is intended to serve as an additional tool for the designer towards the selection of a preferred robust design, complementing any other preference and utility functions that may exist for the specific application of interest. The probability of dominance compares simultaneously the entire set of candidate designs and examines the favorability of each design for all different model parameter values. It is defined as the likelihood that the performance of a design will outperform all other designs in the set. This likelihood is quantified by considering the probabilistic description of the system uncertainties, explicitly incorporating all information available to the designer for comparing the available designs. A multi-stage implementation is also proposed that facilitates increased versatility in the decision-making process (and ultimately robustness) by considering the comparison among smaller subsets within the initial larger set of candidate designs. It should be stressed that this new preference measure requires a probabilistic definition of the uncertainties influencing the performance of the different designs under consideration, i.e. it is not devised for design selection of just any multi-objective problem.

For enhancing the robustness in the definition of the preference measure, the impact of prediction errors is introduced to address potential differences between the real (i.e. as built) system and the model adopted for it and quantify the incomplete information for the latter model (Weber 1987; Beck and Taflanidis 2013). Since inclusion of this error in the analysis has received little attention within the robust optimization literature, different aspects are examined in detail. This extends to proper modeling of the prediction error influence, including selection of a probability model for it, as well as its impact on the probability of dominance and on the RDO formulation. Two different error models are considered, corresponding to either additive or multiplicative influence of the prediction error, and comparisons are drawn between them. The correlation between the errors for different design configurations is also explored.

In the next section, the RDO formulation is reviewed, while in Section 3 the probability of dominance and the multi-stage formulation are introduced. Section 4 discusses the prediction error and then in Section 5 two illustrative examples are presented. The first one considers the design of a tuned mass damper (TMD) for vibration mitigation under harmonic excitations and the second one is a topology optimization problem of minimum compliance. Extensive comparisons are discussed in these two examples, with some emphasis on the influence of the prediction error on the robustness traits of the obtained solutions.

2 RDO problem formulation

Consider a system that involves some controllable parameters defined henceforth as design variables, and let $\mathbf{x}=\left[{x}_1\ {x}_2 \dots {x}_{n_x}\right]\in X\subset {\mathbb{R}}^{n_x}$ be the vector of design variables where X denotes the bounded admissible design space. Moreover, let $\boldsymbol{\uptheta} =\left[{\theta}_1\ {\theta}_2\dots {\theta}_{n_{\theta }}\right]\in \mathtt{\varTheta}\subset {\mathbb{R}}^{n_{\theta }}$ be the vector of uncertain model parameters (random variables) for the system model, where Θ denotes the set of their possible values defining the uncertain space. Α Probability Density Function (PDF) p(θ) - which incorporates our available knowledge about the system into its assumed numerical model - is assigned to these uncertain parameters. In addition, let $h\left(\mathbf{x},\boldsymbol{\uptheta} \right):{\mathbb{R}}^{n_x \times {n}_{\theta }}\to \mathbb{R}$ be the scalar performance function characterizing the favorability of the system’s behavior for the design selection x and model configuration θ. The simplest case for h(.) is to correspond directly to the model response; nevertheless, in many engineering applications other utility functions can be chosen to characterize the system performance. Initially we will assume that the numerical model provides accurate predictions for the performance of the real system. The existence of errors in these predictions will be addressed later, in Section 4.

Under the influence of the uncertain parameters in θ, h(x,θ) is itself a random variable. For RDO, two different statistical measures of h(x,θ) are typically used to characterize and address the impact of uncertainty in the description of the system-model (Doltsinis 2004). The first one is the mean value for h(x,θ), given by

$$ \mu \left(\mathbf{x}\right)=E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]={\displaystyle {\int}_{\varTheta }h\left(\mathbf{x},\boldsymbol{\uptheta} \right)p\left(\boldsymbol{\uptheta} \right)d\boldsymbol{\uptheta}}, $$

(1)

where E[.] stands for expected value, in this case under probability model p(θ), and the second one the standard deviation of h(x,θ), given by

$$ \sigma \left(\mathbf{x}\right)=\sqrt{E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]-E{\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]}^2}=\sqrt{{\displaystyle {\int}_{\varTheta }h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2p\left(\boldsymbol{\uptheta} \right)d\boldsymbol{\uptheta}}-\mu {\left(\mathbf{x}\right)}^2}. $$

(2)

Furthermore, σ ²(x) corresponds to the variance of h(x,θ).

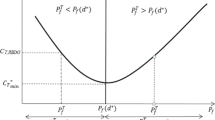
RDO establishes a compromise between the minimization of the mean value of the performance and the minimization of the spread of this performance around this mean value. The latter directly influences the robustness characteristics of the approach by implicitly providing a measure of response variability in the RDO formulation. These two statistical measures, define the feasible objective space, $\mathbf{F}\left(\mathbf{x}\right):=\left[\mu \left(\mathbf{x}\right)\ \sigma \left(\mathbf{x}\right)\right]\in F\subset {\mathbb{R}}^2$, and most often conflict with each other; therefore, the RDO problem can be viewed as a multi-objective minimization of μ(x), and σ(x). A key feature of the objective space F(x) is the utopia point, corresponding to the minimum of μ(x) and σ(x), when each of them is viewed as a separate objective. This point corresponds to the best solution in F, but in general is unattainable. The compromise between μ(x), and σ(x) is typically expressed through the Pareto front, composed (Marler and Arora 2004) of the designs for which no other feasible design exists that will simultaneously improve both competing objectives (in other words, it cannot make one better without making the other worse).

Several different methods have been proposed for formulating/solving the multi-objective RDO problem (Marler and Arora 2004; Kalyanmoy and Gupta 2006). A popular approach for obtaining an approximation to the Pareto front is to employ the weighed sum as objective function, in which a single objective is formed by employing a weighted liner combination of μ(x), and σ(x). This is the approach adopted in this study, leading to the optimization problem

$$ {\mathbf{x}}^{*}=\underset{\mathbf{x}\in X}{ \arg\ \min }f\left(\mathbf{x}\right), $$

(3)

where any constraints are incorporated in the definition of the admissible design space X and the objective function defined as

$$ f\left(\mathbf{x}\right) = \left(1-w\right)\frac{\mu \left(\mathbf{x}\right)}{\mu_n}+w\ \frac{\sigma \left(\mathbf{x}\right)}{\sigma_n}, $$

(4)

where w ∈ [0, 1] is the weight parameter and μ _n , σ _n are normalization constants for the mean and standard deviation respectively. Commonly, μ _n and σ _n are selected as the minimum mean and standard deviation (Lee and Park 2001), denoted by μ _ο and σ _ο that can be obtained by solving (4) when considering w = 0 and w = 1 respectively. Τhe point [μ _ο σ _ο ] is in fact the utopia point (Beyer and Sendhoff 2007). Moreover, the solution to the probabilistic integrals in Eqs. (1) and (2) is challenging to obtain, since often a close form solution does not exist. Thus, different approaches have been proposed for performing the optimization in Eq. (3), mainly differentiated by the methodologies adopted for approximating the aforementioned integrals. The references (Beyer and Sendhoff 2007; Doltsinis 2004) offer a detailed review of these methods in the context of RDO.

Independent of the optimization approach adopted, solution of the multi-objective RDO problem will lead to a set of optimum designs Δ = {x ^* _k , k = 1, …, m} composed of m different designs with corresponding objectives [μ(x _k ^*) σ(x _k ^*)]. Selection of a final design among this set requires the definition of an appropriate utility and preference functions to quantify appropriateness of each considered design. As discussed in the introduction, a common approach within RDO is to use as such preference function the distance in the objective space of each Pareto optimal point from the utopia point, which measures the departure of the established resultant probabilistic performance [μ(x _k ^*) σ(x _k ^*)] from the best (but unachievable) performance [μ _ο σ _ο ] using some appropriate weighted norm to calculate this distance. In this work a new probabilistic measure is introduced as a potential preference function that rather than looking at such resultant probabilistic measures or having to select an ad-hoc normalization, compares designs directly with one another with respect to the performance measure h(x,θ) over the uncertain parameter space.

3 Probability of dominance

Assume that a finite set of candidate designs Δ = {x _k , k = 1,…, m} is provided, where each design is accompanied by their associated performance h(x _k ,θ), and model parameters characterized by probability model p(θ). The framework discussed here ultimately provides a preference measure/index for assessing the appropriateness of each design, to aid the decision maker in the selection of a final design among the set members. Note that the approach is completely decoupled from the process of obtaining the set Δ; it simply assumes that some designs have been provided by the decision maker. This may correspond to a finite number of Pareto-optimal solutions for the problem under consideration, or to any desired set of candidate designs. For this purpose the explicit notation ^* to denote optimal design for x is not used henceforth.

3.1 Formulation for the entire set of candidate designs

The foundation of the method is the introduction of new preference measure, termed probability of dominance. This measure is defined as the likelihood that a candidate design x _i outperforms its rival designs within the set Δ under probability model p(θ) for the uncertain model parameters. Based on the total probability theorem this probability of dominance P _D is given by

$$ {P}_D\left({\mathbf{x}}_i|\Delta \right)={\displaystyle {\int}_{\varTheta }{P}_D\left({\mathbf{x}}_i|\Delta, \boldsymbol{\uptheta} \right)p\left(\boldsymbol{\uptheta} \right)d\boldsymbol{\uptheta}}, $$

(5)

where P _D (x _i |Δ, θ) stands for the probability of dominance given the model configuration θ and is equal to the probability that the performance for the i ^th design will outperform all other designs. Dominance is, thus, probabilistically attained when a particular design x _i has a better performance h(x,θ) relative to other designs under a specific realization of the uncertain parameters θ.

Assuming that a smaller performance is preferable, one has

$$ {P}_D\left({\mathbf{x}}_i|\Delta, \boldsymbol{\uptheta} \right)=P\left[{\displaystyle \underset{k=1,\ k\ne i}{\overset{m}{\cap }}\left(h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)<h\left({\mathbf{x}}_k,\boldsymbol{\uptheta} \right)\right)}\right]. $$

(6)

In the case that no prediction error is assumed for the model (the case with prediction error will be addressed later) this is also given by

$$ P\left[{\displaystyle \underset{k=1,\ k\ne i}{\overset{m}{\cap }}\left(\ h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)<h\left({\mathbf{x}}_k,\boldsymbol{\uptheta} \right)\right)}\right]=P\left[h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)=\underset{k=1,\dots, m}{ \min}\left(\ h\left({\mathbf{x}}_k,\boldsymbol{\uptheta} \right)\right)\right] $$

(7)

and it finally corresponds to the indicator function

$$ {P}_D\left({\mathbf{x}}_i|\Delta, \boldsymbol{\uptheta} \right)=I\left({\Delta}_i,\boldsymbol{\uptheta} \right)=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill \mathrm{if}\ h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)=\underset{k=1,\dots, m}{ \min}\left(\ h\left({\mathbf{x}}_k,\boldsymbol{\uptheta} \right)\right)\hfill \\ {}\hfill 0\hfill & \hfill \mathrm{otherwise},\hfill \end{array}\right. $$

(8)

with the notation I(Δ _i ,θ) used to symbolize the indicator function for the dominance of design i among the designs in set Δ.

The high-dimensional probability integral in (5) can be readily calculated through stochastic (Monte Carlo) simulation, leading to

$$ {\tilde{P}}_D\left({\mathbf{x}}_i|\Delta \right)=\frac{1}{N}{\displaystyle \sum_{j=1}^N{P}_D\left({\mathbf{x}}_i|\Delta, {\boldsymbol{\uptheta}}^j\right)}, $$

(9)

where the N samples for θ, with θ ^j denoting the j ^th sample, are simulated from p(θ). Since we are ultimately interested in the dominant design, corresponding to a high probability, it is anticipated that this approach will yield satisfactorily results (adequate accuracy) without significant computational burden (necessity to select high values for N). The accuracy of the estimation can be assessed through the coefficient of variation of the estimator whereas variance reduction approaches, such as importance sampling, can be used if that accuracy needs to be improved (Robert and Casella 2004).

The probability of dominance ultimately corresponds to a weighted measure of the hyper-volume of the region over Θ where a particular design has a performance that is the best among the candidate designs, with the weight provided by the relative likelihood p(θ) of the model parameters θ within Θ. This probability P _D (x _i |Δ) can be then utilized as a preference index for assessing the appropriateness of each design. If no other indicators are used in the decision making process then the final design may be chosen as the dominant design, i.e. the one corresponding to the maximum P _D (x _i |Δ)

$$ {\mathbf{x}}_D=\underset{i}{\operatorname{argmax}}{P}_D\left({\mathbf{x}}_i|\Delta \right). $$

(10)

An advantage of this measure is that it is independent of the design process, which allows its application to any arbitrary group of designs. However, a caveat of the approach is the fact that the result depends on the exact designs contained in the set Δ, with the final outcome potentially changing even when non-dominant designs are introduced into (or removed from) the set of candidate designs. This can happen if the new design only dominates (that is, provides better performance) in regions of the uncertain space that the previous best design used to dominate, thus detracting from the favorability of the previously dominant design only (and not of any other designs). This may ultimately switch the preference, without this new design emerging as the new dominant.

3.2 Multi-stage formulation

To circumvent the challenge identified at the end of the previous section, and provide enhanced versatility and robustness in the choice of a most appropriate design, a multi-stage formulation is developed. Rather than looking at the dominance over the entire set Δ, the dominance within d-dimensional subsets of Δ containing d total designs is considered (simplest choice for d is 2). A design is then termed as d-dominant if it is the dominant one within the n _d different d-dimensional subsets that include it. To formalize these ideas we will denote S ^d as the set of d-dimensional subsets of d, S ^d _i as the set of d-dimensional subsets including design x _i and will use subscript l to distinguish between the different elements of these sets (so S ^d _l denotes the l ^th subset of Δ containing d designs). For instance, if Δ = {A, B, C, D}, then S ² _C  = {[C A], [C B], [C D]} (thee candidate sets including two designs that have C as a member), S ³ _C  = {[C A B], [C A D]} (two candidate sets including three designs that have C as a member) whereas S ³ = {[C A B], [C A D], [D A B]} (three candidate sets including three total designs). The probability of dominance over subset S ^d _il is then

$$ {P}_D\left({\mathbf{x}}_l|{S}_{il}^d\right)={\displaystyle {\int}_{\varTheta }{P}_D\left({\mathbf{x}}_i|{S}_{il}^d,\boldsymbol{\uptheta} \right)p\left(\boldsymbol{\uptheta} \right)d\boldsymbol{\uptheta}}={\displaystyle {\int}_{\varTheta }P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left(h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)<h\left({\mathbf{x}}_k^{dli},\boldsymbol{\uptheta} \right)\right)}\right]p\left(\boldsymbol{\uptheta} \right)d\boldsymbol{\uptheta}}, $$

(11)

where x ^dli _k denotes the k ^th design within the S ^d _il set. This probability can be evaluated though stochastic simulation as in Eq. (9), employing Eq. (8) to describe the probability function within the integrand. The transformed equations are

$$ {\tilde{P}}_D\left({\mathbf{x}}_i|{S}_{il}^d\right)=\frac{1}{N}{\displaystyle \sum_{j=1}^N{P}_D\left({\mathbf{x}}_i|{S}_{il}^d,{\boldsymbol{\uptheta}}^j\right)}, $$

(12)

with

$$ {P}_D\left({\mathbf{x}}_i|{S}_{il}^d,\boldsymbol{\uptheta} \right)=I\left({S}_{il}^d,\boldsymbol{\uptheta} \right),=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill \mathrm{if}\ h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)=\underset{k=1,\dots, d}{ \min}\left(h\left({\mathbf{x}}_k^{dli},\boldsymbol{\uptheta} \right)\right)\hfill \\ {}\hfill 0\hfill & \hfill \mathrm{otherwise}.\hfill \end{array}\right. $$

(13)

The design x _i is defined to be dominant within the set S ^d _il if it has the largest probability of dominance within the set and it is considered to be d-dominant if it dominates each subset within S ^d _i . The overall preferred design could be taken as the one that is dominant within the lowest possible d-dimensional subsets considered. This does not necessarily mean that the chosen design will be dominant for higher values of d-dimensional subsets, but it exhibits the most robust dominance characteristics for the set Δ. For example, assume that a candidate design exhibits d = 2 dimensional dominance, then if some other design is removed from Δ, the candidate design will still enjoy the dominance property, whereas if an additional design is added, then if the older dominant design outperforms the newly added, it will also preserve its d = 2 dimensional dominance. Note that for certain values of d, it can be the case that no design emerges as dominant. For the example discussed in the first paragraph of this section, this will happen for the two-dimensional (d = 2) comparisons if A dominates B and D, but is dominated by C, whereas C is dominated at least by B. If on the other hand A dominates all B, C, and D (always within the context of individual comparisons) then A is the dominant design for the d = 2 dimensional subsets.

3.3 Quantification of preference within multi-stage implementation

Beyond just the simple notion of absolute dominance discussed above, i.e. which one is the best design, additional information that could be useful to guide the selection process is the relative dominance, i.e. how much better is one design over the next best alternative? To quantify a preference index associated with the relative dominance of a design, we define: (a) the margin of dominance between a particular design x _i and the rest of the designs within set S ^d _il as

$$ {M}_{il}^d={P}_D\left({\mathbf{x}}_i|{S}_{il}^d\right)-\underset{k=1,\dots, d,k\ne i}{ \max }{P}_D\left({\mathbf{x}}_k|{S}_{il}^d\right), $$

(14)

and (b) the degree of dominance of the design over the d-dimensional subsets as

$$ {D}_d\left({\mathbf{x}}_i\right)=\underset{l=1,\dots, {n}_d}{ \min }{M}_{il}^d. $$

(15)

The margin of dominance corresponds to the difference between the probability of dominance for x ⁱ compared to the design among the ones remaining in S ^d _il that has the highest probability of dominance. Positive values for this margin correspond to dominance of x _i in subset S ^d _il . The degree of dominance corresponds to the minimum of the margin of dominance for x _i among all subsets that include it. A positive value for it corresponds to d-dimensional dominance for x _i .

A robust preference towards a design can be then evaluated based on its degree of dominance by adopting a minimum threshold D _t  ≥ 0; The preferred design will be the one satisfying D _d (x) ≥ D _t , if one exists. If no design satisfies that condition, then, as discussed above, a larger value of d needs to be considered. More generally the degree of dominance can be used to provide guidance in the selection process; this is established by calculating D _d (x) for different values of d and using this information to evaluate the different design choices. In this case, the final selection is made by the designer, with D _d (x) serving as a tool aiding this decision. It can be the case that the designer will select a design with negative value D _d (x) as long as (i) that value is close to zero (the opposite means that the design is significantly dominated and thus should probably be avoided) and (ii) the design has some other desired attributes (that ultimately guide the preference towards it).

Note that for all the computations required to identify the dominant design [relying on stochastic simulation as described by Eq. (12)] the same sample set θ ^j can be used. As such, the performance function evaluations (which could be computationally intensive for complex models) used in the estimation of Eq. (12) can be the same ones used for Eq. (9), and the former evaluation merely needs proper comparison of these performance evaluations (not re-computation of the performance). Furthermore, to reduce the overall burden the results from the comparison within the set Δ can be used to guide the priority of comparisons; designs for which P _D (x _i |Δ) is small are not expected to dominate within any considered d-dimensional set and can be given lower priority in the comparisons. Considering these observations, the computational framework for identifying the dominant design within set Δ = {x _i , i = 1,…, m} (i.e. the design with lowest d-dimensional dominance) is the following:

• Step 1 Generate a set of N samples {θ ^j} from p(θ) and evaluate the performance for each one to obtain the set {h(x _i, θ ^j); i = 1,…,m j = 1,…,N}, if h(x _i, θ ^j) is not readily available from the optimization stage.

• Step 2 Calculate the probability of dominance for entire set Δ for each design i = 1,…,m by Eq. (12) utilizing the performance function evaluations from Step 1. Re-order the design based on their dominance P _D (x _i |Δ) to obtain set {${\underset{\bar{\mkern6mu}}{\mathbf{x}}}_c$, c = 1,…,m} and ignore any designs as deemed appropriate.

• Step 3 Set d = 2 and start the comparison form the smallest possible subset class.

• Step 4 Set c = 1 and start by considering the most dominant design based on P _D (x _i |Δ).

• Step 5 For all subsets in S ^d _c including ${\underset{\bar{\mkern6mu}}{\mathbf{x}}}_c$ estimate the probability of dominance for all designs included in it $\left\{{P}_D\left({\underset{\bar{\mkern6mu}}{\mathbf{x}}}_k\Big|{S}_{cl}^d\right);\ l=1,\dots, {n}_d,\ k=1,..,d\right\}$ using approximation in Eq. (12), calculated through the readily available performance function evaluations form Step 1. For the first subset comparisons (when d =2) this corresponds to comparison of a pair of designs and the probability of dominances for the compared designs are complimentary.

• Step 6 Calculate the margin of dominance with Eq. (14) and the degree of dominance with Eq. (15). If the latter is greater than zero (or the chosen threshold D _t ) then ${\underset{\bar{\mkern6mu}}{\mathbf{x}}}_c$ is the overall dominant design and process can stop. Else set c = c + 1 and go back to Step 5, understanding that a lot of the necessary probabilities ${P}_D\left({\underset{\bar{\mkern6mu}}{\mathbf{x}}}_k\Big|{S}_{\left(c+1\right)l}^d\right)$ have been already computed (when considering the smaller valued c’s). Perform Step 5 for the new ${\underset{\bar{\mkern6mu}}{\mathbf{x}}}_c$ only if it could emerge as a dominant one, meaning if it has not yet been dominated by any of the previously considered designs.

• Step 7 If all designs have been examined i.e. c = m, and no dominant design has been identified for the d-dimensional subsets then set d = d + 1 and go back to Step 4.

Through this approach, the design exhibiting the lowest possible d-dimensional dominance is identified. As will be illustrated later, this frequently (but not necessarily always) corresponds to 2-dimensional dominance and to a design having a large associated value of P _D (x _i |Δ). This design is guaranteed to outperform all other designs within the considered class of candidate designs. If the more general approach is adopted, i.e. the degree of dominance is evaluated for different values of d rather than the dominant design identified, the same computational approach is utilized with the only difference that the stopping criteria in Steps 6 and 7 for the identification process are ignored; rather, the evaluation is repeated for all desired values of d and all designs. The entire process will be illustrated in the examples considered later.

4 Impact of prediction error on the probability of dominance

The previous analysis assumed no error between the response of the actual system, denoted h _s(x) henceforth, and that of its assumed model, h(x,θ) [in other words, it was taken that h _s (x) = h(x,θ)]. The notation h _s(x) is used to stress the fact that the real system is dependent on the exact design selection x, and its performance is independent of the numerical model assumed and thus of θ (although θ is obviously related to the system properties). This assumption, i.e. h _s (x) = h(x,θ), is the reason why the probability P _D (x _i |S ^d _il , θ) ultimately corresponds to the indicator function I(S ^d _il , θ) in the analysis discussed in Section 3.

In any engineering application, though, the adopted model cannot describe exactly the behavior of the actual system (Beck 2010); a prediction error always exist and its incorporation in probabilistic analysis can have an impact on the design choices as has been shown recently in (Taflanidis and Beck 2010). This error, e, quantifies the difference between h _s (x) and h(x,θ) and since it is unknown, it can be probabilistically described by assigning a probability density function p(e) for it, treating it like any other uncertain model parameter. This prediction error can be viewed as describing (a) un-modeled characteristics of the system model or (b) un-modeled uncertainties for θ (Beck 2010; Beck and Taflanidis 2013). In this section, the influence of this error on the probability of dominance will be investigated to enhance the robustness in the selection process of the final design. This will extend to the selection of appropriate probability models for this error, a task that has received limited attention for engineering design application. The two most common models will be considered for the impact of the error, these are either additive or multiplicative influence on h(x,θ). Furthermore, the assumption that e is independent of θ will be utilized (this ultimately means independence between p(θ) – or equivalently h(x,θ) – and e). The latter assumption introduces the largest amount of uncertainty in the problem formulation (Taflanidis and Beck 2010; Jaynes 2003) and is the reason adopted here (establishing a greater robustness), as it assumes the least amount of information imposed upon the problem description.

4.1 Correlation of errors between designs

Before moving forward, the correlation between errors for different design selections needs to be addressed, as this correlation will be important in assessing the probability P _D (x _i |S ^d _il , θ). This correlation is expected to depend on the distance between x _i and x _k ; if the two designs are very similar, then any prediction errors for the system numerical model are expected to be the same for both of them since the system models examined (under design configurations x _i and x _k ) are similar. Note that assuming no correlation introduces the largest amount of uncertainty in the problem formulation, but in this case this is not a reasonable choice. In the examples considered later, an exponential function will be assumed for the correlation coefficient ρ _ik between designs i and k given by

$$ {\rho}_{ik} = \exp \left(-\lambda \left|\right|{\mathbf{x}}_i-{\mathbf{x}}_k\left|\right|{}_v^2\right)= \exp \left[-\lambda {\displaystyle \sum_{l=1}^{n_x}{v}_l^2{\left({x}_{il}-{x}_{jl}\right)}^2}\right], $$

(16)

where ||x _i  − x _k || _v stands for the weighted Euclidean norm with v _l weight for each component of vector x, while λ is the assumed decay rate of the exponential function. Exact selection of these terms will be discussed in the examples later. It should be stressed that, even though the use of exponential type of functions to describe correlation is popular in engineering applications (Lophaven et al. 2002), this choice is ultimately ad-hoc, especially due to the dependence on the chosen norm and decay rate λ, and if more information is available for the prediction error and its relationship to the design configuration, some different correlation structure can be adopted (Papadimitriou and Lombaert 2012) (note that this type of information is, though, not available in most practical engineering problems).

For the analysis in this section, a correlation coefficient ρ _ik between designs will be utilized, assumed to be defined by the designer through any appropriate method chosen (Papadimitriou and Lombaert 2012), whereas in the examples, the impact of this correlation on the final design choice will be examined using the correlation function in Eq. (16). Next, the different modeling choices for the prediction error and their impact on the probability of dominance are discussed.

4.2 Additive prediction error

The most commonly used assumption for the prediction error is an additive influence [this agrees with the assumption commonly used for Bayesian system identification applications (Beck and Taflanidis 2013)], leading to

$$ {h}_s\left(\mathbf{x}\right)=h\left(\mathbf{x},\boldsymbol{\uptheta} \right)+e. $$

(17)

The mean for the system model is updated as

$$ {\mu}_s\left(\mathbf{x}\right)=E\left[{h}_s\left(\mathbf{x}\right)\right]=E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)+e\right]=E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]+E\left[e\right]=E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]=\mu \left(\mathbf{x}\right), $$

(18)

where E[e] is taken equal to zero in order to establish unbiased predictions. Similarly, the variance is transformed to

$$ \begin{array}{l}{\sigma}_s^2\left(\mathbf{x}\right)=E\left[{h}_s^2\left(\mathbf{x}\right)\right]-{\mu}_s^2\left(\mathbf{x}\right)=E\left[{\left(h\left(\mathbf{x},\boldsymbol{\uptheta} \right)+e\right)}^2\right]-{\mu}^2\left(\mathbf{x}\right)\\ {}\kern2.5em =E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]+2E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\ e\right]+E\left[{e}^2\right]-{\mu}^2\left(\mathbf{x}\right)\\ {}\kern2.5em = \left(E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]-{\mu}^2\left(\mathbf{x}\right)\right)+E\left[{e}^2\right]+2E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\ \right]E\left[e\right]\\ {}\kern2.5em = {\sigma}^2\left(\mathbf{x}\right)+E\left[{e}^2\right]={\sigma}^2\left(\mathbf{x}\right)+{\sigma}_e^2,\ \end{array} $$

(19)

where σ ² _e is the variance of the prediction error and for the second to last equality the independence between e and h(x,θ) was utilized. These equations show that to characterize the statistics of interest, knowledge of only the mean and variance of the error is necessary, while to establish unbiased predictions the mean needs to be zero. This also agrees with modeling intuition: the error in Eq. (17) should be zero mean (the opposite would indicate a consistent bias in the predictions of the numerical model). Thus, the minimum additional information needed to quantify the error statistically is its variance. Based on this information, the probability model for p(e) is chosen as Gaussian with zero mean and variance σ ² _e . This Gaussian model is the probability model that maximizes the entropy, or equivalently, it incorporates the largest amount of uncertainty in the definition of p(e), assuming that only its mean and variance are known (Jaynes 2003), and is the reason why it is chosen.

Therefore, the only remaining question for the complete description of p(e) is: how should its variance be defined? Note that based on Eq. (17) the error in this case (and so its variance) has same units as the performance function. Rather than choosing the variance to be constant in the design space a reasonable assumption is to take the error statistics to be dependent upon the statistic of the system model. If the error is assumed to represent un-modeled uncertainties then σ ² _e should be set as a fraction of the variance of the system model

$$ {\sigma}_e^2={\gamma}^2{\sigma}^2\left(\mathbf{x}\right), $$

(20)

where γ is a proportionality constant. Note that this constant will typically have a small value since the error is expected to be small, at least if the engineering model predictions are expected to be close to the real system behavior. Through Eq. (20) the error statistics are scaled based on the variability observed for the system model and stemming from the uncertainty in θ; if that variability is small then so will be the error, showing that in fact the error does primarily address un-modeled uncertainties. If, on the other hand, the error is taken to represent also un-modeled characteristics of the system then a more reasonable assumption is to select it proportional to the second moment of the response, scaling the overall magnitude of the response

$$ {\sigma}_e^2={\gamma}^2E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]={\gamma}^2{\sigma}^2\left(\mathbf{x}\right)+{\gamma}^2{\mu}^2\left(\mathbf{x}\right). $$

(21)

The latter components in Eq. (21), i.e. γ ² μ ²(x), can be considered to address the un-modeled characteristics of the real system, with the first component representing the un-modeled uncertainties. Both these assumptions ultimately lead to an error variance that is dependent upon the design configuration σ ² _e  = σ ² _e (x). Modeling assumption in Eq. (20) will be referred hereafter as variance proportional and modeling assumption in Eq. (21) as moment-proportional.

Once the error has been defined, the important question is how to incorporate it in the analysis for the probability of dominance? In other words, how is P _D (x _i |S ^d _il , θ) modified by considering the influence of the prediction error. In this case P _D (x _i |S ^d _il , θ) is expressed with respect to the real system behavior

$$ {P}_D\left({\mathbf{x}}_i|{S}_{il}^d,\boldsymbol{\uptheta} \right)=P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left({h}_s\left({\mathbf{x}}_i\right)<{h}_s\left({\mathbf{x}}_k^{dli}\right)\right)}\Big|\boldsymbol{\uptheta} \right] $$

(22)

and utilizing Eq. (17) to introduce the impact of the prediction error Eq. (22) is transformed to

$$ P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left({h}_s\left({\mathbf{x}}_i\right)<{h}_s\left({\mathbf{x}}_k\right)\right)}\Big|\boldsymbol{\uptheta} \right]=P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left(h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)+{e}_i<h\left({\mathbf{x}}_k,\boldsymbol{\uptheta} \right)+{e}_k\right)}\right], $$

(23)

where the superscript dli is omitted herein for notational simplicity and a subscript is used for e to denote the design configuration that each error term corresponds to. This then leads to

$$ \begin{array}{l}P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left(h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)+{e}_i<h\left({\mathbf{x}}_k,\boldsymbol{\uptheta} \right)+{e}_k\right)}\right]=P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left({e}^i-{e}^k<h\left({\mathbf{x}}_k,\boldsymbol{\uptheta} \right)-h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\right)}\right]\\ {}\kern13em =P\left[\left[\begin{array}{c}\hfill {e}_i-{e}_1\hfill \\ {}\hfill {e}_i-{e}_2\hfill \\ {}\hfill \dots \hfill \\ {}\hfill {e}_i-{e}_d\hfill \end{array}\right]\le \left[\begin{array}{c}\hfill h\left({\mathbf{x}}_1,\boldsymbol{\uptheta} \right)-h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\hfill \\ {}\hfill h\left({\mathbf{x}}_2,\boldsymbol{\uptheta} \right)-h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\hfill \\ {}\hfill \dots \hfill \\ {}\hfill h\left({\mathbf{x}}_d,\boldsymbol{\uptheta} \right)-h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\hfill \end{array}\right]\right]\end{array}, $$

(24)

where the different inequalities in the latter expression are examined component-wise.

Considering now the vector

$$ \left[\begin{array}{c}\hfill {e}_i-{e}_1\hfill \\ {}\hfill {e}_i-{e}_2\hfill \\ {}\hfill \dots \hfill \\ {}\hfill {e}_i-{e}_d\hfill \end{array}\right] $$

(25)

and based on the assumed probability model for each of the error terms, it will follow (Johnson and Wichern 2002) a Gaussian distribution with zero mean and covariance matrix with elements (the k ^th, and q ^th entry is presented below)

$$ \begin{array}{l}E\left[\left({e}_i-{e}_k\right)\left({e}_i-{e}_q\right)\right]=E\left[{e}_i^2\right]-E\left[{e}_i{e}_q\right]-E\left[{e}_k{e}_i\right]+E\left[{e}_k{e}_q\right]\\ {}\kern7.75em ={\sigma}_{ei}^2-{\sigma}_{ei}{\sigma}_{eq}{\rho}_{iq}-{\sigma}_{ei}{\sigma}_{ek}{\rho}_{ki}+{\sigma}_{ek}{\sigma}_{eq}{\rho}_{kq}\end{array}, $$

(26)

where a subscript is used to denote the relationship of the error’s standard deviation to the design configuration since such a relationship has been introduced based on Eqs. (20) or (21). For the diagonal elements of the covariance matrix this relationship simplifies to

$$ E\left[{\left({e}_i-{e}_k\right)}^2\right]={\sigma}_{ei}^2+{\sigma}_{ek}^2-2{\sigma}_{ei}{\sigma}_{ek}{\rho}_{ik}. $$

(27)

Since the probability model for the error vector in Eq. (25) is known, the probability in Eq. (24) corresponds to the associated cumulative distribution function (CDF). This eventually leads to

$$ {P}_D\left({\mathbf{x}}_i|{S}_{il}^d,\boldsymbol{\uptheta} \right)={F}_G\left[D{h}_{il}^d\left(\boldsymbol{\uptheta} \right),0,{\boldsymbol{\Sigma}}_{il}^d\right] $$

(28)

and probability of dominance given by

$$ {P}_D\left({\mathbf{x}}_i|{S}_{il}^d\right)={\displaystyle {\int}_{\varTheta }{F}_G\left[D{h}_{il}^d\left(\boldsymbol{\uptheta} \right),0,{\boldsymbol{\Sigma}}_{il}^d\right]p\left(\boldsymbol{\uptheta} \right)d\boldsymbol{\uptheta}}, $$

(29)

where F _G [Dh ^d _il (θ), 0, Σ ^d _il ] stands for the CDF of the multivariate Gaussian distribution with zero mean, and covariance matrix Σ ^d _il with elements given by Eq. (26) obtained by comparing the error for the i ^th design to the error of each other element of S ^d _il . This CDF is evaluated at the vector of differences between the performances of each of these designs to the performance of the i ^th design (recall this vector does not include the i ^th design), given by

$$ D{h}_{il}^d\left(\boldsymbol{\uptheta} \right)=\left[\begin{array}{c}\hfill h\left({\mathbf{x}}_1^{dli},\boldsymbol{\uptheta} \right)-h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\hfill \\ {}\hfill h\left({\mathbf{x}}_2^{dli},\boldsymbol{\uptheta} \right)-h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\hfill \\ {}\hfill \dots \hfill \\ {}\hfill h\left({\mathbf{x}}_d^{dli},\boldsymbol{\uptheta} \right)-h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\hfill \end{array}\right]. $$

(30)

The introduction of the prediction error leads to modification of the initial indicator function, which was imposing a binary distinction for the system performance (either dominates or not), to a preference function. This function is expressed as the likelihood of dominance based on the difference between the performance of the design of interest and the performance of the other designs under consideration given by Eq. (30), as well as the statistics of the prediction error, introduced through the covariance matrix Σ ^d _il . Note that this ultimately corresponds to analytical integration over the prediction error on the initial probabilistic integral of Eq. (22). Figure 1 illustrates this concept for a two-dimensional example (comparison of two designs). It is evident that increasing the prediction error variance (equivalent in this case to increasing β) provides a smoother transition between the two extreme cases, as the amount of uncertainty in the system description increases, reducing the confidence in assessing the real-system dominance when knowing the dominance characteristics for the model.

Fig. 1

Likelihood function for comparison of x _i against A = {x _k } for different values of β ² = σ ² _ei  + σ ² _ek  − 2σ _ei σ _ek ρ _ik

Computationally, the probability of dominance with the prediction error can be still evaluated by Monte Carlo simulation as in Eq. (12) substituting P _D (x _i |S ^d _il , θ ^j) with F _G [Dh ^d _il (θ ^j), 0, Σ ^d _il ]. The latter multivariate CDF can be estimated by any standard numerical approach. In the example later, the highly efficient algorithm proposed in (Genz 1992) is adopted. For assessing the dominance over the entire set, the approach is same as above and simply needs to utilize Δ instead of S ^d _il .

4.3 Multiplicative prediction error

Modeling prediction errors through a multiplicative assumption is also common in the engineering literature (Taflanidis et al. 2013; Porter et al. 2007), especially for performance function that must take strictly positive values. The relationship between system and model performance in this case is

$$ {h}_s\left(\mathbf{x}\right)=h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\cdot e, $$

(31)

with e > 0 corresponding to a dimensionless quantity. This modeling assumption for the prediction error addresses both un-modeled uncertainties and un-modeled characteristics in the numerical model since it directly scales the entire performance function (the option of addressing only un-model uncertainties does not exist here). The mean and variance for the real system, respectively, are

$$ {\mu}_s\left(\mathbf{x}\right)=E\left[{h}_s\left(\mathbf{x}\right)\right]=E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\cdot e\right]=E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]\cdot E\left[e\right]=E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]=\mu \left(\mathbf{x}\right), $$

(32)

$$ \begin{array}{l}{\sigma}_s^2\left(\mathbf{x}\right)=E\left[{h}_s^2\left(\mathbf{x}\right)\right]-{\mu}_s^2\left(\mathbf{x}\right)=E\left[{\left(h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\ e\right)}^2\right]-{\mu}^2\left(\mathbf{x}\right) = E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]\ E\left[{e}^2\right]-{\mu}^2\left(\mathbf{x}\right)\\ {}\kern2.25em ={\sigma}^2\left(\mathbf{x}\right)+E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]\ \left(E\left[{e}^2\right]-1\right)={\sigma}^2\left(\mathbf{x}\right)+E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]\ {\sigma}_e^2,\end{array} $$

(33)

where E[e] is taken equal to one in order to establish unbiased predictions and the independence between e and θ was used in the third equality in both relationships above. Similarly to the case of additive prediction error, only the mean and variance of the error are necessary to determine the statistics of interest for the real system behavior. To establish unbiased predictions the mean of the error needs to be one. Since in this case the error e is dimensionless and directly scales the model performance, its variance should be independent of the characteristics of the model and so it is assumed to be σ ² _e  = γ ², with γ having typically a small value (similar justification as for additive error). Note that for the same value of γ there is an equivalence for the statistics of the real-system response between the multiplicative error and the additive error with moment-proportional variance modeled through Eq. (21). This is also consistent with the fact that both of these cases address both (i) un-modeled uncertainties and (ii) un-modeled system characteristics.

Furthermore, taking the log of Eq. (31) we have

$$ \log \left({h}_s\left(\mathbf{x}\right)\right)= \log \left(h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right)+ \log (e), $$

(34)

which means then that the log(e) has an additive influence on the log of the performance. Based on this observation the common assumption for the multiplicative prediction error probability model is a lognormal distribution. This also agrees with the most appropriate model based on the maximum entropy principle if the available knowledge is assumed to be on the log of error (rather than the error itself) to circumvent the e > 0 constraint. This means that ε = log(e) follows a Gaussian distribution with mean and variance

$$ \begin{array}{l}{\mu}_{\varepsilon }=-{\sigma}_{\varepsilon}^2/2,\\ {}{\sigma}_{\varepsilon}^2= \log \left({\sigma}_e^2+1\right)\approx {\sigma}_e^2,\end{array} $$

(35)

where the approximation in the second equation is established assuming that σ ² _e is small and the first equality is necessary so that E[e] = 1.

The modification for P _D (x _i |S ^d _il , θ) is in this case

$$ \begin{array}{l}{P}_d\left({\mathbf{x}}_i|{S}_{il}^d,\boldsymbol{\uptheta} \right)=P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left({h}_s\left({\mathbf{x}}_i\right)<{h}_s\left({\mathbf{x}}_k^{dli}\right)\right)}\Big|\boldsymbol{\uptheta} \right]=P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left( \log \left({h}_s\left({\mathbf{x}}_i\right)\right)< \log \left({h}_s\left({\mathbf{x}}_k^{dli}\right)\right)\right)}\Big|\boldsymbol{\uptheta} \right]\\ {}\kern5em =P\left[{\displaystyle \underset{k=1,k\ne i}{\overset{d}{\cap }}\left( \log \left(h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)+{\varepsilon}_i\right)< \log \left(h\left({\mathbf{x}}_k^{dli},\boldsymbol{\uptheta} \right)+{\varepsilon}_k^{dli}\right)\right)}\Big|\boldsymbol{\uptheta} \right]\end{array}, $$

(36)

which is then analyzed in a similar way as for the additive error since ε = log(e) is Gaussian, leading to

$$ {P}_D\left({\mathbf{x}}_i|{S}_{il}^d,\boldsymbol{\uptheta} \right)={F}_G\left[D{l}_{il}^d\left(\boldsymbol{\uptheta} \right),0,{\boldsymbol{\Sigma}}_{il}^d\right], $$

(37)

where Dl ⁱ _dl (θ) is the vectors of the difference between the logarithms of the performance

$$ D{l}_{il}^d\left(\boldsymbol{\uptheta} \right)=\left[\begin{array}{c}\hfill \log \left(h\left({\mathbf{x}}_1^{dli},\boldsymbol{\uptheta} \right)\right)- \log \left(h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\right)\hfill \\ {}\hfill \log \left(h\left({\mathbf{x}}_2^{dli},\boldsymbol{\uptheta} \right)\right)- \log \left(h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\right)\hfill \\ {}\hfill \dots \hfill \\ {}\hfill \log \left(h\left({\mathbf{x}}_d^{dli},\boldsymbol{\uptheta} \right)\right)- \log \left(h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\right)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \log \left(h\left({\mathbf{x}}_1^{dli},\boldsymbol{\uptheta} \right)/h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\right)\hfill \\ {}\hfill \log \left(h\left({\mathbf{x}}_2^{dli},\boldsymbol{\uptheta} \right)/h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\right)\hfill \\ {}\hfill \dots \hfill \\ {}\hfill \log \left(h\left({\mathbf{x}}_d^{dli},\boldsymbol{\uptheta} \right)/h\left({\mathbf{x}}_i,\boldsymbol{\uptheta} \right)\right)\hfill \end{array}\right] $$

(38)

and the covariance matrix Σ ^d _il has elements

$$ E\left[\left({\varepsilon}_i-{\varepsilon}_k\right)\left({\varepsilon}_i-{\varepsilon}_q\right)\right]={\sigma}_{\varepsilon}^2\left(1+{\overline{\rho}}_{kq}-{\overline{\rho}}_{iq}-{\overline{\rho}}_{ki}\right), $$

(39)

where ${\overline{\rho}}_{ik}$ is the correlation between ε _i  = log(e _i ) and ε _k  = log(e _k ), which can be readily obtained (Law and Kelton 2000) based on the correlation of e _i and e _k , ρ _ik , through

$$ {\overline{\rho}}_{ik}=\frac{ \ln \left(1+{\rho}_{ik}{\sigma}_e^2\right)}{ \ln \left(1+{\sigma}_e^2\right)}\approx {\rho}_{ik}\frac{\sigma_e^2}{\sigma_e^2}={\rho}_{ik}, $$

(40)

where the assumption that σ _e is small was used for the approximation in the second equality.

Thus, the evaluation under the impact of multiplicative error follows exactly the same approach as for the additive error, simply replace the CDF in Eq. (28) with a similar CDF given by Eq. (37).

4.4 Impact of prediction error on the RDO formulation

Beyond the impact on the probability of dominance, the influence of the prediction error on the RDO designs can be also examined. In the objective function of Eq. (4) the statistics of the real system are substituted, leading to

$$ f\left(\mathbf{x}\right)=\left(1-w\right)\frac{\mu_s\left(\mathbf{x}\right)}{\mu_{sn}}+w\ \frac{\sigma_s\left(\mathbf{x}\right)}{\sigma_{sn}}, $$

(41)

with [μ _sn σ _sn ] corresponding to the new normalization, selected based on the utopia point for the real system [μ _so σ _so ]. For multiplicative prediction error or for additive prediction error with moment-proportional scaled variance of Eq. (21) this leads to

$$ \begin{array}{l}f\left(\mathbf{x}\right)=\left(1-w\right)\frac{\mu \left(\mathbf{x}\right)}{\mu_{so}}+w\frac{\sqrt{\sigma^2\left(\mathbf{x}\right)+E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]\ {\gamma}^2}}{\sigma_{so}}\\ {}\kern2em =\left(1-w\right)\frac{\mu \left(\mathbf{x}\right)}{\mu_o}+w\frac{\sqrt{E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]\ \left(1+{\gamma}^2\right)-{\mu}^2\left(\mathbf{x}\right)}}{\sigma_{so}}\end{array}, $$

(42)

with μ _so  = μ _o , σ _so  ≠ σ _o . For the additive error with the scaling of Eq. (20) the new objective function is

$$ f\left(\mathbf{x}\right)=\left(1-w\right)\frac{\mu \left(\mathbf{x}\right)}{\mu_{so}}+w\frac{\sigma \left(\mathbf{x}\right)}{\sigma_{so}}\sqrt{1+{\gamma}^2}=\left(1-w\right)\frac{\mu \left(\mathbf{x}\right)}{\mu_o}+w\frac{\sigma \left(\mathbf{x}\right)}{\sigma_o} $$

(43)

with ${\mu}_{so}={\mu}_o,{\sigma}_{so}=\sqrt{1+{\gamma}^2}{\sigma}_o$, and thus it remains identical to the objective function with respect to the system-model performance of Eq. (4) as long as the objective function is normalized with respect to the new utopia point. Note that as mentioned earlier, the expressions of the additive error with moment scaling and the multiplicative error yield the same model variance.

4.5 Summary for modeling/impact of the prediction error

This section addressed the influence of the model prediction error on the probability of dominance as well as on the RDO formulation. The modeling of this error was also extensively discussed and various reasonable modeling assumptions were presented, the most important being that the adopted numerical model for the system provides unbiased predictions for the expected performance. Additive and multiplicative impact of the error were considered and the assumed probability models were suggested to be (i) Gaussian with zero mean and variance scaled according to the statistics of the numerical model and (ii) lognormal with mean unity and a constant variance (independent of the model statistics). The additive prediction error can possibly be chosen to address only un-modeled uncertainties, with its variance scaled according to the response variance of the assumed numerical model (because of the modeled uncertainties θ). In this case, the formulation of the RDO problem is not impacted at all. The additive error can also be selected to address both un-modeled uncertainties and un-modeled system characteristics, with its variance scaled according to the second moment of the numerical model. This is equivalent to the multiplicative prediction error in terms of how it impacts the statistics of the real system performance and ultimately the RDO formulation.

Lastly, the impact of the modeling error on the probability of dominance can be readily addressed by substituting the indicator function describing the favorability of the design given the system model, with a likelihood function dependent upon the assumed probability model of the error and the model performance.

5 Illustrative examples

The proposed framework is now illustrated with two examples. The first example considers the design of a tuned mass damper (TMD) for vibration mitigation of harmonic excitations and extensive comparisons are established for a variety of different cases. These cases mainly vary in the probability models utilized for p(θ) and the error assumptions. Τhe second example discusses the topology optimization problem for minimum compliance and the discussion (due to space constraints) focuses only on specific cases of interest.

5.1 Design of a robust tuned mass damper

Tuned mass dampers (TMDs) are widely used to mitigate vibrations for a variety of different structural systems (Chang 1999; Karrem and Kline 1993; Kwon and Park 2004). They consist (as seen in Fig. 2) of a secondary mass, m _d , connected to the primary mass through a spring with stiffness k _s  = ω ² _d m _s and a dashpot with damping coefficient c _d  = 2ζ _d ω _d m _d , where ω _d represents the damper’s natural frequency and ζ _d its damping ratio. Through the proper tuning of these two design variables (stiffness and damping) significant reduction of the response can be achieved for a variety of dynamic environmental excitations.

Fig. 2

Schematic of single degree of freedom system with tuned mass damper. The equations of motion are also shown in the figure

The RDO of TMDs has been extensively discussed in the literature (Marano et al. 2008; Mohtat and Dehghan-Niri 2011; Debbarma et al. 2010; Zang et al. 2005). Here the design of a TMD to mitigate the vibrations of a bridge structure, modeled as a single degree of freedom (SDOF) system, under harmonic (monochromatic) excitation is considered, a problem similar to the one discussed in (Zang et al. 2005). Fig. 2 shows the details, a SDOF, with mass m _s , stiffness k _s  = ω ² _s m _s , and damping coefficient c _s  = 2ζ _s ω _s m _s (where ω _s represents the natural frequency and ζ _s the damping ratio), equipped with a TMD is considered, under the impact of dynamic excitation F _f (t). The mass of the damper m _d is taken as 0.5 % of the median (i.e., nominal) mass of the structure. The design variables correspond to the damper stiffness and damping coefficient x = [k _d c _d ]^T. The uncertain model parameters correspond to the mass, stiffness, and damping ratio of the structure, θ = [m _s k _s ζ _s ]^T. For all of these, independent lognormal distributions are assumed with coefficient of variation γ _c and median values 17,500 kg for m _s , 3 MN/m for k _s and 3 % for ζ _s . Two cases are considered for γ _c , representing different levels of assumed uncertainty in θ, the first corresponding to 30 % coefficient of variation and the second to 10 % coefficient of variation. These cases will be termed large variability and small variability, respectively.

The performance function is taken as the maximum of the amplification factor, corresponding to the maximum of the dynamic response for a monochromatic excitation over every potential frequency ω. This ultimately leads to (Chang 1999)

$$ \begin{array}{l}h\left(\mathbf{x},\boldsymbol{\uptheta} \right)=\underset{\beta_f}{ \max}\left[\frac{\sqrt{{\left[{\varphi}^2-{\beta}_f^2\right]}^2+{\left(2{\zeta}_d\varphi {\beta}_f\right)}^2}}{\sqrt{E_s^2+{D}_s^2}}\right];\varphi =\frac{\omega_d}{\omega_s},{\beta}_f=\frac{\omega }{\omega_s},\kern0.75em \\ {}{E}_s=\left[1-{\beta}_f^2\right]\left[{\varphi}^2-{\beta}_f^2\right]-4{\zeta}_s{\zeta}_d\varphi {\beta}_f^2-\mu {\varphi}^2{\beta}_f^2,\\ {}{D}_s=2{\beta}_f\left\{{\zeta}_s\left[{\varphi}^2-{\beta}_f^2\right]+\left[1-\left(1+\mu \right){\beta}_f^2\right]{\zeta}_d\varphi \right\},\end{array} $$

(44)

where the auxiliary variables φ and β _f correspond to the tuning ratio for the damper and the non-dimensional excitation frequency, respectively, while μ = m _s /m _d is defined as the mass ratio.

The RDO weight parameter w is varied from 0 to 1 with higher emphasis on lower weight values, w = [0, 0.1, 0.2, 0.3, 0.4, 0.6, 1] (this creates a balanced Pareto-front as will be shown later), leading ultimately to seven different designs configurations. The multivariate probabilistic integrals in Eq. (1) and Eq. (2) needed for the objective function are calculated using stochastic simulation, with the required expected values approximated as

$$ E\left[h\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]\approx \frac{1}{N_r}{\displaystyle \sum_{j=1}^{N_r}h\left(\mathbf{x},{\boldsymbol{\uptheta}}^j\right)},E\left[h{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]\approx \frac{1}{N_r}{\displaystyle \sum_{j=1}^{N_r}h{\left(\mathbf{x},{\boldsymbol{\uptheta}}^j\right)}^2}, $$

(45)

where {θ ^j} is the sample-set used for θ, each element corresponding to a sample from p(θ). The total number of samples to generate the RDO designs is taken as N _r  = 2000 and an exterior sampling approach is adopted (Spall 2003) using the same set {θ ^j} over the entire optimization procedure, thus transforming the RDO problem in Eq. (3) into a standard deterministic optimization problem that can be solved by any numerical optimization approach (an exhaustive search is adopted here). The bounds of the design space X are selected as k _d  = [1 × 10⁴ 1.5 × 10⁴] N/m and c _d  = [100 500] Ns/m.

The following cases are considered for comparison

• i. No prediction error, termed as NE

• ii. Additive prediction error with variance scaling according to Eq. (20) and γ chosen as 10 %. This case is termed as AE.

• iii. Additive prediction error with variance scaling according to Eq. (21) and γ chosen as 5 %. This case is termed as AE _t .

• iv. Multiplicative prediction error with γ chosen same as in AE _t . This case is termed as ME.

As discussed in Section 4, the NE and AE cases and ME and AE _t cases lead to identical RDO designs when normalization is established with respect to the utopia point (as was done here). The higher value for γ chosen for AE compared to the value for AE _t is selected so that similar values are established for the error variance σ ² _e between AE and AE _t .

The results for the optimization are shown in Table 1, and in Figs. 3 and 4. In particular, Table 1 shows for the different weights, the optimal solution for k _d and c _d as well as the performance μ(x) and σ(x) under that optimal design configuration. For the AE _t and ME the variance for the real system σ _s (x) is reported (that is, under the influence of the prediction error). For the AE design this information is omitted since it merely corresponds to multiplication of σ(x) by $\sqrt{1+{\gamma}^2}$. Figure 3 then shows the different optimal solutions in the design space X and Fig. 4 the Pareto-front in the normalized (with respect to utopia point) objective space F. The arrow in this figure represents the closest distance of any design from the utopia point. The closest point corresponds to the w = 0.4 design for all cases considered, and it would have been the preferred design based on this traditional approach for evaluation of appropriateness among RDO design.

Table 1 RDO designs results for all cases considered for the TMD implementation

Fig. 3

Design space along with Pareto optimal designs that compose the set Δ for (a) large variability case, and (b) small variability

Fig. 4

Pareto-front for the TMD RDO implementation of the (a) large and (b) small variability cases. Closest design to utopia point indicated with an arrow

Focusing first on the RDO results, it is evident that the uncertainty in the system description has an important impact on the robust design configuration. Different values for w lead to different optimal designs with the higher variability case (larger uncertainty in system description) contributing, as expected, to higher values of the system statistics (mean and standard deviation). The variation of the normalized values for these statistics is, though, smaller for this case (Fig. 4), and same principle applies for the optimal design configurations. This is easy to explain; because of the higher uncertainty in the system description the TMD has smaller comparative efficiency (more challenging to regulate the performance over the entire Θ region of importance) and as such the differences between the performance for different w values becomes smaller. The prediction error has an impact on the optimal design configuration (as seen by the differences in designs between AE _t /ME and NE/AE) especially for the small variability case, something that is evident in Figs. 3 and 4. This should be attributed to the fact that for that case the impact of the system uncertainty is smaller (smaller variability in system characteristics), which allows the uncertainty induced by the error to influence more prominently the resultant design/performance.

The probability of dominance is examined next. This further requires definition of the correlation characteristics for the prediction error. The exponential function in Eq. (16) is adopted, with normalization weight v _l selected as one over the length of the design domain for each design variable. The decay rate λ is selected so that correlation decrease is equal to ρ _o  = 5 % when the total change in the weighted distance reaches α = 30 %, leading to

$$ \lambda =\frac{- \log \left({\rho}_o\right)}{\alpha }. $$

(46)

This assumption leads to the following correlation matrices ρ _jk between the different designs for the AE design case (due to space constraints the results for AE _t /ME are not reported) for the large and small variability cases, respectively

$$ {\rho}_{jk}=\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill 0.89\hfill & \hfill 0.67\hfill & \hfill 0.44\hfill & \hfill 0.28\hfill & \hfill 0.12\hfill & \hfill 0.03\hfill \\ {}\hfill 0.89\hfill & \hfill 1\hfill & \hfill 0.91\hfill & \hfill 0.72\hfill & \hfill 0.54\hfill & \hfill 0.28\hfill & \hfill 0.09\hfill \\ {}\hfill 0.67\hfill & \hfill 0.91\hfill & \hfill 1\hfill & \hfill 0.93\hfill & \hfill 0.79\hfill & \hfill 0.51\hfill & \hfill 0.21\hfill \\ {}\hfill 0.44\hfill & \hfill 0.72\hfill & \hfill 0.93\hfill & \hfill 1\hfill & \hfill 0.95\hfill & \hfill 0.73\hfill & \hfill 0.38\hfill \\ {}\hfill 0.28\hfill & \hfill 0.54\hfill & \hfill 0.79\hfill & \hfill 0.95\hfill & \hfill 1\hfill & \hfill 0.89\hfill & \hfill 0.56\hfill \\ {}\hfill 0.12\hfill & \hfill 0.28\hfill & \hfill 0.51\hfill & \hfill 0.73\hfill & \hfill 0.89\hfill & \hfill 1\hfill & \hfill 0.83\hfill \\ {}\hfill 0.03\hfill & \hfill 0.09\hfill & \hfill 0.21\hfill & \hfill 0.38\hfill & \hfill 0.56\hfill & \hfill 0.83\hfill & \hfill 1\hfill \end{array}\right], $$

(47)

$$ {\rho}_{jk}=\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill 0.78\hfill & \hfill 0.44\hfill & \hfill 0.26\hfill & \hfill 0.17\hfill & \hfill 0.08\hfill & \hfill 0.03\hfill \\ {}\hfill 0.78\hfill & \hfill 1\hfill & \hfill 0.84\hfill & \hfill 0.64\hfill & \hfill 0.5\hfill & \hfill 0.3\hfill & \hfill 0.16\hfill \\ {}\hfill 0.44\hfill & \hfill 0.84\hfill & \hfill 1\hfill & \hfill 0.94\hfill & \hfill 0.84\hfill & \hfill 0.63\hfill & \hfill 0.41\hfill \\ {}\hfill 0.26\hfill & \hfill 0.64\hfill & \hfill 0.94\hfill & \hfill 1\hfill & \hfill 0.97\hfill & \hfill 0.84\hfill & \hfill 0.63\hfill \\ {}\hfill 0.17\hfill & \hfill 0.5\hfill & \hfill 0.84\hfill & \hfill 0.97\hfill & \hfill 1\hfill & \hfill 0.94\hfill & \hfill 0.77\hfill \\ {}\hfill 0.08\hfill & \hfill 0.3\hfill & \hfill 0.63\hfill & \hfill 0.84\hfill & \hfill 0.94\hfill & \hfill 1\hfill & \hfill 0.94\hfill \\ {}\hfill 0.03\hfill & \hfill 0.16\hfill & \hfill 0.41\hfill & \hfill 0.63\hfill & \hfill 0.77\hfill & \hfill 0.94\hfill & \hfill 1\hfill \end{array}\right], $$

(48)

The probability of dominance over Δ as well as the degree of dominance for 3 different values of d, equal to 2,3, and 4 are then calculated and shown in Tables 2, 3, 4 and 5. It is assumed in this case that the decision maker has chosen not to just identify the dominant design (based on the procedure outlined in Section 3.3), but to calculate the degree of dominance for three different d values (2, 3 and 4). Tables 2 and 4 show the results for the NE and AE designs for the large and small variability cases, respectively. Note that even though the designs corresponding to these cases (AE and NE) are the same, the probability of dominance will not be, since the latter design includes a prediction error (that influences this probability). Subsequently, Tables 3 and 5 show the results for the AE _t and ME in similar fashion. The results will also be different, in this case, because of the different impact of the prediction error. 10,000 samples were used to calculate the statistics reported in these tables, facilitating a high-accuracy comparison.

Table 2 ${\tilde{P}}_D\left({\mathbf{x}}_i\Big|\Delta \right)$ and degree of dominance for NE and AE designs for large variability case

Table 3 ${\tilde{P}}_D\left({\mathbf{x}}_i\Big|\Delta \right)$ and degree of dominance for ME and AEt designs for large variability case

Table 4 ${\tilde{P}}_D\left({\mathbf{x}}_i\Big|\Delta \right)$ and degree of dominance for NE and AE designs for small variability case

Table 5 ${\tilde{P}}_D\left({\mathbf{x}}_i\Big|\Delta \right)$ and degree of dominance for ME and AEt designs for small variability

Based on the probability of dominance P _D (x _i |Δ) over the entire set Δ, the design corresponding to w = 0 is deemed as the dominant one for all cases considered. Before making a final selection, the decision maker should additionally look into the margin of dominance to examine additional robustness traits. For the small variability case, this dominance is preserved when looking at lower dimensional subsets. This agreement provides confidence in the design selection since for all subsets considered, i.e. d = 2, 3, or 4, design w = 0 emerges as the more dominant one (degree of dominance for it has positive value), although the margin of dominance is somewhat reduced, dropping to just 15 % for d = 2 dimensional subsets. Aside from the most dominant design w = 0, the design corresponding to w = 0.1 emerges as the second most appropriate design for all cases considered. It is interesting to note that this design would have also been the second preferable one when looking at the entire set Δ. Introduction of the model prediction error has only a small influence on the estimated statistics, with the overall trend corresponding to a relative reduction of the preference, while degrees of dominance trend closer to 0 (note that this trend does not hold for all instances). No significant changes are reported for the degree of preference towards the w = 0 design. This should be attributed to the fact that the main rival design is w = 0.1, which has high correlation to the dominant design w = 0 based on the assumed correlation characteristics for the prediction error [close to 0.8–0.9 based on matrices Eqs. (47) and (48)]. As such, this error has only a small impact on the calculated statistics (see also discussion later in this section). It should be noted that if only the dominant design was to be identified (based on the framework discussed in Section 3.3) then the evaluation of the degree of dominance for all cases would start from the design corresponding to w = 0 and would immediately stop as soon as the positive degree of dominance for it D ₂(x ₁) was calculated.

For the high variability case, some of these trends change. Similarly, the w = 0 design maintains dominance when looking at the entire set Δ. However, it would not emerge as dominant for some of the cases considered when looking at the lower dimensional subsets. For the NE case, the w = 0.3 design emerges as the dominant one since it exhibits d = 2 dominance, although with a relatively small (degree of dominance 7.4 %). It is interesting to note than when looking at higher values for d, w = 0.3 quickly loses its dominance whereas even when looking at the entire set Δ its associated probability of dominance is rather small (7 %). Another interesting characteristics for the NE case is the fact that no design exhibits dominance for d = 3, 4 dimensional subsets, with all of them having negative values for the degree of dominance. Overall w = 0, w = 1 and w = 0.3 exhibit the highest probability of dominance but w = 0.3 possesses the most favorable degree of dominance based on the proposed multistage approach, focusing on lower d-dimensional dominance. This discussions demonstrate that looking solely at ${\tilde{P}}_D\left({\mathbf{x}}_i\Big|\Delta \right)$ could not be enough, and investigating the dominance within smaller subsets becomes necessary. Comparisons among S ² provide the more trustworthy information, since it is equivalent to one-on-one comparisons of the designs. Looking at larger dimensional subsets, conclusive information is not necessarily established for selecting a particular design, though some valuable insight is provided. It is up to the decision maker then to use this insight for selecting the final design.

The introduction of the error in this case has a bigger impact (compared to the low variability case); for AE the statistics change significantly when compared with the NE case, even though the compared designs are identical. This demonstrates the importance of explicitly accounting for the prediction error in the comparisons for the probability of dominance. For AE, the design w = 0.1 exhibits the lower dimensional dominance (d = 2), though with a very small margin (degree of dominance 3 %), whereas two other designs, w = 0.2 and w = 0.1, show good performance (degree of dominance as large as −5 %). For this instance, (dominance by only a small margin) one would be interested in looking at higher values for d before assessing overall robustness, and in this case it is evident that w = 0 exhibits better robustness characteristics. The previous discussion indicates that beyond the degree of dominance being positive, its value should be also taken into account by the designer in assessing the preferences towards different designs. Looking next at the other cases, for the ME and AE _t cases the characteristics for dominance also change (compared to the NE case), although with smaller margins. For ME w = 0 emerges as the dominant design, exhibiting both d = 2 and d = 4 dominance (but not d = 3 for which no design emerges as dominant, with w = 0 having the better performance overall). For AE _t designs w = 0 and w = 0.1 are practically equal. In this case the decision needs to be based on comparisons of higher order values for d, which tilts the preference towards w = 0. The big impact of the prediction error on the preference towards different designs for the high variability case can be explained based on the inability of the TMD to efficiency suppress vibrations over the entire important Θ region; thus, close performance is established by a few different designs and this is why the different preference for this performance given by the different error-model selections can ultimately shift the dominance towards different designs.

To further examine the influence of the correlation of the error on the results, Table 6 shows the probability of dominance for some of the design-cases considered (AE and ME for small variability case and AE for large variability case) if no such correlation is assumed. Comparison of these results to the results in Table 2 (for AE and large variability), Table 4 (for AE and small variability) and Table 5 (for ME and small variability) shows small differences for the AE case when small variability is assumed for the system description, but large for the other two cases. For the large variability case (AE) the differences are large enough to impact the dominance of the designs over the d = 2 and 3 dimensional subsets; when no correlation is considered for the prediction error the design w = 0 emerges as the dominant design which was not the case before. This discussion shows that the assumed correlation of the prediction error can have an impact on the calculated statistics, so it should be carefully chosen.

Table 6 ${\tilde{P}}_D\left({\mathbf{x}}_i\Big|\Delta \right)$ and degree of dominance for some design cases when no correlation is assumed for prediction error

It is also interesting to note that in no case examined the design selected through the degree of dominance coincides with the one corresponding to the minimum distance from the utopia point (w = 0.4 as previously shown). In all cases examined and for all different values considered for d the latter design has a rather small associated value for the degree of dominance, and thus would have been avoided through the proposed approach. This demonstrates the utility of the new methodology for offering an alternative preference measure in assessing the robustness characteristics of different proposed designs.

5.2 Robust topology optimization for minimum compliance

Topology optimization searches for the structural configuration (shape and connectivity of the structure), contained within a given design domain X, that for some given boundary and loading conditions provides the most favorable response in terms of some chosen performance measure (Bendsøe and Sigmund 2003). A popular approach to obtain the solution is to discretize the domain into finite elements and select the densities of each element as design variables x _e ∈ [0, 1], e = 1,…,N _e (typically interpolated between two states: either void or full material), where N _e corresponds to the total number of elements. The performance objective is typically taken as the minimization of the compliance c(x) for a given structural domain, subject to a prescribed mass fraction constraint m _f such that m _X  ≤ m _f , where m _X denotes the domain’s mass fraction, which can be computed as

$$ {m}_X=\frac{1}{N_e}{\displaystyle \sum_{e=1}^{N_e}{x}_e}. $$

(49)

For a linear elastic material, the compliance is a function of the global displacement U (found through the finite element method) and the global stiffness matrix K (Bendsøe and Sigmund 2003). Here the problem is relaxed by employing the Solid Isotropic Material with Penalization (SIMP) formulation (Rietz 2001), leading to the compliance function given by (Sigmund 2001)

$$ c\left(\mathbf{x}\right)={U}^TKU={\displaystyle \sum_e^{N_e}{x}_e^{p_p}{u}_e^T{k}_o{u}_e}, $$

(50)

where p _p is a penalization factor employed to avoid intermediate densities (i.e. to drive each element towards a particular state: either void or full material), u _e is the local displacement vector for a given element, and k _o is the element’s stiffness matrix which in turn is a function of the poison ratio ν and the modulus of elasticity E _e of the element.

The gradient of the compliance can be analytically obtained (Bendsøe and Sigmund 2003) as

$$ \frac{\partial c\left(\mathbf{x}\right)}{\partial {x}_e}=-{p}_p{\left({x}_e\right)}^{p_p-1}{u}_e^T{k}_o{u}_e,\kern1em e=1,\dots, {N}_e. $$

(51)

More information on the general topology optimization design problem as well as on different solution strategies may be found in (Bendsøe and Sigmund 2003).

The RDO formulation has been extensively employed for addressing uncertainties within topology optimization applications (Chen et al. 2010; Dunning et al. 2011; Tootkaboni et al. 2012; Dunning and Kim 2013). A problem similar to the one presented by Chen et al. (2010) is adopted here: a rectangular design domain, with length double its height, is subjected to a central point load at the bottom with simply supported conditions (Fig. 5). The design domain is discretized into 100x50 elements (resulting in N _e  = 5000) and the mass fraction is taken as m _f  = 0.3 (meaning that 30 % of the domain may be occupied). The uncertain model parameters correspond to (i) the loading conditions, where the component of the load in the horizontal direction F _x is assumed to follow a uniform distribution in [−1, 1] and the component of the load in the vertical direction F _y a uniform distribution in [0, 2], and (ii) to the Young’s moduli for each element, assumed to follow a lognormal distribution with median 1 and coefficient of variation of 0.2. The performance function is directly taken as the compliance of the structure h(x,θ) = c(x,θ).

Fig. 5

Topology optimization RDO problem formulation

The solution to the optimization problem Eq. (3) is obtained with the Method of Moving Asymptotes (MMA) (Svanberg 1987), which is a popular algorithm to solve topology optimization problems. To avoid a solution with intermediate densities, a penalization factor of p _p  = 3 is employed. In addition, to avoid the problem where a checker-board pattern emerges causing artificial stiffness, a filter with size of 1.2 is employed. More details about the selection of these parameters can be found in (Bendsøe and Sigmund 2003). This solution approach ultimately required the gradient of the objective function, meaning the gradients for the mean and variance of the response. Assuming that the functions c(x,θ)p(θ) and ∂c(x,θ)/∂x _i p(θ) are continuous on the domain X × Θ and bounded, while also noting that p(θ) does not depend on x, the differentiation and the expectation operators commute (Spall 2003), leading to the following expressions for the elements of these gradients

$$ \frac{\partial \mu \left(\mathbf{x}\ \right)}{\partial {x}_e}=\frac{\partial E\left[c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)\right]}{\partial {x}_e}=E\left[\frac{\partial c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)}{\partial {x}_e}\right],e=1,\dots, {N}_e, $$

(52)

$$ \begin{array}{l}\frac{\partial\ \sigma \left(\mathbf{x}\ \right)}{\partial {x}_e}=\frac{\partial\ }{\partial {x}_e}\left(\sqrt{E\left[c{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]-E{\left[c\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]}^2}\right)\\ {}\kern3.75em =\frac{E\left[c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)\frac{\partial\ c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)}{\partial {x}_e}\right]-E\left[c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)\right]E\left[\frac{\partial\ c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)}{\partial {x}_e}\right]}{\sqrt{E\left[c{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]-E{\left[c\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]}^2}},e=1,\dots, {N}_e.\end{array} $$

(53)

All expected values required for the above expressions within the optimization algorithm are obtained through stochastic simulation employing again exterior sampling (as in the TMD optimization case) with total of N _r  = 2000 samples. Note that for the case corresponding to the multiplicative error or the moment-proportional additive error, the partial derivatives for the system variance, needed in the objective function of Eq. (42) are transformed to

$$ \frac{\partial\ {\sigma}_s\left(\mathbf{x}\ \right)}{\partial {x}_e}=\frac{E\left[c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)\frac{\partial\ c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)}{\partial {x}_e}\right]\left(1+{\gamma}^2\right)-E\left[c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)\right]E\left[\frac{\partial\ c\left(\mathbf{x}, \boldsymbol{\uptheta} \right)}{\partial {x}_e}\right]}{\sqrt{E\left[c{\left(\mathbf{x},\boldsymbol{\uptheta} \right)}^2\right]\left(1+{\gamma}^2\right)-E{\left[c\left(\mathbf{x},\boldsymbol{\uptheta} \right)\right]}^2}},e=1,\dots, {N}_e. $$

(54)

In this example, the value of w was varied from 0 to 1 with equal steps of 0.2, whereas only the following three cases are considered

• i. No prediction error, termed as NE

• ii. Additive prediction error with variance scaled according to Eq. (20) and γ chosen as 10 %. This case is termed as AE.

• iii. Multiplicative prediction error with γ chosen as 5 %. This case is termed as ME.

The resultant optimal solutions were very similar for the NE/AE and ME cases (almost identical topologies), thus the various results are primarily reported for the former only. The optimal topologies for different values of w are shown in Fig. 6 whereas the statistics (mean and standard deviation) in Table 7. 5,000 samples were used for the statistics reported in this table, facilitating, again, a high-accuracy comparison. Figure 7 shows the Pareto-front in the normalized (with respect to utopia point) objective space F for all three design cases considered. The arrow in this figure represents the closest distance of any design from the utopia point. The closest point corresponds to the w = 1 design for all cases, and it would have been the preferred design based on this traditional approach for evaluation of appropriateness among RDO design.

Fig. 6

Optimal topologies for different values of w for the NE/AE designs

Table 7 Mean and standard deviation of optimal solution for the NE case for the topology optimization problem

Fig. 7

Pareto-front for the Topology RDO implementation. Closest design to utopia point indicated with an arrow

These results agree with the ones reported by Chen et al. (2010) where asymmetry is observed in the optimum designs due to asymmetric boundary conditions. It is possible to observe that the different designs have a similar statistical response even though they correspond to distinct topologies. In fact, the values for μ and σ between the different designs are so similar that it would be very challenging to select a preferred design from the set solely based on these statistics. The probability of dominance, which in this case corresponds to the probability of having a lower compliance over Θ, provides a rational measure for assessing the appropriateness of the candidate designs. For the correlation of the prediction error needed to calculate this probability (and similar to the TMD example), the exponential function in Eq. (16) is adopted, with normalization weight v _l selected as one and decay rate λ selected so that correlation-decay is equal to ρ _o  = 5 % when the total change in the weighted distance between designs reaches α = 30 % [as described by Eq. (46)]. This assumption leads then to the following correlation matrix ρ _jk between the different designs for the AE design case (due to space constraints the results for ME design not reported)

$$ {\rho}_{jk}=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0.63\hfill & \hfill\ 0.34\hfill & \hfill\ 0.11\hfill & \hfill\ 0.07\hfill & \hfill 0.03\hfill \\ {}\hfill 0.63\hfill & \hfill 1\hfill & \hfill\ 0.67\hfill & \hfill 0.19\hfill & \hfill 0.11\hfill & \hfill 0.05\hfill \\ {}\hfill\ 0.34\hfill & \hfill\ 0.67\hfill & \hfill 1\hfill & \hfill 0.37\hfill & \hfill\ 0.20\hfill & \hfill 0.06\hfill \\ {}\hfill\ 0.11\hfill & \hfill 0.19\hfill & \hfill 0.37\hfill & \hfill 1\hfill & \hfill 0.74\hfill & \hfill 0.17\hfill \\ {}\hfill\ 0.07\hfill & \hfill 0.11\hfill & \hfill\ 0.20\hfill & \hfill 0.74\hfill & \hfill 1\hfill & \hfill 0.27\hfill \\ {}\hfill 0.03\hfill & \hfill 0.05\hfill & \hfill 0.06\hfill & \hfill 0.17\hfill & \hfill 0.27\hfill & \hfill 1\hfill \end{array}\right] $$

(55)

The probability of dominance over Δ as well as the degree of dominance for 2 different values of d (equal to 2 and 3) are shown in Table 8. As in the TMD example, rather than just identifying the dominant design based on the procedure outlined in Section 3.2, the degree of dominance for different d values is reported to facilitate a more thorough comparison.

Table 8 ${\tilde{P}}_D\left({\mathbf{x}}_i\Big|\Delta \right)$ and degree of dominance for NE, AE, and ME for the topology optimization problem

For the NE case, design w = 0 emerges as the dominant one when looking at the entire set Δ, with that preference also upheld over d = 2 (S ²) subsets and d = 3 (S ³) dimensional subsets. For the d = 3 case actually no design emerges as dominant [values of D ₃(x _i ) are negative for all of them], though for the w = 0 design the value of D ₃(x _i ) is very close to zero, and much larger than all other designs, indicating a strong preference for it, especially when combined with the information for dominance over Δ and over the two-dimensional subsets. It is interesting to note that design w = 0.2 is close to being dominant over the two dimensional subsets [value of D ₂(x _i ) only slightly negative] but has poor performance when looking at the three dimensional subsets or at the entire set Δ. This stresses the importance of looking at different subsets to evaluate the preference toward a specific design, especially when the dominance properties it exhibits have a narrow margin (values close to zero). When incorporating the additive prediction error in the analysis (AE case in Table 8), we see significant differences in the calculated probabilities. This should be attributed to the fact that the compared designs have very similar statistical characteristics (as shown in Table 7), contributing to stronger influence from the prediction error. Design w = 0 still emerges as the preferred one when looking at lower dimensional subsets (d = 2 or 3, nothing though that for d = 3 there is no dominance) but with much smaller margins compared to the NE case, whereas when looking at the entire set Δ it practically ties with the w = 1 design. Changing the probability model for the prediction error to multiplicative influence (ME case), changes its overall impact. Though the prediction error still has a strong influence on the calculated probability of dominance (changes over the NE case) the relative impact as compared to the AE case changes, without, though, a change in the overall preference (w = 0 is still the dominant design with actually increased robustness margins when looking at the lower dimensional subsets). This validates the previous conclusions that the prediction error model may have an impact on the results.

Finally is also interesting to note that, like the TMD example, in no case examined the design selected through the degree of dominance coincides with the one corresponding to the minimum distance from the utopia point (w = 1 in all cases as previously discussed). Though the w = 1 design has competitive values when considering the probability of dominance over the entire set Δ, for some cases it corresponds to rather small values for the probability of dominance for lower values of d, and would have been avoided through the proposed approach. This further demonstrates the utility of the new methodology for assessing the robustness characteristics of different proposed designs.

6 Conclusions

A novel approach for assessing the appropriateness of a set of candidate designs was introduced based upon the definition of a new robustness measure, termed probability of dominance. This measure is defined as the likelihood that a given design will outperform the rival designs within the candidate set. Given that the resultant probability is a function of the exact designs composing the set, a multi-stage approach was also formulated for enhancing robustness of the chosen solution. This approach compares designs within smaller dimensional subsets and searches for the design that dominates within all subsets that include it. For evaluating the relative preference towards a design the degree of dominance is introduced, which is obtained by comparing the probability of dominance for the candidate design against the probability of dominance of all other designs within all different subset that the candidate design belongs to. This degree of dominance can be utilized as a tool to guide the selection of the final design, with absolute dominance corresponding to a positive value for it. For enhancing the robustness in this selection the impact of prediction errors between the real system and the assumed numerical model was additionally investigated. Two different error models were explored; these correspond to either an additive or multiplicative influence, while reasonable assumptions for selecting the error characteristics were discussed in detail. The additive prediction error can be ultimately chosen to address two different sources of modeling uncertainty. It can be selected to address only un-modeled uncertainties, when its variance is scaled according to the response variance of the assumed numerical model. If this assumption is selected, the formulation of the RDO problem is not impacted at all. This error can also be also selected to address both un-modeled uncertainties and un-modeled system characteristics, when its variance is scaled according to the second moment of the numerical model. This in turn is equivalent to the multiplicative prediction error in terms of how it impacts the statistics of the real system performance and ultimately the RDO formulation. In addition, it was shown that when modeling errors are considered, the impact on the probability of dominance corresponds to substitution of the indicator function, describing the favorability of each design, by a likelihood function dependent upon the assumed probability model of the error and the model performance.

Two RDO illustrative examples were presented, the first considering the design of a tuned mass damper (TMD) for vibration mitigation of harmonic excitations, and the second the robust topology optimization for minimum compliance. It was shown in these examples that the new approach provides an alternative to the established popular methodologies for assessing the appropriateness of the candidate designs. Thus, it ultimately equips designers (decision maker) with an additional tool in the search for a preferred design. The results also showed that looking solely at the probability of dominance (over the entire set) does not always lead to the most appropriate choice. Comparison among smaller dimensional subsets can guide decisions better and further facilitate a deeper understanding of the preference toward each design, even when none emerges as dominant. It was also demonstrated that beyond the degree of dominance being positive, its value should also be taken into account by the designer in assessing the preferences for different designs. Small values for the degree of dominance should be carefully examined by the designer when evaluating the different designs. Moreover, it was shown that explicitly including the prediction error in the comparison can have a significant impact on the assessment. In this case, the assumed correlation of the prediction error between different designs needs to be carefully considered. The influence of the prediction error is especially critical when the compared designs have similar statistical performance despite corresponding to different design configurations. In general, the proposed method showed promising results and provided a rational framework for assessing the appropriateness of a set of candidate robust designs.