1 Introduction

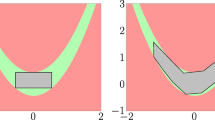
The concept of solution spaces as it is used here, was introduced in Lehar and Zimmermann (2012) in 2012. In the proposed method, a statistical statement is made about a product of intervals, i.e., a box, as shown in Fig. 1. It states, that, if a sample of size N, taken uniformly from this box, contains only feasible sample points, the box holds at least a certain fraction of feasible design space, independent of the dimensionality of the input space. A feasible design is a point which does not violate any constraints g j (x) and for which the model x↦y yields y ≤ y c , with y as a measure for the performance of the system and y c as a threshold value for this performance criterion. In Zimmermann and Hoessle (2013), an algorithm is proposed for identifying these intervals using iterative Monte-Carlo sampling. The size measure Φ of this box is to be maximized while all points x j within the box fulfill all constraints g i (x). This has been extended to the identification of key parameters for design improvement in Fender et al. (2014).

Fig. 1
figure 1

Solution space Ω represented by a box in the input space, which contains only feasible points (o), i.e. for which no included point violates any of the constraint g j (x)

Full size image

Iterative Monte-Carlo sampling requires a large number of function evaluations. In, e.g., vehicle crash design, each function evaluation requires a full vehicle finite element simulation. Such detail model evaluations are computationally expensive. Thus, the stochastic computation of solution spaces relies heavily on highly efficient models, i.e. the use of substructures, see Duddeck (2008), or simplified models, see Fender et al. (2014), Kim et al. (2001), and Carvalho et al. (2011).

Finding the largest box, which contains at least a certain fraction of feasible designs, rather than optimizing x with respect to the performance measure y, has a number of advantages. It decouples the variables in the input space. Given Fig. 1, any x 1∈Δx 1 will likely result in a feasible design if also x 2∈Δx 2. Thus, the parameters are independent with respect to fulfilling the constraints g i (x). This is used to break a large problem down into several smaller classical constrained optimization problems which can be solved independently. In systems engineering, breaking down systems into subsystems is state-of-the-art methodology, see Doyle and Csete (2011). In systems subject to uncertainty, the approach is used to define intervals for each parameter which account for their variability. Finally, defining orthogonal intervals rather than point-solutions means variations in single variables do not have to be accounted for in the other variables as long as all variables are still in their respective intervals.

In lack-of-knowledge problems, where only some of the parameters can be determined, admissible ranges for the unknown parameters are given. These intervals can be refined as more information becomes available.

The approach for identifying the solution space proposed in this paper is different because it does not rely on sampling or stochastics. We state that, given a set of linear constraints g i (x), finding the largest box by a certain performance measure Φ, can be formulated as a linear, convex optimization problem. Then, the problem can be solved directly using the method of Lagrange multipliers. Hence, the computational effort to generate maximized solution spaces can be greatly reduced.

This approach has certain similarities to the so-called lack-of-knowledge theory, see Ladeveze (2002), where an interval analysis is combined with the theory of probabilities. The modeling can then be refined as more information becomes available (model update) (Ladeveze et al. 2006). The difference to the approach discussed here lies in the fact that the lack-of-knowledge is not characterized with probabilities but a high flexibility is aimed for by maximizing the size of the solution space. This is especially attractive for product development in early design phases and can be regarded as a special approach for robustness in early phase design (Duddeck and Wehrle 2015).

2 Problem statement

After establishing why it is desirable to calculate solution spaces, this section provides a formal problem statement for calculating solution spaces in general and for the special case addressed in this paper. With the parameter vector \(\mathbf {x}=(x_{1}, x_{2},\dots , x_{N})\) and the system response y, the mapping

$$ \mathbf{x} \mapsto y \ , $$
(1)

maps a point in parameter space to a scalar output value. This will be referred to as the model. Given a model, classical optimization solves the problem

$$ \mathbf{x} = \arg{\min_{\mathbf{x}}\left( y\right)} \ . $$
(2)

This means finding the point in parameter space for which the output value of the model is minimal: the optimum. With x i,l and x i,u , as the lower and upper bounds for each variable, a solution space is defined as

$$ \Omega = \left[x_{i,l}, x_{i,u}\right]^{N} \subset \mathbf{R}^{N} \ , $$
(3)

with the size measure Φ(Ω). With the constraints g j (x), the optimization problem can be formulated for the solution space:

$$ \Omega= \arg\max_{\Omega}{\left( \Phi(\Omega)\right)} \ . $$
(4)

subject to

$$ g_{j}(\mathbf{x}) \leq 0, \ \forall \ \mathbf{x} \in \Omega, \ \forall j. $$
(5)

The solution is the box with the largest size measure Φ(Ω) for which all points within the box satisfy all constraints g j (x). The stochastic approach provides an estimator for this box. Figure 1 also shows how a box only containing feasible sample points may contain fractions of infeasible design space. In Lehar and Zimmermann (2012), the statistics regarding the fraction of feasible design space and the associated confidence based on sample size are discussed. The stochastic approach requires a model in the sense of (1) which reflects feasibility of the solution in its output value. In the formulation proposed in this work, the constraints are directly evaluated at their respective corners of the box. Compared to the stochastic approach, which relies on a large number of function evaluations, this results in a decrease of calculation time by several orders of magnitudes, even for highly efficient surrogate models. In the approach presented here, there is no need for iterating and the solution exactly satisfies equation (5). The restriction is that it can only be applied to problems of the form

$$ \Phi(\Omega) = \min_{i}\left( \Delta x_{i}\right) \ , $$
(6)

with Δx i =x i,u −x i,l and

$$ g_{j}(\mathbf{x}) = \sum\limits_{i}{a_{i} x_{i}} - b_{j}, $$
(7)

i.e., max-min-problems with linear constraints. The objective function (6) is particularly well suited for the solution space problem because the difficulty of realizing a design for which x i ∈[x i,l ,x i,u ] ∀i is determined by the smallest interval Δx i . Thus, it is advantageous to make the smallest interval as large as possible.

3 Methodology

3.1 The crash load case

This work explores the possibilities of finding an analytical solution for the solution space problem with a focus on crashworthiness design. Appropriate simplifications are derived and formulated. The resulting feasible parameter space is built and then used to solve for the largest hypercube.

In the USNCAP crash load case, the test vehicle is driven against a rigid barrier at full overlap with an initial velocity of 56\(\frac {km}{h}\). The structural performance measures for the USNCAP crash load case are the crash-pulse, i.e., the B-pillar acceleration in the x-direction, see Huang (2002), the firewall intrusion and the order of deformation within the structure, see Fender (2013). The accelerations and deformations in the x-direction are linked to the force-deformation characteristics, see Fender (2013). These force-deformation characteristics are functional properties of the system and constitute the parameters of the system for which constraints are formulated.

Note that the force-deformation characteristics for each component are an output quantity of the detailed FEM crash model but an input quantity of the solution space problem. A detail model directly maps the detail parameters, material and geometry, to full vehicle properties such as accelerations and total deformations. That means that if the force-deformation curves are known from the detail model, the performance of that model is also known. This also means force-deformation curves cannot be directly controlled in the detail model but obtaining a specific force-deformation response is a design problem as well. However designing any single component to deliver a force-deformation response that satisfies certain boundaries is a much smaller problem than simultaneously designing all components of the systems to deliver a specific system response. Thus, deriving intervals for each component which are sufficient for obtaining the desired system response breaks the larger problem down into one smaller problem per component, each of which may be solved independently.

3.2 Formulating linear constraints through discretization

Although the assumption of linear constraints may at first seem very strong and lacking general applicability, it actually holds for a wide variety of problems. E.g. in crash, the two major determining factors are acceleration and energy absorption. The amount of energy absorbed by the structure, E d e f o , over the admissible deformation must be large enough to bring the vehicle to a halt. The absorbed energy can be expressed as the sum of integrals of the crushing force, F j , of each component over its deformation u j . Assuming that the entire vehicle mass is concentrated in the center of gravity of the vehicle, with j indicating the j-th of M components with a deformable length of L j in the vehicle, the constraint is:

$$ E_{defo} = \sum\limits_{j=1}^{M} {\int}_{L_{j}}{F_{j}(u_{j})du_{j} \geq \frac{1}{2} m_{v} {v_{0}^{2}}} \ . $$
(8)

This states that the energy which can be absorbed by all involved components must be greater than the initial kinetic energy related to the initial mass m v and initial velocity v 0. Considering the decrease in mass which has to be decelerated because some of the structure will already be in contact with the barrier and at a velocity of zero before the crash ends, the acting force must be taken in relation to this active mass \(m^{*}_{v,j}(u_{j})\):

$$ \sum\limits_{j=1}^{M} {\int}_{L_{j}}{\frac{F_{j}(u_{j})}{m^{*}_{v,j}(u_{j})}du_{j} \geq \frac{{v_{0}^{2}}}{2}} \ . $$
(9)

In this expression, less energy needs to be absorbed because the kinetic energy of parts hitting the barrier at a certain remaining velocity does not have to be accounted for in vehicle deformation. Note that this is a constraint on a specific energy, having the unit of velocity squared, i.e. \(\frac {\text {m}^{2}}{\text {s}^{2}}\). F j (u j ) for any particular component is an arbitrary function and, in the case of crash, is usually obtained via explicit finite element simulation. However, the integral may be discretized using a zero-order hold approach, yielding

$$ \sum\limits_{j=1}^{M} \sum\limits_{i=1}^{N}{\frac{F_{i,j}}{m^{*}_{i,j}}d_{i,j} \geq \frac{{v_{0}^{2}}}{2}} $$
(10)

as a linear approximation. With L v as the total deformable length of the vehicle, \(m_{i,j}^{*}={\int }_{u_{i,j}}^{L_{v}}{ \frac {dm(x)}{dx} dx}\) is the cumulative mass which is yet to be decelerated at any increment i, opposed to single mass points m i . Although the function of force over deformation is highly non-linear, the dependency of the absorbed energy on this function, or any particular point of this function is linear. This is trivial but it is yet important when trying to formulate constraints for the functions F j (u j ) and not for the underlying geometrical and material properties of the component. Because mathematically it does not matter which component contributes to which energy increment F i,j d u i,j , the index j can be left out and we simply sum all increments over all force-deformation curves of all components:

$$ \sum\limits_{i=1}^{N}{\frac{F_{i}}{m^{*}_{i}}d_{i} \geq \frac{{v_{0}^{2}}}{2}} \ . $$
(11)

This is a linear expression for the total specific energy absorbed by all involved components during a crash as the integral over the force-deformation curves F j (u j ) of each component. Thus, any constraint on the integrals of the exact curves F j (u j ) can instead be formulated for this linear approximation. Particularly, an upper and lower bound F j,u (u j ) and F j,l (u j ) may be defined,

$$ F_{j,l} (u_{j}) \leq F_{j} (u_{j}) \leq F_{j,u} (u_{j}) \ , $$
(12)

where F j,l (u j ), F j,u (u j ) are piecewise constant functions of force over deformation. Any function F j (u j ) which is larger than F j,l (u j ) at every point, i.e. F j,l (u j ) ≤ F j (u j ), will absorb at least as much energy as this piecewise constant lower bound. Also, the same argument can be made for the upper bound of the function. This is illustrated in Fig. 2.

Fig. 2
figure 2

A force-deformation curve F j (u j ) with piecewise constant lower and upper bounds

Full size image

Although energy is the most intuitive example, this holds for any constraint for a sum of integrals, e.g. for a number of arbitrary functions f j (x j ) where the sum over their integrals must be larger than b, i.e.,

$$ \sum\limits_{j=1}^{M} {\int}_{X_{j}}{f_{j}(x_{j})dx_{j}} - b \geq 0 $$
(13)

can be formulated as

$$ \sum\limits_{i=1}^{N} y_{i} dx_{i} - b \geq 0 $$
(14)

with y i =f j (x i,j ). The number of variables in this linear function depends on the discretization. Also note that this is a constraint on the values of the function y i itself rather than the argument of the function, x i .

As mentioned above, the other major constraint in crash is the maximum acceleration. As opposed to the energy, the acceleration depends on the way the components are arranged in relation to one another, i.e., if the order in which two components deform is changed, the total absorbed energy is assumed to not be affected by this, provided the deformation behavior of the components does not change significantly. The acceleration over deformation of the vehicle, a(u v ), however will change. More specifically, the acceleration at any point i during the deformation is, with the index j for M simultaneously deforming components,

$$ a_{c,lo} \leq \frac{1}{m_{i}^{*}}\sum\limits_{j=1}^{M} F_{i,j} \leq a_{c,u} $$
(15)

This results in as many separate linear constraints as the number of piecewise constant segments the x discretization of the structure requires. Finally the order of deformation requires the collapse force of a subsequent component to be larger than the force at any point in deformation of a previously deforming component, which results in another set of linear constraints. This is particularly important for low-speed crashes where the front parts are more easily replaced. From these formulations it becomes clear, that the simplicity of the constraints comes at the price of resulting in a large number of constraints. However, as shown in Fig. 2, the formulation is still correct for very coarse discretizations, although a finer discretization allows for a larger number of feasible solutions. The next section shows why the example front crash problem discussed in this work may be adequately handled with a relatively coarse discretization.

Note that any particular energy, force or deformation over time curves and their derivatives depend highly non-linearly on the behavior of all components and their interaction. The integration schemes used for obtaining the vehicle behavior over time, especially their dependency on geometry or material, cannot be linearized in this manner and constraints directly on the vehicle behavior in time or its geometry or material properties cannot be found using this approach. Also, optimization within the framework of this set of linear constraints is meaningless as the constraints only reliably discriminate between feasible and infeasible designs but hold no information for the exact performance of a design point, regardless whether this point is feasible or not.

However, for constraints on integrated quantities or threshold values as shown above, the method provides a linear model. Furthermore, such a set of linear constraints always results in a convex optimization problem. Although the ansatz is motivated using a given force-deformation curve, this problem is solved without prior knowledge of the component behavior.

Once intervals such as those shown in Fig. 2 have been defined for each component involved in the crash process, the development problem is decoupled. This means that material and geometry of each component can be designed such that its force-deformation characteristic satisfies (12). Any combination of components where all components satisfy their respective constraints will always result in feasible overall system behavior. Therefore components can be designed independently and optimized with respect to other performance measures such as cost, weight, stiffness, etc. as long as the constraints provided by this approach are satisfied, i.e. the design point lies within the solution space.

3.3 The deformation space

The fundamental concept in this approach with respect to crash is that of the deformation space because it enables the construction of the necessary linear constraints g j . As discussed in Section 3.2, it is important for the crash performance in which order and at which relative position the components deform. This map and the resulting necessary discretization is derived from the deformation space.

It is important to note, that for the crash problem, a finer discretization does not necessarily result in a better solution. We assume a distance where the active mass, i.e. the mass which is decelerated by the currently deforming structure, is constant. Also, the number of components which deform in parallel over this distance does not change. Then, for the acceleration, the constraint on the sum over the forces of these components is constant and remains also unchanged over this deformation. Because the energy absorption constrains the integral of the force over deformation, any curve with an equivalent integral is equally viable. Thus, a constant lower bound, to satisfy the energy constraint, maximizes the minimum distance between the two bounds, such as shown for the two piecewise constant sections in Fig. 2. Assuming that for the upper and the lower bound a piecewise constant solution is optimal over a given distance, there is no benefit in finer discretization in this area. Based on this assumption, the structure is divided into sections, where a section is the longest deformable distance over which the involved components and the active mass remain unchanged. Whenever either mass or the contributing components change, a new section with independent degrees of freedom starts.

The deformation space can be obtained from the geometry of the system, see Fig. 3, by mapping geometric coordinates to coordinates of simultaneous deformation, see Fig. 4. We assume, that every component can be compressed to a certain level before it behaves as though it were rigid. Rigid bodies and empty spaces are removed from the geometry. Then, the structure is mapped by order of deformation, i.e., the part of the structure that deforms first, is at the coordinate value zero, the part that deforms next comes after that until all deforming parts of the structure are arranged in ascending order for all parallel load paths.

Fig. 3
figure 3

System geometry with four components and three masses, deformable parts (grey) and undeformable parts (black)

Full size image
Fig. 4
figure 4

The deformation space of the system. Component parts which deform simultaneously lie in parallel, undeformable parts have been removed

Full size image

In the resulting equivalent system, any x-position denotes a point of simultaneous deformation of the parallel components. The dashed lines mark a change of effective mass or involved components. When empty spaces and rigid parts are removed from the geometry, the dashed lines are straight.

For the masses, as discussed in Section 3.2 with respect to active mass, we substitute, \(m^{*}_{1} = m_{1}+m_{2}+m_{3}\), \(m^{*}_{2} = m_{2}+m_{3}\) and \(m^{*}_{3} = m_{3}\). Let F k l be the lower bound for the force in every element and ΔF k l the corresponding interval width, where k denotes the component and l the section that part of the component lies in. Given the design goals defined in Section 3.1, for the system shown in Fig. 4, the constraints are now formulated as follows:

$$\begin{array}{@{}rcl@{}} \text{Pulse} \left\{\begin{array}{ll} F_{11} + \Delta F_{11} + F_{31} + \Delta F_{31} - m^{*}_{1} a_{c}& \leq 0\\ F_{21} + \Delta F_{21} + F_{32} + \Delta F_{32} - m^{*}_{2} a_{c}& \leq 0 \\ F_{22} + \Delta F_{22} + F_{41} + \Delta F_{41} - m^{*}_{3} a_{c}& \leq 0 \end{array}\right. \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} \text{Defo} \left\{\begin{array}{ll} \left( 1-\frac{m^{*}_{1}-m^{*}_{2}}{m^{*}_{1}}\right)\left( F_{11} + \Delta F_{11}\right) \\ - \left( \frac{m^{*}_{1}-m^{*}_{2}}{m^{*}_{1}}\right)\left( F_{31} + \Delta F_{31}\right) - F_{21} \leq 0 \\ \left( 1-\frac{m^{*}_{2}-m^{*}_{3}}{m^{*}_{1}}\right)\left( F_{31} + \Delta F_{31}\right) \\ - \left( \frac{m^{*}_{2}-m^{*}_{3}}{m^{*}_{1}}\right)\left( F_{11} + \Delta F_{11}\right) - F_{41} \leq 0\\ \left( 1-\frac{m^{*}_{2}-m^{*}_{3}}{m^{*}_{2}}\right)\left( F_{32} + \Delta F_{32}\right) \\ - \left( \frac{m^{*}_{2}-m^{*}_{3}}{m^{*}_{2}}\right)\left( F_{21} + \Delta F_{21}\right) - F_{41} \leq 0 \end{array}\right. \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} \text{Energy} \begin{array}{ll} \ &\frac{{v^{2}_{0}}}{2} - \frac{d_{1}}{m^{*}_{1}}\left( F_{11}+F_{12}\right) - \frac{d_{2}}{m^{*}_{2}}\left( F_{21}+F_{22}\right) \\ &- \frac{d_{3}}{m^{*}_{3}}\left( F_{31}+F_{32}\right) \leq 0 \end{array} \end{array} $$
(18)

The set of equations labeled Pulse puts an upper limit of a c on the acceleration in every section. The set labeled Defo ensures that components closer to the barrier deform first and is readily derived from a free body diagram. The constraint labeled Energy puts a lower limit on the integral of the force over the admissible deformation such that the velocity is reduced to zero before the deformation is used up.

3.4 The objective function

In Fender et al. (2014), the volume is given as size measure for the hypercube as it corresponds to the number of feasible solutions contained within the cube. For the design process, however, the smallest interval is most critical for the feasibility. In addition, using the smallest interval width as an objective function makes it possible to use a linear formulation of the problem.

With the the ith interval’s upper bound F u,i , lower bound F l,i and weight ω i , the objective function for the problem is:

$$ \Phi = \Delta F_{\omega,min} = \min_{i}{\left( \frac{F_{u,i} - F_{l,i}}{\omega_{i}}\right)} \ . $$
(19)

The weights ω i represent the relative importance of the individual intervals in the optimization problem. Due to the convex nature of the problem, the size of one interval can only be increased at the cost of the size of the other intervals. The weights ω i are used to control this distribution of interval widths. The optimization goal is to maximize Φ. According to Fender (2013), the supremum for Φ can always be reached while also fulfilling \(\frac {\Delta F_{i}}{\omega _{i}} = \frac {\Delta F_{j}}{\omega _{j}} = \Delta F_{\omega } \forall i, j\). This is intuitive for any vector

\(\mathbf {\Delta F} = \left (\Delta F_{1} , \Delta F_{2} , {\dots } , \Delta F_{N} \right )^{T}\) , and scalar ΔF i ∈ ΔF taken from this vector. With \(\Phi = \min {\left (\mathbf {\Delta F}\right )}\), Φ ≤ ΔF i is always true for any i. Therefore, the objective function value is never improved if the vector contains some ΔF j > ΔF i . At the same time, Φ decreases if there is a ΔF j < ΔF i in the vector. Therefore, the optimal value for Φ can be found by instead maximizing the scalar ΔF under the equality constraint that \(\Delta F_{i} = \Delta F_{j} = \Delta F \ \forall i, j \ \in \ 1,2,\dots ,N\). This is admissible due to the convex nature of the problem which implies that the smallest output value is maximized when all output values are equal.

Therefore, with

$$ \omega_{i}\Delta F_{\omega} = F_{u,i} - F_{l,i} \ , $$
(20)

as a set of additional equality constraints,

$$ \Phi = \Delta F_{\omega}. $$
(21)

is an equivalent objective function to (19).

3.5 The constrained optimization problem

With the objective function Φ = ΔF ω as defined above and for linear constraints

$$ g_{j}(x) = \mathbf{n}_{j}^{T} \mathbf{x} - b_{j} \ , $$
(22)

where n j is the normal vector of the j-th constraint and b j the respective right hand side, the Lagrangian,

$$ L = \Phi[f(\mathbf{x})] - \sum{\lambda_{i} g_{i}(x)} \ , $$
(23)

can be simplified to a linear function using (21):

$$ L = \Delta F_{\omega} - \sum{\lambda_{i} \left( \mathbf{n}_{i}^{T} \mathbf{x} - b_{i}\right)} \ . $$
(24)

The solution is obtained by setting ∇L=0, similarly to, e.g., Nocedal and Wright (1999).

4 A simple example problem

Given the constraints defined in Section 3.3, for the system shown in Fig. 4, and using the objective function, Φ = ΔF ω as defined above, the Lagrangian is

$$ \begin{array}{ll} L = \Delta F_{\omega} &- \lambda_{1} \left( F_{11} \!+ \omega_{11}\Delta F_{\omega} +\! F_{31} + \omega_{31}\Delta F_{\omega} - m^{*}_{1} a_{c} \right) \\ &- \lambda_{2} \left( F_{21} \!+ \omega_{21}\Delta F_{\omega} +\! F_{32} + \omega_{32}\Delta F_{\omega} - m^{*}_{2} a_{c} \right) \\ &- \lambda_{3} \left( F_{22} \!+ \omega_{22}\Delta F_{\omega} +\! F_{41} + \omega_{41}\Delta F_{\omega} - m^{*}_{3} a_{c} \right) \\ &- \lambda_{4} \left( (1-\frac{m^{*}_{1}-m^{*}_{2}}{m^{*}_{1}})(F_{11} + \omega_{11}\Delta F_{\omega})\right. \\ &- \left.\frac{m^{*}_{1}-m^{*}_{2}}{m^{*}_{1}}(F_{31} + \omega_{31}\Delta F_{\omega}) - F_{21} \right) \\ &- \lambda_{5} \left( (1-\frac{m^{*}_{2}-m^{*}_{3}}{m^{*}_{1}})(F_{31} + \omega_{31}\Delta F_{\omega})\right. \\ &- \left.\frac{m^{*}_{2}-m^{*}_{3}}{m^{*}_{1}}(F_{11} + \omega_{11}\Delta F_{\omega}) - F_{41} \right) \\ &- \lambda_{6} \left( (1-\frac{m^{*}_{2}-m^{*}_{3}}{m^{*}_{2}})(F_{32} + \omega_{32}\Delta F_{\omega})\right. \\ &- \left.\frac{m^{*}_{2}-m^{*}_{3}}{m^{*}_{2}}(F_{21} + \omega_{21}\Delta F_{\omega}) - F_{41} \right) \\ &- \lambda_{7} \left( \frac{{v^{2}_{0}}}{2} - \frac{d_{1}}{m^{*}_{1}}(F_{11}+F_{31}) - \frac{d_{2}}{m^{*}_{2}}(F_{21}+F_{32})\right. \\ &- \left.\frac{d_{3}}{m^{*}_{3}}(F_{22}+F_{41}) \right) \end{array} $$
(25)

From ∇L=0, follows that λ 4,5,6=0 and

$$ \begin{array}{ll} \lambda_{1} &= \frac{d_{1}}{m^{*}_{1}}\lambda_{7} \ , \lambda_{2} = \frac{d_{2}}{m^{*}_{2}}\lambda_{7} \ , \lambda_{3} = \frac{d_{3}}{m^{*}_{3}}\lambda_{7} \ , \\ \lambda_{7} &= \frac{1}{2\left( \frac{d_{1}}{m^{*}_{1}} + \frac{d_{2}}{m^{*}_{2}} + \frac{d_{3}}{m^{*}_{3}}\right)} \ . \end{array} $$
(26)

Thus, the order of deformation constraint is not an active constraint for any element. The substitutions \(F^{*}_{i} = {\sum }_{j=1}^{M_{i}}{F_{i,j}}\) and \(\Delta F_{\omega ,i,j} = \frac {\Delta F_{i,j}}{\omega _{i,j}}\) and the condition that ΔF ω,i,j =ΔF ω,k,l ∀i,j,k,l, yields the following linear system of equations:

$$ \left[\begin{array}{llllllll} 0& \frac{d_{1}}{m^{*}_{1}}& \frac{d_{2}}{m^{*}_{2}}& \frac{d_{3}}{m^{*}_{3}}& 0& 0& 0 \\ \omega^{*}_{1}& -1& 0& 0& 1& 0& 0 \\ \omega^{*}_{2}& 0& -1& 0& 0& 1& 0 \\ \omega^{*}_{3}& 0& 0& -1& 0& 0& 1 \\ 0& 0& 0& 0& \frac{1}{m^{*}_{1}}& 0& 0 \\ 0& 0& 0& 0& 0& \frac{1}{m^{*}_{2}}& 0 \\ 0& 0& 0& 0& 0& 0& \frac{1}{m^{*}_{3}} \\ \end{array}\right] \left[\begin{array}{ll} \Delta F_{\omega} \\ F^{*}_{l,1} \\ F^{*}_{l,2} \\ F^{*}_{l,3} \\ F^{*}_{u,1} \\ F^{*}_{u,2} \\ F^{*}_{u,3} \\ \end{array}\right] = \left[\begin{array}{ll} \frac{{v^{2}_{0}}}{2} \\ 0 \\ 0 \\ 0 \\ a_{c} \\ a_{c} \\ a_{c} \\ \end{array}\right] $$
(27)

The solution of this system yields the optimal set of intervals for each section, for any given relative weight ω, as defined in Section 3.4. The remaining equality constraints are used to break these intervals down to the component level:

$$ \left[\begin{array}{lllll} 0& 1& 1& 0& 0 \\ 0& 0& 0& 1& 1\\ \omega_{11}& -1& 0& 1& 0 \\ \omega_{12}& 0& -1& 0& 1 \\ 0& 1& -1& 0& 0 \end{array}\right] \left[\begin{array}{ll} \Delta F_{\omega} \\ F_{l,11} \\ F_{l,31} \\ F_{u,11} \\ F_{u,31} \end{array}\right] = \left[\begin{array}{ll} F^{*}_{l,1} \\ F^{*}_{u,1} \\ 0 \\ 0 \\ 0 \end{array}\right] $$
(28)

The constraint regarding F 32 and F 41 does not need to be considered explicitly in the equations. It is implicitly considered in the Lagrange formalism and in the global solution such that, if all other conditions are satisfied, this condition is not violated under the assumption of optimality of the solution. Therefore, the unique solution obtained by solving (28) is in agreement with this constraint as well. For structual sections two and three, see Fig. 4, the following systems of equations have to be solved:

$$ \begin{array}{ll} & \left[\begin{array}{lllll} 0& 1& 1& 0& 0 \\ 0& 0& 0& 1& 1\\ \omega_{21}& -1& 0& 1& 0 \\ \omega_{22}& 0& -1& 0& 1 \\ 0& 1& 0& 0& 0 \end{array}\right] \left[\begin{array}{ll} \Delta F_{\omega} \\ F_{l,21} \\ F_{l,32} \\ F_{u,21} \\ F_{u,32} \end{array}\right] \\ & = \left[\begin{array}{ll} F^{*}_{l,2} \\ F^{*}_{u,2} \\ 0 \\ 0 \\ \left( 1-\frac{m^{*}_{1}-m^{*}_{2}}{m^{*}_{1}}\right)F_{u,11} -\left( \frac{m^{*}_{1}-m^{*}_{2}}{m^{*}_{1}}\right)F_{u,31} \end{array}\right] \end{array} $$
(29)
$$ \begin{array}{ll} & \left[\begin{array}{lllll} 0& 1& 1& 0& 0 \\ 0& 0& 0& 1& 1\\ \omega_{31}& -1& 0& 1& 0 \\ \omega_{32}& 0& -1& 0& 1 \\ 0& 0& 1& 0& 0 \end{array}\right] \left[\begin{array}{ll} \Delta F_{\omega} \\ F_{l,22} \\ F_{l,41} \\ F_{u,22} \\ F_{u,41} \end{array}\right] \\ & = \left[\begin{array}{ll} F^{*}_{l,3} \\ F^{*}_{u,3} \\ 0 \\ 0 \\ -\left( \frac{m^{*}_{1}-m^{*}_{2}}{m^{*}_{1}}\right)F_{u,11} + \left( 1-\frac{m^{*}_{1}-m^{*}_{2}}{m^{*}_{1}}\right)F_{u,31} \end{array}\right] \end{array} $$
(30)

Note that in (30), the third section is constrained with respect to the order of deformation by the first section. This is valid because the second section is constrained by the first section in the other load path which results in a lower force for this load path in the second section. The resulting force-deformation-intervals for the respective elements are shown in Figs. 5 and 6.

Fig. 5
figure 5

Global solution for the intervals for forces-deformation characteristics

Full size image
Fig. 6
figure 6

Component-wise solution for the intervals for the forces over deformation

Full size image

The active mass decreases over deformation which results in a decreasing total force, shown in Fig. 5, in order to maintain sub-critical accelerations. Also, the order of deformation is as desired despite a monotonously decreasing total force. Each force peak between components is compensated by the parallel load path, see Fig. 6.

The solution space problem is closely related to a constrained optimization problem for the system. In fact, solving the solution space problem can be shown to be of equal complexity as solving the linear optimization problem of minimizing one of the constrained output quantities, e.g. minimizing the maximum acceleration.

By the same reasoning used in the deduction of (21), the problem of minimizing the peak acceleration of the system can, with \({\hat {\mathbf {x}}} = \left (F_{11}, F_{31}, F_{21}, F_{32}, F_{22}, F_{41}\right )^{T}\), be expressed via the Lagrangian

$$ L = - \left( F_{22} + F_{41}\right) - \sum{\lambda_{k} \left( \mathbf{n}_{k}^{T} {\hat{\mathbf{x}}} - b_{k}\right)} \ . $$
(31)

which is very similar to (24). Additionally, the constraints \(F_{22} + F_{41} - \frac {m_{3}}{m_{2} + m_{3}} (F_{22} + F_{32}) = 0\) and \(F_{22} + F_{41} - \frac {m_{3}}{m_{1} + m_{2} + m_{3}} (F_{22} + F_{32}) = 0\), i.e. the acceleration is constant over the length of the structure, are introduced. These constraints substitute the constraints for ΔF which enforced the proportions of the hypercube, i.e. (20).

The problem is still a linear optimization problem with the difference that the dimension of the problem is N rather than 2N+1 as in the solution space problem because the variable ΔF is not needed and only one point, defining the optimal solution, rather than two points to span a hypercube, are sought. (The solution space problem can be reduced to dimension N+1 rather than 2N+1 by substituting of \(F^{*}_{u,i}=F^{*}_{l,i}+\omega _{i} \Delta F_{\omega }\) in the constraints).

In this simple example problem, the optimal solution with respect to acceleration is part of the solution space, more precisely the lower corner of the hypercube. In Figs. 5 and 6, the optimal force over deformation is denoted by the lower bound of each interval. This is not necessarily the case for more complex problems. However, finding an optimal solution with respect to a single output quantity is of the same complexity as finding a solution space to that same problem. Also, for heavily constrained problems, finding a solution space is a problem of the same difficulty as that of finding a feasible solution. If the problem has no feasible solution, a solution space as defined here does not exist.

5 Full vehicle solution

Applying the algorithm to the main load paths of a full vehicle structure is illustrated in Fig. 7. As shown in 3.3, the system is transferred to the deformation space. Then, a section is generated at every point where the active mass or the currently deforming set of components changes. Figure 7 shows the major sections between components. Distributed masses over the structure result in additional sections. Then, based on the generalized form of the global solution, with \(\mathbf {d}^{T} = (d_{1}, d_{2}, \dots , d_{N})\), \(\mathbf {M} = \text {diag}\left (m^{*}_{1}, m^{*}_{2}, \dots , m^{*}_{N}\right )\), \(\mathbf {\omega } = (\omega _{1}, \omega _{2}, \dots , \omega _{M})^{T}\) and I as the unity matrix,

$$ \left[\begin{array}{llll} \mathbf{0}& \textbf{d}^{T}\mathbf{M}^{-1}& \mathbf{0}&\\ \mathbf{\omega}& -\mathbf{I}& \mathbf{I}&\\ \mathbf{0}& \mathbf{0}& \mathbf{M}^{-1}& \end{array}\right] \left[\begin{array}{ll} \Delta F_{\omega} \\ \textbf{F}_{l} \\ \textbf{F}_{u} \end{array}\right] = \left[\begin{array}{ll} \frac{{v_{0}^{2}}}{2} \\ \textbf{0} \\ \textbf{a}_{c} \end{array}\right] \\ , $$
(32)

the global solution can be calculated.

Fig. 7
figure 7

Vehicle structure broken down into one one-dimensional subsystem for the global solution and a number of local subsystems for the component- and section-wise constraints

Full size image

The component solutions are calculated as shown in (28) to (30). This yields an interval for the forces of each section of each component. These intervals can be plotted over the component deformation which results in corridors as described above. Figure 8 shows that the solutions are in good agreement. The analytical solution is much narrower than the solution generated by the stochastic algorithm. The reason for this is shown in Fig. 1. The analytical solution is defined such that all corners of the box fulfill their respective constraints exactly. In high dimensions this results in a much smaller solution space compared to the probabilistic estimate. In particular, the stochastic method generally uses a sample size of N=100 which results, depending on the dimensionality of the problem, in an average difference in the size of the solution space of factor two to three per interval width. An estimator for this loss in solution space size for the direct solution is provided in Fender (2013). Also, the stochastic method, as it is by nature not deterministic, can not exactly detect the boundaries of the feasible domain and may, depending on the quality of the particular sample, over- or underestimate the correct interval width and position.

Fig. 8
figure 8

Solution space for the force-deformation characteristic of two components derived using the method of this paper (solid lines) and the stochastic method (Lehar and Zimmermann 2012) (dashed lines)

Full size image

6 Conclusion

An alternative approach for solving the solution space problem from Zimmermann and Hoessle (2013) has been proposed and described in detail. It was shown, that the method is able to deliver an analytical estimation of the feasible force-deformation intervals for vehicles in a front crash. In reference to previous publications, the method is in good agreement with state-of-the-art methodology for calculating solution spaces. An objective function was formulated which allows for linear representation of the problem, independent of dimensionality. A two-level approach was used to separate the global behavior of the structure as a whole from the singular component contributions. Exploiting the structure of the feasible domain, active constraints are detected prior to solving the problem, removing the need for numerical optimization as preprocessing always results in a linear system of equations of full rank. Hence it was shown here that directly using a linear formulation of the constraints together with a particular choice of objective function yields a very precise and efficient method for the calculation of solution spaces.