1 Introduction

With the continuing updating of CPU and escalation of memory, the computer processing power has been drastically increased, but the computational cost of complex high-fidelity engineering simulations often makes it impractical to exclusively rely on simulation for design optimization (Jin et al. 2001). In order to reduce the computational cost, metamodels are used to replace the expensive simulation models (Queipo et al. 2005; Viana et al. 2010). The most popular metamodels include polynomial model, Kriging (Cressie 1988; Sacks et al. 1989), radial basis functions (RBF) (Fang et al. 2006), support vector regression (SVR), multivariate adaptive regression splines (MARS) (Friedman 1991), least interpolating polynomials (De Boor and Ron 1990), inductive learning (Langley and Simon 1995), and so on.

If only one single predictor is desired, there are two strategies for us to obtain the final prediction metamodel. One is the selection of the most accurate metamodel, which can be done using cross validation (Picard and Cook 1984; Kohavi et al. 1995); The other is the combination of all of the candidate metamodels: Zerpa et al. (2005) proposed a method to determine weight coefficients using prediction variance; Goel et al. (2007) proposed a heuristic method for calculating the weight coefficients, which is known as PRESS (predicted residual sum of squares) weighted average metamodel; Acar and Rais-Rohani (2009) proposed a combining technique with optimized weight coefficients, which were obtained by solving an optimization problem; Viana et al. (2009) got the solution of the weight via Lagrange multipliers, and replaced the real error covariance matrix C with cross-validation error matrix.

Because the choice of metamodel depends on design of experiments (DOEs), selection strategy thus increases the risk of adopting an inappropriate model. Alternatively, since adding inaccurate metamodels may lead to loss of accuracy, combination of all the candidate metamodels also seems not to be a good choice. Therefore, eliminating the redundant metamodels from the set of the candidates before constructing the ensemble is a necessary step. One of the objectives in this paper is to insert a step, where the redundant metamodels are removed, before constructing the final ensemble of metamodels.

Illuminated by the method of variable selection widely used in polynomial regression, a metamodel selection method based on stepwise regression is proposed. In this method, just a subset of n ones (n ≤ p, where p is the number of all of the candidate metamodels) is used. Although a subset of metamodels is also DOE-sensitive (the choice of a subset depends on DOE), using of a subset of metamodels appears to be a more “insure strategy” than selecting one of the “most accurate” metamodel, because there is not less than one individual metamodel used in the construction of the ensemble. Nevertheless, selection of the most accurate metamodel from the candidates only utilizes one metamodel.

The remainder of this paper is organized as follows. In the next section, we present the commonly-used ensemble techniques based on cross validation. In Section 3, the stepwise metamodel selection method is proposed. The arrangement of the experiment is presented in Section 4. The presentation and discussion of results for benchmark functions are displayed in Section 5. And the test for metamodel-based optimization is taken in Section 6. At last, a summary of several important conclusions is discussed in Section 7.

2 Ensemble of metamodels

2.1 BestPRESS

The traditional method of using an ensemble of metamodels is to select the best metamodel among all of the considered models. However, once the choice is made, the metamodel is fixed even though the design of experiments is changed. If the choice is refined for each new DOE, we can include it in the strategies for multiple metamodels, where the model with least error is assigned a weight of one and all others are assigned zero weight. Just as many works do, we also call this strategy BestPRESS, which corresponds to the selection strategy, i.e. the first strategy, mentioned above.

2.2 Heuristic computation of the weight coefficient

Goel et al. (2007) proposed a heuristic method for calculating the weight coefficients, which is known as PRESS weighted average metamodel, where the weight coefficients are computed as:

$$\begin{array}{@{}rcl@{}} w_{i} ={w_{i}^{\ast} } \left/ {\sum\limits_{i=1}^{M} {w_{i}^{\ast} } },w_{i}^{\ast} =(E_{i} +\alpha E_{avg} )^{\beta} ,\right.\\ E_{avg} =\frac{1}{n}\sum\limits_{i=1}^{n} {E_{i} } ,\beta <0,\alpha <1 \end{array} $$
(1)

where E i is the PRESS error of the ith metamodel, α,β are used to control the importance of averaging and individual PRESS (predicted error sum of squares) respectively. Goel et al. (2007) suggested α = 0.05, β = −1. PRESS is actually the leave-one-out (LOO) cross validation error. We firstly construct a metamodel by leaving the jth sample out from training, and then predict the response \(y_{j}^{\prime }\) at the jth sample. Finally, we can get the PRESS, \(\sum \limits _{j=1}^{N} {{{({y_{j}} - y_{j}^{\prime })}^{2}}}\), where N is the number of samples and y j is the real response.

2.3 Computation of the weights for minimum cross validation (especially LOO cross validation)

The optimal weighted metamodel is obtained by minimizing the MSE as:

$$ \underset{\textbf{w}}{\min } \text{{ MSE}} = {\textbf{{w}}^{T}}\textbf{{Cw}} $$
(2)
$$\mathrm{s.t.}~{\textbf{{1}}^{T}}\textbf{{w}} = 1 $$

Using Lagrange multipliers, the solution is obtained as:

$$ \textbf{{w}} = \frac{{{\textbf{{C}}^{- 1}}\textbf{{1}}}}{{\textbf{{1}}^{T}}{\textbf{{C}}^{- 1}}\textbf{{1}}} $$
(3)

where C is approximated by the vectors of cross validation errors, e, especially LOO, which are obtained by using n − 1 samples to construct a metamodel and to predict the rest one sample. The deviation between true value and the predicted value is LOO cross validation error.

$$ {c_{ij}} \simeq \frac{1}{N}{{e}_{i}^{T}}{{e}_{j}} $$
(4)

and N is the number of data points and the i and j indicate different metamodels.

Furthermore, Viana et al. (2009) enforced the weight positive by solving (3) using only the diagonal elements of C. The approach is named OWS d i a g .

According to the classification in Zhou et al. (2011), the ensemble of metamodels can be classified into two groups: some are based on cross-validation; and the others are based on prediction mean square error. All of the above-mentioned ensemble techniques belong to the first group. The second group is not considered in this paper, because the second group of ensemble techniques requires additional test samples. When the number of samples is not large enough, extracting a part of samples for test from the sample set means that the number of samples used to construct the ensemble of metamodels decrease, and thereby the second group of methods greatly impair the prediction capabilities of ensemble of metamodels.

3 Stepwise metamodel selection

Just as polynominal regression model, we can propose an ensemble of model like this:

$$ y = {\beta_{0}} + {\beta_{1}}{f_{1}}(\textbf{{x}}) + {\cdots} + {\beta_{p}}{f_{p}}(\textbf{{x}}) + \varepsilon $$
(5)

Furthermore, if we replace f 1(x) with M 1(x), ..., f p (x) with M p (x) respectively, then (5) becomes

$$ y = {\beta_{0}} + {\beta_{1}}M_{1}(\textbf{{x}}) + {\cdots} + {\beta_{p}}M_{p}(\textbf{{x}}) + \varepsilon $$
(6)

where M 1(x), ..., M p (x) denote individual metamodels. Therefore, (6) can be regarded as a kind of ensemble of metamodels.

Given a dataset, S{X,Y}, consisting of N input-output data pairs {(x (1), y (1)),⋯(x (N), y (N))}, where y is the metamodel response at the design sample point, x, and N is the total number of metamodel runs, the linear regression model becomes a N×(p + 1) system of equations:

$$\begin{array}{@{}rcl@{}} \left( {\begin{array}{c} {{y^{(1)}}} \\ {\vdots} \\ {{y^{(N)}}} \end{array}} \right) &=& \left( {\begin{array}{llll} 1 & {{M_{1}}({\textbf{{x}}^{(1)}})} & {\cdots} & {{M_{p}}({\textbf{{x}}^{(1)}})} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ 1 & {{M_{1}}({\textbf{{x}}^{(N)}})} & {\cdots} & {{M_{p}}({\textbf{{x}}^{(N)}})} \end{array}} \right)\left( {\begin{array}{c} {{\beta_{0}}} \\ {{\beta_{1}}} \\ {\vdots} \\ {{\beta_{p}}} \end{array}} \right) \\&&+ \left( {\begin{array}{c} {{\varepsilon^{(1)}}} \\ {\vdots} \\ {{\varepsilon^{(N)}}} \end{array}} \right) \end{array} $$
(7)

where M i (x (j))(i = 1, ...,p; j = 1, ...,N) is the prediction value of the ith metamodel at the jth design sample point. In the process of construction of the ith metamodel, the jth design sample point is left out from training, and the established metamodel is used to predict the value at the omitted jth design sample point. That is, the samples

$$\begin{array}{@{}rcl@{}} &&\{ ({\textbf{{x}}^{(1)}},{y^{(1)}}), {\ldots} ,({\textbf{{x}}^{(j - 1)}},{y^{(j - 1)}}),({\textbf{{x}}^{(j + 1)}},{y^{(j + 1)}}), \ldots,\\&&({\textbf{{x}}^{(N)}},{y^{(N)}})\} \end{array} $$

can be used to construct the metamodels M 1(⋅),⋯ ,M p (⋅), and then these metamodels are used respectively to predict the values at x (j), finally the predictions M 1(x (j)),⋯ ,M p (x (j)) are obtained. We do this process on all of the samples, then we get the whole matrix of (7). This process is something like LOO cross validation. Finally, the parameter β = (β 0, β 1⋯β p )T can be calculated using least squares method.

There are two purposes for using (6) in this paper: (1) We use it to eliminate the redundant metamodels; and (2) We use it as an ensemble. Nevertheless, if we directly use the ensemble (6) to predict the unknown design point, the redundant metamodels would impair the performance of the ensemble.

Stepwise regression is a systematic method for adding and removing terms from a multilinear model based on their statistical significance in a regression. In this paper, we treat metamodels as terms (or variables) and use the stepwise regression method to reject the redundant individual metamodels.

Before presenting how stepwise regression works to eliminate the redundant metamodels, we detail the process of how to treat these individual metamodels as factors:

Firstly, we use the candidate metamodels (Kriging (denoted by KRG), SVR, RBF and polynomial model (denoted by PRS (polynomial regression surrogate))) to calculate the LOO cross validation predictions, that is, N − 1 samples are employed to predict the omitted one. Then the LOO predictions

$$\left\{ {\begin{array}{c} {y_{RBF}^{(1)}} \\ {\vdots} \\ {y_{RBF}^{(N)}} \end{array}} \right\},\left\{ {\begin{array}{c} {y_{SVR}^{(1)}} \\ {\vdots} \\ {y_{SVR}^{(N)}} \end{array}} \right\},\left\{ {\begin{array}{c} {y_{KRG}^{(1)}} \\ {\vdots} \\ {y_{KRG}^{(N)}} \end{array}} \right\},\left\{ {\begin{array}{c} {y_{PRS}^{(1)}} \\ {\vdots} \\ {y_{PRS}^{(N)}} \end{array}} \right\} $$

for each of the single metamodels at all of the samples are obtained. Combing with the real responses, we can obtain the following new samples

$$\begin{array}{@{}rcl@{}} &(y_{KRG}^{(1)},y_{SVR}^{(1)},y_{RBF}^{(1)},y_{PRS}^{(1)};{y^{(1)}}) {\cdots} &\!(y_{KRG}^{(N)},y_{SVR}^{(N)},y_{RBF}^{(N)},\\&&y_{PRS}^{(N)};{y^{(N)}}), \end{array} $$

where \((y_{KRG}^{(i)},y_{SVR}^{(i)},y_{RBF}^{(i)},y_{PRS}^{(i)})\) for i = 1,⋯,N are regarded as new factors, and y (i) for i = 1, ⋯,N are still regarded as responses.

Furthermore, according to these new samples, we use Stepwise regression method to eliminate the redundant candidate metamodels.

Finally, the remaining metamodels can be used to construct the ensembles according to the techniques such as BP, EG, OWS, and the regression method proposed in formula (6).

In this process, we use cross validation RMSE (especially LOO) to construct ensembles. The LOO cross validation plays a very important role in eliminating of redundant metamodels. And we use prediction RMSE to test the performances of these ensembles, which means that we need extra samples obtained by LHS to test their performances.

Now, let’s go back to how to use Stepwise regression to eliminate the redundant metamodels. The method begins with an initial ensemble and then compares the explanatory power of incrementally larger and smaller ensembles. At each step, the p-value of an F-statistic is computed to test ensembles with and without a potential metamodel. If a metamodel is not currently in the ensemble, the null hypothesis is that the metamodel would have a zero coefficient if added to the ensemble. If there is sufficient evidence to reject the null hypothesis, the metamodel is added to the ensemble. Conversely, if a metamodel is currently in the ensemble, the null hypothesis is that the metamodel has a zero coefficient. If there is insufficient evidence to reject the null hypothesis, the metamodel is removed from the ensemble. The method proceeds as follows:

figure a

Depending on the metamodels included in the initial ensemble and the order in which metamodels are moved in and out, the method may build different ensembles from the same set of potential metamodels. The method terminates when no single step improves the ensemble. There is no guarantee, however, that a different initial ensemble or a different sequence of steps will not lead to a better fit. In this sense, stepwise ensembles are locally optimal, but may not be globally optimal.

Here, there are two comments about the entrance/exit tolerance and the ordering:

(1) The entrance/exit tolerance is important to determine which metamodels should be included in the resulting ensemble. The entrance/exit tolerance can be determined by two ways: one is according to the engineer’s experience, and the other is using cross validation. The second way is employed in this paper. Actually, the entrance/exit tolerance is affected by both candidate metamodels and data set. Therefore, the choice of entrance/exit tolerance depends on the case we confront.

(2) Although the ordering effects which metamodels should be chosen, the ordering strategy adopted in this paper is reasonable. Just as done in step 1 of Algorithm 1, the metamodel with the lowest CV error is chosen as the first metamodel of the ensemble, and the following ordering of adding or removing of metamodels is affected by the first metamodel. This first-metamodel-choosing strategy is advisable, because the lowest-CV metamodel may be more suitable than the others.

At last, we generalize the selection strategy to all of the ensemble techniques, and summarize the procedure of constructing of ensemble as follows:

figure b

Two contributions in this paper are:

  1. (1)

    Adopting the stepwise regression as a metamodel selection method before constructing the final ensemble; and

  2. (2)

    Proposing (6) as a new method of construction of ensemble.

4 Experiments

4.1 Benchmark problems

In order to test the proposed techniques in this paper, we choose the following analytic functions that are commonly used as benchmark problems in literature (Goel et al. 2007; Acar and Rais-Rohani 2009; Viana et al. 2009).

  1. 1.

    CamelBack:

    $$ y(x_{1} ,x_{2} )=(4-2.1{x_{1}^{2}} +\frac{{x_{1}^{4}} }{3}){x_{1}^{2}} +x_{1} x_{2} +(-4+4{x_{2}^{2}} ){x_{2}^{2}} $$
    (8)

    where x 1∈[−3,3],x 2∈[−2,2].

  2. 2.

    Hartman:

    $$\begin{array}{@{}rcl@{}} y({\textbf{x}})=-\sum\limits_{i=1}^{m} {c_{i}} \exp [-\sum\limits_{j=1}^{n}{a_{ij} (x_{j} -p_{ij} )^{2}} ] \end{array} $$
    (9)

    where x i ∈[0,1].

    The six-variables (m = 6) model of this function is considered. The values of function parameters c i , p i j , a i j for Hartman model are given in Table 1.

  3. 3.

    Extended Rosenbrock(denoted by “ER”):

    $$ y(\textbf{{x}}) = \sum\limits_{i = 1}^{m - 1} {[{{(1 - {x_{i}})}^{2}} + 100{{({x_{i + 1}} - {x_{i}^{2}})}^{2}}]} $$
    (10)

    where −5≤x i ≤10.

    The nine-variables (m = 9), twelve-variables (m = 12) and fifteen-variables (m = 15) models of this function are considered.

  4. 4.

    Dixon-Price(denoted by “DP” ):

    $$ y(\textbf{{x}}) = {({x_{1}} - 1)^{2}} + \sum\limits_{i = 2}^{m} {i{{(2{x_{i}^{2}} - {x_{i - 1}})}^{2}}} $$
    (11)

    where −10≤x i ≤10.

Table 1 Parameters used in Hartman function with six variables
Full size table

Fifteen-variables (m = 15) models of this function is considered in this paper.

4.2 Design and analysis of computer experiments

As stated before, the quality of fit depends on the training data (DOE). The performance measures may vary from DOE to DOE. Thus, for all test problems, a set of 500 different DOEs was used as a way of averaging out the DOE dependence of the results. They were created by the MATLAB Latin hypercube function lhsdesign, set with the maxmin option with 5 iterations. Table 2 shows details about the data set generated for each test function. Naturally, the number of points used to fit metamodels increases with dimensionality.

Table 2 Summary of training and test data used in each benchmark problem
Full size table

The accuracies of each individual and ensemble model for the benchmark problems are measured using root mean square error (RMSE), average absolute error (AAE), max absolute error (MAE) and correlation coefficient (denoted by R). Their definitions are expressed as:

Root mean square error:

$$\begin{array}{@{}rcl@{}} RMSE=\sqrt{\left.{{\sum}_{i=1}^{n_{error} } {\left( {y_{i} -\widehat{y}} \right)^{2}} } \right/ {n_{error} }} \end{array} $$

Average absolute error:

$$\begin{array}{@{}rcl@{}} AAE=\left.{{\sum}_{i=1}^{n_{error} } {\left| {y_{i} -\widehat{y}} \right|} } \right/{n_{error} } \end{array} $$

Max absolute error:

$$\begin{array}{@{}rcl@{}} MAE=max\left| {y_{i} -\widehat{y}} \right|, i=1,......,n_{error} \end{array} $$

Correlation coefficient:

$$\begin{array}{@{}rcl@{}} R(y,\widehat{y})&=&\frac{\frac{1}{V}\underset{V}{\int} {(y-\overline y)(\widehat{y}-\overline {\widehat{y}} )dv} }{\delta (y)\delta (\widehat{y})}\\ \frac{1}{V}\underset{V}{\int} {y\widehat{y}dv} &=&\left.{{\sum}_{i=1}^{n_{error} } {y_{i} \widehat{y}_{i} } } \right/ {n_{error} },\\ \overline y&=&\left.{{\sum}_{i=1}^{n_{error} } {y_{i} } } \right/ {n_{error} }, \\ \delta (y)&=&\sqrt{\left.{{\sum}_{i=1}^{n_{error} } {(y_{i} -\overline y )^{2}} } \right/ {n_{error} }} \\ \end{array} $$

In these four definitions above, n e r r o r is the number of samples in the test set, y i is the actual response, \(\overline y \) is average value of actual response, \(\widehat {y}\) is the metamodel response, \(\overline {\widehat {y}} \) is the average value of metamodel response.

Because the experiments are repeated 500 times, the mean and the coefficient of variation (CV) of R, RMAE, AAE, and MAE are used to evaluate the prediction accuracies of each individual metamodel and ensemble model. The definition of CV is expressed as:

$$CV=\left.\delta \right/ \mu $$

where δ is the standard variance of samples, and μ is the mean of samples.

4.3 Individual/ensemble techniques

Four individual metamodels (PRS, KRG, SVR, and RBF), described in “Appendix”, are considered in this paper. These metamodels are used as candidate metamodels.

All the values of the parameters are set using cross validation (LOO is adopted in this paper) such that they minimize the MSE. There are several parameters whose values should be determined in the metamodels mentioned above: the highest order (denoted by d) in PRS, the parameter (c) in multiquadrics of RBF, (C,ε,σ) in SVR, and (𝜃, lob, upb and regression model) in Kriging, where Gauss function is adopted as correlation model.

As to the implementation of Kriging, we use the toolbox proposed by Lophaven et al. (2002), where lob and upb are defined respectively as lower and upper bounds on 𝜃, which are clearly described in Lophaven et al. (2002).

Just as said in Lophaven et al. (2002), 𝜃 0 is just an initial guess on underlying 𝜃, and it doesn’t necessarily be required between lob and upb. If it is larger than upb or smaller than lob, there is a function to reset it into [lob upb]. And in the train function dacefit of Lophaven et al. (2002), the optimal 𝜃-value can be gotten by subfunction boxmin.

The LOO cross-validation results are presented in Table 3.

Table 3 Summary of LOO cross-validation results for the parameters in all of the metamodels, e = 1 1×n , where n is the number of the dimension of x
Full size table

In this paper, we focus on the ensemble techniques based on cross validation: BestPRESS (described in Section 2.1, heuristic method (described in Section 2.2), optimal weighted metamodel (OWS) (described in Section 2.3), and diagonal optimal weighted metamodel (OWS d i a g ) (described in Section 2.3). Just as the denotation in Zhou et al. (2011): BestPRESS is denoted by BP; The heuristic method of Goel et al. (2007) is labeled as EG; OWS d i a g in Viana et al. (2009) is denoted by Od; OWS remains unchanged.

Although BestPRESS is classified into ensemble technique, it also can be regarded as a kind of stand-alone metamodel, because the best metamodel varies with DOE, and actually there is only one metamodel used in the construction of ensemble. Except for BestPRESS, the other ensemble techniques, such as heuristic method (Goel et al. 2007), OWS and OWS d i a g (Viana et al. 2009), can be constructed after eliminating the redundant metamodels using the method proposed in this paper. The eliminated ensembles of EG, Od and OWS are denoted by EG*, Od* and OWS* respectively.

In the process of rejecting of the redundant individual metamodels, the function stepwisefit in MATLAB is used. The parameters penter and premove, which are employed in the step 2 and step 3 of Algorithm 1 in Section 3, are presented in Table 4. They are used to determine which metamodels should be added and which ones should be removed.

Table 4 Setting of the parameters penter and premove used in function stepwisefit for benchmark problems
Full size table

5 Results and analysis of experiments

In this paper, we focus on the comparison among the ensembles (including BestPRESS), without comparing these ensembles with the individual metamodels (PRS, KRG, SVR, and RBF). Actually, we don’t know which individual metamodel can accurately approximate the underlying relationship in practice, it is thus inappropriate to use a same individual metamodel in all of the DOEs, unless we know the underlying relationship. If we have to use an individual metamodel to approximate the underlying relationship, we often adopt BestPRESS to get the best individual metamodel according to a specific DOE, and BestPRESS varies from DOE to DOE. Therefore, we only need to compare ensembles with BestPRESS rather than with the individual metamodels. Although we don’t think that it is necessary to compare the ensembles with the individual metamodels, we still want to present the fact that some of the ensembles even outperform the individual metamodels, which compose the ensembles, in many cases. Therefore, we still present the prediction errors of ensembles and individual metamodels in a same table/figure, but we only compare the prediction errors among ensembles. In order to distinguish ensembles from individual metamodels, we separate ensembles from individual metamodels with the symbol “–” in these tables.

The results of different benchmark problems are shown with the help of boxplots (the description of boxplot is provided in the “Appendix”), and the means and CVs of the error metrics are presented with several tables.

5.1 RMSE

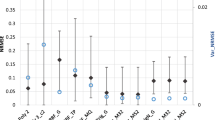
The RMSEs for all of the benchmark functions using individual metamodels and ensembles are presented in Table 5, where we just compare the performance among the ensembles, and the same is done in the following tables in this paper. From this table we can see: 1) the means of RMSEs for EG*, OWS*, Od* and Reg* are smaller than those for EG, OWS, Od and Reg respectively in all of the benchmark problems (Camelback, Hartman, ER-9, ER-12, ER-15 and DP-15), which indicates that it is necessary to get rid of the redundant individual metamodels from the set of candidate ones before constructing the ensemble of metamodels. 2) Od* has better performance in low dimension benchmark problems: Camelback, Hartman; nevertheless, Reg* has the best performance among all of the metamodels (including ensembles and even individual metamodels) in high dimension benchmark problems: ER-9, ER-12, ER-15 and DP-15. 3) In high dimension benchmark problems (ER-9, ER-12, ER-15 and DP-15), OWS and Reg have apparently larger RMSEs than the other ensembles and individual metamodels; OWS* and Reg*, however, sharply reduce the errors after rejecting the redundant individual metamodels.

The intuitional comparison results are presented in Fig. 1. As there are very large outliers in the boxplots of OWS and Reg within subfigures of C, D, E and F (C: ER-9, D: ER-12, E: ER-15, F: DP-15), we constrain these subfigures into [0 5×105] (such treatment is also adopted in AAE and MAE) for the sake of ease of observing, so we can’t observe the outliers larger than 5×105. From Fig. 1 we can observe that OWS and Reg have two very long tails in C, D, E and F, which indicates that OWS and Reg have large variations in high dimension problems. Nevertheless, OWS* and Reg* greatly shorten their tails.

Fig. 1
figure 1

RMSE for different metamodels. (a: Camelback, b: Hartman, c: ER-9, d: ER-12, e: ER-15, f: DP-15)

Full size image

5.2 AAE

Table 6 shows the AAEs using ensembles and individual metamodels on all of the benchmark problems. From this table we find that EG*, OWS*, Od* and Reg* have better performance than EG, OWS, Od and Reg respectively in all of the benchmark problems. And we also can observe that Reg* has the best performance among all of the ensembles, especially in high dimension problems (refer to ER-9, ER-12, ER-15 and DP-15 in this paper), while Od* is the best ensemble in low dimension problems (refer to Camelback and Hartman in this paper). The corresponding comparison results are shown in Fig. 2. These results are similar to those presented in RMSE.

Fig. 2
figure 2

AAE for different metamodels. (a: Camelback, b: Hartman, c: ER-9, d: ER-12, e: ER-15, f: DP-15)

Full size image

5.3 MAE

Table 7 and Fig. 3 show the MAEs of different metamodels for different test functions. From this table and figure we find that except for Camelback, EG*, OWS*, Od* and Reg* still have better performance than EG, OWS, Od and Reg respectively. And Reg* is still the best ensemble in high dimension problems. Furthermore, this table and figure illustrate that rejecting the redundant individual metamodels is still necessary for getting smaller MAEs.

Fig. 3
figure 3

MAE for different metamodels. (a: Camelback, b: Hartman, c: ER-9, d: ER-12, e: ER-15, f: DP-15)

Full size image

5.4 Correlation coefficient

The correlation coefficients for different benchmark functions are shown in Table 8 and Fig. 4, from which we can see: 1) Although OWS* has similar correlation coefficient to Reg* in ER-9, it has the best performance in high dimension problems. 2)Except for Camelback, Od* still has better performance than the other ensembles in low dimension problems. These results demonstrate that we should reject the redundant individual metamodels before constructing the final ensemble.

Fig. 4
figure 4

Correlations between actual and predicted response for different metamodels. (a: Camelback, b: Hartman, c: ER-9, d: ER-12, e: ER-15, f: DP-15)

Full size image

5.5 Discussions

As for RMSE, AAE, MAE and correlation coefficient, we find that ensemble Reg and OWS have unsatisfying results in ER-9, ER-12, ER-15 and DP-15. Why those happen?

On the one hand, in high dimension benchmark problems, some of individual metamodels may not be suitable for these problems. Therefore, these unsuitable individual metamodels may impair the performances of the ensembles, which can explain to a certain extend why Reg and OWS perform badly in these problems. After eliminating those improper metamodels, Reg* and OWS* enhance their performances.

On the other hand, as for Reg, since it doesn’t have a constrain,

$$\sum\limits_{i = 1}^{p} {{\beta_{i}}} = 1 $$

if these coefficients are not proper, the prediction values obtained with the regression model

$$y = {\beta_{0}} + {\beta_{1}}{M_{1}}(\textbf{{x}}) + {\cdots} + {\beta_{p}}{M_{p}}(\textbf{{x}}) $$

maybe largely deviate from the true values, especially in high-dimensional problems, which perhaps is a drawback of the regression model. But after eliminating the redundant metamodels with stepwise method, the regression model can significantly improve its performance. Therefore, using stepwise method to get rid of the redundant metamodels is a necessary and efficient step not only in construction of regression model but also in any other ensemble construction techniques.

Next, let’s analyze the coefficients of variation for these ensembles. After carefully examining the results in Tables 5–8, we find that Reg* has larger coefficients of variation than the other ensembles (it’s still better than Reg), especially in high dimension problems, which means Reg* is not very “robust” in high dimension problems compared with the other ensembles, but its average performance is still good and its coefficients of variation are still nice in low dimension problems. In addition, the coefficients of variation of EG*, OWS* and Od* are similar to those of EG, OWS and Od respectively, and even smaller in some cases. Therefore, the values of these coefficients of variation for ensembles with stepwise, on the whole, are acceptable.

Table 5 Mean and CV (in parenthesis) of RMSE (based on 500 DOEs) for different metamodels, the least value in each category is shown in bold for ease of comparison
Full size table
Table 6 Mean and CV of AAE for different metamodels
Full size table
Table 7 Mean and CV of MAE for different metamodels
Full size table
Table 8 Mean and CV of correlation coefficient between actual and predicted response for different metamodels
Full size table

6 Metamodel-based optimization

After presenting the efficiency of these ensemble models using several benchmark problems, we will take a real-life example, printing ink, to furthermore illustrate their performance in metamodel-based optimization problem.

6.1 The printing ink example

The print ink example is widely used in the works of Box and Draper (1987), Vining and Myers (1990), Del Castillo and Montgomery (1993), Lin and Tu (1995), Copeland and Nelson (1996), Vining and Bohn (1998), Kksoy and Yalcinoz (2005), Shaibu and Cho (2009), and Zhou et al. (2012). The purpose of the experiment was to study the effect of speed, x 1, pressure, x 2, and distance, x 3, upon a printing machine’s ability to apply coloring inks upon package labels. The experiment is 33(n = 27) complete factorial with three runs (m = 3) at each design point for a total of 81 runs. These papers all have considered the situation where we wish to minimize the process variance around a target value of 500 for the response. Table 9 summarizes the data. Following the traditional practice in literature, this table reports the specific settings for the factors in terms of the standard −1 to 1 metric.

Table 9 The printing process data
Full size table

In this problem, the optimization model is

$$\begin{array}{@{}rcl@{}} &&\underset{\textbf{{x}}}{\min } MSE(y) = E[(y-\zeta)^{2}]=Dev^{2}(y)+(E(y)-\zeta)^{2}.\\ &&s.t. 1 \le \textbf{{x}} \le 1 \end{array} $$
(12)

where, E(y) denotes the mean response, and D e v(y) denotes the standard deviation response, ζ represents a target value for the response.

After approximating E(y) and D e v(y) using the ensemble of metamodels, we can get the metamodel-based optimization problem:

$$\begin{array}{@{}rcl@{}} &&\underset{\textbf{{x}}}{\min } \hat{MSE}(y)= \hat{Dev}^{2}(y)+(\hat{E}(y)-\zeta)^{2}.\\ &&s.t. 1 \le \textbf{{x}} \le 1 \end{array} $$
(13)

In this experiment, the p-values in stepwise method are set by cross validation and presented in Table 10.

Table 10 Setting of the parameters penter and premove used in function stepwisefit for Mean and Standard deviation data
Full size table

6.2 Optimization results

In this part, the standard optimization function fmincon in MATLAB is employed. Table 11 summarizes the estimated MSEs and the recommended settings for all of the ensemble models mentioned above. From this table, we can see that all of the ensemble models with stepwise method have the better performance than those without it in terms of MSE and deviation. In this experiment, we hope the objective function (MSE) and the deviation are as small as possible. We also can find that regression model is not very well, but Reg ∗ is still better than Reg, which also indicates that using stepwise to reduce the redundant metamodels is a reasonable strategy.

Table 11 Comparing solution to the MSE optimization (19)
Full size table

7 Conclusion

Illuminated by variable selection method widely used in polynomial regression, we treat metamodels as a variables in polynomial regression, and then propose a methodology of constructing of ensemble from the view of polynomial regression. In addition, considering that including redundant metamodels could impair the prediction accuracy of ensemble, we adopt the stepwise regression method to reject the redundant individual metamodels before constructing the final ensemble of metamodels.

After examining the experiment results, we have the following findings:

  1. 1.

    Stepwise regression method is an useful automatic strategy to reject the inappropriate individual metamodels. This strategy can automatically identify how many individual metamodels should be used to construct the final ensemble of metamodels according to a specify DOE. In the existing methods of constructing of ensembles, the number of individual metamodels is determined before-hand; Nevertheless, the method proposed in this paper doesn’t need to do that. In fact, we have no idea about how many metamodels are fit for the design problems. In other words, it is unknown that how many metamodels should be added to the ensemble. The experiment results show that getting rid of the redundant individual metamodels before constructing the ensemble can greatly enhance the performance of ensemble.

  2. 2.

    After rejecting the redundant metamodels, using the construction method presented in formula (6) from the view of polynomial regression is an optional strategy, especially in high dimension problems, but it is still necessary to be careful of the “robustness” (or stability) in spite of its good average performance.