A new structural reanalysis approach based on the polynomial-type extrapolation methods

Abstract

In this study, a new approach based on the polynomial-type extrapolation methods is applied to the approximate structural reanalysis under multiple and large changes in the initial design. In this approach, the sequences of approximate displacement of the modified structure are constructed by using a fixed-point iteration method. These sequences are then further analyzed by two polynomial-type vector extrapolation methods to find the approximate response of the modified structure more accurately, namely, the minimal polynomial extrapolation (MPE) and the reduced rank extrapolation (RRE). Based on a single initial design, the MPE and RRE methods approximate the displacement vector of the modified structure by solving a least-squares problem which is much smaller than the original system of equations of the exact analysis. The accuracy and efficiency of this reanalysis approach is evaluated on three large scale structural reanalysis problems under multiple and large changes in their initial designs. The obtained reanalysis results demonstrate that the MPE and RRE methods not only yield accurate results, but also are computationally efficient.

1 Introduction

Usually, the structural optimization process requires numerous repeated analyses in order to satisfy code requirements, ensuring safety, and minimizing constructional costs (Jalili et al. 2016a; b; Jalili and Talatahari 2017). For each of the modified structure, a set of finite element equations should be resolved which makes the optimum design procedure very time consuming and computationally expensive. As a matter of fact, it is possible to calculate the response of the modified structure by using approximate structural reanalysis methods without solving the complete set of modified equations. These methods are able to calculate the response of the modified structure with a certain level of accuracy. Typically, the available structural reanalysis methods are classified into two categories: 1) local or single point approximation methods and 2) global or multipoint approximation methods.

As its name suggests, the local or single point approximation methods, such as binomial series expansion and the first order Taylor series expansion about a given initial design, approximate the response of the modified structure based on available information from a single initial design. Although the application of these methods showed good accuracy in approximation of exact response under small changes in the initial design, they were not able to function well on reanalysis problems with relatively larger changes in the design space, and unstable computational results have been observed (Barthelemy and Haftka 1993). On the other hand, global or multipoint approximation methods, such as a polynomial fitting or the reduced basis method (Fox and Miura 1971; Haftka et al. 1987; Noor 1994), calculate the response of the modified structure by considering multiple initial designs. Although, it has been shown that the global methods perform well on the reanalysis problems with a relatively larger changes in the design space, they also have some shortcomings. These methods neglect the higher order terms of series expansion at every initial design point which reduce the accuracy of reanalysis results (Zuo et al. 2012). Moreover, they may require much computational effort in reanalysis problems with a large number of design variables (Wu et al. 2003).

To remedy abovementioned drawbacks of the local and global approximation methods, Kirsch (2000, 2003; Kirsch and Papalambros 2001a) developed a combined approximation (CA) method, which attempts to provide global qualities to the local approximations. By assuming a single initial design, the CA method combines the reduced basis method with the first terms of series expansion to approximate the response of the modified structure. The numerical results in previous studies indicate that the CA method performs well in various reanalysis problems and is able to approximate the response of the modified structure under relatively large changes in the design space (Amir et al. 2008; Kirsch 2010; Kirsch and Bogomolni 2004; Kirsch et al. 2006; Kirsch and Papalambros 2001b; Leu and Huang 2000). Kirsch et al. (2002) proved that the CA method and preconditioned conjugate gradient (PCG) method of using the initial stiffness matrix as the preconditioner are computationally equivalent and they provide theoretically identical results. There have been some studies to improve the accuracy and efficiency of the CA method in structural reanalysis (Sun et al. 2014; Zheng et al. 2015; Zuo et al. 2012). For example, Zuo et al. (2012) proposed a hybrid Fox and Kirsch’s reduced basis method for static structural reanalysis. The hybrid method combines the merits of Fox’s polynomial fitting reanalysis and combined approximation to achieve more accurate results. Although the hybrid method achieves significantly accurate results than the CA method, it requires more computational effort (Zuo et al. 2012). In another work, Sun et al. (2014) developed an adaptive Kirsch method to structural reanalysis. The authors used a K-condition number technique to determine minimum number of basis vectors.

Accuracy and efficiency are two important factors in evaluating the performance of a structural reanalysis method. Most of the available reanalysis methods approximate the response of the modified structure by constructing a series expansion about an available initial design. Usually, they pick a certain terms of constructed series expansion and calculate the approximate response of the structure. However, in most of the reanalysis problems, these series expansions converge to their limits very slowly or even diverge. In this situation, considering higher order terms of series can not only guarantee the accuracy of the results but also lead to computationally expensive solution process. In this context it is necessary to develop new reanalysis procedures based on computational approaches able to find high quality results with fewer computational efforts. From mathematical viewpoint, one practical way to make a given sequence converge more quickly is to apply to them a suitable convergence acceleration method (or equivalently extrapolation method). This paper joins this line of research by using a new structural reanalysis approach based on the polynomial-type extrapolation methods. In this approach, the sequences of approximate displacement of the modified structure are constructed by using a fixed-point iteration method. These sequences are then further analyzed by two polynomial-type extrapolation methods to find the approximate response of the modified structure more accurately, namely, the minimal polynomial extrapolation (MPE) and the reduced rank extrapolation (RRE). The performance of this reanalysis approach is evaluated on three large scale static structural reanalysis problems under multiple and large changes in their initial designs. Numerical results confirm that the new polynomial-type extrapolation-based reanalysis approach is capable of yielding accurate results with fewer amount of computational efforts.

The subsequent sections of this paper are organized as follows. In Section 2, mathematical formulation of static reanalysis problem is presented. Then, details of the new reanalysis approach are introduced in Section 3. In Section 4, the performance of the proposed approach is demonstrated through three large scale structural reanalysis problems. Finally, Section 5 presents the concluding remarks and directions for future research.

2 Problem formulation

The main aim of the static structural reanalysis problem is to calculate the response of the modified structure without resolving complete set of modified equations in such a way that the required computational effort is minimized. Now, let us assume a given initial structural design with n_dof degree of freedoms (DOFs), stiffness matrix ${\boldsymbol{K}}_0\in {\mathbb{C}}^{n_{\mathrm{dof}}\times {n}_{\mathrm{dof}}}$, and load vector ${\boldsymbol{F}}_0\in {\mathbb{C}}^{n_{\mathrm{dof}}}$. In reanalysis problems, it is assumed that the initial displacement vector ${\boldsymbol{r}}_0\in {\mathbb{C}}^{n_{\mathrm{dof}}}$ for initial design has been calculated from the initial analysis as follows:

$$ {\boldsymbol{K}}_0{\boldsymbol{r}}_0={\boldsymbol{F}}_0 $$

(1)

where it is assumed that the decomposed form of initial stiffness matrix K₀ is given as follows:

$$ {\boldsymbol{K}}_0={\boldsymbol{U}}_0^{\mathrm{T}}{\boldsymbol{U}}_0 $$

(2)

in which U₀ denotes a upper triangular matrix.

Now, if we assume that some changes are occurred in the initial structural design, the new stiffness and load vectors for the modified structure can be simply written as:

$$ \boldsymbol{K}={\boldsymbol{K}}_0+\mathbf{\Delta }\boldsymbol{K},\kern6.25em \boldsymbol{K},\mathbf{\Delta }\boldsymbol{K}\in {\mathbb{C}}^{n_{\mathrm{dof}}\times {n}_{\mathrm{dof}}} $$

(3)

$$ \boldsymbol{F}={\boldsymbol{F}}_0+\mathbf{\Delta }\boldsymbol{F},\kern6.50em \boldsymbol{F},\mathbf{\Delta }\boldsymbol{F}\in {\mathbb{C}}^{n_{\mathrm{dof}}} $$

(4)

where K and F are the stiffness matrix and load vector for the modified structure, respectively. Generally speaking, the changes in the stiffness matrix ∆K are a function of cross-sectional properties, length, and material properties of structural elements, while the changes in the load vector ∆F depend on the loading conditions as well as geometrical and physical properties of structure (Kirsch 2000). By assuming these changes in the initial structural design, the purpose of a static reanalysis problem is to calculate the displacement vector $\boldsymbol{r}\in {\mathbb{C}}^{n_{\mathrm{dof}}}$ of the modified structure without solving following complete set of modified equations:

$$ \boldsymbol{Kr}=\boldsymbol{F} $$

(5)

If the displacement vector of the modified structure is given, the stress in the members of structure can be obtained accordingly.

3 Methodology

In this section, we present a new structural reanalysis approach based on the polynomial-type extrapolation methods. Since in the numerical investigations we compare the performance of our approach with the well-known combined approximation (CA) method, we first provide a brief review of the CA method and then explain details of the new reanalysis approach.

3.1 Combined approximation (CA) method

The combined approximation (CA) is a reanalysis method developed by using the reduced basis vectors and the first terms of series expansion. In the CA method, the displacement vector of the modified structure r is approximated as a linear combination of s linearly independent basis vectors as follows:

$$ \boldsymbol{r}={y}_1{\boldsymbol{r}}_1+{y}_2{\boldsymbol{r}}_2+\cdots +{y}_s{\boldsymbol{r}}_s={\boldsymbol{r}}_{\mathrm{B}}\boldsymbol{y},\kern6.5em {\boldsymbol{r}}_{\mathrm{B}}\in {\mathbb{C}}^{n_{\mathrm{dof}}\times s},\boldsymbol{y}\in {\mathbb{C}}^s $$

(6)

$$ {\boldsymbol{r}}_{\mathrm{B}}=\left[{\boldsymbol{r}}_1,{\boldsymbol{r}}_2,\dots, {\boldsymbol{r}}_s\right],\kern1.75em \boldsymbol{y}=\left\{\begin{array}{c}{y}_1\\ {}{y}_2\\ {}\vdots \\ {}{y}_s\end{array}\right\} $$

(7)

where r_B is a matrix consisting of s basis vectors, and y is a vector containing unknown coefficients that should be determined. Substituting (6) in (5) and premultiplying resulting equations by ${\boldsymbol{r}}_{\mathrm{B}}^{\mathrm{T}}$, we can write:

$$ {\boldsymbol{K}}_{\mathrm{R}}\boldsymbol{y}={\boldsymbol{F}}_{\mathrm{R}},\kern6.5em {\boldsymbol{K}}_{\mathrm{R}}\in {\mathbb{C}}^{s\times s},{\boldsymbol{F}}_{\mathrm{R}}\in {\mathbb{C}}^s $$

(8)

where ${\boldsymbol{K}}_{\mathrm{R}}={\boldsymbol{r}}_{\mathrm{B}}^{\mathrm{T}}\boldsymbol{K}{\boldsymbol{r}}_{\mathrm{B}}$ and ${\boldsymbol{F}}_{\mathrm{R}}={\boldsymbol{r}}_{\mathrm{B}}^{\mathrm{T}}\boldsymbol{F}$ are the reduced order stiffness matrix and load vector, respectively. When s ≪ n_dof, the approximate displacement vector of the modified structure can be calculated by solving a system of equations with the size of s × s for y which is much smaller than the original system of equations with the size of n_dof × n_dof. Then, the approximate displacement vector r can be easily calculated by (6).

In the CA method, the basis vectors are obtained based on the binomial series. Back to the load-displacement relation of the modified structure, (5) can be simply written in term of the corresponding changes in stiffness matrix as follows:

$$ \left({\boldsymbol{K}}_0+\Delta \boldsymbol{K}\right)\boldsymbol{r}=\boldsymbol{F} $$

(9)

By rearranging (9), we obtain a recurrence relation as follows:

$$ {\boldsymbol{K}}_0{\boldsymbol{r}}^{\left(k+1\right)}=\boldsymbol{F}-\mathbf{\Delta }\boldsymbol{K}{\boldsymbol{r}}^{(k)} $$

(10)

where r^(k + 1) indicates the value of r in the kth iteration. By assuming an initial vector ${\boldsymbol{r}}^{(1)}={\boldsymbol{K}}_0^{-1}\boldsymbol{F}$, following Neumann series is obtained:

$$ \boldsymbol{r}=\left[\boldsymbol{I}-\boldsymbol{B}+{\boldsymbol{B}}^2-\cdots +{\boldsymbol{B}}^{s-1}\right]{\boldsymbol{r}}^{(1)},\kern2em \boldsymbol{B}\in {\mathbb{C}}^{n_{\mathrm{dof}}\times {n}_{\mathrm{dof}}},{\boldsymbol{r}}^{(1)}\in {\mathbb{C}}^{n_{\mathrm{dof}}}\kern0.75em $$

(11)

where $\boldsymbol{B}={\boldsymbol{K}}_0^{-1}\boldsymbol{\Delta K}$. The basis vectors are thus given by:

$$ {\boldsymbol{r}}_1={\boldsymbol{r}}^{(1)}={\boldsymbol{K}}_0^{-1}\boldsymbol{F},\kern1em {\boldsymbol{r}}_2=-\boldsymbol{B}{\boldsymbol{r}}_1,\dots, \kern1em {\boldsymbol{r}}_{\boldsymbol{s}+1}=-\boldsymbol{B}{\boldsymbol{r}}_s\kern0.5em $$

(12)

As can be seen from above equation, if the initial stiffness matrix is given in the decomposed form of (2), the calculation of basis vectors requires only forward and backward substitutions.

We can now state the step-by-step procedure of the CA method for structural reanalysis as follows:

• Step 1: Calculate the stiffness matrix of the modified structure: K = K₀ + ∆K.

• Step 2: Calculate (n_dof × s) matrix of basis vectors r_B = [r₁, r₂, …, r_s] by (12).

• Step 3: Calculate the reduced stiffness matrix K_R and load vector F_R: ${\boldsymbol{K}}_{\mathrm{R}}={\boldsymbol{r}}_{\mathrm{B}}^{\mathrm{T}}\boldsymbol{K}{\boldsymbol{r}}_{\mathrm{B}}$, ${\boldsymbol{F}}_{\mathrm{R}}={\boldsymbol{r}}_{\mathrm{B}}^{\mathrm{T}}\boldsymbol{F}$.

• Step 4: Solve the reduced system of equations (8) for y.

• Step 5: Calculate the approximate displacement vector of the modified structure by (6).

3.2 New reanalysis approach based on the polynomial-type extrapolation methods

In many problems of engineering approximation, computing the limits of the vector sequences is an essential task. However on many cases of practical interest, due to slow convergence properties of such sequences to their limits, direct using of them to approximate their limits is computationally expensive or even impossible. In mathematical science, the limits of slowly converging sequences or even diverging sequences can be approximated by applying convergence acceleration methods (or equivalently extrapolation methods). From a given vector sequence, extrapolation methods produce a new vector sequence that converges to the former’s limit more quickly when this limit exists. In a certain condition, when the limit of the original vector sequence does not exist, the convergence acceleration methods are able to produce new sequence that either diverge more slowly than former sequence or converges to a meaningful quantity (Sidi 2003). This is a characteristic feature of the extrapolation methods. In this study, we use such an idea to solve static structural reanalysis problems.

Minimal polynomial extrapolation (MPE) developed by Cabay and Jackson (1976) and reduced rank extrapolation (RRE) developed by Kaniel and Stein (1974), Eddy (1979), and Mešina (1977) are two efficient polynomial-type methods for convergence acceleration of vector sequences. Since their emergence, the MPE and RRE methods have been successfully applied to different areas of science and engineering (Bertelle et al. 2011; Duminil et al. 2014, 2015; Loisel and Takane 2011). Some excellent reviews about the polynomial-type extrapolation methods can be found in Refs. (Sidi 2012; Sidi et al. 1986; Smith et al. 1987). In addition, their convergence and stability properties have been investigated by Sidi (1986, 1994), Sidi and Bridger (1988), and Sidi and Shapira (1992, 1998). In the following, we present our reanalysis approach based on the MPE and RRE methods. We only explain those equations which will be used in our approach. For detailed derivations and related mathematical proofs, the interested reader may refer to Ref. (Sidi 2012).

Let us consider the load-displacement relation of the modified structure (5) in term of the corresponding change in the stiffness matrix as follows:

$$ \left({\boldsymbol{K}}_0+\Delta \boldsymbol{K}\right)\boldsymbol{r}=\boldsymbol{F} $$

(13)

by rearranging above equation, we can write it as a recurrence formula as follows:

$$ {\boldsymbol{r}}_{n+1}=\boldsymbol{T}{\boldsymbol{r}}_n+\boldsymbol{b},\kern1em \boldsymbol{b},{\boldsymbol{r}}_n\in {\mathbb{C}}^{n_{\mathrm{dof}}},\kern0.75em \boldsymbol{T}\in {\mathbb{C}}^{n_{\mathrm{dof}}\times {n}_{\mathrm{dof}}} $$

(14)

where

$$ \boldsymbol{T}=-{\boldsymbol{K}}_0^{-1}\mathbf{\Delta }\boldsymbol{K},\boldsymbol{b}={\boldsymbol{K}}_0^{-1}\boldsymbol{F} $$

(15)

and, r_n + 1 and r_n denote the displacement vector of the modified structure at the (n + 1)th and nth iterations, respectively. It should be noted that calculating T and b requires only forward and backward substitutions. Writing (14) in the form (I − T)r = b, it becomes clear that the uniqueness of the solution is guaranteed when the matrix I − T is nonsingular or, equivalently, when T does not have 1 as its eigenvalue. In other words, the convergence of (14) will take place from any r₀ sufficiently close to r_exact provided $\rho \left({\boldsymbol{K}}_0^{-1}\boldsymbol{\Delta K}\right)<1$, where ρ(A) is the spectral radius of the square matrix A. When $\rho \left({\boldsymbol{K}}_0^{-1}\boldsymbol{\Delta K}\right)$ is closer to zero, the convergence speed of the series in (14) is fast. However, the convergence speed of the series is very slow when $\rho \left({\boldsymbol{K}}_0^{-1}\boldsymbol{\Delta K}\right)$ becomes closer to 1. We refer the reader to the book by Süli and Mayers (2003) for more details. In this situation, the obtained series in (14) has a unique solution as ${\boldsymbol{r}}_{\mathrm{exact}}=\underset{n\to \infty }{\lim }{\boldsymbol{r}}_n$. Now, let us consider the displacement vector of the initial design ${\boldsymbol{r}}_0\in {\mathbb{C}}^{n_{\mathrm{dof}}}$ as an initial vector and generate the sequence {r_n} as follows:

$$ {\boldsymbol{r}}_{n+1}=\boldsymbol{T}{\boldsymbol{r}}_n+\boldsymbol{b},\kern1em n=0,1,\dots $$

(16)

Let us also define

$$ {\boldsymbol{u}}_n={\boldsymbol{r}}_{n+1}-{\boldsymbol{r}}_n,\kern2.25em n=0,1,\dots, \kern0.75em {\boldsymbol{u}}_n\in {\mathbb{C}}^{n_{\mathrm{dof}}} $$

(17)

3.2.1 Minimal polynomial extrapolation (MPE)

For vector sequence {r_n} in ${\mathbb{C}}^{n_{\mathrm{dof}}}$, assume an arbitrary positive integer k that is usually much smaller than the number of DOFs of the structure (k ≪ n_dof). Then, construct the matrix U_k − 1 as follows:

$$ {\boldsymbol{U}}_{k-1}=\left[{\boldsymbol{u}}_0\left|{\boldsymbol{u}}_1\right.\left|\cdots \right.\left|{\boldsymbol{u}}_{k-1}\right.\right]\in {\mathbb{C}}^{n_{\mathrm{dof}}\times k} $$

(18)

where u_n is defined in (17). Let assume that c^′ denotes the least-squares solution of the following overdetermined linear system:

$$ {\boldsymbol{U}}_{k-1}{\boldsymbol{c}}^{\prime }=-{\boldsymbol{u}}_k;\kern5.5em {\boldsymbol{c}}^{\prime }={\left[{c}_0,{c}_1,\cdots, {c}_{k-1}\right]}^{\mathrm{T}}\in {\mathbb{C}}^k $$

(19)

In other words, c^′ is a solution of the following minimization problem:

$$ {c}_0,{c}_1,\overset{\min }{\cdots },{c}_{k-1}\left\Vert \sum \limits_{j=0}^{k-1}{c}_j{\boldsymbol{u}}_j+{\boldsymbol{u}}_k\right\Vert $$

(20)

Set c_k = 1 and calculate ${\gamma}_0^{\mathrm{MPE}},{\gamma}_1^{\mathrm{MPE}},\cdots, {\gamma}_k^{\mathrm{MPE}}$ via

$$ {\gamma}_j^{\mathrm{MPE}}=\frac{c_j}{\sum_{i=0}^k{c}_i},\kern1em j=0,1,\cdots, k $$

(21)

It is worth mentioning that $\sum \limits_{i=0}^k{c}_i\ne 0$ (Sidi 2012). Now, the MPE approximation to ${\boldsymbol{r}}_{\mathrm{exact}}=\underset{n\to \infty }{\lim }{\boldsymbol{r}}_n$, denoted by ${\overset{\sim }{\boldsymbol{r}}}_k^{\mathrm{MPE}}$, is obtained as follows:

$$ {\tilde{\boldsymbol{r}}}_k^{\mathrm{MPE}}=\sum \limits_{j=0}^k{\gamma}_j^{\mathrm{MPE}}{\boldsymbol{r}}_j $$

(22)

where r_j represents the displacement vector of the modified structure at the jth iteration obtained from (16).

3.2.2 Reduced rank extrapolation (RRE)

Back to the vector sequence {r_n} in ${\mathbb{C}}^{n_{\mathrm{dof}}}$, assume an arbitrary positive integer k that is usually much smaller than the number of DOFs of the structure (k ≪ n_dof). Then, construct the matrix U_k as follows:

$$ {\boldsymbol{U}}_k=\left[{\boldsymbol{u}}_0\left|{\boldsymbol{u}}_1\right.\left|\cdots \right.\left|{\boldsymbol{u}}_k\right.\right]\in {\mathbb{C}}^{n_{\mathrm{dof}}\times k+1} $$

(23)

Let assume that γ denotes the least-squares solution of the following overdetermined linear system:

$$ {\boldsymbol{U}}_k\boldsymbol{\gamma} =0;\kern5.5em \boldsymbol{\gamma} ={\left[{\gamma}_0,{\gamma}_1,\cdots, {\gamma}_k\right]}^{\mathrm{T}}\in {\mathbb{C}}^{k+1}\kern0.5em $$

(24)

subjected to the constraint ${\sum}_{j=0}^k{\gamma}_j=1$. In other words, γ is the solution of the following constrained minimization problem:

$$ {\displaystyle \begin{array}{l}{\gamma}_0,\overset{\min }{\gamma_1,\cdots },{\gamma}_k\left\Vert \sum \limits_{j=0}^k{\gamma}_j{\boldsymbol{\mu}}_j\right\Vert \\ {}\mathrm{Subject}\ \mathrm{to}:{\sum}_{j=0}^k{\gamma}_j=1\end{array}} $$

(25)

If the solution of minimization problem defined in (25) is denoted by ${\gamma}_j^{\mathrm{RRE}}$, then the RRE approximation to ${\boldsymbol{r}}_{\mathrm{exact}}=\underset{n\to \infty }{\lim }{\boldsymbol{r}}_n$, denoted by ${\overset{\sim }{\boldsymbol{r}}}_k^{\mathrm{RRE}}$, is obtained as follows:

$$ {\tilde{\boldsymbol{r}}}_k^{\mathrm{RRE}}=\sum \limits_{j=0}^k{\gamma}_j^{\mathrm{RRE}}{\boldsymbol{r}}_j $$

(26)

where r_j represents the displacement vector of the modified structure at the jth iteration obtained from (16). For both of the MPE and RRE methods, it can be seen that the approximate structural response is constructed from the knowledge of the k + 1 vectors of iteration r₀, r₁, …, r_k + 1. In the proposed reanalysis process, the complete set of equations of exact analysis with the size of n_dof × n_dof is reduced to the linear least-squares problems with the sizes of n_dof × k and n_dof × k + 1 for the MPE and RRE methods, respectively.

Before leaving this section, we are interested to compare the number of algebraic operations (NAOs) required by the MPE, RRE, and CA methods to compute approximate response of the modified structure. To this end, the approximate total NAOs (multiplications and additions) required by each method are listed in Table 1. As can be seen from the table, the total NAOs for the MPE and RRE methods depend on the value of parameter k. On the other hand, the amount of NAOs for the CA method is mainly related to the number of considered basis vectors (s). In the condition of equal computational effort, we can find the approximate relationship between the parameters of k and s. By setting equality between NAOs of the MPE, RRE, and CA methods, we can see that for the values k and s satisfying the relation $k\cong \frac{3}{2}\left(s-1\right)$, the mentioned methods are computationally equivalent. Our initial investigations show that the both of the MPE and RRE methods are able to produce satisfactory results for very smaller values of k. In our experiments presented in the next section, we compare the required NAOs by each method for different values of k and s.

Table 1 The number of algebraic operations (NAOs) required by the CA, MPE, and RRE methods during the reanalysis process

Now we are ready to summarize main steps of the MPE and RRE methods for the static structural reanalysis as follows:

• MPE method:

  • Step 1: Select an appropriate value for parameter k in such a way that k ≪ n_dof and generate the vectors r₀, r₁, …, r_k + 1 by (16).

  • Step 2: Calculate the vectors u₀, u₁, …, u_k − 1by (17) and construct the matrix U_k − 1 with the size of n_dof × k using (18).

  • Step 3: Calculate c^′ = [c₀, c₁, ⋯, c_k − 1]^T by solving the overdetermined linear system of (19) in the least-square sense.

  • Step 4: Set c_k = 1 and compute ${\gamma}_0^{\mathrm{MPE}},{\gamma}_1^{\mathrm{MPE}},\cdots, {\gamma}_k^{\mathrm{MPE}}$ via (21).

  • Step 5: Calculate the MPE approximation of the displacement vector of the modified structure ${\overset{\sim }{\boldsymbol{r}}}_k^{\mathrm{MPE}}$ by using (22).

• RRE method:

• Step 1: Select an appropriate value for parameter k in such a way that k ≪ n_dof and generate the vectors r₀, r₁, …, r_k + 1 by (16).

• Step 2: Calculate the vectors u₀, u₁, …, u_k by (23) and construct the matrix U_k with the size of n_dof × (k + 1).

• Step 3: Calculate ${\boldsymbol{\gamma}}^{\mathrm{RRE}}={\left[{\gamma}_0^{\mathrm{RRE}},{\gamma}_1^{\mathrm{RRE}},\cdots, {\gamma}_k^{\mathrm{RRE}}\right]}^{\mathrm{T}}$ by solving the overdetermined linear system of (25) in the least-square sense.

• Step 4: Calculate the RRE approximation of the displacement vector of the modified structure ${\overset{\sim }{\boldsymbol{r}}}_k^{\mathrm{RRE}}$ by using (26).

4 Numerical tests and computational results

4.1 Comparison criteria

In this section we evaluate the efficiency and robustness of the presented reanalysis approach based on the MPE and RRE methods against the well-known CA method through a set of three large scale structural reanalysis problems under multiple types of changes in their initial designs. In the investigated test examples, the exact results are obtained by Matlab software. Numerical tests are conducted to asses each method from accuracy and computational viewpoints as described in following subsections.

4.1.1 Accuracy

In the investigates test examples, the accuracy of the MPE, RRE, and CA methods are compared in terms of the average and maximum reanalysis errors occurred in each DOF of the structure. The reanalysis error occurred in each DOF of the structure is evaluated as follows:

$$ {\boldsymbol{E}}_{{\mathrm{DOF}}_i}=\left|\frac{{\boldsymbol{r}}_{{\mathrm{exact}}_i}-{\overset{\sim }{\boldsymbol{r}}}_i}{{\boldsymbol{r}}_{{\mathrm{exact}}_i}}\right|\kern1.75em , for\ i=1,2,\dots, {n}_{\mathrm{dof}} $$

(27)

where ${\boldsymbol{E}}_{{\mathrm{DOF}}_i}$ indicates the reanalysis error occurred in evaluating displacement of the ith DOF of the structure, ${\boldsymbol{r}}_{{\mathrm{exact}}_i}$ and ${\overset{\sim }{\boldsymbol{r}}}_i$ denote the exact and approximated displacements of the ith DOF of the structure, respectively, and n_dof is the total number of DOFs of the structure. For a given reanalysis problem, the average error (E_Av.) and the maximum error (E_Max) obtained from each of the reanalysis method can be calculated as follows:

$$ {E}_{\mathrm{Max}}=\max \left({\boldsymbol{E}}_{{\mathrm{DOF}}_i}\right) $$

(28)

$$ {E}_{\mathrm{Av}.}=\frac{\sum_{i=1}^{n_{\mathrm{dof}}}{\boldsymbol{E}}_{{\mathrm{DOF}}_i}}{n_{\mathrm{dof}}} $$

(29)

Besides, we compared the quality of the approximate displacement vector obtained from each reanalysis method by using following error measuring criteria:

$$ {E}_{\mathrm{Relative}}=\frac{\left\Vert {\boldsymbol{r}}_{\mathrm{exact}}-\overset{\sim }{\boldsymbol{r}}\right\Vert }{\left\Vert {\boldsymbol{r}}_{\mathrm{exact}}\right\Vert } $$

(30)

where E_Relative indicates the relative error, ‖.‖ is the L₂ norm, r_exact denotes the exact displacement vector, and $\overset{\sim }{\boldsymbol{r}}$ is the approximate displacement vector obtained from a reanalysis method. As was already mentioned that, the computational efforts required by the MPE and RRE methods are mainly depend on the value of parameter k. To conduct a fair comparison between the proposed approach and the CA method, we investigated the performance of each method by considering different values for parameters k and s. It should be noted that the appropriate values for the parameters k and s depend on the size of the reanalysis problem and required level of accuracy. In this study, the values of these parameters are selected by a purely trial and error procedure.

4.1.2 Computational consideration

In order to compare the reanalysis methods in term of the computational efficiency, researchers compare the required NAOs by the reanalysis method with the required NAOs by a given exact method. For example, Zuo et al. (2016) defined a speed-up ratio for reanalysis procedure. In this study, the speed-up ratio is also used to compare the efficiency of each method. If the displacement of the modified structure in (5) is obtained by Cholesky decomposition method, the required NAOs is equal to $\frac{{n_{\mathrm{dof}}}^3}{3}+2{n_{\mathrm{dof}}}^2$. Therefore, the speed-up ratio (η) for each reanalysis method can be calculated as follows:

$$ {\eta}_{\mathrm{CA}}=\frac{T_{\mathrm{Direct}}}{T_{\mathrm{CA}}}\approx \frac{\frac{{n_{\mathrm{dof}}}^3}{3}+2{n_{\mathrm{dof}}}^2}{6s{n_{\mathrm{dof}}}^2} $$

(31)

$$ {\eta}_{\mathrm{MPE}}={\eta}_{\mathrm{RRE}}=\frac{T_{\mathrm{Direct}}}{T_{\mathrm{MPE}}}\approx \frac{\frac{{n_{\mathrm{dof}}}^3}{3}+2{n_{\mathrm{dof}}}^2}{\left(4k+6\right){n_{\mathrm{dof}}}^2} $$

(32)

where η_CA, η_MPE, and η_RRE represent the speed-up ratio for the CA, MPE, and RRE methods, respectively, T_Direct, T_CA, and T_MPE are the required NAOs by the direct, CA, and MPE methods, respectively. It should be noted that the required NAOs by both of the MPE and RRE are approximately same.

4.2 A 942-bar tower structure

Figure 1 shows a 942-bar tower structure as the first investigated test example. This structure consists of 244 nodes and 732 DOFs. As displayed in Fig. 2, the structural members are divided into 59 independent design groups. The loading condition for this tower is as follows: 1.12 kips acting in the X and Y directions and −6 kips acting in the Z direction at all nodes of the tower. In the initial design, it is assumed that the all of the structural members have constant Young’s modulus (${E}_i^0$) and cross-sectional area (${A}_i^0\Big)$ equal to 10,000 ksi and 60 in², respectively. Then, we assume a set of multiple changes in the initial design as follows: increasing the cross-sections of design groups 1 through 8 and design groups 12 through 28, and decreasing the Young’s modulus of design groups 47 through 59. Figure 3 shows the modified parts of 942-bar tower structure. To evaluate the performance of the reanalysis methods under different levels of changes in initial design, we considered the modified design as follows:

$$ \mathrm{Modified}\ \mathrm{design}:\left\{\begin{array}{c}{A}_i=\left(1+\alpha \right){A}_i^0\kern0.5em \mathrm{for}\ i=1,2,\dots, 8\\ {}{A}_i=\left(1+\alpha \right){A}_i^0\kern0.5em \mathrm{for}\ i=12,13,\dots, 28\\ {}{A}_i={A}_i^0\kern0.5em \mathrm{otherwise}\\ {}{E}_i=\left(1-\alpha \right){E}_i^0\ \mathrm{for}\ i=47,48,\dots, 59\\ {}{E}_i={E}_i^0\kern0.75em \mathrm{otherwise}\end{array}\right. $$

(33)

where A_i and E_i represent the modified cross-sectional area and Young’s modulus for the ith design group, respectively, and α ∈ [0.2, 0.4] is a constant parameter defined to consider different ranges of the modifications in the structure.

Fig. 1

Schematic of 942-bar tower structure: a 3D view, b side view, and c top view

Fig. 2

Design groups in different sections of 942-bar tower structure: a section 1, b section 2, c section 3

Fig. 3

Modified parts of 942-bar tower structure

As was already mentioned, the convergence of series generated by (16) will take place from any r₀ sufficiently close to r_exact provided $\rho \left({\boldsymbol{K}}_0^{-1}\boldsymbol{\Delta K}\right)<1$. In this test example, $\rho \left({\boldsymbol{K}}_0^{-1}\boldsymbol{\Delta K}\right)$ is equal to 0.20 and 0.40 for the cases of α = 0.2 and α = 0.4, respectively. Therefore, the convergence of series obtained from (16) is guaranteed.

For different values of k and s, Fig. 4 compares the NAOs required by the MPE, RRE, and CA methods to solve 942-bar tower structure problem. As can be seen, all reanalysis methods require a same amount of NAOs when k = s = 3. While for larger values of k and s, both of the MPE and RRE methods requires significantly fewer amount of NAOs than the CA method. Therefore, to conduct a fair numerical comparison between different methods, we investigate the performance of the MPE and RRE methods against the CA method by considering two cases as follows: k = s = 3 and k = s = 8.

Fig. 4

Comparison of the required computational efforts by the MPE, RRE, and CA methods for different values of parameters k and s in 942-bar tower structure problem

When k = s = 3, the reanalysis results obtained from the MPE, RRE, and CA methods are summarized in Table 2. From the results of Table 2 we can see that the accuracy of the MPE and RRE methods is significantly better than the CA method in different levels of changes in design variables. In the all cases, we can see that both of the MPE and RRE methods have a relatively same accuracy and their average, maximum, and relative errors are significantly smaller than the corresponding values yielded by the CA method. The efficiency of the proposed methods is more observable in the cases of larger changes. For example, when the changes in the design variables is 40% (α = 0.4), it can be see that both of the MPE and RRE methods are able to provide accurate results, while the results yielded by the CA method indicate relatively large errors. Back to Table 2, we can see that the maximum error obtained by the CA method is about 16%. While this value is about 0.6% for both of the MPE and RRE methods, which are far less than that is given by the CA method.

Table 2 Reanalysis results of the MPE, RRE, and CA methods for 942-bar tower structure problem (k = 3, s = 3)

For the case of k = s = 8, the reanalysis results have been summarized in Table 3. From the results of Table 3 it can be seen that all of the MPE, RRE, and CA methods obtain more accurate results than the case of k = s = 3. However, accuracy of the MPE and RRE methods is still better than the CA method.

Table 3 Reanalysis results of the MPE, RRE, and CA methods for 942-bar tower structure problem (k = 8, s = 8)

Table 4 compares the required computational efforts by each of the reanalysis method for this test example. From the results of Table 4 we can see that in the case of k = s = 3, a relatively same amount of computational effort is required for all of the MPE, RRE, and CA methods. However, the situation for the case of k = s = 8 is different and both of the MPE and RRE methods are computationally efficient than the CA method. This computational efficiency of the MPE and RRE methods and their accuracy observed in Tables 2 and 3 reveal the distinguished performance of the MPE and RRE methods in the reanalysis process.

Table 4 Comparison of computational efforts required by the CA, MPE, and RRE methods for 942-bar tower structure problem

In order to make comparison more clearly, the relative errors yielded by the MPE, RRE, and CA methods are illustrated in Fig. 5 for the case k = s and α = 0.4. From Fig. 5, we can see that both of the MPE and RRE are capable of yielding more accurate results than the CA method.

Fig. 5

Comparison of the relative errors obtained from the MPE, RRE, and CA methods for different values of parameters k and s in 942-bar tower structure problem (α = 0.4)

4.3 A 4802-bar tower structure

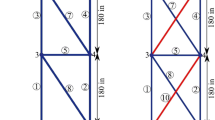
The second test example is a large scale tower structure with 100 stories, 4802 members, 1212 nodes, and 3636 DOFs. The 3D, side, and top views as well as configuration pattern for the first two stories of the structure are illustrated in Fig. 6. The loading condition for this tower is as follows: 1.12 kips acting in the X and Y directions and −6.74 kips acting in the Z direction at all nodes of the tower. For the initial design, it is assumed that the all of the structural members have constant Young’s modulus (${E}_i^0$) and cross-sectional area (${A}_i^0\Big)$ equal to 10,000 ksi and 80 in², respectively. Then, we consider a set of multiple changes in the initial design as follows: increasing the Young’s modulus of structural members in stories 1 through 20 as ${E}_i=\left(1+\alpha \right){E}_i^0$, increasing the cross sectional areas of structural members in stories 40 through 60 as ${A}_i=\left(1+\alpha \right){A}_i^0$, and decreasing the cross sectional areas of structural members in stories 91 through 100 as ${A}_i=\left(1-\alpha \right){A}_i^0$. In this test case, we consider the changes in the design variables within the range 20%–80% (α = 0.2, 0.4, 0.6, 0.8). With these modifications, 2400 structural members (about 50% of total members of the structure) are modified in different directions. The modified parts of the structure are displayed in Fig. 7.

Fig. 6

Schematic of 4802-bar tower structure: a 3D view, b side view, c top view, and d elements pattern for first two stories of the structure

Fig. 7

Modified parts of 4802-bar tower structure

For the changes considered in this test example, the value of $\rho \left({\boldsymbol{K}}_0^{-1}\boldsymbol{\Delta K}\right)$ is equal to 0.2, 0.4, 0.6, and 0.8 for the cases of α = 0.2, α = 0.4, α = 0.6, and α = 0.8, respectively. Hence, the series generated from (16) will converge.

For different values of k and s, Fig. 8 compares the required NAOs by each of the reanalysis methods. Once again, we can see that all of the MPE, RRE, and CA methods require same amount of NAOs for the case of k = s = 3. To reveal the capabilities of the reanalysis methods, like previous test examples, we have compared the performance of the mentioned methods in two different cases of k = s = 3 and k = s = 8.

Fig. 8

Comparison of the required computational efforts by the MPE, RRE, and CA methods for different values of parameters k and s in 4802-bar tower structure problem

When k = s = 3, reanalysis results in terms of the average, maximum, and relative errors are reported in Table 5. Once again, the results of Table 5 demonstrate that both of the MPE and RRE methods provide more accurate results than the CA method. With increasing the amount of changes in the design variables, it can be see that the errors obtained by the CA method grow more rapidly. While the MPE and RRE methods exhibit a good performance in terms of average, maximum, and relative errors. For example, when the change in the design variables is 80% (α = 0.8), the maximum error obtained by the CA method is more than 36%, while it is about 8% and 3% for the MPE and RRE methods, respectively.

Table 5 Reanalysis results obtained by the MPE, RRE, and CA methods for 4802-bar tower structure problem (k = 3, s = 3)

For the case of k = s = 8, reanalysis results have been summarized in Table 6. Results demonstrate that the accuracy of the MPE, RRE, and CA methods is significantly improved by increasing parameters k and s. However, the efficiency of the MPE and RRE methods is also remarkable in comparison to the CA method for this case. For example, when the change in the design variables is 60% (α = 0.6), the maximum errors yielded by the MPE and RRE methods are about 7 × 10⁻⁵%, while it is about 4% for the CA method.

Table 6 Reanalysis results obtained by the MPE, RRE, and CA methods for 4802-bar tower structure problem (k = 8, s = 8)

Table 7 compares the required amount of computational efforts by each method. From this table, we can see that the MPE and RRE methods are cheaper than CA method for the case of k = s = 8. Finally, for the case of k = s and α = 0.8, Fig. 9 compares the relative errors obtained by the MPE, RRE, and CA methods. With increasing parameters k and s, we observe that the difference between the accuracy of the MPE and RRE in comparison with the CA method is more significant.

Table 7 Comparison of computational efforts required by the CA, MPE, and RRE methods for 4802-bar tower structure problem

Fig. 9

Comparison of the relative errors obtained from the MPE, RRE, and CA methods for different values of parameters k and s in 4802-bar tower structure problem (α = 0.8)

4.4 A 3D bracket with hole

In the last test example, we investigate a 3D bracket with a hole as shown in Fig. 10. The finite element model of the bracket consists of 40,092 nodes, 24,200 elements, and 120,276 DOFs. The back face of the bracket is considered as fixed in all directions (see Face 4 in Fig. 10a) and thickness of the horizontal plate is equal to 1 cm. In the initial design, it is assumed that the Young’s modulus (E⁰) and Poisson’s ratio (ν⁰) are equal to 200 GPa and 0.3, respectively. In addition, a distributed load with magnitude of 1 MPa is applied to the front face of the bracket (see Face 8 in Fig. 10a) in negative z-direction. Then, we assume a set of multiple changes in initial design as follows: decreasing Young’s modulus to E = 0.7E⁰, increasing Poisson’s ratio to ν = 1.25ν⁰, and applying a distributed load with magnitude of 1 MPa to the horizontal plate in negative z-direction (see Face 7 in Fig. 10a). With these modifications, the stiffness matrix and load vector are modified simultaneously. Figure 11 compares the displacements of the initial and modified structures in z-direction. As it can be seen, the maximum displacement in z-direction for the initial structure is equal to −0.45 cm, while it is equal to −3.05 cm for the modified structure.

Fig. 10

Schematic of a 3D bracket with a hole: a different faces of bracket, b finite element model

Fig. 11

Comparison of the displacements in z-direction between initial and modified structures: a initial structure, b) modified structure (units are in cm)

For the changes considered in this test example, the value of $\rho \left({\boldsymbol{K}}_0^{-1}\boldsymbol{\Delta K}\right)$ is equal to 0.73. Once again, the convergence of series obtained from (16) is guaranteed for this test example.

Fig. 12 compares the accuracy of the MPE, RRE, and CA methods in term of the relative error obtained from each method for different values of parameters k and s. As we expected, due to large number of DOFs for this problem, the larger values for parameters k and s are needed to achieve adequate level of accuracies. For small values of parameters k and s, it can be seen that accuracy of mentioned methods are relatively same. However, when the values of constant parameters are increased, accuracy of the MPE and RRE methods is significantly better than the CA method. For the case of k = s = 30, the reanalysis results obtained from the mentioned methods are listed in Table 8. As can be seen, unlike the CA and RRE methods, the MPE method can obtain the modified displacement vector with significantly higher level of accuracy. From Table 8, we can see that the maximum error for the MPE method is about 0.02%, which is an appropriate level of accuracy form engineering point of view. However, both of the CA and RRE methods are not able to predict exact displacement values in some DOFs of the structure and some instabilities are observed in their results (see maximum error values). In addition, Fig. 13 compares the required NAOs by each reanalysis method for different values of parameters k and s.

Fig. 12

Comparison of the relative errors obtained from the MPE, RRE, and CA methods for different values of parameters k and s in 3D bracket problem

Table 8 Reanalysis results obtained by the MPE, RRE, and CA methods for 3D bracket problem (k = 30, s = 30)

Fig. 13

Comparison of the required computational efforts by the MPE, RRE, and CA methods for different values of parameters k and s in 3D bracket problem

4.5 Application of the proposed reanalysis methods in structural optimization

As it is mentioned in introduction, attaining optimum designs for structures requires numerous structural analyses during the optimization process. In recent decades, the research toward using meta-heuristic optimization techniques for optimum design of skeletal structures has been increasing enormously (Allen et al. 2013; Jivotovski 2000; Sawada et al. 2011; Stolpe 2016). In comparison to the classical optimization techniques, they are able to solve complex structural optimum design problems without using any gradient information about the objective function and design constraints. However, meta-heuristics do not always guarantee discovering globally optimal solutions in finite time and require thousands of finite element analyses to reach an optimum design. In this subsection, we are interested to know how the proposed reanalysis methods can be employed to reduce the computational time required by meta-heuristics for optimum design of a large scale structure. To this end, we consider 942-bar tower structure shown in Fig. 1 as an optimum design problem. As an efficient meta-heuristic optimization technique, we employed the league championship algorithm (LCA) (Jalili et al. 2016b) to find optimum design for this structure. The optimum design problem of 942-bar tower structure is defined as follows.

$$ {\displaystyle \begin{array}{l}\mathrm{Find}\kern1.25em \boldsymbol{A}=\left[{A}_1,{A}_2,\dots, {A}_{ne}\right]\\ {}\mathrm{To} \operatorname {minimize}\ W\left(\boldsymbol{A}\right)={\sum}_{i=1}^{ne}{\gamma}_i{A}_i{L}_i\end{array}} $$

(34)

where A is the vector containing design variables, ne is the number of members making up the structure, W(.) is the weight of the structure, γ_i is the material density of member i, and A_i is the cross-sectional area of the member i. We assume that the Young’s modulus is 30,450 ksi and the yield stress of steel is 58.0 ksi. The tower is subjected to the single loading condition as follows: 1.12 kips acting in the X and Y directions and −6.0 kips acting in the Z direction at all nodes of the tower. In addition, the range of permitted cross sectional areas varies from 10 in² to 100 in². As design constraints, the optimum design problem is subjected to the following stress and displacement constraints:

• (1) Stress constraint (according to the AISC ASD code (Construction 1989)):

$$ \left\{\begin{array}{c}{\sigma}_i^{+}=0.6{F}_y\kern1em \mathrm{for}\ {\sigma}_i\ge 0\ \\ {}{\sigma}_i^{-}\kern5.5em \mathrm{for}\ {\sigma}_i<0\end{array}\right. $$

(35)

where ${\sigma}_i^{-}$ is calculated according to the slenderness ratio:

$$ \left\{\begin{array}{c}\left[\left(1-\frac{\lambda_i^2}{2{C}_c^2}\right){F}_y\right]/\left(\frac{5}{3}+\frac{3{\lambda}_i}{C_c}-\frac{{\lambda_i}^3}{8{C_c}^3}\right)\kern1.25em \mathrm{for}\kern0.75em {\lambda}_i<{C}_c\ \\ {}\frac{12{\pi}^2E}{23{\lambda}_i^2}\kern12.75em \mathrm{for}\kern0.75em {\lambda}_i\ge {C}_c\end{array}\right. $$

(36)

where E = the modulus of elasticity; F_y = the yield stress of steel; C_C = the slenderness ratio (λ_i) dividing the elastic and inelastic buckling regions$\left({C}_C=\sqrt{2{\pi}^2E/}{F}_y\ \right)$; λ_i = the slenderness ratio (λ_i = kL_i/r_i); k = the effective length factor; L_i = the member length; and r_i = the radius of gyration.

• (2) For all free nodes, the maximum nodal displacements are limited to 3.15 in in all directions.

By using the exact and approximate reanalysis methods during the optimization process, optimal designs obtained through the exact, MPE, RRE, and CA methods are presented in Table 9. The optimization process is terminated when the maximum number of structural analyses is reached. The maximum structural analyses is set to 20,000. These results are obtained by assuming k = s = 8. From Table 9, it can be seen that the reanalysis techniques can significantly reduce computing time of the optimization process. It is worth mentioning that the exact result is obtained by MATLAB software which is extremely fast. Moreover, from the results of Table 9 we can see that both of the MPE and RRE methods are more efficient than the CA method in terms of the accuracy and required CPU time.

Table 9 Optimum designs obtained for 942-bar tower structure by using different reanalysis methods during the optimization process

5 Concluding remarks

In this study, a new approach based on the polynomial-type extrapolation methods is applied to solving static structural reanalysis problems under multiple and large changes in the initial design. In the proposed approach, the sequences of approximate displacement of the modified structure are constructed by using a fixed-point iteration method. These sequences are then further analyzed by two polynomial-type extrapolation methods to find the approximate response of the modified structure more accurately, namely, the minimal polynomial extrapolation (MPE) and the reduced rank extrapolation (RRE). Based on a single initial design, the MPE and RRE methods approximate the displacement vector of the modified structure by solving a least-squares problem which is much smaller than the original system of equations of the exact analysis. To check the efficiency of the MPE and RRE methods, a set of three large scale structural reanalysis problems are investigated under multiple and different levels of changes in their initial designs. In the investigated test examples, the accuracy of the MPE and RRE methods are evaluated against well-known combined approximation (CA) method. Numerical results indicate that both of the MPE and RRE methods are able to provide more accurate results than the CA method for the investigated test examples. Moreover, the computational efforts required by the MPE, RRE, and CA methods are investigated in term of the number of algebraic operations (NAOs). For the same level of accuracy, our investigations show that the MPE and RRE methods are computationally cheaper than the CA method. Besides, application of the MPE and RRE methods in optimum design of a large scale tower structure was also investigated. The results indicate that both of the MPE and RRE methods can significantly reduce computing time of the structural optimization process. Although the MPE and RRE methods were used to static structural reanalysis, their definition is totally independent of the way in which vector sequences are generated. Therefore, the MPE and RRE methods can be used to (hopefully) solve other types of reanalysis problems such as nonlinear, vibrational, and dynamic reanalysis problems under different types of changes.