1 Introduction

The majority of work in structural topology optimization has focused on the minimum compliance (maximum stiffness) design of structures subjected to externally-applied, design-independent mechanical loading. This is likely a result of the simplicity of the structural optimization problem that arises, which due to the underlying mathematics of the problem, makes it comparatively straightforward to solve (Bendsøe and Sigmund 2003). However, there exists entire classes of problems that are not well addressed by this particular formulation (Deaton and Grandhi 2014a). One of these instances is the topological design of structures subject to thermoelastic effects, which are a type of design-dependent load in topology optimization. In fact, due to the material layout capabilities of topology optimization, it holds great promise as a design tool for modern thermal structures applications in the aerospace industry. These include structural design for embedded engine aircraft exhaust structures and thermal protection systems for hypersonic flight vehicles (Haney and Grandhi 2009; Deaton and Grandhi 2014b).

Thermoelastic topology optimization was first investigated by Rodrigues and Fernandes (1995), who used a homogenization method to minimize the compliance of structures with combined temperature and mechanical loading. The problems investigated in their work have been frequently utilized as benchmark problems in many later publications. Li et al. (1999, 2001) utilized an evolutionary method for thermoelastic topology optimization for displacement minimization and problems with non-uniform temperature fields. Kim et al. (2006) and Penmetsa et al. (2006) applied topology optimization to spacecraft thermal protection systems (TPS). Sigmund and Torquato (1997) used topology optimization to generate structures with extremal thermal expansion properties and (Sigmund 2001a, b) developed thermal micro-actuators with topology optimization. In addition, Jog (1996) incorporated nonlinear thermoelasticity. Since these earlier works, thermoelastic topology optimization has been performed using density-based methods to investigate the best interpolation scheme for thermal loading (Gao and Zhang 2010), the level set method (Xia and Wang 2008), and concurrent formulations to optimize both macro and micro-scale topology (Yan et al. 2008). Recently, Pedersen and Pedersen (2010, 2012) questioned the application of the minimum compliance problem to thermoelasticity, which is used in a number of the early research works, because it cannot achieve good performance in minimizing deformation or strength for general problems in thermoelasticity. They proposed an alternative interpolation scheme in addition to a more suitable objective function based on uniform energy density, which was shown to produce superior results from a strength design point-of-view. The conclusion that compliance minimization is not suitable for thermoelastic problems is also supported in the work by Deaton and Grandhi (2013), who demonstrate the inability of compliance minimization to find suitable solutions when thermal effects are significant in comparison to mechanical loads. They circumvent this with alternative formulations based on fictitious mechanical loads to obtain desirable thermoelastic performance for these problems. In another practical application, Wang et al. (2011) proposed a multi-objective optimization model to combine low thermal directional expansion with high structural stiffness. The recent prevalence of alternative formulations for thermoelastic topology optimization indicates that an increasing number of problems are not well addressed by purely compliance-based design. This is further driven by research that shows simple stiffening techniques cannot solve important problems that result from damaging thermal stresses (Haney and Grandhi 2009) and more advanced design techniques that more directly address thermal stresses are necessary.

As a result, we explore stress-based topology optimization, which may be more appropriate for thermoelasticity. Despite the fact that stresses are a primary consideration in any design problem, the topic has received little consideration in the literature compared to stiffness-based objectives until recently. This is due in large part to three primary challenges that make stress-based topological design more difficult than stiffness design. These are: (i) the singularity phenomenon, (ii) the local nature of stresses, and (iii) the highly nonlinear behavior of stress constraints (Le et al. 2010). Early work in the area was completed by Duysinx and Bendsøe (1998). More recently, Pereira et al. (2004), Bruggi and Venini (2008), Bruggi(2008), Guilherme and Fonseca (2007), Le et al. (2010), París et al. 2010a), París et al. (2010b), Lee et al. (2012), Holmberg et al. (2013), and others have explored various aspects of stress-based and stress-constrained topology optimization.

In the following sections, a stress-based topology optimization capability is extended to include thermal stresses and demonstrated using numerical examples. Section 2 discusses the thermoelastic topology optimization formulation, including the finite element parameterization, interpolation schemes, and density filtering. Section 3 gives the techniques for stress-based design including singularity relaxation, an adaptive stress constraint technique, and adjoint sensitivity analysis for thermal stresses including design-dependent thermoelastic effects. Section 4 provides the mathematical statement of the topology problems to be solved. Finally, Section 5 highlights the application of the formulation to numerical example problems followed by concluding remarks in Section 6.

2 Thermoelastic topology formulation

In this section, the framework of a density-based method (Bendsøe and Sigmund 2003; Sigmund and Maute 2013) for topology optimization, in which stress constraints are to be included, is discussed. Discussion includes incorporating the design-dependent thermoelastic effects in the finite element parameterization, selection of interpolation schemes, and density filtering.

2.1 Finite element parameterization

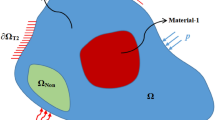
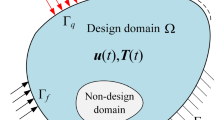
Figure 1 shows a generalized thermoelastic design domain Ω in two dimensions, which contains fixed displacement boundary conditions, externally applied surface tractions, and a prescribed temperature change (with respect to a reference temperature) that may be uniform or spatially varying. The domain consists of regions of fixed void material, fixed solid material (non-designable), and designable areas whose topology is to be determined from optimization.

Fig. 1
figure 1

Generalized two-dimensional thermoelastic structural design domain

Full size image

The design domain is discretized using N finite elements with N d designable and N n d nondesign elements. Each designable element is assigned a density variable ρ e ranging from 0<ρ m i n ≤ ρ e ≤ 1 with e = 1,2,..., N d where densities of 0 and 1 indicate void and solid material, respectively. The density variables are collected in the density vector ρ. In addition to its density ρ e , each designable finite element is assigned a design variable x e , which also 0≤x e ≤ 1 with e = 1,2,..., N d , and are stored in the design variable vector x. The density variables become a function of the design variables as ρ e (x) using the density filter discussed in Section 2.3.

Linear static equilibrium for a finite element representation of the domain, including both mechanical and temperature loading, is given by

$$ \mathbf{K}(\boldsymbol{\rho})\mathbf{U}(\boldsymbol{\rho})=\mathbf{F}(\boldsymbol{\rho}) $$
(1)

where K(ρ) is the global stiffness matrix, U(ρ) is the nodal displacement vector, and F(ρ) is the nodal load vector. In the general case of combined mechanical and thermoelastic load, F consists of design-independent mechanical loading F m and design-dependent thermal loads F th(ρ) as

$$ \mathbf{F}(\boldsymbol{\rho})=\mathbf{F}^{m}+\mathbf{F}^{th}(\boldsymbol{\rho}). $$
(2)

By taking the thermal load vector as a function of the density variables, the appropriate dependency of thermal loading on the design configuration is captured. The stiffness matrix K(ρ) is assembled as the summation of element stiffnesses by

$$ \mathbf{K}(\boldsymbol{\rho})=\sum\limits_{e=1}^{N_{d}}\mathbf{k}_{e}(\rho_{e}) $$
(3)

where

$$ \mathbf{k}_{e}(\rho_{e})={\int}_{{\Omega}_{e}}\mathbf{B}_{e}^{T}\mathbf{C}_{e}(\rho_{e})\mathbf{B}_{e}d{\Omega}. $$
(4)

Here, B e is the element strain-displacement matrix, which consists of derivatives of the element shape functions that are independent of topology design variables. C e is the element elasticity matrix, which for isotropic materials can be written as a function of elastic modulus as

$$ \mathbf{C}_{e}(\rho_{e})=E(\rho_{e})\bar{\mathbf{C}}_{e} $$
(5)

where \(\bar {\mathbf {C}}_{e}\) consists of constant terms related to the material constitutive matrix and E(ρ e ) is the elastic modulus of element e and is dependent on the element’s density variable. Substituting (5) into (4) yields

$$ \mathbf{k}_{e}(\rho_{e})=E(\rho_{e}){\int}_{{\Omega}_{e}}\mathbf{B}_{e}^{T}\bar{\mathbf{C}}_{e}\mathbf{B}_{e}d{\Omega}. $$
(6)

For nondesign elements, the previous equations can be utilized by simply assuming E(ρ e )=E o , where E o is the non-penalized elastic modulus of the material. Based on the forthcoming discussion of interpolation schemes in Section 2.2, in implementation this is equivalent to letting ρ e = 1. The mechanical load vector F m is assembled from externally applied forces on the specified degrees of freedom. The thermal load vector F th(ρ) is parameterized using the thermal stress coefficient (TSC) (Rodrigues and Fernandes 1995; Gao and Zhang 2010) for topology optimization and described as follows.

The nodal load vector for a designable element e is given as

$$ \mathbf{f}_{e}^{th}(\rho_{e})={\int}_{{\Omega}_{e}}\mathbf{B}_{e}^{T}\mathbf{C}_{e} (\rho_{e})\boldsymbol{\epsilon}_{e}^{th}(\rho_{e})d{\Omega} $$
(7)

where \(\boldsymbol {\epsilon }_{e}^{th}(\rho _{e})\) is the thermal strain vector for the element

$$ \boldsymbol{\epsilon}_{e}^{th}(\rho_{e})=\alpha(\rho_{e}){\Delta} T_{e}\boldsymbol{\phi}^{T}. $$
(8)

Here, α(ρ e ) is the thermal expansion coefficient that is also dependent on element density, ΔT e is the temperature change of element e (taken here as the average of nodal temperatures), and ϕ is simply the vector [1 1 0] for two dimensional problems with isotropic materials. Substitution of (5) and (8) into (7) yields

$$ \mathbf{f}_{e}^{th}(x_{e})=E(\rho_{e})\alpha(\rho_{e}){\int}_{{\Omega}_{e}}\mathbf{B}_{e}^{T}\bar{\mathbf{C}}_{e}{\Delta} T_{e}\boldsymbol{\phi}^{T}d{\Omega} $$
(9)

in which we note that both E(ρ e ) and α(ρ e ) are dependent on density variables and thus both necessitate material interpolation. To simplify, we combine these parameters into a single thermal load coefficient as

$$ \beta(\rho_{e})=E(\rho_{e})\alpha(\rho_{e}). $$
(10)

This quantity is then treated as an inherent material property and \(\mathbf {f}_{e}^{th}(\rho _{e})\) can be rewritten as

$$ \mathbf{f}_{e}^{th}(\rho_{e})=\beta(\rho_{e}){\int}_{{\Omega}_{e}}\mathbf{B}_{e}^{T}\bar{\mathbf{C}}{\Delta} T_{e}\boldsymbol{\phi}^{T}d{\Omega}. $$
(11)

Finally, the global thermal load vector is assembled by summing element contributions

$$ \mathbf{F}^{th}(\boldsymbol{\rho})=\sum\limits_{e=1}^{N}\mathbf{f}_{e}^{th}(\rho_{e}). $$
(12)

Again, the element thermal load vector for nondesign elements can be obtained from the previous relations by taking ρ e = 1, which forces β(ρ e )=E o α o through the interpolation scheme in Section 2.2. Here α o is the non-penalized coefficient of thermal expansion for the material.

After solving (1) to determine the displacements, the stress tensor for each element is computed as a post processing step by

$$ \boldsymbol{\mathbf{\sigma}}_{e}=E_{o}\bar{\mathbf{C}}_{e}\mathbf{B}_{e}\mathbf{U}_{e}-E_{o}\bar{\mathbf{C}}_{e}\alpha_{o} \boldsymbol{\phi}^{T}{\Delta} T_{e}, $$
(13)

which we note is only implicitly dependent on the topology through the elemental displacement vector and thus is called the solid stress vector. At this point, the solid stress is utilized to separate the explicit effect of stiffness and thermal load penalization from the elemental stress function that will be utilized in the optimization, which is introduced in Section 3.1. For a two-dimensional continuum element, the stress vector contains two normal stress components, σ x, e and σ y, e , in addition to a shear stress τ x y, e as

$$ \boldsymbol{\mathbf{\sigma}}_{e}=\left[\begin{array}{ccc} \sigma_{x,e} & \sigma_{y,e} & \tau_{xy,e}\end{array}\right]^{T}. $$
(14)

The principal stresses and maximum shear stress in element e can be computed as

$$ \sigma_{1,e}=\frac{\sigma_{x,e}+\sigma_{y,e}}{2}+\sqrt{\left( \frac{\sigma_{x,e}-\sigma_{y,e}}{2}\right)^{2}+\tau_{xy,e}^{2}}, $$
(15)
$$ \sigma_{2,e}=\frac{\sigma_{x,e}+\sigma_{y,e}}{2}-\sqrt{\left( \frac{\sigma_{x,e}-\sigma_{y,e}}{2}\right)^{2}+\tau_{xy,e}^{2}}, $$
(16)
$$ \tau_{max,e}=\sqrt{\left( \frac{\sigma_{x,e}-\sigma_{y,e}}{2}\right)^{2}+\tau_{xy,e}^{2}}. $$
(17)

which yield the most severe (max/min) normal and shear stress conditions in element e for the prescribed stress vector. While failure in an element can be based on the principal or maximum shear stresses, in design various failure metrics are commonly utilized to generalize material failure to states of combined normal (tension and compression) and shear stress. For generality one may assume that a stress failure criterion \(F_{e}^{(g)}\) for element e can be computed as a function of the elements in the solid stress tensor as

$$ F_{e}^{(g)}=F_{e}^{(g)}(\boldsymbol{\sigma}_{e}). $$
(18)

In this work, we take this relation to be the common von Mises failure criterion given by

$$ F_{e}^{(g)}=F_{e}^{vm}=\sqrt{\sigma_{x,e}^{2}-\sigma_{x,e}\sigma_{y,e}+\sigma_{y,e}^{2}+3\tau_{xy,e}^{2}}. $$
(19)

2.2 Interpolation schemes

It is known that in the presence of design-dependent loading, which includes thermal loads, the usual SIMP (Solid Isotropic Material with Penalization) interpolation scheme presents numerical difficulties due in large part to the fact that its sensitivity vanishes with small density values. As a result, the RAMP (Rational Approximation of Material Properties) model is adopted when considering thermal effects. Thus, the stiffness and thermal load are interpolated according to

$$ E(\rho_{e})=\eta_{E}(\rho_{e})E_{o}=\frac{\rho_{e}}{1+R_{E}(1-\rho_{e})}E_{o} $$
(20)
$$ \beta(\rho_{e})=\eta_{\beta}(\rho_{e})E_{o}\alpha_{o}=\frac{\rho_{e}}{1+R_{\beta}(1-\rho_{e})}E_{o}\alpha_{o} $$
(21)

where R E and R β are RAMP penalization parameters. Recall, E o and α o are baseline material properties for the elastic modulus and coefficient of thermal expansion, respectively. For comparison on a room temperature example to be investigated later, we note here the SIMP interpolation on stiffness takes the usual power law form

$$ E(\rho_{e})=\rho_{e}^{p_{E}}E_{o} $$
(22)

where p E is the SIMP penalization parameter on the elastic modulus.

2.3 Density filtering

In order to prevent checker-boarding and enforce length scale we use the density filter (Bruns and Tortorelli 2001) given by (23)

$$ \rho_{e}=\frac{1}{{\sum}_{i\in N_{e}}H_{ei}}\sum\limits_{i\in N_{e}}H_{ei}x_{i} $$
(23)

where ρ e is the physical density of element e, N e is the set of elements i for which the center-to-center distance Δ(e, i) to element e is smaller than the filter radius r m i n , and H e i is the typical linear distance function

$$ H_{ei}=max\left( 0,r_{min}-{\Delta}(e,i)\right). $$
(24)

Here we note the difference between the design variable x and the physical density ρ. The finite element model is parameterized using the density variables contained in ρ, which are now computed by applying the density filter to the design variables x. To maintain consistent sensitivities, the following chain rule is applied where f is an arbitrary response function.

$$ \frac{\partial f}{\partial x_{j}}=\sum\limits_{e\in N_{j}}\frac{\partial f}{\partial\rho_{e}}\frac{\partial\rho_{e}}{\partial x_{j}}=\sum\limits_{e\in N_{j}}\frac{1}{{\sum}_{i\in N_{e}}H_{ei}}H_{je}\frac{\partial f}{\partial\rho_{e}}. $$
(25)

We note that the sensitivity filter (Sigmund and Petersson 1998) was also explored in this work, but the numerical consistency of the sensitivities obtained when using the density filter proved desirable.

3 Methods for stress-based criteria

In this section, the special techniques required to incorporate stress constraints in topology optimization are introduced. In particular, techniques to address the singularity phenomena in the elemental stress function and the need to efficiently treat the local nature of stress constraints are outlined.

3.1 Relaxed stress

In this work, the relaxation method of Le et al. (2010) is adopted to relax elemental stress values and remove the singularity phenomena. This technique works by applying an interpolation on the element failure criterion as defined by (18) according to

$$ F_{e}^{(r)}=\eta_{F}(\rho_{e})F_{e}^{(\mathrm{g})} $$
(26)

where \(F_{e}^{(r)}\) is the relaxed failure criterion and \(\eta _{F}(\rho _{e})=\rho _{e}^{1/2}\) in this work. Since this method was developed for stresses of mechanical origin, the following numerical exercise is provided to demonstrate its effectiveness for stresses due to mechanical, thermal, and combined thermal/mechanical loading. The simple finite element model for the study is shown in Fig. 2. It is constructed using 2D four-node elements in plane stress, the material properties of the structure are taken as E o = 70 GPa, ν o = 0.3, α o = 25×10−6 1/ ∘C, and the thickness is taken as t = 1 cm. The model is analyzed using four different loading cases and boundary conditions, which subject it to various cases of mechanical Fig. 2a and b, thermal c, and d combined stresses.

Fig. 2
figure 2

Model, boundary conditions, and load cases for the validation of the relaxed stress technique. Note dimensions shown in meters. (a, b) Mechanical loading, (c) Thermal loading, and (d) Combined loading

Full size image

Figure 3 gives the von Mises stress in element 1 as a function of its density. In the figure, the dashed lines show the solid stress computed directly from (19) and the multiply colored curves indicate different loading and boundary condition cases. The singularity phenomena is readily evident in the solid stress, which increases significantly as the density in element 1 is reduced. However, when the relaxation is applied to the solid stress according to (26), where the generalized failure criterion has been replaced with the von Mises stress, we observe that the singularity in the stress is arrested as density is decreased. Moreover, as the density nears zero, which corresponds to no material, a state of zero stress is achieved. This is realized for all cases of mechanical, thermal, and combined stress states. In addition, a penalizing effect in terms of stress is observed for intermediate densities. That is, intermediate density material experiences a more severe stress state than both solid and void material, which is desirable in the formulation of the topology optimization to ensure that the non-physical intermediate density is removed in the final design.

Fig. 3
figure 3

Validation of stress relaxation - stress (von Mises) in element 1 plotted as a function of element 1 density

Full size image

3.2 Scaled stress aggregation

Another primary challenge in stress-based topology optimization is effectively capturing the maximum stress at a level of computational expense that is suitable for industrial size topology optimization problems. Since it is computationally impossible to place stress constraints on every element, a modified p-norm function is utilized to aggregate the failure criterion value of many elements into a manageable number of constraints. If the elements in the model are split into n groups, the p-norm function for group m is given by

$$ \text{PN}_{m}=\left[\sum\limits_{e=1}^{N_{m}}\left( \frac{F_{e}^{(r)}}{\bar{F}}\right)^{p}\right]^{1/p} $$
(27)

where N m is the number of elements in group m, p is a tuning parameter, and \(\bar {F}\) is the limit value on the failure criterion \(F_{e}^{(r)}\). In general, higher values of p increase the accuracy of the aggregation with \(\text {PN}_{m}\rightarrow \max (F_{e}^{(r)}/\bar {F})_{m}\) (the maximum value of the normalized failure criterion in group m) for p→∞; however, in practice both numerical and optimization convergence issues occur if the value selected for p is too large. In the optimization literature, when using p-norm functions, suitable values for p are generally found in the range from 4 to 10. This limitation on the values of p ensures that considerable error between PN m and \(\max (F_{e}^{(r)}/\bar {F})_{m}\) is present and we cannot reliably enforce the limit value \(\bar {F}\). To remedy this, a scaling technique is employed to gradually scale the PN m towards \(\max (F_{e}^{(r)}/\bar {F})_{m}\) over the course of the iterative optimization process in the same manner as Le et al. (2010).

If no discrepancy exists between between PN m and \(\max (F_{e}^{(r)}/\bar {F})_{m}\), material failure is predicted if PN m ≥1 and a constraint in the optimization problem can be posed as

$$ g_{m}=\text{PN}_{m}-1\leq0. $$
(28)

If used in a typical gradient-based optimization process, as convergence is reached the value of PN m would converge as well. When considering the inherent discrepancy between PN m and \(\max (F_{e}^{(r)}/\bar {F})_{m}\), the difference approaches a constant value. Exploiting this behavior, the constraint in (28) can be rewritten with an adaptive scaling factor \({s_{m}^{i}}\) as

$$ g_{m}={s_{m}^{i}}\text{PN}_{m}^{i}-1\leq0. $$
(29)

where i indicates the iteration number and \({s_{m}^{i}}\) is the ratio between PN m and \(\max (F_{e}/\bar {F})\) in group m in the previous iteration. This is simply calculated as

$$ {s_{m}^{i}}=\frac{\text{PN}_{m}^{i-1}}{\max(F_{e}^{(r)}/\bar{F})_{m}^{i-1}} $$
(30)

using stored information. We note that the scaling ratio \({s_{m}^{i}}\) is a non-continuous quantity; however, since it approaches a constant value as the optimization progresses, convergence is not impeded so long as excessive step sizes are not permitted between optimization iterations.

3.3 Sensitivity analysis

In the sensitivity analysis implementation, care should be taken to properly treat the stress in elements that are designable (dependent on density) compared to elements that remain solid. In the derivation that follows, this consideration is noted where appropriate.

We begin by differentiating (29) (note that the superscript i that gives the iteration number has been removed for clearer presentation) with respect to a density variable ρ j

$$ \frac{dg_{m}}{d\rho_{j}}=s_{m}\frac{d\text{PN}_{m}}{d\rho_{j}}. $$
(31)

The derivative of the aggregation function PN m with respect to the density variable is

$$\begin{array}{@{}rcl@{}} \frac{d\text{PN}_{m}}{d\rho_{j}} & = & \sum\limits_{e=1}^{N_{m}}\frac{\partial\text{PN}_{m}}{\partial F_{e}^{(r)}}\frac{dF_{e}^{(r)}}{d\rho_{j}}. \end{array} $$
(32)

In (32) the first partial derivative term \(\partial \text {PN}_{m}/\partial F_{e}^{(r)}\) is obtained by differentiating (27) with respect to the relaxed elemental failure criterion \(F_{e}^{(r)}\), which yields

$$ \frac{\partial\text{PN}_{m}}{\partial F_{e}^{(r)}}=\left[\sum\limits_{e=1}^{N_{m}}\left( \frac{F_{e}^{(r)}(\rho_{e})}{\bar{F}}\right)^{p}\right]^{(1/p-1)} \left( \frac{F_{e}^{(r)}(\rho_{e})}{\bar{F}}\right)^{p-1}. $$
(33)

Next we recall that \(F_{e}^{(r)}\) is the product of the stress interpolation η F and, in the most general case, the solid element failure criterion \(F_{e}^{(\mathrm {g})}\) as given in (26). Differentiating this relation yields

$$\begin{array}{@{}rcl@{}} \frac{dF_{e}^{(r)}}{d\rho_{j}} & = & \frac{\partial F_{e}^{(r)}}{\partial\eta_{F}}\frac{d\eta_{F}}{d\rho_{j}}+\left( \frac{\partial F_{e}^{(r)}}{\partial F_{e}^{(\mathrm{g})}}\right)\left( \frac{\partial F_{e}^{(\mathrm{g})}}{\partial\boldsymbol{\sigma}_{e}}\right)^{T}\frac{d\boldsymbol{\sigma}_{e}}{d\rho_{j}}\\ & = & F_{e}^{(\mathrm{g})}\frac{d\eta_{F}}{d\rho_{j}}+\eta_{F}(\rho_{e})\left( \frac{\partial F_{e}^{(\mathrm{g})}}{\partial\boldsymbol{\sigma}_{e}}\right)^{T}\frac{d\boldsymbol{\sigma}_{e}}{d\rho_{j}} \end{array} $$
(34)

where the term d σ e /d ρ j is the derivative of the solid stress tensor of element e with respect to the density variable. This is computed by differentiating (13), which gives

$$ \frac{d\boldsymbol{\sigma}_{e}}{d\rho_{j}}=E_{o}\bar{\mathbf{C}}_{e}\mathbf{B}_{e} \frac{d\mathbf{U}_{e}}{d\rho_{j}}=E_{o}\bar{\mathbf{C}}_{e}\mathbf{B}_{e}\left( \frac{\partial\mathbf{U}_{e}} {\partial\mathbf{U}}\right)^{T}\frac{d\mathbf{U}}{d\rho_{j}} $$
(35)

where ∂ U e /∂ U forms a transformation from local element degrees of freedom to the global degrees of freedom. Substituting (35) into (34) and (34) into (32) yields

$$\begin{array}{@{}rcl@{}} \frac{d\text{PN}_{m}}{d\rho_{j}} &\,=\, & \sum\limits_{e=1}^{N_{m}}\left[\frac{\partial\text{PN}_{m}}{\partial F_{e}^{(r)}}\!\left( \!F_{e}^{(\mathrm{g})}\frac{d\eta_{F}}{d\rho_{j}}\,+\,\eta_{F}(\rho_{e})\!\left( \frac{\partial F_{e}^{(\mathrm{g})}}{\partial\boldsymbol{\sigma}_{e}}\right)^{T}E_{o}\bar{\mathbf{C}}_{e}\mathbf{B}_{e}\right.\right.\\ &&\qquad\;\left.\left.\left( \frac{\partial\mathbf{U}_{e}}{\partial\mathbf{U}}\right)^{T}\frac{d\mathbf{U}}{d\rho_{j}}{\vphantom{F_{e}^{(\mathrm{g})}\frac{d\eta_{F}}{d\rho_{j}}\,+\,\eta_{F}(\rho_{e})\!\left( \frac{\partial F_{e}^{(\mathrm{g})}}{\partial\boldsymbol{\sigma}_{e}}\right)^{T}}}\right)\right]\\ & = & \sum\limits_{e=1}^{N_{m}}\left[\frac{\partial\text{PN}_{m}}{\partial F_{e}^{(r)}}F_{e}^{(\mathrm{g})}\frac{d\eta_{F}}{d\rho_{j}}\right] \\ & & \;\qquad+\!\sum\limits_{e=1}^{N_{m}}\!\left[\!\frac{\partial\text{PN}_{m}}{\partial F_{e}^{(r)}}\eta_{F}(\rho_{e})\!\left( \!\frac{\partial F_{e}^{(\mathrm{g})}}{\partial\boldsymbol{\sigma}_{e}}\!\right)^{T}E_{o}\bar{\mathbf{C}}_{e}\mathbf{B}_{e} \left( \frac{\partial\mathbf{U}_{e}}{\partial\mathbf{U}}\right)^{T}\!\right]\!\frac{d\mathbf{U}}{d\rho_{j}}. \end{array} $$
(36)

We note that the d η F /d ρ j term in the first summation in (36) is nonzero only for e = j. Thus, the summation can be ignored and the equation can be reduced to

$$\begin{array}{@{}rcl@{}} \frac{d\text{PN}_{m}}{d\rho_{j}}&=&\frac{\partial\text{PN}_{m}}{\partial F_{j}^{(r)}}F_{j}^{(\mathrm{g})}\frac{d\eta_{F}}{d\rho_{j}}\\ &&+\sum\limits_{e=1}^{N_{m}}\left[\frac{\partial\text{PN}_{m}}{\partial F_{e}^{(r)}}\eta_{F}(\rho_{e})\left( \frac{\partial F_{e}^{(\mathrm{g})}}{\partial\boldsymbol{\sigma}_{e}}\right)^{T}E_{o}\bar{\mathbf{C}}_{e} \mathbf{B}_{e}\left( \frac{\partial\mathbf{U}_{e}}{\partial\mathbf{U}}\right)^{T}\right]\frac{d\mathbf{U}}{d\rho_{j}}.\\ \end{array} $$
(37)

Differentiating (1) with respect to ρ j and rearranging gives

$$ \frac{d\mathbf{U}}{d\rho_{j}}=\mathbf{K}^{-1}\left( \frac{d\mathbf{F}^{th}}{d\rho_{j}}-\frac{d\mathbf{K}}{d\rho_{j}}\mathbf{U}\right). $$
(38)

Substituting the preceding relation into (37) and introducing the adjoint variable λ yields

$$ \frac{d\text{PN}_{m}}{d\rho_{j}}=\frac{\partial\text{PN}_{m}}{\partial F_{j}^{(r)}}F_{j}^{(\mathrm{g})}\frac{d\eta_{F}}{d\rho_{j}}+\boldsymbol{\mathbf{\lambda}}^{T} \left( \frac{d\mathbf{F}^{th}}{d\rho_{j}}-\frac{d\mathbf{K}}{d\rho_{j}}\mathbf{U}\right) $$
(39)

where the adjoint variable is determined by the solution of the adjoint problem

$$ \mathbf{K}\boldsymbol{\lambda}=\sum\limits_{e=1}^{N_{m}}\left[\frac{\partial\text{PN}_{m}}{\partial F_{e}^{(r)}}\eta_{F}(\rho_{e})\frac{\partial F_{e}^{(\mathrm{g})}}{\partial\boldsymbol{\sigma}_{e}}\left( E_{o}\bar{\mathbf{C}}_{e}\mathbf{B}_{e} \right)^{T}\frac{\partial\mathbf{U}_{e}}{\partial\mathbf{U}}\right]. $$
(40)

Note that (39) and (40) give the sensitivity using a general stress failure criterion. The term \(\partial F_{e}^{(\mathrm {g})}/\partial \boldsymbol {\sigma }_{e}\) varies according to how the selected failure criterion is calculated using the components of the element stress tensor. The sensitivity using the von Mises failure criterion is determined by differentiating (19) with respect to the elements of the stress tensor as

$$ \frac{\partial F_{e}^{(\text{vm})}}{\partial\boldsymbol{\sigma}_{e}}=\left\{ \begin{array}{c} \frac{\partial F_{e}^{(\text{vm})}}{\partial\sigma_{x,e}}\\ \frac{\partial F_{e}^{(\text{vm})}}{\partial\sigma_{y,e}}\\ \frac{\partial F_{e}^{(\text{vm})}}{\partial\tau_{xy,e}} \end{array}\right\} $$
(41)

where

$$ \frac{\partial F_{e}^{(\text{vm})}}{\partial\sigma_{x,e}}=\frac{1}{2F_{e}^{(\text{vm})}}\left( 2\sigma_{x,e}-\sigma_{y,e}\right), $$
(42)
$$ \frac{\partial F_{e}^{(\text{vm})}}{\partial\sigma_{y,e}}=\frac{1}{2F_{e}^{(\text{vm})}}\left( 2\sigma_{y,e}-\sigma_{x,e}\right), $$
(43)
$$ \frac{\partial F_{e}^{(\text{vm})}}{\partial\tau_{xy,e}}=\frac{3\tau_{xy,e}}{F_{e}^{(\text{vm})}}. $$
(44)

3.3.1 Sensitivity analysis validation

Using the models and analysis cases previously given in Fig. 2, the analytical sensitivity analysis formulation for the aggregated measure given by (32) to (44) is validated against finite difference sensitivities. Forward finite difference is utilized in the results presented with a perturbation size of 0.001. The sensitivity of the aggregated measure over various regions with respect to the density of element 1 is found. For each region described in Table 1 (note some regions contain only a single element), the aggregated measure is computed according to (27) using the von Mises failure criterion and \(\bar {F}=350\) MPa. We note that by testing these regions, the sensitivity of regions including only designable elements, only nondesign elements, and regions containing both designable and nondesign elements are evaluated.

Table 1 Region definitions for sensitivity analysis validation of the aggregated stress measure
Full size table

The sensitivity of the aggregated measures with respect to element 1 density are shown in Fig. 4a to d. In each plot, different loading and boundary conditions are indicated by different colors with the analytical sensitivity given by solid lines and finite difference validation points indicated by filled dots. Finally, the variation of the sensitivity with respect to the density of element 1 is plotted (with the density along the horizontal axis) to demonstrate the nonlinear dependence of the stress sensitivities on density. From all the plots in Fig. 4, it is observed that the finite difference points lie on the analytical sensitivity curves, which indicates the accuracy of adjoint formulation.

Fig. 4
figure 4

Validation of analytical sensitivity analysis for the aggregated stress measure with multiple region definitions indicated by color and multiple loading and boundary conditions from Fig. 2

Full size image

3.4 Element grouping

Rather than a single global aggregation, multiple constraints of the form in (29) are utilized with each acting over a group of elements. Elements are grouped according to their stress-level by computing the element stress failure criterion and sorting the values in descending order. For N elements sorted into n groups this can be done as

$$\begin{array}{@{}rcl@{}} &&\overset{\underbrace{F_{1}^{(g)}\geq F_{2}^{(g)}\geq F_{3}^{(g)}\geq...\geq F_{\frac{N}{N_{m}}}^{(g)}}}{\mathrm{region\,}1}\,\,\,\,\overset{\underbrace{\geq...\geq F_{\frac{2N}{N_{m}}}^{(g)}}}{\mathrm{region\,}2}\\ &&{\kern15pt} \overset{\underbrace{\geq...\geq F_{\frac{(n-1)N}{N_{m}}}^{(g)}}}{\mathrm{region\,}n-1}\,\,\,\,\overset{\underbrace{\geq...\geq^{(g)}F_{N}}}{\mathrm{region\,}n} \end{array} $$
(45)

where the first n−1 clusters contain N m elements and the last cluster holds the remaining elements. Note that alternative grouping techniques, along with the resorting of elements during the optimization process, have been explored in the literature (Holmberg et al. 2013) and may hold computational advantages in some problems; however, in this work we sort elements at only the first iteration and maintain the same grouping throughout the optimization.

4 Optimization problem statements

Using the finite element parameterization and additional techniques above, a number of different topology optimization problems can be formulated. The mathematical statement for a generalized topology optimization problem is given by

$$ \begin{array}{ll} {\kern22pt} \mathrm{min:}& f(\boldsymbol{\rho},\mathbf{U}(\boldsymbol{\rho}))\vspace*{5pt}\\ \mathrm{subject\, to:\,\,} & \mathbf{K}(\boldsymbol{\rho})\mathbf{U}(\boldsymbol{\rho})=\mathbf{F}^{m}+\mathbf{F}^{th}(\boldsymbol{\rho}) \vspace*{5pt}\\ & g_{i}(\boldsymbol{\rho},\mathbf{U}(\boldsymbol{\rho}))\leq0\vspace*{5pt}\\ {\kern1.9pt} \mathrm{variables:} & 0<x_{e}\leq1\,\,\text{for}\,\, e=1,2,...,N\end{array} $$
(46)

where f is the objective function and g i is the set of constraints. Using this form, the common minimum compliance (maximum stiffness), material constrained problem is stated as

$$\begin{array}{@{}rcl@{}} \mathrm{min:} & & c(\boldsymbol{\rho})=\mathbf{U}(\boldsymbol{\rho})^{T}\mathbf{K}(\boldsymbol{\rho})\mathbf{U}(\boldsymbol{\rho})\\ \mathrm{subject\, to:} & & \mathbf{K}(\boldsymbol{\rho})\mathbf{U}(\boldsymbol{\rho})=\mathbf{F}^{m}+\mathbf{F}^{th}(\boldsymbol{\rho})\\ & & g_{1}(\boldsymbol{\rho})=\sum\limits_{e=1}^{N_{d}}\left( \rho_{e}v_{e}-V_{f}v_{e}\right)\leq0 \\ \text{variables}: & & 0<x_{min}\leq x_{e}\leq1\,\,\text{for}\,\, e=1,2,...,N_{d} \end{array} $$
(47)

where v e is the elemental volume and V f is the allowable volume fraction. The minimum material, stress-constrained problem is given by

$$\begin{array}{@{}rcl@{}} \mathrm{min:} & & f(\boldsymbol{\rho})=\sum\limits_{e=1}^{N_{d}}\left( \rho_{e}v_{e}\right) \\ \mathrm{subject\, to:} & & \mathbf{K}(\boldsymbol{\rho})\mathbf{U}(\boldsymbol{\rho})=\mathbf{F}^{m}+\mathbf{F}^{th}(\boldsymbol{\rho}) \\ & & g_{m}(\boldsymbol{\rho},\mathbf{U})={s_{m}^{i}}\mathrm{PN(\boldsymbol{\rho},\mathbf{U})}_{m}^{i}-1\leq0\,\,\text{for}\,\, m=1,2,...,n\\ \text{variables}: & & 0<x_{min}\leq x_{e}\leq1\,\,\text{for}\,\, e=1,2,...,N_{d} \end{array} $$
(48)

where a total of n aggregated constraints on stress failure are utilized. Finally, a minimum compliance problem with material usage and stress constraints is useful in the design of high stiffness structures that also satisfy stress limits. Such a problem can be stated as

$$\begin{array}{@{}rcl@{}} \mathrm{min:} & & c(\boldsymbol{\rho})=\mathbf{U}(\boldsymbol{\rho})^{T}\mathbf{K}(\boldsymbol{\rho})\mathbf{U}(\boldsymbol{\rho}) \\ \mathrm{subject\, to:} & & \mathbf{K}(\boldsymbol{\rho})\mathbf{U}(\boldsymbol{\rho})=\mathbf{F}^{m}+\mathbf{F}^{th}(\boldsymbol{\rho}) \\ & & g_{1}(\boldsymbol{\rho})={\sum}_{e=1}^{N_{d}}\left( \rho_{e}v_{e}-V_{f}v_{e}\right)\leq0\\ & & g_{m}(\boldsymbol{\rho},\mathbf{U})={s_{m}^{i}}\mathrm{PN(\boldsymbol{\rho},\mathbf{U})}_{m}^{i}-1\leq0\,\,\text{for}\,\, m=1,2,...,n \\ \text{variables}: & & 0<x_{min}\leq x_{e}\leq1\,\,\text{for}\,\, e=1,2,...,N_{d} \end{array} $$
(49)

We note here the significance of the choice of stress and material limits in the problem statements in (48) and (49) in regards to obtaining a feasible solution. In (48), depending on the magnitude of loading, a feasible solution is not guaranteed within the specified design domain if stress limits are too restrictive. This holds true for (49) as well, where one must also consider the relationship between the selected stress limits and allowed material usage. These types of additional considerations are generally not required when considering the typical minimum compliance design with purely mechanical loading. In this case, a feasible solution is obtained so long as sufficient material is provided to connect points of applied load to boundary conditions.

5 Demonstration examples

Fig. 5
figure 5

Design domain, boundary conditions, and loading for the L-bracket example problem

Full size image

The thermoelastic topology optimization formulation described in the previous sections is demonstrated on two example problems. In both cases, the GCMMA optimizer (Svanberg 2002) has been utilized; however, the algorithm has been modified to take more conservative steps sizes to smooth convergence. All methods, including finite element analysis and topology optimization, have been implemented in MATLAB (MathWorks (2012) Matlab release 2012b). The von Mises failure criterion is utilized for all stress constraints and the density filter radius is taken as twice the element size. For each example, all initial design variable values are taken as 0.5.

5.1 L-bracket

The L-shaped bracket is a popular test example for topology optimization with stress criteria in the literature. This is because the design domain contains a re-entrant corner that causes an initial stress singularity that is not removed when the problem is solved using the typical minimum compliance solution strategy. This problem is used here to demonstrate the effectiveness of the stress-constrained formulation with scaled stress aggregation. It should be noted that for a stress-based topology optimization to be considered successful, the maximum stress in the structure should remain at or below a prescribed limit that is based on realistic failure criterion.

The design domain for the L-bracket is given in Fig. 5. The structure is fixed in all degrees of freedom along its top edge and a 750 N concentrated load is applied as indicated. To prevent an unresolvable stress singularity that would impede the optimization due to the point load, a 2 by 3 region of elements under the load are taken as non-designable and excluded from the stress constraints. The thickness of the structure is assumed to be 1 mm and the material properties are taken as those of 7075-T6 aluminum (shown in Table 2) at room temperature. The domain is discretized using 6400 quadrilateral plane stress finite elements. The minimum material, stress-constrained topology optimization problem is solved according to the statement in (48) with a total of n = 10 stress aggregation regions and the penalization parameter in the p-norm functions is taken as p = 8. In the first set of results (at room temperature) that follow, both the SIMP and RAMP interpolation schemes are utilized, with p E = 3 and R E = 8, respectively, and all design variables are initialized with value of 0.5.

Table 2 Material Properties of 7075-T6 Aluminum (MIL-HDBK-5H 1998)
Full size table

5.1.1 Room temperature

Figure 6 gives the topology optimization results for the L-shaped bracket with only mechanical loading (room temperature) using both the SIMP and RAMP stiffness interpolations.

Fig. 6
figure 6

Topology optimization results for the L-shaped bracket with only mechanical loading for both (a,c,e) SIMP and (b,d,f) RAMP interpolation on stiffness. (a,b) Density distributions, (c,d) von Mises Stress in MPa, and (e,f) Iteration history for material usage and maximum stress

Full size image

We observe in the density distributions in Fig. 6a and b that topologically similar designs are obtained; however, the RAMP design utilizes nearly 6 % more material. It is also apparent that not all of the intermediate density material is removed using RAMP and trace amounts of gray material remain. This creates higher stresses in these regions when compared to the surrounding void material since the relaxation on element stresses only effectively zeros the stresses for nearly zero density. We presume this feature is a result of the fundamental difference between the SIMP and RAMP schemes. Recalling that a limitation of the SIMP interpolation is that it has zero sensitivity at zero density, which RAMP does not. Thus, as material is removed and becomes void, it is much more difficult for it to reappear when utilizing SIMP than RAMP (which is a critical drawback of SIMP for design-dependent loading). When combined with the scaled stress measure, which imparts a small perturbation on the mathematical optimization problem every iteration, the relative insensitivity of SIMP proves to be an advantage. In the RAMP interpolation, the increased sensitivity of responses in low density regions means that the optimization algorithm reacts more strongly to the perturbed problem. This conclusion is supported by the iteration history plots in Fig. in 6e and f. Compared to the SIMP convergence, considerably more oscillation is evident in the maximum stress convergence when using RAMP, which results from a stronger response to the stress scaling process. The most important observation from this problem is found in Fig. 6c and d where we note that the maximum stress limit of \(\bar {F}=275.0\) MPa is satisfied. This indicates the scaled stress technique is successful using both SIMP and RAMP in this problem.

5.1.2 Thermal loading

To investigate the effectiveness of the scaled stress measure in the presence of thermal loading, the L-shaped bracket is now subjected to a uniform elevated temperature of T = 20∘ C. The applied mechanical load of 750 N and boundary conditions remain unchanged. Physically, 20∘ C does not appear to be a significant source of thermal loading; however, considering the two-dimensional context of the problem, where all strain energy is contained in only in-plane degrees-of-freedom, it actually represents a considerable load. To demonstrate this, the optimal design obtained using the RAMP interpolation scheme, previously shown in Fig. 6b, is subjected to the new combined loading environment. The resulting stress distribution is shown in Fig. 7. In the figure, all regions that appear as deep red exceed the previous allowable stress of 275.0 MPa and the maximum stress in the domain is now 346.8 MPa, which represents an increase of approximately 25 %. We note that the elevated stresses occur directly within the connecting structural members. This implies that while such a material layout carries mechanically-induced stresses very well, it may not be appropriate when additional thermal effects are considered.

Fig. 7
figure 7

von Mises stress distribution for the design previously shown in Fig. 6b subjected to combined thermal and mechanical loading (stress in MPa)

Full size image

We now incorporate the combined thermal loading and re-solve the topology optimization problem. The RAMP interpolation scheme is utilized here despite the superior performance of the SIMP scheme in the last section with purely mechanical loads because SIMP is not generally effective in the presence of design-dependent loading. The RAMP penalization parameters are taken as R E = 8 for stiffness and R β = 0 for the thermal load. The resulting density and stress distributions are given in Fig. 8a and b, respectively, and the iteration history for volume usage and maximum stress are shown in Fig. 8c.

Fig. 8
figure 8

Topology optimization results for the L-shaped bracket with combined thermal and mechanical loading. a Density distribution, b von Mises Stress in MPa, and c Iteration history for material usage and maximum stressx

Full size image

In Fig. 8a, we note that a different topological layout is obtained when the effects of the elevated temperature are considered. In this layout, as evidenced by reduced thermal stresses, the material has been redistributed such that structural members do not restrain the thermal expansion of one another. Thus, the stress limit of 275 MPa is satisfied within the tolerances of the optimizer and a nearly identical amount of material has been utilized as the purely mechanical load case. Investigating the iteration history in Fig. 8c, the absence of gray material and significant oscillations in convergence compared to previous results in Fig. 6f is readily evident. This is attributed to the presence of the thermal loading, which due to its design-dependency, serves as a penalty on the reappearance of material. This effectively damps the optimizer’s reaction to the scaling stress measures between each iteration.

5.1.3 Effectiveness of scaled stress measure

To demonstrate the effectiveness of the scaled stress measure in enforcing local limits on maximum stress, even in the presence of thermal loads, the iteration history of the components used to compute it are shown in Fig. 9a and b. The results correspond to the designs in Fig. 6b (mechanical load only) and Fig. 8a (combined thermal and mechanical load), respectively. In the optimization problem, we recall that 10 constraints were utilized based on 10 aggregated regions; however, for demonstration, only results of the first constraint g 1 are shown. In the figure, the blue curve denotes the value of \(\text {PN}_{1}^{i}\) directly computed from the elements in its region according to (27). The red dots denote the actual maximum value of the stress failure criterion (normalized by the limit \(\bar {F}\)) within region 1 in each iteration. The green curve denotes the scaling parameter \({s_{1}^{i}}\) that is computed at each iteration using the value of \(\text {PN}_{1}^{i-1}\) and the maximum value from the previous iteration as stated in (30). The black curve then gives the product \({s_{1}^{i}}\text {PN}_{1}^{i}\), which is the scaled aggregation measure that approximately gives the maximum stress value in the region. This quantity is then constrained to limit maximum stresses according to (29). We observe in both cases, the approximation of the maximum value within the region rapidly approaches the actual maximum value within only a small number of iterations and local limits on stress are enforced effectively.

Fig. 9
figure 9

Iteration history for components of scaled stress measure in constraint 1 for (a) room temperature design and (b) combined mechanical and thermal load design

Full size image

5.2 Bi-clamped thermoelastic domain

The bi-clamped beam problem is a demonstration example that has been used in a limited number of publications regarding thermoelastic topology optimization to demonstrate the behavior of the compliance objective in the presence of thermal loading. It was first introduced by Rodrigues and Fernandes (1995). We note that this objective is not likely to yield a useable solution for general thermoelastic problems and the bi-clamped problem is an exception. In this section, we apply the stress-based formulations to investigate their behavior on a simple problem with combined thermal and mechanical loading. In addition, the conventional minimum compliance problem is solved for comparison since, in this case, the formulation is able to produce solutions. Figure 10 shows the design domain for the structure. It is discretized with four node bi-linear quadrilateral plane stress elements with 60 elements in the horizontal direction and 40 elements in the vertical direction. Black areas in the figure denote non-design regions in the model while gray areas give the designable domain. A mechanical load of F = 150 kN is applied to the center of the bottom edge along with a uniform temperature increase of ΔT = 25∘ C. Similar to the L-shaped bracket example, this temperature level does not seem considerable, but considering the 2D nature of the problem, it in fact represents a significant amount of thermally induced strain energy in the structure. A small non-design region near the application of the mechanical point load is included to prevent a geometrical stress singularity. The material properties are taken as those of 4340 steel at room temperature and are given in Table 3 and a thickness of 1 cm is assumed.

Fig. 10
figure 10

Bi-clamped structural domain with non-design (black) and designable (gray) regions

Full size image
Table 3 Material Properties of 4340 Steel MIL-HDBK-5H (1998)
Full size table

Three different topology optimization problems are solved using the bi-clamped beam domain. First, the minimum volume, stress-constrained problem is solved as stated in (48) using m = 10 stress regions on the von Mises failure criterion. The p-norm parameter in the aggregated stress measures is taken as p = 8. After obtaining the stress-constrained design, another optimization is performed using the standard minimum compliance, volume constrained formulation in (47) where the volume limit is taken as the volume achieved in the stress-constrained problem. Finally, the minimum compliance problem with volume and stress constraints stated in (49) is solved using the constraint limits from the previous problems. In each formulation, the RAMP interpolation model is utilized with a penalization parameter of R E = 8 on the material stiffness and R β = 0.

Figure 11 shows the density and stress distributions and Fig. 12 gives the iteration history for topology optimization of the bi-clamped domain with each of the three formulations.

Fig. 11
figure 11

Density and stress distributions for bi-clamped domain topology optimization with (a) stress-constrained formulation, (b) minimum compliance formulation, and (c) minimum compliance formulation with stress constraints

Full size image
Fig. 12
figure 12

Iteration history for bi-clamped domain topology optimization with (a) stress-constrained formulation, (b) minimum compliance formulation, and (c) minimum compliance formulation with stress constraints

Full size image

Inspecting results of the stress-constrained problem in Fig. 11a, we observe that the stress limit of 400 MPa is satisfied with a material usage of only 14.6 %. In addition, the structure is uniformly stressed, which implies it is an effective layout for carrying the combined thermal and mechanical loading. In Fig. 11b, we see that a significantly different topology is obtained using the minimum compliance formulation even when the material usage is restricted to near that of the stress-constrained design (15 %). A nonuniform stress distribution is also readily evident with significantly higher stresses (note the plots do not use the same color scale in Fig. 11). In fact, the maximum stress observed in the minimum compliance design is 596.6 MPa, or nearly a 50 % increase, compared to the stress-constrained structure. The areas of greatest stress occur adjacent to the non-design elements near the applied loading and at the lower left and right corners, which from a mechanical design perspective, are expected locations. These comparatively increased stresses are likely due in large part to the internal deformation caused by thermal expansion. Compared to the stress-constrained design, where no structural member lies in an orientation directly between the restrained boundaries and expansion can occur with limited bending deformation in the direction of the applied load, expansion in the minimum compliance design is more restrained. This restraint translates into significant internal thermal loading and increased stress levels that cannot be addressed by simply minimizing compliance. This is supported by the results in Fig. 11c, where the stress constraints have been introduced to the minimum compliance problem. In this formulation, results are effectively identical to the purely stress-constrained design, because stress information, which with design-dependent types of loads is not consistent with compliance as with mechanical loading, is directly available to the design optimization problem.

5.2.1 Effectiveness of scaled stress measure

To reaffirm the effectiveness of the scaled stress measure, its components are plotted for the stress constraint corresponding to region 1 in Fig. 13. Similar to the L-shaped bracket problem in Section 5.1.3, the blue curve denotes the value of \(\text {PN}_{1}^{i}\) computed from the elements in its region according to (27). The red dots give the maximum value of the stress failure criterion (normalized by the limit \(\bar {\sigma }\)) within region 1 in each iteration. The green curve denotes the scaling parameter \({s_{1}^{i}}\) that is computed at each iteration using the value of \(\text {PN}_{1}^{i-1}\) and the maximum value from the previous iteration as stated in (30). The black curve then gives the product \({s_{1}^{i}}\text {PN}_{1}^{i}\), which is the scaled aggregation measure that approximately gives the maximum stress value in the region. This quantity is then constrained to limit maximum stresses according to (29). Just as in the previous problem, the approximation of the maximum value within the region quickly reaches the actual maximum value within only a small number of iterations and the local stress limits are satisfied.

Fig. 13
figure 13

Iteration history for scaled stress measure used in constraint 1 in bi-clamped domain topology optimization

Full size image

6 Conclusions

In this paper we have introduced a topology optimization formulation that can efficiently handle stress constraints in a thermoelastic environment. This development was motivated in part by the lack of such a capability in the structural topology optimization field as well as the need for more advanced design techniques for thermal structures in the aerospace industry, including embedded engine aircraft exhaust structures and hypersonic flight applications. Using a consistent finite element parameterization, which incorporates design-dependent thermoelastic effects, and a scaled aggregation technique for elemental stresses, the process was shown to efficiently enforce maximum stress limits on benchmark numerical examples. In addition, results indicate that by utilizing the stress-based formulation, structural configurations can be obtained with superior thermal stress performance when compared to those from the conventional minimum compliance formulation. A valuable continuation of this work would be to expand the structural optimization to include the effects of heat transfer. This will require a coupled analysis procedure to capture the design dependency of heat transfer, which can include combinations of conduction, convection, and radiation, on the topological configuration.