1 Introduction

In engineering optimization, we sometimes encounter very complex systems where many variables have to be considered and it takes considerable efforts to get the relationships among these variables, such as in the simulation using finite element analysis (FEA) and computational fluid dynamics (CFD). Despite the advances in computer capacity and efficiency, the computational cost involved in running complex, high fidelity simulation codes makes it still very hard to rely exclusively on the simulation to explore design alternatives for engineering optimization at the moment (Jin et al. 2001). Computer experiment was developed as a technology exactly in such a background to help engineers to produce surrogate models, also called metamodels (Kleijnen 1987), by using less design points. Applications of the metamodeling methods have been steadily increased in various engineering disciplines today. Simpson et al. (2001b, 2008), Wang and Shan (2007), and Forrester and Keane (2009) provided comprehensive reviews on metamodeling applications in engineering.

Two basic steps are usually required in a typical computer experiment (Chen et al. 2006): (1) to design a series of experiments and (2) to find a statistical fitting model. Different methods have been developed to evaluate the sample data and metamodels.

The early work on comparative study of metamodels focused on two aspects: (1) evaluation of the newly developed data sampling methods and/or metamodels against the existing ones, and (2) evaluation of the different data sampling methods and/or metamodels for specific applications. For example, Koehler and Owen (1996) developed several space filling designs and their corresponding optimum criteria. Simpson et al. (1998) compared polynomial response surface method and kriging method for the design of an aerospike nozzle. Varadarajan et al. (2000) compared ANN method and polynomial response surface method for the design of an engine. Yang et al. (2000) compared four metamodels for building safety functions in automotive analysis. Simpson et al. (2001a) compared some sampling methods in computer experiments. Jin et al. (2002) introduced some sequential sampling methods to be used in computer experiments. Comparative study results considering different metamodeling methods can also be found in the researchers by Giunta et al. (1998), Papila et al. (1999), Koch et al. (1999), Gu (2001), Simpson et al. (2001b), Stander et al. (2004), Fang et al. (2005), Forsberg and Nilsson (2005), Chen et al. (2006), Wang et al. (2006), Xiong et al. (2009), Zhu et al. (2009), and Paiva et al. (2010).

The systematic comparative study of metamodeling techniques was initiated by Jin et al. (2001) considering various metamodels, different characteristics of sample data and multiple evaluation criteria. This research aimed at developing standard procedures for evaluating metamodeling methods. In this research, four metamodels (i.e., polynomial regression, kriging, multivariate adaptive regression splines, and radial basis function), three characteristics of sample data (i.e., nonlinearity properties of the problems: high and low, sample sizes: large, small and scarce, and noise behaviors: smooth and noisy), and five evaluation criteria (i.e., accuracy, robustness, efficiency, transparency and conceptual simplicity) were considered. In the comparative study by Mullur and Messac (2006), four metamodels (i.e., polynomial response surface, radial basis function, extended radial basis function, and kriging), three characteristics of sample data (i.e., sampling methods: Latin hypercube, Hammersley sequence and random, problem dimensions: low and high, sample sizes: low, medium and high), and one evaluation criterion (i.e., accuracy) were considered. In the research by Kim et al. (2009), four metamodels (i.e., moving least squares, kriging, radial basis function, and support vector regression), one characteristic of sample data (i.e., number of variables), and one evaluation criterion (i.e., accuracy) were considered.

The research presented in this paper aims at further improving the comparative study of metamodeling methods considering different characteristics of sample data and multiple evaluation criteria.

Sample data characteristics play an important role to the performance of a metamodeling method. In the past, some basic sample quality merits, such as orthogonality, rotatability, minimum variance and D-optimality, have been developed for the design of experiments (Simpson et al. 2001b). In the comparative study of metamodeling methods, however, only limited categories such as “high” and “low” were used (Jin et al. 2001; Mullur and Messac 2006; Kim et al. 2009). In our research, quantitative merits of sample data, including the sample size, the sample uniformity and the overall sample noise level, have been selected to evaluate their impacts on the performance measures of different metamodels. The quantitative relations between the merits of sample data and performance measures are also plotted as 2-D graphs with the horizontal axes to model the quantitative merits and vertical axes to model the performance measures.

Many metamodeling methods have been developed in the past decades for engineering optimization. In this research, four typical metamodeling methods have been selected. Multivariate polynomial method which is used in the response surface method (Myers and Montgomery 1995), and radial basis function method (Dyn et al. 1986) are two popular methods in metamodeling. Kriging method (Sacks et al. 1989a), as a spatial correlation model which was originated from the geostatistics engineering community, is also included because of its increasing popularity these days. The Bayesian neural network method (MacKay 1991), which places the multi-layer artificial neural networks in a Gaussian process framework, is also included in our discussion.

Many different measures have been developed to evaluate the performance of a metamodeling method, such as mean squared error (MSE), root mean squared error (RMSE), R-square, relative average absolute error (RAAE), relative maximum absolute error (RMAE) and prediction variance (Jin et al. 2001). In our study, a prediction dataset, which is different from the training dataset, is created for each of the testing problems. The following four measures, including (1) RMSE for accuracy, (2) prediction variance for confidence, (3) variance of RMSE for robustness, and (4) regression time for efficiency, are selected for evaluating the performance of the different metamodeling methods.

Compared with the existing studies for evaluating different metamodeling methods, the research presented in this paper provides new contributions in the following aspects:

  1. 1.

    Quantitative measures, instead of qualitative ones, are used in the comparative studies of metamodeling methods to evaluate the characteristics of the sample data.

  2. 2.

    Bayesian neural network method, which is rarely used in metamodeling and has never been considered in comparative studies, is selected in this research as a metamodeling method and compared with other metamodeling methods.

  3. 3.

    A simple guideline is also developed in this research for selecting candidate metamodeling methods based on the sample quality merits and the metamodel performance requirements.

2 Metamodeling methods

Normally the relationship between an input vector \({\boldsymbol{x}}\) and an output parameter Y can be formulated as:

$$ Y=\hat{g}\left({{\boldsymbol{x}}, {\boldsymbol{\beta}}} \right)+\varepsilon $$
(1)

where Y is a random variable, \(\hat{g}\left(\cdot\right)\) is the approximation model, \({\boldsymbol{\beta}}\) is the vector of coefficients, and ε is a stochastic process factor. Metamodeling methods differ to each other in their choices of approximation models and random process formulations. In this research, four typical metamodeling methods, including multivariate polynomial method, radial basis function method, kriging method and Bayesian neural network method, are selected for our comparative study.

2.1 Multivariate polynomial method

The multivariate polynomials here refer to the polynomials used by the response surface method (Myers and Montgomery 1995). The general form of a multivariate polynomial of degree d can be written as:

$$\begin{array}{rll} \hat{g}\left( {{\boldsymbol{x}},\beta } \right)&=&\beta _0 +\sum\limits_i \beta _i x_i +\sum\limits_i \sum\limits_{j>i} \beta _{ij} x_i x_j +\sum\limits_i \beta _{ii} x_i^2 \\&&\! +\!\sum\limits_i \sum\limits_{j>i} \sum\limits_{k>j} \beta _{ijk} x_i x_j x_k +... +\!\sum\limits_i {\beta _{ii...i} x_i^d } \end{array}$$
(2)

Linear least squares estimation can be applied to this linear regression model to obtain the best fit to data. The stepwise forward selection scheme based on mean squared error (Fang et al. 2006) is used to reduce the number of terms in the polynomial.

2.2 Radial basis function method

The general form of a radial basis function can be written as:

$$ \hat{g}\left( {{\boldsymbol{x}},\beta} \right)=\beta_0 +\sum\limits^{m}_{i=1} \beta_{i} b\left( \left\| {\boldsymbol{x}} -{\boldsymbol{x}}_i \right\| \right) $$
(3)

where \({\boldsymbol{x}}_{i}\) is a center point selected from the training data, m is the number of center points, and b(·) is the basis function. In this work, the popular Gaussian function is selected as the basis function due to its effectiveness in metamodeling:

$$ b\left( z \right)=e^{-cz^2} $$
(4)

where z is the distance measure and c is a constant to be optimized. Other basis functions, including the multi-quadratic model and the thin-plate model (McDonald et al. 2007), were also tested in this work and found less effective in the selected cases. The orthogonal least squares method (Chen et al. 1991) is used to select center points and the linear least squares estimation is employed to this linear regression model to obtain the best fit to data.

2.3 Kriging method

Kriging method was originated from the geostatistics community (Matheron 1963) and used by Sacks et al. (1989b) to model computer experiments. Kriging method is based on the assumption that the true response can be modeled by:

$$ Y=\sum\limits^{m}_{i=0} \beta_i f_i \left( {\boldsymbol{x}} \right)+Z\left( {\boldsymbol{x}} \right) $$
(5)

where \(Z({\boldsymbol{x}})\) is a stochastic process with mean of zero and covariance given by:

$$ \emph{Cov}\left( {\mbox{Z}\left( {{\boldsymbol{x}}_j } \right),\mbox{Z}\left( {{\boldsymbol{x}}_k } \right)} \right)=\sigma ^2R_{jk} \left( {{\boldsymbol{\theta}},{\boldsymbol{x}}_j ,{\boldsymbol{x}}_k } \right) $$
(6)

where σ is the process variance and R jk (·) is the correlation function. The linear part of (5) is usually assumed to be a constant (called ordinary kriging), whereas the correlation function R jk (\({\boldsymbol{\theta}}, {\boldsymbol{x}}_{i}, {\boldsymbol{x}}_{k}\)) is generally formulated as:

$$ R_{jk} \left({\boldsymbol{\theta}}, {\boldsymbol{x}}_j, {\boldsymbol{x}}_k \right)= \prod\limits^{p}_{i=1} Q\left(\theta_i, x_{ji}, x_{ki}\right) $$
(7)

where p is the dimension of \({\boldsymbol{x}}\) and Q(·) is usually assumed to be Gaussian as:

$$ Q\left({\theta_i, x_{ji} ,x_{ki}} \right) = \emph{exp} \left( {-\theta_i d_i^2} \right), \quad d_i =\left| {x_{ji} -x_{ki} } \right| $$
(8)

The linear predictor of kriging method is formulated as:

$$ \hat{g}\left( {\boldsymbol{x}} \right)=c^T\left( {\boldsymbol{x}} \right) {\boldsymbol{Y}} $$
(9)

where \(c^{T}({\boldsymbol{x}})\) is the coefficient vector and \({\boldsymbol{Y}}\) is the vector of the observations at the sample sites (\({\boldsymbol{x}}_{1},{\ldots},{\boldsymbol{x}}_{n}\)):

$$ {\boldsymbol{Y}} =\left[ {{\begin{array}{*{20}c} {Y\left( {{\boldsymbol{x}}_1 } \right)} \hfill & \cdots \hfill & {Y\left( {{\boldsymbol{x}}_n } \right)} \hfill \\ \end{array} }} \right]^T $$
(10)

By minimizing the prediction variance \(\sigma_t^2 \):

$$ \sigma _t^2 =E\left[ {\left({\hat{g}\left( {\boldsymbol{x}} \right)-Y} \right)^2} \right] $$
(11)

with respect to the coefficient vector \(c^{T}({\boldsymbol{x}})\), the best linear unbiased predictor (BLUP) is solved as (Lophaven et al. 2002):

$$\begin{array}{rll} \hat{g}\left( {\boldsymbol{x}} \right)&=&{\boldsymbol{r}}^T {\boldsymbol{R}}^{-1}{\boldsymbol{Y}}-\left( {{\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}{\boldsymbol{r}}-{\boldsymbol{f}}} \right)^T\\ &&\times\,\left( {{\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}{\boldsymbol{F}}} \right)^{-1}\left( {{\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}{\boldsymbol{Y}}} \right) \end{array}$$
(12)

where

$$ {\boldsymbol{r}}=\left[ {{\begin{array}{*{20}c} {R\left( {{\boldsymbol{\theta}},{\boldsymbol{x}}_1 ,{\boldsymbol{x}}} \right)} \hfill & \cdots \hfill & {R\left( {{\boldsymbol{\theta}},{\boldsymbol{x}}_n ,{\boldsymbol{x}}} \right)} \hfill \\ \end{array} }} \right]^T $$
(13)
$$ {\boldsymbol{R}}=\left[ {{\begin{array}{*{20}c} {R\left( {{\boldsymbol{\theta}},{\boldsymbol{x}}_1 ,{\boldsymbol{x}}_1 } \right)} \hfill & \cdots \hfill & {R\left( {{\boldsymbol{\theta}},{\boldsymbol{x}}_1 ,{\boldsymbol{x}}_n } \right)} \hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill \\ {R\left( {{\boldsymbol{\theta}},{\boldsymbol{x}}_n ,{\boldsymbol{x}}_1 } \right)} \hfill & \cdots \hfill & {R\left( {{\boldsymbol{\theta}},{\boldsymbol{x}}_n ,{\boldsymbol{x}}_n } \right)} \hfill \\ \end{array} }} \right] $$
(14)
$$ {\boldsymbol{F}}=\left[ {{\begin{array}{*{20}c} {f_0 \left( {{\boldsymbol{x}}_{\rm {\bf 1}} } \right)} \hfill & \cdots \hfill & {f_0 \left( {{\boldsymbol{x}}_{\boldsymbol{n}} } \right)} \hfill \\ \cdots \hfill & \cdots \hfill & \cdots \hfill \\ {f_m \left( {{\boldsymbol{x}}_{\rm {\bf 1}} } \right)} \hfill & \cdots \hfill & {f_m \left( {{\boldsymbol{x}}_{\boldsymbol{n}}} \right)} \hfill \\ \end{array} }} \right]^T $$
(15)
$$ {\boldsymbol{f}}=\left[ {{\begin{array}{*{20}c} {f_0 \left( {\boldsymbol{x}} \right)} \hfill & \cdots \hfill & {f_m \left( {\boldsymbol{x}} \right)} \hfill \\ \end{array} }} \right]^T $$
(16)

2.4 Bayesian neural network method

MacKay (1991) developed a Bayesian framework for neural network computing. Despite of its low computational efficiency, the uncertainties introduced by the neural network can be calculated mathematically by applying this method to the traditional multi-layer artificial neural network. The uncertainties are usually described by the variances of the output measures. This is the reason why we include this method in this research.

In Bayesian neural network method, the prior probability density function of the weighting vector \({\boldsymbol{W}}\) (here we use uppercase and lowercase letters to distinguish a random variable and its value, following the convention of symbols used in probability and statistics studies (Feller 1968)) in a neural network is assumed to be Gaussian as:

$$ p_{\boldsymbol{W}} \left( {\boldsymbol{w}} \right)=\left( {2\pi \omega ^2} \right)^{-\frac{N_W}{2}}\exp \left( {-\frac{\left\| {\boldsymbol{w}} \right\|^2}{2\omega ^2}} \right) $$
(17)

where ω is the expected scale of weight and N W is the number of weighting factors in the neural network. The conditional probability density function of the output Y from the neural network, with a given input vector \({\boldsymbol{x}}\) and a given weighting vector \({\boldsymbol{w}}\), is also assumed to be Gaussian as:

$$ p_{Y\vert {\boldsymbol{x}, \boldsymbol{w}}} \left( y \right)=\big( {2\pi \sigma ^2} \big)^{-\frac{N_Y}{2}}\!\exp \left(\! {-\frac{\left\| {Y-f_N \left( {{\boldsymbol{x}},{\boldsymbol{w}}} \right)} \right\|^2}{2\sigma ^2}} \!\right) $$
(18)

where σ is the inherent noise level of the training data, N Y is the number of output parameters in the neural network, and f N is the neural network relationship.

According to Bayes’ theorem, the posterior probability density function of the weighting vector \({\boldsymbol{w}}\) is calculated by:

$$\begin{array}{rll} p_{{\boldsymbol{w}}\vert {\boldsymbol{D}}} \left( {\boldsymbol{w}} \right)&=&\frac{p_{\boldsymbol{w}} \left({\boldsymbol{w}} \right)p\left({\boldsymbol{D}}\vert {\boldsymbol{w}} \right)}{p\left( {\boldsymbol{D}}\right)}\\&=&\frac{p_{\boldsymbol{W}} \left( {\boldsymbol{w}} \right)\prod\limits^{n}_{i=1}P_{Y_i \vert \boldsymbol{x}_i,\boldsymbol{w}}(y)} {\int_{\Re}p_{\boldsymbol{W}}({\boldsymbol{w}})\prod\limits^{n}_{i=1}P_{Y_i \vert \boldsymbol{x}_i, \boldsymbol{w}}(y)d{\boldsymbol{w}}} \end{array}$$
(19)

where \({\boldsymbol{D}}\) is the training data, \(p({\boldsymbol{D}} \vert {\boldsymbol{w}})\) is the probability that the training data are obtained through the neural network with the given weighting vector \({\boldsymbol{w}}\), \(p({\boldsymbol{D}})\) is called evidence, n is the number of samples in the training data, and \(\Re\) is the value domain of the weighting vector \({\boldsymbol{W}}\). The predicted mean of the output Y for a new input vector \({\boldsymbol{x}}_{n+1}\) is obtained as the mathematical expectation through:

$$ E\left( {Y^{n+1} }\right)=\int_\Re f_N \left({{\boldsymbol{x}}_{n+1}, {\boldsymbol{w}}} \right) p_{{\boldsymbol{w}}\vert {\boldsymbol{D}}} \left( {\boldsymbol{w}} \right)d{\boldsymbol{w}} $$
(20)

3 Sample quality merits

In computer experiments, space filling design is usually used due to the system complexity (Jin et al. 2001). The general idea of a space filling design is to generate a series of points that can be uniformly scattered in the design space. Some popular space filling design methods include orthogonal array (OA) (Hedayat et al. 1999), Latin hypercube sampling (Mckay et al. 1979), uniform design (Fang et al. 2000), etc. The space filling design is independent from the metamodeling methods and some criteria were developed in the past decades for evaluating a space filling design method, such as least integrated mean squared error (IMSE), maximum entropy, minimum maximin distance and maximum minimax distance (Fang et al. 2006). A recent study also shows that it is risky to select the design of experiments based on a single measure (Goel et al. 2008). In this research, we selected three merits that play important roles in influencing the metamodeling performance while can be easily obtained or calculated in actual applications. The three selected merits are: sample size, sample uniformity and sample noise.

3.1 Sample size

Sample size refers to the number of data points in a dataset. It is calculated based on the following equations (Jin et al. 2001):

$$\mbox{Low Dimension:}\;3l\cdot \left( {p+1} \right)\cdot \left( {p+2}\right)$$
(21)
$$\mbox{High Dimension:}\;l\cdot \left( {p+1} \right)\cdot \left( {p+2} \right) $$
(22)

where \({l}=\mbox{0.5}\sim \mbox{2}\) is a scaling parameter and p is the dimension of the input parameter.

3.2 Sample uniformity

Uniformity is a measure to evaluate how uniform a set of points is scattered in a space. Let \(D_{n} = \{ {\boldsymbol{x}}_{1}, {\boldsymbol{x}}_{2},\ldots, {\boldsymbol{x}}_{n}\}\) be a set of design points in the p-dimensional unit cube C p and \(\left[{\boldsymbol{0}},{\boldsymbol{x}} \right)=\left[ {0,x_1} \right)\times \left[ {0,x_2} \right),\cdots,\times \left[ {0,x_p} \right)\) is the Cartesian space defined by \({\boldsymbol{x}}\). The number of points of D n falling in the Cartesian space \([{\boldsymbol{0}}, {\boldsymbol{x}})\) is denoted by \(N(D_{n}, [{\boldsymbol{0}}, {\boldsymbol{x}}))\). The ratio \(N(D_{n}, [\boldsymbol{0},\boldsymbol{x}))/n\) should be as close to the volume of the Cartesian space Vol \(([\boldsymbol{0}, \boldsymbol{x}))\) as possible. Thus, the L q star discrepancy is defined as (Hua and Wang 1981):

$$ D_q \left( {D_n} \right)=\left\{ \int_{C^p} \left| \frac{N(D_n, [\boldsymbol{0},\boldsymbol{x}))}{n} - \emph{Vol} ([\boldsymbol{0}, \boldsymbol{x}))\right|^{q}\right\}^{\frac{1}{q}} $$
(23)

where q is usually selected as 2. The value of L q star discrepancy ranges from 0 to 1 to describe the cases from the extreme uniform to the extreme non-uniform.

Several modified L q discrepancies were proposed by Hickernell (1998) and the centered L 2 discrepancy has been selected for this study because of its appealing properties such as it becomes invariant under reordering the runs. This evaluation measure can be obtained by:

$$\begin{array}{lll} &&{\kern-2pt} \left({\it CD}\left(D_n \right) \right)^2\\ &&\,\,\,= \left(\! \frac{13}{12} \!\right)^p\!-\!\frac{2}{n}\sum\limits_{j=1}^n \prod\limits_{i=1}^p \left[\! 1+\frac{1}{2}\left| x_{ji} -0.5 \right|-\frac{1}{2}\left| x_{ji} -0.5 \right|^2 \!\right]\!\!\!\!\!\!\\ &&\,\phantom{=} +\frac{1}{n^2}\sum\limits_{k=1}^n \sum\limits_{j=1}^n \prod\limits_{i=1}^p \left[1+\frac{1}{2}\big| x_{ki} -0.5 \big| + \frac{1}{2}\left| x_{ji} -0.5 \right| \right. \\ && \qquad\;\;{\kern80pt} \left. - \frac{1}{2}\left| x_{ki} - x_{ji} \right|\right] \end{array}$$
(24)

The value of centered L 2 discrepancy also ranges from 0 to 1 representing the cases from the extreme uniform to the extreme non-uniform.

3.3 Sample noise

The sample data created using a mathematical function, \(f({\boldsymbol{x}})\), do not have any noise. To consider the influence of noises, in this research artificial noises are added to the response values of the output parameter as:

$$ Y=f\left( {\boldsymbol{x}} \right)+l{'}\delta $$
(25)

where \({l}{'} =\mbox{0\% }\sim \mbox{15\%}\) is a scaling parameter and δ is a random number sampled from the standard Gaussian distribution N ∼ (0, 1). In developing engineering applications, multiple tests with the same input parameter values need to be conducted to determine the noise level.

4 Performance measures

In this research, the performance of a metamodel is evaluated from the following four aspects: (1) prediction accuracy, (2) prediction confidence, (3) robustness of the metamodeling method, and (4) computing efficiency. The first three measures are related to the predictability of a metamodel while the last one is related to the regression efficiency to build the metamodel.

4.1 Accuracy

Many accuracy measures have been developed in the past, such as mean squared error (MSE), root mean squared error (RMSE), R-square, relative average absolute error (RAAE) and relative maximum absolute error (RMAE). In our experiments, the RMSE of the prediction dataset is selected to evaluate prediction accuracy:

$$ \emph{RMSE}=\sqrt {\frac{\sum\limits_{i=1}^n {\left( {y_i -\hat{g}_{i}} \right)^2}}{n}} $$
(26)

where y i is the real output value at the point \({\boldsymbol{x}}_{i}\), \(\hat{g}_{i}\) is the estimated output value at the point \({\boldsymbol{x}}_{i}\) and n is the number of points in the prediction dataset. The smaller the RMSE is, the better a metamodel is.

4.2 Confidence

The uncertainties introduced by the metamodeling methods in regression are carried on to prediction. To better understand the predictability, the average confidence level of the prediction dataset is used as a measure to evaluate the confidence of a prediction. The prediction variance is used as the confidence measure. The smaller the prediction variance is, the more confident a metamodel is.

  1. 1.

    For a general linear system, including the multivariate polynomial method and the radial basis function method, the prediction variance is calculated by:

    $$ \sigma_t^2 =\sigma ^2\left[ {1+{\boldsymbol{x}}^T\left( {{\boldsymbol{X}}^T{\boldsymbol{X}}} \right)^{-1}{\boldsymbol{x}}} \right] $$
    (27)

    where \({\boldsymbol{x}}\) is the new design point, \({\boldsymbol{X}}\) is the matrix of training data inputs, and σ is the inherent noise level of training data outputs, which can be estimated by:

    $$ \hat{\sigma }^2=\frac{\sum\limits_{i=1}^n(Y_i - \hat{g}_i)^{2}}{n-m-1} $$
    (28)

    where n is the number of training samples and m is the number of basis functions in the general linear regression models (e.g., (2) and (3) excluding the first constant terms).

  2. 2.

    For the kriging method, the prediction variance can be calculated by (Lophaven et al. 2002):

    $$ \sigma _t^2 =\sigma ^2\left( {1+{\boldsymbol{u}}^T\left( {{\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}{\boldsymbol{F}}} \right)^{-1}{\boldsymbol{u}}-{\boldsymbol{r}}^T{\boldsymbol{R}}^{-1}{\boldsymbol{r}}} \right) $$
    (29)

    where

    $$ {\boldsymbol{u}}={\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}{\boldsymbol{r}}-{\boldsymbol{f}} $$
    (30)

    and σ is estimated by:

    $$ \hat{\sigma}^2=\frac{1}{m}\left( {{\boldsymbol{Y}}- {\boldsymbol{F}}{\boldsymbol{\beta}}^\ast } \right)^T{\boldsymbol{R}}^{-1}\left( {{\boldsymbol{Y}}- {\boldsymbol{F}}{\boldsymbol{\beta}}^\ast } \right) $$
    (31)

    where \({\boldsymbol{\beta}}^\ast\) is the generalized least squares fit to the coefficients. \({\boldsymbol{\beta}}^\ast\) is calculated by:

    $$ {\boldsymbol{\beta}}^\ast =\left( {{\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}{\boldsymbol{F}}} \right)^{-1}{\boldsymbol{F}}^T{\boldsymbol{R}}^{-1}{\boldsymbol{Y}} $$
    (32)
  3. 3.

    For the Bayesian neural network method, the prediction variance is hard to be calculated analytically. In this work, it is estimated based on Gaussian approximation (Bishop 1995) using:

    $$ \sigma _t^2 =\sigma ^2+{\boldsymbol{g}}^T{\boldsymbol{A}}^{-1}{\boldsymbol{g}} $$
    (33)

    where σ is the inherent noise level of training data outputs, \({\boldsymbol{g}}\) is the gradient of neural network output in terms of weighting factors at the most probable point \({\boldsymbol{w}}_{MP}\) calculated by:

    $$ {\boldsymbol{g}}=\left. {\nabla _{\boldsymbol{w}} y} \right|_{{\boldsymbol{w}}_{MP}} $$
    (34)

    and \({\boldsymbol{A}}\) is the Hessian matrix of neural network at the most probable point \({\boldsymbol{w}}_{MP}\) calculated by:

    $$ {\boldsymbol{A}}=\nabla \nabla S_{MP} $$
    (35)

    where S MP is defined as:

    $$ S_{MP} =\frac{1}{2\sigma^2}\sum\limits_{i=1}^n \|Y_i - \hat{g}_i\|^{2} + \frac{1}{2\omega^2} \|{{\boldsymbol{w}}_{MP}}\|^{2} $$
    (36)

4.3 Robustness

The robustness is measured by the variance of RMSE over several experiments for the same sampling configuration (Jin et al. 2001). The standard deviation of RMSE is calculated by:

$$ \emph{STD}(\emph{RMSE})= \sqrt{\frac{{\sum\limits_{i=1}^n \left(\emph{RMSE} - \overline{\emph{RMSE}}\right)}^2}{n-1}} $$
(37)

where n is the number of experiments for the same configuration. The smaller the STD(RMSE) is, the more robust a metamodel is.

4.4 Efficiency

The efficiency is measured by the CPU time consumed in the regression process of a metamodel. The less time the regression process spends, the more efficient a metamodel is.

5 Design of numerical experiments

The testing problems are selected from Hock and Schittkowski (1981) and Jin et al. (2001). We have selected three highly non-linear two-dimensional problems to study the behaviors of the different metamodeling methods in the low dimensional space and three 10-dimensional problems in the high dimensional space.

  1. 1.

    Low dimensional space

    $$\begin{array}{rll} f\left( {\boldsymbol{x}} \right)&=&\sin \left( {x_1 +x_2 } \right)+\left( {x_1 -x_2 } \right)^2\\ &&-\,1.5x_1 +2.5x_2 +1 \end{array}$$
    (38)
    $$ f\left( {\boldsymbol{x}} \right)=\left[ {30+x_1 \sin \left( {x_1 } \right)} \right]\cdot \left[ {4+exp\left( {-x_2^2 } \right)} \right] $$
    (39)
    $$ f\left( {\boldsymbol{x}} \right)=\sin \left( {\frac{\pi x_1 }{12}} \right)\cos \left( {\frac{\pi x_2 }{16}} \right) $$
    (40)
  2. 2.

    High dimensional space

    $$f({\boldsymbol{x}})=\sum\limits_{i=1}^{10} \left[\! ln^2 (x_i - 2) + ln^2 (10 - x_i) \!\right]\! -\! \prod\limits_{i=1}^{10} x_1^2 $$
    (41)
    $$f({\boldsymbol{x}})=\sum\limits_{i=1}^{10} x_i \left(c_i + ln\frac{x_i}{\sum\limits_{i=1}^{10}x_i} \right) $$
    (42)
    $$f({\boldsymbol{x}})=\sum\limits_{i=1}^{10} \emph{exp} (x_i) \left\{c_i + x_i - ln \left[\!\sum\limits_{j=1}^{10} \emph{exp} (x_j)\!\right]\!\right\} $$
    (43)
    $$\begin{array}{rll} c_1 ,c_2 ,...,c_{10} &= &6.089,17.164,34.054,5.914,24.721,\\ && 14.986,24.100,10.708,26.662,22.179 \end{array}$$

The design points for training are generated by the Latin hypercube sampling method or the random sampling method depending on the experimental requirements. For space filling design, the Latin hypercube sampling method can be used to generate uniform designs to study the impact of sample size and noise in the comparative study, whereas the random sampling method can be employed to create unevenly distributed samples to study the impact of sample uniformity. The number of the generated sample points can be adjusted by changing the scaling parameter l in (21) and (22). The noise level can also be adjusted by changing the scaling parameter l ′ in (25). Because the uniformity can only be measured after a set of samples is generated, we first try to generate a sample set then test if its uniformity falls into the range of study. If it does, this sample data will be included. Otherwise new sample data needs to be generated. The prediction dataset is created with additional validation points generated uniformly in the design space for each testing problem. In this work, we use 225 (i.e., 15 × 15 for x 1 and x 2) grid points in the design space to test the low dimensional problems, and 900 points created using Latin hypercube sampling method to test the high dimensional problems. Because of the randomness of the sample data generated by using the same sampling configuration (e.g., to use the Latin hypercube sampling method to generate 50 design points for training), each configuration in an experiment (e.g., sample size changes from 18 to 72 and all other sampling parameter values are kept unchanged) will be tested many times (75–500). The mean value of a performance measure of a metamodeling method over these test runs for a configuration is used to represent the value of the performance measure of the metamodeling method for the configuration. The number of test runs is determined when the changes of the values of the performance measures of a metamodeling method over all the configurations in an experiment become stable. The configuration parameters of each of the metamodeling methods are first set with their initial values (Table 1) and then adjusted during each run with optimization.

Table 1 Configuration parameters and their initial values of the metamodeling methods
Full size table

Since the six testing problems given in (38–43) are classified into two groups: low dimensional problems and high dimensional problems, comparative studies are also carried out considering these two groups of testing problems. For the three testing functions in each group, the boundaries of the input parameters are selected in such a way that changes of the three output functions are in the same scale and comparable. The mean value of the three performance measures obtained using the three testing functions is selected as the final performance measure in the comparative study.

All the testing cases were run on the West Grid Linux server and all the metamodeling methods were written as MATLAB programs. The codes for the multivariate polynomial method and the radial basis function method were developed directly on MATLAB. The codes for running the kriging method were developed based on DACE (Lophaven et al. 2002) and the codes for running the Bayesian neural network method were developed based on NETLAB (Ian 2004).

6 Results and comparative study

6.1 Sample size

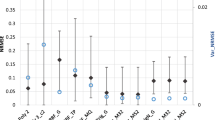
The impact of sample size is examined by using the Latin hypercube sampling method to generate uniformly scattered samples of different sizes in the design space. In the Figs. 1, 2, 3, 4, 5, 6, the multivariate polynomial method is denoted as ply, the radial basis function method is denoted as rbf, the kriging method is denoted as krg, and the Bayesian neural network method is denoted as bnn.

Fig. 1
figure 1

Impact of sample size for low dimensional problems

Full size image
Fig. 2
figure 2

Impact of sample size for high dimensional problems

Full size image
Fig. 3
figure 3

Impact of sample uniformity for low dimensional problems

Full size image
Fig. 4
figure 4

Impact of sample uniformity for high dimensional problems

Full size image
Fig. 5
figure 5

Impact of sample noise for low dimensional problems

Full size image
Fig. 6
figure 6

Impact of sample noise for high dimensional problems

Full size image

For the low dimensional problems (Fig. 1), when the sample size is increased, the accuracy, confidence and robustness will be increased whereas the efficiency will be decreased. For the accuracy, most of the metamodeling methods do not show good performance when the sample size is low except for the multivariate polynomial method. This could be an indication that the sample size is not sufficient for the metamodeling methods to capture the general features of the problems. Regarding the rate of accuracy performance improvement, the kriging method is the fastest and the multivariate polynomial method is almost not affected when the sample size is above the intermediate level. For the confidence, the kriging method is the worst when the sample size is low. This is because that the kriging method tries to interpolate data. When the sample size is increased to the intermediate level, the confidence performance of the kriging method and the radial basis function method is increased to an acceptable level. The confidence performance of the Bayesian neural network method is the best among all the four metamodeling methods. However, regarding the rate of the confidence performance improvement, the kriging method is the fastest whereas the multivariate polynomial method and the Bayesian neural network method are not so affected by the sample size. For the robustness, the multivariate polynomial method is the most robust among all the four metamodeling methods and the kriging method becomes as robust as the multivariate polynomial method when the sample size is sufficiently high. Regarding the rate of robustness performance improvement, it seems that the radial basis function method and the kriging method follow one pattern of change whereas the multivariate polynomial method and the Bayesian neural network method follow another. For the efficiency, it is obvious that the Bayesian neural network method is an order slower than the other metamodeling methods and its efficiency performance is decreased at a faster rate.

For the high dimensional problems (Fig. 2), the basic performance trends are similar to those in the low dimensional problems. For the accuracy, the Bayesian neural network method and the radial basis function method are poor compared with the kriging method and the multivariate polynomial method. The accuracy performance of the kriging method is the best among all the four metamodeling methods, especially when the sample size is high. Regarding the rate of accuracy performance improvement, the kriging method is also the fastest. For the confidence, the Bayesian neural network method is still the best among all the four metamodeling methods whereas the multivariate polynomial method is the worst and not sensitive to the change of the sample size. For the robustness, the multivariate polynomial method is still the most robust one among all the four metamodeling methods. The robustness performance of the radial basis function method is almost not affected when the sample size is above the intermediate level. For the efficiency, the radial basis function method and the kriging method will increase the regression time a lot when the sample size is increased. Especially for the radial basis function method, its efficiency performance is decreased considerably when the sample size is high and at a faster rate than the other metamodeling methods. However, the efficiency performance of the multivariate polynomial method and the Bayesian neural network method are not so affected by the sample size.

The study on influence of sample size in metamodeling also plays an important role in the design of experiments to select the proper number of samples considering costs of the experiments. When the performance is not significantly influenced by the sample size, creation of a small number of sample data should be considered to reduce the cost of design experiments.

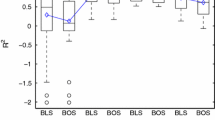
6.2 Sample uniformity

The impact of sample uniformity is examined when the sample size is kept the same at a low value and the random sampling method is used to generate data with different uniformities.

For the low dimensional problems (Fig. 3), when the central discrepancy is increased, representing that the uniformity is decreased, the accuracy and robustness will normally decrease whereas all the other performance measures are not so affected. For the accuracy, the multivariate polynomial method is the best among all the four metamodeling methods. The accuracy performance of the kriging method is almost not affected. For the robustness, the multivariate polynomial method is still the best among all the four metamodeling methods whereas the Bayesian neural network method is the worst. However, the robustness performance of the multivariate polynomial method is also decreased rapidly when the samples become highly non-uniform.

For the high dimensional problems (Fig. 4), the basic performance trends are similar to those in the low dimensional problems but with lower scales of changes. For the accuracy, the performance of the kriging method is the best among all the four metamodeling methods and it is not affected by the change of the uniformity. For the robustness, the multivariate polynomial method is still the best among all the four metamodeling methods. The robustness performance of the Bayesian neural network method is the most affected one and is decreased at a faster rate than other metamodeling methods.

6.3 Sample noise

The impact of sample noise is examined by using the Latin hypercube sampling method to generate uniformly scattered samples in the design space and adding artificial noises to the response data.

For the low dimensional problems (Fig. 5), when the noise level is increased, the accuracy and confidence will be decreased. The robustness measures exhibit different patterns for different metamodeling methods and the efficiency is not so affected. For the accuracy, the radial basis function method and the kriging method are the most affected. Especially, the accuracy performance of the radial basis function method is decreased at a faster rate than other metamodeling methods. The multivariate polynomial method and the Bayesian neural network method are almost not affected by the change of the noise level. For the confidence, the performance of the kriging method and the radial basis function method is decreased fast, especially the kriging method. The confidence performance of the multivariate polynomial method and the Bayesian neural network method is not affected. For the robustness, the multivariate polynomial method is still the best among all the four metamodeling methods and is not affected by the change of the noise level whereas the radial basis function method and the kriging method are the most affected. It should be noted that only the normal kriging method was tested in our comparative study. Since the normal kriging method tries to interpolate the sample data, this method is sensitive to the noises. Non-interpolative kriging method with nugget effect has been developed to smooth the nose data (Montès 1994). Our research is limited to the normal kriging method.

For the high dimensional problems (Fig. 6), when the noise level is increased, the accuracy, confidence and robustness will normally be decreased at a slower rate. The efficiency is not affected.

7 Discussions

By comparing the results achieved so far, we tentatively summarize all the evaluation results into a table (Table 2), so that it can help engineers in the selection of the metamodeling methods when sample quality merits are available.

Table 2 Comparison results
Full size table

Selection of an appropriate metamodeling method is conducted through four steps: (1) to determine the performance measures to be considered, (2) to obtain the sample quality merits, (3) to find the recommended metamodeling methods considering each of the sample quality merits obtained in step (2), and (4) to select the metamodeling methods that best satisfy the performance requirements. For example, suppose we are going to develop a metamodel for a low dimensional problem. For this metamodel, accuracy and efficiency are selected as the performance measures. From the sample data, the sample quality merits are obtained as: low sample size, high uniformity and high noise. By using Table 2, the following metamodeling methods (Table 3) are recommended considering each of the sample quality merits.

Table 3 Recommended metamodeling methods
Full size table

From Table 3, we can see that the multivariate polynomial method (ply) will be selected as the first candidate for metamodeling, since it tops most of the evaluation rankings in Table 3.

Due to the complex nature of the relationships among metamodeling methods, sample quality merits, and performance measures, the results achieved in this research can only be used as the generic guidelines for the selection of metamodeling methods.

8 Summary

In this research, we designed a series of experiments to examine the relationships between the sample quality merits and the performance measures of several metamodeling methods. By artificially adjusting the sample quality merits through changing sample data, we observed how the performance measures of each of the metamodeling methods are influenced. In addition, we also ranked the different metamodeling methods considering the sample quality merits and the performance measures. These results can serve as the general guidelines for engineers in selecting the effective metamodeling methods based on the available sample data and the performance requirements.

Significance and contributions of this research are summarized as follows.

  1. (1)

    Quantitative measures, instead of qualitative ones, are used in this comparative study of metamodeling techniques to evaluate the characteristics of the sample data. The result from this research can show how the changes of the sample quality merits quantitatively influence the changes of the performance measures of the different metamodeling methods.

  2. (2)

    In addition to the popular metamodeling methods, the Bayesian neural network method, which is rarely used in metamodeling, has been selected in this work and compared with other metamodeling methods for the first time. The Bayesian neural network method is more effective compared with the traditional neural network method when the uncertainties in the metamodel have to be considered.

  3. (3)

    A simple guideline to select candidate metamodeling methods based on the sample quality merits and the performance requirements has also been proposed in this work.

A number of issues need to be further addressed in our future work. (1) More metamodeling methods, including the variations of the popular metamodeling methods (e.g., the nugget kriging method), should be studied because some of the problems can be better solved by these methods. (2) Some measures to evaluate the metamodel performance can be further improved. For example, cross-validation or predicted R-squared may be considered in the future to evaluate the accuracy of prediction. (3) Weighing factors of the performance measures, representing the importance of these measures, should be considered in the decision-making process to select the best metamodeling method. (4) Comparative study considering multiple quality merits and multiple performance measures simultaneously should be carried out. (5) More sample quality merits and performance measures should be considered.