1 Introduction

The design of transonic airfoils for civil aviation applications has been a major engineering challenge in the last fifty years. The design process has been aided significantly by improvements in experimental methods and facilities, which led initially to the design of supercritical airfoils (Whitcomb 1974). These airfoils have good transonic behavior while maintaining acceptable performance at lower speeds. A description of all the development phases of the supercritical airfoils can be found in Harris (1990).

Advances in computational methods applicable to transonic flow (Jameson 1974; Drela and Giles 1987) have allowed engineers to analyze and evaluate candidate designs without the need for prototype construction and subsequent testing in the wind tunnel. Furthermore, the recent development of aerodynamic shape optimization techniques has provided designers with a tool to obtain airfoil shapes with the desirable performance characteristics. One of the first such methods, which is based on control theory, was developed by Jameson (1988). Recently, researchers have attempted to perform aerodynamic shape optimization using evolutionary algorithms (Jones et al. 1998; Giannakoglou 2002).

Aircraft noise has been a major source of noise pollution since the beginning of the utilization of jet engines in civil transport aircraft. The aircraft noise produced during take-off and landing causes considerable nuisance to the population living near the airports. Airframe noise, engine noise, and the noise generated due to the interference between engine and airframe comprise the main components of aircraft noise. In recent years, statutory limits regarding noise levels have been set by the International Civil Aviation Organization (ICAO 2008). At the same time, considerable research effort has been made towards reducing aircraft noise. For example, the introduction of the high-bypass ratio turbofan engine has significantly reduced the amount of engine radiated noise.

Airframe noise is generated through the interaction of turbulent flows with sharp-edged bodies (Howe 1978), e.g., lifting surfaces. The highest levels of airframe noise occur while the aircraft is in the final approach to landing (Lilley 2001). In this case, the landing gear and high lift devices, e.g., trailing edge flaps and leading edge slats, are the main sources of airframe noise. The trailing edge noise is another source of airframe noise; it becomes the dominant source for a clean wing configuration, i.e., an aircraft with the high lift devices and the landing gear stowed.

If one of the design requirements is to obviate the need for high lift devices, the minimization of the trailing edge noise becomes a significant part of the aerodynamic shape optimization problem. The prediction of the trailing edge noise can be done through the computation of the far-field noise intensity per unit volume of acoustic sources at the trailing edge of a wing using the equation derived in Goldstein (1976) and later modified in Lilley (2001). A formulation which is easy to implement in a simulation-based optimization problem was later derived in Hosder et al. (2010).

In the current paper, the aerodynamic and aeroacoustic shape optimization problem is treated using a multi-objective approach. The goal is to design a transonic airfoil with low drag during cruise and low levels of trailing edge noise during the approach to landing. The results presented in Hosder et al. (2010) and Jouhaud et al. (2007) reveal that there is a trade-off between the aforementioned objectives, thus, there is no single globally optimal solution. For this reason, it was decided to solve this optimization problem using a multi-objective approach. During the last fifteen years, various design methodologies have been utilized by researchers to solve aerospace design optimization problems (Sobieszczanski-Sobieski and Haftka 1997; Jones et al. 1998; Leifsson et al. 2006).

The flow analysis was performed using computational fluid dynamics (CFD). The CFD results obtained at specific points within the design variable space were subsequently utilized in order to build surrogate models for the objective functions and constraints of the optimization problem. In this way, the computational time required to solve the problem could be signicantly reduced (Yang et al. 2002; Jin 2005; Wang et al. 2011).

The main objective of the current paper is to demonstrate the effectiveness and efficiency of an optimization framework based on swarm intelligence and surrogate models when applied to a multi-objective optimization problem. The general definition of a multi-objective optimization problem, the multi-objective optimizer, and the surrogate models utilized in this research project are discussed in Section 2. The theoretical background of the trailing edge noise calculation is presented in Section 3. The shape optimization procedure is described in Section 4. The optimization results are presented in Section 5, in addition to a comparison between selected Pareto-optimal airfoil sections. Finally, conclusions and some directions for future research are provided in Section 6.

2 Components of multi-objective design optimization framework

2.1 Multi-objective optimization

The general multi-objective optimization problem, assuming minimization of the objective functions, can be stated as follows:

$$ \label{eq1} \mbox{Minimize}\quad f_i ({\rm {\bf x}}),\quad i=1,...,I $$
(1)
$$ \label{eq2} \mbox{subject}\;\mbox{to}\quad g_m ({\rm {\bf x}})\le 0,\quad m=1,...,M $$
(2)
$$ \label{eq3} h_n ({\rm {\bf x}})=0,\quad n=1,...,N $$
(3)

where

$$ \textbf{x }(x_{1}, x_{2},...,x_{D}), x_{jl} \le x_{j} \le x_{ju}, j = 1,...,D. $$

In unconstrained multi-objective optimization problems, a solution vector A dominates another solution vector B, if and only if the following two conditions for Pareto dominance are satisfied:

  • The objective vector that corresponds to solution A (x A ) is no worse than the objective vector that corresponds to solution B (x B ) in all objectives.

  • Solution A is strictly better than solution B in at least one objective.

If x A is not dominated by any other solution, it is called a Pareto-optimal solution. The corresponding objective function vector belongs to the set of vectors that comprise the Pareto front. In constrained problems, x A constraint-dominates x B if any of the following conditions are satisfied (Deb 2001):

  • Both x A and x B are feasible and x A dominates x B , based on the aforementioned conditions for Pareto dominance.

  • Both x A and x B are infeasible but x A has a smaller constraint violation.

  • Solution x A is feasible and solution x B is not.

The constraints listed in (2) and (3) can have a significant impact on the Pareto front and the corresponding Pareto-optimal set. Parts of the unconstrained Pareto front, or in some cases the entire unconstrained Pareto front, might become infeasible in the presence of constraints. Furthermore, constraints might be active in different regions of the search space. A multi-objective optimizer needs to be capable of handling the additional search requirements of a constrained optimization problem.

2.2 Description of the ACMOPSO algorithm

The Pareto-optimal solutions of the multi-objective design problem were obtained using the Adaptive Coevolutionary Multi-Objective Particle Swarm Optimizer (ACMOPSO), which was presented in Kotinis (2011). ACMOPSO explores the design variable space using the search mechanism of PSO combined with random mutation. The swarm is divided into a number of equi-sized smaller swarms at the end of each algorithmic iteration; each of these swarms focuses on a specific region of the computed Pareto front, which consists of the non-dominated solutions stored in an external archive. The latter is divided into a number of segments equal to the number of swarms. Two members of the Pareto-optimal set within each segment are randomly selected to act as leaders of the kth swarm particle for each design variable j:

$$\begin{array}{rll} \label{eq4} v_{kj} (t+1)&=&w\cdot v_{kj} (t)+c_1 \cdot (x_{ndlr1,j} (t)-x_{kj} (t)) \\ &&+c_1 \cdot rand_j (0,1)\cdot (x_{ndlr2,j} (t)-x_{kj} (t)) \end{array}$$
(4)

where v kj is the movement of particle k within the range of j, x ndlr1,j (t) and x ndlr2,j (t) are the jth position coordinates of the two randomly selected leaders, x kj (t) is the corresponding jth position coordinate of the kth particle, w is the inertia weight, c 1 is the social coefficient, and rand j (0,1) is a random number uniformly distributed in (0,1). The kth particle’s position is updated in every iteration (t + 1) by adding the velocity vector over a single time increment to the current position vector:

$$ \label{eq5} {\rm {\bf x}}_k (t+1)={\rm {\bf x}}_k (t)+{\rm {\bf v}}_k (t+1) $$
(5)

This procedure is followed for 80% of the swarm particles. The remaining particles are substituted with randomly selected non-dominated archived solutions, which are subsequently mutated with a mutation rate p mut  = 10%. The inclusion of a mutation operator, combined with particle substitution, enhances the algorithm’s capability to solve problems with multiple local Pareto fronts, and also counterbalances the high selective pressure due to the utilization of a Pareto ranking procedure to manage the external archive. It needs to be mentioned that if the number of non-dominated solutions exceeds the nominal capacity of the archive, the crowding distance operator (Deb et al. 2000) is employed to maintain the solutions that reside in the least crowded areas.

The values of the algorithmic parameters, w and c 1, are adapted on-line for each swarm using the feedback provided by two metrics. The first metric takes into account the effectiveness of each swarm in producing new non-dominated solutions during the current iteration. The second metric represents the overall ability of the swarms to produce solutions capable of entering the external archive.

In the current research project, a parallelized version of ACMOPSO with five swarms was utilized. It was shown in Kotinis (2011) that the utilization of five swarms, in most cases, results in very fast convergence to the true Pareto front. The parallelization process, which involves the computation of the objective functions and constraints, was performed using the OpenMP (Chapman et al. 2008) interface, and specifically a work-sharing parallel do construct. The results reported in Kotinis (2011) regarding an application of the parallelized version of ACMOPSO to an engineering design optimization problem demonstrated near-linear speedup and high parallel efficiency.

2.3 Surrogate models

The approximation of the objective functions and constraints can lead to significant savings in terms of both time and resources utilized in the optimization process. However, it is of the utmost importance to provide surrogate models that are able to generalize well, i.e., provide accurate predictions when presented with previously unseen data. It was decided to compare the effectiveness of different surrogate models for each objective and constraint function of the optimization problem, first, and then select the most appropriate model for each function. For this purpose, the University of Waikato’s open source data mining software WEKA (Hall et al. 2009) was utilized. WEKA provides the user with the capability to evaluate and compare different metamodeling techniques through a very user-friendly interface. Three such techniques were selected and utilized: Artificial neural networks (ANNs), support vector regression (SVR), and linear regression. The effectiveness of each metamodel was assessed using ten-fold cross-validation. A brief description of ANNs and SVR is provided in the following paragraphs. The selection of the aforementioned techniques (ANNs and SVR) was based on a preliminary extensive investigation, which showed that these two methods had the best overall performance in a number of benchmark problems. Linear regression was also tested and utilized wherever its performance was better or even comparable to ANNs and SVR, as it provides a significantly less complex metamodeling solution.

2.3.1 Artificial neural networks

Artificial neural networks have been used extensively across many fields of scientific research. A review of ANN applications and history can be found in Eberhart and Shi (2007). The primary reason for the use of ANNs is their universal approximation capability given an adequate number of hidden nodes. It was proven in Cybenko (1989) that a network with linear output nodes and a single hidden layer of sigmoid nodes is sufficient for uniform approximation of any continuous function in the unit hypercube. Although, there are many types and topologies of ANNs, it was decided to utilize a feedforward fully-connected network consisting of an input layer, a single hidden layer with varying number of sigmoid neurons (nodes), and a linear output layer. A typical feedforward ANN is shown in Fig. 1. The ANNs were trained in WEKA using the backpropagation algorithm (Rumelhart et al. 1986) for a fixed number of epochs (training iterations). Assuming I input nodes, J hidden nodes, a bias node added to the input (I + 1) and to the hidden layer (J + 1), and a single output node, the equation that provides the network prediction y can be written as follows:

$$ \label{eq6} y=\sum\limits_{j=1}^{J+1} {w_j f\left( {\sum\limits_{i=1}^{I+1} {u_{ji} x_i } } \right)} $$
(6)

where u ji is the weight of the connection between input node x i and hidden node h j , w j is the weight of the connection between hidden node h j and the output node, and f is the activation function, which for this specific application corresponds to the sigmoid function:

$$ \label{eq7} f(x)=\frac{1}{1+\mbox{e}^{-x}} $$
(7)
Fig. 1
figure 1

Feedforward ANN with a single hidden layer

Full size image

2.3.2 Support vector regression

Support vector regression (SVR) is a machine learning technique based on the support vector machine (SVM) algorithm developed at AT&T Bell Laboratories by Vapnik and co-workers (Boser et al. 1992). SVR utilizes a nonlinear mapping function, typically based on kernels, in order to map the data from the input variable space to the feature space. Given a data set of training points (features), the algorithm attempts to provide a regression function where the predicted values of the training points are within a specified distance ε from the actual values and also the function is as flat as possible. Because such a function might not exist, slack variables are introduced to the problem to deal with distances larger than ε. The trade-off between flatness and the amount up to which deviations larger than ε are accepted is controlled by a parameter C. A review of SVR can be found in Smola and Schölkopf (2004). The SVR model utilized in WEKA is based on the algorithm presented in Shevade et al. (2000). For the purpose of the current research, the mapping was performed using a kernel based on the universal Pearson VII function (PUK) as suggested in Üstün et al. (2006). The SVR prediction is given through a regression function f as follows:

$$ \label{eq8} f({\rm {\bf x}})=\sum\limits_{i=1}^n {(a_i -a_i^\ast )k({\rm {\bf x}},{\rm {\bf x}}_i )+b} $$
(8)

where a i and \(a_{i}^{\ast}\) are the Lagrange multipliers, 0 ≤ a i , \(_{\thinspace }a_{i}^{\ast } \le C\), and x i is a training point. The PUK kernel function k(x, x i ) is given by the equation:

$$ \label{eq9} k({\rm {\bf x}},{\rm {\bf x}}_i )=\frac{1}{\left[1+\left(\frac{2\sqrt{\|{\rm{\bf x}}-{\rm{\bf x}}_{i}\|^2}\sqrt{2^{1/\omega}-1}}{\sigma}\right)^2\right]^\omega} $$
(9)

where the parameters σ and ω control the shape of the function.

3 Trailing edge noise metric

The basis for the noise metric formulation is the expression derived in (Goldstein 1976). For low Mach numbers, the far-field noise intensity per unit volume of acoustic sources is formulated as:

$$ \label{eq10} I=\frac{\rho_\infty }{2\pi^3c_\infty^2 }\omega_0 u_0^4 \cos^3\beta \frac{D(\theta ,\phi )}{H^2} $$
(10)

where ρ  ∞  is the freestream density, c  ∞  is the freestream speed of sound, ω 0 is the characteristic source frequency, u 0 is the characteristic velocity scale of turbulence, H is the distance to the ground (receiver), β is the trailing edge sweep angle, D(θ, ϕ) is the directivity term, and θ and ϕ are the polar and azimuthal directivity angles (shown in Fig. 2), respectively.

Fig. 2
figure 2

Parameters used in the definition of the far-field noise intensity

Full size image

The directivity term is equal to 2sin2(θ/2)sinϕ. For most conventional wings the sweep angle term can be neglected. Assuming a constant value of the Strouhal relation for turbulent flow ((ω 0 ℓ0 )/u 0 ), as proposed in (Lilley 2001), we can rewrite (10) as:

$$ \label{eq11} I\approx \frac{\rho_\infty }{2\pi^3c_\infty^2 }\ell_0^{-1} u_0^5 \frac{D(\theta ,\phi )}{H^2} $$
(11)

where ℓ0 is the characteristic length scale of turbulence. Using the following expression (Hosder et al. 2010) for a correlation volume per unit span at the trailing edge:

$$ \label{eq12} dV=\ell_0^2 dy $$
(12)

we can integrate (11) over the wing span, b, to obtain the expression for the noise intensity indicator:

$$ \label{eq13} I_{NI} =\frac{\rho_\infty }{2\pi^3c_\infty^2 }\int\limits_0^b {\ell_0 u_0^5 \frac{D(\theta ,\phi )}{H^2}dy} $$
(13)

The noise intensity metric that was proposed in Hosder et al. (2010) models the characteristic turbulent velocity at a spanwise location of the wing trailing edge as equal to the maximum value of the turbulent kinetic energy (TKE) profile at that particular spanwise location:

$$ \label{eq14} u_0 =\max \left( {\sqrt {TKE(n)} } \right) $$
(14)

where n is the direction normal to the wing surface. Similarly, the characteristic length scale of turbulence at a spanwise location can be modeled as:

$$ \label{eq15} \ell_0 =\frac{\max \left( {\sqrt {TKE(n)} } \right)}{\omega } $$
(15)

where ω is the turbulence frequency (specific dissipation rate of TKE) observed at the position of maximum TKE at the spanwise location under consideration. The noise intensity indicator can be scaled using a reference value of the noise intensity (I ref = 10 − 12 W/m2) in order to obtain the following metric for the trailing edge noise (in dB):

$$ \label{eq16} NM(\mbox{dB})=10\log_{10} \frac{I_{\emph{NI}} }{I_{\emph{ref}} }=120+10\log_{10} I_{NI} $$
(16)

It needs to be mentioned that only the upper surface of the airfoil was taken into consideration when computing the noise metric, as the contribution of the lower surface boundary layer to the far-field radiated trailing edge noise is generally minimal; this was also confirmed by the CFD results.

4 Multi-objective shape optimization of transonic airfoil sections

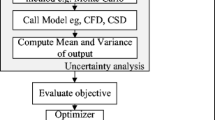
The flowchart of the optimization framework is depicted in Fig. 3. In the following sections, each step is explained and details regarding its implementation are provided.

Fig. 3
figure 3

Flowchart of optimization framework

Full size image

4.1 Selection of operating points

The aircraft is assumed to be at an altitude of 120 m in the approach condition with the receiver located directly below the aircraft, where the noise certification measurements are taken (ICAO 2008). The directivity angles in (13) are set equal to 90°. Therefore H = 120 m and D(θ, ψ) is equal to unity. During cruise the corresponding altitude is 35,000 ft. The mean aerodynamic chord (mac) value was assumed to be equal to 5.67 m, a value typical of transport aircraft. The Mach number was set equal to 0.80 and 0.215 for cruise and approach, respectively. The corresponding Reynolds number values, based on mac, are 35.6·106 and 28.1·106. The angle of attack was assumed to be equal to 2.5° during cruise and 10° during approach.

4.2 Formulation of the multi-objective optimization problem

The goal is to find the airfoil sections that correspond to the solution of the following shape optimization problem: Minimize the noise metric given in (16) during approach (A) and maximize the lift-to-drag ratio during cruise (C). Constraints were imposed on the pitching moment coefficient value during cruise, the lift coefficient value during approach, and the maximum thickness-to-chord ratio of the section. It needs to be mentioned that the RAE-2822 airfoil was used as a baseline design in the optimization procedure. The reason for selecting a subsonic airfoil as a baseline design, i.e., instead of a supercritical airfoil, was to avoid biasing the search towards shapes with good performance in one objective. The problem was formulated as follows:

$$ \label{eq17} \mbox{Minimize}:f_1 ({\rm {\bf x}})=(NM)_A $$
(17)
$$ \label{eq18} \mbox{Maximize}\;f_2 ({\rm {\bf x}})=(C_L /C_D )_C $$
(18)
$$ \label{eq19} \mbox{subject}\;\mbox{to}:g_1 ({\rm {\bf x}})=(C_{M@0.25c} )_C \ge -0.11 $$
(19)
$$ \label{eq20} g_2 ({\rm {\bf x}})=(C_L )_A \ge 1.10 $$
(20)
$$ \label{eq21} g_3 ({\rm {\bf x}})=(t/c)_{\max } \ge 0.105 $$
(21)

where C L is the lift coefficient, C D is the drag coefficient, C M@0.25c is the pitching moment coefficient about the quarter-chord position, and t/c is the thickness ratio of the section. The vector of fourteen design variables, x, is defined as:

$$ \textbf{x }(x_{1}, x_{2},...,x_{14}), x_{jl} \le x_{j} \le x_{ju}, j = 1,...,14. $$

4.3 Parameterization of the airfoil shape

The airfoil shape was parameterized using two cubic B-splines; one for the upper and one for the lower airfoil surface. The B-splines are generated by utilizing nine control points for each surface as shown in Fig. 4. Assuming that the chord length is equal to one, the first control point, which is common to both surfaces, is placed on the leading edge with coordinates (0,0). The last control point is placed on the trailing edge with coordinates (1,0). Seven additional control points are placed at intermediate positions on each surface. The x-coordinates of these points, which are listed in Table 1, are kept fixed and the y-coordinates are allowed to vary in the ranges displayed in Table 2. The y-coordinates of the fourteen control points form the vector of design variables x; the ranges listed in Table 2 correspond to the boundary constraints of the optimization problem. These ranges were based on the values that were used to generate the baseline design (RAE-2822 airfoil).

Fig. 4
figure 4

Control points of the cubic B-splines

Full size image
Table 1 Values of x-coordinate of control points
Full size table
Table 2 Ranges of y-coordinate of control points
Full size table

4.4 Design of experiments

The optimization problem was solved using surrogate models of the objective functions and constraints. These models were developed and trained using a data set of points selected from within the design variable space. For this purpose, an experimental design methodology was utilized. Uniform design (Fang 1980; Fang et al. 2000), which is a kind of fractional factorial design, has been shown (Simpson et al. 2001) to be a very effective sampling strategy even when small data sets are available. Therefore, it was decided to use a U90(914) uniform design for 90 runs with fourteen factors (design variables) each having nine discrete levels. Given the continuous nature of the design variables, each one of the ranges listed in Table 2 was discretized into nine equi-spaced values. The 90 airfoil sections were analyzed using the ANSYS® FLUENT® software as described in Section 4.5. The results were combined to create five datasets; one for each objective and constraint function.

4.5 Analysis of performance of airfoil sections

The analysis of the steady flow around the airfoils in both cruise and approach conditions was performed in FLUENT®, a general-purpose CFD software, at the operating points described in Section 4.2. The flow domain is shown in Fig. 5. A C-type grid was created with 54,000 cells (540 cells in the streamwise direction and 100 cells in the normal direction). The airfoil shapes that were generated using B-splines were analyzed by first creating files containing discrete data points on the airfoil surface. These files were imported into GAMBIT®, a general-purpose preprocessor for CFD analysis, where the mesh of the flow domain was created. The flow analysis was performed by solving the governing equations for mass, momentum, and energy using the density-based implicit numerical solver of FLUENT®, which is based on a finite volume method with the flow properties calculated at the cell centers. The convection terms were discretized using a second-order upwind scheme and the diffusion terms with a central-differencing scheme. Gradients were computed using a least squares cell-based method. The inviscid fluxes were calculated using the Roe flux-difference splitting scheme. Turbulence was modeled using the shear-stress transport (SST) model (Menter 1994). At least ten cells in the direction normal to the airfoil surface were placed within the turbulent boundary layer in order to provide adequate flow resolution in that region. A pressure far-field boundary condition was imposed on the flow boundaries, where the turbulence intensity value was set equal to 0.1%.

Fig. 5
figure 5

Flow domain for CFD analysis

Full size image

The CFD simulations for each airfoil were terminated when the scaled residuals of all the governing equations had been reduced by at least five orders of magnitude, provided that the lift and drag coefficients had also converged. The values of the lift, drag, and pitching moment coefficients were recorded and the profiles of the turbulent kinetic energy and the specific dissipation rate at the trailing edge were extracted. These were subsequently analyzed to find the location of maximum turbulent kinetic energy and the value of the specific dissipation rate at that location.

4.6 Surrogate models

Using the results obtained from the flow analysis, surrogate models for the objective and constraint functions were generated in WEKA. Instead of using a single type of surrogate model, it was decided to evaluate a number of different models for each function. Specifically, the models that were included in the evaluation process were the following: Feedforward ANNs with a single hidden layer and number of hidden nodes varying between two and ten, SVR with the PUK kernel, and linear regression. The model evaluation was performed using ten-fold cross-validation on the data set of 90 points using the root mean squared error as the evaluation metric. Different parameter values for each model were tested. The surrogate model with the best performance for each function was utilized by the optimization algorithm.

4.7 Running the ACMOPSO optimizer

ACMOPSO was run for 100 iterations per optimization cycle using five swarms with twenty particles each. At the end of the first cycle, as shown in Fig. 3, five points were selected from the computed Pareto front and the corresponding airfoil shapes were generated using B-splines and subsequently analyzed in FLUENT®. The results were added to the existing data set and the surrogate models were reconstructed. This iterative process was repeated until the computed Pareto front showed minimal changes between two successive iterations. A total of five optimization cycles was required in order to obtain the final Pareto front.

5 Multi-objective shape optimization results and discussion

The representation in the objective function space of a subset of the initial data set of 90 sample points is depicted in Fig. 6. Some of these points correspond to infeasible solutions. The Pareto front consists of only three members. During the iterative optimization process, a total of twenty new points, as shown in Fig. 6, were evaluated and added to the existing data set. In the same figure, the final Pareto front is also depicted. The effectiveness of the iterative optimization procedure is demonstrated by the fact that the optimal values in both objectives, i.e., at the extreme points on the Pareto front, were significantly improved compared to the solutions in the initial data set. The surrogate models that were used to approximate the objective functions enabled the optimizer to converge to the final Pareto front in only five iterations. Even though, there is no guarantee that this is the global Pareto front, the improvement in the objective function values is definitely noteworthy considering that it was achieved with only twenty additional problem evaluations. A comparison between the surrogate models that were tested and the corresponding optimal parameter values is displayed in Table 3. The optimal parameter values were obtained manually. Minimization of the root mean squared error (RMSE) value, which was obtained using ten-fold cross-validation, was utilized as the selection criterion. The RMSE values of the models that were selected as surrogates of the problem objectives/constraints in order to produce the final Pareto front are listed in bold font.

Fig. 6
figure 6

Multi-objective optimization results

Full size image
Table 3 Comparison between surrogate models
Full size table

5.1 Comparison between two Pareto-optimal solutions

It was decided to compare two solutions from the final Pareto-optimal set. The first Pareto-optimal solution (airfoil #1) that was selected was the computed solution with the maximum lift-to-drag ratio value. The second Pareto-optimal solution (airfoil #2) was chosen from the ‘knee’ section, which contains solutions that provide a balanced trade-off between high lift-to-drag ratio and low noise metric values. The shapes of the airfoil sections are displayed in Fig. 7. The main geometric characteristics of the two airfoil sections are listed in Table 4, while their aerodynamic performance characteristics are presented in Table 5. It can be observed from Table 5 that the predicted objective function values (pr) for these two points on the Pareto front are very close to the actual values (ac), i.e., the values obtained from a flow analysis in FLUENT®; a fact that demonstrates the good prediction capabilities of the utilized surrogate models.

Fig. 7
figure 7

Pareto-optimal airfoil section #1 (solid line) and #2 (dashed line)

Full size image
Table 4 Maximum thickness (t max ) and camber (f max ) of two Pareto-optimal airfoils
Full size table
Table 5 Aerodynamic performance of two Pareto-optimal airfoils
Full size table

Both solutions have a thickness ratio close to the minimum allowable value, however, the position of maximum thickness of airfoil #2 is located closer to the leading edge (a distance equal to approximately two per cent of the chord length) than the corresponding location on airfoil #1. The curvature on the upper surface of airfoil #1, particularly in the mid-chord region, is significantly smaller than the curvature on the upper surface of airfoil #2, as shown in Fig. 7. Both solutions have a relatively large leading edge radius. Small curvature along the upper surface, combined with a large leading edge radius, is an important design element of the shape of supercritical airfoils.

A comparison of the corresponding pressure coefficient distributions, displayed in Fig. 8, reveals that the shock strength in the case of airfoil #1 is much weaker than in the case of airfoil #2. Furthermore, the shock wave occurs further aft in the case of airfoil #1. The maximum Mach number value of the flow over airfoil #1 is 1.32, as shown in Table 5, compared to a maximum Mach number value of 1.36 for airfoil #2. Even though, the lift coefficient values during cruise are not significantly different, airfoil #1 has a significantly lower drag coefficient value, which can be attributed to the aforementioned observations regarding the shock wave and the maximum Mach number value.

Fig. 8
figure 8

Pressure coefficient distribution of two Pareto-optimal airfoil sections

Full size image

The values of the noise metric for the two airfoils are also listed in Table 5. Airfoil #2 has a significantly smaller value than airfoil #1 due to the low value of maximum turbulent kinetic energy at the trailing edge of the former airfoil. The value of the drag coefficient is also lower for airfoil #2 in the approach condition.

6 Conclusions

A multi-objective particle swarm optimizer (ACMOPSO) was utilized for the shape optimization of transonic airfoil sections. The computed Pareto-optimal set includes solutions that provide a trade-off between maximizing the lift-to-drag ratio during cruise and minimizing the trailing edge noise during the approach to landing. Five iterations of the optimization process were performed. Significant improvements in both objectives were observed in the values of the final Pareto front compared to the front obtained after the initial sampling of the design variable space. The utilization of various metamodels and the selection of the most appropriate for each objective and constraint function resulted in very accurate predictions and, thus, in a smaller number of required problem evaluations.

The inclusion of robustness in the shape optimization problem objectives, in addition to methods capable of increasing the level of automation within the optimization framework will be investigated in future research projects.