Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

One of the major challenges in aerospace design is to improve aircraft efficiency during operation, a requirement borne from the need to accommodate for rising fuel prices and the mitigation of emissions. The research effort in aircraft design is primarily driven by this incentive. One of most widely-used strategies by modern aircraft is using movable control surfaces to improve flight performance. For example, flaps and slats, whilst traditionally used during take-off and landing manoeuvres, can also be used to introduce a variable camber to the wing, thus providing scope for determining the optimum configuration for a given flight condition. However, when constrained by limited freedom of movement, it is unlikely that optimal solutions for every possible cruise condition are attainable. Furthermore, control surface devices result in geometrical discontinuities, which can often reduce the aerodynamic efficiency. In contrast, a morphing wing can potentially conform to provide optimal performance at any desired flight condition. Morphing wing technology can be used for flow-control, aerodynamic tailoring, improved flight dynamics during manueveres, and improve the aeroelastic performance and dynamic load response of military aircraft [1, 4, 5, 7].

In this paper a conceptual two-dimensional study is considered. The upper section of the trailing edge is deformable, since it is possible to achieve similar results to a fully morphing airfoil [2] without the drastic increase in complexity and weight. A multi-swarm heuristic, combining surrogate models for the alleviation of the computational effort are considered. Surrogates are used in lieu of the computationally expensive computational fluid dynamic (CFD) model, whereby the swarm directly navigates the surrogate landscape in order to find the region in the design space where the optimal solutions are likely located [3].

The dynamic optimization framework is developed to characterize the entire flight envelope, providing the best aerodynamic design, including morphing parameters as well, for that configuration. The framework allows for the identification of different optimal solutions, where the transition between different flight configurations (and therefore different shape topologies) is ultimately dependent on minimum energy expenditure during morphing. This ensures that during transition of flight configurations, the algorithm places a priority to solutions which avoid drastic changes between successive configurations, with minimal structural and logistic problems.

Fig. 1.
figure 1

An example of a morphed airfoil, compared with the original one, the design variables in input are: inputs = [1,0,1,0].

Full size image

2 Geometrical Parametrization

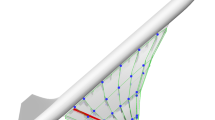
The original (i.e. base) airfoil selected is the NACA 23012, which is a mildly-cambered low-speed airfoil. The topology of the morphing trailing edge is controlled using four control points, situated along the upper trailing edge section, as shown in Fig. 1. We choose as original airfoil a NACA 23012. The morphing is theoretically achieved by manipulating the vertical (i.e. y) coordinate of the control points. Since the exact configuration is not known in advance, a random population of design candidates is first generated, and the optimization framework hones in on the optimal deviation of the vertical (i.e. y) coordinates from the original position. The boundaries of the design space are restricted to \(\mathbf {y} \in [-0.015, 0.015]\), to ensure a robust topology the and manufacturable shape is guaranteed. To facilitate the optimization process, the boundaries are normalized to unity, where a value of 0 corresponds to the lowest position for the y coordinate and 1 to the highest position. The four control points provide the basis for shape morphing, where a piecewise cubic Hermite polynomial interpolation scheme is used.

3 Surrogate Model

A major obstacle in using population-based optimization frameworks is the often prohibitive computational expense of the numerical model. To this end, the pursuit of higher-order shape parameterization techniques, able to define arbitrarily complex shapes with minimal design variables, is highly desirable. Nevertheless, for true multi-disciplinary aircraft design, the numerical model is the most prohibitive element of the framework. The use of surrogate models are very popular for aerospace design applications since they can be used in lieu of the original and more costly computational model of the problem [3]. In this context, the surrogate model can play a very valuable role in increasing the feasibility of using population-based algorithms in conceptual aircraft design. The surrogates are constructed using data obtained from the high-fidelity numerical model, and provide cheap approximations of the original objective functions and constraints at new locations.

3.1 Kriging Method

Of particular significance in surrogate models is the methodology used. In this study, the approximated values are modeled by a Gaussian process governed by prior covariances, known as Kriging (Krige, 1951), which is an interpolating method featuring the observed data at all sample points. Kriging provides a statistical prediction of the function at an arbitrary location by minimizing its mean squared error (MSE).

Kriging methods rely on the notion of autocorrelation. Correlation is usually thought of as the tendency for two types of variables to be related. For the derivation of Kriging, the output of a deterministic computer experiment is treated as a realization of a random function (or stochastic process), which is defined as the sum of a global trend function \(f^T(\mathbf {x})\beta \) and a Gaussian random function Y(x) as the following:

$$\begin{aligned} y(\mathbf {x})=f^T(\mathbf {x})\beta +Y(x),\qquad \mathbf {x}\in \mathfrak {R}^m, \end{aligned}$$
(1)

where \(f(\mathbf {x})\) is defined by a set of regression basis functions and \(\beta \) denotes the vector of the corresponding coefficients, m is the number of dimensions, and \(\mathbf {x}\) is the vector of design variables. Now we can obtain the correlation function of our variables which is only dependent on the Euclidean distance between any two points \(\mathbf {x}^{(i)}\) and \(\mathbf {x}^{(l)}\) in the design space. The random variables are correlated with each other using the basis expression:

$$\begin{aligned} Corr[Y(\mathbf {x})^{(i)},\,\,Y(\mathbf {x})^{(l)}]=\,exp\,\biggl (-\sum _{j=1}^{k}\theta _j|x_j^{(i)}-x_j^{(l)}|^{p_j}\biggr ). \end{aligned}$$
(2)

The correlation depends on the Euclidean distance and two undefined parameters \(\theta \) and p that have to be obtained by means of a numerical optimization technique. At this point it is possible to formulate the prediction expression:

$$\begin{aligned} \hat{y}(\mathbf {x})=\hat{(\mu )}+\psi ^T\varPsi ^{-1}(\mathbf {y}-\mathbf {1}\hat{\mu }), \end{aligned}$$
(3)

where \(\psi \) is the vector of the basis function, \(\varPsi \) is the correlation matrix, \(\mathbf {1}\) is a vector of one, centered around the n sample points and are added to a mean base term \(\hat{\mu }\).

4 Particle Swarm Optimization

Particle Swarm Optimization (PSO) is a population-based stochastic optimization technique, inspired by social behavior of bird flocking or fish schooling, and belongs to the family of swarm intelligence techniques [13]. The potential candidates, called particles, navigate the objective landscape, with their movements guided by the best known position of each particle as well as the entire swarm’s best known position. The process is iterated until a satisfactory (or converged) solution is found. Each particle keeps track of its coordinates in the problem space, which are associated with the best solution (in terms of fitness) it has achieved so far. This position is called pbest. Another position that is tracked by the standard version of the particle swarm optimizer is the overall best position, and its fitness value, obtained so far by any particle in the population. This location is called gbest.

The particle swarm optimization (PSO) search process consists of, at each time step, changing the velocity (accelerating) of each particle towards its pbest and gbest locations (standard version of PSO). Acceleration is weighted by a random term, with separate random numbers being generated for acceleration towards the pbest and gbest locations.

figure a

The original process for implementing the standard version of PSO is provided in Algorithm 1. In the algorithm, a, b and c are constants that separately control the importance of the three directions which determine the next velocity and position of the particle. The three components are usually referred to as inertia (\(v_{ti}\)), cognitive influence (\(p_{bti}-x_{ti}\)), and social influence (\(g_{bt} - x_{ti}\)).

4.1 Optimization in a Dynamic Environment

Many real-world problems are dynamic in the sense that the global optimum location and value may change with time. The task for the optimization algorithm is to track this shifting optimum. In this context it is possible to adapt the particle swarm to work in a dynamic environment and in presence of multiple peaks. The choice of using PSO is obvious, since it shows very useful characteristics for a dynamic environment: simple implementation, very few algorithm parameters, very efficient global search algorithm, and insensitive to the scaling of design variables. However the standard PSO is affected by two problems: outdated memory; and diversity loss [16]. The first one happens as the environment changes when the optima may shift in location and/or value. Particle memory (namely the best location visited in the past, and its corresponding fitness) may no longer be consistent after the change, with potentially sub-optimal effects on the search. The problem of outdated memory is typically solved by either assuming that the algorithm knows just when the environment change occurs, or that it can detect changes. In either case, the algorithm must act with an appropriate response. Equally troubling as outdated memory is an insufficient diversity after change. The population takes time to re-diversify and re-converge, resulting in being unable to track a moving optimum. Loss of diversity arises when a swarm converges onto a peak. There are two possibilities: when a change occurs, the new optimum location may either be within or outside the collapsing swarm. In the former case, there is a good chance that a particle will find itself close to the new optimum within a few iterations and the swarm will successfully track the moving target, assuming that the swarm as a whole has sufficient diversity. However, if the optimum shift is significantly far from the swarm, the low velocities of the particles will inhibit re-diversification and tracking, and the swarm can even oscillate about a false attractor and along a line perpendicular to the true optimum, in a phenomenon known as linear collapse [14].

In this study we resolve this issue by combining two techniques to treat the dynamic problems: Charged Particle Swarm Optimization (CPSO) [14] and Multi-swarm Particle Swarm Optimization (MPSO) [14]. CPSO introduces a repulsive mechanism that can either be between particles, or from an already detected optimum. In this model, a swarm is comprised of a charged and a neutral sub-swarm. Charge enhances diversity in the vicinity of the converging PSO sub-swarm, so that optimum shifts within this cloud should be trackable. Implementing the charged PSO is simple, since its structure is similar to the canonical one, with the addition of an acceleration term in the swarm equations of motion, which is called electrostatic acceleration \(\mathbf {a_i}\) [15]. The main idea behind MPSO is to split the population of particles into several interacting swarms. The aim of these swarms is to position each on different promising peaks of the fitness landscape. Splitting the main swarm into independent sub-swarms is unlikely to be effective, since the swarms will not interact. The idea is to use some parameters to control the interaction between swarms, including two mechanisms known as exclusion and anti-convergence [17].

Exclusion controls the local interaction between swarms, preventing swarms from staying on the same peak. Anti-convergence deals with the issue as each swarm converges onto a peak, i.e., the particles of the swarms are in close proximity to the attractor. The problem is that if there are more peaks than the number of swarms, it is necessary to ensure that at least one swarm is kept free for detecting any possible change in the environment.

5 Implementation of the Surrogate Model

Given that the operating principles of optimization and surrogates are defined; their synergy and integration into the framework must be considered. The surrogate is treated as a partially-online black-box emulating function, with inputs as the normalized control points, and the airfoil lift coefficient (\(C_L\)), which defines the flight condition. A local surrogate is referred to cases where \(C_L\) is fixed (and so the flight condition). Alternatively, the global surrogate refers to cases where \(C_L\) is an additional participating input variable.

The difference between the two objective landscapes is that the local model ensures more accuracy for a defined flight condition, whereas the global provides a better prediction for the whole objective landscape. For this reason, it is possible to discern at least three different approaches:

  1. 1.

    Local surrogates (four variables, i.e. the four control points):

    1. (a)

      Apply optimization directly to the surrogate model.

    2. (b)

      Optimize the surrogate with CFD and compute the optimization.

  2. 2.

    Global surrogates (five variables, i.e. the four control points and the lift \(C_L\)):

    1. (a)

      Apply optimization directly to the surrogate model.

    2. (b)

      Optimize the surrogate with CFD and execute the optimization.

  3. 3.

    Mixed approach: using a global surrogate with local surrogates optimized with CFD.

A direct application of an optimization method without using the surrogate is rare, since the computational cost is very high. Each above approach can be evaluated in terms of: flexibility to the designer, computational intensity and accuracy. The mixed approach proved to be most efficient. In this case the global surrogate provides the general information of the space design and the local surrogates are used as swarms to locate the optima.

6 Application

The practical application of the framework is based on a generic modular, long endurance unmanned aerial system which intends to fulfil the primary roles of unarmed reconnaissance, data collection, and surveillance. The morphing optimization will be performed for a hypothetical flight path. This is composed of three mission objectives which correspond to three different configurations. We want to find the three optimal configurations to minimize the objective of the specific phase as restricting the energy spent when performing the morphing. The three mission objectives considered are:

  • Maximum range

  • Maneuvering at a defined angle of attack

  • Maximum endurance

Both the range and endurance depend on the rate of fuel consumption of the propulsion system, and therefore, on the type of engine. The range is considered to be the maximum distance the aircraft can fly and the endurance as the maximum possible flight duration (irrespective of distance covered, i.e. loitering). As one might expect, there is a flight condition (attitude and velocity) that will provide the best range for a given aircraft, and a different flight condition that will give us maximum endurance. It is clear that if we want to maximize flight endurance for a defined configuration, we have to minimize the function \(f^*=\frac{C_D}{C_L}\), where \(C_D\) is the aerodynamic drag coefficient. Alternatively, to maximize the range, the cost function to be minimized is \(f^*=\frac{C_D}{C_L^{1/2}}\). The maneuvering has been performed for a fixed angle of attack trying to minimize \(f^*=(\frac{1}{CL^2})\). There are six design parameters to define both range and endurance, which are four morphing control points, as well as the wing angle of attack (\(\alpha \)) and airspeed (V). For simplicity, the altitude is fixed.

7 Results

The optimal framework approach in terms of accuracy, flexibility and computational cost is the mixed approach. Different combinations of parameters were considered, to determine the optimal swarm population size, number of swarms, and size of the initial training dataset (i.e. number of samples), and are consolidated in Table 1. It is important to note the time of change: such that after every 40 iterations the optimization framework dynamically changes its objective.

Table 1. Input parameters for MPSO
Full size table
Table 2. Results for range, maneuvering and endurance.
Full size table

The velocities are obtained after having optimized the airfoil without morphing and found out which are the best to accomplish each objective. The results obtained for each case are shown in Table 2. Each optimization routine provides four ideal shapes for each objective, with each solution ranked according to the percentage of improvement and energy expenditure. The improvement, except for the maneuvering phase, is quite small. Indeed, for range and endurance, the average improvement is of the order of 1%. Minimum energy expenditure is determined based on the minimum amount of structural deformation required to transition between successive states. After this trade-off was performed, the best three profiles for completing the mission are obtained, which can be seen in Fig. 2. It is interesting to note the effects of the morphing on the aerodynamic performance coefficients. For the range the result does not change much, as compared to the original, instead for the maneuvering we have some interesting improvements. After the first input point there is a regain in pressure and consequently an increase of lift, this is exactly what we want to achieve during this phase. Furthermore, the pitching moment \(C_M\) is affected by the morphing.

Fig. 2.
figure 2

Best airfoils shape for range, maneuvering and endurance.

Full size image

8 Conclusion

This paper has presented a dynamic optimization of a morphing trailing edge. A population-based dynamic optimization framework is developed, utilizing the Multi-swarm Particle Swarm Optimization algorithm, in combination with Kriging surrogate models, used to alleviate the computational effort of the high-fidelity numerical solver. The conceptual study illustrated significant improvement in the flight performance is attainable, with the major improvement experienced during the phase of maneuvering. In this context an improvement in aerodynamic performance of approximately 5% is observed, as compared to the original profile. Cruise aerodynamic performance was improved by 1% to 3%, which is still significant since minimal energy expenditure in morphing the trailing edge topology of the original profile is considered. Starting from this and passing from an experimental validation of the numerical analysis, morphing could, in future, replace the current use of multiple aerodynamic devices (such as flaps and slats). The framework developed provides a clear scope for future research direction. The conceptual application simply considers a static two-dimensional analysis, the real benefits of adopting a dynamic swarm framework would be to consider the optimal execution of time-accurate aircraft maneuvers.