Genomic prediction of dichotomous traits with Bayesian logistic models

Abstract

Bayesian methods are a popular choice for genomic prediction of genotypic values. The methodology is well established for traits with approximately Gaussian phenotypic distribution. However, numerous important traits are of dichotomous nature and the phenotypic counts observed follow a Binomial distribution. The standard Gaussian generalized linear models (GLM) are not statistically valid for this type of data. Therefore, we implemented Binomial GLM with logit link function for the BayesB and Bayesian GBLUP genomic prediction methods. We compared these models with their standard Gaussian counterparts using two experimental data sets from plant breeding, one on female fertility in wheat and one on haploid induction in maize, as well as a simulated data set. With the aid of the simulated data referring to a bi-parental population of doubled haploid lines, we further investigated the influence of training set size (N), number of independent Bernoulli trials for trait evaluation (n _i ) and genetic architecture of the trait on genomic prediction accuracies and abilities in general and on the relative performance of our models. For BayesB, we in addition implemented finite mixture Binomial GLM to account for overdispersion. We found that prediction accuracies increased with increasing N and n _i . For the simulated and experimental data sets, we found Binomial GLM to be superior to Gaussian models for small n _i , but that for large n _i Gaussian models might be used as ad hoc approximations. We further show with simulated and real data sets that accounting for overdispersion in Binomial data can markedly increase the prediction accuracy.

Introduction

Genomic prediction (Meuwissen et al. 2001) methodology is now well established for quantitative traits that follow approximately a Gaussian phenotypic distribution. However, many important traits in plant breeding are dichotomous. Especially reproductive traits such as haploid induction ability and spontaneous chromosome duplication rate, two traits important for doubled-haploid (DH) production in maize (Prigge et al. 2012; Kleiber et al. 2012), seed emergence (Yousefabadi and Rajabi 2012; Goggi et al. 2007), male and female fertility (Sellamuthu et al. 2011; Dou et al. 2010) and hybrid sterility (Zhao et al. 2006) fall into this category. Using a Gaussian likelihood function here ignores important features of the data, namely its restriction to positive values and the dichotomous nature of the observations.

In human genetics, dichotomous traits, such as outbreak of a disease or not, are commonly observed (Wray et al. 2008) and genomic prediction methodology was already successfully applied to such data sets (Lee et al. 2011). In plant breeding, however, phenotypic observations are usually made on independent, repeated Bernoulli trials. Thus, the underlying phenotypic distribution of the data can be characterized as being Binomial. An extension of the genomic prediction methodology to Binomial generalized linear models (GLM) with appropriate link function is therefore needed.

A common choice of link function is the logit link. Logistic GLM predict the log-odds ratio of observing a certain outcome (e.g., a seed being haploid). A great advantage of logistic GLM is that they allow convenient and efficient Gibbs-sampling computations also for Binomial data, when using the auxiliary mixture sampling parametrization developed by Frühwirth-Schnatter et al. (2009).

A phenomenon commonly associated with Binomial and other types of count data is overdispersion (Dey et al. 1997). Overdispersion means that the data observed are more heterogeneous than expected under a Binomial model, in which case the predicted variance is a direct function of the conditional mean (conditional on the set of predictors, e.g., the markers). The linkage disequilibrium (LD) between markers and quantitative trait loci (QTL) is seldom complete. Overdispersion can, therefore, always be a problem in genomic prediction because under incomplete LD, the Binomial sampling process is not the only source of uncertainty. This is especially the case when phenotyping is done in field trials, where in addition to genetic differences also non-genetic sources of variation are present that cannot be fully accounted for. Under overdispersion, a simple Binomial model will not fit the data optimally, which can reduce the prediction accuracy. Genomic prediction methodology for Binomial phenotypes therefore needs to be able to account for overdispersion for successful application to real world data sets.

Bayesian methods are a popular choice for genomic prediction of genotypic values (Kärkkäinen and Sillanpää 2012). They might be coarsely separated into (1) marker effects methods and (2) polygenic or total genetic effects methods, where genetic effects are associated directly with individuals (Kärkkäinen and Sillanpää 2012). The latter might be understood as Bayesian versions of the popular non-Bayesian GBLUP method. Numerous results point to a superiority of GBLUP (both Bayesian and non-Bayesian) when the trait is controlled by a large number of QTL with small effects and to a superiority of marker effects methods for traits with a more oligogenic architecture (Kärkkäinen and Sillanpää 2012; Hayes et al. 2010; Clark et al. 2011; Zhong et al. 2009). However, such a comparison is lacking for traits with a Binomial phenotypic distribution.

Binomial GLM are the only statistically valid way of analyzing Binomial data. However, practitioners applying genomic prediction are mostly interested in identifying superior genotypes for selection purposes. For this, a standard Gaussian GLM might provide a useful ad hoc approximation after an appropriate transformation of the data. Furthermore, Binomial GLM can be associated with considerable implementational and computational overhead and complexity. Therefore, it seems worthwhile to investigate whether and under which circumstances Gaussian GLM are sufficient for practical applications.

Our objectives were to (1) implement logistic GLM for genomic prediction of dichotomous traits with Binomial phenotypic distribution that can account for overdispersion and (2) compare for these traits the performance of Bayesian GBLUP and marker effect-based methods. Thereby we based our investigation on real and simulated plant breeding data sets.

Materials and methods

We consider a segregating population of genotypes such as F₂ individuals or DH lines from a bi-parental cross, the genotypes of which are genotyped and progeny of them are either produced by self-pollination or cross-pollination with a common tester. Let n _i be the number of progeny derived from genotype i. Each offspring was phenotyped for a dichotomous trait, receiving a phenotypic value of either one or zero, depending on which of two possible events occurred (e.g., seed viable or not, seed haploid or not). Thus, each offspring can be viewed as an independent Bernoulli trial. The sum s _i over all n _i offspring is the phenotypic score of genotype i, which consequently follows a Binomial distribution.

Marker effects methods

To analyze this kind of data, we first used a Binomial GLM based on marker effects

$$ s_i \sim {\fancyscript{B}}(p_i,n_i) $$

(1)

$$ p_i = {\fancyscript{L}}(\beta_0 + \boldsymbol{X}_i\boldsymbol{u}), $$

where p _i is the probability of observing the “successful” outcome for the ith individual and $\fancyscript{L}(\beta_0 +{\varvec{X}}_i\boldsymbol{u})$ its linear predictor, with $\fancyscript{L}(\cdot)$ denoting the logit link function. The intercept is denoted by β ₀. The row vector ${\varvec{X}}_i$ is a known marker genotype incidence vector of the ith individual, for the additive marker effects in ${\varvec{u}}.$ The whole matrix ${\varvec{X}}$ has dimensions N × M (N = number of individuals, M = number of biallelic markers). The marker genotypes were coded with 1 and −1 for the two homozygous genotypes and 0 for the heterozygous genotype and were scaled and centered prior to analysis by subtracting the mean and dividing by the standard deviation, a common practice in regression models as discussed by de los Campos et al. (2012). The term $\fancyscript{B}(\cdot)$ denotes the Binomial probability function with n _i being known.

The auxiliary mixture sampling method (Frühwirth-Schnatter et al. 2009) was used to facilitate Gibbs-sampling. Briefly, in auxiliary mixture sampling, an aggregated latent variable $y_{i}^{*}=log(\beta_0 + {\varvec{X}}_i\boldsymbol{u}) + \epsilon_i$ is introduced for each Binomial observation. The distribution of the residuals $\epsilon_i$ is a negative log-gamma distribution, which is approximated by a Gaussian mixture distribution. A second latent variable r _i is introduced as an indicator of the component of the mixture. Then, conditional on y ^* _i and r _i , model (1) reduces to a linear model with Gaussian likelihood function, y ^* _i as response and heteroscedastic but fixed residual variances, which are determined by r _i . The major advantage of this procedure is that then standard Gibbs-sampling methodology developed for Gaussian models can be used.

The parameters (i.e., weights, means and variances) of the components of the Gaussian mixture distributions were precomputed and remained fixed during Gibbs-sampling. We used the Matlab function “compute_mixture”, obtained by request to Frühwirth-Schnatter et al. (2009), for precomputing these parameters. For convenience, we provide them tabulated up to n _i  = 3,500 in supplemental file S1.

The joint hierarchical prior distribution was

$$ p(\beta_0) \times p(\boldsymbol{u}_j|\sigma^2_{u_j}) \times p(\sigma^2_{u_j}|\pi,\nu,S^2) \times p(\pi|a,b) \times p(S^2) \times p(\nu). $$

The priors for β ₀ and the marker effects were p(β ₀) ∝ 1 and $p({\varvec{u}}_j|\sigma^2_{u_j}) =\mathcal{N}(0,\sigma^2_{u_j}).$

The prior variance of the effect of the jth marker ($\sigma^2_{u_j}$) was

$$ p(\sigma^2_{u_j} |\nu,S^2)\left\{\begin{array}{ll} = 0& \hbox{with probability }\pi\\ = \chi^{-2}(\nu,S^2)&\hbox{with probability } (1 -\pi).\end{array}\right. $$

(2)

From Eq. (2) follows that our method falls into the class, the priors for the marker effects of which can be parametrized as Student’s t distributions with a non-zero probability mass over zero. Specifically, because the prior probability mass over zero is introduced through $\sigma^2_{u_j}$ instead of through an explicit indicator variable, our method belongs to the “BayesB” class (Meuwissen et al. 2001). Therefore, it is referred to as “Binomial BayesB GLM” in the remainder of this treatise.

Following Yang and Tempelman (2012) and Technow et al. (2012), the hyperparameters π, ν and S ² were associated with prior distributions too and, thus, were estimated from the data. The prior of S ² was a Gamma distribution with shape and rate parameter equal to 0.1, and for ν we used the uninformative improper prior distribution

$$ p(\nu) \left\{\begin{array}{ll} \propto (\nu + 1)^{-2} &\rm{ if } \, 0 < \nu < 100 \\ = 0 & \hbox{else}.\end{array}\right. $$

(3)

The prior for π was a Beta distribution. Its parameters were different for each data set and are specified together with their description given below.

We employed finite mixture models to account for overdispersion (Frühwirth-Schnatter 2006). Model (1) now generalizes to

$$ s_i \sim \sum_{k=1}^{K}\eta_k {\fancyscript{B}}(p_{ik},n_i) $$

(4)

$$ p_{ik} ={\fancyscript{L}}(\beta_{0,k} + \boldsymbol{X}_i\boldsymbol{u}_k),$$

where k indexes the mixture component, K is the number of components used and η _k the weight of the kth component. The marker genotypes were not scaled and centered, because the sampling algorithm used would have required a constant re-centering and re-scaling, which would have been computationally prohibitive. The number of components K is a constant, but we fitted the model with K ranging from 2 to 12 and report results for the value of K that gave best results. Further note that for K = 1, model (4) reduces to the standard Binomial GLM in (1).

The joint prior distribution then is indexed by k as well and a uniform Dirichlet distribution with concentration parameter $\alpha_1,\dots,\alpha_K =4$ was used as prior for the weights η _k . We used the data augmentation technique as described by Fruhwirth-Schnatter (2006, sect. 3.5) for sampling from model (4). Here, a group indicator $S_i \in \{1, 2,\ldots,K\},$ is introduced as missing data. Then, the parameters and hyperparameters for the kth mixture component are sampled conditional on knowing S _i (i.e., from all observations in group S _i  = k) and S _i conditional on knowing the parameters and hyperparameters. Adopting this data augmentation method has the advantage that conditional on S _i , the parameters can be sampled with standard Gibbs-sampling methodology, while sampling S _i conditional on the parameters reduces to a straightforward classification problem.

As a baseline method for comparison purposes, we also fitted a Gaussian BayesB GLM commonly used for Gaussian data in the literature (e.g., Technow et al. 2012; Yang and Tempelman 2012). The model was

$$ w_i \sim{\mathcal{N}}(p_i,\sigma^2_e) $$

(5)

$$ p_i = \beta_0 +\boldsymbol{X}_i\boldsymbol{u} $$

Here, $w_i =arcsin(\sqrt{s_i/n_i}),\, \mathcal{N}(\cdot)$ denotes the Gaussian density function and $\sigma^2_{e}$ the residual variance. We scaled and centered w _i prior to the analysis. Note that p _i is not confined to the probability scale as for the Binomial GLM above. The same joint hierarchical prior distribution as for the Binomial BayesB GLM was used here. The additional parameter σ ² _e was associated with an uninformative scaled inverse Chi-square prior.

Samples from the joint posterior distribution of the parameters were drawn by Gibbs-sampling, with a single chain of 250,000 iterations, of which the first 100,000 were discarded as burn-in and only samples from every 50th iteration were stored. Details on the sampling strategy for auxiliary mixture sampling can be found in Frühwirth-Schnatter et al. (2009) and details on data augmentation for sampling from finite mixture models in Frühwirth-Schnatter (2006). The fully conditional distributions (FCD) and Gibbs-sampling strategy for BayesB are described in Yang and Tempelman (2012). For sampling from the FCD of $\sigma^2_{u_j}$ and ν, Metropolis–Hastings algorithms were used as described by Technow et al. (2012). For the standard Binomial BayesB GLM as well as the Gaussian BayesB GLM, the posterior means of β ₀ and the marker effects u _j were used as point estimates for predicting genotypic values.

In finite mixture models, the estimates of the posterior means might be sensitive to “label switching” (Frühwirth-Schnatter 2006). Therefore, we used the mean of the posterior predictive distribution for predicting the genotypic values of new observations. The posterior predictive distribution is robust against label switching (Frühwirth-Schnatter 2006).

All BayesB algorithms were implemented as C routines compatible with the R software environment (R Development Core Team 2011). The source code is provided in supplemental file S2. The R package “coda” (Plummer et al. 2010) was used to estimate effective sample sizes (ESS) of marker effects for the standard Binomial and Gaussian GLM. Because of “label switching”, there seems to be no straightforward way to estimate an ESS for our finite mixture models.

Bayesian GBLUP methods

The Binomial GBLUP GLM was

$$ s_i \sim {\fancyscript{B}}(p_i,n_i) $$

(6)

$$ p_i = {\fancyscript{L}}(\beta_0 + a_i), $$

with a _i denoting the total genetic effect of the ith individual.

We used the JAGS Gibbs-sampling environment (Plummer 2003) for GBLUP, which allows for convenient specification and implementation of standard models. The JAGS environment is very similar to the BUGS/OpenBUGS environment (Thomas et al. 2006), but platform independent and designed for integration with R. JAGS uses auxiliary mixture sampling as well, however, its implementation might differ somewhat from ours used for BayesB.

The joint hierarchical prior distribution was

$$ p(\beta_0) \times p(a_i|\sigma^2_{a}) \times p(\sigma^2_{a}) $$

(7)

Again we used an uniform prior for β ₀. The prior for the total genetic effects was $\mathcal{MVN}({\varvec{0}},\boldsymbol{A}\sigma^2_a),$ where ${\varvec{A}}$ is the genomic relationship matrix, computed according to Method 1 of VanRaden (2008) and σ ² _a the additive genetic variance component. We associated 1/σ ² _a with an uninformative Gamma prior with shape and rate parameters equal to 0.01.

In this case too, we considered a Gaussian GBLUP GLM version as

$$ w_i \sim {\mathcal{N}}(p_i,\sigma^2_e) $$

(8)

$$ p_i = \beta_0 + a_i. $$

The set-up for the joint hierarchical prior distribution was identical to the Binomial GBLUP GLM, with 1/σ ² _e also associated with an uninformative Gamma prior with shape and rate parameters equal to 0.01.

Sampling was done by running three independent Gibbs-sampling chains for 10,000 iterations each. The first 5,000 iterations of each chain were discarded as burn-in and only samples from every 3rd iteration stored afterwards. The JAGS source code is provided in supplemental file S3.

Wheat female fertility data set

The data comprises a bi-parental wheat (Triticum aestivum L.) F₂ population of size 243, genotyped with 28 markers. The Binomial phenotypic scores are the number of seeded spikelets (s _i ) from a total number of spikelets per plant (n _i ). The average s _i was 19.13, and the average n _i was 25.15. For the majority of plants, the ratio s _i /n _i was around 0.9, some plants had a ratio close to or exactly zero and there were only few intermediate observations. We therefore performed the analysis additionally for a subset of the data with plants for which s _i /n _i  > 0.75 (“high fertility subset”). The number of remaining observations was 186, with an average s _i of 23.88 and an average n _i of 25.04. The phenotypic and the marker data were obtained by request to the authors of Che and Xu (2012), who previously analyzed the data. A more detailed description of the data set is given in Dou et al. (2009).

Given the rather small number of markers, the Beta distribution prior for π was Beta(a = 1, b = 9), meaning that almost all markers are expected to have an effect a priori. We used fivefold cross-validation (CV) for assessing the performance of our models. Here, the whole data set is split into five distinct subsets and each subset is in turn predicted by a model fitted using the data from the remaining four subsets as training set. The statistics of interest are determined each time and averaged at the end over the five runs. This whole process was repeated 25 times, with independent random splits each time. All models were fitted on the same subsets and the differences between them assessed for significance using standard frequentist paired t tests. The recorded statistic was the Pearson correlation coefficient of predicted and observed phenotypic values in the prediction set (predictive ability). We refrained from calculating prediction accuracies commonly obtained by dividing the predictive ability by the square root of the trait heritability (h ²) because obtaining sensible estimates of h ² for dichotomous traits is not trivial if n _i varies.

Maize haploid induction rate data set

In maize (Zea mays L.), DH lines are generated in-vivo by pollinating source germplasm with pollen from so-called “inducer” genotypes. A proportion of the so obtained seeds then contain embryos with haploid genome of maternal origin. The proportion of haploid seeds in the total number of seeds produced is commonly referred to as the haploid induction rate (HIR).

Our example data set comprised a bi-parental experimental maize F₂ population used in a recently published study on QTL mapping for HIR (Prigge et al. 2012). The parents of the population were the European inducer line UH400 and the Chinese inducer line CAUHOI. UH400 has a HIR of around 0.08 (Prigge et al. 2012), CAUHOI of around 0.02 (Li et al. 2009). The N = 185 F₂ individuals were genotyped with 90 polymorphic simple sequence repeat (SSR) markers. The HIR was determined by pollinating a tester genotype with pollen from each F₂ individual and counting the number of haploid seeds in the progeny. The average number of pollinated test cross seeds per F₂ individual was 1,108 but ranged from below 166 to 3,279. The average HIR was 0.053. The marker data were retrieved from the supporting material of Prigge et al. (2012), and the phenotypic data were obtained by request to the authors of cited publication.

As previous research suggests an oligogenic or even monogenic inheritance of HIR (Barret et al. 2008; Lashermes et al. 1988), we chose Beta(a = 8, b = 2) as prior for π, which concentrates most of the probability mass around 0.8. Here, we used 25 times repeated tenfold CV, which results in larger training sets as compared with fivefold CV.

Simulated data set

For investigating the influence of factors such as genetic architecture, population size and number of Bernoulli trials, we simulated a bi-parental DH population with size 500. The genome consisted of 10 chromosomes, each of 100 cM length. There were 50 equally spaced markers and 15 QTL per chromosome. The meiosis events for generating the DH lines in silico were simulated according to the Haldane mapping function, using the R package “hypred” (Technow 2011). The polygenic trait architecture was simulated by assigning additive effects, defined according Falconer and Mackay (1996), drawn from a standard Gaussian distribution to all 150 QTL. To simulate an oligogenic architecture with small and large QTL, we assigned additive effects drawn from a Gamma distribution with parameters scale = 1.66 and shape = 0.4 (Meuwissen et al. 2001) to a random subset of five of the QTL per chromosome and effects of zero to the remaining QTL. The QTL effects were summed according to the QTL genotypes of each DH line to create a raw genotypic score g _i , which was additionally scaled and centered. These scores were then transformed to the probability scale by computing $p_i =\phi(\phi(g_i/max(g_i)_{i = 1\dots 500}) - 2.12),$ where ϕ is the standard Gaussian cumulative distribution function. This transformation assured that the true probability parameters of the genotypes were within the interval [0, 0.1]. Phenotypes were simulated by drawing the number of observed events s _i from a Binomial distribution with probability parameter equal to p _i . The number of independent Bernoulli trials n _i was n ^* _i  + 1, where n ^* _i is a random number from a Poisson distribution. The rate parameter λ of this distribution was set to 25, 50, 100, 250 and 500. For each combination of trait architecture and λ, we created 50 independent subdivisions of the data into training and prediction set. The training set was used for fitting the model. As sizes of the training set, we considered N = 100, 200 and 300. The true genotypic values p _i were known from simulation. Thus, we could compute the prediction accuracy of the models as the Pearson correlation between predicted and true p _i values for the prediction set individuals.

To avoid incorporating information on the genetic architecture that might be unavailable in practice, we used Beta(a = 0.9, b = 0.9) as prior for π. This prior has its probability peaks close to zero and close to one. It suggests that we either expect a polygenic or oligogenic trait architecture, without completely ruling out anything in between. We observed better convergent properties with this prior than with a completely uniform prior. To facilitate computations, the number of independent Gibbs-sampling chains for GBLUP was reduced to 1.

The marker and QTL genotypes of the 500 individuals, their phenotypes and true probability parameters as well as the simulated QTL effects are provided as supplemental file S4.

We further performed a simulation to investigate the effects of overdispersion on the prediction accuracies and to compare the standard Binomial BayesB GLM with the finite mixture implementation. For this we used the marker data described above together with the n _i values corresponding to λ = 25 and the p _i values from the oligogenic trait. Overdispersion was simulated according to a Beta-Binomial sampling process by drawing p ^* _i from a Beta distribution with parameters α = κ p _i and β = κ(1 − p _i ). Then we redrew s _i from a Binomial distribution with probability parameter equal to p ^* _i and size parameter equal to n _i , as shown above. Thus, p ^* _i was drawn from a Beta distribution with mean equal to p _i and a standard deviation (SD) that is determined largely by κ. The smaller κ, the higher the SD and thereby the degree of extra-binomial variation or overdispersion. For the simulations, we considered κ = 10 (100, 1,000). The exact value of the SD also depends on p _i , but to give an example, for p _i  = 0.05, κ = 10 results in a SD of 0.066, κ = 100 in a SD of 0.022 and κ = 1,000 in a SD of just 0.007. The simulation was repeated 50 times for each combination of κ and N (for which we again considered N = 100 (200, 300)).

Identifiability is always a problem in GLM when the number of parameters is larger than the number of observation, i.e., when N < M. However, by using proper, informative prior distributions, parameter estimation, Bayesian learning and posterior prediction is still possible (Gelfand and Sahu 1999). The huge success of Bayesian marker effects methods for genomic prediction (Kärkkäinen and Sillanpää 2012) shows that especially posterior prediction seems not to be affected by the lack of identifiability in these cases. However, as discussed by Frühwirth-Schnatter (2006), finite mixture regression models suffer especially from nonidentifiability due to the added complexity and flexibility. Consequently, trying to fit model (4) with the full set of M = 500 markers led to non-convergent Gibbs-sampling chains and non-sense results. We therefore reduced the number of markers to 250 for N = 100 to 300 for N = 200 and to 350 for N = 300 by randomly sampling from the full marker set. For direct comparison, the standard Binomial GLM (1) was fitted with these reduced marker sets as well and in addition with the full set of M = 500 markers.

Results

Wheat female fertility data set

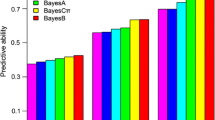
For the full data set, a finite mixture Binomial BayesB GLM with K = 12 gave the highest average predictive ability of 0.555. The predictive abilities observed for the other models were significantly lower at around 0.500 (Table 1).

Table 1 Average predictive ability of the wheat female fertility data set, the high fertility subset of this data set and maize haploid induction data from 25 replications of fivefold (wheat) and tenfold (maize) cross-validation for the Binomial and Gaussian BayesB and GBLUP generalized linear models (GLM)

For the “high fertility subset”, the highest average predictive ability of 0.202 was observed for the standard Binomial BayesB GLM (Table 1). The Binomial GLM had generally significantly higher predictive abilities than their Gaussian counterparts, for both the BayesB as well as the GBLUP methods. For both the standard Binomial and the Gaussian GLM, method BayesB had a significantly higher predictive ability than GBLUP.

Maize haploid induction rate data set

Here, the highest average predictive ability was 0.684 observed for the Gaussian BayesB GLM (Table 1). For this data set, the Gaussian GLM had significantly higher predictive abilities than their Binomial counterparts. BayesB had again a significantly higher predictive ability than GBLUP, for both the Binomial and the Gaussian GLM. A finite mixture Binomial BayesB GLM with K = 2 yielded a slightly but significantly higher predictive ability than the standard Binomial BayesB GLM.

The ESS for marker effects (BayesB) and total genetic effects (GBLUP) for the Gaussian models were in most cases close to the actual sample sizes (3,000 for BayesB and 5,000 for GBLUP) (Table 2). The ESS for the Binomial models, however, were considerably lower than the actual sample sizes but always above 400.

Table 2 Mean effective sample size of marker effects (BayesB) and total genetic values (GBLUP), for the standard Binomial and Gaussian BayesB and GBLUP GLM, averaged over cross-validation runs for the wheat female fertility and maize haploid induction data sets

Simulated data sets

Results for the polygenic trait architecture showed that the average prediction accuracy increased with increasing N, from 0.686 at N = 100, to 0.781 at N = 200 and to 0.819 at N = 300 and with increasing λ, from 0.567 at λ = 25, to 0.801 at λ = 100 and to 0.898 at λ = 500 (Table 3). The increase in prediction accuracy with increasing λ thereby depended on the size of N. For example, the average increase from λ = 25 to λ = 100 amounted to 0.282 at N = 100 and 0.230 at N = 200, but just 0.190 at N = 300. Analogously, the increase in prediction accuracy with increasing N depended on the level of λ. For example, the increase of N from 100 to 200 increased the prediction accuracy by 0.156 at λ = 25, by 0.105 at λ = 100, but only by 0.050 at λ = 500.

Table 3 Average prediction accuracy over 50 replications for the simulated data set with polygenic and oligogenic trait architecture, for the Binomial and Gaussian BayesB and GBLUP generalized linear models

Binomial GLM tended to have higher prediction accuracies than Gaussian GLM for λ < 250, but for greater values of λ the prediction accuracy of the Gaussian GLM was equal or higher (Table 3). The superiority of Binomial over the Gaussian GLM was highest for λ = 25. GBLUP had in most cases a slightly higher prediction accuracy than BayesB, but there were no obvious trends regarding the relative superiority of BayesB and GBLUP with respect to N or λ.

Virtually, the same trends with regard to N and λ as for the polygenic trait architecture were observed for the oligogenic trait architecture (Table 3). In the case of BayesB, the Binomial GLM had always significantly higher prediction accuracy compared with Gaussian GLM, with greater differences for lower values of λ. For GBLUP, Binomial GLM had higher prediction accuracy until λ = 100, after which Gaussian GLM had prediction accuracies of equal or slightly higher size. On average (across Binomial and Gaussian GLM), BayesB was only slightly superior to GBLUP. However, the differences between the Binomial BayesB GLM, which had the highest prediction accuracy in all cases, and the Binomial GBLUP GLM were considerably greater than this.

For the simulated overdispersion data sets, by far the lowest prediction accuracies were observed for κ = 10, i.e., for strong overdispersion (Table 4). The highest prediction accuracies were observed for κ = 1,000, but the average difference to κ = 100 was with 0.052 marginal compared with the average difference between κ = 10 and κ = 100, which was 0.288. The average prediction accuracies increased with increasing N, from 0.435 at N = 100 to 0.549 at N = 200 and to 0.609 at N = 300 (Table 4).

Table 4 Average prediction accuracy over 50 replications for the simulated data set with overdispersion using the Binomial BayesB GLM

The standard Binomial BayesB GLM fitted with M = 500 tended to have slightly higher prediction accuracies than the same model fitted with the reduced marker sets (Table 4). Because the differences were marginal, the comparison between models will be focused on the comparison between the standard GLM with M = 500 and the finite mixture Binomial GLMs (with K = 2). For κ = 10, the highest prediction accuracies were observed for the finite mixture Binomial GLM (Table 4). The difference thereby increased with increasing N, from 0.044 at N = 100, to 0.130 at N = 200, to 0.171 at N = 300. The increase in difference thereby mostly came from an increased prediction accuracy of the finite mixture Binomial GLM. The prediction accuracy of the standard Binomial GLM changed only marginally. For κ = 100 and κ = 1, 000, however, the standard Binomial GLM had higher (at N = 100 and N = 200) or virtually equal (at N = 300) prediction accuracies (Table 4).

Discussion

Influence of training set size and number of Bernoulli trials

Prediction accuracies increased with increasing N, as expected and already observed in previous research for Gaussian traits (Zhong et al. 2009). We also observed a considerable increase in prediction accuracy with increasing λ, i.e., n _i . The higher n _i , the better will s _i represent the true probability parameter p _i of the individual. Thus, an increase in λ will have the same effect as an increase in h ², which was previously recognized as major factor influencing prediction accuracy (Villumsen et al. 2009).

Interestingly, a high λ could almost compensate for low N. For example, for N = 100 and λ = 500 the prediction accuracies were as high or even higher than at N = 300 and λ = 100. An elaborate study about the optimal allocation of resources, taking the relative costs of increasing N and λ into account, should be conducted to investigate the optimal combination of N and λ under a restricted total budget. We speculate that λ should always be raised to high values, because this would be absolutely neutral with respect to genotyping costs. However, we recognize that λ is biologically constrained in many cases, for example by the number of progeny seeds of a plant. We limited ourselves to p _i within the interval [0, 0.1]. The effect of λ will likely be smaller for values of p _i closer to 0.5, where a Gaussian distribution will be approached already for much lower values of λ. However, while increasing λ has the effect of better representing the information in the data provided by the N biological replicates, the actual amount of information can only be increased by increasing N. Conversely, if N and thereby the information content of the data becomes too low, the prediction accuracy will inevitably deteriorate strongly, regardless of how high λ is. Therefore, the most critical factor remains N. This is apparent from the fact that even at very low λ, accurate prediction is possible when N is high. This is in fact the typical scenario encountered in human genetic studies, where n _i  = 1 but often N ≫ 1,000 (Wray et al. 2008; Lee et al. 2011).

Model comparison based on simulated data sets

As expected, BayesB tended to be superior under an oligogenic trait architecture and GBLUP under a polygenic trait architecture. Numerous researchers found similar results for traits displaying a Gaussian phenotypic distribution (Kärkkäinen and Sillanpää 2012; Hayes et al. 2010; Clark et al. 2011; Zhong et al. 2009). Kärkkäinen and Sillanpää (2012) previously also reported that Bayesian marker effect models are superior to GBLUP models under an oligogenic trait architecture for binary traits (i.e., with n _i  = 1 for all i). Thus, we can confirm these observations for Binomial phenotypic distributions, too. However, the differences between BayesB and GBLUP were rather small, especially under the polygenic trait architecture. The choice between BayesB and GBLUP might therefore be driven by convenience considerations regarding computation and implementation. However, computational requirements of Binomial GBLUP GLM were not necessarily lower than those of Binomial BayesB GLM in our study. We used MCMC algorithms also for the Gaussian models. We are aware that approximate but fast expectation–maximization algorithms are available, for which computation times are almost negligible (Kärkkäinen and Sillanpää 2012). Nevertheless, it seems that our BayesB method, with hyperpriors on hyperparameters, cannot be fitted by them (Kärkkäinen and Sillanpää 2012). We furthermore decided against their use to be able to compare Binomial and Gaussian GLM on exactly the same terms. Recently, an improved auxiliary mixture sampler for logistic GLM was developed, which has the potential of substantially decreasing the computation times for the Binomial GLM due to increased efficiency (Fussl et al. 2012).

The greatest gains in prediction accuracy by using Binomial GLM were observed for smaller values of λ, where the distribution of the data is definitely non-Gaussian, and for p _i values far removed from 0.5. For higher values of λ, the distribution of the data will rapidly approach a Gaussian distribution. Consequently, results from Gaussian and Binomial GLM converged for the highest values of λ considered, at least under the polygenic trait architecture. Under the oligogenic trait architecture, the best Binomial model (BayesB) remained consistently superior over its Gaussian counterparts, albeit with reduced differences. We speculate that this is so because usage of the correct model and likelihood function is more important when estimating effects of single markers than when estimating total genetic effects of individuals, because the latter might be more robust with regard to the distribution underlying the data. With true probability parameters p _i closer to 0.5, the distribution of the data would approach a Gaussian distribution earlier, i.e., for lower values of λ. However, the range of p _i chosen by us reflects the most interesting situation of traits deviating substantially from a Gaussian distribution, where finding better alternatives than the standard Gaussian GLM is most important. This range seems also of greatest relevance in practice. For example, both experimental data sets used in this study exhibit probability parameters close to 1.0 or 0.0. This will also be the case for traits such as seed emergence, where the emergence rate of reasonably well-adapted material almost always exceeds 0.90 (Goggi et al. 2007).

The standard Gaussian GLM used commonly in genomic prediction, which we used as baseline for comparison with our Binomial GLM, make the simplifying assumption of homogeneous residual variances. Thus, they ignore that some individuals will have been phenotyped more precisely than others, depending on the size of n _i . Our Binomial GLM automatically incorporate the differences in n _i , via heteroscedastic residual variances (Frühwirth-Schnatter et al. 2009). The resulting weighing of the observations in the training set by n _i is therefore another advantage of Binomial GLM over the standard Gaussian GLM. However, in Gaussian GLM as well, records could be explicitly weighted by 1/n _i , which could alleviate this disadvantage.

Our results suggest that a Gaussian GLM might indeed provide a useful approximation on an ad hoc basis when the phenotypic distribution approaches a Gaussian distribution. However, real-world data are too complex to know in advance when exactly this will be the case. Therefore, when dealing with Binomial data, the performance of a Binomial GLM should always be evaluated before relying on a Gaussian approximation.

Modeling overdispersion

Our simulations clearly showed that accounting for overdispersion with finite mixture models is vital and improves prediction accuracy considerably, when there is strong overdispersion present in the data. Nonetheless, nonidentifiability still was an issue, especially for N = 100, where the finite mixture models performed significantly worse than the standard model under higher values of κ, i.e., when overdispersion was less pronounced. The better performance for κ = 10, however, showed that under strong overdispersion the greater flexibility of the finite mixture models overcompensates for problems due to nonidentifiability.

Comparing the results for κ = 1,000 with the results of the corresponding scenario in Table 3 (for which conceptually $\kappa =\infty$) shows that even low degrees of overdispersion can depress prediction accuracies. Thus, finite mixture models could still be of advantage under low degrees of overdispersion, but presumably only with very high N.

How much nonidentifiability depresses prediction accuracy will depend on the size of N compared with M. At higher N, we were able to fit more markers without severe nonidentifiability problems, as long as the increase in M was under proportional to the increase in N.

Owing to extensive long-range LD in bi-parental populations, a high marker density is not required for accurate genomic predictions. This is apparent from the only very marginal difference in prediction accuracy between the standard Binomial GLM fitted with the full and reduced marker sets. Reducing the number of markers for improving identifiability of finite mixture GLM therefore does not reduce the LD between markers and QTL to such an extent as to negatively affect the performance of the model. In most other types of populations encountered in animal or plant breeding, the marker density will be much more critical. How finite mixture Binomial GLM can be applied under such scenarios remains to be studied.

Wheat female fertility data set

The typical value of n _i observed in this data set corresponds to our λ = 25 scenario in the simulated data. Thus, in line with our findings on the clear superiority of Binomial GLM under low λ, we found that Binomial GLM performed better than the Gaussian alternatives. For the full data set, the best model was the finite mixture Binomial BayesB GLM, indicating that there indeed was overdispersion present in this data set. The standard Binomial BayesB GLM was the best model for the “high fertility subset”, however. Thus, either there was no overdispersion, or it could not be modeled due the nonidentifiability problems mentioned above.

Che and Xu (2012), who previously analyzed this data set, also found that using a Binomial GLM (with probit link, though) delivers considerably better QTL detection results than a Gaussian GLM. They also strongly argued in favor of using Binomial GLM for Binomial data, if only for the sake of statistical rigor, regardless of the quality of the approximation by Gaussian GLM. The authors also reported the presence of major QTL, explaining why BayesB tended to outperform GBLUP.

The low level of the predictive ability generally observed for the “high fertility subset” is most likely attributable to the low marker density, which left some of the chromosomes completely uncovered. The fertility rates of the full data set are concentrated at very high and very low values. Therefore, the model mostly captures the differentiation between these two groups. Thus, what is predicted is mainly whether a new observation has a very low or very high fertility. Doing this correctly is obviously easier than to predict the right order within any of these two groups (e.g., within the “high fertility subset”) and may be done with lower marker coverage, which may explain the higher predictive ability observed for the full data set.

The presence of a number of observations far from the bulk of the data, with numbers of seeded spikelets very close to or exactly zero, might be an indication of zero-inflation, i.e., the presence of more zeros in the data than expected from the (overdispersed) Binomial model. Thus, incorporating zero-inflation into the models, as is often done for Poisson data (Meng 1997), might be worthwhile.

Maize haploid induction data set

Our results for the maize data set indicated that in bi-parental populations an average of about ten markers per chromosome is sufficient for obtaining decent levels of predictive ability. Results of our simulations showed that Binomial and Gaussian GLM converged for the highest value of λ = 500. Therefore, we did not expect the Binomial GLM to perform notably better than the Gaussian GLM for this data set, where the typical value of n _i was greater than 1,000. That the finite mixture Binomial BayesB GLM yielded a higher prediction accuracy than the standard Binomial GLM is again an indication of overdispersion in the data.

Prigge et al. (2012) detected several major QTL within this data set, again explaining why BayesB outperformed GBLUP significantly. To generate a sufficient number of DH lines and to exploit the entire genetic variance present in the source germplasm, a high HIR of the inducers is desired, especially because many of the haploid seedlings will not survive the subsequent chromosomal doubling process. Currently, the HIR of known inducers rarely exceeds 8 %. Therefore, breeding efforts are underway for improving HIR and based on our results, genomic prediction of HIR could be a valuable tool in this process, given the generally high predictive abilities observed.

In summary, we found that Binomial GLM, based either on marker effects or on total genetic values, can increase the accuracy of the predictions considerably as compared with Gaussian GLM. We further found that accounting for overdispersion can increase prediction accuracy and is vital under strong overdispersion.