Robust Sparse Normalized LMAT Algorithms for Adaptive System Identification Under Impulsive Noise Environments

Abstract

It is known that the conventional adaptive filtering algorithms can have good performance for non-sparse systems identification, but unsatisfactory performance for sparse systems identification. The normalized least mean absolute third (NLMAT) algorithm which is based on the high-order error power criterion has a strong anti-jamming capability against the impulsive noise, but reduced estimation performance in case of sparse systems. In this paper, several sparse NLMAT algorithms are proposed by inducing sparse-penalty functions into the standard NLMAT algorithm in order to exploit the system sparsity. Simulation results are given to validate that the proposed sparse algorithms can achieve a substantial performance improvement for a sparse system and robustness to impulsive noise environments.

1 Introduction

Adaptive filtering algorithms have received much attention over the past decades and are widely used for diverse applications such as system identification, adaptive beamforming, interference cancelation and channel estimation [15, 19, 30, 35]. The least mean square (LMS) algorithm, introduced by Widrow and Hoff [41], has become one of the most popular methods for adaptive system identification due to its simplicity and low computational complexity. The normalized least mean square (NLMS) was also proposed to further improve the identification performance [34, 41]. There is a trade-off between lower steady-state error and fast convergence rate in LMS and NLMS. However, their major drawbacks are slow convergence and performance degradation with colored input signals or in the presence of heavy-tailed impulsive interferences [33]. Therefore, in order to overcome these limitations, a normalized robust mixed-norm RMN (NRMN) algorithm [26, 27] was presented by using the variable step size instead of the fixed step size of the RMN algorithm [7]. Nevertheless, it needs to know the variance of the white noise and impulsive noise. In the recent years, adaptive filtering algorithms that were based on high-order error power (HOEP) conditions were proposed [13, 28, 39] which can improve the convergence rate performance and mitigate the noise interference effectively. The least mean absolute third (LMAT) algorithm is based on the minimization of the mean of the absolute error value to the third power [12, 13]. The error function is a perfect convex function with respect to the filter coefficients, so there is no local minimum for the LMAT algorithm. The LMAT algorithm often converges faster than the LMS algorithm and is suitable for various noise conditions [23]. To alleviate the dependence of the input signal power effect, a normalized form of LMAT (NLMAT) algorithm is proposed in [43]. The NLMAT algorithm exhibits good stability and can mitigate non-Gaussian impulsive noise.

In many physical scenarios, the unknown systems to be identified exhibit sparse representation, i.e., their impulse response has few nonzero (dominant) coefficients, while most of the coefficients are zero or close to zero. Such systems are encountered in many practical applications such as wireless multipath channels [1], acoustic echo cancelers [4] and digital TV transmission channels [31]. The channel impulse response in an acoustic system is relatively long due to the presence of echoes, but is zero for most of the time. Such a system is said to be sparse, meaning that many of the terms in the impulse response are zero, while only a few terms are nonzero. It is worthy to note that if the a priori knowledge about the system sparsity is properly utilized, the identifying performance can be improved. However, all of the above-mentioned algorithms do not take into account such sparse prior information present in the system and may lose some estimation performance.

Recently, many sparse adaptive filter algorithms that exploit system sparsity have been proposed, notable among them being the proportionate normalized LMS (PNLMS) algorithm [17] and its variants [5, 11, 14, 22]. On the other hand, motivated by the least absolute shrinkage and selection operator (LASSO) [38] and the recent research in compressive sensing [3, 6, 16], an alternative approach to identify sparse systems has been proposed in [10]. The approach applies ℓ₁ relaxation, to improve the performance of the LMS algorithm. To achieve further performance improvement, adaptive sparse channel estimation methods using reweighted ℓ1-norm sparse-penalty LMS (RL1-LMS) [36, 37] and non-uniform norm constraint LMS (NNC-LMS) [42] were also proposed. Under the Gaussian noise model assumption, these algorithms exhibit improved performance in comparison with the traditional adaptive filters. Recently, a novel ℓ0-norm approximate method based on the correntropy-induced metric (CIM) [32] is widely used in sparse channel estimation [18, 21, 24, 40]. However, these methods may be unreliable in estimating the system under non-Gaussian impulsive noise environments. In [25], the impulsive noise is modeled as a sparse vector in the time domain and proved useful for a powerline communication application. Fractional adaptive identification algorithms have been applied for parameter estimation in channel equalization, linear and nonlinear control autoregressive moving average model [2, 8, 9, 29]. It is observed that fractional-based identification algorithms outperform standard estimation methods in terms of accuracy, convergence, stability and robustness. The theoretical development for the case in which both sparsity and impulsive noise are present is out of the scope of this paper.

The normalized LMAT algorithm has been successfully validated for system identification under impulsive noise environments [43]. To the best of our knowledge, no paper has reported on sparse NLMAT algorithms. In this paper, we propose sparse NLMAT algorithms based on different sparsity penalty terms to deal with sparse system identification under impulsive noise environment and various noise distributions. The following algorithms that integrate similar approaches presented above are proposed: the zero-attracting NLMAT (ZA-NLMAT), reweighted zero-attracting NLMAT (RZA-NLMAT), reweighted ℓ1-norm NLMAT (RL1-NLMAT), non-uniform norm constraint NLMAT (NNC-NLMAT) and correntropy-induced metric NLMAT (CIM-NLMAT).

The remaining part of the paper is organized as follows. Section 2 reviews the known LMAT and NLMAT algorithms. In Sect. 3, the sparse NLMAT algorithms are derived. In Sect. 4, we compare the proposed algorithms in terms of computational complexity. The performances of the proposed algorithms are demonstrated in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Review of LMAT and Normalized LMAT Algorithm

The general block diagram of sparse system identification using an adaptive filter is shown in Fig. 1.

Fig. 1

Block diagram of sparse system identification

The desired response $d(n)$ of the adaptive filter is calculated as $d(n) = {\mathbf{h}}^{T} \bar{x}(n) + v(n)$, where superscript T indicates transpose of matrix or vector, ${\mathbf{h}}$ denotes the weight vector of the unknown system of length L, $\bar{x}(n) = \left[ {x(n),x(n - 1), \ldots x(n - L + 1)} \right]^{T}$ is the input vector of the system, and $v(n)$ is the system background noise. The system noise consists of the impulsive noise along with different noise distributions (Gaussian, uniform, Rayleigh and exponential).

2.1 LMAT Algorithm

The objective function of LMAT algorithm is

$$ \begin{aligned} J_{\text{LMAT}} (n) & = \left| {e(n)} \right|^{3} \\ & = \left| {d(n) - y(n)} \right|^{3} \\ \end{aligned} $$

(1)

where $y(n) = \bar{W}^{T} (n)\bar{x}(n)$ is the output of the adaptive filter, $e(n) = d(n) - y(n)$ denotes the error signal, and $\bar{W}(n) = \left[ {w_{1} (n),w_{2} (n), \ldots w_{L} (n)} \right]^{\text{T}}$ is the weight vector of the adaptive filter.

The gradient descent method is used to minimize $J_{\text{LMAT}} (n)$ which can be expressed as

$$ \bar{W}(n + 1) = \bar{W}(n) - \frac{\mu }{3}\frac{{\partial J_{\text{LMAT}} (n)}}{{\partial \bar{W}(n)}} $$

(2)

By substituting Eq. (1) in the above equation, the weight update rule of the LMAT algorithm is given by

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]\bar{x}(n) $$

(3)

where the positive constant $\mu$ is the step-size parameter.

$\text{sgn} (x)$ denotes the sign function of $x$ which is defined as

$$ \begin{aligned} \text{sgn} (x) & = \frac{x}{\left| x \right|},\quad x \ne 0 \\ & = 0 ,\quad x = 0\\ \end{aligned} $$

(4)

The drawback of the LMAT algorithm is that its convergence performance is highly dependent on the power of the input signal.

2.2 Normalized LMAT Algorithm

To avoid the limitation of the LMAT algorithm, the NLMAT algorithm [43] is derived by considering the following minimization problem [34]:

$$ \mathop {\hbox{min} }\limits_{{\bar{W}(n + 1)}} \left\{ {\frac{1}{3}\left| {d(n) - \bar{W}^{T} (n + 1)\bar{x}(n)} \right|^{3} + \frac{1}{2}\left\| {\bar{x}(n)} \right\|^{2} \left\| {\bar{W}(n + 1) - \bar{W}(n)} \right\|^{2} } \right\} $$

(5)

where $\left\| \bullet \right\|$ is the Euclidean norm of a vector.

Derivating Eq. (5) with respect to $\bar{W}(n + 1)$ and equating to zero yields

$$ \bar{W}(n + 1) = \bar{W}(n) + \frac{{e^{2} (n)\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{T} (n)\bar{x}(n)}} $$

(6)

The weight update equation for the NLMAT algorithm is given by

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu \frac{{e^{2} (n)\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{T} (n)\bar{x}(n) + \delta }} $$

(7)

where $\mu$ is a step-size parameter, and $\delta$ is a small positive constant to prevent division by zero when $\bar{x}^{T} (n)\bar{x}(n)$ vanishes.

In the presence of impulsive noises, the squared error term $e^{2} (n)$ in Eq. (7) might degrade the NLMAT algorithm in the convergence performance, and hence, we consider assigning an upper-bound $e_{\text{up}}$ to $e^{2} (n)$.

Thus, the NLMAT algorithm is modified as

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu \frac{{\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{T} (n)\bar{x}(n) + \delta }}\hbox{min} \left\{ {e^{2} (n),e_{\text{up}} } \right\} $$

(8)

where $e_{\text{up}}$ is the upper-bound assigned to $e^{2} (n)$ in Eq. (7).

The posteriori error $e_{p} (n)$ is defined as

$$ \begin{aligned} e_{p} (n) & = d(n) - \bar{W}^{T} (n + 1)\bar{x}(n) \\ & = e(n)\left[ {1 - \mu \frac{{e(n)\text{sgn} [e(n)]\bar{x}^{T} (n)\bar{x}(n)}}{{\delta + \bar{x}^{T} (n)\bar{x}(n)}}} \right] \\ \end{aligned} $$

(9)

For convenience, we can neglect the small parameter δ in Eq. (9) and have

$$ e_{p} (n) = e(n)[1 - \mu e(n)\text{sgn} [e(n)]] $$

(10)

Taking the mathematical expectation of both sides of Eq. (10),

$$ E\text{[}e_{p} (n)\text{]} = E\text{[}e(n)\text{]} - E\text{[}\mu e^{2} (n)sgn\text{[}e(n)\text{]]} $$

(11)

Denoting $\bar{\mu } = \mu e^{2} (n)$ [20], Eq. (11) is rewritten as

$$ E[e_{p} (n)] = E[e(n)] - E[\bar{\mu }\text{sgn} [e(n)]] $$

(12)

By using the Price’s theorem in [12], Eq. (12) can be simplified as

$$ E[e_{p} (n)] = E[e(n)] - \sqrt {\frac{2}{\pi }} \frac{1}{{\sigma_{e} (n)}}E[\bar{\mu }e(n)] $$

(13)

where $\sigma_{e} (n)$ is the standard deviation of the error e(n).

In steady-state condition, the algorithm is assumed to be converged such that the error e(n) is considerably smaller. Hence,

$$ E[\bar{\mu }e(n)] = E[\bar{\mu }]E[e(n)] $$

(14)

Thus, substituting Eq. (14) into Eq. (13), we get

$$ E[e_{p} (n)] = E[e(n)]\left[ {1 - \sqrt {\frac{2}{\pi }} \frac{1}{{\sigma_{e} (n)}}E[\bar{\mu }]} \right] $$

(15)

The magnitude of the a posteriori error $E[e_{p} (n)]$ does not exceed that of the priori error $E[e(n)]$, and then, the following inequality must be satisfied [20]

$$ \left| {1 - \sqrt {\frac{2}{\pi }} \frac{1}{{\sigma_{e} (n)}}E[\bar{\mu }]} \right| < 1 $$

(16)

Finally, by solving Eq. (16), we can obtain the upper-bound of ${\text{e}}_{\text{up}}$ as

$$ e_{\text{up}} = \frac{{\sqrt {2\pi } \sigma_{e} (n)}}{\mu } $$

(17)

The standard deviation $\sigma_{e} (n)$ is estimated by the following probabilistic method [7, 26, 27]

$$ \sigma_{e} (n) = \sqrt {\frac{{O^{T} (n)T_{w} O(n)}}{{N{}_{w} - K}}} $$

(18)

where $T_{w}$ is the diagonal matrix defined as, $T_{w} = {\text{diag}}[1, \ldots ,1,0, \ldots 0],$ that sets the last $K$ elements of $O(n)$ to zero, and forms an unbiased estimate $\sigma_{e} (n)$ by using the remaining ($N{}_{w} - K$) elements.

$O(n) = {\text{sort}}\left( {\left[ {\left| {e(n)} \right|, \ldots ,\left| {e(n - N_{w} + 1)} \right|} \right]^{T} } \right)$ contains the $N_{w}$ most recent values of $e(n)$ arranged in the increasing order of the absolute value.

In general, $N{}_{w}$ and $K$ are chosen as $N_{w} = L$ and $K \ge 1 + \left\lfloor {L\Pr } \right\rfloor$ where $\left\lfloor \bullet \right\rfloor$ is the floor operator which rounds a number to the next integer and $\Pr$ is the probability of the impulsive noise occurrence.

3 Proposed Sparse NLMAT Algorithms

To exploit the system sparsity and robustness against impulsive noise, several sparse NLMAT algorithms are proposed by inducing effective sparsity constraints into the standard NLMAT, namely zero-attracting NLMAT, reweighted zero-attracting NLMAT, reweighted ℓ1-norm (RL1)-NLMAT, non-uniform norm constraint (NNC)-NLMAT and correntropy-induced metric (CIM)-NLMAT.

The update equation of LMAT sparse adaptive filter can be generalized as

$$ \bar{W}(n + 1) = \underbrace {{\underbrace {{\bar{W}(n) + {\text{ Adaptive}}\;{\text{error}}\;{\text{update}}}}_{\text{LMAT}} + {\text{Sparse}}\;{\text{penalty}}}}_{{{\text{sparse}}\;{\text{LMAT}}}} $$

(19)

3.1 Zero-Attracting NLMAT (ZA-NLMAT)

The cost function of ZA-LMAT filter with ℓ1-norm penalty is given by

$$ J_{\mathrm{ZA}} (n) = \frac{1}{3}\left| {e(n)} \right|^{3} + \lambda_{\mathrm{ZA}} \left\| {\bar{W}(n)} \right\|_{1} $$

(20)

The updating equation of ZA-LMAT filter can be written as

$$ \bar{W}(n + 1) = \bar{W}(n) - \mu \frac{{\partial J_{ZA} (n)}}{{\partial \bar{W}(n)}} $$

(21)

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]\bar{x}(n) - \rho_{\mathrm{ZA}} \text{sgn} (\bar{W}(n) $$

(22)

where $\rho_{\mathrm{ZA}} = \mu \lambda_{\mathrm{ZA}}$.

Based on the updated Eq. (7), the NLMAT-based sparse adaptive updated equation can be generalized as

$$ \bar{W}(n + 1) = \underbrace {{\underbrace {\begin{aligned} \bar{W}(n) + {\text{Normalized}}\;{\text{Adaptive}} \hfill \\ {\text{ error}}\;{\text{update}} \hfill \\ \end{aligned} }_{\text{NLMAT}} + {\text{ Sparse}}\;{\text{penalty}}}}_{{{\text{sparse}}\;{\text{NLMAT}}}} $$

(23)

In order to avoid the stability issues of Eq. (22), the modified form can be represented as

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu \frac{{e^{2} (n)\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{T} (n)\bar{x}(n) + \delta }} - \rho_{\mathrm{ZA}} \text{sgn} (\bar{W}(n)) $$

(24)

Equation (24) corresponds to the updated equation of sparse NLMAT filter.

The update equation of the modified sparse NLMAT algorithm is given by

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu \frac{{\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{T} (n)\bar{x}(n) + \delta }}\hbox{min} \left\{ {e^{2} (n),e_{\text{up}} } \right\} - \rho_{\mathrm{ZA}} \text{sgn} (\bar{W}(n)) $$

(25)

which is termed as the zero-attracting NLMAT (ZA-NLMAT).

The ZA-NLMAT algorithm based on ℓ1-norm penalty is easy to implement and performs well for the systems that are highly sparse, but struggles as the system sparsity decreases. This behavior comes from the fact that the shrinkage parameter in the ZA-NLMAT cannot distinguish between zero taps and nonzero taps. Since all the taps are forced to zero uniformly, its performance would deteriorate for less sparse systems.

3.2 Reweighted Zero-Attracting NLMAT (RZA-NLMAT)

The cost function of the Reweighted ZA-LMAT algorithm is derived by introducing the log-sum penalty

$$ J_{\mathrm{RZA}} (n) = \frac{1}{3}\left| {e(n)} \right|^{3} + \lambda_{\mathrm{RZA}} \sum\limits_{i = 1}^{L} {\log \left( {1 + \varepsilon_{\mathrm{RZA}} \left| {w_{i} (n)} \right|} \right)} $$

(26)

The ith filter coefficient is then updated as

$$ \begin{aligned} w_{i} (n + 1) & = w_{i} (n) - \mu \frac{{\partial J_{\mathrm{RZA}} (n)}}{{\partial w_{i} (n)}} \\ & = w_{i} (n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]x_{i} (n) - \rho_{\mathrm{RZA}} \frac{{\text{sgn} (w_{i} (n))}}{{1 + \varepsilon_{\mathrm{RZA}} \left| {w_{i} (n)} \right|}} \\ \end{aligned} $$

(27)

The RZA-LMAT update equation can be expressed in vector form as

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]\bar{x}(n) - \rho_{\mathrm{RZA}} \frac{{\text{sgn} (\bar{W}(n))}}{{1 + \varepsilon_{\mathrm{RZA}} \left| {\bar{W}(n)} \right|}} $$

(28)

By using $\lambda_{\mathrm{RZA}} \sum\nolimits_{i = 1}^{L} {\log (1 + \varepsilon_{\mathrm{RZA}} \left| {w_{i} (n)} \right|)}$ as a sparse penalty in Eq. (23), the RZA-NLMAT update equation can be expressed as

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu \frac{{\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{T} (n)\bar{x}(n) + \delta }}\hbox{min} \left\{ {e^{2} (n),e_{up} } \right\} - \rho_{\mathrm{RZA}} \frac{{\text{sgn} (\bar{W}(n))}}{{1 + \varepsilon_{\mathrm{RZA}} \left| {\bar{W}(n)} \right|}} $$

(29)

where $\rho_{\mathrm{RZA}} = \mu \lambda_{\mathrm{RZA}} \varepsilon_{\mathrm{RZA}}$ and $\lambda_{\mathrm{RZA}} > 0$ is the regularization parameter for RZA-NLMAT.

A logarithmic penalty that resembles the ℓ0-norm which is the exact measure of sparsity is considered in RZA-NLMAT. This makes RZA-NLMAT to exhibit a better performance than the ZA-NLMAT. However, the cost function Eq. (26) is not convex and the convergence analysis is problematic for Eq. (29).

3.3 Reweighted ℓ1-Norm NLMAT (RL1-NLMAT)

Since the complexity of using the ℓ0-norm penalty is high, a term more similar to the ℓ0-norm, i.e., the reweighted ℓ1-norm penalty is used in the proposed RL1-NLMAT algorithm. This penalty term is proportional to the reweighted ℓ1-norm of the coefficient vector.

The cost function of the reweighted ℓ1-norm LMAT algorithm is given by

$$ J_{{{\text{RL}}1}} (n) = \frac{1}{3}\left| {e(n)} \right|^{3} + \lambda_{{{\text{RL}}1}} \left\| {\bar{f}(n)\bar{W}(n)} \right\|_{1} $$

(30)

where $\lambda_{{{\text{RL}}1}}$ is the parameter associated with the penalty term and the elements of $\bar{f}(n)$ are set to

$$ \left[ {\bar{f}(n)} \right]_{i} = \frac{1}{{\delta_{{{\text{RL}}1}} + \left| {\left[ {\bar{W}(n - 1)} \right]_{i} } \right|}},\quad i = 0,1, \ldots L - 1 $$

(31)

with $\delta_{{{\text{RL}}1}}$ being some positive number, and hence, $\left[ {\bar{f}(n)} \right]_{i} > 0$ for $i =0,1, \ldots\break L - 1.$ Differentiating Eq. (30) with respect to $\bar{W}(n),$, the update equation of RL1-LMAT is

$$ \begin{aligned} \bar{W}(n + 1) & = \bar{W}(n) - \mu \frac{{\partial J_{{{\text{RL}}1}} (n)}}{{\partial \bar{W}(n)}} \\ & = \bar{W}(n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]\bar{x}(n) - \rho_{{{\text{RL}}1}} \frac{{\text{sgn} \left( {\bar{W}(n)} \right)}}{{\delta_{{{\text{RL}}1}} + \left| {\bar{W}(n - 1)} \right|}} \\ \end{aligned} $$

(32)

According to the NLMAT in Eq. (8), the update equation of RL1-NLMAT can be written as

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu \frac{{\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{\text{T}} (n)\bar{x}(n) + \delta }}\hbox{min} \left\{ {e^{2} (n),e_{\text{up}} } \right\} - \rho_{RL1} \frac{{\text{sgn} \left( {\bar{W}(n)} \right)}}{{\delta_{{{\text{RL}}1}} + \left| {\bar{W}(n - 1)} \right|}} $$

(33)

where $\rho_{{{\text{RL}}1}} = \mu \lambda_{{{\text{RL}}1}}$.

The cost function Eq. (30) is convex unlike the cost function for the RZA-NLMAT. Therefore, the algorithm is guaranteed to converge to the global minimum under some conditions.

3.4 Non-uniform Norm Constraint NLMAT (NNC-NLMAT)

In all the above algorithms, there is no adjustable factor which can effectively adapt the norm penalty itself to the unknown sparse finite impulse response of the system. In order to further improve the performance of sparse system identification, the non-uniform p-norm-like constraint is incorporated into NLMAT algorithm.

Let us consider the cost function of sparse NLMAT with p-norm-like constraint as

$$ J(n) = \frac{1}{3}\left| {e(n)} \right|^{3} + \lambda \left\| {\bar{W}(n)} \right\|_{p}^{p} $$

(34)

where $\left\| {\bar{W}(n)} \right\|_{p}^{p} = \sum\limits_{i = 1}^{L} {\left| {w_{i} (n)} \right|}^{p}$ is called $L_{p}^{p} {\text{ - norm}}$ or p-norm like, $0 \le p \le 1$.

The gradient of the cost function $J(n)$ with respect to $\bar{W}(n)$ is

$$ \nabla J(n) = \frac{{\partial \left( {\frac{1}{3}\left| {e(n)} \right|^{3} } \right)}}{{\partial \bar{W}(n)}} + \lambda \frac{{\partial \left\| {\bar{W}(n)} \right\|_{p}^{p} }}{{\partial \bar{W}(n)}} $$

(35)

Thus, the gradient descent recursion of the filter coefficient vector is

$$ \begin{aligned} w_{i} (n + 1) & = w_{i} (n) - \mu \nabla J(n) \\ & = w_{i} (n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]x(n - i) - \rho \frac{{p\text{sgn} (w_{i} (n))}}{{\left| {w_{i} (n)} \right|^{1 - p} }},\quad \forall 0 \le i < L \\ \end{aligned} $$

(36)

Similar to the sparse algorithms created by using ℓ0-norm and ℓ1-norm, the zero attractor term in Eq. (36) which is produced by the p-norm-like constraint will cause an estimation error for the desired sparsity exploitation. To solve this problem, the non-uniform p-norm-like definition which uses a different value of p for each of the L entries in $\bar{W}(n)$ is provided,

$$ \left\| {\bar{W}(n)} \right\|_{p,L}^{p} = \sum\limits_{i = 1}^{L} {\left| {w_{i} (n)} \right|}^{{p_{i} }}, \quad 0\le {{p}}_{{i}} \le 1 $$

(37)

The new cost function using the non-uniform p-norm-penalty is given as

$$ J_{\text{NNC}}^{{}} (n) = \frac{1}{3}\left| {e(n)} \right|^{3} + \lambda_{\text{NNC}} \left\| {\bar{W}(n)} \right\|_{p,L}^{p} $$

(38)

The corresponding gradient descent recursion equation is

$$ w_{i} (n + 1) = w_{i} (n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]x(n - i) - \rho_{NNC} \frac{{p_{i} \text{sgn} (w_{i} (n))}}{{\left| {w_{i} (n)} \right|^{{1 - p_{i} }} }},\quad \forall 0 \le i < L $$

(39)

$$ g(n) = E\left[ {\left| {w_{i} (n)} \right|} \right],\quad \forall 0 \le i < L $$

(40)

$$ w_{i} (n + 1) = w_{i} (n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]x(n - i) - \rho_{\text{NNC}} f_{i} \text{sgn} (w_{i} (n)),\quad \forall 0 \le i < L $$

(41)

where

$$ f_{i} = \frac{{\text{sgn} \left[ {g(n) - \left| {w_{i} (n)} \right|} \right] + 1}}{2},\quad \forall 0 \le i < L $$

(42)

and $\rho_{\text{NNC}} = \mu \lambda_{\text{NNC}}$.

The reweighted zero attraction which is used to reduce the bias is introduced to Eq. (41).

The weight update equation of NNC-LMAT algorithm is written as

$$ w_{i} (n + 1) = w_{i} (n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]x(n - i) - \, \rho_{NNC} \frac{{f_{i} \text{sgn} (w_{i} (n))}}{{1 + \varepsilon_{\text{NNC}} \left| {w_{i} (n)} \right|}},\quad \forall 0 \le i < L $$

(43)

where $\varepsilon_{\text{NNC}} > 0.$

The weight update equation of NNC-NLMAT algorithm can be written in vector form as

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu \frac{{\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{T} (n)\bar{x}(n) + \delta }}\hbox{min} \left\{ {e^{2} (n),e_{\text{up}} } \right\} - \frac{{\rho_{\text{NNC}} F\text{sgn} (\bar{W}(n))}}{{1 + \varepsilon_{\text{NNC}} \left| {\bar{W}(n)} \right|}} $$

(44)

where $\varvec{F}$ is defined as

$$ \varvec{F} = \left[ \begin{aligned} f_{0} \hfill \\ 0 \hfill \\ \vdots \hfill \\ 0 \hfill \\ \end{aligned} \right.\left. \begin{aligned} 0 \cdots 0 \hfill \\ f_{1} \cdots 0 \hfill \\ 0 \ddots 0 \hfill \\ 0 \cdots f_{L - 1} \hfill \\ \end{aligned} \right]_{L \times L} $$

(45)

3.5 Correntropy-Induced Metric NLMAT (CIM-NLMAT)

Due to the superiority of the correntropy-induced metric (CIM) for approximate the ℓ0-norm, CIM is used as the penalty term in the CIM-NLMAT algorithm. CIM favors sparsity and can be used as a sparsity penalty term in the sparse channel estimation.

The similarity between two random vectors $\varvec{p} = \left\{ {p_{1} ,p_{2} , \ldots p_{L} } \right\}$ and $\varvec{q} = \left\{ {q_{1} ,q_{2} , \ldots q_{L} } \right\}$ in kernel space can be measured using CIM which is described as

$$ {\text{CIM(}}\varvec{p,q} )= \left( {{{k(0)}} - \hat{V} (\varvec{p,q} )} \right)^{{{\raise0.7ex\hbox{$ 1$} \!\mathord{\left/ {\vphantom { 12}}\right.\kern-0pt} \!\lower0.7ex\hbox{$ 2$}}}} $$

(46)

where

$$ k(0) = \frac{1}{{\sigma \sqrt {2\pi } }}, {\text{and}} $$

(47)

$$ \hat{V} (\varvec{p,q} )= \frac{1}{L}\sum\limits_{i = 1}^{L} {k(p_{i} ,q_{i} )} $$

(48)

For the Gaussian kernel,

$$ k(p,q) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left( { - \frac{{e^{2} }}{{2\sigma^{2} }}} \right) $$

(49)

here ${{e}} = {{p}} - {{q}}$ and $\sigma$ is the kernel width.

The CIM provides a good approximation for the ℓ0-norm that can be represented as

$$ \left\| \varvec{p} \right\|_{0} \sim{\text{CIM}}^{2} (\varvec{p},0) = \frac{k(0)}{L}\sum\limits_{i = 1}^{L} {\left( {1 - \exp \left( { - \frac{{\left( {p_{i} } \right)^{2} }}{{2\sigma^{2} }}} \right)} \right)} $$

(50)

The Gaussian kernel-based CIM is integrated into the cost function of the LMAT algorithm which is given by

$$ \begin{aligned} J_{\text{CIM}} (n) & = \frac{1}{3}\left| {e(n)} \right|^{3} + \lambda_{\text{CIM}} {\text{CIM}}^{2} (\bar{W}(n),0) \\ & = \frac{1}{3}\left| {e(n)} \right|^{3} + \lambda_{\text{CIM}} \frac{k(0)}{L}\sum\limits_{i = 1}^{L} {\left( {1 - \exp \left( { - \frac{{\left( {w_{i} (n)} \right)^{2} }}{{2\sigma^{2} }}} \right)} \right)} \\ \end{aligned} $$

(51)

The gradient of the cost function $J_{\text{CIM}} (n)$ with respect to $\bar{W}(n)$ is

$$ \begin{aligned} \nabla J_{\text{CIM}} (n) & = \frac{{\partial J_{\text{CIM}} (n)}}{\partial W(n)} \\ & = - e^{2} (n)\text{sgn} \left[ {e(n)} \right]x(n - i) + \lambda_{\text{CIM}} \frac{1}{{L\sigma^{3} \sqrt {2\pi } }}w_{i} (n)\exp \left( { - \frac{{\left( {w_{i} (n)} \right)^{2} }}{{2\sigma^{2} }}} \right) \\ \end{aligned} $$

(52)

The weight update equation of CIM-LMAT is expressed as

$$ \begin{aligned} w_{i} (n + 1) & = w_{i} (n) - \mu \nabla J_{\text{CIM}} (n) \\ & = w_{i} (n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]x(n - i) - \rho_{\text{CIM}} \frac{1}{{L\sigma^{3} \sqrt {2\pi } }}w_{i} (n)\exp \left( { - \frac{{\left( {w_{i} (n)} \right)^{2} }}{{2\sigma^{2} }}} \right) \\ \end{aligned} $$

(53)

where $\rho_{\text{CIM}} = \mu \lambda_{\text{CIM}} > 0$ is a regularization term which balances the estimation error and sparsity penalty.

Equation (53) can be rewritten in matrix form as

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu e^{2} (n)\text{sgn} \left[ {e(n)} \right]\bar{x}(n) - \rho_{\text{CIM}} \frac{1}{{L\sigma^{3} \sqrt {2\pi } }}\bar{W}(n)\exp \left( { - \frac{{\left\| {\bar{W}(n)} \right\|^{2} }}{{2\sigma^{2} }}} \right) $$

(54)

By using $\lambda_{\text{CIM}} \frac{k(0)}{L}\sum\limits_{i = 1}^{L} {\left( {1 - \exp \left( { - \frac{{\left( {w_{i} (n)} \right)^{2} }}{{2\sigma^{2} }}} \right)} \right)}$ as a sparse penalty in Eq. (23), the CIM-NLMAT update equation is given by

$$\begin{aligned} w_{i} (n + 1) &= w_{i} (n) + \mu \frac{{\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\sum\nolimits_{i = 0}^{L - 1} {(x(n - i))^{2} } + \delta }}\hbox{min} \left\{ {e^{2} (n),e_{\text{up}} } \right\}x(n - i)\\ & - \rho_{\text{CIM}} \frac{1}{{L\sigma^{3} \sqrt {2\pi } }}w_{i} (n)\exp \left( { - \frac{{\left( {w_{i} (n)} \right)^{2} }}{{2\sigma^{2} }}} \right),\end{aligned} $$

(55)

The matrix form of CIM-NLMAT algorithm is expressed as

$$ \bar{W}(n + 1) = \bar{W}(n) + \mu \frac{{\text{sgn} \left[ {e(n)} \right]\bar{x}(n)}}{{\bar{x}^{T} (n)\bar{x}(n) + \delta }}\hbox{min} \left\{ {e^{2} (n),e_{\text{up}} } \right\} - \rho_{\text{CIM}} \frac{1}{{L\sigma^{3} \sqrt {2\pi } }}\bar{W}(n)\exp \left( { - \frac{{\left( {\bar{W}(n)} \right)^{2} }}{{2\sigma^{2} }}} \right) $$

(56)

Pseudocodes for the proposed sparse NLMAT algorithms are summarized in Table 1.

Table 1 Pseudocodes

4 Computational Complexity

The numerical complexity of the proposed sparse algorithms in terms of additions, multiplications, divisions, square roots and comparisons per iteration is shown in Table 2.

Table 2 Comparison of computational complexity of the investigated algorithms

5 Simulation Results

In this section, the performance of the proposed sparse algorithms is evaluated in the context of system identification using various noise distributions and impulsive noise environment. The unknown system, h, is of length L = 16, and its channel impulse response (CIR) is assumed to be sparse in the time domain. The adaptive filter is also assumed to be of the same length. The proposed algorithms are compared under different sparsity levels S = 1 and S = 4. The active coefficients are uniformly distributed in the interval (− 1, 1), and the position of the nonzero taps in the CIR is randomly chosen. The Gaussian white noise with variance $\sigma_{x}^{2} = 1$ is considered as the input signal $x(n)$. The correlated signal $\bar{z}(n)$ is obtained using a first-order autoregressive process, AR(1), with a pole 0.5 and is given by $\bar{z}(n) = 0.5\bar{z}(n - 1) + \bar{x}(n)$. The system background noise consists of impulsive noise combined with different noise distributions such as (1) white Gaussian noise with $N(0,1)$, (2) uniformly distributed noise within the range (-1, 1), (3) Rayleigh distribution with 1 and (4) an exponential distribution with 2. The impulsive noise is modeled by a Bernoulli–Gaussian (BG) process and is given as $\xi (n) = a(n)I(n)$, where $a(n)$ is a white Gaussian signal with $N\left( {0,\sigma_{a}^{2} } \right)$ and $I(n)$ is a Bernoulli process described by the probability $p\left\{ {I(n) = 1} \right\} = \Pr$, $p\left\{ {I(n) = 0} \right\} = 1 - \Pr ,$ where $Pr$ represents the probability of the impulsive noise occurrence. We choose $Pr$ = 0.01 and $\sigma_{a}^{2} = {\raise0.7ex\hbox{${10^{4} }$} \!\mathord{\left/ {\vphantom {{10^{4} } {12}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${12}$}}$.

The mean square deviation (MSD) and excess mean square error (EMSE) are used as the performance metrics to measure the performance of the proposed algorithms which are expressed as

$$ {\text{MSD}}({\text{dB}}) = 10\log_{10} \left( {\left\| {\varvec{h} - \bar{W}(n)} \right\|_{ 2}^{ 2} } \right) $$

(57)

and

$$ {\text{EMSE(dB)}} = 1 0 {\text{log}}_{ 1 0} \left[ {\varepsilon (n)} \right]^{ 2} , {\text{respectively}}. $$

(58)

$\varepsilon (n) = \theta^{T} (n)\bar{x}(n),$ where $\theta (n) = \varvec{h} - \bar{W}(n).$

The average of 100 independent trials with SNR = 20 dB is used in evaluating the results.

In order to show the effectiveness of the proposed sparse NLMAT algorithms, a comparison with the NRMN algorithms is performed. In Fig. 2, the simulation results for the proposed algorithms are shown for the white Gaussian input and when the background noise consists of only white Gaussian noise for the system with sparsity S = 1. The simulation results shown in Fig. 3 are carried out for the white Gaussian input with background noise consisting of white Gaussian noise and impulsive noise with sparsity level S = 1. It can be seen from Figs. 2 and 3 that the proposed sparse NLMAT algorithms exhibit better performance than NLMAT and NRMN algorithms in terms of MSD for the very sparse system. Moreover, the proposed CIM-NLMAT algorithm achieves lower steady-state error value.

Fig. 2

MSD Comparison of the proposed algorithms with white Gaussian noise as the background noise and the Gaussian white input signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 5 \times 10^{ - 5} ,$$\rho_{\mathrm{RZA}} = 3 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 1 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 3

MSD Comparison of the proposed algorithms with white Gaussian noise and impulsive noise as the background noise and the white Gaussian input signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 4 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 1 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

In Fig. 4, the simulation results for the proposed algorithms are shown for the white Gaussian input, while the background noise has white noise with uniform distribution within the range (−1, 1) and impulsive noise for the system with sparsity S = 1. In Fig. 5, the input is white Gaussian with background noise consisting of Rayleigh distributed noise with 1 and impulsive noise for the system with sparsity S = 1. In Fig. 6, the input is white Gaussian signal and the background noise is composed of an exponential distribution of 2 and impulsive noise for the system with sparsity S = 1.

Fig. 4

MSD Comparison of the proposed algorithms when the background noise is composed of white noise with uniform distribution within the range (−1, 1) and impulsive noise and the white Gaussian input signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 4 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 1 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 5

MSD Comparison of the proposed algorithms with background noise comprising of a Rayleigh distributed noise with 1 and impulsive noise and the input is white Gaussian signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 3 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01$$\rho_{\text{NNC}} = 1 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 6

MSD Comparison of the proposed algorithms with background noise comprising of an exponential distribution with 2 and impulsive noise and the white Gaussian input signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 3 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 2 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

It can be easily seen from Figs. 4, 5 and 6 that the proposed sparse NLMAT algorithms provide better performance than NLMAT and NRMN algorithms in terms of MSD for the very sparse system. As shown above, the proposed CIM-NLMAT algorithm achieves lower steady-state error too.

The EMSE values of the proposed algorithms obtained for different noises with uncorrelated input and system sparsity S = 1 are given in Table 3. It is confirmed that the proposed sparse algorithms outperform the NLMAT algorithm in identifying a sparse system.

Table 3 Comparison of EMSE values for different NLMAT algorithms with uncorrelated input signal and system sparsity S = 1

In the simulations shown in Figs. 7, 8, 9, 10, 11, the input signal is the correlated/colored input and the system sparsity is S = 1. In Fig. 7, the system noise is only white Gaussian noise, while for Fig. 8 is both white Gaussian noise and impulsive noise. The system noise for simulations shown in Fig. 9 consists of white noise with uniform distribution within the range (−1, 1) and impulsive noise. In the case of Fig. 10, the system noise has Rayleigh distributed noise of 1 and impulsive noise, while for Fig. 11 consists of an exponential distribution of 2 and impulsive noise. It is observed from Figs. 7, 8, 9, 10 and 11 that the proposed sparse NLMAT algorithms exhibit better performance than NLMAT and NRMN algorithms in terms of MSD for the very sparse system. Moreover, like for the previous simulations, the proposed CIM-NLMAT algorithm achieves the lowest steady-state error value.

Fig. 7

MSD Comparison of the proposed algorithms with white Gaussian noise as the background noise and the input is the correlated signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 5 \times 10^{ - 5} ,$$\rho_{\mathrm{RZA}} = 3 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 1 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 8

MSD Comparison of the proposed algorithms with white Gaussian noise and impulsive noise as the background noise and the input is the correlated signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 4 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 1 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 9

MSD Comparison of the proposed algorithms when the background noise is comprised of white noise with uniform distribution within the range (−1, 1) and impulsive noise and the correlated input signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 3 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 1 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 10

MSD Comparison of the proposed algorithms with background noise comprising of a Rayleigh distributed noise with 1 and impulsive noise and the input is the correlated signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 3 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 3 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 1 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 11

MSD Comparison of the proposed algorithms with background noise comprising of an exponential distribution with 2 and impulsive noise and the input is the correlated signal for the system with sparsity S = 1. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{ZA} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 4} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 3 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 2 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 2 \times 10^{ - 3} ,$$\sigma = 0.05$

The EMSE values of the proposed algorithms obtained for different noises with correlated/colored input and system sparsity S = 1 are given in Table 4. It can be easily noticed that the proposed sparse algorithms outperform the NLMAT algorithm in identifying a sparse system.

Table 4 Comparison of EMSE values for different NLMAT algorithms with correlated/colored input signal and system sparsity S = 1

In Figs. 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, the performance of the proposed algorithms when the system sparsity is changed to S = 4 is shown.

Fig. 12

MSD Comparison of the proposed algorithms with white Gaussian noise as the background noise and the Gaussian white input signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 4} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 13

MSD Comparison of the proposed algorithms with white Gaussian noise and impulsive noise as the background noise and the white Gaussian input signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 5 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 8 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 14

MSD Comparison of the proposed algorithms when the background noise is composed of white noise with uniform distribution within the range (−1, 1) and impulsive noise and the white Gaussian input signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 4} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 8 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 15

MSD Comparison of the proposed algorithms with background noise comprising of a Rayleigh distributed noise with 1 and impulsive noise and the input is white Gaussian signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 4} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 16

MSD Comparison of the proposed algorithms with background noise comprising of an exponential distribution with 2 and impulsive noise and the white Gaussian input signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 5 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 8 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 6 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 17

MSD Comparison of the proposed algorithms with white Gaussian noise as the background noise and the input is the correlated signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 1 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 4} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 18

MSD Comparison of the proposed algorithms with white Gaussian noise and impulsive noise as the background noise and the input is the correlated signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 4 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 4 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 8 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{CIM} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 19

MSD Comparison of the proposed algorithms when the background noise is comprised of white noise with uniform distribution within the range (− 1, 1) and impulsive noise and the correlated input signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 3 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 7 \times 10^{ - 5} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 8 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 20

MSD Comparison of the proposed algorithms with background noise comprising of a Rayleigh distributed noise with 1 and impulsive noise and the input is the correlated signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 2 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 1 \times 10^{ - 4} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 8 \times 10^{ - 3} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

Fig. 21

MSD Comparison of the proposed algorithms with background noise comprising of an exponential distribution with 2 and impulsive noise and the input is the correlated signal for the system with sparsity S = 4. The simulation parameters for sparse NLMAT algorithms are given as $\mu = 0.8,$$\delta = 1 \times 10^{ - 3} ,$$\rho_{\mathrm{ZA}} = 2 \times 10^{ - 4} ,$$\rho_{\mathrm{RZA}} = 5 \times 10^{ - 3} ,$$\varepsilon_{\mathrm{RZA}} = 20,$$\rho_{{{\text{RL}}1}} = 2 \times 10^{ - 4} ,$$\delta_{{{\text{RL}}1}} = 0.01,$$\rho_{\text{NNC}} = 1 \times 10^{ - 2} ,$$\varepsilon_{\text{NNC}} = 20,$$\rho_{\text{CIM}} = 5 \times 10^{ - 3} ,$$\sigma = 0.05$

In Fig. 12, the simulation results for the proposed algorithms are shown for the white Gaussian input and when the background noise consists of only white Gaussian noise for the system with sparsity S = 4. The simulation results shown in Fig. 13 are carried out for the white Gaussian input with background noise consisting of white Gaussian noise and impulsive noise with sparsity level S = 4. It can be seen from Figs. 12 and 13 that the proposed sparse NLMAT algorithms exhibit better performance than NLMAT and NRMN algorithms in terms of MSD even after changing the system sparsity to S = 4.

In Fig. 14, the simulation results for the proposed algorithms are shown for the white Gaussian input, while the background noise has white noise with uniform distribution within the range (− 1, 1) and impulsive noise for the system with sparsity S = 4. In Fig. 15, the input is white Gaussian with background noise consisting of Rayleigh distributed noise with 1 and impulsive noise for the system with sparsity S = 4. In Fig. 16, the input is white Gaussian signal and the background noise is composed of an exponential distribution of 2 and impulsive noise for the system with sparsity S = 4.

It can be easily seen from Figs. 14, 15 and 16 that the proposed sparse NLMAT algorithms provide better performance than NLMAT and NRMN algorithms in terms of MSD even after changing the system sparsity to S = 4. As shown above, the proposed CIM-NLMAT algorithm achieves lower steady-state error too.

The EMSE values of the proposed algorithms obtained for different noises with uncorrelated input and system sparsity S = 4 are given in Table 5. It is confirmed that the proposed sparse algorithms outperform the NLMAT algorithm in identifying a sparse system.

Table 5 Comparison of EMSE values for different NLMAT algorithms with uncorrelated input signal and system sparsity S = 4

In the simulations shown in Figs. 17, 18, 19, 20 and 21, the input signal is the correlated/colored input and the system sparsity is changed to S = 4. In Fig. 17, the system noise is only white Gaussian noise, while for Fig. 18 is both white Gaussian noise and impulsive noise. The system noise for simulations shown in Fig. 19 is comprised of white noise with uniform distribution within the range (− 1, 1) and impulsive noise. In the case of Fig. 20, the system noise has Rayleigh distributed noise of 1 and impulsive noise, while for Fig. 21 consists of an exponential distribution of 2 and impulsive noise. It is observed from Figs. 17, 18, 19, 20 and 21 that the proposed sparse NLMAT algorithms exhibit better performance than NLMAT and NRMN algorithms in terms of MSD even after changing the system sparsity to S = 4. Moreover, like for the previous simulations, the proposed CIM-NLMAT algorithm achieves the lowest steady-state error.

The EMSE values of the proposed algorithms obtained for different noises with correlated/colored input and system sparsity S = 4 are given in Table 6. It can be shown that the proposed sparse algorithms outperform the NLMAT algorithm in identifying a sparse system.

Table 6 Comparison of EMSE values for different NLMAT algorithms with correlated/colored input signal and system sparsity S = 4

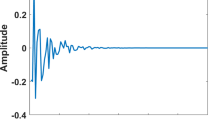
Let us now consider a network echo cancelation (NEC) system with the echo path impulse response of length L = 512 as shown in Fig. 22. This is a sparse impulse response.

Fig. 22

Network echo path impulse response

In Fig. 23, the simulation results for the proposed algorithms are shown for the white Gaussian input and when the background noise consists of both white Gaussian noise with SNR = 20 dB, and impulsive noise. It can be seen from Fig. 23 that the proposed sparse NLMAT algorithms exhibit better performance than the NLMAT algorithm for long echo paths with sparse impulse response.

Fig. 23

MSD Comparison of the proposed algorithms in a NEC sparse system with white Gaussian noise and impulsive noise as the background noise and the input is white Gaussian signal

In Fig. 24, the input signal is the correlated/colored input and the system noise is comprised of both white Gaussian noise and impulsive noise. It is observed that the proposed sparse NLMAT algorithms exhibit better performance than NLMAT algorithm. Moreover, like for the previous simulations, the proposed CIM-NLMAT algorithm achieves the lowest steady-state error for long echo paths with sparse impulse response.

Fig. 24

MSD Comparison of the proposed algorithms in a NEC sparse system with white Gaussian noise and impulsive noise as the background noise and the input is the AR(1) correlated signal

6 Conclusion

The normalized LMAT algorithm based on high-order error power (HOEP) criterion achieves improved performance and mitigates the noise interference effectively, but it does not promote sparsity. Hence, in this paper, we have proposed different sparse normalized LMAT algorithms in the sparse system identification context. From the simulation results, it is verified that our proposed sparse algorithms are capable of exploiting the system sparsity as well as providing robustness to impulsive noise. Moreover, the proposed CIM-NLMAT algorithm exhibits superior performance in the presence of different types of noise. The comparison of the proposed algorithms with the fractional adaptive algorithms will be investigated in a future paper.