1 Introduction

Sparse representations are typical in unknown systems, when they are being identified, signifying that only a certain portion of their impulse response's coefficients are nonzero (dominant), while the bulk of them are 0 or almost 0. Many real-world applications, including digital TV transmission channels [1], acoustic echo cancelers [2], and wireless multipath channels [3], involve such systems.

The conventional algorithms like the least mean square (LMS) [4], least mean square/fourth (LMS/F) [5], normalized least mean square (NLMS) [6], least mean kurtosis (LMK) [7] algorithms, etc., based on gradient descent technique were developed for different applications. Later Lyapunov adaptive filtering (LA) algorithms [8, 9] were proposed to overcome drawbacks encountered by gradient descent-based techniques like local minima problem, slow rate of convergence, but the aforementioned algorithms failed to work for sparse systems. Therefore, researchers have shown interest in developing adaptive algorithms to identify sparse systems [10,11,12,13,14,15,16,17]. When there are many more small-magnitude coefficients than large-magnitude coefficients, a system is said to be sparse. Sparsity norm-based and proportionate-type adaptive algorithms are two general categories of sparsity-aware adaptive algorithms for recognizing sparse systems [13]. In the sparsity norm-based approach, an additional regularization term that promotes sparsity is introduced to push the smaller coefficients approaching zero. When using a proportionate-based approach, the convergence is quickened by adjusting the gain term, that is proportional with the filter weights; in other words, it is larger for effective filter coefficients and lower for inert coefficients. The proportionate type is favored and employed in this study because of the difficulties in choosing the regularization factor in sparsity norm employing algorithms and being unable to operate with systems that may not be exactly sparse but still feature a reasonably sparse structure.

The majority of proportionate adaptive algorithms rely on the Gaussian assumption and are established on mean square error (MSE) criterion. In [11], a filter proportionate normalized least mean square (FPNLMS) method was proposed for a compressed input signal by the utilization of variable step size to adapt sparse systems. This resulted in improved performance compared to the other existing algorithms like PNLMS [12], improved PNLMS (IPNLMS) [14], and µ-law PNLMS (MPNLMS) [15] algorithms. But in actual time, the noise encountered is frequently impulsive, and the conventional methods struggle with this situation. The maximum correntropy criterion (MCC), a new robust optimum criterion, was recently utilized effectively in adaptive filtering [18, 19]. MCC cost becomes an effective selection in an impulsive interference environment because correntropy is resistive to outliers for suitable kernel width. For effective utilization in sparse systems some specific proportionate-type adaptive filtering approaches relying on maximum correntropy criteria (MCC) [20] and the proportional minimum error entropy (MEE) method [21] were created to counter impulsive noise. An improved proportionate algorithm utilizing the maximum correntropy criteria (IP-MCC) was presented to detect the system with changing sparsity under the impulsive noise environment [22], but the inclusion of double-sum operations and exponential components led these techniques to have a high computational cost. Adaptive filter established on the maximum versoria criteria (MVC) has recently acquired a lot of interest because, compared to other competing approaches, it performs better under non-Gaussian noise and requires fewer computations [23]. Later the proportionate MVC (P-MVC) method combined the MVC features of resilience to impulsive noise with the proportional notion to leverage sparsity for identifying sparse systems [24].

It is possible to enhance the robustness of adaptive algorithms by using saturation characteristics of nonlinearities in errors like arctangents. Hence a novel cost function framework was introduced and established on this characteristic of an arctangent function where the typical cost function was featured within the arctangent framework. This brought about the establishment of arctangent families of robust algorithms like the arctangent LMS (ALMS), arctangent least mean fourth (ALMF) [25], and arctangent LMS/F (ALMS/F) for system identification [26]. However, the above-mentioned algorithms were sparse agnostic.

The filter proportional (FP) adaptation concept is applied to the ALMS algorithm and is known as a filter proportionate arctangent LMS (FP-ALMS) method in response to the facts and drawbacks listed above. The following are the paper's key contributions: 1. The ALMS is subjected to FP adaptation ideas, resulting in the FP-ALMS algorithm that takes advantage of the system's sparseness properties. 2. It is investigated how the proportionate factor affects the final excess mean square error (EMSE) and the stability restriction for the step size. 3. The steady-state EMSE of the FP-ALMS algorithm is established, and the computational complexity is analyzed. 4. The proposed algorithm’s performance is tested for several sparse systems under the effect of impulsive noise. The following is a summary of the paper's structure. In Sect. 2, a novel FP-ALMS algorithm is developed. The FP-ALMS algorithm's performance is investigated in Sect. 3. Steady-state performance and computational complexity are analyzed in Sect. 4. In Sect. 5, the simulated outcomes are compiled. Lastly Sect. 6 of this brief deals with the conclusion.

2 Proposed FP-ALMS algorithm

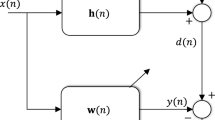
Consider an unknown sparse system where \({\mathbf{x}}\left( k \right) = [x\left( k \right), x\left( {k - 1} \right), . . . , x\left( {k - M + 1} \right)]^{T}\) signifies the input signal with length \(M\). The unknown physical system vector is denoted by \({\varvec{w}}_{0}\) of size \(M \times 1\), whereas the desired signal \(d\left( k \right) = {\varvec{w}}_{0}^{T} {\varvec{x}}\left( k \right) + \eta \left( k \right)\) with \(\eta \left( k \right)\) being the noise signal. The error \(e\left( k \right)\) in the system’s output is stated as

$$ e\left( k \right) = d\left( k \right) - \hat{y}\left( k \right) $$
(1)

with \(\hat{y}\left( k \right) = \hat{\user2{w}}^{T} {\varvec{x}}\left( k \right)\) characterizes the adaptive filter’s output having \(\hat{\user2{w}}\left( k \right) = [\hat{w}_{1} , \hat{w}_{2} , . . . , \hat{w}_{M} ]^{T}\) represents the adaptive filter’s weight vector. The ALMS algorithm’s cost function is given as [25]

$$ J\left( k \right) = \tan^{ - 1} \left[ {\gamma \zeta \left( k \right)} \right] $$
(2)

where \(\zeta \left( k \right) = E\left[ {e^{2} \left( k \right)} \right]\) is the LMS algorithm’s cost function [4] and \(\gamma\) > 0 suggests the steepness of the arctangent framework. Utilizing the gradient descent technique, the ALMS algorithm’s weight update representation is written as [25]

$$ \hat{\user2{w}}\left( {k + 1} \right) = \hat{\user2{w}}\left( k \right) - \mu ^{\prime}\frac{\partial J\left( k \right)}{{\partial \hat{\user2{w}}\left( k \right)}} $$
(3)

In Eq. (3), µ′ representing step size Eqs. (1) and (3) is combined to produce the following result:

$$ \hat{\user2{w}}\left( {k + 1} \right) = \hat{\user2{w}}\left( k \right) + \mu \frac{{e\left( k \right){\varvec{x}}\left( k \right)}}{{(1 + [\gamma \left( {e^{2} \left( k \right)} \right]^{2} )}} $$
(4)

with the cumulative step-size factor denoted by \(\mu = \mu^{\prime } \gamma\). Equation (4) is represented as

$$ \hat{\user2{w}}\left( {k + 1} \right) = \hat{\user2{w}}\left( k \right) + \mu f\left( {e\left( k \right)} \right){\varvec{x}}\left( k \right) $$
(5)

with the nonlinear function \(f\left( {e\left( k \right)} \right)\) is indicated as

$$ f(e\left( k \right) = \frac{e\left( k \right)}{{(1 + [\gamma \left( {e^{2} \left( k \right)} \right]^{2} )}} $$
(6)

It is seen that for large values of \(e\left( k \right)\), the nonlinear function \(f\left( {e\left( k \right)} \right)\) becomes 0. This results in an improvement of the robustness of the ALMS algorithm to impulsive noise. Meanwhile when \(\gamma \to 0\), the ALMS algorithm is identical to the LMS algorithm, and when \(\gamma \to \infty\), \(f\left( {e\left( k \right)} \right)\) approaches 0 thus reducing the convergence rate. Using filter proportionate adaptation concepts, the ALMS algorithm can take advantage of the system’s sparsity by multiplication of the proportionate gain matrix \({\varvec{Q}}\left( k \right)\) with a weight update vector to benefit from the sparsity and thus increasing the convergence time. The weight vector formula of the novel filter proportionate ALMS (FP-ALMS) algorithm is stated as

$$ \hat{\user2{w}}\left( {k + 1} \right) = \hat{\user2{w}}\left( k \right) + \mu \left( k \right)f\left( {e\left( k \right)} \right){\varvec{Q}}\left( k \right){\varvec{x}}\left( k \right) $$
(7)

where \( {\varvec{Q}}\left( k \right) = {\text{diag}}(q_{1} \left( k \right),q_{2} \left( k \right) \ldots q_{M} \left( k \right)\)). The gain factor elements are given as [14]

$$ q_{l} \left( k \right) = \frac{1 - \theta }{{2M}} + \left( {1 + \theta } \right)\frac{{\left| {\hat{w}_{l} \left( k \right)} \right|}}{ {2\left\| {\widehat{\varvec{w}}\left( k \right)_{1} } \right\|} + \varepsilon } $$
(8)

where \(l = 1,2, \ldots M\), \(- 1 \le \theta \le 1,\) and ε is a positive number that avoids division by 0 in Eq. (8). The step size in Eq. (7) is revised in accordance with the filter coefficient and is written as

$$ \mu \left( {k + 1} \right) = \mu \left( k \right) + \beta \left( {1 - l_{\infty }{\prime} \left( k \right)} \right)e\left( k \right)e\left( {k - 1} \right) $$
(9)

where

$$ l_{\infty } \left( k \right) = \max \left\{ {\left| {\hat{w}_{1} \left( k \right)} \right|,\left| {\hat{w}_{2} \left( k \right)} \right|, \ldots \left| {\hat{w}_{M} \left( k \right)} \right| } \right\} $$
(10)

When all the filter coefficients are 0 initially, a slight medication is done in \(l_{\infty } \left( k \right)\) to avoid the step size of stalling and is written as

$$ l_{\infty }{\prime} \left( k \right) = \max \left\{ { \delta ,l_{\infty } \left( k \right) } \right\} $$
(11)

where \(\delta\) is a small positive value that becomes ineffective post-first iteration [11].

3 Performance analysis

This segment presents the performance study of the suggested FP-ALMS algorithm. The step size limits needed to satisfy the convergence requirement and how proportionate terms affect steady-state behavior are discussed using the transformed domain model [24]. The proposed FP-ALMS algorithm utilizes the transformed matrix \({\varvec{Q}}^{\frac{1}{2}} \left( k \right)\) given as

$$ {\varvec{Q}}^{\frac{1}{2}} \left( k \right) = {\text{diag}}[q_{1}^{\frac{1}{2}} \left( k \right), q_{2}^{\frac{1}{2}} \left( k \right) \ldots q_{M}^{\frac{1}{2}} \left( k \right)] $$
(12)

and the transformed input vector \({\varvec{x}}_{t} \left( k \right) = {\varvec{Q}}^{\frac{1}{2}} \left( k \right){\varvec{x}}\left( k \right)\). Similarly, the transformed filter coefficients \(\hat{\user2{w}}_{t} \left( k \right) = {\varvec{Q}}^{{ - \frac{1}{2}}} \left( k \right)\hat{\user2{w}}\left( k \right)\). From the equations written above we get \(\hat{\user2{w}}_{t}^{T} \left( k \right){\varvec{x}}_{t} \left( k \right) = \hat{\user2{w}}^{T} \left( k \right){\varvec{x}}\left( k \right)\). Let the weight error vector is set as \(\tilde{\user2{w}}\left( k \right) = {\varvec{w}}_{o} - \hat{\user2{w}}\left( k \right)\), in the transformed domain we get \(\tilde{\user2{w}}_{t} \left( k \right) = {\varvec{Q}}^{{ - \frac{1}{2}}} \left( k \right)\left( {{\varvec{w}}_{o} - \hat{\user2{w}}\left( k \right)} \right) = {\varvec{Q}}^{{ - \frac{1}{2}}} \left( k \right){\varvec{w}}_{o} - \hat{\user2{w}}_{t} \left( k \right)\). Therefore \(e\left( k \right)\) is written as

$$ e\left( k \right) = e_{a} \left( k \right) + \eta \left( k \right) = \tilde{\user2{w}}^{T} \left( k \right){\varvec{x}}\left( k \right) + \eta \left( k \right) = \tilde{\user2{w}}_{t}^{T} \left( k \right){\varvec{x}}_{t} \left( k \right) + \eta \left( k \right) $$
(13)

where \(e_{a} \left( k \right) = \tilde{\user2{w}}^{T} \left( k \right){\varvec{x}}\left( k \right) = \tilde{\user2{w}}_{t}^{T} \left( k \right){\varvec{Q}}^{\frac{1}{2}} \left( k \right){\varvec{Q}}^{{ - \frac{1}{2}}} \left( k \right){\varvec{x}}_{t} \left( k \right) = \tilde{\user2{w}}_{t}^{T} \left( k \right){\varvec{x}}_{t} \left( k \right)\) is the apriori error. Expressing Eq. (7) with reference to the weight error vector \(\tilde{\user2{w}}_{t} \left( k \right)\) and assuming that \({\varvec{Q}}\left( k \right)\) varies slowly as used in [22, 24], we get

$$ \tilde{\user2{w}}_{t} \left( {k + 1} \right) = \tilde{\user2{w}}_{t} \left( k \right) - \mu \left( k \right)f\left( {e\left( k \right)} \right){\varvec{x}}_{t} \left( k \right) $$
(14)

The mean square performance evaluation for the FP-ALMS algorithm is obtained using the conservation of energy equation.

$$ E\left[{\left\| {\tilde{\user2{w}}_{t} \left( {k + 1} \right) } \right\|}^{2}\right] = E\left[ {\left\|{\tilde{\user2{w}}_{t} \left( k \right) } \right\|}^{2}\right] - 2\mu E\left[ {\tilde{\user2{w}}_{t}^{T} \left( k \right){\varvec{x}}_{t} \left( k \right)f\left( {e\left( k \right)} \right)} \right] + \mu^{2} E[{\varvec{x}}_{t}^{T} \left( k \right)f(e\left( k \right))f\left( {e\left( k \right)){\varvec{x}}_{t} \left( k \right)} \right] $$
(15)

Substituting \(e_{a} \left( k \right)\) in Eq. (15) and assuming \(E\left[ {\left\|{{\varvec{x}}_{t} \left( k \right) } \right\|}^{2}\right]\) is asymptotically not dependent of \(f^{2} \left( {e\left( k \right)} \right)\), the relationship shown below is attained

$$ E\left[ {\left\|{\tilde{\user2{w}}_{t} \left( {k + 1} \right)} \right\|}^{2}\right] = E\left[{\left\| {\tilde{\user2{w}}_{t} \left( k \right) } \right\|}^{2}\right] - 2\mu E\left[ {e_{a} \left( k \right)f\left( {e\left( k \right)} \right)} \right] + \mu^{2} \left( k \right)E\left[ {\left\|{{\varvec{x}}_{t} \left( k \right) }\right\|^{2}} \right]E\left[ {f^{2} (e\left( k \right))} \right] $$
(16)

For steady-state conditions as \(k \to \infty\),

$$ E\left[ {\left\|{\tilde{\user2{w}}_{t} \left( {k + 1} \right) }\right\|}^{2} \right] \le E\left[{\left\| {\tilde{\user2{w}}_{t} \left( k \right) } \right\|}^{2}\right] $$
(17)

This, the stability condition concerning µ is provided by

$$ \mu \left( k \right) \le \frac{{2E[e_{a} \left( k \right)f\left( {e\left( k \right)} \right]}}{{E\left[{\left\| {{\varvec{x}}_{t} \left( k \right) }\right\|^{2}} \right]E\left[ {f^{2} \left( {e\left( k \right)} \right)} \right]}} $$
(18)

If we utilize the premise that \({\varvec{Q}}\left( k \right)\) is not dependent on \({\varvec{x}}_{t} \left( k \right)\) then

$$ \begin{gathered} E\left[ {\left\| {{\varvec{x}}_{t} \left( k \right) }\right\|^{2}} \right] = E\left[ {{\varvec{x}}_{t}^{T} \left( k \right){\varvec{x}}_{t} \left( k \right)} \right] = E\left[ {{\text{Tr}}\left[ {{\varvec{x}}_{t} \left( k \right){\varvec{x}}_{t}^{T} \left( k \right)} \right]} \right] \hfill \\ {\text{Tr}}[E\left[ {{\varvec{x}}_{t} \left( k \right){\varvec{x}}_{t}^{T} \left( k \right)} \right] = {\text{Tr}}\left[ {E\left[ {{\varvec{Q}}^{\frac{1}{2}} \left( k \right){\varvec{x}}\left( k \right){\varvec{x}}^{T} \left( k \right){\varvec{Q}}^{\frac{1}{2}} \left( k \right)} \right]} \right] \hfill \\ \end{gathered} $$
(19)

If \({\mathbf{S}}\left( k \right) = E\left[ {{\mathbf{Q}}^{\frac{1}{2}} \left( k \right){\varvec{R}}_{{\varvec{x}}} {\mathbf{Q}}^{\frac{1}{2}} \left( k \right)} \right]\), then

$$ E\left[{\left\| {{\mathbf{x}}_{t} \left( k \right) } \right\|^{2}}\right] = Tr\left[ {{\mathbf{S}}\left( k \right)} \right] $$

where \({\varvec{R}}_{x}\) is the autocorrelation matrix and \({\text{Tr}}\) is the trace operator. Using Eq. (19) in Eq. (18) we get

$$ \mu \left( k \right) \le \frac{{2E[e_{a} \left( k \right)f\left( {e\left( k \right)} \right]}}{{{\text{Tr}}\left[ {{\varvec{S}}\left( k \right)\left] E \right[f^{2} \left( {e\left( k \right)} \right)} \right]}} $$
(20)

Equation (20) illustrates that the stability bound matches up to that of the ALMS algorithm if \({\varvec{Q}}\left( k \right) = {\varvec{I}}\). Equation (20) can also be written as

$$ \mu \left( k \right) < \mu_{m} = \frac{{2E[e_{a} \left( k \right)f\left( {e\left( k \right)} \right]}}{{Tr\left[ {{\mathbf{S}}\left( k \right)\left] E \right[f^{2} \left( {e\left( k \right)} \right)} \right]}} $$
(21)

where \(\mu_{m}\) represents the step-size upper limit.

4 Steady-state performance

The steady-state EMSE in the context of an impulsive noise scenario as well as the impact of the proportionate gain factor over the final EMSE is investigated here. The steady-state EMSE is determined by calculating \(\mathop {{\text{Lim}}}\limits_{{k \to \infty }} \;E\left[ {\| {e_{a} \left( k \right) } \|^{2}} \right] \). Substituting Eq. (17) into Eq. (16) and using Eq. (19), we get

$$ 2E\left[ {e_{a} \left( k \right)f\left( {e\left( k \right)} \right] = \mu_{m} {\text{Tr}}} \right[{\varvec{S}}\left( k \right)\left] E \right[f^{2} (e\left( k \right))] $$
(22)

The Taylor series is used to expand the nonlinear component of error as seen below.

$$ f(\left( {e\left( k \right)} \right) = f\left( {e_{a} \left( k \right) + \eta \left( k \right)} \right) = f\left( {\eta \left( k \right)} \right) + f^{\prime}\left( {\eta \left( k \right)} \right)e_{a} \left( k \right) + \frac{1}{2}f^{\prime\prime}\left( {\eta \left( k \right)} \right)e_{a}^{2} \left( k \right) + O\left( {e_{a}^{2} \left( k \right)} \right) $$
(23)

where \(O\left( {e_{a}^{2} \left( k \right)} \right)\) denotes the third- and higher-order terms of \(e_{a} \left( k \right) \), whereas \(f^{\prime}\left( {\eta \left( k \right)} \right)\) and \(f^{\prime\prime}\left( {\eta \left( k \right)} \right)\) represent the 1st- and 2nd-order derivation of \(f\left( {\eta \left( k \right)} \right)\) and is written as

$$ f^{\prime}\left( \eta \right) = \frac{{1 - 3\gamma^{2} \eta^{4} }}{{\left[ {1 + \gamma^{2} \eta^{4} } \right]^{2} }} $$
(24)

and

$$ f^{\prime\prime}\left( \eta \right) = \frac{{4\gamma^{2} \eta^{3} \left( {3\gamma^{2} \eta^{4} - 5} \right)}}{{\left[ {1 + \gamma^{2} \eta^{4} } \right]^{3} }} $$
(25)

The left half of Eq. (22) is obtained as

$$ \begin{gathered} 2\mathop {{\text{Lim}}}\limits_{k \to \infty } \;E\left[ {e_{a} \left( k \right)f\left( {e\left( k \right)} \right] = 2\mathop {{\text{Lim}}}\limits_{k \to \infty } \;E} \right[e_{a} \left( k \right)(f\left( {\eta \left( k \right)} \right) + f^{\prime}\left( {\eta \left( k \right)} \right)e_{a} \left( k \right) \hfill \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{1}{2}f^{\prime \prime } \left( {\eta \left( k \right)} \right)e_{a}^{2} \left( k \right) + O\left( {e_{a}^{2} \left( k \right)} \right)} \right] \hfill \\ \end{gathered} $$
(26)

Utilizing the premise that the noise \(\eta \left( k \right)\) is i.i.d. (independent and identically distributed) having mean 0 and uncorrelated to the signal that serves as the input \({\varvec{x}}\left( k \right), \) together with a priori error \(e_{a} \left( k \right)\) having 0 mean and uncorrelated to the noise \(\eta \left( k \right)\) and ignoring the high-order components [22, 24], Eq. (26) is

$$ 2\mathop {{\text{Lim}}}\limits_{k \to \infty } E\left[ {e_{a} \left( k \right)f\left( {e\left( k \right)} \right] = 2{\text{EMSE}}\mathop {{\text{Lim}}\;E[}\limits_{k \to \infty } f^{\prime} \left( {\eta \left( k \right)} \right)} \right] $$
(27)

Similarly, the RHS of (22) is given as

$$ \begin{gathered} \mathop {{\text{Lim}}}\limits_{k \to \infty } \mu_{m} {\text{Tr}}\left[ {S\left( k \right)} \right]E[f^{2} \left( {e\left( k \right)} \right] = \mu_{m} \mathop {{\text{Lim}}}\limits_{k \to \infty } {\text{Tr}}\left[ {S\left( k \right)} \right]\left( {E\left[ {f^{2} \left( {\eta \left( k \right)} \right)} \right]} \right. \hfill \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + E\left[ {\left( {f\left( {\eta \left( k \right)} \right)f^{\prime \prime } \left( {\eta \left( k \right)} \right)} \right)\left| {f^{\prime } \left( {\eta \left( k \right)} \right)} \right|^{2} } \right]{\text{EMSE}}} \right) \hfill \\ \end{gathered} $$
(28)

The EMSE expression of the novel FP-ALMS algorithm is produced by removing EMSE from Eqs. (27) and (28) and utilizing the derivatives obtained from Eqs. (24) and (25).

$$ EMSE = \frac{{\mu_{m} Tr\left[ {{\mathbf{S}}\left( k \right)} \right]E[f^{2} \left( {\eta )} \right]}}{{2E\left[ {f^{\prime}\left( \eta \right)} \right] - \mu_{m} Tr\left[ {{\mathbf{S}}\left( k \right)} \right]E\left[ {\left( {f\left( \eta \right)f^{\prime\prime}\left( \eta \right)} \right)\left| {f^{\prime}\left( \eta \right)} \right|^{2} } \right]}} $$
(29)

The expectation terms in Eq. (29) can be obtained by integration [17]. Equation (29) illustrates the steady-state EMSE for the FP-ALMS algorithm and is analogous to the ALMS algorithm [27] which indicates the calculation is true.

The PMCC algorithm, IP-MCC algorithm, P-MVC algorithm, and the suggested algorithm’s computational complexity are illustrated in Table. 1. The complexity is measured using the required number of additions, multiplications, divisions, and exponential operations. Table 1 shows that the proposed FP-ALMS algorithm needs extra 2 additions, 7 multiplications, and 1 division terms in comparison with the P-MVC criterion-based algorithm.

Table 1 Computational complexity evaluation
Full size table

5 Simulation study

Three distinct experiments were assessed to determine the impact of the proposed approach. The suggested FP-ALMS algorithm was compared against the PMCC, IP-MCC, and P-MVC-based algorithms. The mean square deviation \({\text{MSD}} \left( {{\text{dB}}} \right) = 20\log_{10} {\|{\hat w}}\left( k \right) - {\varvec{{w}}_{{0}}\|_{2}}\) is the measurement metric employed to assess the proposed algorithm’s performance.

5.1 Experiment-I

The unidentified system to be simulated comprising of 120 samples is symbolized by the impulse response \(h\left( n \right)\) and is shown in Fig. 1. It is generated as \(h\left( n \right) = \exp \left( { - \beta n} \right)r\left( n \right)\), where the sequence \(\beta\) is a uniformly distributed group of data lying from -0.5 to 0.5 and determines the decay rate of the envelope. The signal that serves as the input for computation is a random signal with a variance of 1 and a mean of 0. The system noise consists of a mix of white Gaussian noise having to mean of 0 and variance of 0.01 with impulsive noise \(v_{i} \left( n \right)\) such that \(\eta \left( n \right) = v_{w} \left( n \right) + v_{i} \left( n \right)\). \(v_{i} \left( n \right)\) is generated as \(v_{i} \left( n \right) = B\left( n \right)I\left( n \right)\), in which the Bernoulli process is denoted by \(B\left( n \right)\) with occurrence probability \({\text{Pr}}\left( {B\left( n \right) = 1} \right) = P\) where \(P\) is the success probability. \(I\left( n \right)\) is the Gaussian process featuring 0 mean and variance of \(1000\). The parameters for simulation utilized in this experiment for the various algorithms are as follows: PMCC \((\mu = 0.001, \;p = 0.75,\;\sigma = 1.25),\) IPMCC \(\left( {\mu = 0.001,\; p = 0.75,\;\sigma = 1.25, \;\epsilon = 0.01} \right)\), PMVC \(\left( {\mu = 0.001, \;p = 1,\; \tau = 0.1} \right)\), and proposed \(\left( {\mu = 0.001,\; p = 0.75,\; \gamma = 0.6} \right)\). Figure 2 depicts the MSD curve of the suggested approach with \(P = 0.05\). The suggested FP-ALMS algorithm converges at around 793 iterations, whereas the PMVC, IPMCC, and PMCC converge at around 1692, 2600, and 648 iterations, respectively. Though the PMCC algorithm converges fast, it achieves higher MSD value. The MSD values obtained by PMCC, IP-MCC, P-MVC, and the proposed algorithm are − 12.84, − 20, − 19.99, and − 20 dBs, respectively. This suggests that the proposed approach can be considered over the other algorithms.

Fig. 1
figure 1

Echo path’s impulse response

Full size image
Fig. 2
figure 2

MSD curve of the proposed algorithm

Full size image

Figure 3 depicts the simulated and theoretical values of the proposed FP-ALMS algorithm's steady-state MSE. The step size was changed from 0.2 to 0.6. Equation (29) provides the theoretical values.

Fig. 3
figure 3

MSE analysis of the suggested algorithm

Full size image

5.1.1 Choice of parameters γ and θ

To examine the impact of the various parameters \(\gamma {\text{ and}}\,\, \theta\) on the performance of the proposed algorithm, the MSD curves of the proposed algorithm are obtained using Experiment-I. The behavior for different values of \(\gamma \,\,{\text{and}}\,\, \theta\) is compared and plotted in Fig. 4 and Fig. 5 accordingly. Figure 4 depicts that for \(\gamma = 6\), the proposed FP-ALMS algorithm converges slowly but converges fast for both values of \(\gamma = 1\) and \(\gamma = 0.6\). For Experiment-I, \(\gamma = 0.6\) is considered as it achieved a lower MSD value of − 20.05 dB compared to − 19.9 dB for \(\gamma = 1\). Figure 5 shows that for \(\theta = 0.75\), the proposed FP-ALMS algorithm converges slightly faster compared to \(\theta = 0.9\) and \(\theta = - 0.75\), but the MSD values almost remain the same for different values of \(\theta\). Similarly, the optimized values of \(\gamma \, {\text{and}}\, \theta \) are obtained through simulation for Experiment-II.

Fig. 4
figure 4

Choice of parameter \(\gamma\)

Full size image
Fig. 5
figure 5

Choice of parameter \(\theta\)

Full size image

5.2 Experiment-II

An experiment is put out to determine the room’s acoustic transfer function to compare the resilience of the FP-ALMS algorithm to PMCC, IP-MCC, and P-MVC criterion-based algorithms. The block diagram representation of the different components employed in the setup of the experiment is shown in Fig. 6. The setup comprises a dSPACE MicroLab Box which is a small development system for the laboratory that brings together great performance and versatility with a small size and affordability. It can be used in signal processing and other research areas like medical engineering, vehicle engineering, etc. The dSPACE MicroLab Box has numerous analogs-to-digital converters (ADC) and digital-to-analog converters (DAC) ports programmed by the MATLAB-Simulink software. One of the MicroLab Box's DAC ports uses an input random noise to stimulate the speaker and produce acoustic noise. To drive the speaker, a connection is done from the DAC port to the speaker via the reconstruction filter and the power amplifier. The speaker excitation signal acts as the input of the unidentified transfer function, whereas the received microphone signal acts as the output. The input signal's sampling frequency is 10 kHz, and there is a 65-cm gap between the speaker and the microphone. Inside a laboratory room are kept a speaker and a microphone. The room’s impulse response is produced by the LMS algorithm which runs in real time in the identical MicroLab Box lasting for about 5 min [11]. Figure 7 shows the impulse response that was so acquired. The input signal needed for determining the room transfer function is a random signal with a variance of 4 and a mean of 0. The system noise is generated as per the first experiment. The parameters for simulation utilized in this experiment for the various algorithms are as follows: PMCC (\(\mu = 0.001,\; p = 0.5,\;\sigma = 1.25),\) IPMCC \(\left( {\mu = 0.001,\; p = 0.5,\;\sigma = 1.25, \;\epsilon = 0.01} \right)\), PMVC \(\left( {\mu = 0.001,\; p = 4, \;\tau = 0.1,\;p = 0.5} \right)\), and proposed \(\left( {\mu = 0.001,\; p = 0.5, \;\gamma = 0.9} \right)\). Figure 8 illustrates the MSD curve of the suggested algorithm. The PMCC, IP-MCC, P-MVC, and the suggested algorithm are used to further identify the transfer function as the unknown system. The MSD value obtained by the PMCC algorithm is − 25.8 dB, the IP-MCC algorithm is − 20.95 dB, the P-MVC algorithm is − 24.45 dB, and the proposed algorithm is −  26.07dB respectively, which shows that the proposed algorithm attains the lowest MSD value when compared to the current algorithms.

Fig. 6
figure 6

Experimental setup block diagram

Full size image
Fig. 7
figure 7

Experimentally obtained impulse response

Full size image
Fig. 8
figure 8

MSD curve of the proposed algorithm

Full size image

6 Conclusion

The paper introduced a novel filter proportionate arctangent framework based on the least mean square to identify sparse systems. The FP-ALMS algorithm's step size is adjusted proportionally to the filter coefficient. To evaluate the effectiveness of the FP-ALMS algorithm, the steady-state EMSE is obtained using the Taylor expansion approach. Simulations demonstrate that the FP-ALMS algorithm outperforms other modern algorithms in terms of robustness in an impulsive noise environment.