New Stability Criteria for Uncertain Nonlinear Stochastic Time-Delay Systems

Abstract

This paper deals with the problem of robust stabilization and non-fragile robust control for a class of uncertain stochastic nonlinear time-delay systems that satisfy a one-sided Lipschitz condition. The parametric uncertainties are assumed to be real time-varying and norm bounded. Based on the one-sided Lipschitz condition including useful information of the nonlinear part, a new stability criterion for this class of nonlinear systems is provided. A memoryless non-fragile state-feedback controller is designed to guarantee robust stochastic stability of closed-loop systems. The approach of linear matrix inequalities is proposed to solve the robust stability for stochastic nonlinear systems with time-varying delay, and to obtain new delay-dependent sufficient conditions. Numerical examples are given to illustrate the validity and advantages of the proposed theoretical results.

1 Introduction

During the last decades, the stability analysis of uncertain stochastic time-delay systems satisfying some special nonlinearities has become very important due to the fact that nonlinearities are inherent characteristics of many dynamic systems such as biological systems, air pollution systems, and electrical networks. In the existing literature, the nonlinearities were restricted to satisfying the case of boundedness condition. And the nonlinear part was regarded as the unknown disturbance in the stability analysis [1, 9, 10, 18, 21, 26–28, 32, 33]. Reference [21] considered the robust stability problems for a class of stochastic time-delay interval systems with nonlinear disturbances. A model transformation of the systems was used to solve the robust stabilization problem, and a memoryless state-feedback controller was designed to stabilize the closed-loop system. Non-fragile guaranteed cost control for uncertain stochastic systems with time-invariant delay and nonlinearity was studied in [26, 27], and delay-independent/delay-dependent results ensuring the system robust stability had been obtained. Both the robust $H_{\infty }$ control of uncertain stochastic systems with time-varying delay and nonlinearity have been investigated in [18], and also a memoryless non-fragile state-feedback controller guaranteeing stochastic stability and prescribed $H_{\infty }$ performance of the closed-loop system was obtained. The robust stability of linear time-varying discrete delay systems with nonlinear perturbations by using a decomposition technique of the delay term matrix and an integral inequality was studied in [6]. The problem of state-feedback inverse optimal stabilization in the probability sense for high-order stochastic nonlinear system has been in [11], and an optimal state-feedback controller with respect to meaningful cost functionals was designed, which guarantees that the equilibrium of the closed-loop system is globally asymptotically stable in the probability sense. A delay-dependent criterion for robust stability was studied by using the relation between $x(t-\tau (t))$ and $x(t)-\int _{t-\tau (t)}^{t}\dot{x}(s)\hbox {d}s$ together with the free-weighting matrices in [22]. A sufficient condition for exponential stability in mean square for uncertain stochastic systems with a multiple time-delay was obtained by applying both a descriptor model transformation of the system and Moons inequality for bounding cross terms in [2]. Sufficient conditions to the robust exponential stability for both nonlinear stochastic systems and linear stochastic systems were presented in [8]. A delay-dependent sufficient condition of robust $H_{\infty }$ control was presented by using cone complementarity linearization algorithm for a class of uncertain neutral stochastic systems with mixed delays in [19]. In [20], authors established a global asymptotical mean square stability criterion for stochastic time-delay genetic regulatory networks based on a delay fractioning approach.

On the other hand, a useful one-sided Lipschitz condition was introduced in [4]. Since the nonlinear part satisfying the one-sided Lipschitz condition can make positive contributions to the stability of systems, one-sided Lipschitz condition was introduced to solve the observer design problem for nonlinear systems [7, 24, 31]. Inspired by the above work, we investigate the robust stability for one-sided Lipschitz stochastic nonlinear systems.

In this paper, applying a Lyapunov–Krasovskii functional combined with the linear matrix inequality (LMI) technique, we develop a new delay-dependent stability criterion based on a one-sided Lipschitz condition and a quadratic inner-boundedness condition. Two main contributions of this paper are as follows: ➀ the one-sided Lipschitz condition is extended to time-delay systems, and ➁ the less conservative stability conditions of uncertain stochastic nonlinear time-delay systems are developed in terms of LMI, and a non-fragile state-feedback controller which can guarantee the robust stability of the closed-loop systems is designed. Numerical examples are given to show the validity of the proposed method.

We work on the complete probability space $(\varOmega ,\mathcal {F},\mathcal {P})$ with the filtration $\mathcal {F}_{t\{t\ge 0\}}$ satisfying the usual conditions. $\mathbb {R}^{n}$ and $\mathbb {R}^{m\times n}$ denote, respectively, the $n\hbox {-dimensional}$ Euclidean space and the set of all $m\times n$ real matrices. $C^{2,1}(\mathbb {R}^{n}\times \mathbb {R}_{+};\mathbb {R}_{+})$ denotes the family of all nonnegative functions $V(x(t),t)$ on $\mathbb {R}^{n}\times \mathbb {R}_{+}$ that are continuously twice differentiable in $x$ and once differentiable in $t$. Let $\tau >0$ and denote by $C([-\tau ,0];\mathbb {R}^{n})$ the family of continuous functions $\varphi$ from $[-\tau ,0]$ to $\mathbb {R}^{n}$ with the norm $\Vert \varphi \Vert =\sup _{\theta \in [-\tau ,0]} |\varphi (\theta )|$, where $\Vert \cdot \Vert$ is the usual Euclidean norm in $\mathbb {R}^{n}$. $<\cdot ,\cdot >$ stands for a Euclidean inner product on the corresponding Euclidean norm. In the matrix, $(i,j)$ denote $(i,j)$-block element of the matrix. $\mathbb {E}(x)$ stands for the expectation of stochastic variable $x$, $B^\mathrm{T}$ represents the transposed matrix of $B$, moreover, $\begin{bmatrix}A&B\\ *&D\end{bmatrix}=\begin{bmatrix}A&B\\ B^\mathrm{T}&D\end{bmatrix}$. $I$ denotes the identity matrix of a compatible dimension.

2 Preliminaries

Consider the following stochastic time-delay systems described in the It${\hat{\mathrm{o}}}$’s form:

$$\begin{aligned} \hbox {d}x(t)&=[(A+\varDelta A(t))x(t)+(A_{\tau }+\varDelta A_{\tau }(t))x(t-\tau (t))+f(x(t),x(t-\tau (t)))\nonumber \\&\quad +Bu(t)]\hbox {d}t+[(H+\varDelta H(t))x(t)+(H_{\tau }+\varDelta H_{\tau }(t))x(t-\tau (t))]\hbox {d}\omega (t), \end{aligned}$$

(1a)

$$\begin{aligned} x(t)=\varphi (t),~~t\in [-\tau , 0], \end{aligned}$$

(1b)

where $x(t)\in \mathbb {R}^{n}$ is the state vector, $u(t)\in \mathbb {R}^{p}$ is the control input, $\tau (t)$ is the unknown time-varying delay satisfying $0\le \tau (t)<\tau$ and $\dot{\tau }(t)\le d$ with real constants $\tau , d$. $f(x(t),x(t-\tau (t)))\in \mathbb {R}^{n}$ is a nonlinear function with respect to the state $x(t)$ and the delayed state $x(t-\tau (t))$, $f(0,0)=0$. $\varphi (t)\in C([-\tau ,0];\mathbb {R}^{n})$ is a continuous vector-valued initial function, and $\omega (t)$ is a one-dimensional Brownian motion satisfying

$$\begin{aligned} \mathbb {E}[\hbox {d}\omega (t)]=0, \quad \mathbb {E}[\hbox {d}\omega (t)]^{2}=\hbox {d}t. \end{aligned}$$

Here $A\in \mathbb {R}^{n\times n},A_{\tau }\in \mathbb {R}^{n\times n},B\in \mathbb {R}^{n\times p}, H\in \mathbb {R}^{n\times n}, and H_{\tau }\in \mathbb {R}^{n\times n}$ are known real constant matrices of appropriate dimensions. Moreover, $\varDelta A(t), \varDelta A_{\tau }(t), \varDelta H(t)$, and $\varDelta H_{\tau }(t)$ are unknown matrices representing time-varying parameter uncertainties, and assumed to be in the form

$$\begin{aligned} \begin{bmatrix}\varDelta A(t)&\quad \varDelta A_{\tau }(t)\\ \varDelta H(t)&\quad \varDelta H_{\tau }(t)\end{bmatrix}=\begin{bmatrix}E_{1}\\E_{2}\end{bmatrix}F(t)\begin{bmatrix}G_{1}&G_{2}\end{bmatrix}, \end{aligned}$$

(2)

where $E_{1},E_{2},G_{1}$, and $G_{2}$ are known real constant matrices and $F(t)$ is an unknown time-varying matrix function satisfying

$$\begin{aligned} F(t)^\mathrm{T}F(t)\le I, \quad \forall t. \end{aligned}$$

The parameter uncertainties $\varDelta A(t), \varDelta A_{\tau }(t), \varDelta H(t)$, and $\varDelta H_{\tau }(t)$ are said to be admissible if both (2) and (3) hold.

Remark 1

Uncertain stochastic time-delay systems in the form of (1) is widely used in many real applications [16, 23]. We know that time-delay and uncertainties often destroy the stability of systems [12, 15, 29, 30]. It is observed that, in system (1), parameter uncertainties, It${\hat{\mathrm{o}}}$-type stochastic disturbances, and time-delay are considered simultaneously. The aim of this paper is to discuss the robust stochastic stabilization of system (1).

We first introduce the following several definitions and lemmas.

Definition 1

The nonlinear function $f(x,y)$ is said to be one-sided Lipschitz, if there exist $\alpha _{1}$ and $\alpha _{2}\in \mathbb {R}$ satisflying

$$\begin{aligned} \langle f(x,y),x\rangle \le \alpha _{1}x^\mathrm{T}x+\alpha _{2}y^\mathrm{T}y, \end{aligned}$$

(3)

for $\forall x, y\in \mathbb {R}^{n}$, where constant $\alpha _{1}$ and $\alpha _{2}$ are positive, zero or even negative, which are called the one-sided Lipschitz constant for $f(x,y)$ with respect to $x$ and $y$.

Remark 2

The one-sided Lipschitz condition is different from the standard one. Reviewing the definition of classical Lipschitz condition [14], that is, for nonlinear function $f(x(t),x(t-\tau (t)))\in \mathbb {R}^{n}$ with zero initial conditions, there is a constant $c>0$ such that

$$\begin{aligned} \Vert f(x(t),x(t-\tau (t)))\Vert <c(\Vert x(t)\Vert +\Vert x(t-\tau (t))\Vert ), \end{aligned}$$

(4)

where $c$ is Lipschitz constant. Note that while the Lipschitz constant must be positive, the one-sided Lipschitz constant may be non-positive. Any Lipschitz function is also one-sided Lipschitz, but the converse is not true [5]. From the definition of the one-sided Lipschitz condition, we can see that the one-sided Lipschitz constant can be non-positive, the nonlinear part is able to contribute to the stability of nonlinear systems. For example, the system $\dot{x}=x$ is unstable, but for the system $\dot{x}=x-4x/(1+\cos ^{2}(x))$, we can choose the Lyapunov function $V(x)=x^{2}$, the derivative is given by $\dot{V}=2x\dot{x}=2x^{2}+2\langle -4x/(1+\cos ^{2}(x)),x\rangle <-2x^{2}$. Therefore, $V(x)<0$ ensures the stability of nonlinear systems $\dot{x}=x-4x/(1+\cos ^{2}(x))$.

Definition 2

The nonlinear function $f(x,y)$ is called quadratic inner-boundedness in the region $\mathcal {C}$, if for any $x,y\in \mathcal {C}$ there exist $\beta _{1},\beta _{2},\gamma \in \mathbb {R}$ such that

$$\begin{aligned} f(x,y)^\mathrm{T}f(x,y)\le \beta _{1}x^\mathrm{T}x+\beta _{2}y^\mathrm{T}y+\gamma \langle x,f(x,y)\rangle . \end{aligned}$$

(5)

Lemma 1

(Schur Complement) For a given symmetric matrix $X=\begin{bmatrix} X_{11}&\quad X_{12}\\ X_{12}^\mathrm{T}&\quad X_{22} \end{bmatrix}$, the following conditions are equivalent:

• (a) $X<0$;

• (b) $X_{11}<0,X_{22}-X_{12}^\mathrm{T}X_{11}^{-1}X_{12}<0$;

• (c) $X_{22}<0,X_{11}-X_{12}X_{22}^{-1}X_{12}^\mathrm{T}<0$.

Lemma 2

[17] Let $G,H$ and $F(t)$ be real matrices of appropriate dimensions with $F(t)$ satisfying $F(t)^\mathrm{T}F(t)\le I$. Then, for any scalar $\varepsilon >0$, we have

$$\begin{aligned} GF(t)H+H^\mathrm{T}F(t)^\mathrm{T}G^\mathrm{T}\le \varepsilon GG^\mathrm{T}+\varepsilon ^{-1}H^\mathrm{T}H. \end{aligned}$$

3 Main Results

Let $h(t)=F(t)[G_{1}x(t)+G_{2}x(t-\tau (t))]$, $z(t)=Ax(t)+A_{\tau }x(t-\tau (t))+f(x(t),x(t-\tau (t)))+Bu(t)+E_{1}h(t)$, then the system (1) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\hbox {d}}x(t)=z(t)\hbox {d}t+(Hx(t)+H_{\tau }x(t-\tau (t))+E_{2}h(t)]\hbox {d}\omega (t)\\ h(t)^\mathrm{T}h(t)\le (G_{1}x(t)+G_{2}x(t-\tau (t)))^\mathrm{T}(G_{1}x(t)+G_{2}x(t-\tau (t))) \end{array}\right. }. \end{aligned}$$

(6)

Next, we will deal with the problem of robust stability for uncertain stochastic time-varying delay systems (6) with $u(t)=0$ by constructing the appropriate Lyapunov–Krasovskii functional and introducing free-weighting matrix. A new delay-dependent stability criteria is derived for a stochastic asymptotic stability of the zero solution of this system by using a Lyapunov stability theorem.

Theorem 1

Consider the stochastic time-delay system (6) with $u(t)=0$. The nonlinear function $f(x(t),x(t-\tau (t)))$ holds (3) and (5). For given scalars $\tau$ and $d$, if there exist matrices $P>0, Q_{1}>0, Q_{2}>0$, $M_{i}>0,(i=1,2,3)$, and $N_{i}(i=1,2)$ of appropriate dimensions and positive scalars $\varepsilon _{1}>0,\varepsilon _{2}>0,\varepsilon _{3}>0$ satisfying the following LMIs:

$$\begin{aligned} \begin{bmatrix}(1{,}1)&(1{,}2)&0&(1{,}4)&PE_{1}+H^\mathrm{T}PE_{2}&A^\mathrm{T}R&\bar{M_{1}}\\ *&(2{,}2)&(2{,}3)&0&H_{\tau }^\mathrm{T}PE_{2}&A_{\tau }^\mathrm{T}R&\bar{M_{2}}\\ *&*&(3{,}3)&0&0&0&\bar{M_{3}}\\ *&*&*&-\varepsilon _{3}I&0&R&0\\ *&*&*&*&E_{2}^\mathrm{T}PE_{2}-\varepsilon _{1}I&E_{1}^\mathrm{T}R&0\\ *&*&*&*&*&-\tau ^{-1}R&0\\ *&*&*&*&*&*&-\bar{M}\\ \end{bmatrix}<0, \end{aligned}$$

(7)

$$\begin{aligned} \begin{bmatrix}-M_{1}&0&0&0\\ *&-M_{2}&0&-N_{1}\\ *&*&-M_{3}&0\\ *&*&*&-R\\ \end{bmatrix}<0,\ \ \ \begin{bmatrix}-M_{1}&0&0&0\\ *&-M_{2}&0&0\\ *&*&-M_{3}&-N_{2}\\ *&*&*&-R\\ \end{bmatrix}<0, \end{aligned}$$

(8)

with

• $(1{,}1) =PA+A^\mathrm{T}P+Q_{1}+Q_{2}+H^\mathrm{T}PH+\varepsilon _{1}G_{1}^\mathrm{T}G_{1}+\varepsilon _{2}\alpha _{1}I+\varepsilon _{3}\beta _{1}I,$

• $(1{,}2)=PA_{\tau }+H^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{1}^\mathrm{T}G_{2}+N_{1}^\mathrm{T},$

• $(1{,}4) =P-\frac{1}{2}\varepsilon _{2}I+\frac{1}{2}\varepsilon _{3}\gamma I,$

• $(2{,}2) =-(1-d)Q_{1}+H_{\tau }^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{2}^\mathrm{T}G_{2}+\varepsilon _{2}\alpha _{2}I+\varepsilon _{3}\beta _{2}I-N_{1}-N_{1}^\mathrm{T},$

• $(2{,}3) =N_{2}^\mathrm{T},$

• $(3{,}3) =-Q_{2}-N_{2}-N_{2}^\mathrm{T},$

$\bar{M}=\mathrm{diag}\{\tau ^{-1}M_{1},\tau ^{-1}M_{2},\tau ^{-1}M_{3}\},$

$\bar{M_{1}}=[M_{1}\ \ 0\ \ 0],$ $\bar{M_{2}}=[0\ \ M_{2}\ \ 0],$ $\bar{M_{3}}=[0\ \ 0\ \ M_{3}],$ then the null solution of the stochastic time-delay system (6) is asymptotically stable in the mean square.

Proof

Choose the following Lyapunov–Krasovskii functional:

$$\begin{aligned} V(x(t),t)=\,&x^\mathrm{T}(t)Px(t)+\int _{t-\tau (t)}^{t}x^\mathrm{T}(s)Q_{1}x(s)\hbox {d}s+\int _{t-\tau }^{t}x^\mathrm{T}(s)Q_{2}x(s)\hbox {d}s\nonumber \\&+\int _{-\tau }^{0}\int _{t+\theta }^{t}z^\mathrm{T}(s)Rz(s)\hbox {d}s\hbox {d}\theta . \end{aligned}$$

(9)

By using It${\hat{\mathrm{o}}}$’s formula [13], we obtain the stochastic differential as

$$\begin{aligned} \hbox {d}V(x(t),t)=\mathcal {L}V(x(t),t)\hbox {d}t+2x^\mathrm{T}(t)P(Hx(t)+H_{\tau }x(t-\tau (t))+E_{2}h(t))\hbox {d}\omega (t), \end{aligned}$$

(10)

where

$$\begin{aligned} \mathcal {L}V(x(t),t)=\,&2x^\mathrm{T}(t)P[Ax(t)+A_{\tau }x(t-\tau (t))+f(x(t),x(t-\tau (t)))+E_{1}h(t)]\\&{+}\,x^\mathrm{T}(t)Q_{1}x(t){-}(1-\dot{\tau }(t))x^\mathrm{T}(t-\tau (t))Q_{1}x(t{-}\tau (t)){+}x^\mathrm{T}(t)Q_{2}x(t)\\&-\,x^\mathrm{T}(t-\tau )Q_{2}x(t-\tau )+[Hx(t)+H_{\tau }x(t-\tau (t))+E_{2}h(t)]^\mathrm{T}\\&\times \, P[Hx(t)+H_{\tau }x(t-\tau (t))+E_{2}h(t)]+\tau [Ax(t)+A_{\tau }(t-\tau (t))\\&+\,f(x(t),x(t-\tau (t)))+E_{1}h(t)]^\mathrm{T}R[Ax(t)+A_{\tau }(t-\tau (t))\\&+\,f(x(t),x(t-\tau (t)))+E_{1}h(t)]-\int _{t-\tau }^{t}z^\mathrm{T}(s)Rz(s)\hbox {d}s. \end{aligned}$$

Taking the expectation of both sides of (10), we can obtain the following formula [3]:

$$\begin{aligned} \mathbb {E}\hbox {d}V(x(t),t)=\mathbb {E}\mathcal {L}V(x(t),t)\hbox {d}t. \end{aligned}$$

(11)

Specifically, we have the following equations by using the Leibniz–Newton formula:

$$\begin{aligned}&2x^\mathrm{T}(t-\tau (t))N_{1}\left( x(t)-x(t-\tau (t))-\int _{t-\tau (t)}^{t}z(s)\hbox {d}s\right. \nonumber \\&\left. \qquad \qquad \qquad \qquad -\int _{t-\tau (t)}^{t}(Hx(s)+H_{\tau }x(s-\tau (s))+E_{2}h(s))\hbox {d}\omega (s)\right) =0, \end{aligned}$$

(12)

$$\begin{aligned}&2x^\mathrm{T}(t-\tau )N_{2}\left( x(t-\tau (t))-x(t-\tau )-\int _{t-\tau }^{t-\tau (t)}z(s)\hbox {d}s\right. \nonumber \\&\left. \qquad \qquad \qquad \qquad -\int _{t-\tau }^{t-\tau (t)}(Hx(s)+H_{\tau }x(s-\tau (s))+E_{2}h(s))\hbox {d}\omega (s)\right) =0, \end{aligned}$$

(13)

where $N_{i}(i=1,2)$ are arbitrary matrices with appropriate dimensions. And using the properties of the stochastic integral ( see Theorem 1.5.8 in [13]), we know that

$$\begin{aligned} \mathbb {E}\left\{ x^\mathrm{T}(t-\tau (t))N_{1}\int _{t-\tau (t)}^{t}(Hx(s)+H_{\tau }x(s-\tau (s))+E_{2}h(s))\hbox {d}\omega (s)\right\} =0, \end{aligned}$$

$$\begin{aligned} \mathbb {E}\left\{ x^\mathrm{T}(t-\tau )N_{2}\int _{t-\tau }^{t-\tau (t)}(Hx(s)+H_{\tau }x(s-\tau (s))+E_{2}h(s))\hbox {d}\omega (s)\right\} =0. \end{aligned}$$

This way, adding the left sides of Eqs. (12) and (13) on to $\mathcal {L}V(x(t),t)$, then Eq. (11) becomes

$$\begin{aligned} \mathbb {E}\hbox {d}V(x(t),t)=\mathbb {E}\mathcal {L}\hat{V}(x(t),t)\hbox {d}t, \end{aligned}$$

(14)

where

$$\begin{aligned} \mathcal {L}\hat{V}(x(t),t)=\,&\mathcal {L}V(x(t),t)+2x^\mathrm{T}(t-\tau (t))N_{1}(x(t)-x(t-\tau (t))-\int _{t-\tau (t)}^{t}z(s)\hbox {d}s)\nonumber \\&+2x^\mathrm{T}(t-\tau )N_{2}(x(t-\tau (t))-x(t-\tau )-\int _{t-\tau }^{t-\tau (t)}z(s)\hbox {d}s). \end{aligned}$$

On the other hand, by using the one-sided Lipschitz and the quadratically inner-bounded conditions (3) and (5), we obtain the following inequality:

$$\begin{aligned} \alpha _{1}x^\mathrm{T}(t)x(t)+\alpha _{2}x^\mathrm{T}(t-\tau (t))x(t-\tau (t))-x^\mathrm{T}(t)f(x(t),x(t-\tau (t)))\ge 0, \end{aligned}$$

(15)

$$\begin{aligned}&\beta _{1}x^\mathrm{T}(t)x(t)+\beta _{2}x^\mathrm{T}(t-\tau (t))x(t-\tau (t))-f(x(t),\nonumber \\&\quad x(t-\tau (t)))^\mathrm{T}f(x(t),x(t-\tau (t)))+\gamma x^\mathrm{T}(t)f(x(t),x(t-\tau (t)))\ge 0. \end{aligned}$$

(16)

Using the S-procedure in [25], we can see that $\mathcal {L}\hat{V}(x(t),t)<0$ is implied if there exist positive scalars $\varepsilon _{1}>0, \varepsilon _{2}>0$, and $\varepsilon _{3}>0$ satisfying

$$\begin{aligned}&\mathcal {L}\hat{V}(x(t),t)+\varepsilon _{1}(G_{1}x(t)+G_{2}x(t{-}\tau (t)))^\mathrm{T}(G_{1}x(t)+G_{2}x(t{-}\tau (t))){-}\varepsilon _{1}h^\mathrm{T}(t)h(t)\nonumber \\&\quad +\varepsilon _{2}\alpha _{1}x^\mathrm{T}(t)x(t)+\varepsilon _{2}\alpha _{2}x^\mathrm{T}(t-\tau (t))x(t-\tau (t))-\varepsilon _{2}x^\mathrm{T}(t)f(x(t),x(t-\tau (t)))\nonumber \\&\quad +\varepsilon _{3}\beta _{1}x^\mathrm{T}(t)x(t)+\varepsilon _{3}\beta _{2}x^\mathrm{T}(t-\tau (t))x(t-\tau (t))-\varepsilon _{3}f(x(t),x(t-\tau (t)))^\mathrm{T}\nonumber \\&\quad \times f(x(t),x(t-\tau (t)))+\varepsilon _{3}\gamma x^\mathrm{T}(t)f(x(t),x(t-\tau (t)))<0. \end{aligned}$$

(17)

Moreover, the following formula holds for any positive definite matrix $M_{1}(M_{2},M_{3})$ of appropriate dimensions:

$$\begin{aligned} \tau x^\mathrm{T}(t)M_{1}x(t)-\int _{t-\tau }^{t}x^\mathrm{T}(t)M_{1}x(t)\hbox {d}s=0. \end{aligned}$$

(18)

We decompose the integration interval $[t-\tau ,t]$ into two subintervals, that is $[t-\tau , t-\tau (t)]$ and $[t-\tau (t), t]$, and combined with Eq. (18) we can gain the following inequality by rearranging Eq. (17):

$$\begin{aligned}&\xi ^\mathrm{T}(t)\varSigma \xi (t)+\tau [Ax(t)+A_{\tau }x(t-\tau (t))+f(x(t),x(t-\tau (t)))+E_{1}h(t)]^\mathrm{T}R[Ax(t)\nonumber \\&\quad +A_{\tau }x(t-\tau (t))+f(x(t),x(t-\tau (t)))+E_{1}h(t)]\nonumber \\&\quad +\int _{t-\tau }^{t-\tau (t)}\eta ^\mathrm{T}(t,s)\Xi \eta (t,s)\hbox {d}s+\int _{t-\tau (t)}^{t}\eta ^\mathrm{T}(t,s)\varPi \eta (t,s)\hbox {d}s<0, \end{aligned}$$

(19)

where $\xi (t)=\begin{bmatrix}x^\mathrm{T}(t)&x^\mathrm{T}(t-\tau (t))&x^\mathrm{T}(t-\tau )&f^\mathrm{T}(x(t),x(t-\tau (t)))&h^\mathrm{T}(t)\end{bmatrix}^\mathrm{T},$ $\eta (t,s)=\begin{bmatrix}x^\mathrm{T}(t)&x^\mathrm{T}(t-\tau (t))&x^\mathrm{T}(t-\tau )&z^\mathrm{T}(s)\end{bmatrix}^\mathrm{T},$ and

$$\begin{aligned} \varSigma =\begin{bmatrix}(1{,}1)&(1{,}2)&0&(1{,}4)&PE_{1}+H^\mathrm{T}PE_{2}\\ *&(2{,}2)&(2{,}3)&0&H_{\tau }^\mathrm{T}PE_{2}\\ *&*&(3{,}3)&0&0\\ *&*&*&-\varepsilon _{3}I&0\\ *&*&*&*&E_{2}^\mathrm{T}PE_{2}-\varepsilon _{1}I\\ \end{bmatrix}, \end{aligned}$$

$$\begin{aligned} \varXi =\begin{bmatrix}-M_{1}&0&0&0\\ *&-M_{2}&0&-N_{1}\\ *&*&-M_{3}&0\\ *&*&*&-R\\ \end{bmatrix},\quad \varPi =\begin{bmatrix}-M_{1}&0&0&0\\ *&-M_{2}&0&0\\ *&*&-M_{3}&-N_{2}\\ *&*&*&-R\\ \end{bmatrix}, \end{aligned}$$

with

• $(1{,}1) =PA+A^\mathrm{T}P+Q_{1}+Q_{2}+H^\mathrm{T}PH+\varepsilon _{1}G_{1}^\mathrm{T}G_{1}+\varepsilon _{2}\alpha _{1}I+\varepsilon _{3}\beta _{1}I+\tau M_{1},$

• $(1{,}2) =PA_{\tau }+H^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{1}^\mathrm{T}G_{2}+N_{1}^\mathrm{T},$

• $(1{,}4) =P-\frac{1}{2}\varepsilon _{2}I+\frac{1}{2}\varepsilon _{3}\gamma I,$

• $(2{,}2) =-(1-d)Q_{1}+H_{\tau }^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{2}^\mathrm{T}G_{2}+\varepsilon _{2}\alpha _{2}I+\varepsilon _{3}\beta _{2}I -N_{1}-N_{1}^\mathrm{T}+\tau M_{2},$

• $(2{,}3) =N_{2}^\mathrm{T},$

• $(3{,}3) =-Q_{2}-N_{2}-N_{2}^\mathrm{T}+\tau M_{3},$

and $M_{1},M_{2},M_{3}$ are arbitrary symmetric matrices. By utilizing Lemma 1 again, we see that $\xi ^\mathrm{T}(t) \varSigma \xi (t)+\tau [Ax(t)+A_{\tau }(t-\tau (t))+f(x(t),x(t-\tau (t)))+E_{1}h(t)]^\mathrm{T}R[Ax(t) +A_{\tau }(t-\tau (t))+f(x(t),x(t-\tau (t)))+E_{1}h(t)]<0$ in Eq. (19) is equivalent to the LMI

$$\begin{aligned} \begin{bmatrix}(1{,}1)&(1{,}2)&0&(1{,}4)&PE_{1}+H^\mathrm{T}PE_{2}&A^\mathrm{T}&\bar{M_{1}}\\ *&(2{,}2)&(2{,}3)&0&H_{\tau }^\mathrm{T}PE_{2}&A_{\tau }^\mathrm{T}&\bar{M_{2}}\\ *&*&(3{,}3)&0&0&0&\bar{M_{3}}\\ *&*&*&-\varepsilon _{3}I&0&I&0\\ *&*&*&*&E_{2}^\mathrm{T}PE_{2}-\varepsilon _{1}I&E_{1}^\mathrm{T}&0\\ *&*&*&*&*&-\tau ^{-1}R^{-1}&0\\ *&*&*&*&*&*&-\bar{M}\\ \end{bmatrix}<0, \end{aligned}$$

(20)

where $(1,1)=PA+A^\mathrm{T}P+Q_{1}+Q_{2}+H^\mathrm{T}PH+\varepsilon _{1}G_{1}^\mathrm{T}G_{1}+\varepsilon _{2}\alpha _{1}I+\varepsilon _{3}\beta _{1}I,$ $(2,2)=-(1-d)Q_{1}+H_{\tau }^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{2}^\mathrm{T}G_{2}+\varepsilon _{2}\alpha _{2}I+\varepsilon _{3}\beta _{2}I -N_{1}-N_{1}^\mathrm{T},$ $(3,3)=-Q_{2}-N_{2}-N_{2}^\mathrm{T}$, $\bar{M}= \mathrm{diag}\{\tau ^{-1}M_{1},\tau ^{-1}M_{2},\tau ^{-1}M_{3}\}, \bar{M_{1}}=[M_{1}\ \ 0\ \ 0], \bar{M_{2}}=[0\ \ M_{2}\ \ 0]$, and $\bar{M_{3}}=[0\ \ 0\ \ M_{3}],$ the other notations are defined as Eq. (19). Pre- and post-multiplying Eq. (20) by $\text{ diag }\{I,I,I,I,I,R,I\}$, we readily obtain the LMI (7). Combining with $\varXi <0,\varPi <0$, we find that $\mathbb {E}\mathcal {L}\hat{V}(\xi (t),t)<0,$ i.e., it guarantees the asymptotic stability of the system (6) in the mean square.

If uncertain parameters $\varDelta A(t)=\varDelta A_{\tau }(t)=\varDelta H(t)=\varDelta H_{\tau }(t)=0$ in systems (1), then the system is simplified to the following deterministic stochastic system:

$$\begin{aligned} \hbox {d}x(t)&=[Ax(t)+A_{\tau }x(t-\tau (t))+f(x(t),x(t-\tau (t)))]\hbox {d}t\nonumber \\&\quad \,+[Hx(t)+H_{\tau }x(t-\tau (t))]\hbox {d}\omega (t), \end{aligned}$$

(21a)

$$\begin{aligned} x(t)=\varphi (t), \quad t\in [-\tau , 0], \end{aligned}$$

(21b)

The following conclusion of the robust asymptotic stability is obtained by Theorem 1 for the deterministic stochastic system (21).

Corollary 1

Consider the stochastic time-delay system (21). The nonlinear function $f(x(t),x(t-\tau (t)))$ holds (3) and (5). For given scalars $\tau$ and $d$, if there exist matrices $P>0, Q_{1}>0, Q_{2}>0$, $M_{i}>0 (i=1,2,3)$, and matrices $N_{i}(i=1,2)$ of appropriate dimensions and positive scalars $\varepsilon _{2}>0,\varepsilon _{3}>0$ satisfying the following LMIs:

$$\begin{aligned} \begin{bmatrix}(1{,}1)&(1{,}2)&0&(1{,}4)&A^\mathrm{T}R&\bar{M_{1}}\\ *&(2{,}2)&(2{,}3)&0&A_{\tau }^\mathrm{T}R&\bar{M_{2}}\\ *&*&(3{,}3)&0&0&\bar{M_{3}}\\ *&*&*&-\varepsilon _{3}I&R&0\\ *&*&*&*&-\tau ^{-1}R&0\\ *&*&*&*&*&-\bar{M}\\ \end{bmatrix}<0, \end{aligned}$$

(22)

$$\begin{aligned} \begin{bmatrix}-M_{1}&0&0&0\\ *&-M_{2}&0&-N_{1}\\ *&*&-M_{3}&0\\ *&*&*&-R\\ \end{bmatrix}<0, \quad \begin{bmatrix}-M_{1}&0&0&0\\ *&-M_{2}&0&0\\ *&*&-M_{3}&-N_{2}\\ *&*&*&-R\\ \end{bmatrix}<0, \end{aligned}$$

(23)

with

• $(1{,}1) =PA+A^\mathrm{T}P+Q_{1}+Q_{2}+H^\mathrm{T}PH+\varepsilon _{2}\alpha _{1}I+\varepsilon _{3}\beta _{1}I,$

• $(1{,}2) =PA_{\tau }+H^\mathrm{T}PH_{\tau }+N_{1}^\mathrm{T},$

• $(1{,}4) =P-\frac{1}{2}\varepsilon _{2}I+\frac{1}{2}\varepsilon _{3}\gamma I,$

• $(2{,}2) =-(1-d)Q_{1}+H_{\tau }^\mathrm{T}PH_{\tau }+\varepsilon _{2}\alpha _{2}I+\varepsilon _{3}\beta _{2}I-N_{1}-N_{1}^\mathrm{T},$

• $(2{,}3) =N_{2}^\mathrm{T},$

• $(3{,}3) =-Q_{2}-N_{2}-N_{2}^\mathrm{T},$

$\bar{M}= \mathrm{diag}\{\tau ^{-1}M_{1},\tau ^{-1}M_{2},\tau ^{-1}M_{3}\},$ $\bar{M_{1}}=[M_{1}\ \ 0 \ \ 0], \ \bar{M_{2}}=[0\ \ M_{2}\ \ 0], \ \,\mathrm{and}\,\bar{M_{3}}=[0\ \ 0\ \ M_{3}],$ then the null solution of the stochastic time-delay system (21) is asymptotically stable in the mean square.

Remark 3

If $\dot{\tau }(t)$ is unknown, then a delay-dependent and rate-independent sufficient conditions are provided by setting $Q_{1}=0$ in Theorem 1. Moreover, it is worth mentioning that new stability criteria reduce the computational cost. Making use of the LMI toolbox of MATLAB, we can solve feasibility problem of a new criterion easily.

4 Non-fragile Robust Stabilization Problem

In the previous section, we discussed the stability of uncertain stochastic one-sided Lipschitz nonlinear time-delay systems (1) with $u=0$, and presented a sufficient condition in the form of LMIs which make the null solution of the system asymptotically stable in the mean square. In this section, we will design a non-fragile state-feedback controller $u(t)=(K+\varDelta K(t))x(t)$ guaranteeing robust stability for the closed-loop systems with parameter uncertainties and time delay. In the state-feedback controller, $K$ is the controller gain, and $\varDelta K(t)$ represents the gain perturbations with the following assumption:

$$\begin{aligned} \varDelta K(t)=E_{3}F(t)G_{3}, \end{aligned}$$

(24)

where $E_{3}$ and $G_{3}$ are known real constant matrices with appropriate dimensions.

Theorem 2

Consider the stochastic time-delay system (6). The nonlinear function $f(x(t),x(t-\tau (t)))$ satisfies (3) and (5). For given scalars $\tau$ and $d$, if there exist matrices $P>0, Q_{1}>0, Q_{2}>0$, $M_{i}>0,(i=1,2,3)$, and matrices $N_{i}(i=1,2)$ of appropriate dimensions and positive scalars $\varepsilon _{1}>0,\varepsilon _{2}>0,\varepsilon _{3}>0,\varepsilon _{4}>0,$ and $\sigma >0$ satisfying the following LMIs:

$$\begin{aligned} \begin{bmatrix}(1{,}1)&(1{,}2)&0&(1{,}4)&PE_{1}+H^\mathrm{T}PE_{2}&A^\mathrm{T}R&\bar{M_{1}}&J_{1}&0\\ *&(2{,}2)&(2{,}3)&0&H_{\tau }^\mathrm{T}PE_{2}&A_{\tau }^\mathrm{T}R&\bar{M_{2}}&0&0\\ *&*&(3{,}3)&0&0&0&\bar{M_{3}}&0&0\\ *&*&*&-\varepsilon _{3}I&0&R&0&0&0\\ *&*&*&*&E_{2}^\mathrm{T}PE_{2}-\varepsilon _{1}I&E_{1}^\mathrm{T}R&0&0&0\\ *&*&*&*&*&-\tau ^{-1}R&0&0&L_{1}\\ *&*&*&*&*&*&-\bar{M}&0&0\\ *&*&*&*&*&*&*&-J&0\\ *&*&*&*&*&*&*&*&-L\\ \end{bmatrix}<0, \end{aligned}$$

(25)

$$\begin{aligned} \begin{bmatrix}-M_{1}&0&0&0\\ *&-M_{2}&0&-N_{1}\\ *&*&-M_{3}&0\\ *&*&*&-R\\ \end{bmatrix}<0, \quad \begin{bmatrix}-M_{1}&0&0&0\\ *&-M_{2}&0&0\\ *&*&-M_{3}&-N_{2}\\ *&*&*&-R\\ \end{bmatrix}<0, \end{aligned}$$

(26)

with

• $(1{,}1) =PA+A^\mathrm{T}P+Q_{1}+Q_{2}+H^\mathrm{T}PH+\varepsilon _{1}G_{1}^\mathrm{T}G_{1}+\varepsilon _{2}\alpha _{1}I+\varepsilon _{3}\beta _{1}I+2\varepsilon _{4}G_{3}^\mathrm{T}G_{3},$

• $(1{,}2)=PA_{\tau }+H^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{1}^\mathrm{T}G_{2}+N_{1}^\mathrm{T},$

• $(1{,}4) =P-\frac{1}{2}\varepsilon _{2}I+\frac{1}{2}\varepsilon _{3}\gamma I,$

• $(2{,}2) =-(1-d)Q_{1}+H_{\tau }^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{2}^\mathrm{T}G_{2}+\varepsilon _{2}\alpha _{2}I+\varepsilon _{3}\beta _{2}I-N_{1}-N_{1}^\mathrm{T},$

• $(2{,}3) =N_{2}^\mathrm{T},$

• $(3{,}3) =-Q_{2}-N_{2}-N_{2}^\mathrm{T},$

• $\bar{M} = \mathrm{diag}\{\tau ^{-1}M_{1},\tau ^{-1}M_{2},\tau ^{-1}M_{3}\},$

• $\bar{M_{1}} = [M_{1} \, 0 \, \, 0],$ $\bar{M_{2}}=[0 \, \, M_{2}\, \, 0],$ $\bar{M_{3}}=[0\, \, 0\, \, M_{3}],$

• $J = \mathrm{diag}\{\frac{1}{2}\sigma I,\varepsilon _{4}I,\sigma I\}$, $J_{1}=[PB PBE_{3} PB],$

• $L = \mathrm{diag}\{\varepsilon _{4}I,\sigma I\}$, $L_{1}=[RBE_{3} RB],$

then the closed-loop system is asymptotically stable in the mean square with the non-fragile state-feedback controller $K=\sigma ^{-1}B^\mathrm{T}P$.

Proof

By using the controller $u(x)=\sigma ^{-1}B^\mathrm{T}Px(t)$, and let $z(t)=(A+B(K+\varDelta K(t)))x(t)+A_{\tau }x(t-\tau (t))+f(x(t),x(t-\tau (t)))+E_{1}h(t)$, the system (6) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \hbox {d}x(t)=z(t)\hbox {d}t+(Hx(t)+H_{\tau }x(t-\tau (t))+E_{2}h(t)]\hbox {d}\omega (t)\\ h(t)^\mathrm{T}h(t)\le (G_{1}x(t)+G_{2}x(t-\tau (t)))^\mathrm{T}(G_{1}x(t)+G_{2}x(t-\tau (t))) \end{array}\right. }\!\!. \end{aligned}$$

(27)

Similar to Theorem 1, $\mathbb {E}\mathcal {L}\hat{V}(\xi (t),t)<0$ is guaranteed by the matrix inequality $\varOmega <0$, where

$$\begin{aligned} \varOmega =\begin{bmatrix}(1{,}1)&(1{,}2)&0&(1{,}4)&PE_{1}+H^\mathrm{T}PE_{2}&(1,6)&\bar{M_{1}}\\ *&(2{,}2)&(2{,}3)&0&H_{\tau }^\mathrm{T}PE_{2}&A_{\tau }^\mathrm{T}R&\bar{M_{2}}\\ *&*&(3{,}3)&0&0&0&\bar{M_{3}}\\ *&*&*&-\varepsilon _{3}I&0&R&0\\ *&*&*&*&E_{2}^\mathrm{T}PE_{2}-\varepsilon _{1}I&E_{1}^\mathrm{T}R&0\\ *&*&*&*&*&-\tau ^{-1}R&0\\ *&*&*&*&*&*&-\bar{M}\\ \end{bmatrix}\!, \end{aligned}$$

(28)

with

• $(1{,}1) =P(A+BK)+(A+BK)^\mathrm{T}P+Q_{1}+Q_{2}+H^\mathrm{T}PH+\varepsilon _{1}G_{1}^\mathrm{T}G_{1}+\varepsilon _{2}\alpha _{1}I+\varepsilon _{3}\beta _{1}I + PBE_{3}F(t)G_{3}+G_{3}^\mathrm{T}F^\mathrm{T}(t)E_{3}^\mathrm{T}B^\mathrm{T}P,$

• $(1{,}2)=PA_{\tau }+H^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{1}^\mathrm{T}G_{2}+N_{1}^\mathrm{T},$

• $(1{,}4) =P-\frac{1}{2}\varepsilon _{2}I+\frac{1}{2}\varepsilon _{3}\gamma I,$

• $(1{,}6) =A^\mathrm{T}R+K^\mathrm{T}B^\mathrm{T}R+G_{3}^\mathrm{T}F^\mathrm{T}(t)E_{3}^\mathrm{T}B^\mathrm{T}R,$

• $(2{,}2) =-(1-d)Q_{1}+H_{\tau }^\mathrm{T}PH_{\tau }+\varepsilon _{1}G_{2}^\mathrm{T}G_{2}+\varepsilon _{2}\alpha _{2}I+\varepsilon _{3}\beta _{2}I-N_{1}-N_{1}^\mathrm{T},$

• $(2{,}3) =N_{2}^\mathrm{T},$

• $(3{,}3) =-Q_{2}-N_{2}-N_{2}^\mathrm{T},$

$\bar{M}= \mathrm{diag}\{\tau ^{-1}M_{1},\tau ^{-1}M_{2},\tau ^{-1}M_{3}\},$ $\bar{M_{1}}=[M_{1}\ \ 0\ \ 0],\ \ \bar{M_{2}}=[0\ \ M_{2}\ \ 0],\ \,\mathrm{and}\,\bar{M_{3}}=[0\ \ 0\ \ M_{3}].$ Noting condition (24), we have

$$\begin{aligned} \varOmega =\bar{\varOmega }+\bar{E}\bar{F}\bar{G}+\bar{E}^\mathrm{T}\bar{F}^\mathrm{T}\bar{G}^\mathrm{T}+\bar{K}\bar{R}+\bar{R}^\mathrm{T}\bar{K}^\mathrm{T}, \end{aligned}$$

(29)

where

$$\begin{aligned} \bar{\varOmega }=\begin{bmatrix}(1{,}1)&(1{,}2)&0&(1{,}4)&PE_{1}+H^\mathrm{T}PE_{2}&(1,6)&\bar{M_{1}}\\ *&(2{,}2)&(2{,}3)&0&H_{\tau }^\mathrm{T}PE_{2}&A_{\tau }^\mathrm{T}R&\bar{M_{2}}\\ *&*&(3{,}3)&0&0&0&\bar{M_{3}}\\ *&*&*&-\varepsilon _{3}I&0&R&0\\ *&*&*&*&E_{2}^\mathrm{T}PE_{2}-\varepsilon _{1}I&E_{1}^\mathrm{T}R&0\\ *&*&*&*&*&-\tau ^{-1}R&0\\ *&*&*&*&*&*&-\bar{M}\\ \end{bmatrix}, \end{aligned}$$

(30)

with

• $(1{,}1) = P(A+BK)+(A+BK)^\mathrm{T}P+Q_{1}+Q_{2}+H^\mathrm{T}PH+\varepsilon _{1}G_{1}^\mathrm{T}G_{1}+\varepsilon _{2}\alpha _{1}I+\varepsilon _{3}\beta _{1}I$

• $(1{,}6) = A^\mathrm{T}R.$

The other notations are defined in Eq. (28), and $\bar{E}=\{(PBE_{3})_{1,1},(RBE_{3})_{6,2}\}$ denotes a block matrix with appropriate dimensions whose all nonzero blocks are the (1,1)-block $PBE_{3}$, the (6,2)-block $PBE_{3}$ and all other blocks are zero matrices. Similarly, $\bar{G}=\{(G_{3})_{1,1},(G_{3})_{2,1}\}$, $\bar{K}=\{(K^\mathrm{T})_{1,1}\}$ and $\bar{R}=\{(B^\mathrm{T}R)_{1,6}\}$. According to Lemma 2, for any scalars $\varepsilon _{4}>0$ and $\sigma >0$, we have

$$\begin{aligned} \varOmega <\bar{\varOmega }+\varepsilon _{4}^{-1}\bar{E}\bar{E}^\mathrm{T}+\varepsilon _{4}\bar{G}^\mathrm{T}\bar{G}+\sigma \bar{K}\bar{K}^\mathrm{T}+\sigma ^{-1}\bar{R}^\mathrm{T}\bar{R}. \end{aligned}$$

(31)

Let $K=\sigma ^{-1}B^\mathrm{T}P$. By using the Schur Lemma, $\bar{\varOmega }+\varepsilon _{4}^{-1}\bar{E}\bar{E}^\mathrm{T}+\varepsilon _{4}\bar{G}^\mathrm{T}\bar{G}+\sigma \bar{K}\bar{K}^\mathrm{T}+\sigma ^{-1}\bar{R}^\mathrm{T}\bar{R}<0$ if LMI (25) is satisfied.

5 Numerical Examples

In order to illustrate the flexibility and less conservative nature of the proposed results, we present numerical examples in this section.

Example 1

[6] Consider the stochastic nonlinear time-delay system (1) with $A=\begin{bmatrix} -1.2&\quad 0.1\\ -0.1&\quad -1 \end{bmatrix} \,\mathrm{and}\,A_{\tau }= \begin{bmatrix} -0.6&\quad 0.7\\ -1&\quad -0.8 \end{bmatrix}\!.$ We consider these two situations for comparison:

System I: Let $f(x(t),x(t-\tau (t)))=\begin{bmatrix}\frac{0.1}{\sin ^{2}x_{2}-2}x_{1}(t-\tau (t))\\ \frac{0.1}{\sin ^{2}x_{1}-2}x_{2}(t-\tau (t))\end{bmatrix}.$

Since $-0.1<\frac{0.1}{\sin ^{2}x_{2}-2}x_{2}(t)<-0.05,$ we have $f(x(t),x(t-\tau (t)))^\mathrm{T}f(x(t),x(t-\tau (t)))\le 0.01x^\mathrm{T}(t-\tau (t))x(t-\tau (t))$ and $\langle f(x(t),x(t-\tau (t))),x(t)\rangle \le 0.5x^\mathrm{T}(t)x(t)+0.005x^\mathrm{T}(t-\tau (t))x(t-\tau (t))$, i.e., $\alpha _{1}=0.5,\alpha _{2}=0.005$ in Eq. (3). It can be found that $f(x(t),x(t-\tau (t)))$ is quadratic inner-boundedness with $\gamma =5, \beta _{1}=-2.5, \beta _{2}=-0.015$.

System II: Let $f(x(t),x(t-\tau (t)))=\!\small \begin{bmatrix}\frac{0.1}{(2-\sqrt{2})\sin ^{2}x_{1}-2}x_{1}(t){+}\frac{0.1}{(2-\sqrt{2})\sin ^{2}x_{2}-2}x_{1}(t{-}\tau (t))\\ \frac{0.1}{(2-\sqrt{2})\sin ^{2}x_{2}-2}x_{2}(t){+}\frac{0.1}{(2-\sqrt{2})\sin ^{2}x_{1}-2}x_{2}(t{-}\tau (t))\end{bmatrix}\!\!.$

Since $-0.05\sqrt{2}<\frac{0.1}{(2-\sqrt{2})\sin ^{2}x_{2}-2}x_{2}(t)<-0.05,$ we have $f(x(t),x(t-\tau (t)))^\mathrm{T}f(x(t),x(t-\tau (t)))\le 0.01x^\mathrm{T}(t)x(t)+0.01x^\mathrm{T}(t-\tau (t))x(t-\tau (t)),$ and $\langle f(x(t),x(t-\tau (t))),x(t)\rangle \le 0.45x^\mathrm{T}(t)$  $x(t)+0.0025x^\mathrm{T}(t-\tau (t))x(t-\tau (t))$, i.e., $\alpha _{1}=0.45$ and $\alpha _{2}=0.0025$ in Eq. (3). It can be found that $f(x(t),x(t-\tau (t)))$ is quadratic inner-boundedness with $\gamma =5, \beta _{1}=-2.24$, and $\beta _{2}=0.0025$.

We can obtain the allowable upper bound of time-delay $\tau$ by Corollary 1 for the two above systems. In the literature, a nonlinear function is assumed to be bounded in the form: $\Vert f(x(t),x(t-\tau (t)))\Vert < c_{1}\Vert x(t)\Vert +c_{2}\Vert x(t-\tau (t))\Vert$, where $c_{1}$ and $c_{2}$ are positive real constants. We can see that $f(x(t),x(t-\tau (t)))$ is a Lipschitz function with Lipschitz constant $c=\max \{c_{1},c_{2}\}$ when $f(x(t),x(t-\tau (t)))$ is known. Because the nonlinear part is able to contribute to the stability of nonlinear systems with negative one-sided Lipschitz constant, the methods introduced in this paper expand the range of feasible solution. The allowable upper bound of $\tau$ on the basis of the stability criteria in this paper and in [1, 6, 28, 33] are listed in Table 1. It is seen that the criteria of [1, 6] fail when $d>1$, but our method still works. Comparing the maximal allowable value of the time-delay, it is seen from Table 1 that our results are less conservative than the ones in the existing references.

Table 1 Allowable upper bounds of $\tau$ for different $d$, $a_{1}$, and $a_{2}$

Example 2

Consider the uncertain stochastic nonlinear time-delay system (1) with

$$\begin{aligned} A&= \begin{bmatrix} \, -2&\quad 0.1 \\ 0.5&\quad 0.48 \\ \end{bmatrix}, \quad A_{\tau }= \begin{bmatrix} 1&\quad 0.5\\ \, -0.8&\quad -0.2\\ \end{bmatrix}, \quad B= \begin{bmatrix} 1\\ 2\\ \end{bmatrix}, \quad H= \begin{bmatrix} 0.2&\quad 0.1\\ 0&\quad 0.3\\ \end{bmatrix}, \\ H_{\tau }&= \begin{bmatrix} \, -0.1&\quad 0.5\\ \, -0.5&\quad 0.2\\ \end{bmatrix}, \quad E_{1}= \begin{bmatrix} 0.1&\quad 0\\ 0&\quad 0.1 \end{bmatrix}, \quad E_{2}= \begin{bmatrix} 0.2&\quad 0 \\ 0&\quad 0.2 \end{bmatrix}, \quad G_{1}= \begin{bmatrix} 0.3&\quad 0 \\ 0&\quad 0.3 \end{bmatrix}, \\ G_{2}&= \begin{bmatrix} 0.1&\quad 0 \\ 0&\quad 0.1 \end{bmatrix},\quad E_{3}= \begin{bmatrix} 0.5&0.5 \end{bmatrix}, \quad G_{3}= \begin{bmatrix} 1&\quad 0 \\ 0&\quad 1 \end{bmatrix}. \end{aligned}$$

For a nonlinear function $f(x(t),x(t-\tau (t)))$ in System II and $d=1$, we solve LMI (25) and (26) to obtain the maximum allowable bound $\tau =1.0831$. Hence, for any time delay $\tau$ satisfying $0<\tau \le 1.0831$, there exists a non-fragile state-feedback controller such that the closed-loop system is asymptotically stable in the mean square. For this example, if we choose the time-delay as $\tau =0.2,$ according to Theorem 2, we can obtain a set of solutions as follows:

$$\begin{aligned} P&= \begin{bmatrix} 2.0060&\quad -0.7109 \\ -0.7109&\quad 0.4135 \end{bmatrix}, Q_{1}= \begin{bmatrix} 1.3055&\quad -0.1193 \\ -0.1193&\quad 0.9815 \end{bmatrix}, \quad Q_{2}= \begin{bmatrix} 2.4912&\quad -0.0422 \\ -0.0422&\quad 1.9912 \end{bmatrix}, \\ R&= \begin{bmatrix} 7.7136&\quad -2.3326 \\ -2.3326&\quad 3.0880 \end{bmatrix}, \quad N_{1}= \begin{bmatrix} 5.0804&\quad -0.0880 \\ -0.0880&\quad 3.0065 \end{bmatrix}, \quad N_{2}= \begin{bmatrix} 1.2431&\quad -0.3190 \\ -0.3190&\quad 1.0327 \end{bmatrix}, \\ \varepsilon _{1}&=7.0568, \varepsilon _{2}=293.2912,\varepsilon _{3}=70.9524,\varepsilon _{4}=1.9531,\sigma =25.7089. \end{aligned}$$

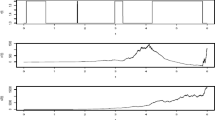
We can obtain the desired state-feedback matrix $K{\,=\,}\sigma ^{-1}B^\mathrm{T}P{\,=\,}\begin{bmatrix}0.0294&0.0040\end{bmatrix}$. For the sake of the simulation, the initial conditions have been chosen as $x(0)=[1~~-1]^\mathrm{T}$. State response trajectories for the open-loop and closed-loop systems are given. In Figs. 1 and 2, we see that the proposed methods are effective.

Fig. 1

State response trajectories for the open-loop systems

Fig. 2

State response trajectories for the closed-loop systems

6 Conclusions

We have investigated the robust stability for stochastic nonlinear time-delay systems. Both one-sided Lipschitz condition and a quadratic inner-boundedness condition are introduced to stochastic nonlinear time-delay systems. Unlike the methods in the existing literature, the new stability condition extracts more useful information of the nonlinear part using the one-sided Lipschitz condition. Delay-dependent sufficient condition has been proposed by constructing an appropriate Lyapunov–Krasovskii functional and using the free-weighting matrices method. We have constructed a memoryless non-fragile state-feedback controller to guarantee the closed-loop system asymptotical stability. Numerical examples have illustrated the advantages and effectiveness of our results, and shown that the proposed method is less conservative.