Robust H _∞ Control for a Class of Uncertain Neutral Stochastic Systems with Mixed Delays: a CCL Approach

Abstract

In this paper, the problem of robust H _∞ control for a class of uncertain neutral stochastic systems with mixed delays is investigated. The parameter uncertainties are assumed to be norm-bounded. A delay-dependent sufficient condition is derived in terms of the nonlinear matrix inequality by constructing proper Lyapunov–Krasovskii functional, using matrix inequality techniques and introducing free weighting matrices. The new result obtained in this paper can be tested numerically by using the so-called cone complementarity linearization (CCL) algorithm. Two examples provided in the literature show the effectiveness of the proposed approach.

1 Introduction

Dynamical systems modeled by neutral functional differential equations are generally called neutral systems in the literature. Neutral systems are frequently encountered in many practical situations such as chemical reactors, water pipes, population ecology and so on [12]. It is well known that time-delay and stochastic perturbations are often a source of instability and/or poor performance of many systems (see [6, 8] and the references therein). Also, in practice, the systems almost present some uncertainties because it is very difficult to obtain an exact mathematical model due to environmental noise, uncertain or slowly varying parameters, etc. Therefore, the problems of analysis and control for uncertain neutral stochastic systems with delays have attracted considerable attention (see [2, 3, 6–9, 11] and the references therein) in recent decade. It should be emphasized that the achieved results mainly focus on uncertain neutral stochastic systems with discrete and neutral delays, while few results concerning robust H _∞ control problem for uncertain neutral stochastic systems with discrete, distributed, and neutral delays can be found. In general, the problems of robust H _∞ control are solved by constructing Lyapunov–Krasovskii functional and applying the linear matrix inequality (LMI) technique, and hence the achieved results are described by LMIs which can be solved by the LMI Control Toolbox of MATLAB. However, in order to obtain LMIs criteria, some nonlinear items in the infinitesimal operators of Lyapunov–Krasovskii functionals have to be transformed into linear ones, which may bring certain conservativeness.

Motivated by the above causes, in this paper we consider the problem of robust H _∞ control for a class of uncertain neutral stochastic systems modeled in [6]. By constructing a new Lyapunov–Krasovskii functional, using matrix inequality techniques and introducing free-weighting matrices, a novel delay-dependent sufficient condition is derived in terms of the nonlinear matrix inequality, which can be tested effectively by using the so-called CCL algorithm. Two examples are given to show the effectiveness of our results as compared to the results obtained by the method in [6].

Notation: ℝⁿ denotes the n-dimensional Euclidean space. A ^T and A ⁻¹ represent the transpose and inverse of a matrix A, respectively. For real symmetric matrices X and Y, the notation X≥Y (respectively, X>Y) means that the matrix X−Y is positive semi-definite (respectively, positive definite). I is the identity matrix of appropriate dimensions. We denote by 0 _m×n the m×n zero matrix. ρ(⋅) denotes the spectral radius of matrix. In a symmetric matrix, ∗ denotes the entries implied by symmetry. L ₂[0,∞) is the space of square-integrable functions over [0,∞) with the norm ∥⋅∥₂. ∥⋅∥ will refer to the Euclidean vector norm. $(\varOmega, \mathcal{F}, \mathcal{P})$ is a probability space, where Ω is the sample space, $\mathcal{F}$ is the σ-algebra of subsets of the sample space, and $\mathcal{P}$ is the probability measure on $\mathcal{F}$. The notation $\mathbb{E}$ stands for the mathematical expectation operator. We denote by $\mathcal{L}_{2}[\varOmega,\mathbb{R}^{k})$ the space of square-integrable ℝ^k-valued vector functions on the probability space $(\varOmega, \mathcal{F}, \mathcal{P})$. We also denote by $\mathcal{L}_{2}[[0,\infty),\mathbb{R}^{k})$ the space of nonanticipatory square-integrable stochastic processes f(⋅)=[f(t)] _t∈[0,∞) in ℝ^k with respect to $(\mathcal{F}_{t})_{t\in[0,\infty)}$ satisfying

$$\|f\|_{E_2}^{2}=\mathbb{E} \biggl[ \int_{0}^{\infty} \big\|f(t) \big\|^{2}\,\mathrm{d}t \biggr]= \int_{0}^{\infty} \mathbb{E} \big\|f(t) \big\|^{2}\,\mathrm{d} t<\infty. $$

2 Problem Formulation

Consider the following uncertain neutral stochastic system with mixed delays:

(1a)

(1b)

(1c)

where x(t) is the n-dimensional state vector, u(t) is the m-dimensional control input vector, y(t) is the q-dimensional controlled output vector, v(t) is the p-dimensional disturbance input vector which belongs to L ₂[0,∞), ϕ(s) is an ℝⁿ-valued continuous initial function specified on [−max{2τ ₁,τ ₂},0], τ ₁ and τ ₂ are positive scalars representing the system delays, ω(t) is a scalar Brownian motion defined on a complete probability space $(\varOmega, \mathcal{F}, \mathcal{P})$, C, D, B ₂, E, F ₁, F ₂, and F ₃ are known real constant matrices of appropriate dimensions, and A(t), A ₁(t), A ₂(t), and B ₁(t) are matrix functions with time-varying uncertainties, that is,

(2)

and A, A ₁, A ₂, and B ₁ are known real constant matrices of appropriate dimensions.

Throughout this paper, we make the following assumptions.

Assumption 1

ρ(D)<1.

Assumption 2

The time-varying uncertainties ΔA(t), ΔA ₁(t), ΔA ₂(t), and ΔB ₁(t) are assumed to be of the form

$$ \bigl[\Delta A(t)\quad \Delta A_1(t) \quad \Delta A_2(t)\quad \Delta B_1(t)\bigr] =MF(t) [S\quad S_1\quad S_2\quad S_3] , $$

(3)

where M, S, S ₁, S ₂, and S ₃ are known real constant matrices of appropriate dimensions, and F(t) is a time-varying uncertain matrix satisfying

$$ F^T(t)F(t)\leq I\quad \forall t\geq0. $$

(4)

Remark 1

Assumption 1 guarantees that the zero solution of the homogeneous difference equation $\mathcal{D}x_{t}:=x(t)-Dx(t-\tau_{1})=0$ is asymptotically stable.

When the state feedback controller

$$ u(t)=Kx(t), $$

(5)

where K is a constant gain to be designed, is applied to system (1a)–(1c), the resultant closed-loop system is as follows:

(6a)

(6b)

(6c)

Next, we will give the concepts of mean-square asymptotic stability and robustly stochastic stabilization with disturbance attenuation level γ for system (1a)–(1c).

Definition 1

For system (1a) with u(t)=0 and v(t)=0, the equilibrium point 0 is said to be mean-square asymptotically stable if $\lim_{t\rightarrow\infty}\mathbb{E}\|x(t)\|^{2}=0$ for any t≥0 and all admissible uncertainties satisfying (3) and (4).

Definition 2

For a given positive constant γ, system (1a)–(1c) is said to be robustly stochastically stabilizable with disturbance attenuation level γ if there exists a state feedback controller (5) such that, for all admissible uncertainties satisfying (3) and (4), the closed-loop system (6a)–(6c) with v(t)=0 is mean-square asymptotically stable and, under the zero-initial condition, the inequality $\|y\|_{E_{2}}<\gamma\|v\|_{2}$ holds for any nonzero disturbance input.

The aim of this paper is to design a state feedback controller of the form (5) which robustly stochastically stabilizes system (1a)–(1c) with disturbance attenuation level γ.

The following lemmas will be useful to realize our aim.

Lemma 1

[10]

Let D,S, and W ^T=W>0 be real matrices of appropriate dimensions. Then for any nonzero vectors x and y of appropriate dimensions, we have

$$2x^TDSy\leq x^TDWD^Tx+y^TS^TW^{-1}Sy. $$

Lemma 2

(Jensen Inequality) [5]

Let x(t) be a vector-valued function which is integrable on the interval [a,b]. Then

$$(b-a) \int_{a}^{b}x^{T}(s)Rx(s)\, \mathrm{d}s\ge \int_{a}^{b}x^{T}(s)\, \mathrm{d}sR \int_{a}^{b}x(s)\,\mathrm{d}s $$

for any matrix R=R ^T>0.

Lemma 3

[1]

Let U,W and X ^T=X be real matrices of appropriate dimensions. Set ${\mathcal{S}}= \{V:V^{T}V\le I \}$. Then

$$X+UVW+W^TV^TU^T<0\quad \forall V\in{ \mathcal{S}} $$

if and only if there exists a scalar ε>0 such that

$$X+\varepsilon^{-1} UU^T+\varepsilon W^TW<0. $$

3 Main Results

In this section, we will investigate a new delay-dependent sufficient condition for the solvability of the robust H _∞ control problem for a class of uncertain neutral stochastic systems with mixed delays. We have the following theorem.

Theorem 1

For given γ>0,τ ₁>0, and τ ₂>0, the uncertain neutral stochastic system (1a)–(1c) is robustly stochastically stabilizable with disturbance attenuation level γ if there exist real matrices $\hat{P}^{T}=\hat{P}>0$, R ^T=R>0, $Q_{i}^{T}=Q_{i}>0$, $W_{i}^{T}=W_{i}>0$ (i=1,2), $\hat{K}$ and $\hat{L}$, and a scalar ϵ>0 such that

(7)

where

In this case, a desired state feedback gain can be obtained as $K=\hat{K}^{T}\hat{P}^{-1}$.

Proof

By the Schur complementary lemma, inequality (7) is equivalent to

(8)

Pre- and post-multiplying by with

on the both sides of (8), one can easily derive that

$$ \varPi+ \epsilon\hat{M}^T\hat{M}+ \epsilon^{-1}\hat{S}\hat{S}^T <0, $$

(9)

where

The combination of Lemma 3 and (9) gives that

$$\varPi+\hat{S}F^T(t)\hat{M}+\hat{M}^TF(t) \hat{S}^T<0 $$

for any uncertainty F(t) satisfying (4). This, together with the Schur complementary lemma, implies that

$$ \varPi_{1}+\varPi_2+e_1^TP \hat{A}(t)+\hat{A}^T(t)Pe_1+\hat {A}^T(t) (P+ \tau_1R)\hat{A}(t)<0, $$

(10)

where

For convenience, let

$$ \xi(t)= \left [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} x^T(t)&x^T(t-\tau_1)(I+D)^T&x^T(t-2\tau_1)D^T& \int_{t-\tau _2}^{t}x^{T}(s)\,\mathrm{d}s&v^T(t) \end{array} \right ] ^T. $$

(11)

Then the closed-loop system (6a)–(6c) becomes

$$ \mathrm{d}\mathcal{D}x_t =g_1(t)\, \mathrm{d}t+g_2(t)\,\mathrm{d}\omega(t), $$

(12)

where

$$ g_1(t)=\hat{A}(t)\xi(t),\quad\quad g_2(t)=\hat{F} \xi(t). $$

(13)

Define a Lyapunov–Krasovskii functional candidate for the closed-loop system (6a)–(6c) as

$$ V(t)=V_1(t)+V_2(t)+V_3(t)+V_4(t)+V_5(t), $$

(14)

where

Using Itô’s formula, we get from Lemmas 1 and 2 that

(15)

(16)

(17)

(18)

(19)

By the Newton–Leibniz formula, it is easy to achieve from (12) that

Using Lemma 1, we have that

and

Therefore,

(20)

This, together with (15)–(19), implies that

$$ \mathbb{E}\mathcal{L}V(t)\leq \mathbb{E} \bigl\{ \xi^T(t) \bigl[\varPi_1+e_{1}^TPA(t)+A^T(t)Pe_{1}+A^T(t) (P+\tau_1R)A(t) \bigr]\xi(t) \bigr\}. $$

(21)

When v(t)=0, it follows from (10), (11), and (21) that

$$\mathbb{E}\mathcal{L}V(t)<-\lambda \mathbb{E}\big\|\xi(t)\big\|^2\quad( \forall t\ge0), $$

where λ is some positive scalar, which implies that

i.e., $\int_{0}^{t}\mathbb{E}\|x(s)\|^{2}\,{\mathrm{d}}s\le \frac{1}{\lambda}\mathbb{E}V(0)$. Since $\mathbb{E}V(0)$ is a finite number, it follows that lim _t→∞∥x(t)∥=0, that is, the closed-loop system (6a)–(6c) is asymptotically mean-square stable for all admissible uncertainties satisfying (3) and (4).

Next, for any nonzero v(t), under the zero initial condition we consider the index

$$J(t)=\mathbb{E} \int_{0}^{t} \bigl[y^T(s)y(s)- \gamma^2v^T(s)v(s) \bigr]\, \mathrm{d} s. $$

Clearly,

$$J(t)\leq \int_{0}^{t}\mathbb{E} \bigl[y^T(s)y(s)-\gamma^2v^T(s)v(s)+ \mathcal{L}V(s) \bigr]\,\mathrm{d} s. $$

This, together with

$$y^T(s)y(s)=x^T(s) \bigl(C^T+K^TB_2^T \bigr) (C+B_2K)x(s), $$

implies that

Hence, from (10) we have J(t)<0 for any t>0. Therefore, under the zero initial condition, $\|y(t)\|_{E_{2}}<\gamma\|v(t)\|_{2}$ is satisfied for any nonzero disturbance input and all admissible uncertainties satisfying (3) and (4). This completes the proof. □

Remark 2

Comparing with the corresponding results in [6, 7], we construct a new Lyapunov–Krasovskii functional (for example, the item V ₃(t) is introduced) in the proof of Theorem 1, which may reduce the conservativeness of results. This will be tested by numerical examples in Sect. 5. Moreover, a CCL algorithm will be offered in Sect. 4 below to solve the nonlinear inequality proposed in Theorem 1, which avoids transforming some nonlinear items into linear ones. This may reduce the conservativeness of results but may increase the computational complexity.

4 A CCL Algorithm to Design State Feedback Gains

Due to the existence of the terms like $\hat{P}R\hat{P}$, inequality (7) in Theorem 1 is not an LMI, and hence no state feedback gain K can be obtained directly by using the LMI Control Toolbox. In order to solve the nonlinear inequality (7), in this section we will design a CCL algorithm.

Motivated by the idea of the so-called CCL algorithm [4], we require to introduce the matrix variables P>0, $\hat{R}>0$, $\hat{Q}_{i}>0$, $\hat{W}_{i}>0\ (i=1,2)$, X _j >0, and $\hat{X}_{j}>0\ (j=1,2,3,4)$ satisfying

(22)

Obviously, inequality (7) is feasible if (22) and

(23)

are satisfied, where V _1i (i=2,3,4) and are defined as in Theorem 1, and

Based on the preparation above, now we can give the following CCL algorithm to compute the maximum of τ ₂ for given τ ₁>0 and γ>0 under the premise that the LMI (7) is feasible.

Algorithm 1

(Compute the Maximum of τ ₂ for Given τ ₁>0 and γ>0)

Step 1 Choose a sufficiently small τ ₂ such that there exists a feasible solution to (23) and

(24)

Set τ _max=τ ₂.

Step 2 Find a feasible set of R ₀, $\hat{R}_{0}$, P ₀, $\hat{P}_{0}$, Q _i0, $\hat{Q}_{i0}$, W _i0, $\hat{W}_{i0}$ (i=1,2), X _j0, $\hat{X}_{j0}$ (j=1,2,3,4), $\hat{L}_{0}$, ϵ ₀, and $\hat{K}_{0}$ satisfying (23) and (24). Set k=0.

Step 3 Solve the following LMI problem for the variables $R,\hat{R},P,\hat{P},Q_{i},\hat{Q}_{i}$, $W_{i},\hat{W}_{i}\ (i=1,2), X_{j}, \hat{X}_{j}\ (j=1,2,3,4),\hat{L},\epsilon$, and $\hat{K}$:

$$\min_{\mathrm{subject\ to}\ (\scriptsize23)\ \mathrm{and}\ (\scriptsize24)} \operatorname{tr} \varPsi, $$

where

Set $R_{k+1}=R,\ \hat{R}_{k+1}=\hat{R},\ P_{k+1}=P,\ \hat{P}_{k+1}=\hat {P},\ Q_{i k+1}=Q_{i}, \hat{Q}_{i k+1}=\hat{Q}_{i}, W_{i k+1}=W_{i},\ \hat {W}_{i k+1}=\hat{W}_{i},\ X_{j k+1}=X_{j},\ \hat{X}_{j k+1}=\hat{X}_{j}\ (i=1,2, j=1,2,3,4)$.

Step 4 If the following LMI (25) is feasible for the variables $\hat{K}$, ϵ, Q _i , W _i (i=1,2), $\hat{L}$, and the matrices $\hat{P}$ and R obtained in Step 3, then set τ _max=τ ₂, increase τ ₂ by a small amount, and return to Step 2. If LMI in (25) is infeasible within a specified number k _max of iteration, then stop; otherwise, set k=k+1 and go to Step 3.

(25)

where

and V ₁₁, V ₁₂, V ₂₂, and are defined as in Theorem 1.

5 Numerical Examples

In this section, we offer the following two examples to present that the theoretical results proposed in the paper may be less conservative than those in [6].

Example 1

[6] Consider system (1a)–(1c) with the following parameters:

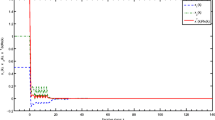
Case 1: τ ₁=τ ₂. When γ=0.5, the maximum allowable upper bounds of τ ₂ and corresponding state feedback gains K obtained from [6, Theorems 2] and Theorem 1 (i.e., Algorithm 1) of this paper are listed in Table 1. When F(t)≡1, v(t)≡0, τ ₁=τ ₂=3.35, and the initial values $x(t)= [ 10 \mathrm{e}^{\frac{t}{2}} \ \ 20 \mathrm{e}^{\frac{t}{2}} ] ^{T}$ for t∈[−6.7, 0], Fig. 1 illustrates the mean-square asymptotical stability of the closed-loop system (6a)–(6c) for a given scalar Brownian motion ω(t).

Fig. 1

State responses when F(t)≡1, v(t)≡0, and τ ₁=τ ₂=3.35

Table 1 The maxτ ₂ and state feedback gains K (Example 1)

Case 2: $\tau_{1}\not= \tau_{2}$. By using Theorem 1 (i.e., Algorithm 1), when γ=0.5, Table 2 shows the maximum allowable upper bounds of τ ₂ for different prescribed values of τ ₁ and k _max. When τ ₁=0.1 and τ ₂=3.53, a state feedback gain obtained from Theorem 1 is given by

$$K= \left [\begin{array}{c@{\quad}c} -1.6823 & 0.1892\\[4pt] -0.3642 & -0.9437 \end{array} \right ] . $$

Besides, Fig. 2 presents an illustrative simulation of the mean-square asymptotical stability of the closed-loop system (6a)–(6c) for a given scalar Brownian Motion ω(t) when F(t)≡1, v(t)≡0 and the initial values $x(t)= [ 10 \mathrm{e}^{\frac{t}{2}} \ \ 20 \mathrm{e}^{\frac{t}{2}} ] ^{T}$ for t∈[−3.53, 0].

Fig. 2

State responses when F(t)≡1, v(t)≡0, τ ₁=0.1, and τ ₂=3.53

Table 2 The maxτ ₂ for different τ ₁ and k _max (Example 1)

Remark 3

Example 1 shows that Theorem 1 in this paper can provide less conservative results than [6, Theorem 2]. On the other hand, this reduced conservatism is at the price of some additional computation, for example, for Case 1 of Example 1, we can easily calculate that the running time is approximately 3313 seconds when Theorem 1 is used (k _max =10), but the corresponding running time is only approximately 13 seconds when [6, Theorem 2] is used.

Example 2

[6]

Consider system (1a)–(1c) with the following parameters:

Case 1: τ ₁=τ ₂. When γ=0.5, the maximum allowable upper bounds of τ ₂ obtained from [6, Theorems 2] and Theorem 1 (i.e., Algorithm 1) of this paper are listed in Table 3.

Table 3 The maxτ ₂ (Example 2)

Case 2: $\tau_{1}\not= \tau_{2}$. By using Theorem 1 (i.e., Algorithm 1), when γ=0.5 and k _max=10, Table 4 shows the maximum allowable upper bounds of τ ₂ for different prescribed values of τ ₁.

Table 4 The maxτ ₂ for different τ ₁ (Example 2)

The above two examples show that the method proposed in this paper may be less conservative than one reported in [6] when τ ₁=τ ₂, while for the case $\tau_{1}\not= \tau_{2}$, the method proposed in [6] is not available.

6 Conclusions

In this paper, the problem of robust H _∞ control for a class of uncertain neutral stochastic systems with mixed delays is investigated. A less conservative result was presented in terms of a nonlinear matrix inequality. To solve the H _∞ control problem, a CCL algorithm has been designed, and thereby, a desired state feedback controller can be constructed. The numerical examples show that the method proposed in this paper maybe less conservative than one reported in [6].