1 Introduction

In the adaptive filtering algorithm, the least mean square (LMS) algorithm uses the least mean square of the error as the cost function and has been widely studied and applied in the Gaussian noise environment because of its simplicity and robustness [15]. To improve the convergence speed and steady-state accuracy of the algorithm, researchers introduced the normalization LMS (NLMS) algorithm based on the LMS algorithm [8, 14], which uses normalization to reduce the impact of large impulse responses on the LMS algorithm and enhance the stability performance of the algorithm. In addition, based on the normalized algorithm, Chien proposed several improved affine projection algorithms (APAs) [4,5,6], which alleviated the contradiction between the convergence speed and the steady-state misalignment of the NLMS algorithm and increased its adaptability to different sparse and noise characteristics of the system. Duttweiler [9] first proposed the proportional NLMS (PNLMS) algorithm, which references the step control matrix \(G(n)\) [17] based on the traditional LMS algorithm, so that the step parameters at each moment vary with the weight coefficients of the filter at the current moment, with larger coefficients obtaining a larger step size and smaller coefficients obtaining a smaller step size, thus both speeding up the convergence of the adaptive filtering algorithm and reducing the steady-state error of the adaptive filtering algorithm.

However, whether LMS, NLMS, APAs or PNLMS, the convergence performance will deteriorate or even fail to converge in a non-Gaussian noise environment. This is due to the poor resistance of the least mean-square error criterion (MSE) to impulse response. To solve this problem researchers have proposed various solutions, and the least mean p-power error criterion (MPE) [18, 19] instead of the MSE is one of the most commonly used methods at present. When \(p = 2\), the LMP algorithm is equivalent to the LMS algorithm, and when \(p < 2\), the LMP algorithm can obtain good performance in a non-Gaussian noise environment.

Based on the above analysis, in this paper we propose an improved proportional normalized least mean p-power algorithm (PNLMP). Based on the LMP algorithm, a proportional control factor and an improved error high-order tongue-line function are introduced for normalization processing. The stability and convergence of the algorithm and the influence of parameters on the performance of the algorithm are analyzed. Experiments show that the PNLMP algorithm has a faster convergence speed and stronger system tracking ability than some comparison algorithms.

2 Least Mean P-Power (LMP) Algorithm

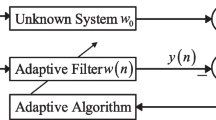
Figure 1 shows the general structure of the adaptive filter. where \({\varvec{u}}(n)\) is the input signal at the nth moment of the filter, and the expected signal \({\varvec{d}}(n)\) is the \({\varvec{u}}(n)\) that passes through the unknown system \({\varvec{w}}_{0}\) and is affected by the noise signal \({\varvec{v}}(n)\). Set \({\varvec{y}}(n)\) as the output signal of the adaptive filter, to make \({\varvec{y}}(n)\) as close as possible to \({\varvec{d}}(n)\). To achieve the best filtering effect, a cost function \(J(n)\) is needed to gradually reduce the error signal \({\varvec{e}}(n) = {\varvec{d}}(n) - {\varvec{y}}(n)\) by iteration so that the filter weight vector \({\varvec{w}}(n)\) approaches the unknown system impulse response \({\varvec{w}}_{0}\)

where \({\varvec{u}}(n) = [u(n),u(n - 1), \cdot \cdot \cdot ,u(n - M + 1)]^{{\text{T}}}\) is the input vector; \(M\) is the length of the adaptive filter; \({\varvec{w}}_{0}\) is the unknown system that can be estimated; and the superscript \(( \cdot )^{{\text{T}}}\) is the transpose of a vector or matrix. The desired signal can be expressed as.

$$ {\varvec{d}}(n) = {\varvec{w}}_{0}^{{\text{T}}} {\varvec{u}}(n) + {\varvec{v}}(n) $$
(1)
Fig. 1
figure 1

Adaptive filter structure for system identification

Full size image

The instantaneous error of the filter can be expressed as

$$ e(n) = d(n) - y(n) = d(n) - {\varvec{w}}^{{\text{T}}} (n){\varvec{u}}(n) $$
(2)

The cost function the LMS algorithm is based on the least mean square error criterion (MSE).

$$ \min J(n) = E\left[ {\left| {e(n)} \right|^{2} } \right] = \left| {e(n)} \right|^{2} $$
(3)

Under α stable distribution impulse noise environment, is used to the least mean p-power replace the least mean square of error. Therefore, the cost function can be expressed as \(\min J(n) = \left| {e(n)} \right|^{p}\), and the weight update of the LMP algorithm is obtained by using the stochastic gradient algorithm.

$$ {\varvec{w}}(n + 1) = {\varvec{w}}(n) + \mu \frac{{\partial J_{LMP} (n)}}{\partial w(n)} = {\varvec{w}}(n) + \mu p\left| {e(n)} \right|^{p - 1} {\text{sgn}} (e(n)){\varvec{u}}(n) $$
(4)

In [24], the weight vector update of the adaptive filtering algorithm is summarized as a nonlinear even function with respect to the error in three shapes, V-shaped, Λ-shaped, and M-shaped algorithms, and \(\mu > 0\) is the step size. The weight update with error nonlinearity can also be defined as.

$$ {\varvec{w}}(n + 1) = {\varvec{w}}(n) + \mu f(e(n))e(n){\varvec{u}}(n) $$
(5)

Since the Λ-shaped algorithms cannot converge quickly in both Gaussian and non-Gaussian noises, we want to find an algorithm that has V-shaped and M-shaped characteristics. Inspired by [17] and [24], the robust proportional normalization least mean p-power (PNLMP) algorithm is proposed.

3 PNLMP Algorithm

In this paper, we present a novel robust proportional normalized least mean p-power (PNLMP) algorithm to improve the steady-state accuracy and convergence speed of the algorithm, which introduced the proportional control matrix algorithm and normalization method. First, the proportional control matrix \(G(n)\) is introduced for Eq. (5).

$$ {\varvec{w}}(n + 1) = {\varvec{w}}(n) + \mu G(n)f(e(n))e(n){\varvec{u}}(n) $$
(6)

where \(G(n) = diag\left[ {g_{1} (n),g_{2} (n),...,g_{M} (n)} \right]\) is a time-varying step control matrix with the following expressions for the diagonal elements.

$$ g_{s} (n) = \frac{{u_{s} (n)}}{{\sum\nolimits_{i = 1}^{M} {u_{i} (n)} }},(1 \le s \le M) $$
(7)
$$ F_{\max } = \max \left\{ {\theta ,F(w_{1} (n),...,F(w_{M} (n))} \right\} $$
(8)
$$ u_{s} (n) = \max \left[ {\rho F_{\max } ,F(w_{s} (n))} \right] $$
(9)
$$ F(w_{s} (n)) = \left| {w_{s} (n)} \right| $$
(10)

The parameters \(\theta\) and \(\rho\) are both smaller positive numbers, which are used to avoid stopping the algorithm from updating because the filter coefficients are too small.

It is proposed in [24] that the \(f(e(n))\) shape should be related to the power of the estimation error, so it is proposed that in the \(f(e(n))\) weight update, the p-order moments of the input vector are used instead of the commonly used 2-norm, and the (p-q)-order moments of the error are used to perform the normalization. The weight update equation is obtained.

$$ {\varvec{w}}(n + 1) = {\varvec{w}}(n) + \mu \frac{{G({\text{n}})\left| {e(n)^{p - 1} } \right|sign\left[ {e(n)} \right]}}{{\left\| {{\varvec{u}}(n)} \right\|_{2}^{P} \left| {e(n)} \right|^{p - q} + a}}{\varvec{u}}(n) $$
(11)

where \(a\) is a positive constant and \(p\) is a constant from 0 to 2. It is mentioned in [17] that since the pulsed excitation signal can make the algorithm unstable, \(\left\| {{\varvec{u}}(n)} \right\|_{2}^{P}\) is rewritten as \(\left\| {{\varvec{u}}(n)} \right\|_{G}^{P} = {\varvec{u}}^{T} (n)G(n){\varvec{u}}(n)\). The resulting nonlinear function is

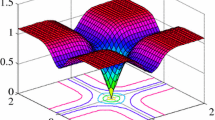
$$ f(e(n)) = \frac{{G(n)\left| {e(n)} \right|^{p - 2} }}{{\left\| {{\varvec{u}}(n)} \right\|_{G}^{p} \left| {e(n)} \right|^{p - q} + a}} $$
(12)

Assume that the input signal is a smooth sequence of independent zero-mean Gaussian random variables with finite variance \(\delta_{u}^{2} = 0.01\) and dimension \(N = 128\). Setting \(p = 4\), \(a = 1\), \(G(n) = I(n)\) unit diagonal matrix, we plot Eq. (12) with respect to the error in Fig. 2, where \({\varvec{u}}(n)\) is the average of 200 independent runs. As shown in Fig. 2\(f(e(n))\) is usually an M-shaped algorithm, but when \(q = 2\) \(f(e(n))\) is a V-shaped algorithm.

Fig. 2
figure 2

Nonlinear function surface of error e(n)

Full size image

In [23], it is proposed that when \(q\) is a fixed value, \(p - q\) is also a fixed value, so the algorithm can only filter the fixed noise environment. According to the adaptive filtering algorithm, in Fig. 2 it is seen that when the errors are large, we need a small \(q\) to ensure the convergence; in contrast, when the errors are small, we need a large \(q\) to improve the steady-state performance. Therefore, to obtain the varying \(q\), we design \(q(n)\) as a monotonically decreasing function about \(e(n)\), and the function has lower and upper bounds of 0 and 2 to ensure stability and filtering accuracy, which is also explained in [19, 24]. At the same time, motivated by the “S” shape function of the sigmoid function, we design \(q(n)\) as a tongue-like curve monotone decreasing function about the error and symmetry about the y-axis and use the previous moment error and the current error to control the step size of \(q(n)\). The improved algorithm can switch well between V-shaped and M-shaped algorithms. Therefore, \(q(n)\) with different \(p\) can be applied in different noise environments.

The standard tongue-like curve function in [16] is \(Y = \frac{1}{{1 + X^{2} }}\), which is also explained in [3]. \(q(n) \in (0,2]\) is chosen to ensure the stability and filtering accuracy, so we adjust the amplitude of the function, and the \(q(n)\) nonlinear function can be defined as

$$ q(n) = \frac{2}{{1 + \beta \left| {e(n)} \right|\left| {e(n - 1)} \right|}} $$
(13)

In (13), \(\beta\) is the smaller positive constant. Combined with (11), (12) and (19), we obtain the PNLMP algorithm weight update formula in this paper. The pseudo code process of the PNLMP algorithm is shown in Table 1.

$$ {\varvec{w}}(n + 1) = {\varvec{w}}(n) + \mu G(n)\frac{{\left| {e(n)^{p - 1} } \right|sign\left[ {e(n)} \right]}}{{\left\| {{\varvec{u}}(n)} \right\|_{G}^{p} \left| {e(n)} \right|^{p - q(n)} + a}}{\varvec{u}}(n) $$
(14)
Table 1 the PNLMP algorithm
Full size table

4 Algorithm Analysis

In this section, the mean square performance analysis is performed to theoretically verify the convergence performance of the PNLMP algorithm. Define the \(n\) moment error vector as (11).

$$ \tilde{\user2{w}}(n) = {\varvec{w}}(n) - {\varvec{w}}_{0} $$
(15)

Using \({\text{E}}\left[ {\left\| {\tilde{\user2{w}}{\text{(n)}}} \right\|^{{2}} } \right]\) to represent the mean squared error (MSD) to estimate the accuracy of the filter, we obtain the error as follows:

$$ \begin{aligned} e(n) &= d(n) - y(n) \\ &= \left( {{\varvec{w}}_{o} (n) - {\varvec{w}}(n - 1)} \right)^{{\text{T}}} {\varvec{u}}(n) + {\varvec{v}}(n) \\ &= \tilde{\user2{w}}(n){\varvec{u}}(n) + {\varvec{v}}(n) \\ \end{aligned} $$
(16)

For theoretical analysis, the following assumptions need to be given.

  • A1: \({\varvec{u}}(n)\) is a zero-mean smooth series of independent and uniformly distributed (i.i.d.) Gaussian random variables with finite variance \(\sigma_{u}^{2}\).

  • A2: The noise \({\varvec{v}}(n)\) is zero-mean, independently and identically distributed, and independent of the input signal \({\varvec{u}}(n)\), with variance \(\sigma_{v}^{2}\).

  • A3: The a priori error \(e_{a} (n) = \tilde{\user2{w}}^{{\text{T}}} (n){\varvec{u}}(n)\) is zero-mean, has a Gaussian distribution and is independent of the noise.

  • A4: The filter runs long enough, \(\left\| {{\varvec{u}}(n)} \right\|_{G}^{P}\) and \(e^{2} (n)\) are asymptotically independent.

Assumptions A1~A4 have been widely used in the theoretical analysis of adaptive filters [3, 21].

4.1 Convergence Analysis

Combining (1) and (10) generates

$$ \tilde{\user2{w}}(n + 1) = \tilde{\user2{w}}(n) - \mu G(n)f(e(n)){\varvec{u}}(n) $$
(17)

Taking the square of both sides of the above equation and squaring the expectation gives.

$$ \begin{aligned} E\left[ {\left\| {\tilde{\user2{w}}(n{ + }1)} \right\|^{2} } \right] = & E\left[ {\left\| {\tilde{\user2{w}}(n)} \right\|^{2} } \right] - 2\mu E\left[ {\tilde{\user2{w}}^{{\text{T}}} (n){\varvec{u}}(n)f(e(n))G(n)} \right] \\ & + \mu^{2} E\left[ {(G(n)f(e(n)){\varvec{u}}(n))^{{\text{T}}} G(n)f(e(n)){\varvec{u}}(n)} \right] \\ \end{aligned} $$
(18)

In the LMS algorithm, when the step size is satisfied \(0 < \mu < \frac{2}{3tr(R)}\) the algorithm converges. \(tr( \cdot )\) denotes the trace of the matrix and \(R = E[{\varvec{u}}^{{\text{T}}} ({\text{n}}){\varvec{u}}(n)]\) is the autocorrelation matrix of \({\varvec{u}}(n)\). Therefore, as when \(n \to \infty\) the filter reaches a steady state, in (18) the first term on the right side is equal to the left, so we can simplify the above equation as:

$$ 0 < \mu < \frac{{2E\left[ {\tilde{\user2{w}}^{{\text{T}}} (n)f(e(n)){\varvec{u}}(n))} \right]}}{{E\left[ {\left( {f(e(n)){\varvec{u}}(n)} \right)^{T} G(n)f(e(n)){\varvec{u}}(n)} \right]}} $$
(19)

For analytical convenience, for \(p = 2\), while \(q(n)\) converges to 2 when the steady state is reached, \(\left| {e(n)} \right|^{p - q(n)}\) converges to 1; then, \(W\) is defined as the molecular part and simplified as

$$ \begin{aligned} W & = 2E\left[ {\tilde{\user2{w}}^{{\text{T}}} (n)f(e(n)){\varvec{u}}(n))} \right] \\ &= 2E[e(n)f(e(n))]/E\left[ {e^{2} (n)} \right] \\ &= 2E\left[ {\frac{{\left| {e(n)} \right|^{2} }}{{\left[ {\left\| {{\varvec{u}}(n)} \right\|^{2} + \alpha } \right]}}} \right]/E\left[ {e^{2} (n)} \right] \\ & = 2E\left\{ {\frac{1}{{\left\| {{\varvec{u}}(n)} \right\|^{2} }}} \right\} \\ \end{aligned} $$
(20)

Similarly, defining the denominator as \(K\), the derivation yields \(K\).

$$ \begin{aligned} K &= E\left[ {{\varvec{u}}^{{\text{T}}} (n)G(n)u(n)} \right]E\left[ {f^{2} (e(n)} \right] \\ &= Tr\left[ {R_{u} } \right]E\left\{ {\frac{{\left| {e(n)} \right|^{2p - 2} }}{{\left[ {\left\| {{\varvec{u}}(n)} \right\|_{G}^{p} \left| {e(n)} \right|^{p - q(n)} + \alpha } \right]^{2} }}} \right\} \\ & \approx Tr\left[ {R_{u} } \right]E\left\{ {\frac{{\left| {e(n)} \right|^{2p - 2} }}{{\left[ {\left\| {{\varvec{u}}(n)} \right\|_{{}}^{2} \left| {e(n)} \right|^{2} + \alpha } \right]^{2} }}} \right\} \\ & = Tr\left[ {R_{u} } \right]E\left\{ {\frac{1}{{\left\| {{\varvec{u}}(n)} \right\|^{4} }}} \right\} \\ \end{aligned} $$
(21)

where \(\left\| {{\varvec{u}}(n)} \right\|^{2} = {\varvec{u}}^{{\text{T}}} (n){\varvec{u}}(n) \approx N\delta_{u}^{2}\), which is valid when \(N\) is assumed to be sufficiently large under assumption A1 [11, 12]. Bringing \(W\) and \(K\) respectively into (17), it is derived that the convergence condition of the algorithm needs to be satisfied.

$$ 0 < u < \frac{{2N\delta_{u}^{2} }}{{Tr\left[ {R_{u} } \right]}} $$
(22)

4.2 Stability Analysis

To evaluate the filtering accuracy, the instantaneous mean square deviation (MSD) and the excess mean-square error (EMSE) are used to measure the steady-state performance. Thus, we evaluate the limit on both sides of (16).

$$ \begin{aligned} \mathop {\lim }\limits_{n \to \infty } E\left[ {\left\| {\tilde{\user2{w}}(n{ + }1)} \right\|^{2} } \right] = & E\left[ {\left\| {\tilde{\user2{w}}(n)} \right\|^{2} } \right] - 2\mu \mathop {\lim }\limits_{n \to \infty } E\left[ {\tilde{\user2{w}}^{{\text{T}}} (n){\varvec{u}}(n)f(e(n))G(n)} \right] \\ & + \mu^{2} \mathop {\lim }\limits_{n \to \infty } E\left[ {\left( {G(n)f(e(n)){\varvec{u}}(n)} \right)^{{\text{T}}} G(n)f(e(n)){\varvec{u}}(n)} \right] \\ \end{aligned} $$
(23)

When the filter reaches steady state, we have \(y(n) = y(n - 1)\), \(\mathop {\lim }\limits_{n \to \infty } E\left[ {\left\| {\tilde{\user2{w}}(n{ + }1)} \right\|^{2} } \right] = \mathop {\lim }\limits_{n \to \infty } E\left[ {\left\| {\tilde{\user2{w}}(n)} \right\|^{2} } \right]\), and the above equation simplifies to.

$$ 2\mathop {\lim }\limits_{n \to \infty } E\left[ {\tilde{\user2{w}}^{{\text{T}}} (n){\varvec{u}}(n)f(e(n))} \right] = \mu \mathop {\lim }\limits_{n \to \infty } E\left[ {\left( {G(n)f(e(n)){\varvec{u}}(n)} \right)^{{\text{T}}} f(e(n)){\varvec{u}}(n)} \right] $$
(24)

Combined with assumption A3, we find

$$ y(\infty ) = \frac{1}{2}\mu \frac{{\mathop {\lim }\limits_{n \to \infty } E\left[ {\left\| {{\varvec{u}}(n)} \right\|^{2} } \right]K}}{{\delta_{u}^{2} \mathop {\lim }\limits_{n \to \infty } W}} \approx \frac{{uN\sigma {}_{v}^{2} }}{{2N\sigma {}_{u}^{2} - \mu T_{r} \left[ {R_{u} } \right]}} $$
(25)

Meanwhile, the EMSE denoted by \(\xi (\infty )\) is used to evaluate the steady-state performance and tracking capability of the adaptive filtering algorithm. defined as.

$$ \xi (\infty ) = E\left[ {e_{a}^{2} (n)} \right] = E\left[ {\left[ {\tilde{\user2{w}}^{{\text{T}}} (n){\varvec{u}}(n)} \right]^{{\text{T}}} \tilde{\user2{w}}^{{\text{T}}} (n){\varvec{u}}(n)} \right] $$
(26)

Combining (23) with (24), we generate.

$$ \xi (\infty ) = \sigma {}_{u}^{2} y(\infty ) = \frac{1}{2}\mu T_{r} \left( {R_{g} } \right)\frac{{\mathop {\lim }\limits_{n \to \infty } K}}{{\mathop {\lim }\limits_{n \to \infty } W}} \approx \frac{{u\sigma {}_{v}^{2} T_{r} \left[ {R_{u} } \right]}}{{2N\sigma {}_{u}^{2} - \mu T_{r} \left[ {R_{u} } \right]}} $$
(27)

When \(p = 2\), the steady-state EMSE and MSD of PNLMP are the same as those of PNLMS. When \(0 < p < 2\) to ensure the convergence of the algorithm, then \(q(n)\) converges as close as possible to 2 to achieve algorithmic convergence. In fact, when \(a\) is small, the validity of the derived EMSE and MSD can be guaranteed as long as \(\mu\) or \(\beta\) is small enough.

5 Simulation

5.1 Algorithm Verification

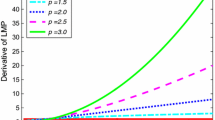
To verify the effectiveness of the PNLMP algorithm under α stable distribution impulse noise environment, the parameters \(a\) and \(\beta\) introduced in (9) are analyzed for \(p = 1.55\) and applied to the simulation experiments at a signal-to-noise ratio of 5 dB with the impulse noise parameters \(N1 \, = \, [1.4, \, 0, \, 0.3, \, 0]\). The trial-and-error method [10] was used to obtain the optimal values, setting \(a = 0.01, \, \beta = 2*10^{ - 1} , \, \beta = 2*10^{ - 2} ,\beta = 2*10^{ - 3} ,\beta = 2*10^{ - 4}\) and \(\beta = 0.002\) \( \, a = 0.05, \, a = 0.1, \, a = 0.15, \, a = 0.2\), and the algorithm performance curves are shown in Figs. 2 and 3.

Fig.3
figure 3

PNLMP performance curve under different values of β

Full size image

Figures 3 and 4 show that the \(a\) variation has a small effect on the convergence speed of the algorithm, and the parameter \(\beta\) mainly affects the steady-state error when the algorithm converges.

Fig.4
figure 4

PNLMP performance curve under different values of β

Full size image

5.2 Algorithm Comparison

To verify the performance of the PNLMP algorithm, we compare it with the PNRMS of [24], the LMP of [1], the NLMS of [20], the GVC of [13], and the GMCC of [2] in the cases of \(a = 0.2\), \(\beta = 0.002\) and their nonlinear functions \(f(e(n))\), as shown in Table 2.

Table 2 The Examples of f(e(n))
Full size table

Simulation experiments were applied at a signal-to-noise ratio of 15 dB with other parameters unchanged, the simulated system noise parameters were \(N2 \, = \, [2, \, 0, \, 0.03, \, 0]\), and the simulated MSD was averaged over 100 independent runs. and the system mutates at the \(1 \times 10^{4}\) sampling point moment, i.e., the unknown system weight vector changes from \({\varvec{w}}\) to \(- {\varvec{w}}\), and the algorithm results are shown in Figs. 5 and 6. It can be seen that the PNLMP algorithm converges after approximately 900 iterations, and the MSD value is reduced by 4.17 dB and 5.76 dB compared with the traditional PNRMS and GMCC algorithms, which shows that the PNLMP algorithm can achieve better convergence and system tracking performance under both Gaussian noise and impulsive noise conditions.

Fig. 5
figure 5

Comparison of the MSDs in N2 = [2, 0, 0.03, 0]

Full size image
Fig. 6
figure 6

Comparison of the MSDs in N2 = [2, 0, 0.03, 0] with impulse noise

Full size image

5.3 Application of Channel Identification

To further investigate the performance of each algorithm, [7] states that the noise parameter of an offshore domain can be represented by \(N3 \, = \, [1.82, \, 0, \, 0.0317, \, 0]\), so this parameter is chosen as the impulse noise parameter in this section. Figure 7 shows the measured channel impact response [22] for a moment in time in the Qingjiang River, Yichang, with a channel length of 400, and this is chosen as the unknown system response to be identified in this section. The five algorithms in the previous comparison are applied to the system at this location while the number of sampling points is \(2 \times 10^{4}\), and at the \(1 \times 10^{4}\) sampling moment, the system undergoes a sudden change, i.e., the channel impulse response is inverted, and the convergence curves of each algorithm are shown in Fig. 8.

Fig. 7
figure 7

Impulse response of a measured hydroacoustic channel

Full size image
Fig. 8
figure 8

Comparison of MSDs performance of real hydroacoustic channel algorithms

Full size image

It is obvious that the PNLMP algorithm proposed in this paper has better convergence speed and stronger system tracking capability under different noise and SNR conditions by comparing the simulated and real environment.

6 Conclusion

In this paper, we analyze several existing nonlinear adaptive filtering algorithms and propose a new PNLMP algorithm. This algorithm is based on the error surface of the nonlinear function, which introduces the proportional control matrix and the tongue-line function about the error to change the p-power of the nonlinear function to ensure that it can switch between V-shaped and M-shaped algorithms. Simulation experiments demonstrate that in the α stable distribution environment, whether it is Gaussian noise or impulse noise, the PNLMP algorithm has faster convergence and greater system tracking capability compared to the conventional adaptive algorithm.