1 Introduction

A switched system is a hybrid dynamic system consisting of a series of subsystems, which are generally described by the differential equation or difference equation and a rule to supervise the switching among the subsystems [2, 11]. Switched systems have been applied in many fields, such as power systems, mechanical manufacturing, traffic control and many others [3, 4, 26]. The study on switched systems have attracted great attention in the last decades. Many results have been obtained on switched systems [6, 14, 19]. For example, a switching system approach was proposed to solve the output tracking control problem for the networked systems [20]. The survey of the developments in the stability and design of the switched systems was given in [12]. A linear descriptor reduced-order observer and a descriptor sliding mode observer were designed for the switched system in [24].

Actuator saturation is one of the most common actuator nonlinearities which is inevitable in reality. In view of the limitation of mechanical device, the magnitude or rate of an actuator input are always bounded. When an actuator reaches its maximum boundary, the actuator saturation happens. When the actuator saturates, the control system does not work according to the designed controller which will degrade the control system performance or make the control system unstable. Therefore, the study on the actuator saturation is challenging and intricate [21, 27, 28]. Many control methods on switched systems with input saturation have been developed in recent years [15, 22, 29]. The stabilization conditions were established based on a time-dependent switching signals and multiple Lyapunov function in [5]. The output feedback robust controller was designed for a class of switched fuzzy systems with input saturation in [25]. The \(l_{2}\)-gain analysis for switched systems with input saturation based on mode-dependent average dwell time was studied in [30]. The disturbance tolerance and rejection of discrete switched systems with actuator saturation was studied in [16], and the stability analysis for a class of nonlinear systems with input saturation was given in [17]. In spite of the fruitful research results, most of the above results concentrated on the symmetrical input saturation of switched systems and the control system analysis and design were heavily based on a symmetrical saturation function. In fact, we often encounter the control systems with non-symmetrical input saturation, such as the missile system and the spacecraft system [23]. Meanwhile, a symmetrical saturation function can be considered as a special case of a non-symmetrical saturation function, thus, the study on the non-symmetrical input saturation problem has less conservatism comparing with the symmetrical one. It is more theoretical and practical to study the non-symmetrical input saturation switched systems.

Based on the foregoing analysis, we will design a state feedback controller for switched systems with non-symmetry input saturation based on the two classes of PRE. The exponential stability of the switched system is investigated through using the good properties of PRE, such as the matrix \(P(\varepsilon )\) is differentiable and monotonically increasing with the parameter \(\varepsilon \) and \(\underset{\varepsilon \rightarrow 0^{+}}{ \lim }P \left( \varepsilon \right) =0\), the details can be found in the following Lemmas 1 and 2. The main contributions of this paper are:

  1. (1)

    By appropriate mathematical transformation, we transform a switched system with non-symmetrical input saturation to a switched system with multiple equilibrium points and symmetrical input saturation;

  2. (2)

    The exponential stability analysis of the switched system with the subsystems having the open-loop critical stable poles is given by using the good properties of the two classes of PRE and multiple Lyapunov function;

  3. (3)

    The designed controller can be easily computed by solving the parametric Riccati equation. In reality, the controller is easy to implement.

The rest of this paper is structured as follows. The system description and preliminaries are given in Sect. 2. Section 3 presents the main results. The numerical simulation results can be found in Sect. 4. Section 5 draws the conclusion.

Notations In the whole paper, we use \(\mathrm {tr}(A)\) to stand the trace of the matrix A and \(A^{\mathrm {T}}\) to denote the transpose of the matrix A. \(I_{n}\) denotes the n-dimensional identity matrix. \(P>0\) means a real symmetric positive definite matrix. Let \(\lambda _{\min }\left( P\right) \) and \(\lambda _{\max }\left( P\right) \) stand the minimum and maximum eigenvalues of a matrix \(P (P>0)\), respectively.

2 System Description and Preliminaries

Consider the following switched system with non-symmetrical input saturation

$$\begin{aligned} {\dot{x}}(t)=A_{\delta \left( t\right) }x(t)+B_{\delta \left( t\right) }\mathrm {SAT}(u), \end{aligned}$$
(1)

where \(x\in \mathrm {R}^{n}\) and \(u\in \mathrm {R}^{m}\) are the system state and the control input, respectively. The switching signal \(\delta \left( t\right) \) is a piecewise constant function \(\delta \left( t\right) :\left[ 0,\infty \right) \rightarrow \Psi =\left\{ 1,2,\ldots ,M\right\} \) and M \((M>1)\) denotes the number of the subsystem. When \(\delta \left( t\right) =i \in \Psi \) , the i-th subsystem is activated. The matrices \(A_{i}\) and \(B_{i}\) are known with the appropriate dimensions. And the non-symmetrical input saturation is defined as

$$\begin{aligned} \mathrm {SAT}(u)=\left[ \begin{array}{ccc} \mathrm {SAT}\left( u_{1}\right)&\begin{array}{cc} \mathrm {SAT}\left( u_{2}\right)&\cdots \end{array}&\mathrm {SAT}\left( u_{m}\right) \end{array} \right] ^{\mathrm {T}} \end{aligned}$$

in which

$$\begin{aligned} \mathrm {SAT}\left( u_{j}\right) =\left\{ \begin{array}{llll} d _{j},u_{j}\ge d _{j}, \\ u_{j},-f _{j}\le u_{j}\le d _{j}, \\ -f _{j},u_{j}\le -f _{j}, \end{array} \right. \end{aligned}$$

with \(d_{j}>0\), \(f_{j}>0\) and \(d_{j}\ne f_{j}, j=1,2,\ldots ,m\).

Assumption 1

Assume that the matrices \(A_{i}\) are invertible and whose eigenvalues are all on the closed left-half plane, where \(i\in \Psi \), the matrix pairs \((A_{i},B_{i})\) are controllable. Without loss of generality, we assume that the matrix pairs \((A_{i},B_{i}), i\in \Psi \) have the following form

$$\begin{aligned} A_{i}=\left[ \begin{array}{cc} A_{i,s} &{} \quad 0 \\ 0 &{} \quad A_{i,c} \end{array} \right] ,B_{i}=\left[ \begin{array}{c} B_{i,s} \\ B_{i,c} \end{array} \right] , \end{aligned}$$
(2)

where, \(A_{i,s}\in \ R^{n_{i,s}\times n_{i,s}}\) include all the eigenvalues with negative real parts of the matrices \(A_{i}\) and \(A_{i,c}\in R^{n_{i,c}\times n_{i,c}}\) include all the eigenvalues of matrices \(A_{i}\), which are on the imaginary axis, \(n_{i,s}+n_{i,c}=n\).

From [1], we give the following definition

$$\begin{aligned} \Lambda _{j}=u_{j}-\frac{d _{j}-f _{j}}{2}. \end{aligned}$$
(3)

Then, the non-symmetrical input saturation can be rewritten as

$$\begin{aligned} \mathrm {SAT}\left( u_{j}\right) =\mathrm {sat}_{\rho _{j}}\left( \Lambda _{j}\right) +\frac{d _{j}-f _{j}}{2}, \end{aligned}$$
(4)

where \(\mathrm {sat}_{\rho _{j}}\left( \Lambda _{j}\right) \) is a symmetrical non-standard saturation function defined as

$$\begin{aligned} \mathrm {sat}_{\rho _{j}}\left( \Lambda _{j}\right) =\left\{ \begin{array}{lll} \rho _{j},\Lambda _{j}\ge \rho _{j},\\ \Lambda _{j},-\rho _{j}\le \Lambda _{j}\le \rho _{j}, \\ -\rho _{j},\Lambda _{j}\le -\rho _{j}, \end{array} \right. \end{aligned}$$
(5)

where \(\rho _{j}=\frac{d_{j}+f_{j}}{2}\). Set

$$\begin{aligned} \upsilon _{j}=\Lambda _{j}\frac{1}{\rho _{j}}. \end{aligned}$$
(6)

According to (3) and (6), we have

$$\begin{aligned} u_{j}=\frac{d_{j}+f _{j}}{2}\upsilon _{j}+\frac{d_{j}-f_{j}}{2}, \end{aligned}$$
(7)

that is

$$\begin{aligned} u=\frac{{\mathscr {Q}}_{d }+{\mathscr {Q}}_{f}}{2}\upsilon +\frac{{\mathscr {Q}}_{d}-{\mathscr {Q}}_{f }}{2}\Delta , \end{aligned}$$
(8)

where \({\mathscr {Q}}_{d }=\mathrm {diag}\left\{ \begin{array}{cccc} d _{1}&\quad d _{2}&\quad \cdots&\quad d _{m} \end{array} \right\} , {\mathscr {Q}}_{f }=\mathrm {diag}\left\{ \begin{array}{cccc} f_{1}&\quad f _{2}&\quad \cdots&\quad f _{m} \end{array} \right\} \) and \(\Delta =\left[ \begin{array}{cccc} 1&\quad 1&\quad \cdots&\quad 1 \end{array} \right] ^{\mathrm {T}}\in \mathrm {R}^{m}.\) Thus, we can obtain

$$\begin{aligned} \mathrm {SAT}(u)=\frac{{\mathscr {Q}}_{d }+{\mathscr {Q}}_{f }}{2}\mathrm {sat}\left( \upsilon \right) +\frac{{\mathscr {Q}}_{d }-{\mathscr {Q}}_{f }}{2}\Delta , \end{aligned}$$
(9)

where,

$$\begin{aligned}\mathrm {sat}\left( \upsilon _{j}\right) =\left\{ \begin{array}{c} 1,\upsilon _{j}\ge 1,\\ \upsilon _{j},-1\le \upsilon _{j}\le 1, \\ -1,\upsilon _{j}\le -1. \end{array} \right. \end{aligned}$$

Obviously, system (1) can be rewritten as

$$\begin{aligned} {\dot{x}}(t)=A_{\delta \left( t\right) }x(t)+{\mathscr {B}}_{\delta \left( t\right) }\mathrm {sat}\left( \upsilon \right) +\phi _{\delta \left( t\right) }, \end{aligned}$$
(10)

where \({\mathscr {B}}_{\delta \left( t\right) }= B_{\delta \left( t\right) }\frac{{\mathscr {Q}}_{d }+{\mathscr {Q}}_{f}}{2}\), \(\phi _{\delta \left( t\right) }=B_{\delta \left( t\right) }\frac{{\mathscr {Q}}_{d }-{\mathscr {Q}}_{f }}{2}\Delta \) and \(\Delta ^{\mathrm {T}}\Delta =m\).

Consider Assumption 1, let \(x_{\delta \left( t\right) }^{*}=-A_{\delta \left( t\right) }^{-1}\phi _{\delta \left( t\right) }\), then, system (10) becomes

$$\begin{aligned} {\dot{x}}(t)=A_{\delta \left( t\right) }\left( x(t)-\ x_{\delta \left( t\right) }^{*}\right) +{\mathscr {B}}_{\delta \left( t\right) }\mathrm {sat}\left( \upsilon \right) . \end{aligned}$$
(11)

Remark 1

In fact, system (11) is a switched system with multiple equilibrium points. Based on the above analysis, switched system (1) is recast to a switched system with multiple equilibrium points and symmetrical input saturation through mathematical transformation.

Let

$$\begin{aligned} {\mathscr {X}}(t)=x(t)-x_{\delta \left( t\right) }^{*}, \end{aligned}$$
(12)

then, system(11) becomes

$$\begin{aligned} \dot{{\mathscr {X}}}(t)=A_{\delta \left( t\right) }{\mathscr {X}}(t)+{\mathscr {B}}_{\delta \left( t\right) }\mathrm {sat}\left( \upsilon \right) , \end{aligned}$$
(13)

where \(\upsilon =\digamma {\mathscr {X}}(t)\), the state feedback gain \(\digamma \in \mathrm {R}^{m\times n} \) and

$$\begin{aligned} {\mathscr {B}}_{\delta (t)}=\left[ \begin{array}{c} {\mathscr {B}}_{\delta (t),s} \\ {\mathscr {B}}_{\delta (t),c} \end{array} \right] , \end{aligned}$$
(14)

with

$$\begin{aligned} {\mathscr {B}}_{\delta (t),s}=B_{\delta (t),s}\frac{{\mathscr {Q}}_{d }+{\mathscr {Q}}_{f }}{2} \end{aligned}$$
(15)

and

$$\begin{aligned} {\mathscr {B}}_{\delta (t),c}=B_{\delta (t),c}\frac{{\mathscr {Q}}_{d }+{\mathscr {Q}}_{f}}{2}. \end{aligned}$$
(16)

Remark 2

It follows from Assumption 1 that the matrix pairs \((A_{i},B_{i})\) are controllable, obviously, \((A_{i},{\mathscr {B}}_{i})\) are also controllable.

Now, we will give some lemmas which are useful for the derivation of the main results.

Lemma 1

[13] Assume that the matrix A is a Hurwitz matrix and the matrix pair (A, B) is controllable, then the matrix \(P(\varepsilon _{s} )\) is the unique positive-definite solution to the following PRE

$$\begin{aligned} P\left( \varepsilon _{s} \right) A+A^{\mathrm {T}}P\left( \varepsilon _{s}\right) -P\left( \varepsilon _{s} \right) BB^{\mathrm {T}}P\left( \varepsilon _{s}\right) =-\varepsilon _{s} I_{n_{s}}, \end{aligned}$$
(17)

where, \(\varepsilon _{s} >0\) is a low gain parameter. The properties of PRE (17) are given in the following

  1. (1)

    \(\frac{\mathrm {d}P\left( \varepsilon _{s} \right) }{\mathrm {d}\varepsilon _{s}}>0\);

  2. (2)

    \(\underset{\varepsilon _{s} \rightarrow 0^{+}}{ \lim }P \left( \varepsilon _{s} \right) =0\).

Lemma 2

[31] Assume that all the eigenvalues of the matrix A are on the imaginary axis and the matrix pair (A, B) is controllable, the matrix \(P(\varepsilon _{c} )\) is the unique positive-definite solution to the following PRE

$$\begin{aligned} P\left( \varepsilon _{c} \right) A+A^{\mathrm {T}}P\left( \varepsilon _{c} \right) -P \left( \varepsilon _{c} \right) BB^{\mathrm {T}}P\left( \varepsilon _{c} \right) =-\varepsilon _{c} P\left( \varepsilon _{c} \right) , \end{aligned}$$
(18)

where, \(\varepsilon _{c} >0\) is a low gain parameter. The properties of PRE (18) are given in the following

  1. (1)

    \(\frac{\mathrm {d}P \left( \varepsilon _{c}\right) }{\mathrm {d}\varepsilon _{c} }>0\);

  2. (2)

    \(\underset{\varepsilon _{c} \rightarrow 0^{+}}{ \lim }P\left( \varepsilon _{c} \right) =0\);

  3. (3)

    \(\mathrm {tr}\left( B^{\mathrm {T}}P\left( \varepsilon _{c} \right) B\right) =n_{c} \varepsilon _{c} \).

Lemma 3

[10] Consider the switching signal \(\delta \left( t\right) \) and any \(T\geqslant t\geqslant 0\). The switching number of the switched system over the time interval \(\left[ t,T\right] \) is denoted by \(N_{\delta \left( t\right) }\left( T,t\right) , j\in \Psi \). If there exist positive real numbers \(N_{0}\) and \(\tau _{a}\) satisfy the following inequality

$$\begin{aligned} N_{\delta \left( t\right) }\left( t,T\right) \le N_{0}+\frac{T-t }{\tau _{a}}, \end{aligned}$$
(19)

then, the parameters \(\tau _{a}\) and \(N_{0}\) are termed as the average dwell time and the chatter bound, respectively.

Problem 1

In this paper, we will consider the following problems:

  1. 1.

    The non-symmetrical input saturation problem;

  2. 2.

    The controller design for the switched system with the subsystems having the open-loop critical stable poles;

  3. 3.

    The stability analysis of the switched system with average dwell time and multiple equilibrium points.

3 Main Results

Theorem 1

Consider Assumption 1 and Lemmas 1–3. The matrices \(P_{i,s}\) are the solutions to PRE (17) and matrices \(P_{i,c}\) are the solutions to PRE (18) with the given low gain parameters \(\varepsilon _{i,c}>0 \), \(\varepsilon _{i,s}>0,i\in \Psi \) and \(\mu <\underset{i\in \Psi }{\min }\left( \varepsilon _{i,c}\right) \). Then, design the following controller

$$\begin{aligned} \upsilon =\digamma _{i} {\mathscr {X}}(t),i\in \Psi , \end{aligned}$$
(20)

in which \(\digamma _{i}=-{\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}\) and

$$\begin{aligned} {\mathscr {P}}_{i} =\left[ \begin{array}{cc} \varsigma _{i} P_{i,s} &{} \quad 0 \\ 0 &{} \quad P_{i,c} \end{array} \right] , \end{aligned}$$
(21)

with the given constant \(\varsigma _{i}>0\) satisfying

$$\begin{aligned} \varsigma _{i}>\frac{1}{\lambda _{\max }\left( \Theta _{i}\right) }, \end{aligned}$$
(22)

where,

$$\begin{aligned} \Theta _{i} = \Sigma _{i} ^{-\frac{1}{2} }P_{i,s}{\mathscr {B}}_{i,s}\left( I_{m}+\frac{1}{\mu -\varepsilon _{i,c}} {\mathscr {B}}_{i,c}^{\mathrm {T}}P_{i,c}{\mathscr {B}}_{i,c}\right) {\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s}\Sigma _{i} ^{-\frac{1}{2}} \end{aligned}$$
(23)

and

$$\begin{aligned} \Sigma _{i} =A_{i,s}^{\mathrm {T}}P_{i,s}+P_{i,s}A_{i,s}+\mu P_{i,s}. \end{aligned}$$
(24)

If there exists \(\eta >1\) such that

$$\begin{aligned} {\mathscr {P}}_{k}\le \eta {\mathscr {P}}_{k-1}, k=2,3,\ldots ,M, \end{aligned}$$
(25)

then, the designed controller (20) makes the closed-loop system exponentially stable with the average dwell time

$$\begin{aligned} \tau _{a}\ge \frac{\ln \eta }{\mu }. \end{aligned}$$
(26)

Proof

In view of system (13) and the designed controller (20), the closed-loop system of i-th subsystem is

$$\begin{aligned} \dot{{\mathscr {X}}}(t)=A_{i}{\mathscr {X}}(t)+{\mathscr {B}}_{i}\mathrm {sat}\left( -{\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {X}}(t)\right) , i\in \Psi . \end{aligned}$$
(27)

In view of the properties of PRE (17) and PRE (18) that \(\underset{\varepsilon _{i,s} \rightarrow 0^{+}}{ \lim }P \left( \varepsilon _{i,s} \right) =0\) and \(\underset{\varepsilon _{i,c} \rightarrow 0^{+}}{ \lim }P\left( \varepsilon _{i,c} \right) =0\), we can get

$$\begin{aligned} \underset{\varepsilon _{i,s}\rightarrow 0^{+},\varepsilon _{i,c}\rightarrow 0^{+}}{\lim }{\mathscr {P}}_{i} =0. \end{aligned}$$
(28)

Thus, we can obtain

$$\begin{aligned} \mathrm {sat}\left( \upsilon \right) =\upsilon \end{aligned}$$
(29)

by choosing the appropriate small value of the low gain parameters \(\varepsilon _{i,c}\) and \(\varepsilon _{i,s}\). Consider the following Lyapunov function

$$\begin{aligned} V_{i}\left( t\right) ={\mathscr {X}}^{\mathrm {T}}(t){\mathscr {P}}_{i}{\mathscr {X}}(t). \end{aligned}$$

The derivative of the Lyapunov function \(V_{i}\left( t\right) ={\mathscr {X}}^{\mathrm {T}}(t){\mathscr {P}}_{i}{\mathscr {X}}(t)\) along the trajectories of the closed-loop system (27) is

$$\begin{aligned} {\dot{V}}_{i}\left( t\right)= & {} 2\dot{{\mathscr {X}}}^{\mathrm {T}}(t){\mathscr {P}}_{i}{\mathscr {X}}(t) \nonumber \\= & {} 2\left( A_{i}{\mathscr {X}}(t)+{\mathscr {B}}_{i}\left( - {\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {X}}(t)\right) \right) ^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {X}} (t)\nonumber \\= & {} {\mathscr {X}}^{\mathrm {T}}(t)\left( {\mathscr {P}}_{i}A_{i}+A_{i}^{\mathrm {T}}{\mathscr {P}}_{i}\right) {\mathscr {X}}(t)-2{\mathscr {X}}^{\mathrm {T}}(t){\mathscr {P}}_{i} {\mathscr {B}}_{i}{\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {X}}(t). \end{aligned}$$
(30)

By considering the matrix structure of matrices (2), (14), (15) and (16), we have

$$\begin{aligned} {\dot{V}}_{i}\left( t\right) +\mu V_{i}\left( t\right) =-{\mathscr {X}}^{\mathrm {T}}(t)\Upsilon _{i} {\mathscr {X}}(t), \end{aligned}$$

where,

$$\begin{aligned} \Upsilon _{i}=\left[ \begin{array}{cc} \Upsilon _{i,1} &{} \quad \Upsilon _{i,2} \\ \Upsilon _{i,2}^{\mathrm {T}} &{} \quad \Upsilon _{i,4} \end{array} \right] , \end{aligned}$$
(31)

with

$$\begin{aligned} \Upsilon _{i,1}= & {} -(\varsigma _{i}A_{i,s}^{\mathrm {T}}P_{i,s}+\varsigma _{i}P_{i,s}A_{i,s}-\varsigma _{i}^{2}P_{i,s}{\mathscr {B}}_{i,s}{\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s}+\mu \varsigma _{i}P_{i,s}), \end{aligned}$$
(32)
$$\begin{aligned} \Upsilon _{i,2}= & {} \varsigma _{i}P_{i,s}{\mathscr {B}}_{i,s}{\mathscr {B}}_{i,c}^{\mathrm {T}}P_{i,c}, \end{aligned}$$
(33)

and

$$\begin{aligned} \Upsilon _{i,4}&=-(P_{i,c}A_{i,c}+A_{i,c}^{\mathrm {T}}P_{i,c}-P_{i,c} {\mathscr {B}}_{i,c}{\mathscr {B}}_{i,c}^{\mathrm {T}}P_{i,c}+ \mu P_{i,c}) \nonumber \\&=(\varepsilon _{i,c}-\mu )P_{i,c}\nonumber \\&>0 . \end{aligned}$$
(34)

According to Schur complement lemma [8], we have

$$\begin{aligned} \Phi _{i}= & {} -\varsigma _{i}\Sigma _{i} +\varsigma _{i}^{2}P_{i,s}{\mathscr {B}}_{i,s}{\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s}- \left( \frac{1}{-\mu +\varepsilon _{i,c}}\right) \varsigma ^{2} _{i}P_{i,s}{\mathscr {B}}_{i,s} {\mathscr {B}}_{i,c}^{\mathrm {T}}\nonumber \\&\times P_{i,c}P_{i,c}^{-1}P_{i,c}{\mathscr {B}}_{i,c} {\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} \nonumber \\= & {} -\varsigma _{i}\Sigma _{i} +\varsigma _{i}^{2}P_{i,s}{\mathscr {B}}_{i,s} {\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} -\left( \frac{\varsigma _{i}^{2}}{-\mu +\varepsilon _{i,c}}\right) P_{i,s}{\mathscr {B}}_{i,s}{\mathscr {B}}_{i,c}^{\mathrm {T}}\nonumber \\&\times P_{i,c}{\mathscr {B}}_{i,c}{\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} \nonumber \\= & {} -\varsigma _{i}\Sigma _{i}+\varsigma _{i}^{2}P_{i,s}{\mathscr {B}}_{i,s} {\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} +\left( \frac{\varsigma _{i}^{2}}{\mu -\varepsilon _{i,c}}\right) P_{i,s}{\mathscr {B}}_{i,s}{\mathscr {B}}_{i,c}^{\mathrm {T}} P_{i,c}{\mathscr {B}}_{i,c}{\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} \nonumber \\= & {} -\varsigma _{i}\left( \Sigma _{i} -\varsigma _{i}P_{i,s}{\mathscr {B}}_{i,s}{\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} -\left( \frac{\varsigma _{i}}{\mu -\varepsilon _{i,c}}\right) P_{i,s}{\mathscr {B}}_{i,s}{\mathscr {B}}_{i,c}^{\mathrm {T}} P_{i,c}{\mathscr {B}}_{i,c}{\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s}\right) \nonumber \\= & {} -\varsigma _{i}\left( \Sigma _{i}-\varsigma _{i}\left( P_{i,s} {\mathscr {B}}_{i,s}\left( I_{m}+\frac{1}{\mu -\varepsilon _{i,c}}{\mathscr {B}}_{i,c}^{\mathrm {T}}P_{i,c} {\mathscr {B}}_{i,c}\right) {\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s}\right) \right) , \end{aligned}$$
(35)

where

$$\begin{aligned} \Sigma _{i}= & {} A_{i,s}^{\mathrm {T}}P_{i,s}+P_{i,s}A_{i,s}+\mu P_{i,s} \\= & {} -\varepsilon _{i,s}I_{n_{i,s}}+P_{i,s}{\mathscr {B}}_{i,s}{\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s}+\mu P_{i,s}. \end{aligned}$$

There will always exist parameters \(\varepsilon _{i,s}\) and \(\mu \) to make \(\Sigma _{i}>0\). Multiplying both sides of equality (35) by \(\Sigma _{i}^{-\frac{1}{2}}\), we have

$$\begin{aligned} \Pi _{i}= & {} -\varsigma _{i}\left( \Sigma _{i} ^{-\frac{1}{2}}\Sigma _{i} \Sigma _{i} ^{-\frac{1}{2 }}-\varsigma _{i}\Theta _{i}\right) \nonumber \\= & {} -\varsigma _{i}\left( I_{n_{i,s}}-\varsigma _{i}\Theta _{i}\right) \end{aligned}$$
(36)

where,

$$\begin{aligned} \Theta _{i} = \Sigma _{i} ^{-\frac{1}{2} }P_{i,s}{\mathscr {B}}_{i,s}\left( I_{m}+\frac{1}{\mu -\varepsilon _{i,c}}{\mathscr {B}}_{i,c}^{\mathrm {T}}P_{i,c}{\mathscr {B}}_{i,c}\right) {\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s}\Sigma _{i} ^{-\frac{1}{2}}. \end{aligned}$$

It follows from (22) that \(\Pi _{i}>0\). Obviously, we have

$$\begin{aligned} {\dot{V}}_{i}\left( t\right) <-\mu V_{i}\left( t\right) . \end{aligned}$$
(37)

It can be easily computed by (37) that

$$\begin{aligned} V_{i}\left( t\right) \le e^{-\mu \left( t-t_{i}\right) }V_{i}\left( t_{i}\right) ,\forall t\in \left[ t_{i},t_{i+1}\right) . \end{aligned}$$
(38)

In view of (25) and (38), for any \(k=2,3,\ldots ,M\), \(i=1,2,\ldots \), we have

$$\begin{aligned} V_{k}\left( t\right)\le & {} \eta ^{(k-1)}e^{-\mu \left( t-t_{0}\right) }V_{1}\left( t_{0}\right) ,\forall t\in \left[ t_{i},t_{i+1}\right) . \end{aligned}$$

It follows from (19) that \(N_{\delta }\left( t_{0},t\right) =k-1 \le N_{0}+\frac{\left( t-t_{0}\right) }{\tau _{a}},\) then

$$\begin{aligned} V_{k}\left( t\right)&\le \eta ^{(N_{0}+\frac{t-t_{0}}{\tau _{a}} )}e^{-\mu \left( t-t_{0}\right) }V_{1}\left( t_{0}\right) \nonumber \\&=e^{-\lambda \left( t-t_{0}\right) }V_{1}\left( t_{0}\right) , \end{aligned}$$
(39)

where \(\lambda =\mu -\frac{\ln \eta }{\tau _{a}}.\) In order to guarantee \(\lambda >0\), the average dwell-time should satisfy

$$\begin{aligned} \tau _{a}> \frac{\ln \eta }{\mu }. \end{aligned}$$

From (39), we have

$$\begin{aligned} \left\| {\mathscr {X}}\left( t\right) \right\| \le \frac{\underset{i\in \Psi }{ \max }\left( \lambda _{\max }\left( {\mathscr {P}}_{i}\right) \right) }{\underset{i\in \Psi }{\min }\left( \lambda _{\min }\left( {\mathscr {P}}_{i}\right) \right) }e^{-\frac{ \lambda }{2}(t-t_{0})}\left\| {\mathscr {X}}\left( t_{0}\right) \right\| . \end{aligned}$$

Thus, the closed-loop switched system is exponentially stable and the exponential decay rate is \(\frac{\lambda }{2}\). \(\square \)

Corollary 1

The explanation of (29) in the above proof. When \({\mathscr {X}}(t)\in E_{i}\), we have

$$\begin{aligned} \mathrm {sat}\left( \upsilon \right) =\upsilon , \end{aligned}$$

where,

$$\begin{aligned} \begin{aligned} E_{i}(t)=\{{\mathscr {X}}:(\varsigma _{i}\mathrm {tr} ({\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s}{\mathscr {B}}_{i,s}) +n_{i,c}\varepsilon _{i,c}){\mathscr {X}}^{\mathrm {T}}{\mathscr {P}}_{i} {\mathscr {X}}\le 1\}, \end{aligned} \end{aligned}$$
(40)

and

$$\begin{aligned} L_{i}(t)=\{{\mathscr {X}}:\Vert {\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {X}}\Vert \le 1\}, \end{aligned}$$
(41)

\(L_{i}(t)\) denotes the area in the state space where the actuator is unsaturated. The ellipsoid set \(\cup _{i=1}^{M}E_{i}\) is the stability region of system (13).

Proof

Without loss of generality, we assume \(\varepsilon _{i,c}=\varepsilon _{i,s}=\varepsilon _{i}\). In view of (20), we have

$$\begin{aligned} \begin{aligned} \Vert {\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {X}}\Vert ^{2}&={\mathscr {X}}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {B}}_{i} {\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {X}}\\&\le {\mathscr {X}}^{\mathrm {T}}{\mathscr {P}}_{i}^{\frac{1}{2}} \mathrm {tr}({\mathscr {P}}_{i}^{\frac{1}{2}}{\mathscr {B}}_{i} {\mathscr {B}}_{i}^\mathrm {T}{\mathscr {P}}_{i}^{\frac{1}{2}}) {\mathscr {P}}_{i}^{\frac{1}{2}}{\mathscr {X}}\\&={\mathscr {X}}^{\mathrm {T}}{\mathscr {P}}_{i}^{\frac{1}{2}} \mathrm {tr}({\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {B}}_{i}) {\mathscr {P}}_{i}^{\frac{1}{2}}{\mathscr {X}}\\&=\left( \varsigma _{i}\mathrm {tr}({\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} {\mathscr {B}}_{i,s})+\mathrm {tr}({\mathscr {B}}_{i,c}^{\mathrm {T}}P_{i,c} {\mathscr {B}}_{i,c})\right) {\mathscr {X}}^{\mathrm {T}}{\mathscr {P}}_{i}{\mathscr {X}}\\&=\left( \varsigma _{i}\mathrm {tr}({\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} {\mathscr {B}}_{i,s})+n_{i,c}\varepsilon _{i,c}\right) {\mathscr {X}}^{\mathrm {T}} {\mathscr {P}}_{i}{\mathscr {X}}, \end{aligned} \end{aligned}$$
(42)

which implies that

$$\begin{aligned} E_{i}(t)\subseteq L_{i}(t), \forall t\ge 0. \end{aligned}$$
(43)

Obviously, there exist the appropriate value of the parameters \(\varepsilon _{i,c}\) and \(\varepsilon _{i,s}\) to ensure the actuator unsaturated or we have \({\mathscr {X}}\in E_{i}(t)\Rightarrow \mathrm {sat}\left( \upsilon \right) =\upsilon \). \(\square \)

Remark 3

The parameters \(\varepsilon _{i}\) can be computed by solving the following equation

$$\begin{aligned} (\varsigma _{i}\mathrm {tr}({\mathscr {B}}_{i,s}^{\mathrm {T}}P_{i,s} {\mathscr {B}}_{i,s})+n_{i,c}\varepsilon _{i}\big ){\mathscr {X}}^{\mathrm {T}} {\mathscr {P}}_{i}{\mathscr {X}}=1. \end{aligned}$$

Remark 4

Comparing with the work in [23] and [1], the main differences are reflected in the following aspects: (1) the system models are different and this paper focused on the switched systems; (2) this paper transformed a non-symmetrical input saturation control problem to a control problem of switched systems with multiple equilibrium points and symmetrical input saturation, however, the results in [23] and [1] transform the non-symmetrical input saturation control problem to the control problem of the system with input saturation and constant disturbance;(3) we consider the systems whose eigenvalues are in the closed left-half plan.

Remark 5

In Theorem 1, (25) is a stability boundary condition for the switched system with the designed controller (20).

Remark 6

The link between the designed controller \(\upsilon \) in (20) and the controller u in (1) can be found in (8), that is,

$$\begin{aligned} u={\mathscr {D}}\upsilon +\varpi \end{aligned}$$

where, \({\mathscr {D}}=\frac{{\mathscr {Q}}_{d }+{\mathscr {Q}}_{f }}{2}\) and \(\varpi =\frac{{\mathscr {Q}}_{d}-{\mathscr {Q}}_{f}}{2}\Delta \).

Remark 7

From the above analysis, the low gain parameters \(\varepsilon _{i,c}\) and \(\varepsilon _{i,s}\) will affect the state convergent speed of the closed-loop system. On the other hand, in view of \(\frac{\mathrm {d}P\left( \varepsilon _{s} \right) }{\mathrm {d}\varepsilon _{s}}>0\) and \(\frac{\mathrm {d}P\left( \varepsilon _{c} \right) }{\mathrm {d}\varepsilon _{c}}>0\), the norms of the designed control gains \(\digamma _{i}=-{\mathscr {B}}_{i}^{\mathrm {T}}{\mathscr {P}}_{i}\) increase with the increase in the low gain parameters \(\varepsilon _{i,s}\) and \(\varepsilon _{i,c}\). However, in order to get \(\mathrm {sat}(v)=v\), we should choose the appropriate small value of the parameters \(\varepsilon _{i,c}\) and \(\varepsilon _{i,s}\). In reality, we should make a trade-off between the system dynamic performance and the input saturation when choosing the parameters \(\varepsilon _{i,c}\) and \(\varepsilon _{i,s}\).

Fig. 1
figure 1

The state x with \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.6,i=1,2\)

Full size image
Fig. 2
figure 2

The control input \(\mathrm {sat}(\upsilon )\) with \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.6,i=1,2\)

Full size image

4 Numerical Simulation

In this section, we will give a numerical example to illustrate the effectiveness of the proposed method. Considering switched system with

$$\begin{aligned} A_{1,s}= & {} \left[ \begin{array}{cc} 0 &{} \quad 1 \\ -0.2 &{} \quad -0.5 \end{array} \right] ,B_{1,s}=\left[ \begin{array}{c} 1 \\ 0.5 \end{array} \right] , \\ A_{2,s}= & {} \left[ \begin{array}{cc} -0.7 &{} \quad 0.1 \\ -0.1 &{} \quad -1 \end{array} \right] ,B_{2,s}=\left[ \begin{array}{c} 0.1 \\ 1 \end{array} \right] , \\ A_{1,c}= & {} \left[ \begin{array}{cc} 0 &{} \quad -1 \\ 1 &{} \quad 0 \end{array} \right] ,B_{1,c}=\left[ \begin{array}{c} 0 \\ 1 \end{array} \right] , \\ A_{2,c}= & {} \left[ \begin{array}{cc} 0 &{} \quad 1 \\ -2 &{} \quad 0 \end{array} \right] ,B_{2,c}=\left[ \begin{array}{c} -1\\ 1 \end{array} \right] . \end{aligned}$$

We set \({\mathscr {Q}}_{d }=1,{\mathscr {Q}}_{f}=0.5\), \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.6,i=1,2\). The initial state is \(x\left( 0\right) =\left[ \begin{array}{cccc} -0.5&\quad -0.2&\quad 1&\quad -1.5 \end{array} \right] .\) By the above parameters, we compute the equilibrium points \(x_{1}^{*}=\left[ \begin{array}{cccc} 1.25&\quad -0.25&\quad -0.25&\quad 0 \end{array} \right] ^{\mathrm {T}},x_{2}^{*}=\left[ \begin{array}{cccc} 0.0704&\quad 0.243&\quad 0.125&\quad 0.25 \end{array} \right] ^{\mathrm {T}}\), \(\varsigma _{1}=21,\) \(\varsigma _{2}=45,\) \(\eta =2\), \(\mu =0.5\), \(\tau _{a}> 1.3863\) and

$$\begin{aligned}&{\mathscr {P}}_{1}=\left[ \begin{array}{cccc} 15.7231 &{} \quad 6.8928 &{} \quad 0 &{} \quad 0 \\ 6.8928 &{} \quad 19.1303 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 2.5173 &{} \quad -0.6400 \\ 0 &{} \quad 0 &{} \quad -0.6400 &{} \quad 2.1333 \end{array} \right] ,\\&{\mathscr {P}}_{2}=\left[ \begin{array}{cccc} 19.2174 &{} \quad 0.1975 &{} \quad 0 &{} \quad 0 \\ 0.1975 &{} \quad 12.5347 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1.1804 &{} \quad -0.0284 \\ 0 &{} \quad 0 &{} \quad -0.0284 &{} \quad 0.8960 \end{array} \right] . \end{aligned}$$
Fig. 3
figure 3

The switching signal \(\delta \left( t\right) \) with \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.6,i=1,2\)

Full size image
Fig. 4
figure 4

The state x with \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.6,i=1,2\)

Full size image
Fig. 5
figure 5

The control input \(\mathrm {sat}(\upsilon )\) with \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.6,i=1,2\)

Full size image
Fig. 6
figure 6

The switching signal \(\delta \left( t\right) \) with \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.6,i=1,2\)

Full size image
Table 1 The value of \(\left\| \digamma \right\| \) with different \(\varepsilon _{i}\)
Full size table
Fig. 7
figure 7

The state x with \(i=1,2\)

Full size image
Fig. 8
figure 8

The control input \(\mathrm {sat}(\upsilon )\) with \(i=1,2\)

Full size image
Fig. 9
figure 9

The curve of d with \(d=\sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}}\), where A1 denotes the proposed approach, A2 denotes the approach in [23]

Full size image

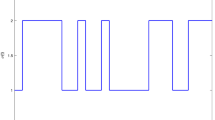
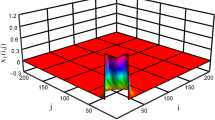
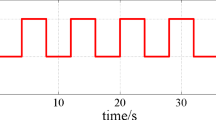
From Figs. 1 and 4, we can see that the system state can convergent to the equilibrium points. From Figs. 2 and 5, we can see that the control input is unsaturated. The switching signal is recorded in Figs. 3 and 6 . The curves of the state and the control input in Figs. 1 and 2 are corresponding to the switching signal \(\delta \left( t\right) \) in Fig. 3, while, Figs. 4 and  5 are corresponding to the switching signal \(\delta \left( t\right) \) in Fig. 6. For comparing, we choose \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.3\), \(\varepsilon _{i,s}=\varepsilon _{i,c}=0.05,i=1,2\) to carry out the simulation. From Table 1, we can see that the norms of the designed control gains \(\digamma _{i}\) increase with the increase in the parameters \(\varepsilon _{i,s}\) and \(\varepsilon _{i,c},i=1,2\). From Figs. 7 and 8, we can see that the convergent speed of the states is affected by the low gain parameters \(\varepsilon _{i,s}\) and \(\varepsilon _{i,c},i=1,2\), that is, the larger the value of the low gain parameter, the faster the state convergence speed. We also compare the proposed mathematical transformation approach manipulating the non-symmetrical input saturation with the approach in [23]. When the system is stable, the state trajectory in [23] is farther from the origin than the proposed approach due to introducing the constant disturbance, that is, the static error of the proposed method is smaller. From Fig. 9, we can see that the state trajectory in [23] converges to 0.485, while, the state trajectory converges to 0.377 with the proposed method.

5 Conclusion

This paper studied the exponential stability of switched systems with non-symmetrical input saturation and average dwell time. We transform a switched system with non-symmetrical input saturation to a switched system with multiple equilibrium points and symmetrical input saturation. The state feedback controller was designed based on the two classes of PRE. The designed controller can be easily computed by solving PRE. The numerical simulation results show the usefulness of the proposed method. In our future work, we will optimize the designed parameters to improve the dynamic performance of the switched system with non-symmetrical input saturation and extend the proposed method to the Markov jump systems [7, 9, 18].