1 Introduction

Differential equations of fractional orders can be used to simulate phenomena in various scientific disciplines, thereby enhancing our understanding of natural phenomena across a wide range of fields, including engineering, electronics, biology, business, computer science, and physics. Throughout history, notable scientists such as Bernoulli, Liouville, Euler, L’Hopital, and Wallis have made substantial contributions to the development of fractional calculus, furthering our understanding of these equations. However, due to the inherent challenges in finding exact and analytical solutions for fractional differential equations, numerical methods are employed to study and analyze these solutions.

Since its invention by Heaviside in 1880, telegraph equations have been used to solve a wide variety of issues in numerous scientific areas. In addition to their applications in the study of wave propagation in cable transmission, wave phenomena, and electric signals, the proposed equation is also applied in the fields of telephone lines, wireless signals, and radio frequency [1].

The distance and time of electric transmissions with current and voltage are described by the telegraph equation [1]. Through the use of several numerical and analytical techniques, including the Adomian decomposition method, telegraph equations of fractional orders were solved (ADM) in [2], He’s homotopy perturbation method (HPM) [3], Laplace transforms combined with HPM [4], and the reduced differential transform technique [5]. Chebyshev tau method is used to solve the hyperbolic telegraph equation [6]. The variation iteration method is used to find the solution to the proposed problem and obtained the same result as obtained by (ADM) with fewer computations [7], explicit finite difference method [8], and the modified Adomian decomposition method (MADM) [9]. A novel enhanced variation iteration Laplace transform approach is applied to time-fractional differential equations [10].

The homotopy perturbation method (HPM) is another important semi-analytical technique for solving differential equations [11,12,13]. It is an efficient technique for studying various types of nonlinear functional equations. Volterra–Fredholm nonlinear systems were solved by HPM [14], also hyperbolic PDEs [15], and Zakharov–Kuznetsov [16], and a system of nonlinear differential equations [17] are solved by HPM.

The solutions to both integer- and fractional-order linear and nonlinear differential equations have been extensively described over the past decade. Methods such as Laplace Adomian decomposition method, Laplace homotopy perturbation method, and more recently, the Elzaki homotopy transformation perturbation method have been employed to solve various problems, including a family of differential equations [18], spatial diffusion of biological population [19], nonlinear oscillators [20], and system of linear and nonlinear PDEs of fractional orders [21]. The solution of the fractional telegraph equation is examined in this study using the Elzaki transform together with a novel variation iteration method and homotopy perturbation method. The fractional reduced differential transform technique is utilized to solve differential equations with fractional and integer orders in [22,23,24,25,26]. The Adomian decomposition Sumudu transform approach is employed to solve differential equations with fractional and integer orders in [27,28,29].

Elzaki integral transform is a modification of the Laplace and Sumudu transforms which was invented by Tarig [30], and Elzaki transformation is an efficient and powerful technique that has found the exact solutions to several differential equations which cannot be solved by Sumudu transform [31]. Elzaki integral equation is a powerful and efficient technique that has been used to solve many differential equations of integer and fractional orders; see [32,33,34,35,36,37,38,39].

The objective of this paper is to expand the applications of HEM and illustrate the efficiency of the proposed method. Therefore, we consider the fractional telegraph equation

Nanoelectromechanical systems have a significant impact on detection and actuation. However, the design of nanoelectromechanical processes is adversely affected by nonlinearity. Noise, response instability, and bifurcation phenomena are characteristics of the complicated behaviors of nonlinear vibration systems. Consequently, it is crucial to manage nonlinear vibrations in nanoelectromechanical systems to produce stable vibrations.

$$\begin{aligned} \frac{\partial ^{\beta }u}{\partial x^{\beta }}+K\frac{\partial ^{\alpha }w}{\partial t^{\alpha }}+Jw= & {} 0 \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial ^{\beta }w}{\partial x^{\beta }}+M\frac{\partial ^{\alpha }r}{\partial t^{\alpha }}+Lu= & {} 0. \end{aligned}$$
(2)

By differentiating Eq. (1) with respect to time t and Eq. (2) with respect to position x, and subsequently solving the resulting system, we obtain the following equations:

Differentiate Eq. (1) concerning t and (2) concerning x, then solving the system, the following equation is obtained as

$$\begin{aligned} \frac{\partial ^{2\beta }w}{\partial x^{2\beta }}+R\left[ -K\frac{\partial ^{\alpha }w}{\partial t^{\alpha }}-Jw \right] +L\left[ -K\frac{\partial ^{2\alpha }w}{\partial t^{2\alpha }}-J\frac{\partial ^{\alpha }w}{\partial t^{\alpha }} \right] =0 \end{aligned}$$

Assume that \(\varepsilon =\frac{L}{M}\epsilon =\frac{J}{K}\delta ^{2}=\frac{1}{MK}\) substituting these values in the above equation, we obtain

$$\begin{aligned} \frac{\partial ^{2\alpha }w}{\partial t^{2\alpha }}+(\varepsilon +\epsilon )\frac{\partial ^{\alpha }w}{\partial t^{\alpha }}+\varepsilon \epsilon w=\delta ^{2}\frac{\partial ^{2\beta }w}{\partial x^{2\beta }} \end{aligned}$$
(3)

Equation (3) is a telegraph equation which arises in electromagnetic waves.

2 Preliminaries

In this section, we introduce some definitions and properties of fractional calculus and the Elzaki transform, which are used in this article.

Definition 2.1

[40] A real-valued function \(\textrm{g}\left( \textrm{y} \right) \mathrm {, y>0}\) is belong to the space \(\textrm{C}_{\mathrm {\sigma }}\mathrm {, \sigma \in R}\) if there exists at least a real number \(\mathrm {d>\sigma ,}\) such that \(\textrm{g}\left( \textrm{y} \right) \mathrm {=}\textrm{y}^{\textrm{d}}\textrm{g}_{\textrm{1}}\mathrm {(y)}\) where \(\textrm{g}_{\textrm{1}}\mathrm {(y)\in }\textrm{C}\left( \mathrm {0,\infty } \right) \) and it is said to be in the space \(\textrm{C}_{\mathrm {\sigma }}^{\textrm{n}}\) if\({\textrm{ g}}^{\textrm{n}}\mathrm {\in }R_{\mathrm {\sigma }}\mathrm {, n\in N}\)

Definition 2.2

[41] The function \(\textrm{f}\left( \textrm{u} \right) \)is called Riemann–Liouville fractional integral of order \(\alpha >0\) if it defines as:

$$\begin{aligned} J^{\alpha }f\left( w \right) =\frac{1}{\varGamma \left( \alpha \right) }\mathop {\int }\limits _0^w \left( w-t \right) ^{\alpha -1} f\left( t \right) dt, t>0 \end{aligned}$$

In particular, \(J^{0}f\left( w \right) =f\left( w \right) \)

For \(\mathrm {\theta \ge 0}\) and\(\mathrm { \vartheta \ge -1}\), some properties of the operator \(\textrm{J}^{\mathrm {\alpha }}\)

  1. 1.

    \(J^{\alpha }J^{\theta }f\left( w \right) =J^{\alpha +\theta }f\left( w \right) \)

  2. 2.

    \(J^{\alpha }J^{\theta }f\left( w \right) =J^{\theta }J^{\alpha }f\left( w \right) \)

  3. 3.

    \(J^{\alpha }y^{\vartheta }=\frac{\varGamma \left( \vartheta +1 \right) }{\varGamma \left( \alpha +\vartheta +1 \right) }y^{\alpha +\vartheta }.\)

Definition 2.3

[41] The function \(\mathrm {f\in }\textrm{C}_{\mathrm {-1}}^{\textrm{n}}\mathrm {, n\in N}\), is called Caputo fractional derivative if it defines as

$$\begin{aligned} D^{\alpha }f\left( w \right) =\frac{1}{\varGamma \left( n-\alpha \right) }\mathop {\int }\limits _0^w \left( w-t \right) ^{n-\alpha -1} f^{n}\left( t \right) dt, n-1<\alpha \le n \end{aligned}$$

Definition 2.1

[42] The Elzaki transform of the function \(\mathrm {f(u)}\) is defined as:

$$\begin{aligned} E\left[ f\left( w \right) \right] =T\left( v \right) =v\mathop {\int }\limits _0^\infty {f\left( w \right) e^{\frac{-u}{v}}dw} \quad u>0. \end{aligned}$$

The Laplace transform of the Caputo fractional derivative has the form

$$\begin{aligned} L\left[ D_{x}^{\alpha }g\left( x,w \right) \right] =s^{\alpha }G\left( s \right) -\sum \limits _{i=0}^{n-1} {s^{\alpha -1-i}g^{\left( i \right) }\left( x,0 \right) n-1<\alpha \le n} \end{aligned}$$
(4)

where \(G\left( s \right) \) represents the Laplace transform of\( g\left( x \right) \)

The Elzaki form of the Caputo operators is as follows [33]:

$$\begin{aligned} E\left[ D_{x}^{\alpha }g\left( x,w \right) \right] =\frac{G\left( s \right) }{s^{\alpha }}-\sum \limits _{i=0}^{n-1} {s^{2-\alpha +i}g^{\left( i \right) }\left( x,0 \right) n-1<\alpha \le n} \end{aligned}$$
(5)

3 He–Elzaki method (HEM)

To obtain the constrained recurrence relation needed to define the Lagrange multiplier, the Elzaki transform for fractional differential equations is employed in this letter. The integral computation and the convolution terms are avoided using this method. Elzaki transform’s constraints on nonlinear components require the usage of the HPM to reduce calculations. The novel and altered strategy are built up as follows:

The Lagrange multiplier is identified by multiplying the Elzaki transform of the proposed differential equation by the Lagrange multiplier, which is performed using a variational approach. The suggested problem’s nonlinear terms are calculated using the Adomain polynomial, and the series solution is then discovered using the well-known homotopy perturbation approach.

To clarify the implementation of our modified method, consider the following nonlinear equation.

$$\begin{aligned} Rw-Nw-m=0. \end{aligned}$$
(6)

Applying the Elzaki transform, we have

$$\begin{aligned} E[Rw-Nw-m]=0. \end{aligned}$$

Now, we take the Lagrange multiplier\( \mu (v)\)

$$\begin{aligned} \mu \left( v \right) \left\{ E\left[ Rw-Nw-m \right] \right\} =0 \end{aligned}$$

Here, we can have the following recurrence relation:

$$\begin{aligned} W_{j+1}\left( v \right) =W_{j}\left( v \right) +\mu \left( v \right) \left\{ E\left[ Rw-Nw-m \right] \right\} \end{aligned}$$
(7)

The recurrence relation reflects the modified Elzaki variant, and we use the following relation to incorporate the Lagrange multiplier \(\mu \left( v \right) \) while applying the optimal condition

$$\begin{aligned} \frac{\rho W_{j+1}\left( v \right) }{\rho W_{j}\left( v \right) }=0. \end{aligned}$$

Now, taking the inverse of Elzaki transform of Eq. (7) to achieve the solution of Eq. (3)

$$\begin{aligned} w_{j+1}\left( v \right) =w_{j}\left( v \right) +E^{-1}\left[ \mu \left( v \right) \left\{ E\left[ Rw_{j}]-E[A_{j}+m \right] \right\} \right] . j=0,1,2,3, \ldots \end{aligned}$$

where \(A_{j}\) represents the Adomian polynomial as follows:

$$\begin{aligned} A_{j}=\frac{1}{j!}\frac{d^{j}}{d\tau ^{j}}\left( N\left( \sum \limits _{j=0}^\infty u_{j}\tau ^{j}\right) \right) . \end{aligned}$$
(8)

Finally, to investigate the series approximate solution the homotopy perturbation method is considered by equating the powers of the embedded parameter\( p\)

4 Homotopy perturbation method (HPM)

In this section, we study the concept of HPM for the solution to our problem. Consider the following differential equation

$$\begin{aligned} Rw-Nw=m \end{aligned}$$
(9)

where m represents a source term, R and N represent linear and nonlinear operators, respectively, and w represents the solution function.

According to Homtopy theory\( H\left( u,p \right) \), \(H\left( u,p \right) :R\times \left[ 0,1 \right] \rightarrow R\) that satisfies the equation

$$\begin{aligned} H\left( u,p \right) =\left( 1-p \right) \left[ R\left( u \right) -R\left( u_{0} \right) \right] +p\left[ R\left( u \right) -N\left( u \right) -m \right] =0 \end{aligned}$$

Using simple calculations, we obtain

$$\begin{aligned} R\left( u \right) -pN\left( u \right) =m \end{aligned}$$
(10)

where the embedding parameter \(p\in [0,1]\), and \(u_{0}\) represents the initial approximation of the solution of Eq. (3); further, w is the homotopy function with \(R\left( w_{0} \right) =m\).

Thus, w can be written as:

$$\begin{aligned} u={\lim \limits _{p \rightarrow 1}}{({u}_{0}+{pu}_{1}+p^{2}u_{2}+ \ldots )} \end{aligned}$$
(11)

Using (10) and (11), we have

$$\begin{aligned} u_{0}+{pu}_{1}+p^{2}u_{2}+p^{3}u_{3}\ldots =m+pN\left( u \right) \end{aligned}$$

Equating the powers of p can be written as follows:

$$\begin{aligned} p^{0}: u_{0}= & {} m, \\ p^{1}: u_{1}= & {} N\left( u_{0} \right) , \\ p^{2}: u_{2}= & {} u_{1}N^{'}(u_{0}), \\ p^{3}: u_{3}= & {} N^{'}(u_{0})+\frac{u_{1}^{2}N^{''}\left( u_{0} \right) }{2}, \\&\vdots&\end{aligned}$$

Finally, as p approach to 1 the approximate solution of (3) is

$$\begin{aligned} {w=u}_{0}+u_{1}+u_{2}+u_{3}\ldots \quad . \end{aligned}$$
(12)

5 Applications

The effectiveness and precision of the novel method for solving the telegraph equation are verified using numerical patterns. We use several examples to explain our modification approach to the suggested problem for this aim.

Example 5.1

Consider the following nonlinear telegraph equation of fractional order \(0<\alpha \le 1\)

$$\begin{aligned} \frac{\partial ^{2\alpha }}{\partial t^{2\alpha }}z(x,t)={-z}^{2}(x,t)-\frac{\partial ^{\alpha }}{\partial t^{\alpha }}z(x,t)+z_{xx}(x,t)+f(x,t), \quad tx\ge 0, \end{aligned}$$
(13)

with the initial conditions\( z\left( x,0 \right) =x-x^{2}, z_{t}\left( x,0 \right) =0\). The exact solution of the Eq. (13) when \(\alpha =1\) is

$$\begin{aligned} z\left( x,t \right) =(x-x^{2})(t^{3}+1). \end{aligned}$$

Assume that \(f\left( t,x \right) =\left( x-x^{2} \right) \left( \frac{6t^{3-2\alpha }}{\varGamma \left( 4-2\alpha \right) }+\frac{6t^{3-\alpha }}{\varGamma \left( 4-\alpha \right) }+\left( t^{3}+1 \right) \left( x-x^{2} \right) \right) +2(t^{3}+1)\).

Taking the Elzaki transform of Eq. (13)

$$\begin{aligned} E\left[ \frac{\partial ^{2\alpha }z(x,t)}{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }z\left( x,t \right) }{\partial t^{\alpha }}-\frac{\partial ^{2}z\left( x,t \right) }{\partial x^{2}}+z^{2}\left( x,t \right) +f(x,t) \right] =0. \end{aligned}$$

Now, we multiply both sides of above equation by \(\mu (v)\)

$$\begin{aligned} \mu (v)E\left[ \frac{\partial ^{2\alpha }z(x,t)}{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }z\left( x,t \right) }{\partial t^{\alpha }}-\frac{\partial ^{2}z\left( x,t \right) }{\partial x^{2}}+z^{2}\left( x,t \right) +f(x,t) \right] =0. \end{aligned}$$

The recurrence relation has the following form

$$\begin{aligned} Z_{j+1}\left( x,v \right) =Z_{j}\left( x,v \right) +\mu \left( v \right) E\left[ \frac{\partial ^{2\alpha }z_{i}(x,t)}{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }z_{i}(x,t)}{\partial t^{\alpha }}-\frac{\partial ^{2}z_{i}(x,t)}{\partial x^{2}}+z_{i}^{2}\left( x,t \right) \right] . \end{aligned}$$
(14)

Taking the variation of the above equation and using Elzaki property (5), we obtain

$$\begin{aligned} {\rho Z}_{j+1}\left( x,v \right)= & {} \rho Z_{j}\left( x,v \right) +\mu \left( v \right) \rho \left\{ \frac{Z_{j}\left( x,v \right) }{v^{2\alpha }}-v^{2-2\alpha }\hat{Z}_{j}\left( x,0 \right) -v^{3-2\alpha }\frac{\partial ^{\alpha }\hat{Z}_{j}\left( x,0 \right) }{\partial t}\right. \nonumber \\{} & {} \left. -E\left[ \frac{\partial ^{\alpha }\hat{z}_{j}\left( x,t \right) }{\partial t^{\alpha }}-\frac{\partial ^{2}\hat{z}_{j}\left( x,t \right) }{\partial x^{2}}+\hat{z}_{j}^{2}\left( x,t \right) \right] \right\} .\\ {\rho Z}_{j+1}\left( x,v \right)= & {} {\rho Z}_{j}\left( x,v \right) +\frac{1}{v^{2\alpha }}\mu \left( v \right) {\rho Z}_{j}\left( x,v \right) \nonumber \end{aligned}$$
(15)

The variables \(\hat{z}_{j}=\hat{z}_{j}\left( x,0 \right) =\hat{Z}_{j}(x,0)\) are restricted variables, since \(\rho \hat{z}_{j}\left( x,0 \right) ={\rho \hat{Z}}_{j}\left( x,0 \right) =0\) and\( \frac{{\rho Z}_{j+1}\left( x,v \right) }{{\rho Z}_{j}\left( x,v \right) }=0\)

Therefore, the Lagrange multiplier\( \mu \left( v \right) =-v^{2\alpha }\)

Table 1 Exact solution and approximate solution at different values of x and \(t\alpha =1\), for Eq. (12), illustrate the exact and approximate solutions of (12) for different values of t and\( \alpha \) using HETM. It is clear that the value \(\alpha =1\) using HEM gives almost the exact solution of the Eq. (12)
Full size table

Substituting the Lagrange multiplier in Eq. (14), we obtain

$$\begin{aligned} Z_{j+1}\left( x,v \right) =Z_{j}\left( x,v \right) -v^{2\alpha }E\left[ \frac{\partial ^{2\alpha }\hat{z}_{j}\left( x,t \right) }{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }\hat{z}_{j}\left( x,t \right) }{\partial t^{\alpha }}-\frac{\partial ^{2}\hat{z}_{j}\left( x,t \right) }{\partial x^{2}}+\hat{z}_{j}^{2}\left( x,t \right) \right] \end{aligned}$$

Applying Elzaki inverse, we get

$$\begin{aligned} z_{j+1}\left( x,v \right) =z_{j}\left( x,v \right) -E^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{2\alpha }z_{j}(x,t)}{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }z_{j}(x,t)}{\partial t^{\alpha }}-\frac{\partial ^{2}z_{j}(x,t)}{\partial x^{2}}+z_{j}^{2}\left( x,t \right) \right] \right] \end{aligned}$$

Since\( \frac{\partial ^{\alpha }z_{j}}{\partial t^{\alpha }}=0, j=0,1,2,3\ldots \) to get He’s polynomial, we apply HPM

$$\begin{aligned} z_{0}+{pz}_{1}+p^{2}z_{2}+p^{3}z_{3}\ldots =z_{j}\left( x,t \right) -pE^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{\alpha }z_{j}(x,t)}{\partial t^{\alpha }}-\frac{\partial ^{2}z_{j}(x,t)}{\partial x^{2}}-A_{j} \right] \right] \end{aligned}$$
(16)

where\({ A}_{j}\) are the Adomian polynomials of \((z_{0}, z_{1}, z_{2}, z_{3}\ldots )\); we use (8) to calculate the Adomian polynomials:

$$\begin{aligned} { A}_{0}= & {} z_{0}^{2}, { A}_{1}=2z_{0}z_{1},\\ { A}_{2}= & {} 2z_{0}z_{2}+{ z}_{1}^{2}, { A}_{3}=2z_{0}z_{3}+2z_{1}z_{2}. \end{aligned}$$

Equating the highest powers of\( p\), and substituting the Adomian polynomials in (16), leads to

$$\begin{aligned} p^{0} : z_{0}= & {} z_{0}\left( x,t \right) +{tz_{0}}_{t}\left( x,t \right) + E^{-1}\left[ v^{2\alpha }E\left[ f(x,t) \right] \right] \\ p^{1} : z_{1}= & {} -E^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{2}z_{0}}{\partial x^{2}}-\frac{\partial ^{\alpha }z_{0}}{\partial t^{\alpha }}-z_{0}^{2} \right] \right] \\ p^{2} : z_{2}= & {} -E^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{2}z_{1}}{\partial x^{2}}-\frac{\partial ^{\alpha }z_{1}}{\partial t^{\alpha }}-2z_{0}z_{1} \right] \right] \\ p^{3} : z_{3}= & {} -E^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{2}z_{0}}{\partial x^{2}}-\frac{\partial ^{\alpha }z_{0}}{\partial t^{\alpha }}-2z_{0}z_{2}-{ z}_{1}^{2} \right] \right] \end{aligned}$$

Here, the HEM solution for Eq. (13) is

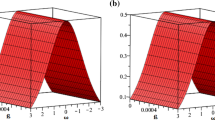
$$\begin{aligned} z=z_{0}+z_{1}+z_{2}+z_{3}+\ldots . \end{aligned}$$

In Fig. 1, graph (a) and graph (b) represent the exact solution and HEM solution of Eq. (12) at\( \alpha =1\), respectively. It is clear that the exact and HEM solutions are in a good agreement. In Fig. 2, graph (a) and graph(b) represent the HEM solution of Eq. (13) at \(\alpha =0.95\) and\( \alpha =0.90\), respectively.

Fig. 1
figure 1

Exact solution and the approximate solution of z(x, t) of Eq. (13) at \( \alpha =1\)

Full size image
Fig. 2
figure 2

approximate solutions of z(x, t) of equation (13) at \( \alpha =0.95\) and 0.9.

Full size image

Example 5.2

Consider the following nonlinear telegraph equation with fractional order \(0<\alpha \le 1\)

$$\begin{aligned} \frac{\partial ^{2\alpha }}{\partial t^{2\alpha }} z(x,t)={-z}^{2}(x,t)-\frac{\partial ^{\alpha }}{\partial t^{\alpha }}z(x,t)+\frac{\partial ^{2}z}{\partial x^{2}}(x,t)+f(x,t) \le t,0<x<\pi \end{aligned}$$
(17)

with the initial conditions\( z\left( x,0 \right) =\sin \left( x \right) , z_{t}\left( x,0 \right) =0\). The exact solution of the Eq. (17) when \(\alpha =1\) is

$$\begin{aligned} z\left( x,t \right) =\sin \left( x \right) (t^{3}-1). \end{aligned}$$

Assume that \(f\left( t,x \right) =\mathrm {sin?}(x)\left( \frac{6t^{3-2\alpha }}{\varGamma \left( 4-2\alpha \right) }+\frac{6t^{3-\alpha }}{\varGamma \left( 4-\alpha \right) }+\left( t^{6}-2t^{3}+1 \right) \mathrm {sin?}(x)+t^{3}-1 \right) \).

Taking the Elzaki transform of Eq. (17)

$$\begin{aligned} E\left[ \frac{\partial ^{2\alpha }z(x,t)}{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }z\left( x,t \right) }{\partial t^{\alpha }}-\frac{\partial ^{2}z\left( x,t \right) }{\partial x^{2}}+z^{2}\left( x,t \right) +f(x,t) \right] =0. \end{aligned}$$

Now, we multiply both sides of above equation by \(\mu (v)\)

$$\begin{aligned} \mu (v)E\left[ \frac{\partial ^{2\alpha }z(x,t)}{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }z\left( x,t \right) }{\partial t^{\alpha }}-\frac{\partial ^{2}z\left( x,t \right) }{\partial x^{2}}+z^{2}\left( x,t \right) +f(x,t) \right] =0. \end{aligned}$$

The recurrence relation has the following form

$$\begin{aligned} Z_{j+1}\left( x,v \right) =Z_{j}\left( x,v \right) +\mu \left( v \right) E\left[ \frac{\partial ^{2\alpha }z_{i}(x,t)}{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }z_{i}(x,t)}{\partial t^{\alpha }}-\frac{\partial ^{2}z_{i}(x,t)}{\partial x^{2}}+z_{i}^{2}\left( x,t \right) \right] . \end{aligned}$$
(18)

Taking the variation of the above equation and using Elzaki property (5), we obtain

$$\begin{aligned} {\rho Z}_{j+1}\left( x,v \right)= & {} \rho Z_{j}\left( x,v \right) +\mu \left( v \right) \rho \left\{ \frac{Z_{j}\left( x,v \right) }{v^{2\alpha }}-v^{2-2\alpha }\hat{Z}_{j}\left( x,0 \right) -v^{3-2\alpha }\frac{\partial ^{\alpha }\hat{Z}_{j}\left( x,0 \right) }{\partial t}\right. \nonumber \\{} & {} \left. -E\left[ \frac{\partial ^{\alpha }\hat{z}_{j}\left( x,t \right) }{\partial t^{\alpha }}-\frac{\partial ^{2}\hat{z}_{j}\left( x,t \right) }{\partial x^{2}}+\hat{z}_{j}^{2}\left( x,t \right) \right] \right\} .\\ {\rho Z}_{j+1}\left( x,v \right)= & {} {\rho Z}_{j}\left( x,v \right) +\frac{1}{v^{2\alpha }}\mu \left( v \right) {\rho Z}_{j}\left( x,v \right) \nonumber \end{aligned}$$
(19)

The variables \(\hat{z}_{j}=\hat{z}_{j}\left( x,0 \right) =\hat{Z}_{j}(x,0)\) are restricted variables, since \(\rho \hat{z}_{j}\left( x,0 \right) ={\rho \hat{Z}}_{j}\left( x,0 \right) =0\) and \( \frac{{\rho Z}_{j+1}\left( x,v \right) }{{\rho Z}_{j}\left( x,v \right) }=0\)

Therefore, the Lagrange multiplier\( \mu \left( v \right) =-v^{2\alpha }\)

Table 2 Approximate solutions of (12) for different values of tx and\( \alpha \) using HEM. It is clear that as the value \(\alpha \) approach to 1 gives better solutions
Full size table

Substituting the Lagrange multiplier in Eq. (18), we obtain

$$\begin{aligned} Z_{j+1}\left( x,v \right) =Z_{j}\left( x,v \right) -v^{2\alpha }E\left[ \frac{\partial ^{2\alpha }\hat{z}_{j}\left( x,t \right) }{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }\hat{z}_{j}\left( x,t \right) }{\partial t^{\alpha }}-\frac{\partial ^{2}\hat{z}_{j}\left( x,t \right) }{\partial x^{2}}+\hat{z}_{j}^{2}\left( x,t \right) \right] \end{aligned}$$

Applying Elzaki inverse, we get

$$\begin{aligned} z_{j+1}\left( x,v \right) =z_{j}\left( x,v \right) -E^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{2\alpha }z_{j}(x,t)}{\partial t^{2\alpha }}+\frac{\partial ^{\alpha }z_{j}(x,t)}{\partial t^{\alpha }}-\frac{\partial ^{2}z_{j}(x,t)}{\partial x^{2}}+z_{j}^{2}\left( x,t \right) \right] \right] \end{aligned}$$

Since\( \frac{\partial ^{\alpha }z_{j}}{\partial t^{\alpha }}=0 j=0,1,2,3\ldots \) to get He’s polynomial, we apply HPM

$$\begin{aligned} z_{0}+{pz}_{1}+p^{2}z_{2}+p^{3}z_{3}\ldots =z_{j}\left( x,t \right) -pE^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{\alpha }z_{j}(x,t)}{\partial t^{\alpha }}-\frac{\partial ^{2}z_{j}(x,t)}{\partial x^{2}}-A_{j} \right] \right] \end{aligned}$$
(20)

where\({ A}_{j}\) and \(B_{j}\)are the Adomian polynomials of \((z_{0}, z_{1}, z_{2}, z_{3}\ldots )\); we use (8) to calculate the Adomian polynomials:

$$\begin{aligned} { A}_{0}= & {} z_{0}^{2}, { A}_{1}=2z_{0}z_{1},\\ { A}_{2}= & {} 2z_{0}z_{2}+{ z}_{1}^{2}, { A}_{3}=2z_{0}z_{3}+2z_{1}z_{2}. \end{aligned}$$

Equating the highest powers of\( p\), and substituting the Adomian polynomials in (16) leads

$$\begin{aligned} p^{0} : z_{0}= & {} z_{0}\left( x,t \right) +{tz_{0}}_{t}\left( x,t \right) + E^{-1}\left[ v^{2\alpha }E\left[ f(x,t) \right] \right] \\ p^{1} : z_{1}= & {} -E^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{2}z_{0}}{\partial x^{2}}-\frac{\partial ^{\alpha }z_{0}}{\partial t^{\alpha }}-z_{0}^{2} \right] \right] \\ p^{2} : z_{2}= & {} -E^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{2}z_{1}}{\partial x^{2}}-\frac{\partial ^{\alpha }z_{1}}{\partial t^{\alpha }}-2z_{0}z_{1} \right] \right] \\ p^{3} : z_{3}= & {} -E^{-1}\left[ v^{2\alpha }E\left[ \frac{\partial ^{2}z_{0}}{\partial x^{2}}-\frac{\partial ^{\alpha }z_{0}}{\partial t^{\alpha }}-2z_{0}z_{2}-{ z}_{1}^{2} \right] \right] \end{aligned}$$

Here, the HEM solution for Eq. (17) is

$$\begin{aligned} z=z_{0}+z_{1}+z_{2}+z_{3}+\ldots . \end{aligned}$$
Table 3 Error analysis for Eq. (17) at different values of x and t were \(\alpha =1\) illustrates the error analysis of Eq. (16) for different values of t and\( x\) using HETM. It is clear that the value \(\alpha =1\) using HEM gives almost the exact solution of the Eq. (16)
Full size table
Fig. 3
figure 3

Exact solution and the approximate solution z(x, t) of Eq. (17) at \( \alpha =1\)

Full size image
Fig. 4
figure 4

Approximate solutions of z(x, t) of Eq. (17) at\( \alpha =0.9\) and 0.8

Full size image

In Fig. 3, graph (a) and graph (b) represent the exact solution and HEM solution of Eq. (13) at\( \alpha =1\), respectively. It is clear that the exact and HEM solutions are in a good agreement. In Fig. 2, graph (a) and graph(b) represent the HEM solution of Eq. (13) at \(\alpha =0.9\) and\( \alpha =0.8\), respectively.

6 Conclusion

To study the solution of time-fractional telegraph equations, a novel computational technique called Elzaki integral transform is merged with He’s variation iteration method in this paper. The fractional derivatives are defined in the Caputo sense. The suggested method was applied to a new model with one dimension, and the exact and approximate solutions were found. The beauty of the innovative procedure is that one needs to depend on neither the integration nor the convolution theorem in recurrence relation to define the Lagrange multiplier. Convolution and integral computation terms are avoided by using this method. The HPM and Adomian polynomial is used to reduce calculations due to the Elzaki transform’s restrictions on nonlinear components. Finally, we found that the He–Elzaki transform method (HEM), which has been successfully implemented in solving the time-fractional telegraph model, is an efficient method for solving differential equations of integer and fractional orders.

NOMENCLATURE

 

\(\textrm{N}\)

Neutral number

\(\mu \left( . \right) \)

Lagrange multiplier

\(A_{j}\)

Adomian polynomials

\(E\left[ . \right] \)

Elzaki transform

\(\alpha \)

Fractional-order derivative

p

Embedding parameter

t

Time parameter