1 Introduction

Significant advancements have been achieved in the basic understanding (Okal 2015), warning methodology (Bernard and Titov 2015), and pre-disaster preparedness against tsunamis, since the 2004 Indian Ocean (Synolakis and Bernard 2006) and, especially, after the 2011 Japan (Kânoğlu et al. 2015) events. One of the key advancements was the establishment of the standards for tsunami numerical models, which were introduced as a set of analytical, experimental, and field data by Synolakis et al. (2008). Hence, the validated and verified tsunami numerical models (Synolakis et al. 2008) consistently show predictions with excellent agreements with field measurements, i.e., deep ocean, tide gauge, and runup data (Titov et al. 2016).

The nonlinear shallow water-wave (NSW) models have been widely used in tsunami modeling. The National Oceanic and Atmospheric Administration’s operational tsunami forecast system is based on validated and verified NSW model called the method of splitting tsunami (MOST), and has been used for every significant tsunami during the in-house development since 2003 and at the operational warning centers since 2013 (Titov et al. 2016; Bernard and Titov 2015). The analytical solutions of the NSW equations and its linear approximation, the linear shallow water-wave (LSW) equations, have been extensively used as key instruments in fundamental understanding of the maximum runup of long waves—tsunamis—as well as swash zone dynamics (Antuono and Brocchini 2010; Madsen and Fuhrman 2008; Kânoğlu 2004; Kânoğlu and Synolakis 1998; Brocchini 1997; Brocchini and Peregrine 1996; Synolakis 1987). An extensive number of analytical studies on the NSW equations employs the state-of-the-art hodograph transformation introduced by Carrier and Greenspan (1958). The Carrier–Greenspan transformation converts the nonlinear set of equations into a single linear equation, which is solvable by standard methods. However, this unique transformation did not find many applications for a very long time, probably due to difficulty in implementing geophysically meaningful initial wave profiles.

This restriction was overcome by Synolakis (1987) with a boundary value problem (BVP) formulation. The Carrier–Greenspan transformation was used by Synolakis (1987) to solve the nonlinear propagation and runup problem over a sloping beach as a BVP, taking the boundary condition at the toe of the beach from the solution of the LSW equations for the canonical problem—wave propagation first over a constant depth and then over a sloping beach. Later, Tadepalli and Synolakis (1994) used the methodology of Synolakis (1987) to solve the LSW equations and showed that the leading-depression N-waves run up higher than their counterparts, i.e., leading-elevation N-waves. Madsen and Schäffer (2010) extended the work of Synolakis (1987), and Tadepalli and Synolakis (1994) by avoiding the classical solitary wave tie between wavenumber and wave height to depth ratio, and providing solutions for the temporal variation of the shoreline motions for solitary waves and N-waves for the canonical problem.

Carrier and Greenspan (1958) used the Hankel transform in their original formulation with two very specific initial wave profiles. Carrier et al. (2003) improved the Carrier and Greenspan (1958) solution in terms of initial wave profiles, again using the Hankel transform and representing the solution in terms of a Green function, which involves the complete elliptic integral of the first kind, having singularity. This singularity becomes important, especially, when the initial wave has velocity. Hence, Carrier et al. (2003) were able to compute the wave field satisfactorily only for small values of the initial amplitude when there is an initial velocity. Kânoğlu (2004) adopted the original solution of Carrier and Greenspan (1958), but linearized the hodograph transformation to derive the initial conditions in the transform space. This approach led to simpler solution integrals and allowed the use of more realistic initial waveforms. Later, Kânoğlu and Synolakis (2006) showed how to incorporate the exact nonlinear initial wave velocity into the hodograph transform technique.

In terms of analytical solutions for more general bathymetric profiles, Kânoğlu and Synolakis (1998) used the LSW equations to evaluate the amplification factor for long wave propagation over piecewise linear slopes. They then extended their solution into a three-dimensional problem of long wave propagation and runup around a conical island. Later, Fuentes et al. (2015) augmented Kânoğlu and Synolakis (1998)’s runup estimate for the continental shelf and slope bathymetric profile to more general ones. The hodograph transformation technique has also been utilized to obtain the runup of long waves on more general bathymetries, such as non-plane beaches (Choi et al. 2008), inclined channels with parabolic cross sections (Didenkulova and Pelinovsky 2011a), and U- and V-shaped bays of single (Harris et al. 2016; Didenkulova and Pelinovsky 2011b) and piecewise (Anderson et al. 2017) slopes. Recently, Rybkin et al. (2014) presented an exact analytical solution of the NSW equations for wave runup over inclined channels of arbitrary cross-section generalizing previous studies on wave runup for a plane beach and channels of parabolic cross sections.

An alternate analytical solution for the NSW equations was provided by Aydın (2011), and Aydın and Kânoğlu (2007) in the context of the wind set-down relaxation problem, considering a long and shallow bay connected to a deep ocean. They first presented an explicit analytical solution for the steady-state wind set-down phase—description of the sea surface state in the presence of a continuously blowing wind in seaward direction—and they then modeled the relaxation phase—the subsequent wave motion after the wind stops blowing—analytically. They expressed the flow field in terms of an eigenfunction expansion combined with the hodograph transformation technique. Their formulation for the relaxation phase led to an initial-boundary value problem (IBVP) involving the solution of the NSW equations over a linearly sloping beach and was suitable for a solution in terms of a Fourier–Bessel series.

Furthermore, a limited number of studies attempted to generalize the hodograph transformation into three-dimensions and succeeded in providing analytical solutions, at least in the weak form, for obliquely incident waves with a small angle of incidence (Brocchini and Peregrine 1996; Carrier and Noiseux 1983). Recently, Kânoğlu et al. (2013) used the LSW equations in three-dimensional propagation of an N-wave to show the focusing effect in the direction of depression, where abnormal wave height could be observed. They conjectured that some of the extreme runup values observed in the field such as the ones during 27 July 2006 Java and 11 March 2011 Japan tsunamis could be explained through focusing.

Here, we use the hodograph transformation and solve the NSW equations through eigenfunction expansion as IBVP for the classical problem of long wave evolution and runup over a sloping beach. We evaluate the methodology with a wide class of initial wave profiles with and without initial velocity.

2 Analytical Solution

The non-dimensional form of the NSW equations is given as

$$\begin{aligned} \eta _t&+ \big [(h+\eta )u\big ]_x = 0,\end{aligned}$$
(1a)
$$\begin{aligned} u_t&+ u u_x + \eta _x = 0, \end{aligned}$$
(1b)

where \(h(x)=x\) and subscripts denote derivatives with respect to the arguments. Here, \(\eta (x, t)\) and u(x, t) represent the free-surface elevation and the depth-averaged velocity, respectively. The non-dimensional quantities in (1) are defined as

$$\begin{aligned} x&=\tilde{x}/\tilde{l}, \quad (h,\eta )=(\tilde{h},\tilde{\eta })/(\tilde{l} \tan \beta ), \nonumber \\ u&=\tilde{u}/\sqrt{g \, \tilde{l} \tan \beta }, \quad {\mathrm{and}}\quad t=\tilde{t}/\sqrt{\tilde{l} / (g \tan \beta )}, \end{aligned}$$
(2)

where \(\tilde{l}\), g, and \(\beta\) are the characteristic horizontal length scale, the gravitational acceleration, and the beach angle with the horizontal, respectively (Fig. 1).

Figure 1
figure 1

Definition sketch (not to scale)

Full size image

We introduce the hodograph transformation similar to Carrier and Greenspan (1958) as

$$\begin{aligned}&\sigma = \sqrt{x+\eta },\end{aligned}$$
(3a)
$$\begin{aligned} &\lambda = t-u, \end{aligned}$$
(3b)

which allows to transform (1) into

$$\begin{aligned}&(\sigma ^2 u)_{\sigma } + 2 \sigma (\eta +\frac{u^2}{2})_{\lambda } = 0,\end{aligned}$$
(4a)
$$\begin{aligned}&2 \sigma \, u_{\lambda } + (\eta +\frac{u^2}{2})_{\sigma } = 0, \end{aligned}$$
(4b)

by replacing the independent variables (x, t) with the respective auxiliary variables \((\sigma ,\lambda )\). Furthermore, defining a potential function as

$$\begin{aligned} \varphi = \eta +\frac{u^2}{2}, \end{aligned}$$
(5)

and eliminating u in (4), a single second-order linear differential equation results for the potential function \(\varphi\)

$$\begin{aligned} 4\,\varphi _{\lambda \lambda } - \frac{1}{\sigma } (\sigma \varphi _{\sigma })_{\sigma } = 0, \end{aligned}$$
(6)

as the governing equation. Notably, this transformation maps the moving shoreline tip in the physical coordinates onto a fixed point in the hodograph space (\(\sigma =0\) at \(x_s=-\eta _s\)) through (3a).

The common practice has been to use the integral transform techniques to solve (6). However, here, we consider an IBVP and pursue a solution through an eigenfunction expansion, under the most general case, i.e., an initial wave height distribution, \(\eta (x,t=0)=\eta _0(x)\), with a corresponding velocity profile, \(u(x,t=0)=u_0(x) \ne 0\). These conditions are expressed in the hodograph space by directly approximating x through the linearized form of (3a), \(x \approx \sigma ^2\), as in Kânoğlu (2004). Then, the initial conditions in the \((\sigma ,\lambda )\)-space can be expressed as \(\eta (\sigma ,\lambda =\lambda _0)=\eta _0(\sigma )\) and \(u(\sigma ,\lambda =\lambda _0)=u_0(\sigma )\), or specifically for the governing equation (6) as

$$\begin{aligned}&\varphi (\sigma ,\lambda =\lambda _0) = \eta _0 (\sigma ) + \frac{u_0 ^2 (\sigma )}{2} \equiv P (\sigma ), \end{aligned}$$
(7a)
$$\begin{aligned}&\varphi _{\lambda }(\sigma ,\lambda =\lambda _0) = -u_0 (\sigma ) - \frac{\sigma }{2} \frac{du_0(\sigma )}{d\sigma } \equiv F (\sigma ), \end{aligned}$$
(7b)

following from (5) and (4a), respectively. Here, we note that \(u(x,t=0)=u_0(x) \ne 0\) in the (x, t)-space corresponds to \(\lambda _{0}=-u_{0} (\sigma )\ne 0\) in the \((\sigma ,\lambda )\)-space through (3b) (Kânoğlu and Synolakis 2006) and, hence, \(\lambda _0=0\) at \(t=0\) in the absence of initial velocity.

In terms of boundary conditions, the solution needs to be bounded everywhere, including at the shoreline. In addition, we use homogeneous boundary condition at the seaward boundary, \(\sigma =\sqrt{x_l+\eta }\approx \sqrt{x_l}=L\), to formulate the solution simply through eigenfunction expansion. We first adopt the Dirichlet (first-type) condition, \(\varphi (\sigma =L,\lambda ) = 0\). Therefore, the boundary conditions in the \((\sigma ,\lambda )\)-space are

$$\begin{aligned}&\vert \varphi (\sigma =0,\lambda )\vert < \infty ,\end{aligned}$$
(8a)
$$\begin{aligned}&\varphi (\sigma =L,\lambda ) = 0. \end{aligned}$$
(8b)

The IBVP formulated above is now a classical separation of variables problem, i.e., \(\varphi (\sigma ,\lambda )=S(\sigma )T(\lambda )\). The series expansion for the potential function becomes

$$\begin{aligned} \varphi (\sigma ,\lambda ) = \sum _{n=1} ^{\infty } J_0 (2\alpha _n \sigma ) \, [A_n \, \cos (\alpha _n \lambda ) + B_n \, \sin (\alpha _n \lambda )], \end{aligned}$$
(9)

through (6) applying the condition given in (8a) and denoting \(\alpha _n=z_n/(2L)\), where the \(z_n\) are the zeros of the Bessel function of the first kind of order zero, \(J_0 (\bullet )\), following from (8b)Footnote 1. To calculate the unknown coefficients \(A_n\) and \(B_n \, (n \ge 1)\), the initial conditions given in (7) are considered:

$$\begin{aligned} A_n=\frac{2}{\alpha _n\,L^2 \,J_1^2 (z_n)}\big [\alpha _nP_n\cos (\alpha _n \lambda _0) -F_n\sin (\alpha _n \lambda _0)\big ],\end{aligned}$$
(10a)
$$\begin{aligned} B_n&=\frac{2}{\alpha _n\,L^2 \,J_1^2 (z_n)}\big [F_n\cos (\alpha _n \lambda _0) +\alpha _nP_n\sin (\alpha _n \lambda _0)\big ], \end{aligned}$$
(10b)

where

$$\begin{aligned} \left\{ \begin{array}{l} P_n\\ F_n\\ \end{array} \right\} = \int _{0} ^{L} \sigma ^* \, \left\{ \begin{array}{l} P(\sigma ^*)\\ F(\sigma ^*)\\ \end{array} \right\} \, J_0 (2 \alpha _n\sigma ^*) \, d\sigma ^*. \end{aligned}$$
(11)

This completes the solution of the IBVP defined by (6)–(8) in the hodograph space.

The depth-averaged velocity \(u(\sigma ,\lambda )\) follows from (4b) and (9) as

$$\begin{aligned} u(\sigma ,\lambda ) = \sum _{n=1} ^{\infty } \frac{J_1 (2\alpha _n \sigma )}{\sigma } \big [A_n \, \sin (\alpha _n \lambda )-B_n \, \cos (\alpha _n \lambda )\big ]. \end{aligned}$$
(12)

The apparent singularity of (12) at the shoreline (\(\sigma =0\)) can easily be resolved with the use of \(\lim _{z \rightarrow 0} J_1 (\xi z) / z = \xi / 2\), and the shoreline velocity hence becomes

$$\begin{aligned} u_s (\lambda ) = \sum _{n=1} ^{\infty } \alpha _n \, \big [ A_n \, \sin (\alpha _n \lambda ) - B_n \, \cos (\alpha _n \lambda )\big ]. \end{aligned}$$
(13)

Once \(\varphi (\sigma ,\lambda )\) and \(u(\sigma ,\lambda )\) are calculated in the hodograph \((\sigma ,\lambda )\)-space, the solution in the physical (x, t)-space follows as

$$\begin{aligned}&\eta = \varphi -\frac{u^2}{2},\end{aligned}$$
(14a)
$$\begin{aligned}&x = \sigma ^2-\eta ,\end{aligned}$$
(14b)
$$\begin{aligned}&t = \lambda +u. \end{aligned}$$
(14c)

The temporal variation of the shoreline position is calculated explicitly using (13) and (14), employing \(\sigma =0\):

$$\begin{aligned}&x_s(\lambda )=\frac{u_s ^2(\lambda )}{2}-\varphi (0,\lambda ),\end{aligned}$$
(15a)
$$\begin{aligned}&t_s(\lambda )=\lambda +u_s(\lambda ). \end{aligned}$$
(15b)

Moreover, \(\eta (x, t)\) and u(x, t) can be evaluated at any time \(t=t^*\) or at any location \(x=x^*\) through the following Newton–Raphson algorithms:

$$\begin{aligned}&\lambda _{i+1}=\lambda _{i}-\frac{t^{*}-t(\sigma , \lambda _{i})}{\left[ -1-u_{\lambda }\right] _{(\sigma , \lambda _{i})}},\end{aligned}$$
(16a)
$$\begin{aligned}&\sigma _{i+1}=\sigma _{i}-\frac{x^{*}-x(\sigma _{i}, \lambda )}{\left[ -2 \sigma +\varphi _{\sigma }-u\,u_{\sigma }\right] _{(\sigma _i, \lambda )}}, \end{aligned}$$
(16b)

respectively (Kânoğlu 2004; Synolakis 1987).

In addition to the Dirichlet condition at the seaward, we also consider the Neumann (second-type) boundary condition, \(\varphi _{\sigma }(\sigma =L,\lambda ) = 0\). Then, the series expansion for the potential function becomes

$$\begin{aligned} \varphi (\sigma ,\lambda ) = A_0+\sum _{n=1} ^{\infty } J_0 (2\beta _n \sigma ) \big [A_n \cos (\beta _n \lambda )+B_n \sin (\beta _n \lambda )\big ], \end{aligned}$$
(17)

\(\beta _n=w_n/(2L)\), under this boundary condition. In the Fourier–Bessel series, again, \(J_0 (\bullet )\) is the Bessel function of the first kind of order zero and the \(w_n\) are the zeros of the function \(w J'_0 (w)=0\) (or \(w J_1 (w)=0\))Footnote 2, due to the Neumann-type boundary condition at \(\sigma =L\). Since \(w J_1 (w)=0\) has a double root at \(w=0\), Dini’s expansion of order zero yields the constant term \(A_0\) in the series solution (17) (Bowman 1958), which is given by

$$\begin{aligned} A_0 = \frac{2}{L^2} \, \int _{0} ^{L} \sigma ^* \, P (\sigma ^*) \, d\sigma ^*. \end{aligned}$$
(18)

The unknown coefficients (\(A_n\), \(B_n\)) for \(n \ge 1\) are calculated from (10) replacing \(\alpha _n=z_n/(2L)\) with \(\beta _n=w_n/(2L)\). The rest of the solution is the same.

We note that the choice of Dirichlet or Neumann boundary condition at the seaward boundary implies \(\eta (x=x_l, t)=0\) or \(u(x=x_l, t)=0\), respectively, and both result in wave reflection from the artificial seaward boundary. However, the overall main interest in these analytical solutions is the shoreline quantities and, at most, flow properties close to the shoreline. Therefore, the accurate calculation of shoreline quantities before reflected wave from artificial seaward boundary reaching to the domain of interest can be achieved with the choice of the domain (\(x_l\)) large enough.

3 Applications

We apply the solution method described above to a number of previously studied initial wave profiles. We first consider

$$\begin{aligned}&\eta _0 ^ g(x) = H_1 \,{\mathrm{e}}^{-c_1(x-x_1)^2},\end{aligned}$$
(19a)
$$\begin{aligned}&\eta _0 ^n (x)= H_1 \,{\mathrm{e}}^{-c_1(x-x_1)^2}-H_2 \,{\mathrm{e}}^{-c_2(x-x_2)^2}, \end{aligned}$$
(19b)

namely, Gaussian waves and N-waves, respectively, as suggested by Carrier et al. (2003) (Fig. 2). Carrier et al. (2003) evaluated the time evolution of shoreline position and velocity for two different sets of parameters for the profiles given in (19), using the Hankel transform. Kânoğlu (2004) obtained the same results by avoiding elliptic integrals in Carrier et al. (2003), as briefly described in §1. We evaluate the shoreline position \(\eta _s(t)\) and velocity \(u_s(t)\) for the initial wave profiles without initial velocity proposed by Carrier et al. (2003) and compare them with Kânoğlu (2004) observing perfect agreement, hence with Carrier et al. (2003).

Figure 2
figure 2

Initial waveforms of a a Gaussian and b a negative Gaussian with \(H_1 =0.017\), \(c_1 =4.0\) and \(x_1 =1.69\) in (19a), and leading-depression N-waves with c \(H_1 =0.02\), \(c_1 =3.5\), \(x_1 =1.5625\), \(H_2 =0.01\), \(c_2 =3.5\) and \(x_2 =1.0\), and d \(H_1 =0.006\), \(c_1 =0.4444\), \(x_1 =4.1209\), \(H_2 =0.018\), \(c_2 =4.0\) and \(x_2 =1.6384\) in (19b). The time variations of the shoreline e–h positions and i–l velocities under \(u_0(x,t=0)=0\). Solid lines represent the present solution, while circles represent the solution of Kânoğlu (2004)

Full size image
Figure 3
figure 3

Time variations of the shoreline a–d positions and e–h velocities, for initial wave profiles given in Fig. 2a–d, respectively, with different approximations of the initial velocities. Solid lines represent the present solution with the nonlinear initial velocity profile defined by (20), while circles and dashed lines represent the results of the linear (21) and the asymptotic (22) initial velocity approximations, respectively

Full size image

We also investigate the effect of different initial velocity approximations. Note that, while cases without initial velocity represent tsunamis generated in near-field, cases with initial velocity represent tsunamis coming from far-field. We consider three previously used relations for the initial velocity, i.e., the exact nonlinear relation (Kânoğlu and Synolakis 2006)

$$\begin{aligned} u_0(x)=2\sqrt{h(x)}-2\sqrt{h(x)+\eta _0(x)}, \end{aligned}$$
(20)

the linear approximation given by Carrier et al. (2003)

$$\begin{aligned} u_0(x) \approx -\eta _0(x)/\sqrt{h(x)}, \end{aligned}$$
(21)

and the classic asymptotic relation discussed by Pritchard and Dickinson (2007)

$$\begin{aligned} u_0(x) \approx -\eta _0(x). \end{aligned}$$
(22)

In Fig. 3, we compare the shoreline motions and velocities for three different approximations of the initial velocities for the initial wave profiles presented by Carrier et al. (2003). We observe that while the exact nonlinear (20) and linear (21) relations produce almost identical results, as also noted by Kânoğlu and Synolakis (2006), the asymptotic relation (22) produces slightly higher runup.

We then consider the initial waveforms of Tinti and Tonini (2005), who obtained evolution and runup of long waves resulting from earthquakes that occur in near-field. They solved the NSW equations as an IVP after utilizing the hodograph transformation with the initial waveform of

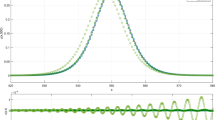
$$\begin{aligned} \eta _0 (\sigma ) = \sum _{k=0} ^{3} c_k (1+\sigma ^2)^{-(k+3/2)} , \end{aligned}$$
(23)

having zero initial velocity. The coefficients \(c_k\) are obtained using a curve fitting procedure, which approximates the initial sea surface profile obtained from Okada’s ( 1992, 1985) dislocation model. The initial wave profile (23) allows analytical expressions for the quantities of interest. Tinti and Tonini (2005) produced spatial variations of the water surface elevations along with the shoreline motions and velocities for different earthquake configurations. Leaving the details to Tinti and Tonini (2005), in Fig. 4, we reproduce results for one of the cases they presented and compare their results with that of our methodology. We obtain an excellent agreement.

Figure 4
figure 4

a Initial wave profile (23) of Tinti and Tonini (2005) with \(c_0=7.1062\times 10^{-3}\), \(c_1=-1.4383\times 10^{-2}\), \(c_2=2.7970\times 10^{-4}\) and \(c_3=6.8806\times 10^{-3}\), and its evolution at b \(\tilde{t}=1\) min and c \(\tilde{t}=3\) min. Note that \(\tilde{x}\) is decreasing in the seaward direction as in Tinti and Tonini (2005). d Time variations of the shoreline position (solid line) and velocity (dashed line). In this figure lines represent current solution while circles represent results of Tinti and Tonini (2005). The dimensional quantities are presented with the characteristic length of \(\tilde{l}=50\) km and beach slope of \(\tan \beta =1/25\), leading to the characteristic depth of \(\tilde{l} \tan \beta =2000\) m

Full size image

In terms of practical applications, the methodology presented here could be efficiently used for the initial consideration of the locations of tsunami-prone devices and structures, such as oscillating wave surge converters or tsunami shelters, against tsunami attack. O’Brien et al. (2015) considered oscillating wave surge converters and evaluated whether they could withstand force due to an incoming tsunami. Fritz et al. (2012) analyzed eyewitness videos recorded at a location near a surviving coast guard building during the 11 March 2011 Japan tsunami and determined the time history of the tsunami flood at that location with high-end particle tracking methodologies. As pointed out by Kânoğlu et al. (2013), such measurements are incredibly useful for civil defense to help inform communities at risk of how quickly overland depths can change. They also emphasized that such calculations are needed for every tsunami shelter in the tsunami prone regions around the world. It is clear that these shelters need to be built at least outside of the regions, where absolute maximum tsunami onshore and offshore velocities occur. Even though a detailed computational analysis is required, the analytical solution presented here might be useful during the preliminary analysis, at least as a first-order estimate, in determining where these devices or shelters should not be located.

4 Conclusions

We modeled nonlinear propagation of long waves climbing up on a linearly sloping beach as an IBVP by combining the eigenfunction expansion method with the hodograph transformation introduced by Carrier and Greenspan (1958). We considered a wide class of initial wave profiles with and without initial velocity and evaluated shoreline quantities using our methodology. Our methodology allows accurate estimation of the quantities of interest and our results are in excellent agreement with integral transform solutions (Kânoğlu and Synolakis 2006; Tinti and Tonini 2005; Kânoğlu 2004; Carrier et al. 2003). Moreover, our methodology is more flexible compared to the integral transform methods in terms of using different initial wave profiles. We also analyzed the effects of exact nonlinear, linearized, and asymptotic initial velocity assumptions on the shoreline quantities, confirming that the exact nonlinear and linear initial velocities produce almost identical results (Kânoğlu and Synolakis 2006). In addition, our solution is computationally efficient over the integral transform methods, i.e., it requires much less computational effort. One disadvantage of our methodology is that the evolving wave may possibly be contaminated by the wave reflected from the artificial seaward boundary. However, the shoreline quantities are of the most interest, and therefore, this difficulty can simply be avoided by choosing a sufficiently large computational domain. Postacioglu et al. (2016) considered radiation damping to the deep sea, which could be applied here to avoid the reflection from seaward boundary. Nevertheless, in our view, this would complicate the solution presented here and will not contribute in terms of shoreline behavior, which is the interest in our analytical solution.

The methodology we presented here can easily be used in benchmarking of numerical models for their shoreline runup algorithms (Synolakis et al. 2008), in further relating tsunami flow parameters to earthquake source (Sepulveda and Liu 2016), and in evaluating coastal structures and devices against tsunami attacks, at least, during the preliminary design phase. Moreover, we note that even numerical solutions of Boussinesq-type equations usually revert to temperamental NSW algorithms during runup. Our methodology which does not involve the occasional calculation of singular integrals holds promise for implementation in runup algorithms in several kinds of numerical computations, the latter remaining fairly ad-hoc, almost three decades after being proposed by Hibberd and Peregrine (1979).