Run-up of nonlinear long waves in U-shaped bays of finite length: analytical theory and numerical computations

Abstract

Run-up of long waves in sloping U-shaped bays is studied analytically in the framework of the 1-D nonlinear shallow water theory. By assuming that the wave flow is uniform along the cross section, the 2-D nonlinear shallow water equations are reduced to a linear semi-axis variable-coefficient 1-D wave equation via the generalized Carrier-Greenspan transformation (Rybkin et al. in J Fluid Mech 748:416–432, 2014). A spectral solution is developed by solving the linear semi-axis variable-coefficient 1-D equation via separation of variables and then applying the inverse Carrier-Greenspan transform. To compute the run-up of a given long wave, a numerical method is developed to find the eigenfunction decomposition required for the spectral solution in the linearized system. The run-up of a long wave in a bathymetry characteristic of a narrow canyon is then examined.

1 Introduction

Tsunamis pose a major hazard to coastal regions and can result in casualties fatalities and property damage. In 2004, the Indian Ocean tsunami caused more than 228,000 fatalities and had an estimated economic impact of 10 billion USD (Geist et al. 2006; Bernard and Robinson 2009). More recently, the 2011 Tohoku tsunami resulted in 15,889 fatalities and an estimated economic cost of over 250 billion USD (National Police Agency of Japan 2014; Nanto et al. 2011). Tsunami run-up and its associated inundation are the most devastating stage of a tsunami and therefore accurate models for the tsunami run-up process are critical for any attempt to minimize the damages caused by tsunamis.

The societal impact of a tsunami depends on both the level of preparation in the coastal communities and the efficiency of evacuation plans. In turn, the actions taken by emergency managers and harbor masters depend strongly on the information bulletins issued by tsunami warning centers (Borrero et al. 2005, 2015; Barberopoulou et al. 2011; Ewing 2011, 2015; Wilson and Miller 2014). Typical actions taken by emergency managers range from limiting access to the waterfront to a full evacuation of the near-shore areas. Under certain circumstances, emergency managers need to adjust evacuation plans; overly conservative evacuation may result in heavy costs to businesses, and potentially damage public confidence in response activities (Kiffer 2012; Wilson and Miller 2014).

Quick and robust assessment of the incoming tsunami is paramount to the determination of an emergency plan. To generate such assessments, warning centers process all available data to provide a forecast for potential inundation at selected locations (Tang et al. 2009). Quick and efficient estimates for the potential wave height at locations where forecasts by the Warning Centers are not yet available are important to select an appropriate evacuation procedure.

Recent studies of the 2011 Tohoku tsunami have suggested that the local bathymetry is a key component in predicting the local run-up, narrower bays having larger run-up than wider bays (Didenkulova and Pelinovsky 2011b; Shimozono et al. 2012, 2014; Liu et al. 2013; Kim et al. 2013). An understanding of the run-up characteristics in such bays may help communities where no timely forecast is available.

The 2-D nonlinear shallow water theory is commonly used to predict the propagation of long waves in the ocean and the subsequent inundation of coastal areas (Synolakis and Bernard 2006; Kanoglu et al. 2015). The classical 2-D nonlinear shallow water wave equations are the system

$$\begin{aligned}&\frac{\partial \eta }{\partial t}+\nabla \cdot ([\eta +h]~\mathbf {U})=0\end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial \mathbf {U}}{\partial t}+(\mathbf {U}\cdot \nabla )~\mathbf {U}=-g~\nabla \eta \end{aligned}$$

(2)

where $\mathbf {U}(x,y,t)=\langle U(x,y,t),V(x,y,t)\rangle$ is a velocity vector, $\eta (x,y,t)$ is the water level displacement, h(x, y) is the still water depth and g is the constant of gravity. In the case of long, narrow channels and fjords, (1, 2) can be depth averaged into 1-D equations (Stoker 1957; Pelinovsky and Troshina 1994; Didenkulova and Pelinovsky 2011b; Rybkin et al. 2014). For such bays, the conservation of mass and linear momentum become the shallow water wave equations

$$\begin{aligned}&\frac{\partial S}{\partial t} + \frac{\partial }{\partial x}(uS) = 0,\end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + g \frac{\partial H}{\partial x} = g \frac{\mathrm{d}h}{\mathrm{d}x}. \end{aligned}$$

(4)

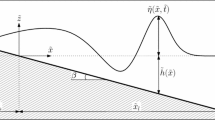
In this system, $u=u(x,t)$ is the cross-sectional average velocity, $H=H(x,t)$ and $h=h(x,0)$ are, respectively, the total water depth and unperturbed water depth along the main axis of the bay, g is the acceleration due to gravity, and S(x, t) is the cross-sectional area under water at the point (x, t). We assume that S can be written as a function of the total depth H only; i.e., the cross section of the bay does not change with respect to the distance from shoreline. We denote the average water displacement as $\eta (x,t)=H(x,t)- h(x,0)$. A sketch of a U-shaped bay and wave profile are shown in Fig. 1.

Fig. 1

Top left A (x, z) cross-sectional view of an N-wave in a constantly sloping parabolic bay. Top right A (y, z) cross-sectional view of a parabolic bay with water displacement $\eta (x,t)$, and bottom the 3-D view of the bay and N-wave given by the two cross sections

The 1-D non-linear shallow water wave equations have been extensively studied analytically. In 1958, Carrier and Greenspan developed a hodograph transform, known as the classical Carrier-Greenspan transform, which transforms the system (3, 4) into a linear second order wave equation. The classical Carrier-Greenspan transform is only valid in the case of a plane sloping beach, $h(x)=\alpha x$ where, $\alpha >0$ (Carrier and Greenspan 1957), and has been an invaluable tool in the development of solutions to shallow water wave equations (Shuto 1973; Spielfogel 1976; Synolakis 1987; Liu et al. 1991; Pelinovsky and Mazova 1992; Tadepalli and Synolakis 1994; Pelinovsky 1995; Massel and Pelinovsky 2001; Carrier et al. 2003; Kanoglu 2004; Tinti and Tonini 2005; Zahibo et al. 2006; Aydin 2011). In particular, a Green’s function for (3, 4) with a zero initial velocity condition, $u(x,0)=0$, was found by Carrier et al. (2003) and a Green’s function for (3, 4) which is valid for a nonzero initial velocity profile was developed by Kanoglu and Synolakis (2006).

In 2011, Didenkulova and Pelinovsky generalized the classical Carrier-Greenspan transformation to the case of sloping bays with parabolic cross sections (i.e., bays with bathymetry of the form $\gamma y^2-\alpha x$ for some constants $\alpha >0$, and $\gamma >0$) and U-shaped and V-shaped cross sections i.e., bays with bathymetry of the form

$$\begin{aligned} h(x,y)=\gamma |y|^m-\alpha x \end{aligned}$$

(5)

for some positive constants $m,~\alpha ,\text { and}~\gamma$ (Didenkulova and Pelinovsky 2011a, b). Note that V-shaped bays are characterized by $0<m\le 1$ and U-shaped bays by $1<m$. This generalization led to an analytic solution for wave run-up in a constantly sloping parabolic bay (Didenkulova and Pelinovsky 2011b), a d’Alembert solution for a parabolic bay of infinite length (Didenkulova and Pelinovsky 2011b), and a spectral solution for U-shaped and V-shaped bays of infinite length (Garayshin 2013). Rybkin et al. (2014) further generalized the Carrier-Greenspan transform to the case of sloping bays with arbitrary cross section which was then numerically implemented by Harris et al. (2015).

These recent generalizations prompt interest in the viability of the Carrier-Greenspan transform to long wave run-up in U-shaped and V-shaped bays. Such bays are of interest since they are good approximations to the bathymetry of many inlets, fjords, and river canyons.

In this paper, we develop a spectral solution for the tsunami run-up problem for U-shaped and V-shaped bays of finite length. We first discuss the Carrier-Greenspan transform in U-shaped and V-shaped bays as developed by Didenkulova and Pelinovsky (2011b). Then, we develop an initial value boundary problem for wave run-up in U-shaped and V-shaped bay of finite length similar to the work by Aydin and Kanoglu (2007) and Aydin (2011). The resulting initial value boundary problem is solved via separation of variables, numerically implemented, and tested for validity. In particular, we validate our method against the analytic solution for an infinite sloping bay with parabolic cross sections developed by Didenkulova and Pelinovsky (2011b). In this validation, we examine the effects that the wavelength of the initial wave and the length of the bay have on the error in the approximation of the maximum run-up. Since this analytic solution is valid for bays of infinite length, these comparisons test the validity and applicability of our solution to bays of infinite length. We then verify our solution by modeling the process of wind setdown in a 2000 m long, narrow, steeply sloping canyon and comparing our results to the 2-D verified and validated numerical model FUNWAVE (Tehranirad et al. 2012a, b; Synolakis et al. 2008). These comparisons are encouraging, and our solutions agree more than one might expect when comparing a 1-D depth averaged model to a 2-D model. In particular the two models agree on most aspects of the wave run-up and run-down process.

2 Carrier-Greenspan transform for U- and V-shaped bays

In this section, we provide a brief overview of the Carrier-Greenspan transformation by Rybkin et al. (2014) for a linearly inclined bay of U-shaped or V-shaped cross section [bays given by (5) where m, $\gamma$, and $\alpha$ are positive constants] followed by the development of an initial value boundary problem for run-up in such bays. See Fig. 1 for an example of a U-shaped bay.

Following Rybkin et al. (2014) we define a new coordinate system with respect to the bathymetry. A key step for analytically computing the generalized Carrier-Greenspan transform is finding the cross-sectional area, S(x, t), as a function of the effective depth H(x, t). For U-shaped and V-shaped bays we have $S(H)\sim \frac{m}{m+1}H^{(m+1)/m}$. Consequently. we define the new coordinate system $(\sigma ,\lambda )$ by

$$\begin{aligned} \lambda (x,t) = u(x,t) + \alpha gt\quad \text {and} \end{aligned}$$

(6)

$$\begin{aligned} \sigma (x,t) = \int _0^{H(x,t)} \sqrt{\frac{g}{S(h)}~\frac{\mathrm{d}S}{\mathrm{d}h}} ~\mathrm{d}h=2\sqrt{\frac{g(m+1)}{m}~H(x,t)}.\nonumber \\ \end{aligned}$$

(7)

The variable $\lambda$ is related to time, while $\sigma \ge 0$ is associated with the spatial variable. Note that the moving shoreline is represented by $H(x,t)=0$ and thus the above definition for $\sigma$ implies that the moving shoreline corresponds to $\sigma =0$. Examining (6) we see that initial data at $t=0$ corresponds to data at $\lambda =0$ if and only if the initial velocity, $u_0(x)=u(x,0)$, is zero. We assume that $u_0(x)=0$, unlike the work done by Kanoglu and Synolakis (2006) and Aydin (2011).

In order to exploit the convenient properties of the $\sigma -\lambda$ system, Rybkin et al. (2014) defined a function $F=F(\sigma )$ and a potential $\Phi =\Phi (\sigma , \lambda )$ via

$$\begin{aligned} F(\sigma )=2\sqrt{gS~\frac{\mathrm{d}h}{\mathrm{d}S}}, \quad u = \frac{\Phi _\sigma }{F(\sigma )}. \end{aligned}$$

(8)

For U-shaped and V-shaped bays, $H(\sigma )=\frac{m}{4g(m+1)}~\sigma ^2$ and we obtain

$$\begin{aligned} F(\sigma ) =\frac{m}{m+1} ~\sigma , \quad u = \frac{(m+1)}{m\sigma }~\Phi _\sigma . \end{aligned}$$

(9)

In terms of $F(\sigma )$, (3, 4) can be written as the linear second order wave equation

$$\begin{aligned} \Phi _{\lambda \lambda } - \Phi _{\sigma \sigma } - \frac{m+2}{m\sigma }~\Phi _\sigma = 0. \end{aligned}$$

(10)

Finally, using Eqs. (6, 7) and (9) we find the water disturbance $\eta (x,t)$ and velocity u(x, t) for U-shaped and V-shaped bays through the nonlinear transformation

$$\begin{aligned}&u= \frac{m+1}{m\sigma }~\Phi _\sigma , \quad \eta = \frac{1}{2g}\left( \Phi _\lambda - u^2\right) , \nonumber \\&x = \frac{1}{2g\alpha } \left( \Phi _\lambda - 2g~H - u^2 \right) , \quad t = \frac{\lambda - u}{\alpha g}. \end{aligned}$$

(11)

It is conceivable that there are some non-breaking initial wave profiles where (11) ceases to be one-to-one. In such cases, (11) is not invertible and thus the generalized Carrier-Greenspan transform cannot be used to solve (3, 4). Rybkin et al. (2014) have shown that the Jacobian of (11) vanishes precisely when the wave as predicted by (3, 4) breaks. Since the Jacobian of a differential coordinate transform is nonzero if and only if the coordinate transform is a bijection, the work by Rybkin et al. (2014) ensures that the generalized Carrier-Greenspan transform can predict the run-up for all non-breaking initial profiles. Note that wave breaking in the system (3, 4) corresponds to a gradient catastrophe and not the more complicated breaking process that is present in real-world tsunami waves (Liu et al. 1991).

We now develop our initial boundary value problem for bays of finite length. For the shoreline boundary condition at $\sigma =0$ we follow the work by Aydin (2011); Carrier et al. 2003); Rybkin et al. 2014) and Kanoglu and Synolakis (2006) and assume that the water velocity is bounded. In transformed coordinates the boundedness of the velocity, u, at the shoreline along with (11) gives the condition

$$\begin{aligned} \left. \Phi _\sigma (\sigma ,\lambda )\right| _{\sigma =0} = 0. \end{aligned}$$

(12)

At the offshore boundary, $x_L\gg 1$, we assume there is a physical wall, and thus we assume $u(x_L,t)=0$. For a discussion of this wall condition the interested reader may consult (Antuono and Brocchini 2007; Aydin 2011). For our method of solving (10), it is convenient for $\sigma _L=\sigma (x_L,t)$ to be constant. However, imposing that $\sigma _L$ is constant is problematic since the CG transform (11) implies that $x_L=\alpha ^{-1}(\eta (\sigma _L,\lambda )-H(x_L,t))$. Thus if the wave height at the offshore boundary is not constant, then both $\sigma _L$ and $x_L$ cannot simultaneously be constants. To solve this potential problem, we note that when $\eta (\sigma _L,\lambda ) \ll H(\sigma _L)$ for all relevant $\lambda$ then $x_L$ is approximately a constant for some fixed $\sigma _L$. This argument was previously made by Synolakis (1987). Thus we compute the initial $\sigma _L$ from (6). Physically, we are assuming that the perturbation at the wall is small when compared to the depth of the unperturbed water height at the wall. With this assumption, our condition that $u(x_L,t)=0$ with (11) becomes

$$\begin{aligned} \left. \Phi _\sigma (\sigma ,\lambda )\right| _{\sigma =\sigma _L}=0. \end{aligned}$$

(13)

For the initial conditions at $t=0$ we use the physical wave height $\eta _0(x)$ and physical velocity profile $u_0(x)=0$. Exploiting (11), our physical initial conditions are

$$\begin{aligned}&\Phi (\sigma ,0) =\frac{m}{m+1}~\int _0^\sigma u_0(\sigma (x'))~ \sigma '~d\sigma '=0 \quad \text {and}\nonumber \\&\Phi _\lambda (\sigma ,\lambda )|_{\lambda =0}=2g~\eta _0(\sigma (x)) \end{aligned}$$

(14)

with the mapping between x and $\sigma$ defined as in (6), and where $\sigma '$ is a dummy integration variable.

We now note that (10) along with our Neumann boundary conditions (12, 13) and our initial conditions (14) form a consistent system. Finally one should note that unlike the work of Aydin and Kanoglu (2007) and Aydin (2011) we use Neumann boundary conditions instead of Dirichlet conditions.

3 Spectral solution to the SWEs for U-shaped and V-shaped bays of finite length

The tsunami run-up problem in U-shaped and V-shaped bays of finite length is formulated as

$$\begin{aligned} \Phi _{\lambda \lambda }=\Phi _{\sigma \sigma }+\frac{m+2}{m\sigma }~\Phi _{\sigma }, \end{aligned}$$

(15)

with the boundary conditions

$$\begin{aligned} \left. \Phi _\sigma (\sigma ,\lambda )\right| _{\sigma =0}=0 \quad \text { and } \quad \left. \Phi _\sigma (\sigma ,\lambda )\right| _{\sigma =\sigma _L}=0, \end{aligned}$$

(16)

and the initial conditions

$$\begin{aligned} \Phi (\sigma ,0)=0 \quad \text {and} \quad \left. \Phi _\lambda (\sigma ,\lambda )\right| _{\lambda =0}=2g~\eta _0(\sigma (x)). \end{aligned}$$

(17)

Before presenting our method of solving the system (15)–(17), we would like to note that our solution is found via a generalization of the works over a sloping beach by Aydin and Kanoglu (2007) and Aydin (2011) to U-shaped bays. Since this (15)–(17) forms a linear system, we look for a separable solution (Brown and Churchill 1993) to (15) of the form $\Phi (\sigma ,\lambda )=\chi (\sigma )\Lambda (\lambda )$ and obtain

$$\begin{aligned} \left( \chi ''(\sigma )+\frac{m+2}{m\sigma }\chi '(\sigma )\right) \frac{1}{\chi (\sigma )}=-v^2=\frac{\Lambda ''(\lambda )}{\Lambda (\lambda )}. \end{aligned}$$

(18)

The choice of a negative separation constant, $-v^2$, facilitates wave-like solutions (Brown and Churchill 1993). One of the difficulties involved in solving this system is finding the function $\chi (\sigma )$. Computing $\chi (\sigma )$ is equivalent to solving the ODE boundary value problem

$$\begin{aligned}&\chi ''(\sigma )+\frac{m+2}{m\sigma }\chi '(\sigma )=-v^2\chi (\sigma ) \nonumber \\&\quad \text { where, } \quad \chi '(0)=\chi '(\sigma _L)=0. \end{aligned}$$

(19)

To solve (19), we transform it into Bessel’s equation of order $m^{-1}$. This is accomplished by multiplying (19) by $\sigma ^{(1/m)+1}$, introducing the parameter $\beta =1/m$, assuming $\chi (\sigma )=\sigma ^{-\beta } \varphi (\sigma )$ where $\varphi (\sigma )$ is an arbitrary function, and finally introducing the change of variables $\sigma =\gamma /\sqrt{v}$. Under this transformation, (19) becomes Bessel’s equation

$$\begin{aligned} \gamma ^2\varphi _{\gamma \gamma }+\gamma \varphi _\gamma +(\gamma ^2-\beta ^2)~\varphi =0 \end{aligned}$$

with boundary conditions

$$\begin{aligned} \varphi (0)=0 \quad \text {and}\quad \sigma _L\varphi _\gamma (\sigma _L)-\beta \varphi (\sigma _L)=0. \end{aligned}$$

(20)

The general solution to Bessel’s equation is

$$\begin{aligned} \varphi (\sigma )=C_1J_\beta (\sigma v)+C_2Y_\beta (\sigma v), \end{aligned}$$

where $J_\beta (\sigma )$ and $Y_\beta (\sigma )$ are Bessel functions of the first and second kinds, respectively (Abramowitz and Stegun 1965). After applying our boundary conditions (20) to $\varphi (\sigma )$, we have that $C_2=0$ and the constant v must be a positive solution to the equation

$$\begin{aligned} \sigma _L J'_\beta (\sigma _Lv)-\beta J_\beta (\sigma _Lv)=0. \end{aligned}$$

(21)

After solving (18) for $\Lambda (\lambda )$, we have

$$\begin{aligned} \Phi _n(\sigma ,\lambda )=J_\beta (\sigma v_n)~\sigma ^{-\beta }~ \left( A_n \sin (v_n\lambda )+B_n \cos (v_n\lambda )\right) \end{aligned}$$

where $v_n$ is the nth positive root of (21) solves (15) and satisfies the boundary conditions (16). To satisfy the initial conditions (17), we utilize the principle of linear superposition and find the Fourier-Bessel series,

$$\begin{aligned} \Phi (\sigma ,\lambda ) =\sum _{n=1}^\infty \Phi _n(\sigma ,\lambda )= & {} \sum _{n=1}^\infty \Bigg (\frac{J_\beta (\sigma v_n)}{\sigma ^{\beta } }~\left( A_n \sin (v_n\lambda )\right. \nonumber \\&\left. +B_n \cos (v_n\lambda )\right) \Bigg ) \end{aligned}$$

(22)

which is an exact solution of (15), subject to (16). We will refer to (22) as the spectral solution. Applying our initial conditions (17) to the function (22) we note that

$$\begin{aligned}&\sum _{n=1}^\infty B_n\frac{J_\beta (\sigma v_n)}{\sigma ^{\beta } }=0 \quad \text {and} \quad \sum _{n=1}^\infty A_n\frac{J_\beta (\sigma v_n)}{\sigma ^{\beta } } v_n\nonumber \\&\quad =2g ~\eta _0(\sigma (x)). \end{aligned}$$

(23)

In order to solve for our coefficients $A_n$ and $B_n$, we apply an orthogonality condition for the family of functions $\{ J_\beta (\sigma v_n)\sigma ^{-\beta } \}_{n= 1}^\infty$. We thus note that the left hand side of (18) can be written as

$$\begin{aligned} \frac{d^2\chi }{d \sigma ^2}+\frac{m+2}{m\sigma }\frac{d\chi }{d \sigma }=\frac{1}{\sigma ^{1+2\beta }}~\frac{d}{d \sigma }\left( \sigma ^{1+2\beta }~\frac{d\chi }{d\sigma } \right) , \end{aligned}$$

and then utilize Sturm-Liouville (Al-Gwaiz 2007) theory to obtain the orthogonality condition

$$\begin{aligned}&\int _0^{\sigma _L} \left( J_\beta (\sigma v_n)~\sigma ^{-\beta }\right) \left( J_\beta (\sigma v_m)~\sigma ^{-\beta } \right) ~ \sigma ^{1+2\beta }~d\sigma \nonumber \\&\quad =\delta _{nm}\int _0^{\sigma _L}J^2_\beta (\sigma v_n)~\sigma ~d\sigma , \end{aligned}$$

where $\delta _{nm}$ is the Kronecker delta. Consequently, multiplying (23) by $J_{\beta }(\sigma v_m)\sigma ^{1+\beta }$ and integrating with respect to $\sigma$ from 0 to $\sigma _L$ we obtain

$$\begin{aligned} B_n= 0, \end{aligned}$$

(24)

and

$$\begin{aligned} A_n= & {} \frac{2g}{v_n~\int _0^{\sigma _L}J_\beta ^2(\sigma v_n)\sigma ~d\sigma }~\int _0^{\sigma _L}\eta _0(x(\sigma ,0))\nonumber \\&\times J_\beta (v_n\sigma )~\sigma ^{1+\beta }~d\sigma . \end{aligned}$$

(25)

A straightforward modification of the work by Stempak (2002) implies that (22) with coefficients defined via (24) and (25), converges a.e. for any $m\ge -2$, as long as the initial condition $\Phi _\lambda (\sigma ,\lambda )|_{\lambda =0}=2g~\eta _0(\sigma (x))$, belongs to $L^{p}(0,\sigma _L)$ for some $p\in (4/3,\infty ]$. Thus, for any U-shaped and V-shaped bay and any bounded initial data, the convergence of our spectral solution is assumed.

Using this analytical spectral solution to (15), we develop a numerical method to evaluate our spectral solution (22). In our algorithm, we consider with an initial number of coefficients, $\{A_n\}_{n=1}^P$, compute the approximation to (15), check for convergence in the approximation of the initial condition and then increase the number of coefficients until our numerical approximation agrees with the initial condition to within the desired accuracy. Convergence of our algorithm for continuous initial data is given by the convergence of our spectral solution. The necessary computational steps to evaluate (22) are:

• 1. Use the physical bay length and the initial wave height to compute $\sigma _L$ and $\sigma (x,0)$. In particular, recall that Eq. (6) gives the transformation from (x, t) to $\sigma$ and thus $\sigma _L$ and $\sigma (x,0)$ can be computed by applying Newton’s method to

  $$\begin{aligned} \sigma (x,0) - 2\sqrt{\frac{g(m+1)}{m}~(\eta _0(x,0)-\alpha x)}=0. \end{aligned}$$

• 2. Compute the first P eigenvalues, $v_n$, for some natural number P by finding the first P positive roots of (21). We accomplish this by utilizing the open-source software Chebfun (Trefethen 2013).

• 3. Compute $A_n$ and $B_n$ for each eigenvalue under consideration from (25) and (24) and thus compute the potential $\Phi (\sigma ,\lambda )$ via (22).

• 4. Find the corresponding physical solution by computing (11) via the following algorithm:

  • (a) Compute $\Phi _\sigma$ and $\Phi _\lambda$ by utilizing (22).

  • (b) Compute $u(x(\sigma ,\lambda ),t(\sigma ,\lambda ))$ via the equation

    $$\begin{aligned} u=\frac{m+1}{m\sigma }~\Phi _\sigma . \end{aligned}$$

  • (c) Compute the wave height $\eta (x(\sigma ,\lambda ),t(\sigma ,\lambda ))$ through the equation

    $$\begin{aligned} \eta =\frac{1}{2g}~(\Phi _\lambda -u^2). \end{aligned}$$

  • (d) Calculate $x(\sigma ,\lambda )$ via

    $$\begin{aligned} x=\frac{1}{2g\alpha } \left( \Phi _\lambda - 2g~H - u^2 \right) . \end{aligned}$$

  • (e) Compute $t(\sigma ,\lambda )$ via the equation

    $$\begin{aligned} t=\frac{\lambda -u}{\alpha g}. \end{aligned}$$

• 5. Check for the error in the approximation of the initial condition. If the error is not below the desired tolerance, repeat steps 2–4 with one more eigenvalue.

• 6. The resulting (x, t) points will not be on an even grid. Interpolate the solution onto an even grid (Harris et al. 2015).

We note that the above algorithm requires around a CPU minute to run on a midrange 2012 CPU.

4 Validation of the spectral solution

In this section, we validate our spectral solution (22) by comparing it to an analytic solution found by Didenkulova and Pelinovsky (2011b) in a parabolic bay ($m=2$) of infinite length. The analytic solution we utilize is the d’Alembert solution to (10),

$$\begin{aligned} \hat{\Phi }(\sigma \ge 0,\lambda ;A,\sigma _0,\rho )&=\frac{A}{\sigma }\left[ e^{-\left( \frac{\sigma +\lambda -\sigma _0}{\rho }\right) ^2}-e^{-\left( \frac{\sigma -\lambda -\sigma _0}{\rho }\right) ^2}\right. \nonumber \\&\qquad \left. +e^{-\left( \frac{\sigma +\lambda +\sigma _0}{\rho }\right) ^2}-e^{-\left( \frac{\sigma -\lambda +\sigma _0}{\rho }\right) ^2} \right] \nonumber \\ \end{aligned}$$

(26)

for an initial N-wave profile given by

$$\begin{aligned} \hat{\eta }_0(\sigma ;A,\sigma _0,\rho )= & {} -\frac{4A}{gp^2}\left[ \frac{\sigma -\sigma _0}{\sigma }e^{-\left( \frac{\sigma -\sigma _0}{\rho }\right) ^2}\right. \nonumber \\&+\left. \frac{\sigma +\sigma _0}{\sigma }e^{-\left( \frac{\sigma +\sigma _0}{\rho }\right) ^2}\right] \quad \text {and} \quad \hat{u}_0(\sigma )=0,\nonumber \\ \end{aligned}$$

(27)

where A is related to the amplitude of the wave, $\rho$ is the wave length, and $\sigma _0$ is the distance of the wave from the shore in $\sigma$ coordinates. Since the dynamics of the (26) are analytically known, we compute $\hat{\Phi }_\sigma$ and $\hat{\Phi }_\lambda$ from (26) and thus compute the corresponding wave run-up in physical coordinates using the transformation (11).

Our validation involves four tests. We first examine the space-time dynamics of a sample N-wave; then we examine the effect of the wavelength, $\rho$, of the initial condition on the accuracy of the shoreline dynamics. Finally, the accuracy of a using finite length bay to approximate a bay of infinite length is then examined.

For each test, we fix some initial bay length and compare our spectral solution (22) at the moving shoreline. For consistency we use a bay slope of $\alpha =0.01$ for all comparisons with (26) and for notational convenience we denote the wave predicted by the spectral solution, (22), by $\eta _s(x,t)$ and the wave predicted by the analytic solution, (26), by $\eta _a(x,t)$.

4.1 Test 1: run-up of an N-wave

For our first test we examine run-up of the wave given by the initial profile $\hat{\eta }_0(\sigma ;A=300,\sigma _0=25,\rho =7)$ where $\hat{\eta }$ is defined in equation (27). These coefficients generate an N-wave centered at 1200 m with a height of 0.13 m and a length of 1200 m (see the top right plot in Fig. 2). The offshore boundary in non-physical coordinates is fixed at $\sigma _L=55$, which corresponds to an initial physical bay length of $x_L=5139.3$ m. This distance was chosen arbitrarily, but a discussion of the effect of the bay length on our spectral solution is given in Sect. 4.3.

Fig. 2

Left A plot of the first 20 coefficients for our spectral solution $\eta _s(x,t)$ given in (22) corresponding to the initial condition, $\hat{\eta }_0(\sigma ;A=300,\sigma _0=25,\rho =7)$ where $\hat{\eta }_0$ is defined in (27). Note the decaying nature of the coefficients $A_n$. Right-top Initial condition given by $\hat{\eta }_0(\sigma ;A=300,\sigma _0=25,\rho =7)$ where $\hat{\eta }_0$ is given in (27). Right-bottom The error in the our spectral approximation, $\eta _s(x,0)$, of the initial condition. The discrepancy between the initial condition and our spectral approximation to the initial condition is small having 0.00028 and 0.00036 % relative error at the maximum and minimum points of our initial wave respectfully

Figure 2 shows the values of $A_n$ for the eigenfunction decomposition of the N-wave $\hat{\eta }_0(\sigma ;A=300,\sigma _0=25,\rho =7)$. Note that $A_n$ has periodic behaviour and quickly decreases to zero and also that for $n\ge 15$ the magnitude of $A_n$ is small as compared to the coefficient values for $n<15$. The right-hand plots in Fig. 2 shows our initial condition, $\hat{\eta }_0(\sigma ;A=300,\sigma _0=25,\rho =7)$, and the error in the wave height of our spectral approximation to the initial condition. It is notable that the error is of the order of 6$\times 10^{-6}$ m for a wave with height of 0.13 m.

We now examine the time evolution of this wave. The top left plot in Fig. 3 shows the space-time behavior of the analytic solution, $\eta (x,t)$, for the infinite bay. Note that the initial N-wave splits into two waves: one that travels away from the shore and one that interacts with the shore line and then reflects off the shore. This is consistent with the investigation of N-waves preformed by Kanoglu et al. (2013). The behavior of the spectral solution, $\eta _s(x,t)$, is shown in the top right plot of Fig. 3. Its behavior differs from the analytic solution in that the waves reaching the offshore boundary reflect back towards the shore. Thus, to examine the differences between the analytic solution and the spectral solution, we consider $|\eta _a(x,t)-\eta _s(x,t)|$ in a region where the reflected wave has not yet reached the shore. This region is defined by the black lines in the top two plots in Fig. 3. The error, $|\eta _a(x,t)-\eta _s(x,t)|$, in this region is given in the bottom plot of Fig. 3. Note that the error is small, and peaks near the maximum wave run-up and minimum wave run-down. The relative error at the maximum run-up and minimum run-down are readily computed as 0.0042 and 0.0053 %, respectively. This shows that the spectral solution, $\eta _s(x,t)$, and the analytic solution, $\eta _a(x,t)$, are in good agreement.

Fig. 3

Top left The space-time evolution of the analytic solution, $\eta _a(x,t)$ given in (26). Note that the analytic solution does not interact with the wall. Top right The space-time evolution of the spectral solution $\eta _s(x,t)$ given in (22). Note that in this model, the waves interact with the boundary and reflect back towards the shoreline. The black box defines the domain for the bottom figure. Bottom The absolute value of the difference in the analytical and spectral solutions within the black box in the top plots. Note that the error within the region where the two solutions represent the same physical model is of the order of $10^{-5}$ m and the wave height is of the order of 0.1 m

4.2 Test 2: affect of a N-wave’s wavelength on the spectral solution’s error

We now examine the effect that the wavelength ($\rho$) of an initial N-wave profile has on the accuracy of the spectral solution $\eta _s$. In particular, we study three initial profiles that are centered at the same point, have the same initial maximum height, and have different wavelengths. For an accurate comparison of our spectral solution’s accuracy, we choose the number of coefficients, P, in our expansion so that P is the smallest integer such that

$$\begin{aligned} \frac{\sqrt{\sum _{i=1}^N (\eta _s(x_i,0)-\hat{\eta }_0(x_i;A,\sigma _0,\rho ))^2}}{\sqrt{\sum _{i=1}^N (\hat{\eta }_0(x_i;A,\sigma _0,\rho ))^2}}<0.01. \end{aligned}$$

In other words, we pick the smallest integer P such that the $\ell ^2$ norm of the difference between our spectral solution’s approximation to the initial condition weighted by the reciprocal of the $\ell ^2$ norm of the initial condition in question is below 1 %.

We choose to examine the initial conditions given by $\hat{\eta }_0(\sigma ;A=31.6,\sigma _0=50,\rho =11)$, $\hat{\eta }_0(\sigma ;A=15.9,\sigma _0=50,\rho =5)$, and $\hat{\eta }_0(\sigma ;A=9.9,\sigma _0=50,\rho =3)$. Figure 4 shows these three profiles. It is notable that the waves in order of large wavelength to small wavelength require 18, 32, and 57 coefficients to obtain the 0.01 error bound on the initial condition. The maximum run-up of these waves in order of longest to shortest wave is 0.015, 0.038, and 0.066 m respectively. Moreover, the absolute relative errors at the maximum run-up location ordered from longest wave to shortest wave are 0.003, 0.013, and $0.059\,\%$, respectively. This suggests that our spectral solution better approximated long waves than short waves. We believe that this loss of accuracy is due to the larger number of coefficients which must be computed to approximate the initial condition for short wavelengths. In practice, the loss of accuracy when approximating short waves is not a limitation since our model is only valid for long waves.

Fig. 4

Three initial profiles that have the same initial maximum height, are centered at the same point but have different wavelengths. Note that $\hat{\eta }_0(\sigma ;A,\sigma _0,\rho )$ is given in Eq. (27)

4.3 Test 3: error due to approximating an infinite bay by a finite bay

We now examine the effect that the length of a finite bay has on the approximation of a bay of infinite length. In particular, we are interested in the relationship between the length of the finite bay and the error in the approximation of the maximum run-up in the bay of infinite length. Note that if the length of the finite bay is too small, the wave will reflect off of the offshore boundary and interfere with the run-up process. Thus, we must ensure that the finite bay is sufficiently long to prevent error. Moreover, even if the bay is larger than this minimum distance, the fact that the physical length of our bay changes over time may affect the run-up of the spectral solution.

To test for effects of the length of the wall on the run-up, we examine the run-up of the initial profile $\hat{\eta }_0(\sigma ,A=300,\sigma _0=30,\rho =7)$ where $\hat{\eta }_0(\sigma ;A.\sigma _0,\rho )$ is defined in (27). Note that this initial condition was used in the experiment in Sect. 4.1. Figure 5 plots the error versus our choice of wall location $x_L$. Here, we see that the relative error for bays shorter than 4500 m is rather chaotic but on average, quickly decreases. For bays longer than 4500 m, the error is relatively constant. This is evident that the length of the bay does not have much effect on the maximum run-up, once it exceeds a certain length and also shows that the bay length in the experiment in Sect. 4.1 (5239.3 m) was large enough to ensure no reflection errors.

Fig. 5

The effect that the length of the bay has on the error of the approximation of the analytical solution, $\eta _a$ (26), by the spectral solution, $\eta _s$ given in (22). We consider the run-up of the initial condition $\hat{\eta }_0(\sigma ,A=300,\sigma _0=30,\rho =7)$ where $\hat{\eta }_0(\sigma ;A.\sigma _0,\rho )$ is defined in (27). Furthermore, the formulas $100*|(\max (\eta _a)-\max (\eta _s))/\max (\eta _a)|$ and $100*|(\min (\eta _a)-\min (\eta _s))/\min (\eta _a)|$ are used to compute the relative errors shown in the blue circles and red triangles respectively. Note that the error is very sensitive to the change in the length of the bay until the we consider bay larger than 4500 m

5 Verification of the spectral solution

To verify that our method properly captures real-world water dynamics, we preform two numerical experiments comparing our spectral solution to the 2-D nonlinear shallow water wave model FUNWAVE-TVD 1.0 (Shi et al. 2012). FUNWAVE is a phase-resolving, time-stepping 2-D Boussinesq model for ocean surface wave propagation. The version of FUNWAVE we use is based on the MUSCLE-TVD finite volume scheme with adaptive Runge Kutta time-stepping. In the current paper, FUNWAVE was restricted to run without dispersion so that FUNWAVE solves the classical 2-D shallow water wave equations (1, 2). We would like to note that FUNWAVE has been verified and validated by Tehranirad et al. (2012a, b) according to an exhaustive suite of tests proposed by (Synolakis et al. 2008). The interested reader may consult (Shi et al. 2012) for further details about FUNWAVE. Note, that we are comparing a 1-D model to a 2-D model, and should therefore expect some differences between the two models. For convenience of notation, we denote the wave predicted by our spectral solution (22) by $\eta _s(x,t)$ and the wave predicted by the FUNWAVE model (in the middle of the bay) by $\eta _f(x,t)$.

For our verification experiments, we choose a bathymetry and two initial profiles representative of the wind setdown problem. Wind setdown is the process where a relatively constant gust of wind blows toward the wall of a dam, canyon or glacier. This wind causes water to be pushed away from the shore and towards the wall of the canyon (Nof and Paldor 1992; Aydin and Kanoglu 2007). When the wind stops blowing, a wave propagates and floods the coast (Didenkulova and Pelinovsky 2011b). Figure 6 depicts the type of initial condition that is used in the wind setdown problem. The dashed line represents the unperturbed water height, the blue region shows the new water equilibrium position and the back triangle and rectangle represent the bathymetry of the canyon.

Fig. 6

Diagram for the wind setdown problem. The black regions are the bathymetry of the canyon, the dashed line represents the normal water height, and the blue region shows the new water equilibrium position due the force of the wind on the water

Note that within the framework of the employed model, (3)–(4), the equation resulting from employing the generalized CG transform, (10), does not depend on the coefficient $\gamma$ in (5). Thus for simplicity we assume that $\gamma =1$ and consider a narrow (cross section defined by $|y|^{3/2}$) constantly sloping, 2000 m long bathymetry with a wall depth of 30 m ($\alpha =0.015$). Figure 7 contains a 3-D view of the canyon as well as its cross section, and a plot of our model’s first four eigenfunctions at $t=0$ for this canyon.

Fig. 7

Top Example of a canyon. The canyon is 2000 m long by 30 m deep. The slope along the canyon is 0.015. The steepness of the side walls are simulated by letting the cross section be defined by $|y|^{3/2}$. Bottom-left The $y-z$ cross section of the canyon. Bottom-right The plots of the first four eigenfunctions at $t=0$ for this canyon as a function of distance from the shore. The second eigenfunction is marked with circles as it is the eigenfunction that is used as the initial condition for our first validation experiment. The fourth eigenfunction multiplied by $-1$ is shown in the 3-D canyon picture

5.1 Perturbations due to an initial disturbance parameterized by a single eigenfunction

For our first validation experiment, our initial condition is simply multiple of the second eigenfunction. In particular, we use an initial condition given by

$$\begin{aligned} \tilde{\eta }_0(\sigma )=-200\frac{J_{\beta }(\sigma \sqrt{v_1})}{\sigma ^{\beta } } \quad \text {and} \quad \tilde{u}_0(\sigma )=0, \end{aligned}$$

(28)

where $v_1$ is the second eigenvalue. Figure 7 shows this initial condition in the canyon under consideration. This profile was chosen over the initial condition used in Aydin and Kanoglu (2007) because it is given by a single eigenfunction and thus allows for an analysis of the error due to a single eigenfunction. Unlike Aydin and Kanoglu (2007), who started with the balance equations by Nof and Paldor (1992), our initial condition may not by physical significant. The interested reader is suggested to see Aydin and Kanoglu (2007) for a discussion of initial conditions for the wind setdown problem that are known to be physically relevant.

Note that for $\tilde{\eta }_0$ one can analytically compute $\eta (x,t)$ for all points (x, t) in terms of $v_1$. Thus, some of the behavior of this solution can be studied via analytic methods. In particular, the maximum run-up values, minimum run-down values, and the behavior of the solution at both the wall and shore can be analytically described in terms of the parameter $v_1$. Unfortunately, the value of $v_1$ changes the period of the solution with respect to both space and time; thus, such analytic descriptions are not useful in practice. Instead, we apply the numerical method described in Sect. 3 to generate pictures of the wave dynamics of $\tilde{\eta }_0$ in our canyon.

Figure 8 shows the wave run-up predicted by the spectral solution. The left plot shows the solution for the first two run-up values. Note the periodic nature of our solution in both space and time. In particular, the spatial part of the canyon is split into two zones which correspond to the zeros of the second eigenfunction and these zones oscillate in time similar to a sine wave with period $2\pi v_1^{-1/2}$. Recall that the derivation of our spectral solution (22) required the length of the bay to be fixed at some $\sigma _L$ (in this case $\sigma _L=44.4027$), but physically the length of bay is assumed to be fixed at some offshore distance $x_L$. Figure 8 shows that this assumption is violated; the maximum relative error in the movement of the wall is 0.9 %.

Fig. 8

Left Surface plots for the spectral solution, $\eta _s(x,t)$, corresponding to the initial condition $\tilde{\eta }_0(\sigma (x)))$ (defined in (28)) for the wave run-up problem in a 2 km long canyon. Note the periodic nature of the solution in terms of both x and t. Right A near-wall view of the error in our stationary wall assumption. Note that the largest relative error in the walls location from 2 km is 0.9 % and that the initial length of the canyon is 2 km corresponding the length of our physical canyon

Figure 9 shows the comparison between $\eta _f(x,t)$ and $\eta _s(x,t)$ for particular instances in time. We see that there is good agreement between $\eta _f(x,t)$ and $\eta _s(x,t)$ during the process of the first run-up (Fig. 9a, b) and the shoreline extrema (Fig. 9c–f). On the other hand, Fig. 9 shows that there is error (0.0042 and 0.0053 % at the first minimum run-down and maximum run-up respectively) in the wave during the run-down process.

Fig. 9

Comparison of the water level computed by the spectral solution (22) and the FUNWAVE model for the initial condition $\tilde{\eta }_0(\sigma )$ (28). a The waves 5 s into the run-up process where they agree with each other very well. b The wave in the run-up process after 100 s. c The first maximum run-up at 200 s. Again the predictions of the FUNWAVE model and the spectral solution agree. In d the wave is retreating from its maximum run-up point. During the run-down process the FUNWAVE model predicts slower water movement than our spectral solution does. In e we see the minimum run-down; at this point the two models agree with each other but there is some slight viable difference. Finally in f the waves are at run-up again and agree with each other

In order to better compare the two solutions, we compare the shoreline dynamics of the models. Figure 10 shows the shoreline wave heights predicted by both FUNWAVE, $\eta _f(x,t)$, and our spectral solution, $\eta _s(x,t)$. The curves labeled with symbols a-f correspond to the times in Fig. 9a–f. The behaviour of the solution at the shoreline is clearly seen. In particular, the two solutions agree remarkably well for the first run-up, and only begin to differ during the first run-down. Note, that the shoreline displacement predicted by FUNWAVE during the first run-down abruptly changes from the prediction given by the spectral solution. Following this abrupt change, the two solutions show similar behavior, but disagree with a time delay. Overall, after 295 s the FUNWAVE model tends to predict earlier run-up and run-down than the spectral solution. Despite these differences, the two solutions closely agree on the height and time of the wave extrema. The discrepancies we observe may be due to differences between the classical 2-D shallow water wave equations (1, 2) and our 1-D cross-sectionally averaged system (3, 4). Considering the differences in the underlying physics of the two models, the solutions agree rather well. Furthermore due to the steepness of the bay, the FUNWAVE model required 48 h (using parallelization on a super-computer) to compute the space-time dynamics of the wave run-up while the spectral solution only required only 22 s (using a single core of a personal computer) to compute the space-time dynamics of the corresponding 1-D wave.

Fig. 10

Comparison of the shoreline dynamics computed by the spectral solution (22) and FUNWAVE models. The initial condition is given by $\tilde{\eta }_0(\sigma )$ defined in (28). Note that the two models agree well until 300 s. After this time the models disagree on the space-time location of the shore location but still predict similar behavior. The dashed lines correspond to the plots shown in Fig. 9a–f

5.2 Perturbations due to an initial disturbance parameterized by the weighted sum of three eigenfunctions

In the second experiment, we use an initial condition given by a weighted sum of the first three nontrivial eigenfunctions (Fig. 7). In particular, we chose the initial condition

$$\begin{aligned} \bar{\eta }_0(\sigma )=-200\sum _{n=1}^3\frac{J_{\beta }(\sigma \sqrt{v_n})}{3^n\sigma ^{\beta } } \quad \text {and} \quad \bar{u}_0(\sigma )=0 \end{aligned}$$

(29)

where $v_n$ is the nth nontrivial eigenvalue (see Fig. 11). This initial condition was chosen because in physical coordinates the condition has the basic shape of a typical wind setdown profile and allows for an examination of the error of a more complicated eigenvalue decomposition than the initial profile used in the first experiment.

Fig. 11

Initial wave height, $\bar{\eta }_0(\sigma (x))$ defined in (29), for the second wave run-up experiment. Note that the sloping black line in the left of the figure represents the bottom of the bay and the dashed black line represents the unperturbed water level

Figure 12 shows the shoreline position predictions of both our spectral solution, $\eta _s(x,t)$, and the FUNWAVE model, $\eta _f(x,t)$. Notice that the two solutions agree rather well during the first three major run-up times, at 200, 600, and 1000 s. Additionally, both models predict similar general behavior throughout the entire time domain. There are, however, some noticeable differences during the run-down process. Specifically, there are major differences during the second and third major run-down at 700 and 1100 s respectively. Again these discrepancies may be do to the fact that we are comparing a 1-D model to a 2-D model. Similar to the last experiment, the FUNWAVE model required 48 h to compute the wave dynamics on a supercomputer whereas it required only 28 s on a single core of a mid-range 2012 CPU to compute the wave dynamics via our spectral solution.

Fig. 12

Comparison of the shoreline water level computed by the spectral solution, $\eta _s(x,t)$ (22), and the prediction of the FUNWAVE model, $\eta _f(x,t)$, for the initial condition $\bar{\eta }_0(\sigma )$ shown in Fig. 11. Note both models predict similar behavior for the shoreline and are in agreement for many of the maximum run-up values and minimum run-down values

6 Conclusions

In this paper, we developed a spectral solution to the long wave run-up problem in bays of finite length and an algorithm for its implementation. The derived solution is valid for the long wave run-up problem in constantly sloping bays of finite length with cross section given by $\gamma |y|^m$ for any positive constants m and $\gamma$. In addition, the finite bays under consideration have physical walls at some fixed offshore boundary which is typical of dams, canyons, and glaciers. The initial conditions considered were restricted to long waves with zero velocity. For the technique used in this paper, the restriction on the initial velocity is not superficial, but for small initial velocities it is possible to extend our solution by linearizing the generalized CG transform for the initial time (Carrier et al. 2003; Kanoglu 2004). The accuracy of this approximation for the methodology used in this paper is topic of future research. The choice of a zero initial velocity profile is an appropriate model to approximate physical phenomena such as wind setdown (Aydin and Kanoglu 2007; Nof and Paldor 1992; Didenkulova and Pelinovsky 2011b).

Our spectral solution has been extensively validated and verified. Several comparisons of our solution to an analytic solution for the parabolic bay of infinite length (Didenkulova and Pelinovsky 2011b) reveal that our method agrees with the analytic solution for a variety of different waves. In particular, our solution correctly predicts run-up for initial waves of varying wavelength. The effect of approximating an infinite bay by one on finite length was analyzed and it was found that our spectral solution predicts the correct shoreline behaviour given that the wall is sufficiently far from the shore. The bay length that is sufficient depends on the initial wave perturbation. Moreover, after conducting numerous experiments, we found that the length of the bay does not seem to affect the first run-up given that the bay is sufficiently long so that reflections do not interfere with the initial run-up.

The spectral solution has also been verified on the wind setdown problem via a comparison to the verified and validated nonlinear shallow water wave model FUNWAVE. The experiments show that our spectral solution agrees with the dynamics of the run-up process that are predicted by FUNWAVE. The comparisons we made with FUNWAVE suggest that our spectral solution could be used to predict some aspects of 2-D wave dynamics even though our spectral method solves the 1-D cross-sectionally averaged nonlinear shallow water wave equations. One should note that our 1-D cross-sectionally averaged model does not allow for a study of the effect of the width of the bay on the run-up and such a study is a topic for future research.

It is notable that our spectral solution is an extreme improvement over the FUNWAVE model in term of runtime. For the cases considered in this manuscript, we computed the spectral solution approximately 1500 times faster than it took to run the FUNWAVE model. Finally, one should note that throughout this manuscript only U-shaped bays were considered but the method presented here is also valid for V-shaped bays.