1 Introduction

Many of the geological structures in mineral and oil exploration can be classified into four categories: spheres, cylinders, thin sheets and geological contacts. These four simple geometric forms are convenient approximations to common geological structures often encountered in the interpretation of magnetic data. Few methods have been developed to determine simultaneously both the depth and the shape of a buried structure from magnetic data. Barbosa et al . (1999), Hsu (2002) and Gerovska and Arauzo-Bravo (2003) presented criteria for determining the correct structural index that is related to the shape of the source and is applied in magnetic interpretation using the Euler deconvolution method. Abdelrahman and Hassanein (2000) developed a parametric–curves method (window–curves method) to determine simultaneously the shape and the depth of a buried structure from a residual magnetic anomaly profile. Salem et al . (2004) presented a method for interpreting a residual magnetic anomaly where a linear equation involving a symmetric anomalous field and its horizontal gradient is derived to provide the depth and the shape of the buried structures. Abdelrahman et al. (2013) described a procedure for automated determination of the best-fit model parameters including the depth and shape of the buried structure from magnetic data. Abdelrahman and Essa (2005) developed a least-squares depth–shape curves method to simultaneously define the shape and the depth of a buried structure from a residual magnetic anomaly profile. It is evident from this review that the accuracy of the results obtained by most of these methods depends upon the accuracy to which the residual anomaly can be separated from the observed magnetic data.

Finally, to address the above regional–residual separation problem, Abdelrahman et al. (2007) developed a least-squares method to define simultaneously the shape and the depth of a buried structure from magnetic data. The method is based on computing the variance of depths determined from all second-derivative anomaly profiles. The variance is considered a criterion for determining the correct shape and depth of the buried structure. On the other hand, Abdelrahman et al. (2002) presented a semi-automatic method to determine the depth to the local and deep-seated structures from a magnetic anomaly profile and suggested a procedure to estimate the shape of both structures. However, the above two methods are generally lengthy and tedious in determining the shape and the depth of the buried structure.

In the present paper we have developed a simple and fast numerical method to determine simultaneously the depth and shape of a buried structure from second-horizontal derivative anomalies obtained from magnetic data with filters of successive window lengths using a new formula representing the magnetic anomaly expressions produced by simple geological structures. This method can be applied to residuals as well as to the observed magnetic data. The method was applied to synthetic data with and without random errors and tested on three field examples from India, Brazil and the USA.

2 Theory

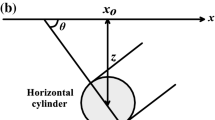
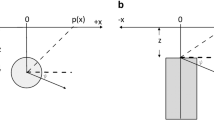
Careful examination of the total, vertical and horizontal magnetic anomaly expressions of the sphere (meridian profile) (Rao et al. 1977; Prakasa Rao and Subrahmanyam 1988), the horizontal cylinder (Prakasa Rao et al. 1986) and the thin sheet (Gay 1963) led to the following generalized formula which represents magnetic anomalies produced by most simple geologic models:

$$T(x_{i} ,z) = K\frac{{Az^{2}+ Bx_{i} + Cx_{i}^{2} }}{{(x_{i}^{2} + z^{2} )^{q} }},i = 0,1,2,3, \ldots ,N,$$
(1)

where

$$A = \left\{ \begin{gathered} 3\sin^{2} \theta - 1 \hfill \\ 2\sin \theta \hfill \\ - \cos \theta \hfill \\ \cos \theta \hfill \\ \cos \theta /z \hfill \\ \end{gathered} \right.,\;B = \left\{ \begin{gathered} - 3z\sin \theta \hfill \\ - 3z\cos \theta \hfill \\ - 3z\sin \theta \hfill \\ 2z\sin \theta \hfill \\ - \sin \theta \hfill \\ \end{gathered} \right.,\;C = \left\{ \begin{gathered} \,3\cos^{2} \theta - 1 \hfill \\ - \sin \theta \hfill \\ 2\cos \theta \hfill \\ - \cos \theta \hfill \\ 0 \hfill \\ \end{gathered} \right., \; \begin{gathered} for \, a \, sphere \, (total \, field) \hfill \\ for \, a \, sphere \, (vertical \, field) \hfill \\ for \, a \, sphere \, (horizontal \, field) \hfill \\ for \, a \, horizontal \, cylinder, \, thin \, sheet \, (FHD),\, geological \, contact \, (SHD) \, (all \, fields) \hfill \\ for \, a \, thin \, sheet, \, geological\, contact \, (FHD)\, (all \, fields). \hfill \\ \end{gathered}$$

for a sphere (total field) for a sphere (vertical field) for a sphere (horizontal field) for a horizontal, cylinder, thin sheet (FHD), geological contact (SHD) (all fields) for a thin sheet, geological contact (FHD) (all fields).

In Eq. (1) z is the depth of the body, x i is the position coordinate, K is the amplitude coefficient, θ is an inclination parameter, FHD and SHD denote the first and the second horizontal derivatives of the magnetic anomaly, respectively, and q is the shape factor. As examples, the shape factors for a sphere, a horizontal cylinder, and a thin sheet are 2.5, 2.0, and 1.0, respectively. Examples of K and θ for the case of the sphere are the magnetic moment and effective angle of magnetization in the plane of the principle profile coinciding with the x-direction, respectively. In the case of thin sheet and horizontal cylinder, the values of K and θ are shown in Table 1.

In Table 1 k is magnetic susceptibility contrast; I o is the true inclination of the geomagnetic field; \({\text{T}}_{\text{o}}^{'} \; {\text{and}}\) \({\text{I}}_{\text{o}}^{'}\)are, respectively, the effective intensity and effective inclination of the geomagnetic field in the vertical plane normal to the strike of the body; t and d are, respectively, the thickness and the dip of the thin sheet; S is the cross-sectional area of the horizontal cylinder; α is the azimuth of the body measured in a clockwise direction from magnetic north. In all cases the values of C and θ can be used for detailed interpretation.

Table 1 Characteristic amplitude coefficient K and inclination parameter θ for vertical, horizontal and total magnetic field anomalies due to thin sheets and horizontal cylinders (after Gay 1963, 1965)
Full size table

Equation (1) is similar to Eq. (6) of Abdelrahman et al. (2013) but not identical because their equation depends on the anomaly value at the origin and can be only used to interpret residual magnetic anomalies. However, our new formula (Eq. 1) can be used to develop new methods to interpret both residual and observed magnetic anomalies as follows.

Let us consider four observation points (x i – 2s, x i  − s, x i  + s, x i  + 2s) along the anomaly profile where s = 1, 2, 3,…, m spacing units is called the window length or graticule spacing of any residual or derivative filter (Hammer 1977). Using Eq. (1) the 1st horizontal derivative magnetic anomaly using a central difference formula is given by:

$$T_{x} (x_{i} ,z,s) = \frac{K}{2s}\left\{ {\frac{{Az^{2} \, + B\left( {x_{i} + s} \right) + C\left( {x_{i} + s} \right)^{2} }}{{\left( {\left( {x_{i} + s} \right)^{2} + z^{2} } \right)^{q} }} - \frac{{Az^{2} + B\left( {x_{i} - s} \right) + C\left( {x_{i} - s} \right)^{2} }}{{\left( {\left( {x_{i} - s} \right)^{2} + z^{2} } \right)^{q} }}} \right\}.$$
(2)

The 2nd horizontal derivative magnetic anomaly is obtained from Eq. (2) as

$$T_{xx} (x_{i} ,z,s) = \frac{K}{{4s^{2} }}\left\{ {\frac{{Az^{2} + B\left( {x_{i} + 2s} \right) + C\left( {x_{i} + 2s} \right)^{2} }}{{\left( {\left( {x_{i} + 2s} \right)^{2} + z^{2} } \right)^{q} }} - 2\frac{{Az^{2} + Bx_{i} + Cx_{i}^{2} }}{{(x_{i}^{2} + z^{2} )^{q} }} + \frac{{Az^{2} + B\left( {x_{i} - 2s} \right) + C\left( {x_{i} - 2s} \right)^{2} }}{{\left( {\left( {x_{i} - 2s} \right)^{2} + z^{2} } \right)^{q} }}} \right\}.$$
(3)

Following Abdelrahman and Abo-Ezz (2001), Eq. (3) gives the following numerical second derivative values at x i  = s

$$T_{xx} (s) = \frac{K}{{4s^{2} }}\left\{ {\frac{{Az^{2} + 3Bs + 9Cs^{2} }}{{(9s^{2} + z^{2} )^{q} }} - 2\frac{{Az^{2} + Bs + Cs^{2} }}{{(s^{2} + z^{2} )^{q} }} + \frac{{Az^{2} - Bs + Cs^{2} }}{{(s^{2} + z^{2} )^{q} }}} \right\},$$

which is reduced to:

$$T_{xx} (s) = \frac{K}{{4s^{2} }}\left\{ {\frac{{Az^{2} + 3Bs + 9Cs^{2} }}{{(9s^{2} + z^{2} )^{q} }} - \frac{{Az^{2} + 3Bs + Cs^{2} }}{{(s^{2} + z^{2} )^{q} }}} \right\},x_{i} = + s$$
(4)

Similarly, Eq. (3) gives the following numerical derivative values at x i  = −s, x i  = +2s, and x i  = −2s, respectively

$$T_{xx} ( - s) = \frac{K}{{4s^{2} }}\left\{ {\frac{{Az^{2} - 3Bs + 9Cs^{2} }}{{(9s^{2} + z^{2} )^{q} }} - \frac{{Az^{2} - 3Bs + Cs^{2} }}{{(s^{2} + z^{2} )^{q} }}} \right\},x_{i} = - s$$
(5)
$$T_{xx} ( + 2s) = \frac{K}{{4s^{2} }}\left\{ {\frac{{Az^{2} + 4Bs + 16Cs^{2} }}{{(16s^{2} + z^{2} )^{q} }} - 2\frac{{Az^{2} + 2Bs + 4Cs^{2} }}{{(4s^{2} + z^{2} )^{q} }} + Az^{2 - 2q} } \right\},x_{i} = + 2s$$
(6)
$$T_{xx} ( - 2s) = \frac{K}{{4s^{2} }}\left\{ {Az^{2 - 2q} - 2\frac{{Az^{2} - 2Bs + 4Cs^{2} }}{{(4s^{2} + z^{2} )^{q} }} + \frac{{Az^{2} - 4Bs + 16Cs^{2} }}{{(16s^{2} + z^{2} )^{q} }}} \right\},x_{i} = - 2s.$$
(7)

Subtracting Eq. (5) from Eq. (4) we obtain

$$T_{xx} ( + s) - T_{xx} ( - s) = \frac{3KB}{2s}\left\{ {\frac{1}{{(9s^{2} + z^{2} )^{q} }} - \frac{1}{{(s^{2} + z^{2} )^{q} }}} \right\},$$
(8)

and subtracting Eq. (7) from Eq. (6) we obtain

$$T_{xx} ( + 2s) - T_{xx} ( - 2s) = \frac{2KB}{s}\left\{ {\frac{1}{{(16s^{2} + z^{2} )^{q} }} - \frac{1}{{(4s^{2} + z^{2} )^{q} }}} \right\}.$$
(9)

In this way we are able to eliminate A and C from Eq. (3) by introducing four pieces of information, namely, T xx (+s), T xx (−s), T xx (+2s), and T xx (−2s).

Dividing Eq. (8) by Eq. (9) we obtain the following non-linear equation in z:

$$f(z,q,s) = \left( {\frac{3}{4}\left\{ {\frac{{\left[ {\left( {s^{2} + z_{j}^{2} } \right)^{q} - \left( {9s^{2} + z_{j}^{2} } \right)^{q} } \right]\left( {16s^{2} + z_{j}^{2} } \right)^{q} \left( {4s^{2} + z_{j}^{2} } \right)^{q} }}{{\left( {9s^{2} + z_{j}^{2} } \right)^{q} \left( {s^{2} + z_{j}^{2} } \right)^{q} \left[ {\left( {4s^{2} + z_{j}^{2} } \right)^{q} - \left( {16s^{2} + z_{j}^{2} } \right)^{q} } \right]}}} \right\} - F} \right) = 0.$$
(10)

where

$$F = \frac{{T_{xx} ( + s) - T_{xx} ( - s)}}{{T_{xx} ( + 2s) - T_{xx} ( - 2s)}}.$$

In this way we are able to eliminate K and B from Eqs. (8) and (9).

Equation (10) can be solved for z using standard methods for non-linear equation. Here it is solved by a fixed point iteration method. The iteration form is obtained by multiplying Eq. (10) by \(\frac{z}{F}\)and rearranging the right and left sides of the equation to be of the form z = ψ(z). The result is as follows:

$$z_{f} = \frac{{3z_{j} }}{4F}\left\{ {\frac{{\left[ {\left( {s^{2} + z_{j}^{2} } \right)^{q} - \left( {9s^{2} + z_{j}^{2} } \right)^{q} } \right]\left( {16s^{2} + z_{j}^{2} } \right)^{q} \left( {4s^{2} + z_{j}^{2} } \right)^{q} }}{{\left( {9s^{2} + z_{j}^{2} } \right)^{q} \left( {s^{2} + z_{j}^{2} } \right)^{q} \left[ {\left( {4s^{2} + z_{j}^{2} } \right)^{q} - \left( {16s^{2} + z_{j}^{2} } \right)^{q} } \right]}}} \right\},$$
(11)

where z j is the initial depth parameter and z f is the revised depth parameter; z f will be used as the z j for the next iteration. The iteration stops when |z f  − z j | ≤ e, where e is a small predetermined real number close to zero.

The advantage of this method over the other methods that use a second derivative filter is that the effect of a second-order regional polynomial is removed completely. This is because of the fact that the second derivative filter will reduce the 2nd-order regional effect to a constant regional field and at the same time the subtraction of the numerical value of T xx (−s) from the value of T xx (+s) and the subtraction of the value T xx (−2s) from The value of T xx (+2s) (Eqs. 8, 9) will eliminate the constant regional field in the data.

The depth is determined by solving one non-linear equation in z. One value of s is theoretically sufficient to determine the depth to the buried structure from Eq. (11), but in practice more than one value of s is desirable because of the presence of noise and interference from neighboring sources. However, the accuracy of the result obtained using Eq. (11) depends up on the accuracy with which the shape factor can be determined from other geological and/or geophysical data.

3 Solution Using the Window Curves Method

Because the shape of the buried structure is sometimes difficult to determine from geological and/or other geophysical data, Eq. (11) can be used not only to determine the depth but also to estimate simultaneously the shape of the buried structure. The procedure is as follows:

  1. 1.

    Determine the origin of the anomaly profile (x i  = 0) using the method described by Stanley (1977) in case of no other geological or geophysical data. A straight line joining the maximum to the minimum of the anomaly profile will intersect the anomaly curve at the point x i  = 0.

  2. 2.

    Digitize the anomaly profile at several points including the central point x i  = 0.

  3. 3.

    Subject the digitized values to a separation technique using the second derivative method. The numerical second derivative anomaly value at point x i is computed from observed magnetic data (T(x i )) using the equation

$$T_{xx} (x_{i} ) = \frac{{T(x_{i} + 2s) - 2T(x_{i} ) + T(x_{i} - 2s)}}{{4s^{2} }}.$$
(12)
  1. 4.

    Apply several second derivative filters of successive window lengths to the input data. In this way several second derivative magnetic anomaly profiles are obtained.

  2. 5.

    Apply Eq. (11) to each of the second derivative anomaly profiles, yielding depth solutions (z) for all possible q values. Then the computed depths are plotted against the shape factors representing a parametric family of the curves (window curves). The correct solution for z and q occurs at the common intersection of the window curves.

4 Theoretical Examples

4.1 Noise Free Data

The composite magnetic anomaly in nanoteslas of Fig. 1 consisting of the combined effect of a total magnetic anomaly due to a thin sheet (K = 200 nT; z = 3 m; θ = 45°; q = 1.0) and 2nd-order regional polynomial was computed by the following expression:

Fig. 1
figure 1

A composite total magnetic anomaly consisting of the combined effects of a residual component due to a thin sheet (profile length = 60 m; K = 200 nT; z = 3 m; θ = 45°; q = 1.0) and a regional component represented by a second-order polynomial

Full size image
$$\begin{gathered} T(x_{i} ) = 200\frac{{3\cos \left( {45^o} \right) - x_{i} \sin \left( {45^o} \right)}}{{\left( {x_{i}^{2} + 3^{2} } \right)}} + 0.03x_{i}^{2} - 2x_{i} + 10, \hfill \\ {\text{Thin}}\;{\text{sheet}}\;{\text{model}}+{\text{second-order}}\;{\text{regional}}\;{\text{polynomial}} .\hfill \\ \end{gathered}$$
(13)

The magnetic anomaly T(x i ) is processed using five free parameters (window length) (s = 1, 2, 3, 4 and 5 m). The numerical second derivative anomaly was computed from the input data using Eq. (12).

Equation (11) was applied to each of the five second horizontal derivative magnetic anomaly profiles (Fig. 2) yielding depth solutions for all possible (q) values. The range of the shape factor value is chosen to be from 0.8 to 2.5. The spacing of the q values is chosen to be 0.1. The computed depths are plotted against the shape factors representing the parametric family of the window curves. The results are summarized in Fig. 3. The correct solution for q and z occurs at the common intersection of the window curves. Figure 3 shows the intersection at the correct location of q = 1.0 and z = 3.0 m. The depth and the shape of the buried structure are in excellent agreement with the actual depth and shape of the thin sheet model.

Fig. 2
figure 2

Data analysis of Fig. 1 using the present second derivative method

Full size image
Fig. 3
figure 3

The family of window curves of z as a function of q for s = 1, 2, 3, 4 and 5 m as obtained from noise free magnetic anomaly (Eq. 13) using the present approach. Estimates of q and z are, respectively, 1.0 and 3.0 m

Full size image

The five window curves shown in Fig. 3 intersect at a single point representing the correct solution for the shape factor and depth parameters. When using the correct q value we obtained the correct z value for any s value while using wrong q values different z-solutions are obtained for each s value. This is true because when the correct q value is used the original Eq. (1) is correct and therefore the second derivative approximation expressions are valid and f(z, q, s) = 0 is valid and has the same solution for any value of s. By contrast, with a wrong value of q the solution f(z, q, s) = 0 is incorrect and different for every value of s as shown in Fig. 3.

It is also shown in Fig. 3 that the iteration method (Eq. 11) does not converge to a depth solution in some cases when we use a smaller q value than the actual q value. This criterion can be used to inform us about the range of the shape factor. When there is no convergence the actual shape factor must be greater than the assumed shape factor.

4.2 Effect of Random Noise

We have computed a composite magnetic anomaly consisting of the combined effect of a total magnetic anomaly due to a sphere (K = 3,000 nT; z = 6 m; θ = 60°; q = 2.5) and 2nd-order regional polynomial (Fig. 4) using the following expression:

Fig. 4
figure 4

A noisy composite total magnetic anomaly consisting of the combined effects of a residual component due a sphere (profile length = 60 m; K = 3,000 nT; z = 6 m; θ = 60°; q = 2.5) and a regional component represented by a second-order polynomial

Full size image
$$\begin{gathered} T(x_{i} ) = 3,000\left\{ {\frac{{x_{i}^{2} \left( {3\cos^{2} \left( {60^o} \right) - 1} \right) - 18x_{i} \sin \left( {120^o} \right) + 36\left( {3\sin^{2} \left( {60^o} \right) - 1} \right)}}{{\left( {x_{i}^{2} + 6^{2} } \right)^{2.5} }}} \right\} + 0.01x_{i}^{2} + x_{i} - 15, \hfill \\ {\text{sphere}}\;{\text{model}} + {\text{second-order}}\;{\text{regional}}\;{\text{polynomial}} .\hfill \\ \end{gathered}$$
(14)

To test the stability of our method in the presence of noise the computed magnetic anomaly T(x i ) was contaminated with random errors with a noise level of 10 nT (Fig. 4). The numerical second horizontal derivative magnetic anomaly profiles obtained from the noisy composite magnetic anomaly using five window lengths (s = 1, 2, 3, 4 and 5 km) are shown in Fig. 5. Following the same interpretation method the results are shown in Fig. 6.

Fig. 5
figure 5

Data analysis of Fig. 4 using the present second derivative method

Full size image
Fig. 6
figure 6

The family of window curves of z as a function of q for s = 1, 2, 3, 4 and 5 m as obtained from the noisy composite total magnetic anomaly (Eq. 14) using the present approach. Estimates of q and z are, respectively, 2.46 and 5.90 m

Full size image

Figure 6 shows the window curves intersect at approximately q = 2.46 and z = 5.9 m. This demonstrates that the present method will give reliable model parameters (z and q) even when the magnetic anomaly is contaminated with noise. However, when interpreting highly noisy data there is no unique intersection point. In this case it is recommended to use the standard deviation or variance of depths for each q value to obtain the reasonable results. The minimum of standard deviation or variance of depths is considered as a criterion for determining the correct depth and shape of the buried structure (Abdelrahman et al. 2006a, b).

4.3 Effect of a Wrong Origin

This procedure begins with selecting the origin (x i  = 0) using Stanley’s (1977) method and may lead to errors in the depth and the shape when interpreting real data. We investigate this problem in this subsection.

We computed a composite total magnetic anomaly consisting of the combined effect of a total magnetic anomaly due to a horizontal cylinder (K = 5,000 nT; z = 10 m; θ = −55°; q = 2) and 2nd-order regional polynomial (Fig. 7) from the following expression after introducing an error of 1 m to the horizontal coordinate:

Fig. 7
figure 7

A composite total magnetic anomaly consisting of the combined effects of a residual component due a horizontal cylinder (profile length = 60 m; K = 500 nT; z = 4 m; θ = −55°; q = 2.0) in which an error of 1 m is introduced into the horizontal position x i and a regional component represented by a second-order polynomial

Full size image
$$\begin{gathered} T(x_{i} ) = 5,000\frac{{\left( {100 - (x_{i}^{{}} + 1)^{2} } \right)\cos \left( { - 55^o} \right) + 20(x_{i} + 1)\sin \left( { - 55^o} \right)}}{{\left( {(x_{i}^{{}} + 1)^{2} + 10^{2} } \right)^{2} }} - 0.03x_{i}^{2} + 2x_{i} - 5, \hfill \\ {\text{Horizontal}}\;{\text{cylinder}}\;{\text{model}} + {\text{second-order}}\;{\text{regional}}\;{\text{polynomial}} .\hfill \\ \end{gathered}$$
(15)

A separation technique using a second derivative method was applied to the composite magnetic anomaly T(x i ). Five successive second derivative window lengths (s = 1, 2, 3, 4 and 5 m) were applied to the composite anomaly (Fig. 8). We applied our interpretation method to the second derivative anomalies thus obtained. The results are shown in Fig. 9.

Fig. 8
figure 8

Data analysis of Fig. 7 using the present second derivative method

Full size image
Fig. 9
figure 9

The family of window curves of z as a function of q for s = 1, 2, 3, 4 and 5 m as obtained from the composite total magnetic anomaly (Eq. 15) using the present approach. Estimates of q and z are, respectively, 2.2 and 10.3 m

Full size image

Figure 9 shows the parametric curves intersect at approximately z = 10.3 m and q = 2.2. The errors in depth and shape factor are about 3 and 10 %, respectively. This demonstrates that the present method will give reasonable model parameters (z and q) even when the origin of the magnetic anomaly profile is determined approximately.

4.4 Application to a Dipping Dike Model

The geometrical shape of the dipping dike is different from the simple geometries described in Eq. (1). In this subsection we will investigate the applicability of the present method to the magnetic anomaly of a buried dipping dike.

We computed a composite total magnetic anomaly consisting of the combined effect of a total magnetic anomaly due to a dipping dike (K = 100 nT; h = 4 m; d = 2 m; α = 40°) and 2nd-order regional polynomial (Fig. 10) from the following expression:

Fig. 10
figure 10

A composite total magnetic anomaly consisting of the combined effects of a residual component due to a dipping dike (h = 4 m; d = 2 m; α = 40°; K = 100 nT; profile length = 60 m; sampling interval = 1 m) and a regional component represented by a second-order polynomial

Full size image
$$\begin{gathered} T(x_{i} ) = K\sin \alpha \left[ {\tan^{ - 1} \left( {\frac{{x_{i} + d}}{h}} \right) - \tan^{ - 1} \left( {\frac{{x_{i} - d}}{h}} \right) - \frac{\cos \alpha }{2}\ln \left( {\frac{{\left( {x_{i} + d} \right)^{2} + h^{2} }}{{\left( {x_{i} - d} \right)^{2} + h^{2} }}} \right)} \right] - 0.01x_{i}^{2} + x_{i} - 15, \hfill \\ {\text{dipping}}\;{\text{dike}}\;{\text{model}} + {\text{second-order}}\;{\text{regional}}\;{\text{polynomial}} .\hfill \\ \end{gathered}$$
(16)

where h is the depth to the top of the dike from the plane of observation, d is the half-width of the dike and α is the index parameter and K is the amplitude coefficient (McGrath and Hood 1970).

A separation technique using a second derivative method was applied to the composite magnetic anomaly T(x i ). Four successive second derivative window lengths (s = 2, 3, 4 and 5 m) were applied to the composite anomaly (Fig. 11). We applied our interpretation method to the second derivative anomalies thus obtained and the results are shown in Fig. 12.

Fig. 11
figure 11

Data analysis of Fig. 10 using the present second derivative method

Full size image
Fig. 12
figure 12

A family of window curves of z as a function of q for s = 1, 2, 3, 4 and 5 m as obtained from the composite total magnetic anomaly (Eq. 16) using the present approach. Estimates of q and z are, respectively, 1.23 and 5.3 m

Full size image

Figure 12 shows the window curves intersect at approximately z = 5.3 m and q = 1.23. This suggests that the shape of the dipping dike is slightly different from the shape of thin sheet model (q = 1.0). Accordingly, our interpretation method may be extended to infer a distinction in shape between a thin sheet, horizontal cylinder and a dipping dike.

4.5 Application to Complicated Regionals and Interferences

The composite vertical magnetic anomaly of Fig. 13 consisting of the combined effects of an intermediate structure of interest (thin sheet with K = 200 nT; z = 5 m; q = 1; θ = 40°), a deep-seated structure (sphere with K = 80,000 nT; z = 15 m; q = 2.5; θ = 10°) and an interference from neighboring magnetic rocks (horizontal cylinder with K = 80 nT; z = 2 m; q = 2; and θ = 30°) was computed by the following expression:

Fig. 13
figure 13

A composite vertical magnetic anomaly consisting of the combined effect of an intermediate structure (thin sheet with K = 200 nT; z = 5 m; q = 1; θ = 40°) (anomaly 1), a deep-seated structure (sphere with K = 80,000 nT; z = 15 m; q = 2.5; θ = 10°) (anomaly 2) and an interference from neighboring magnetic rocks (horizontal cylinder with K = 80 nT; z = 2 m; q = 2; θ = 30°) (anomaly 3)

Full size image
$$\begin{aligned} T(x_{i} ) &= 200\frac{{5\cos \left( {40^o} \right) - x_{i} \sin \left( {40^o} \right)}}{{\left( {x_{i}^{2} + 5^{2} } \right)}} \hfill \\ &\qquad{\text{Thin}}\;{\text{sheet}}\; ( {\text{vertical}}\;{\text{component)}} \hfill \\ &\quad+ 80{,}000\frac{{\left( {450 - \left( {x_{i} + 60} \right)^{2} } \right)\sin (10^o) - 45\left( {x_{i} + 60} \right)\cos (10^o)}}{{((x_{i} + 60)^{2} + 15^{2} )^{2.5} }} \hfill \\ &\qquad{\text{Sphere}}\; ( {\text{vertical}}\,{\text{component)}} \hfill \\ &\quad+ 80\frac{{\left( {4 - \left( {x_{i} - 25} \right)^{2} } \right)\cos (30^o) + 4\left( {x_{i} - 25} \right)\sin (30^o)}}{{((x_{i} - 25)^{2} + 2^{2} )^{2} }}. \hfill \\ &\qquad{\text{Horizontal}}\;{\text{cylinder}}\; ( {\text{vertical}}\,{\text{component)}} \hfill \\ \end{aligned}$$
(17)

In this Figure anomaly 1 is the anomaly due to the intermediate structure of our interest, anomaly 2 is the anomaly due to the deep-seated structure and anomaly 3 is the anomaly due to the interference from neighboring sources. The origin of the sphere model (deep-seated structure) is located at x i  = −60 m and the origin of the horizontal cylinder model (neighboring source) is located x i  = 25 m as shown in Eq. (17).

The composite magnetic anomaly (T(x i )) is subjected to a separation technique using the second derivative method. Five successive second derivative windows were applied to input data (Fig. 14). Equation (11) was applied to each of the five second derivative profiles yielding depth solutions for each shape factor. The results are given in Fig. 15.

Fig. 14
figure 14

Data analysis of Fig. 13 using the present second derivative method

Full size image
Fig. 15
figure 15

The family of window curves of z as a function of q for s = 1, 2, 3, 4 and 5 m as obtained from the composite vertical magnetic anomaly (Eq. 17) using the present approach. Estimates of q and z are, respectively, 1.05 and 5.05 m

Full size image

Figure 15 shows most of the curves intersect at z = 5.05 m and q = 1.05. The results are generally in excellent agreement with the model parameters shown in Eq. (17). When magnetic data have a complicated regional and interference from neighboring sources the maximum error in depth is 1 % and in shape is 5 %. Good results are obtained by using the present algorithm for depth and shape determinations, which are of primary concern in magnetic prospecting and other geophysical work.

5 Field Examples

To examine the applicability of the present method the following three mineral field examples are presented.

5.1 Bankura Anomaly

Figure 16 shows a vertical magnetic anomaly profile from Bankura area, west Bengal, India (Verma and Bandopadhyay 1975). It represents a vertical anomaly due to a spherical mass of Gabbroic composition. The origin of the vertical anomaly profile (x i  = 0) was determined using the method described by Prakasa Rao and Subrahmanyam (1988). The anomaly profile was digitized at an interval of 62.5 m. Four successive windows (s = 312.5, 375, 437.5 and 500 m) were used to obtain the second horizontal derivative magnetic anomalies (Fig. 17). Equation (11) was applied on the anomaly profiles to determine the depths for each q value. The range of q values was taken from 1.5 to 2.5 every 0.1. The results are shown in Fig. 18. Figure 18 shows the curves intersect each other at z = 1,430 m and q = 2.58. This suggests that the shape of the buried structure resembles a spherical model buried at a depth of 1,430 m. The shape and the depth of the ore body obtained by the present method agrees very well with those obtained by Rao et al. (1973), Verma and Bandopadhyay (1975), Prakasa Rao and Subrahmanyam (1988), and Abdelrahman et al. (2007, 2013) as summarized in Table 2.

Fig. 16
figure 16

A vertical magnetic anomaly over a spherical feature in the Bankura area, West Bengal, India (after Verma and Bandopadhyaya 1975)

Full size image
Fig. 17
figure 17

Data analysis of Fig. 16 using the present second derivative method

Full size image
Fig. 18
figure 18

The family of window curves of z as a function of q for s = 312.5, 375.0, 437.5 and 500.0 m as obtained from the Bankura magnetic anomaly using the present approach. Estimates of q and z are, respectively, 2.58 and 1,430 m

Full size image
Table 2 Comparative results of the Bankura field example
Full size table

5.2 Parnaiba Basin Dike Anomaly

Figure 19 presents a total magnetic anomaly above a Mesozoic diabase dike intruded into Paleozoic sediments from the Parnaiba basin, Brazil (Silva 1989, Fig. 10). The depth to the outcropping dike (sensor height) is 1.9 m. This anomaly profile of 21.56 m was digitized at an interval of 0.385 m. Three successive windows (s = 0.77, 1.155 and 1.54 m) were used to obtain the second horizontal derivative magnetic anomalies (Fig. 20). Adapting the same technique applied in the above example using a range of q values from 0.5 to 2.5 every 0.1 produced the results given in Fig. 21. The curves nearly intersect within a narrow region defined by 2 m < z < 2.5 m and 0.9 < q < 1.25. Averaging over the three intersections yields the solution q = 1.02 and z = 2.35 m. This suggests that the shape of the buried structure resembles a perfect thin sheet model buried at depth of 2.35 m. This result agrees very well with the surface geology given by Silva (1989).

Fig. 19
figure 19

A total magnetic anomaly over a Paraniaba dike, Brazil (Silva 1989, Fig. 10)

Full size image
Fig. 20
figure 20

Data analysis of Fig. 19 using the present second derivative method

Full size image
Fig. 21
figure 21

The family of window curves of z as a function of q for s = 0.77, 1.155 and 1.54 m as obtained from the Paraniaba magnetic anomaly using the present approach. Estimates of q and z are, respectively, 1.02 and 2.35 m

Full size image

5.3 Pima Copper Mine Anomaly

Figure 22 shows a vertical magnetic anomaly from the Pima copper mine, Arizona (Gay 1963, Fig. 10) that represents an anomaly due to a thin dike. Drilling information showed the mineralized zone to be 11 m thick which is much less than the actual depth to the top of the body (64 m). This profile of 750 m was digitized at an interval of 6.25 m. The digitized values were subjected to a separation technique using the second derivative method [Eq. (12)]. Three successive window lengths (s = 43.75, 50 and 56.25 m) were applied (Fig. 23). Adapting the same technique applied in the above examples using a range of q values from 0.5 to 2.5 every 0.1 produced the results given in Fig. 24. The curves nearly intersect within a narrow region defined by 46 m < z < 70 m and 0.8 < q < 1.2. Averaging over the three intersections yields the solution q = 0.95 and z = 60 m. This suggests that the shape of the buried structure resembles a perfect thin sheet model buried at depth of 60 m. The depth agrees very well with the depth of 64 m obtained from drilling (Gay 1963).

Fig. 22
figure 22

A vertical magnetic anomaly from the Pima copper mine, Arizona (Gay 1963, Fig. 10)

Full size image
Fig. 23
figure 23

Data analysis of Fig. 22 using the present second derivative method

Full size image
Fig. 24
figure 24

The family of window curves of z as a function of q for s = 43.75, 50.0 and 56.25 m as obtained from the Pima magnetic anomaly using the present approach. Estimates of q and z are, respectively, 0.95 and 60 m

Full size image

6 Conclusions

The problem of determining the shape and depth of a buried structure from magnetic data can be solved using the present method. A simple and rapid numerical approach is formulated to use the anomaly values at four characteristic points on the second derivative anomaly profile for determining simultaneously the shape and the depth of the buried structure. The iterative equation for z (Eq. 11) is ready for computation to construct the window-curves. The advantages of this method over the least-squares methods that use second derivative anomalies to determine the depth and shape of a buried structure is that this method does not require computation of analytical or numerical derivatives with respect to the model parameters. It is also emphasized that the present method can be applied not only to residuals but also to measured magnetic data and can be used to gain geologic insight concerning the subsurface as illustrated in the three field examples.

Finally, we envisage use of the new formula that represents the magnetic effect of most simple geometric bodies (Eq. 1) in developing new methods to interpret magnetic data.