Trigonometric Integrable Tops from Solutions of Associative Yang–Baxter Equation

Abstract

We consider a special class of quantum nondynamical R-matrices in the fundamental representation of $\mathrm{GL}_N$ with spectral parameter given by trigonometric solutions of the associative Yang–Baxter equation. In the simplest case $N=2$, these are the well-known 6-vertex R-matrix and its 7-vertex deformation. The R-matrices are used for construction of the classical relativistic integrable tops of the Euler–Arnold type. Namely, we describe the Lax pairs with spectral parameter, the inertia tensors and the Poisson structures. The latter are given by the linear Poisson–Lie brackets for the nonrelativistic models and by the classical Sklyanin-type algebras in the relativistic cases. In some particular cases, the tops are gauge equivalent to the Calogero–Moser–Sutherland or trigonometric Ruijsenaars–Schneider models.

1 Introduction

In this paper, we discuss $\mathrm{GL}_N$ integrable Euler–Arnold-type tops [1,2,3,4,5,6,7] defined by the equations of motion

$$\begin{aligned} {\dot{S}}=[S,J(S)],\quad S=\sum \limits _{i,j=1}^N E_{ij}S_{ij}\in \mathrm{Mat}(N,{\mathbb {C}}) , \end{aligned}$$

(1.1)

where $\{S_{ij},\ i,j=1,\ldots ,N\}$ is the set of dynamical variables, $\{E_{ij}\}$ is the standard basis in $\mathrm{Mat}(N,{\mathbb {C}})$ and J(S) is a linear map¹ on S

$$\begin{aligned} J(S)=\sum \limits _{i,j,k,l=1}^N J_{ijkl}E_{ij}S_{lk}\in \mathrm{Mat}(N,{\mathbb {C}}) \end{aligned}$$

(1.2)

with components $J_{ijkl}$ independent of dynamical variables. The model is not integrable in the general case but for special choices of J(S) only. The construction of integrable tops under consideration goes back to Sklyanin’s paper [8] (see also [9]). The idea was to formulate the classical analogue of the models described by the inverse scattering method. In this way, the classical spin chains were described and the quadratic Poisson structures were obtained via the classical limit of the exchange (RLL) relations.

The $\mathrm{GL}_N$ top can be viewed as the model obtained through the classical limit from the 1-site spin chain. The rational models of this type were described in [10,11,12]. Here, we use a specification of the above-mentioned results based on trigonometric R-matrices satisfying the associative Yang–Baxter equation (AYBE) [13, 14]:

$$\begin{aligned} R^\hbar _{12}(z_{12}) R^{\eta }_{23}(z_{23})=R^{\eta }_{13}(z_{13})R_{12}^{\hbar -\eta }(z_{12})+ R^{\eta -\hbar }_{23}(z_{23})R^\hbar _{13}(z_{13}),\quad z_{ab}=z_a-z_b. \end{aligned}$$

(1.3)

It was shown in [15] that solution of (1.3) satisfying also additional properties of skew-symmetry²

$$\begin{aligned} \displaystyle { R^\hbar _{12}(z)=-R_{21}^{-\hbar }(-z)=-P_{12}R_{12}^{-\hbar }(-z)P_{12}, \quad P_{12}=\sum \limits _{i,j=1}^N E_{ij}\otimes E_{ji}, } \end{aligned}$$

(1.4)

unitarity

$$\begin{aligned} \begin{array}{c} \displaystyle { R^\hbar _{12}(z) R^\hbar _{21}(-z) = f^\hbar (z)\,\,1_N\otimes 1_N } \end{array} \end{aligned}$$

(1.5)

and the local expansions³

$$\begin{aligned} \begin{array}{c} \displaystyle { \mathop {\hbox {Res}}\limits \limits _{\hbar =0}R^\hbar _{12}(z)=1_N\otimes 1_N=1_{N^2},\quad \mathop {\hbox {Res}}\limits \limits _{z=0}R^\hbar _{12}(z)=P_{12} } \end{array} \end{aligned}$$

(1.6)

($1_N$ – is $N\times N$ identity matrix) leads to explicit constructions of the Lax pair $L(z),M(z)\in \mathrm{Mat}(N,{\mathbb {C}})$. That is the Lax equations

$$\begin{aligned} {\dot{L}}(z)=[L(z),M(z)] \end{aligned}$$

(1.7)

are equivalent to the equations of motion (1.1) identically in spectral parameter z. All the data of the models including their Hamiltonians, the Lax pairs, the Poisson structures and the inertia tensors (i.e., J(S)) are given in terms of coefficients of expansion of the R-matrices near $\hbar =0$ and $z=0$. For example, in the relativistic case, the Lax pair is as follows:

$$\begin{aligned} \begin{array}{c} \displaystyle { L^\eta (z)=\mathrm{tr}_2(R^\eta _{12}(z)S_2),\quad M^\eta (z)=-\mathrm{tr}_2(r_{12}(z)S_2), } \end{array} \end{aligned}$$

(1.8)

where $S_2=1_N\otimes S$ and $r_{12}(z)$ is the classical r-matrix. See Sect. 3 for details. The Planck constant plays the role of the relativistic deformation parameter $\eta$. In some special case, it is identified with the corresponding parameter in the Ruijsenaars–Schneider model.

Notice that together with properties (1.4) and (1.5), a solution of (1.3) satisfies also the custom Yang–Baxter equation

$$\begin{aligned} R_{12}^\hbar (z_1-z_2)R_{13}^\hbar (z_1-z_3)R_{23}^\hbar (z_2-z_3)= R_{23}^\hbar (z_2-z_3)R_{13}^\hbar (z_1-z_3)R_{12}^\hbar (z_1-z_2), \end{aligned}$$

(1.9)

so that such solution of (1.3) is then a true quantum R-matrix by convention. Sometimes the following property holds true as well⁴:

$$\begin{aligned} \begin{array}{c} \displaystyle { R^\hbar _{12}(z)P_{12}=R^{z}_{12}(\hbar ). } \end{array} \end{aligned}$$

(1.10)

This allows to relate the coefficients of expansion (of R-matrices) near $\hbar =0$ and $z=0$ to each other.

The paper is organized as follows. In Sect. 2, we describe the set of well-known trigonometric R-matrices satisfying conditions (1.3)–(1.6) and briefly describe the general classification of such solutions of (1.3) suggested by Schedler and Polishchuk [17, 18]. We will show that a representative example of the classification is given by the so-called nonstandard trigonometric R-matrix [19], which generalizes the $\mathrm{GL}_2$ 7-vertex R-matrix [20] for $N>2$. In Sect. 3, we review the construction of integrable tops and evaluate all the data for the general case and the nonstandard R-matrix. Using (1.3), we also prove that the classical quadratic r-matrix structure provides the classical Sklyanin-type Poisson structure. This results in getting the classification of the trigonometric Sklyanin-type Poisson structures, and it is parallel to the classification of solutions of the associative Yang–Baxter equation. In Sect. 4, we consider a special top corresponding to rank one matrix S and related to the nonstandard R-matrix. It turns out that this model is gauge equivalent to the Ruijsenaars–Schneider [21, 22] or the Calogero–Moser–Sutherland [23,24,25,26] models. Explicit changes in variables are described.

2 Trigonometric R-matrices and AYBE

We begin with the properties of well-known R-matrices and then proceed to the general case.

2.1 Standard and Nonstandard R-matrices

Consider the following examples of R-matrices:

$$\begin{aligned} \begin{array}{c} \displaystyle { R^{\eta }_{12}(z)=\sum \limits _{i,j,k,l=1}^N R^\eta _{ijkl}(z)E_{ij}\otimes E_{kl} } \end{array} \end{aligned}$$

(2.1)

$\bullet$ The ${\mathbb {Z}}_N$-invariant $A_{N-1}$ trigonometric R-matrix [20, 27, 28]:

$$\begin{aligned} (R_1)^{\eta }_{ij,kl}(z)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N}{2}\,\Big (\coth (Nz/2)+\coth (N\eta /2)\Big )\nonumber \\&+\, \delta _{ij}\delta _{kl}\varepsilon (i\ne k)\frac{N e^{(i-k)\eta -\hbox {sign}(i-k)N\eta /2}}{2\sinh (N\eta /2)}\nonumber \\&+\,\delta _{il}\delta _{kj} \varepsilon (i\ne k)\frac{N e^{(i-k)z-\hbox {sign}(i-k)Nz/2}}{2\sinh (Nz/2)}, \end{aligned}$$

(2.2)

where hereinafter we use

$$\begin{aligned} \begin{array}{l} \varepsilon (\hbox {A})=\left\{ \begin{array}{ll} 1,&{}\quad \hbox {if\;\; A is true},\\ 0,&{}\quad \hbox {if\;\; A is false}.\end{array}\right. \end{array} \end{aligned}$$

(2.3)

$\bullet$ Baxterization of the (trigonometric) Cremmer–Gervais R-matrix [19, 29]:

$$\begin{aligned} (R_2)^{\eta }_{ij,kl}(z)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N}{2}\,\Big (\coth (Nz/2)+\coth (N\eta /2)\Big ) \nonumber \\&+\, \delta _{ij}\delta _{kl}\varepsilon (i\ne k)\frac{N e^{(i-k)\eta -\hbox {sign}(i-k)N\eta /2}}{2\sinh (N\eta /2)}\nonumber \\&+\,\delta _{il}\delta _{kj} \varepsilon (i\ne k)\frac{N e^{(i-k)z-\hbox {sign}(i-k)Nz/2}}{2\sinh (Nz/2)}\, \nonumber \\&+\,N\delta _{i+k,j+l}\Big (\varepsilon (i{<}j{<}k) e^{(i-j)z+(j-k)\eta }\nonumber \\&-\, \varepsilon (k{<}j{<}i) e^{(i-j)z+(j-k)\eta }\Big ). \end{aligned}$$

(2.4)

It differs from the previous one (2.2) by the last line. Let us comment on how it is related to the Cremmer–Gervais R-matrix. First, one should perform the gauge transformation

$$\begin{aligned} \begin{array}{c} \displaystyle { R_{12}^\eta (z-w)\rightarrow {\tilde{R}}_{12}^\eta (z,w)=D_1(z) D_2(w) R^{\eta }_{12}(z) D_1^{-1}(z)D_2^{-1}(w) } \end{array} \end{aligned}$$

(2.5)

with the diagonal matrix $D_{ij}(z)=\delta _{ij}e^{-jz}$. For (2.4) ${\tilde{R}}_{12}^\eta (z,w)={\tilde{R}}_{12}^\eta (z-w)$. The result is

$$\begin{aligned} (\tilde{R}_2)^{\eta }_{ij,kl}(z)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N}{2}\,\Big (\coth (Nz/2)+\coth (N\eta /2)\Big ) \nonumber \\&+\, \delta _{ij}\delta _{kl}\varepsilon (i\ne k)\frac{N e^{(i-k)\eta -\hbox {sign}(i-k)N\eta /2}}{2\sinh (N\eta /2)}\nonumber \\&+\,\delta _{il}\delta _{kj} \varepsilon (i\ne k)\frac{N e^{\hbox {sign}(i-k)Nz/2}}{2\sinh (Nz/2)}\, \nonumber \\&+\,N\delta _{i+k,j+l}\Big (\varepsilon (i{<}j{<}k) e^{(j-k)\eta }-\varepsilon (k{<}j{<}i) e^{(j-k)\eta }\Big ). \end{aligned}$$

(2.6)

Consider the Cremmer–Gervais R-matrix [30]. It is free of spectral parameter:

$$\begin{aligned} R^{\mathrm{CG,q}}_{12}= & {} q^{-1/N}\left( q\sum \limits _{i=1}^N E_{ii}\otimes E_{ii} +q\sum \limits _{i>j}^N q^{-2(i-j)/N} E_{ii}\otimes E_{jj}\right. \nonumber \\&\left. +\,q^{-1}\sum \limits _{i<j}^N q^{-2(i-j)/N} E_{ii}\otimes E_{jj} \right. \nonumber \\&\left. -\,(q-q^{-1})\sum \limits _{i<j}^N\sum \limits _{k=1}^{j-i-1}q^{2k/N} E_{j-k,i}\otimes E_{i+k,j}\right. \nonumber \\&\left. +\,(q-q^{-1})\sum \limits _{i>j}^N\sum \limits _{k=0}^{i-j-1}q^{-2k/N} E_{j+k,i}\otimes E_{i-k,j}\right) . \end{aligned}$$

(2.7)

Next, introduce

$$\begin{aligned} \begin{array}{c} \displaystyle { R^{\mathrm{CG,q}}_{12}(x)=xR_{12}^{\mathrm{CG,q}}-x^{-1}\left( R_{21}^\mathrm{CG,q}\right) ^{-1}. } \end{array} \end{aligned}$$

(2.8)

Finally,

$$\begin{aligned} \begin{array}{c} \displaystyle { (\tilde{R}_2)^{\eta }_{12}(z)=-\frac{N}{4\sinh (Nz/2)\sinh (N\eta /2)}\,R^\mathrm{CG,q}_{12}(x)^T, } \end{array} \end{aligned}$$

(2.9)

where ”T” means the transpose of matrix ($R_{ij,kl}{\mathop {\rightarrow }\limits ^{T}}R_{ji,lk}$) and $x=e^{-\eta /2-Nz/2}$, $q=e^{-N\eta /2}$.

$\bullet$ Nonstandard trigonometric R-matrix [19]:

$$\begin{aligned} R^{\eta }_{ij,kl}(z)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N}{2}\,\Big (\coth (Nz/2)+\coth (N\eta /2)\Big ) \nonumber \\&+\, \delta _{ij}\delta _{kl}\varepsilon (i\ne k)\frac{N e^{(i-k)\eta -\hbox {sign}(i-k)N\eta /2}}{2\sinh (N\eta /2)}\nonumber \\&+\,\delta _{il}\delta _{kj} \varepsilon (i\ne k)\frac{N e^{(i-k)z-\hbox {sign}(i-k)Nz/2}}{2\sinh (Nz/2)}\, \nonumber \\&+\,N\delta _{i+k,j+l}\Big (\varepsilon (i{<}j{<}k) e^{(i-j)z+(j-k)\eta }-\varepsilon (k{<}j{<}i) e^{(i-j)z+(j-k)\eta }\Big ) \nonumber \\&+\, N \delta _{i+k,j+l+N}\Big (\delta _{iN}e^{-jz-l\eta }-\delta _{kN}e^{lz+j\eta }\Big ). \end{aligned}$$

(2.10)

It differs from the previous one (2.4) by the last line, which provides in $N=2$ case the 7-vertex deformation [20] of the 6-vertex R-matrix.

Properties of R-matrices.

Briefly, all the R-matrices (2.2), (2.4) and (2.10) satisfy the associative Yang–Baxter equation (1.3), the skew-symmetry property (1.4), the unitarity property (1.5) and therefore, the Yang–Baxter equation (1.9). Moreover, all of them satisfy the Fourier symmetry (1.10). The gauge-transformed R-matrix (2.6) does not satisfy (1.10) while the rest of the properties hold true.

In order to summarize the properties of the above R-matrices, introduce notations for the last lines of (2.4) and (2.10): $\Delta _1R^{\eta }(z)=(R_2)^{\eta }(z)-(R_1)^{\eta }(z)$ and $\Delta _2R^{\eta }(z)=(R)^{\eta }(z)-(R_2)^{\eta }(z)$, i.e.,

$$\begin{aligned} \Delta _1R^{\eta }_{ij,kl}(z)= & {} N\delta _{i+k,j+l}\Big (\varepsilon (i{<}j{<}k) e^{(i-j)z+(j-k)\eta }\nonumber \\&-\,\varepsilon (k{<}j{<}i) e^{(i-j)z+(j-k)\eta }\Big ), \end{aligned}$$

(2.11)

$$\begin{aligned} \Delta _2R^{\eta }_{ij,kl}(z)= & {} N \delta _{i+k,j+l+N}\Big (\delta _{iN}e^{-jz-l\eta }-\delta _{kN}e^{lz+j\eta }\Big ) \end{aligned}$$

(2.12)

and consider the following linear combination:

$$\begin{aligned} \begin{array}{c} \displaystyle { \mathbf{R}^\eta (z)=A_0(R_1)^\eta (z)+A_1\Delta _1R^{\eta }(z)+A_2\Delta _2R^{\eta }(z),} \end{array} \end{aligned}$$

(2.13)

where $A_0$, $A_1$ and $A_2$ are some constants. For example, for $A_0=A_1=A_2=1$, (2.13) yields (2.10). To summarize:

Proposition 2.1

For any $A_0$, $A_1$ and $A_2$ , (2.13) satisfies the properties (1.4), (1.10) and (1.5) with

$$\begin{aligned} \begin{array}{l} \displaystyle { f^\eta (z)=A_0^2\frac{N^2}{4}\left( \frac{1}{\sinh ^2(N\eta /2)}-\frac{1}{\sinh ^2(Nz/2)}\right) ,} \end{array} \end{aligned}$$

(2.14)

that is (2.13) is nondegenerated iff $A_0\ne 0$.

The associative Yang–Baxter equation (1.3) holds true for all R-matrices (2.2), (2.4) and (2.10). The linear combination (2.13) satisfies (1.3) in the following cases:

• 1. $A_0=A_1\ne 0$, $A_2$ – any,

• 2. $A_0\ne 0$, $A_1=A_2=0$

• 3. $A_0=A_1=0$, $A_2$ – any.

The latter means that the R-matrix (2.12) satisfies (1.3).

Let us also mention two special cases:

• a. In the case⁵$N=2,3$, the combination (2.13) satisfies (1.3) for $A_0$, $A_1$—any, and $A_2=0$.

• b. for $N=4$ and $A_0=A_2=0$, (2.13) does not satisfy (1.3) while the Yang–Baxter equation (1.9) holds true.

Case 2 from the proposition can be verified directly. Instead of a direct proof of cases 1 and 3, we will show (in the next subsection) that the nonstandard R-matrix (2.10) is contained in the general classification. Next, we can apply the gauge transformation (2.5) with

$$\begin{aligned} \begin{array}{l} \displaystyle { D_{ij}=\delta _{ij} e^{-j\Lambda } } \end{array} \end{aligned}$$

(2.15)

to (2.10). In terms of components, it leads to $R^{\eta }_{ij,kl}(z) \rightarrow e^{(j+l-i-k)\Lambda }R^{\eta }_{ij,kl}(z)$. Therefore, the last line of (2.10) is multiplied by $e^{-N\Lambda }$:

$$\begin{aligned} R^{\eta }_{ij,kl}(z)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N}{2}\,\Big (\coth (Nz/2)+\coth (N\eta /2)\Big ) \nonumber \\&+\, \delta _{ij}\delta _{kl}\varepsilon (i\ne k)\frac{N e^{(i-k)\eta -\hbox {sign}(i-k)N\eta /2}}{2\sinh (N\eta /2)}\nonumber \\&+\,\delta _{il}\delta _{kj} \varepsilon (i\ne k)\frac{N e^{(i-k)z-\hbox {sign}(i-k)Nz/2}}{2\sinh (Nz/2)}\, \nonumber \\&+\, N\delta _{i+k,j+l}\Big (\varepsilon (i{<}j{<}k) e^{(i-j)z+(j-k)\eta }\nonumber \\&-\,\varepsilon (k{<}j{<}i) e^{(i-j)z+(j-k)\eta }\Big ) \nonumber \\&+\, N e^{-N\Lambda } \delta _{i+k,j+l+N}\Big (\delta _{iN}e^{-jz-l\eta }-\delta _{kN}e^{lz+j\eta }\Big ). \end{aligned}$$

(2.16)

By taking the limit $\Lambda \rightarrow \pm \infty$, we come to cases 1 with $A_2=0$ or to case 3.

At last, consider

$\bullet$R-matrix for the affine quantized algebra ${\hat{{\mathcal {U}}}}_q(\mathrm{gl}_N)$ [31, 32]:

$$\begin{aligned} R^{\mathrm{xxz,}\eta }_{12}(z)= & {} \frac{N}{2}\Big (\coth (Nz/2)+\coth (N\eta /2)\Big )\sum \limits _{i=1}^N E_{ii}\otimes E_{ii}\nonumber \\&+\,\frac{(N/2)}{\sinh (N\eta /2)}\sum \limits _{i\ne j}^N E_{ii}\otimes E_{jj}\nonumber \\&+\,\frac{(N/2)}{\sinh (Nz/2)}\sum \limits _{i< j}^N \left( E_{ij}\otimes E_{ji}\,e^{Nz/2}+E_{ji}\otimes E_{ij}\,e^{-Nz/2}\right) .\nonumber \\ \end{aligned}$$

(2.17)

It is used for construction of $\mathrm{GL}_N$ XXZ spin chains and is usually written in different normalization:

$$\begin{aligned} {\tilde{R}}^{\mathrm{xxz,}q}_{12}(x)= & {} \frac{4}{N}\,\sinh (Nz/2)\sinh (N\eta /2)\,R^{\mathrm{xxz,}\eta }_{12}(z) \nonumber \\= & {} \left( xq-\frac{1}{xq}\right) \sum \limits _{i=1}^N E_{ii}\otimes E_{ii}+ \left( x-\frac{1}{x}\right) \sum \limits _{i\ne j}^N E_{ii}\otimes E_{jj}\nonumber \\&+\, \left( q-\frac{1}{q}\right) \sum \limits _{i\ne j}^N x^{\hbox {sign}(j-i)} E_{ij}\otimes E_{ji}, \end{aligned}$$

(2.18)

where $x=e^{Nz/2}$, $q=e^{N\eta /2}$. The XXZ R-matrix is the Baxterization of the Drinfeld’s one [33]:

$$\begin{aligned} \begin{array}{l} \displaystyle { \left( { R}^{\mathrm{Dr,}q}_{12}\right) ^{\pm 1} =q^{\pm 1}\sum \limits _{i=1}^N E_{ii}\otimes E_{ii}+ \sum \limits _{i\ne j}^N E_{ii}\otimes E_{jj}\pm (q-q^{-1})\sum \limits _{i>j}^N E_{ij}\otimes E_{ji}. } \end{array} \end{aligned}$$

(2.19)

Namely,

$$\begin{aligned} \begin{array}{l} \displaystyle { {\tilde{R}}^{\mathrm{xxz,}q}_{12}(x)=xR^{\mathrm{Dr,}q}_{21}-x^{-1}\left( R^{\mathrm{Dr,}q}_{12}\right) ^{-1}. } \end{array} \end{aligned}$$

(2.20)

The R-matrix (2.17) satisfies Yang–Baxter equation (1.9). It is skew-symmetric and unitary (1.5) with

$$\begin{aligned} \begin{array}{l} \displaystyle { f^\eta (z)=\frac{N^2}{4}\left( \frac{1}{\sinh ^2(N\eta /2)}-\frac{1}{\sinh ^2(Nz/2)}\right) .} \end{array} \end{aligned}$$

(2.21)

The associative Yang–Baxter equation (1.3) for (2.17) holds true in the $N=2$ case. For $N>2$, the difference of the l.h.s. and the r.h.s. from (1.3) is not zero though it is independent of spectral parameters:

$$\begin{aligned}&R^\hbar _{12}(z_{12}) R^{\eta }_{23}(z_{23})-R^{\eta }_{13}(z_{13})R_{12}^{\hbar -\eta }(z_{12})- R^{\eta -\hbar }_{23}(z_{23})R^\hbar _{13}(z_{13}) \nonumber \\&\quad =-\frac{N^2}{8\cosh (N\hbar /4)\cosh (N\eta /4)\cosh (N(\hbar -\eta )/4)}\nonumber \\&\qquad \times \,\sum \limits ^N_{i\ne j\ne k\ne i} E_{ii}\otimes E_{jj}\otimes E_{kk}. \end{aligned}$$

(2.22)

The latter statement is verified by direct computation. We do not consider the XXZ R-matrix for construction of integrable tops in this paper. It is of course possible, but our method requires (1.3) to be valid.

2.2 General Classification

Here, we briefly describe the classification [17, 18] of trigonometric solutions to associative Yang–Baxter equation (1.3) with the properties of skew-symmetry (1.4) and unitarity (1.5). As noted previously, this is sufficient condition for satisfying the Yang–Baxter equation (1.9) as well. So that we deal with the quantum nondynamical R-matrices. Another goal of the section is to show how the nonstandard R-matrix (2.10) arises from the classification.

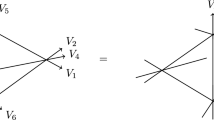
General solution of (1.3) is given in terms of combinatorial construction called the associative Belavin–Drinfeld structure. Consider $S=\{1,\ldots ,N\}$—a finite set of N elements. Say, S is the set of N vertices on a circle numerated from 1 to N (the extended Dynkin diagram of $A_{N-1}$ type). Let $C_0$ be a transitive cyclic permutation acting on S and $\Gamma _{C_0}$ be its graph, i.e., the set of ordered pairs $\Gamma _{C_0}=\{(s,C_0(s)),s\in S\}$.

Define another one transitive cyclic permutation C and a pair of proper subsets $\Gamma _1,\Gamma _2\subset \Gamma _{C_0}$ related by C: $(C\times C)\Gamma _1=\Gamma _2$, where the action means $(C\times C) (i,j)=(C(i),C(j))$. So that $C\times C$ provides the induced bijective map $\tau$: $\Gamma _1{\mathop {\longrightarrow }\limits ^{C\times C}}\Gamma _2$. The set $(\Gamma _1,\Gamma _2,\tau )$ is an example of the Belavin–Drinfeld triple [34].

Here, the action of $\tau$ is extended to larger sets. Namely, it is extended to $\tau :\, P_1{\mathop {\longrightarrow }\limits ^{C\times C}}P_2$, where $P_{1,2}$ are the following sets:

$$\begin{aligned} P_i= & {} \{ (s,C^k_0(s)):\, (s,C_0(s))\in \Gamma _i, \ldots ,(C^{k-1}_0(s),C^k_0(s))\in \Gamma _i,\nonumber \\&(C_0^k(s),C^{k+1}_0(s))\notin \Gamma _i \}. \end{aligned}$$

(2.23)

From the transitivity of C and the choice of $\Gamma _{1,2}$ to be proper subsets of $\Gamma _{C_0}$, it follows that there exists a number k such that $(C\times C)^k\Gamma _1\notin \Gamma _1$. Similarly, there exist $k_1,k_2$ with the property $(C_0\times C_0)^{k_{i}+1}\Gamma _{i}\notin \Gamma _{i}$, $i=1,2$. Therefore, $P_i$ are well-defined finite sets, and $\tau$ is the bijective map between them.

Then, the general answer for trigonometric R-matrix based on $(C_0,C,\Gamma _1,\Gamma _2)$ is as follows:

$$\begin{aligned} R^{\eta }_{12}(z)= & {} \frac{N}{2}\Big (\coth (Nz/2)+\coth (N\eta /2)\Big )\sum _{i} E_{ii}\otimes E_{ii} \nonumber \\&+\,\frac{N}{e^{N\eta }-1}\sum \limits _{0<n<N,\, i=C^n(k)} e^{n\eta }E_{ii}\otimes E_{kk}\nonumber \\&+\,\frac{N}{e^{Nz}-1}\sum \limits _{0<m<N,\,k=C^m_0(i)} e^{mz} E_{ik}\otimes E_{ki} \nonumber \\&+\,\sum \limits _{\mathrm {\begin{array}{c}0<m<N,\,n>0,\\ i=C^m_0(j), \,\tau ^n(j,i)=(k,l)\end{array}}} \nonumber \\&\times \,N \left( e^{-n\eta -mz}E_{ij}\otimes E_{kl}- e^{n\eta +mz}E_{kl}\otimes E_{ij}\right) , \end{aligned}$$

(2.24)

where the sums are over all possible values of indices—elements of S. In particular, the last sum is over all $i,j,k,l\in \{1,\ldots ,N\}$ and positive m, n for which the $\tau ^n(j,i)$ is defined, i.e., $(j,i)\in P_1$ and $\tau ^n(j,i)=(k,l)\in P_2$ with $i=C^m_0(j)$. The R-matrix is skew-symmetric and unitary (1.5) with $f^\eta (z)$ (2.21). Answer (2.24) is given e up to some gauge transformations. See the details in [17, 18].

Example

Consider example with the cyclic permutations

$$\begin{aligned} C_0:\quad \begin{array}{|c|c|} \hline \hline \ \ s\ \ &{} C_0(s) \\ \hline 1 &{} N \\ \hline 2 &{} 1 \\ \hline 3 &{} 2 \\ \hline \vdots &{} \vdots \\ \hline N &{} N-1 \\ \hline \hline \end{array} \qquad \qquad \qquad C=C_0^{-1}:\quad \begin{array}{|c|c|} \hline \hline s &{} C(s) \\ \hline 1 &{} 2 \\ \hline 2 &{} 3 \\ \hline \vdots &{} \vdots \\ \hline N-1 &{} N \\ \hline N &{} 1 \\ \hline \hline \end{array} \end{aligned}$$

(2.25)

and the proper subsets $\Gamma _{1,2}\subset \Gamma _{C_0}=\{(s,C_0(s))$ given by

$$\begin{aligned} \Gamma _1= & {} \Big \{ (1,N), (2,1), (3,2), \ldots , (N-1,N-2) \Big \}, \end{aligned}$$

(2.26)

$$\begin{aligned} \Gamma _2= & {} (C\times C)\Gamma _1=\Big \{ (2,1), (3,2), \ldots , (N-1,N-2), (N,N-1) \Big \}.\nonumber \\ \end{aligned}$$

(2.27)

To construct $P_1$, consider the action of $C_0\times C_0$ on the elements of $\Gamma _1$ (2.26):

$$\begin{aligned}&(1,N)\,{\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, (N,N-1)\not \subset \Gamma _1, \nonumber \\&(2,1)\,{\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, (1,N)\,{\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, (N,N-1)\not \subset \Gamma _1, \nonumber \\&(3,2)\,{\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, (2,1)\,{\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, (1,N)\,{\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, (N,N-1)\not \subset \Gamma _1, \nonumber \\&\vdots \nonumber \\&(N-1,N-2)\,{\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, \ldots {\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\,(2,1)\,{\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, (1,N)\nonumber \\&\quad {\mathop {\longrightarrow }\limits ^{C_0\times C_0}}\, (N,N-1)\not \subset \Gamma _1. \end{aligned}$$

(2.28)

According to definition (2.25), we get the following set for $P_1$:

$$\begin{aligned} P_1=\left\{ \begin{array}{l} \displaystyle { (1,N), }\\ (2,1), (2,N), \\ (3,2), (3,1), (3,N), \\ \qquad \qquad \vdots \\ (N\!-\!1,N\!-\!2), (N\!-\!1,N\!-\!3), \ldots , (N\!-\!1,1), (N\!-\!1,N) \end{array} \right\} \end{aligned}$$

(2.29)

In a similar way from (2.27), we obtain the set of $P_2$:

$$\begin{aligned} \begin{array}{l} P_2=(C\times C)P_1=\left\{ \begin{array}{l} \displaystyle { (2,1), }\\ (3,2), (3,1), \\ (4,3), (4,2), (4,1), \\ \qquad \qquad \vdots \\ (N,N\!-\!1), (N,N\!-\!2), \ldots , (N,2), (N,1) \end{array} \right\} \end{array} \end{aligned}$$

(2.30)

The bijection between $P_1$ and $P_2$ induced by $C\times C$ is the map $\tau$.

Proposition 2.2

The R-matrix (2.24) reproduces the nonstandard one (2.10) for the case of the associative Belavin–Drinfeld structure (2.25)–(2.27).

Proof

The first lines of (2.24) and (2.10) coincide. Consider the first term from the second line of (2.24):

$$\begin{aligned}&\frac{N}{e^{N\eta }-1}\sum \limits _{0<n<N, \, i=C^n(k)} e^{n\eta }E_{ii}\otimes E_{kk}\nonumber \\&\quad =\frac{Ne^{-N\eta /2}}{2\sinh (N\eta /2)}\sum \limits _{0<n<N, \, i=C^n(k)} e^{n\eta }E_{ii}\otimes E_{kk} \end{aligned}$$

(2.31)

Due to the definition of C (2.25) for the summation index n, we have: $n=i-k$ if $i>k$ and $n=N-k+i$ for $i<k$. In this way, we reproduce the first term in the second line of (2.10). Similar consideration for the second term in the second line of (2.24) yields that the total second line of (2.24) coincides with the second line of (2.10).

Next, consider the first sum in the last line of (2.24) and subdivide it into two parts:

$$\begin{aligned}&\sum \limits _{\mathrm {\begin{array}{c}0<m<N, \,n>0,\\ i=C^m_0(j), \,\tau ^n(j,i)=(k,l)\end{array}}} N e^{-n\eta -mz}E_{ij}\otimes E_{kl}\nonumber \\&\quad =\Big ({\sum }'+{\sum }''\Big ) N e^{-n\eta -mz}E_{ij}\otimes E_{kl}, \end{aligned}$$

(2.32)

where the sums ${\sum }'$ and ${\sum }''$ are defined as follows. The total sum is over i, j, k, l such that $(j,i)\in P_1$ (and $(k,l)\in P_2$). Then, the sum ${\sum }''$ is over the diagonal elements (1, N), ...,$(N-1,N)$ among $(j,i)\in P_1$ (2.29), and the sum ${\sum }'$ is over the rest of the elements among $(j,i)\in P_1$ [it is the lower triangular part of (2.29)].

From (2.29) and (2.30), it follows that $j>i$ and $k>l$ for the elements in the ${\sum }'$. Moreover, $i+k=j+l$ for these elements,⁶ and $k>j$ since the map $P_1\rightarrow P_2$ is generated by $C\times C$. Therefore, $i<j<k$ holds true. Also, from $i=C^m_0(j)$ we have $m=j-i$. And finally, $C^n(j)=k$, so that $n=k-j$. In this way, we showed that the sum ${\sum }'$ provides the first term in the third line of (2.10).

For the elements of the sum ${\sum }''$, we have $i=N>j$ and $i+k=j+l+N$. Since $N=C_0^m(j)$, we have $j=m$. On the other hand, $C^n(N)=k$, so that $k=n$. In this way, the sum ${\sum }''$ is shown to be the first term in the last line of (2.10).

In the same way (by subdividing into two parts), the second term in the last line of (2.31) is shown to be equal to the sum of the second terms in the third and the fourth lines of (2.10). $\square$

Let us comment on the origin of the general classification. It comes from nontrivial limiting procedures (trigonometric limits) [19, 35, 36] starting from the elliptic case, where the classification is rather simple. It is based on the M. Atiyah’s classification of bundles over elliptic curves. The elliptic R-matrix is fixed by its poles structure (1.6) and quasiperiodic boundary conditions on a torus given by powers of $N\times N$ matrices $I_1^k$, $I_2^l$$(k,l=1,\ldots ,N-1)$, where $I_1=\mathrm{diag}(\exp (2\pi \imath /N),\exp (4\pi \imath /N),\ldots ,1)$ and $(I_2)_{ij}=\varepsilon (i=j+1\,\mathrm{mod}\, N)$. The nondynamical R-matrix corresponds to g.c.d.$(k,N)=1$ and g.c.d.$(l,N)=1$. Otherwise, elliptic moduli appear, which play the role of dynamical variables.

3 Integrable Tops

Below, we describe the relativistic and the nonrelativistic tops constructed by means of R-matrices satisfying (1.3)–(1.6). Our consideration uses results of [11, 12, 15]. For the relativistic models, the classical r-matrix structure is quadratic, while in the nonrelativistic case it is linear. In its turn, the relativistic models admit two natural (and equivalent) Lax representations: The first one includes explicit dependence on the relativistic parameter $\eta$. It is based on the quantum R-matrix. And the second one is based on the classical r-matrix. The Lax pair in this description is independent of $\eta$.

Consider a solution of the associative Yang–Baxter equation (1.3) with the properties⁷ (1.4) and (1.5) and the following expansions near $\hbar =0$ (the classical limit):

$$\begin{aligned} \begin{array}{c} \displaystyle { R^\hbar _{12}(z)=\frac{1}{\hbar }\,1_N\otimes 1_N+r_{12}(z)+\hbar \, m_{12}(z)+O(\hbar ^2) } \end{array} \end{aligned}$$

(3.1)

and near $z=0$

$$\begin{aligned} R^\hbar _{12}(z)= & {} \frac{1}{z}\,P_{12}+R^{\hbar ,(0)}_{12}+zR^{\hbar ,(1)}_{12}+O(z^2), \nonumber \\ \end{aligned}$$

(3.2)

$$\begin{aligned} R^{\hbar ,(0)}_{12}= & {} \frac{1}{\hbar }\,1_N\otimes 1_N+r^{(0)}_{12}+O(\hbar ), \quad r_{12}(z)=\frac{1}{z}\,P_{12}+r^{(0)}_{12}+O(z).\nonumber \\ \end{aligned}$$

(3.3)

From the skew-symmetry (1.4), we have

$$\begin{aligned} r_{12}(z)= & {} -r_{21}(-z), \quad m_{12}(z)=m_{21}(-z), \nonumber \\ R^{\hbar ,(0)}_{12}= & {} -R^{-\hbar ,(0)}_{21}, \quad r_{12}^{(0)}=-r_{21}^{(0)}. \end{aligned}$$

(3.4)

If the Fourier symmetry (1.10) holds true⁸ as well then

$$\begin{aligned} R^{z,(0)}_{12}= & {} r_{12}(z)P_{12}, \nonumber \\ R^{z,(1)}_{12}= & {} m_{12}(z)P_{12}, \nonumber \\ r_{12}^{(0)}= & {} r_{12}^{(0)}P_{12}. \end{aligned}$$

(3.5)

Let us summarize the results from [15]. Consider R-matrix, which obeys Equations (1.3)–(1.6) and has expansions (3.1)–(3.3). Then, the Lax equations

$$\begin{aligned} {\dot{L}}(z,S)=[L(z,S),M(z,S)] \end{aligned}$$

(3.6)

are equivalent to equations

$$\begin{aligned} {\dot{S}}=[S,J(S)] \end{aligned}$$

(3.7)

in the following cases

$\bullet$ Relativistic top:

$$\begin{aligned} \begin{array}{l} \displaystyle { L^\eta (z,S)=\mathrm{tr}_2(R^\eta _{12}(z)S_2), \quad M^\eta (z,S)=-\mathrm{tr}_2(r_{12}(z)S_2) } \end{array} \end{aligned}$$

(3.8)

and

$$\begin{aligned} \begin{array}{l} \displaystyle { J^{\eta }(S)=\mathrm{tr}_2\Big ((R^{\eta ,(0)}_{12}-r_{12}^{(0)})S_2\Big ). } \end{array} \end{aligned}$$

(3.9)

$\bullet$ Nonrelativistic top:

$$\begin{aligned} \begin{array}{l} \displaystyle { L(z,S)=\mathrm{tr}_2(r_{12}(z)S_2), \quad M(z,S)=\mathrm{tr}_2(m_{12}(z)S_2) } \end{array} \end{aligned}$$

(3.10)

and

$$\begin{aligned} \begin{array}{l} \displaystyle { J(S)=\mathrm{tr}_2(m_{12}(0)S_2). } \end{array} \end{aligned}$$

(3.11)

These formulae can be easily written through R-matrix components (2.1). For example, the Lax matrix (3.8) is of the form

$$\begin{aligned} \begin{array}{c} \displaystyle { L^\eta (z,S)=\sum \limits _{i,j,k,l=1}^N R^{\eta }_{ijkl}(z)S_{lk} E_{ij}, } \end{array} \end{aligned}$$

(3.12)

due to $\mathrm{tr}(E_{kl}S)=S_{lk}$. Equivalently,

$$\begin{aligned} \begin{array}{c} \displaystyle { L^\eta (z,S)=\sum \limits _{i,j=1}^N L^{\eta }_{ij}(z,S) E_{ij}, \quad L^{\eta }_{ij}(z,S)=\sum \limits _{k,l=1}^N R^{\eta }_{ijkl}(z)S_{lk}, } \end{array} \end{aligned}$$

(3.13)

and for (3.9), (3.11)

$$\begin{aligned} J^{\eta }(S)= & {} \sum \limits _{i,j=1}^N E_{ij}J^\eta _{ij}(S), \quad J^\eta _{ij}(S)=\sum \limits _{k,l=1}^N (R^{\eta ,(0)}_{ij,kl}-r^{(0)}_{ij,kl})S_{lk}, \nonumber \\ J(S)= & {} \sum \limits _{i,j=1}^N E_{ij}J_{ij}(S), \quad J_{ij}(S)=\sum \limits _{k,l=1}^N m_{ij,kl}(0)S_{lk}. \end{aligned}$$

(3.14)

Classical Sklyanin Algebras and r-Matrix Structures. In this subsection, we show that any solution of the associative Yang–Baxter equation (1.3) with the properties provides (1.4)–(1.6) and the local expansions (3.1)–(3.4) provide the quadratic Poisson structures of Sklyanin type. The quadratic r-matrix structure [8]

$$\begin{aligned} \begin{array}{c} \displaystyle { c_2\{L^\eta _1(z,S),L^\eta _2(w,S)\}=[L^\eta _1(z,S)L^\eta _2(w,S),r_{12}(z-w)], } \end{array} \end{aligned}$$

(3.15)

where $c_2\ne 0$ is arbitrary constant, leads to the following Poisson brackets:

$$\begin{aligned} \begin{array}{c} \displaystyle { c_2\{S_1,S_2\}=[S_1 S_2,r_{12}^{(0)}]+[L^{\eta ,(0)}_1(S)S_2,P_{12}], \quad L^{\eta ,(0)}_1(S)=\mathrm{tr}_3(R_{13}^{\eta ,(0)}S_3). } \end{array} \end{aligned}$$

(3.16)

for the defined above Lax matrices. These brackets are easily obtained (see [11, 12]) by taking residues at $z=0$ and $w=0$ of both sides of (3.15). Being written in components (3.16) takes the form:

$$\begin{aligned} c_2\{S_{ij},S_{kl}\}=\left( L_{il}^{\eta ,(0)}S_{kj}-L_{kj}^{\eta ,(0)}S_{il}\right) + \sum _{a,b=1}^{N}\left( S_{ia}S_{kb}r^{(0)}_{aj,bl}-r^{(0)}_{ia,kb}S_{aj}S_{bl}\right) , \end{aligned}$$

(3.17)

where

$$\begin{aligned} L^{\eta ,(0)}_{ij}=\sum \limits _{k,l=1}^N R^{\eta ,(0)}_{ij,kl}S_{lk}. \end{aligned}$$

(3.18)

The proof of equivalence of (3.16) and (3.17) is based on the degeneration of (1.3)

$$\begin{aligned} \begin{array}{c} \displaystyle { R^\hbar _{12}(x) R^{\hbar }_{23}(y)=R^{\hbar }_{13}(x+y)r_{12}(x)+r_{23}(y)R^\hbar _{13}(x+y)-\partial _\hbar R_{13}^\hbar (x+y), } \end{array} \end{aligned}$$

(3.19)

obtained by taking the limit $\eta \rightarrow \hbar$ in (1.3).

Proposition 3.1

For the Lax matrix (3.8) defined by R-matrix satisfying the associative Yang–Baxter equation (1.3) together with properties (3.1)–(3.5), the Poisson brackets (3.16) are equivalently written in the r-matrix form (3.15).

Proof

Plugging the Lax matrix (3.8) into (3.15), we get the following expression for the l.h.s. of (3.15) up to $c_2$:⁹

$$\begin{aligned}&\mathrm{tr}_{3,4}\Big (R^\eta _{13}(z)R^\eta _{24}(w)\{S_3,S_4\}\Big )\nonumber \\&\quad {\mathop {=}\limits ^{(3.16)}} \mathrm{tr}_{3,4}\Big ( R^\eta _{13}(z)R^\eta _{24}(w)\Big ([S_3 S_4,r_{34}^{(0)}]+[L^{\eta ,(0)}_3(S)S_4,P_{34}]\Big )\Big ), \nonumber \\ \end{aligned}$$

(3.20)

and we are going to prove that it is equal to the r.h.s. of (3.15):

$$\begin{aligned} \begin{array}{c} \displaystyle { \mathrm{r.h.s.}=\mathrm{tr}_{3,4}\Big (\Big ( R^\eta _{13}(z)R^\eta _{24}(w)r_{12}(z-w)-r_{12}(z-w)R^\eta _{13}(z)R^\eta _{24}(w)\Big )S_3S_4\Big ).} \end{array} \end{aligned}$$

(3.21)

Let us rewrite the expression in the brackets of (3.21) using (3.19), which we represent in the form (the skew-symmetry (1.4) is also used)

$$\begin{aligned} \begin{array}{c} \displaystyle { R_{24}^\eta (w) r_{12}(z-w)=-R_{21}^\eta (w-z)R^\eta _{14}(z)+r_{14}(z)R_{24}^\eta (w)-\partial _\eta R_{24}^\eta (w) } \end{array} \end{aligned}$$

(3.22)

for the first term in (3.21), and

$$\begin{aligned} \begin{array}{c} \displaystyle { r_{12}(z-w)R_{24}^\eta (w) =-R^\eta _{14}(z)R_{21}^\eta (w-z)+R_{24}^\eta (w)r_{14}(z)-\partial _\eta R_{24}^\eta (w) } \end{array} \end{aligned}$$

(3.23)

for the second one. Due to $[R^\eta _{13}(z),\partial _\eta R^\eta _{24}(w)]=0$, we have

$$\begin{aligned}&R^\eta _{13}(z)R^\eta _{24}(w)r_{12}(z-w)-r_{12}(z-w)R^\eta _{13}(z)R^\eta _{24}(w) \nonumber \\&\quad =R^\eta _{14}(z)R_{21}^\eta (w-z)R_{13}^\eta (z)-R_{13}^\eta (z)R_{21}^\eta (w-z)R^\eta _{14}(z) \nonumber \\&\qquad +\,R^\eta _{13}(z)r_{14}(z)R_{24}^\eta (w)-R_{24}^\eta (w)r_{14}(z)R^\eta _{13}(z). \end{aligned}$$

(3.24)

The second line of (3.24) is canceled out after substitution into (3.21) since it is skew-symmetric under renaming the numbers of the tensor components $3\leftrightarrow 4$. Therefore, expression (3.21) is simplified to

$$\begin{aligned} \begin{array}{c} \displaystyle { \mathrm{r.h.s.}=\mathrm{tr}_{3,4}\Big (\Big (R^\eta _{13}(z)r_{14}(z)R_{24}^\eta (w)-R_{24}^\eta (w)r_{14}(z)R^\eta _{13}(z)\Big )S_3S_4\Big ). } \end{array} \end{aligned}$$

(3.25)

Next, transform the latter expression using further degeneration of (1.3), corresponding to $z\rightarrow 0$ in (3.22) and (3.23):

$$\begin{aligned} R_{13}^\eta (z)r_{14}(z)= & {} r_{34}^{(0)}R_{13}^\eta (z)+R_{14}^\eta (z)R_{43}^{\eta ,(0)} -\partial _z R_{14}^\eta (z)P_{34}+\partial _\eta R_{13}^\eta (z), \end{aligned}$$

(3.26)

$$\begin{aligned} r_{14}(z)R_{13}^\eta (z)= & {} R_{13}^\eta (z)r_{34}^{(0)}+R_{43}^{\eta ,(0)}R_{14}^\eta (z) -\partial _z R_{13}^\eta (z)P_{34}+\partial _\eta R_{13}^\eta (z).\nonumber \\ \end{aligned}$$

(3.27)

Then, the expression in the brackets of (3.25) transforms into

$$\begin{aligned}&R^\eta _{13}(z)r_{14}(z)R_{24}^\eta (w)-R_{24}^\eta (w)r_{14}(z)R^\eta _{13}(z)\nonumber \\&\quad =r_{34}^{(0)}R_{13}^\eta (z)R_{24}^\eta (w)-R_{24}^\eta (w)R_{13}^\eta (z)r_{34}^{(0)}\nonumber \\&\qquad +\,R_{14}^\eta (z)R_{43}^{\eta ,(0)}R_{24}^\eta (w)-R_{24}^\eta (w)R_{43}^{\eta ,(0)}R_{14}^\eta (z)\nonumber \\&\qquad +\,R_{24}^\eta (w)\partial _z R_{13}^\eta (z)P_{34}-\partial _z R_{14}^\eta (z)P_{34}R_{24}^\eta (w). \end{aligned}$$

(3.28)

The last line of (3.28) vanishes being substituted into (3.21). Indeed, on the one hand

$$\begin{aligned} \begin{array}{c} \displaystyle { \mathrm{tr}_{3,4}\Big ( \partial _z R_{14}^\eta (z)P_{34}R_{24}^\eta (w)S_3S_4\Big ) = \mathrm{tr}_{3,4}\Big ( P_{34}\partial _z R_{13}^\eta (z)R_{24}^\eta (w)S_3S_4\Big ), } \end{array} \end{aligned}$$

(3.29)

and, on the other hand,

$$\begin{aligned} \mathrm{tr}_{3,4}\Big ( R_{24}^\eta (w)\partial _z R_{13}^\eta (z)P_{34} S_3S_4\Big )= & {} \mathrm{tr}_{3,4}\Big ( \partial _z R_{13}^\eta (z) R_{24}^\eta (w)P_{34} S_3S_4 \Big )\nonumber \\= & {} \mathrm{tr}_{3,4}\Big ( \partial _z R_{13}^\eta (z) R_{24}^\eta (w) S_3S_4P_{34} \Big ) \nonumber \\= & {} \mathrm{tr}_{3,4}\Big ( P_{34}\partial _z R_{13}^\eta (z) R_{24}^\eta (w) S_3S_4 \Big ).\qquad \end{aligned}$$

(3.30)

The second line of (3.28) after substitution into (3.21) results in the first term of the r.h.s. of (3.20):

$$\begin{aligned}&\mathrm{tr}_{3,4}\Big ( \Big ( r_{34}^{(0)}R_{13}^\eta (z)R_{24}^\eta (w)-R_{24}^\eta (w)R_{13}^\eta (z)r_{34}^{(0)} \Big )S_3S_4\Big )\nonumber \\&\quad =\mathrm{tr}_{3,4}\Big ( R^\eta _{13}(z)R^\eta _{24}(w)\Big ([S_3 S_4,r_{34}^{(0)}]\Big )\Big ). \end{aligned}$$

(3.31)

Finally, the third line of (3.28) after substitution into (3.21) results in the second term of the r.h.s. of (3.20):

$$\begin{aligned}&\mathrm{tr}_{3,4}\Big ( \Big (R_{14}^\eta (z)R_{43}^{\eta ,(0)}R_{24}^\eta (w)-R_{24}^\eta (w)R_{43}^{\eta ,(0)}R_{14}^\eta (z) \Big )S_3S_4\Big )\nonumber \\&\quad = \mathrm{tr}_{3,4}\Big ( R^\eta _{13}(z)R^\eta _{24}(w)\Big (L^{\eta ,(0)}_3(S)S_4P_{34}-P_{34}L^{\eta ,(0)}_3(S)S_4\Big )\Big ). \end{aligned}$$

(3.32)

The latter equality is verified as follows. Let us show that the first terms in the upper and lower lines of (3.32) are equal to each other (the equality of the second terms is verified similarly):

$$\begin{aligned}&\mathrm{tr}_{3,4}\Big (R^\eta _{13}(z)R^\eta _{24}(w)L^{\eta ,(0)}_3(S)S_4P_{34} \Big )= \mathrm{tr}_{3,4}\Big ( R^\eta _{13}(z)L^{\eta ,(0)}_3(S)S_4P_{34} R^\eta _{24}(w)\Big ) \nonumber \\&\quad =\mathrm{tr}_{3,4,5}\Big (R^\eta _{13}(z)R_{35}^{\eta ,(0)}S_5S_4P_{34}R^\eta _{24}(w) \Big ) = \mathrm{tr}_{3,4,5}\Big (P_{34} R^\eta _{14}(z)R_{45}^{\eta ,(0)}S_5S_3R^\eta _{24}(w) \Big ) \nonumber \\&\quad =\mathrm{tr}_{3,4,5}\Big (P_{34} R^\eta _{14}(z)R_{45}^{\eta ,(0)}R^\eta _{24}(w) S_5S_3\Big )= \mathrm{tr}_{3,4,5}\Big ( R^\eta _{14}(z)R_{45}^{\eta ,(0)}R^\eta _{24}(w) S_5S_3P_{34}\Big )\nonumber \\&\quad = \mathrm{tr}_{3,4,5}\Big ( R^\eta _{14}(z)R_{45}^{\eta ,(0)}R^\eta _{24}(w) S_5P_{34}S_4\Big ) \end{aligned}$$

(3.33)

The last step is to take the trace over the third tensor component (then $P_{34}$ vanishes) and rename the component $5\leftrightarrow 3$.

To summarize, we deduce the r-matrix structure (3.15) from brackets (3.16). The converse statement (when the brackets (3.16) are derived from the r-matrix structure(3.15)) follows from the local behavior (3.2). Indeed, by now we have proved that the r-matrix structure (3.15) is equivalent to the condition $\mathrm{tr}_{3,4}(R^\eta _{13}(z)R^\eta _{24}(w)A_{34})=0$ with $A_{12}=c_2\{S_1,S_2\}-[S_1 S_2,r_{12}^{(0)}]-[L^{\eta ,(0)}_1(S)S_2,P_{12}]$, which is the difference between l.h.s. and r.h.s. of (3.16). In order to prove that $A_{12}=0$, consider the expression ${\mathcal A}_{12}(z,w)=\mathrm{tr}_{3,4}( R^\eta _{13}(z)R^\eta _{24}(w)A_{34})$ locally near $z=0$ and $w=0$. Then, from (3.2), we have ${\mathcal A}_{12}(z,w)=z^{-1}w^{-1}\mathrm{tr}_{3,4}(P_{13}P_{24}A_{34})+\cdots =z^{-1}w^{-1}A_{12}+\cdots$. Therefore, $A_{12}=0$ follows from ${\mathcal A}_{12}(z,w)=0$. $\square$

In the nonrelativistic limit, we are left with the linear r-matrix structure

$$\begin{aligned} \begin{array}{c} \displaystyle { c_1\{L_1(z,S),L_2(w,S)\}=[L_1(z,S)+L_2(w,S),r_{12}(z-w)], } \end{array} \end{aligned}$$

(3.34)

which provides the Poisson–Lie brackets on $\mathrm{gl}_N^*$ Lie coalgebra ($c_1\ne 0$ is an arbitrary constant):

$$\begin{aligned} \begin{array}{l} \displaystyle { c_1\{S_1,S_2\}=[S_2,P_{12}] } \end{array} \end{aligned}$$

(3.35)

or

$$\begin{aligned} \begin{array}{l} \displaystyle { c_1\{S_{ij},S_{kl}\}=S_{kj}\delta _{il}-S_{il}\delta _{kj}. } \end{array} \end{aligned}$$

(3.36)

The Poisson structures (3.15)–(3.16) and (3.34)–(3.35) provide the Hamiltonians generating the Euler–Arnold equations (3.7). In the relativistic case, the Hamiltonian is given by

$$\begin{aligned} \begin{array}{l} \displaystyle { H^{\mathrm{rel}}=\frac{1}{c_2}\,\mathrm{tr}(S), } \end{array} \end{aligned}$$

(3.37)

and for the nonrelativistic case we have

$$\begin{aligned} \begin{array}{l} \displaystyle { H^{{\text {non-rel}}}=\frac{1}{2c_1}\,\mathrm{tr}(SJ(S)). } \end{array} \end{aligned}$$

(3.38)

In the relativistic case, the Hamiltonian is linear, while the Poisson structure is quadratic (in variables S), and vice versa for nonrelativistic models.

3.1 The Case of Nonstandard R-matrix

In order to describe the tops explicitly, it is enough to write down all R-matrices and related coefficients of expansions entering (3.8)–(3.14). Below is the summary based on the R-matrix (2.16):

$$\begin{aligned} R^{\eta }_{ij,kl}(z)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N}{2}\,\Big (\coth (Nz/2)+\coth (N\eta /2)\Big ) \nonumber \\&+\, \delta _{ij}\delta _{kl}\varepsilon (i\ne k)\frac{N e^{(i-k)\eta -\hbox {sign}(i-k)N\eta /2}}{2\sinh (N\eta /2)}\nonumber \\&+\,\delta _{il}\delta _{kj} \varepsilon (i\ne k)\frac{N e^{(i-k)z-\hbox {sign}(i-k)Nz/2}}{2\sinh (Nz/2)}\, \nonumber \\&+\,N\delta _{i+k,j+l}e^{(i-j)z+(j-k)\eta }\Big (\varepsilon (i{<}j{<}k) -\varepsilon (k{<}j{<}i) \Big ) \nonumber \\&+\, N e^{-N\Lambda } \delta _{i+k,j+l+N}\Big (\delta _{iN}e^{-jz-l\eta }-\delta _{kN}e^{lz+j\eta }\Big ). \end{aligned}$$

(3.39)

The classical r-matrix:

$$\begin{aligned} r_{ij,kl}(z)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N}{2}\,\coth (Nz/2) \nonumber \\&+\, \delta _{ij}\delta _{kl}\varepsilon (i\ne k) \Big ((i-k)-\frac{N\hbox {sign}(i-k)}{2}\Big ) \nonumber \\&+\,\delta _{il}\delta _{kj} \varepsilon (i\ne k)\frac{N e^{(i-k)z-\hbox {sign}(i-k)Nz/2}}{2\sinh (Nz/2)}\, \nonumber \\&+\, Ne^{(i-j)z}\delta _{i+k,j+l}\Big (\varepsilon (i{<}j{<}k) -\varepsilon (k{<}j{<}i) \Big ) \nonumber \\&+\, N e^{-N\Lambda } \delta _{i+k,j+l+N}\Big (e^{-jz}\delta _{iN}-e^{lz}\delta _{kN}\Big ). \end{aligned}$$

(3.40)

The next coefficient in expansion (3.1):

$$\begin{aligned} m_{ij,kl}(z)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N^2}{12}+ \, \delta _{ij}\delta _{kl}\varepsilon (i\ne k) \left( \frac{(i-k)^2}{2}-\frac{N^2}{12}-\frac{N}{2}|i-k|\right) \nonumber \\&+\, N(j-k)e^{(i-j)z}\delta _{i+k,j+l}\left( \varepsilon (i{<}j{<}k) -\varepsilon (k{<}j{<}i) \right) \nonumber \\&-\, N e^{-N\Lambda }\delta _{i+k,j+l+N}\left( l\,e^{-jz}\delta _{iN}+j\,e^{lz}\delta _{kN}\right) . \end{aligned}$$

(3.41)

Its value at $z=0$ entering the inverse inertia tensor in the nonrelativistic case (3.11) or (3.14):

$$\begin{aligned} m_{ij,kl}(0)= & {} \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N^2}{12}+ \, \delta _{ij}\delta _{kl}\varepsilon (i\ne k) \left( \frac{(i-k)^2}{2}-\frac{N^2}{12}-\frac{N}{2}|i-k|\right) \nonumber \\&+\, N(j-k)\delta _{i+k,j+l}\left( \varepsilon (i{<}j{<}k) -\varepsilon (k{<}j{<}i) \right) \nonumber \\&-\, N e^{-N\Lambda } \delta _{i+k,j+l+N}\left( l\,\delta _{iN}+j\,\delta _{kN}\right) . \end{aligned}$$

(3.42)

The coefficient from expansions (3.2) and (3.3) entering the relativistic inverse inertia tensor (3.9) or (3.14):

$$\begin{aligned} R^{\eta ,(0)}_{ij,kl}= & {} r_{ilkj}(\eta )= \delta _{ij}\delta _{kl}\delta _{ik}\,\frac{N}{2}\coth (N\eta /2)\nonumber \\&+\, \delta _{ij}\delta _{kl}\varepsilon (i\ne k)\frac{N e^{(i-k)\eta -\hbox {sign}(i-k)N\eta /2}}{2\sinh (N\eta /2)}\nonumber \\&+\,\delta _{il}\delta _{kj} \varepsilon (i\ne k) \left( (i-k)-\frac{N\hbox {sign}(i-k)}{2}\right) \nonumber \\&+\, Ne^{(j-k)\eta }\,\delta _{i+k,j+l}\left( \varepsilon (i{<}j{<}k) -\varepsilon (k{<}j{<}i) \right) \nonumber \\&+\, N e^{-N\Lambda } \delta _{i+k,j+l+N}\left( e^{-l\eta }\delta _{iN}-e^{j\eta }\delta _{kN}\right) \end{aligned}$$

(3.43)

and

$$\begin{aligned} r_{ij,kl}^{(0)}= & {} \left( \delta _{ij}\delta _{kl}\varepsilon (i\ne k) +\delta _{il}\delta _{kj} \varepsilon (i\ne k)\right) \left( (i-k)-\frac{N\hbox {sign}(i-k)}{2}\right) \nonumber \\&+\,N\delta _{i+k,j+l}\left( \varepsilon (i{<}j{<}k) -\varepsilon (k{<}j{<}i) \right) \nonumber \\&+\,N e^{-N\Lambda } \delta _{i+k,j+l+N}\left( \delta _{iN}-\delta _{kN}\right) . \end{aligned}$$

(3.44)

Lax Pairs. The Lax matrix of the relativistic top constructed by means of (3.39) is of the following form. For $i=j$:

$$\begin{aligned} L_{ii}^{\eta }(z)= & {} \frac{N}{2}\big (\coth (Nz/2)+\coth (N\eta /2)\big )S_{ii}\nonumber \\&+\,\frac{N}{2\sinh (N\eta /2)}\left( e^{-N\eta /2}\sum _{k=1}^{i-1}e^{(i-k)\eta }S_{kk}\right. \nonumber \\&\left. +\,e^{N\eta /2}\sum _{k=i+1}^{N}e^{(i-k)\eta }S_{kk}\right) , \end{aligned}$$

(3.45)

for $i<j$:

$$\begin{aligned} L_{ij}^{\eta }(z)= & {} \frac{N\exp (Nz/2+(i-j)z)}{2\sinh (Nz/2)}S_{ij}\nonumber \\&+\,N\sum _{k=j+1}^{N}e^{(i-j)z+(j-k)\eta }S_{i-j+k,k}, \end{aligned}$$

(3.46)

and for $i>j$:

$$\begin{aligned} L_{ij}^{\eta }(z)= & {} \frac{N\exp (-Nz/2+(i-j)z)}{2\sinh (Nz/2)}S_{ij}-N\sum _{k=1}^{j-1}e^{(i-j)z+(j-k)\eta }S_{i-j+k,k}\nonumber \\&-\,Ne^{-N\Lambda } e^{(i-j)z+j\eta }S_{i-j,N}\nonumber \\&+\,\delta _{iN}Ne^{-N\Lambda }\sum _{k=j+1}^{N}e^{-jz+(j-k)\eta }S_{k-j,k}. \end{aligned}$$

(3.47)

From definitions (3.8), (3.10) and the expansion (3.1), it follows that

$$\begin{aligned} \begin{array}{c} \displaystyle { -M^\eta (z)=L(z)=\mathop {\hbox {Res}}\limits \limits _{\eta =0}\Big (\eta ^{-1}L^{\eta }(z)\Big ), \quad M(z)=\mathop {\hbox {Res}}\limits \limits _{\eta =0}\Big (\eta ^{-2}L^{\eta }(z)\Big ). } \end{array} \end{aligned}$$

(3.48)

Similarly, expansion (3.2) near $z=0$ yields

$$\begin{aligned} \begin{array}{c} \displaystyle { L^\eta (z)=\frac{1}{z}S+L^{\eta ,(0)}(S)+O(z), \quad L^{\eta ,(0)}(S)=\mathrm{tr}_2\Big (R_{12}^{\eta ,(0)}S_2\Big )=\mathop {\hbox {Res}}\limits \limits _{z=0}\Big (z^{-1}L^{\eta }(z)\Big ).} \end{array} \end{aligned}$$

(3.49)

Example: $GL_2$Top. In this case, we deal with the following quantum:

$$\begin{aligned} \begin{array}{l} R^\hbar (z)=\left( \begin{array}{llll} \coth (z)+\coth (\hbar ) &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \sinh ^{-1}(\hbar ) &{}\quad \sinh ^{-1}(z) &{}\quad 0 \\ 0 &{}\quad \sinh ^{-1}(z) &{}\quad \sinh ^{-1}(\hbar ) &{}\quad 0 \\ -\,4\,e^{-2\Lambda }\sinh (z+\hbar ) &{}\quad 0 &{}\quad 0 &{}\quad \coth (z)+\coth (\hbar ) \end{array} \right) \end{array} \end{aligned}$$

(3.50)

and classical

$$\begin{aligned} \begin{array}{l} r(z)=\left( \begin{array}{llll} \coth (z)&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \sinh ^{-1}(z)&{}\quad 0 \\ 0 &{}\quad \sinh ^{-1}(z )&{}\quad 0 &{}\quad 0\\ -\,4\,e^{-2\Lambda }\sinh (z)&{}\quad 0&{}\quad 0&{}\quad \coth (z) \end{array} \right) \end{array} \end{aligned}$$

(3.51)

R-matrices. In the relativistic case, this provides the Lax pair

$$\begin{aligned} L^\eta (z,S)= & {} \left( \begin{array}{ll} \displaystyle { S_{11}(\coth (z)+\coth (\eta ))+\frac{S_{22}}{\sinh (\eta )} } &{}\quad \displaystyle { \frac{S_{12}}{\sinh (z)} }\\ \displaystyle { \frac{S_{21}}{\sinh (z)}-4e^{-2\Lambda }S_{12}\sinh (z+\eta ) }&{}\quad \displaystyle { S_{22}(\coth (z)+\coth (\eta ))+\frac{S_{11}}{\sinh (\eta )} } \end{array} \right) \end{aligned}$$

(3.52)

$$\begin{aligned} M^\eta (z,S)= & {} -\left( \begin{array}{ll} \displaystyle { \coth (z)S_{11} } &{}\quad \displaystyle { \frac{\textstyle S_{12}}{\textstyle \sinh (z)}}\\ \displaystyle { \frac{\textstyle S_{21}}{\textstyle \sinh (z)}-4e^{-2\Lambda }\sinh (z)S_{12} }&{}\quad \displaystyle { \coth (z)S_{22} } \end{array} \right) \end{aligned}$$

(3.53)

and the inverse inertia tensor

$$\begin{aligned} \begin{array}{l} J^\eta (S)=\left( \begin{array}{ll} \coth (\eta )S_{11}+\frac{\textstyle S_{22}}{\textstyle \sinh (\eta )} &{}\quad 0 \\ -\,4e^{-2\Lambda }\sinh (\eta )S_{12} &{}\quad \frac{\textstyle S_{11}}{\textstyle \sinh (\eta )}+\coth (\eta )S_{22} \end{array}\right) \end{array} \end{aligned}$$

(3.54)

In the nonrelativistic case, the Lax matrix is defined by (3.53): $L(z,S)=-M^\eta (z,S)$. The accompanying matrix is as follows:

$$\begin{aligned} \begin{array}{l} \displaystyle { M(z,S)=\frac{1}{6}\left( \begin{array}{ll} 2S_{11}-S_{22} &{}\quad 0 \\ \ \\ -\,24\,e^{-2\Lambda }\cosh (z)S_{12} &{}\quad -\,S_{11}+2S_{22}\end{array}\right) } \end{array} \end{aligned}$$

(3.55)

The inverse inertia tensor acquires the form:

$$\begin{aligned} \begin{array}{l} \displaystyle { J(S)=\frac{1}{6}\left( \begin{array}{ll} 2S_{11}-S_{22} &{}\quad 0 \\ \ \\ -\,24\,e^{-2\Lambda }S_{12} &{}\quad -\,S_{11}+2S_{22}\end{array}\right) } \end{array} \end{aligned}$$

(3.56)

$\bullet$ Relativistic top ($\eta$-independent description):

Another one description for the relativistic top is available, which is similar to original construction [8]. Instead of usage of the quantum R-matrix (3.8), consider the traceless part of the nonrelativistic Lax matrix and supplement it by the scalar term $s_01_N$:

$$\begin{aligned} \begin{array}{c} \displaystyle { {{\tilde{L}}}(z,S)=s_01_N+L(z,S)-\frac{1_N}{N}\,\mathrm{tr}L(z,S), \quad s_0=\frac{\mathrm{tr}S}{N}, } \end{array} \end{aligned}$$

(3.57)

where $s_0$ is a dynamical variable. In fact, it is the Hamiltonian since $\mathrm{tr}{{\tilde{L}}}=Ns_0$. The Lax equations do not change because L(z, S) and ${{\tilde{L}}}(z,S)$ differ from each other by only a scalar matrix. So that the M-matrix for (3.57) is the same as in (3.8). However, the Poisson structures are different (see below). It happens because of the bi-Hamiltonian structure in this kind of models [11, 12, 37].

As mentioned in [11, 12] (see also [38]), there is a relation between the Lax matrices (3.8) and (3.57). Similarly, to the rational case, we have

$$\begin{aligned} \begin{array}{c} \displaystyle { L^\eta \left( z-\frac{\eta }{N},{{\tilde{L}}}\left( \frac{\eta }{N},S\right) \right) =\frac{\mathrm{tr}\left( L^\eta \left( z-\frac{\eta }{N},S\right) \right) }{\mathrm{tr}(S)}{{\tilde{L}}}(z,S). } \end{array} \end{aligned}$$

(3.58)

This relation can be verified directly using explicit formulae (3.45)–(3.47).

The quadratic Poisson structure takes the form

$$\begin{aligned} \begin{array}{c} \displaystyle { \{{{\tilde{L}}}_1(z,S),{{\tilde{L}}}_2(w,S)\}=\frac{1}{c_2}\,[{{\tilde{L}}}_1(z,S){{\tilde{L}}}_2(w,S),r_{12}(z-w)], } \end{array} \end{aligned}$$

(3.59)

and provides the following Poisson brackets:

$$\begin{aligned} \begin{array}{c} \displaystyle { c_2 \{S_1,S_2\}=s_0[S_2,P_{12}]+\left[ S_1S_2,r^{(0)}_{12}\right] +\left[ \mathrm{tr}_3(r_{13}^{(0)}S_3)S_2,P_{12}\right] .} \end{array} \end{aligned}$$

(3.60)

The latter is verified similarly to the $\eta$-dependent case (3.15)–(3.16).

3.2 The Case of General R-matrix

The summary of the integrable tops data in the general case is based on the expansions of the R-matrix (2.24):

$$\begin{aligned} R^{\eta }_{12}(z)= & {} \frac{N}{2}\Big (\coth (Nz/2)+\coth (N\eta /2)\Big )\sum _{i} E_{ii}\otimes E_{ii}\nonumber \\&+\,\frac{N}{e^{N\eta }-1}\sum \limits _{0<n<N,\, i=C^n(k)} e^{n\eta }E_{ii}\otimes E_{kk}\nonumber \\&+\, \frac{N}{e^{Nz}-1}\sum \limits _{0<m<N,\,k=C^m_0(i)} e^{mz} E_{ik}\otimes E_{ki}\nonumber \\&+\,\sum \limits _{\mathrm {\begin{array}{c}0<m<N,\,n>0,\\ i=C^m_0(j),\,\tau ^n(j,i)=(k,l)\end{array}}} \nonumber \\&\times \, N \left( e^{-n\eta -mz}E_{ij}\otimes E_{kl}- e^{n\eta +mz}E_{kl}\otimes E_{ij}\right) , \end{aligned}$$

(3.61)

The classical r-matrix and the next coefficient of the classical limit (3.1) are as follows:

$$\begin{aligned} r_{12}(z)= & {} \frac{N}{2}\coth (Nz/2)\sum _{i} E_{ii}\otimes E_{ii}\nonumber \\&+\,\sum \limits _{0<n<N,\, i=C^n(k)} \left( n-\frac{N}{2}\right) E_{ii}\otimes E_{kk}\nonumber \\&+ \frac{N}{e^{Nz}-1}\sum \limits _{0<m<N,\,k=C^m_0(i)} e^{mz} E_{ik}\otimes E_{ki}\nonumber \\&+\,\sum \limits _{\mathrm {\begin{array}{c}0<m<N,\,n>0,\\ i=C^m_0(j),\,\tau ^n(j,i)=(k,l)\end{array}}} \nonumber \\&\times \, N \left( e^{-mz}E_{ij}\otimes E_{kl}- e^{mz}E_{kl}\otimes E_{ij}\right) \end{aligned}$$

(3.62)

and

$$\begin{aligned} m_{12}(z)= & {} \frac{N^2}{12}\sum _{i} E_{ii}\otimes E_{ii} +\frac{1}{12}\sum \limits _{0<n<N,\, i=C^n(k)} \Big (6n^2-6nN+N^2\Big )E_{ii}\otimes E_{kk} \nonumber \\&-\,\sum \limits _{\mathrm {\begin{array}{c}0<m<N,\,n>0,\\ i=C^m_0(j),\,\tau ^n(j,i)=(k,l)\end{array}}} \nonumber \\&\times \, Nn \left( e^{-mz}E_{ij}\otimes E_{kl}+ e^{mz}E_{kl}\otimes E_{ij}\right) . \end{aligned}$$

(3.63)

The first nontrivial coefficients from expansions (3.2), (3.3) are of the form:

$$\begin{aligned} R^{\eta ,(0)}_{12}= & {} \frac{N}{2}\coth (N\eta /2)\sum _{i} E_{ii}\otimes E_{ii}\nonumber \\&+\,\frac{N}{e^{N\eta }-1}\sum \limits _{0<n<N,\, i=C^n(k)} e^{n\eta }E_{ii}\otimes E_{kk}\nonumber \\&+\, \sum \limits _{0<m<N,\,k=C^m_0(i)} \left( m-\frac{N}{2}\right) E_{ik}\otimes E_{ki} \nonumber \\&+\,\sum \limits _{\mathrm {\begin{array}{l}0<m<N,\,n>0,\\ i=C^m_0(j),\,\tau ^n(j,i)=(k,l)\end{array}}} \nonumber \\&\times \,N \left( e^{-n\eta }E_{ij}\otimes E_{kl}- e^{n\eta }E_{kl}\otimes E_{ij}\right) \end{aligned}$$

(3.64)

and

$$\begin{aligned} r^{(0)}_{12}= & {} \sum \limits _{0<n<N,\, i=C^n(k)} \left( n-\frac{N}{2}\right) E_{ii}\otimes E_{kk}+ \sum \limits _{0<m<N,\,k=C^m_0(i)} \left( m-\frac{N}{2}\right) E_{ik}\otimes E_{ki}\nonumber \\&+\,\sum \limits _{\mathrm {\begin{array}{c}0<m<N,\,n>0,\\ i=C^m_0(j),\,\tau ^n(j,i)=(k,l)\end{array}}} N \left( E_{ij}\otimes E_{kl}- E_{kl}\otimes E_{ij}\right) . \end{aligned}$$

(3.65)

4 Relation to Ruijsenaars–Schneider Model

Introduce the matrix [19]¹⁰

$$\begin{aligned} \begin{array}{l} \displaystyle { g(z, q)=\Xi (z,q)D^{-1}(q)\in \mathrm{Mat}(N,{\mathbb {C}}) , } \end{array} \end{aligned}$$

(4.1)

where

$$\begin{aligned} \begin{array}{l} \displaystyle { \Xi _{ij}(z,q)=e^{(i-1)(z-{{\bar{q}}}_j)}+(-1)^{N}e^{-(z-{{\bar{q}}}_j)}\delta _{iN}} \end{array} \end{aligned}$$

(4.2)

and

$$\begin{aligned} \begin{array}{l} \displaystyle { D_{ij}( q)=\delta _{ij} \prod \limits _{k\ne i}\left( e^{-{{\bar{q}}}_i}-e^{-{{\bar{q}}}_k}\right) . } \end{array} \end{aligned}$$

(4.3)

The matrices depend on z and the set of variables $q_1,\ldots ,q_N$. The variables ${{\bar{q}}}_1,\ldots ,{{\bar{q}}}_N$ are obtained by transition to the center of mass frame:

$$\begin{aligned} \begin{array}{c} \displaystyle { {{\bar{q}}}_i=q_i-\frac{1}{N}\sum \limits _{k=1}^Nq_k. } \end{array} \end{aligned}$$

(4.4)

The determinant of the matrix $\Xi$ is as follows:

$$\begin{aligned} \begin{array}{c} \displaystyle { \det \Xi (z,q)=e^{zN(N-1)/2}(1-e^{-Nz})\prod \limits _{i>j}^N\left( e^{-{{\bar{q}}}_i}-e^{-{\bar{q}}_j}\right) . } \end{array} \end{aligned}$$

(4.5)

That is $\Xi (z,q)$ is degenerated at $z=0$.

Our statement is that the following matrix

$$\begin{aligned} \begin{array}{l} \displaystyle { { L}^{\mathrm{RS}}(z)= g^{-1}(z) g(z+\eta )e^{P/c},\quad P=\mathrm{diag}(p_1,p_2,\ldots ,p_N) } \end{array} \end{aligned}$$

(4.6)

is the Lax matrix of the trigonometric Ruijsenaars–Schneider model. More precisely,

$$\begin{aligned} L^{\mathrm{RS}}_{ij}(z)= & {} e^{\frac{N-2}{2}\,\eta }\sinh (\eta /2) \left( \coth \left( \frac{Nz}{2}\right) +\coth \left( \frac{q_i-q_j+\eta }{2}\right) \right) e^{p_j/c}\nonumber \\&\times \,\prod ^N_{k\ne j}\frac{\sinh \left( \frac{q_j-q_k-\eta }{2}\right) }{\sinh \left( \frac{q_j-q_k}{2}\right) }. \end{aligned}$$

(4.7)

The proof is obtained by direct verification, which is similar to calculations performed in [10,11,12] in the rational case. One should introduce the set of elementary symmetric polynomials $\sigma _k(q)$ of N variables $\{e^{-{{\bar{q}}}_1},\ldots ,e^{-{{\bar{q}}}_N}\}$

$$\begin{aligned} \begin{array}{c} \displaystyle { \prod _{k=1}^N(\zeta -e^{-{{\bar{q}}}_k})=\sum _{k=0}^N(-1)^k\zeta ^k\sigma _k(q)} \end{array} \end{aligned}$$

(4.8)

and N sets of similar functions $\{\check{\sigma }_{k,i}(q),i=1,\ldots ,N\}$ defined for the sets $\{e^{-{{\bar{q}}}_1},\ldots ,e^{-{{\bar{q}}}_N}\}\backslash \{e^{-{\bar{q}}_i}\}$ of $N-1$ variables each:

$$\begin{aligned} \begin{array}{c} \displaystyle { \prod _{k\ne i}^N(\zeta -e^{-{\bar{q}}_k})=\sum _{k=0}^N(-\,1)^k\zeta ^k\check{\sigma }_{k,i}(q). } \end{array} \end{aligned}$$

(4.9)

The inverse of $\Xi$ is then written as follows:

$$\begin{aligned} \begin{array}{c} \displaystyle { (\Xi ^{-1})_{ij}(z, q)=\frac{(-1)^{j-1}e^{(N-j+1)z}}{e^{Nz}-1} \frac{\left( \check{\sigma }_{j-1,i}(q)+e^{-{{\bar{q}}}_i}\check{\sigma }_{j,i}(q)e^{-Nz}\right) }{\prod \nolimits _{k\ne i}\left( e^{-{{\bar{q}}}_i}-e^{-{{\bar{q}}}_k}\right) }. } \end{array} \end{aligned}$$

(4.10)

Consider the gauge-transformed Lax matrix

$$\begin{aligned} \begin{array}{l} \displaystyle { L^\eta (z)=g(z){\tilde{L}}^{RS}(z)g^{-1}(z)=g(z+\eta )e^{P/c}g^{-1}(z) } \end{array} \end{aligned}$$

(4.11)

Then,¹¹

$$\begin{aligned} \begin{array}{l} \displaystyle { L^\eta (z)=\mathrm{tr}\left( R_{12}^\eta (z)S_2(p,q)\right) } \end{array} \end{aligned}$$

(4.12)

with the nonstandard R-matrix (2.16), where $\Lambda =\sqrt{-1}\pi$. Put it differently, matrix (4.12) coincides with (3.45)–(3.47) when $\Lambda =\sqrt{-1}\pi$. The change of variables is as follows:

$$\begin{aligned} \begin{array}{c} \displaystyle { S_{ij}(p,q)=\frac{(-1)^{j}\sigma _{j}(q)e^{(i-1)\eta }}{N}\sum _{n=1}^{N}\frac{e^{p_n/c}}{\prod \nolimits _{k:k\ne n}(e^{-{{\bar{q}}}_n}-e^{-{{\bar{q}}}_k})}\left( e^{-(i-1){{\bar{q}}}_n}+\frac{(-\,1)^N \delta _{iN}}{e^{N\eta -{{\bar{q}}}_n}}\right) . } \end{array} \end{aligned}$$

(4.13)

The Poisson structure for (p, q) variables is canonical, i.e.,

$$\begin{aligned} \begin{array}{c} \displaystyle { \{p_i,q_j\}=\delta _{ij}\quad \hbox {or}\quad \{p_i,{{\bar{q}}}_j\}=\delta _{ij}-\frac{1}{N}. } \end{array} \end{aligned}$$

(4.14)

After some tedious calculations, it can be verified that the Poisson brackets $\{S_{ij}(p,q),S_{kl}(p,q)\}$ evaluated through (4.14) coincide with (3.17) with $c_2=Nc$ and $r_{12}^{(0)}$ from (3.44). In particular, it is useful to notice for the proof that matrix (4.13) is of rank 1, i.e.,

$$\begin{aligned} S_{ij}(p,q)= & {} a_i(p,q)b_j(q), \nonumber \\ a_i(p,q)= & {} \frac{e^{(i-1)\eta }}{N}\sum _{n=1}^{N}\frac{e^{p_n/c}}{\prod \nolimits _{k:k\ne n}(e^{-{{\bar{q}}}_n}-e^{-{{\bar{q}}}_k})}\left( e^{-(i-1){{\bar{q}}}_n}+\frac{(-1)^N \delta _{iN}}{e^{N\eta -{{\bar{q}}}_n}}\right) ,\nonumber \\ \quad b_j(q)= & {} (-\,1)^{j}\sigma _{j}(q). \end{aligned}$$

(4.15)

In this case, $S_{ij}S_{kl}=S_{il}S_{kj}$, and the Poisson structure (3.17) takes the (relatively simple) form:

$$\begin{aligned} \{S_{ij},S_{kl}\}= & {} \frac{1}{Nc}(L_{il}^{\eta ,(0)}S_{kj}-L_{kj}^{\eta ,(0)}S_{il})+\frac{2}{Nc}(k-i)S_{ij}S_{kl} \nonumber \\&+\,\frac{\varepsilon (i{>}k)}{c}\sum _{p=0}^{i-k-1}S_{i-p,j}S_{k+p,l}-\frac{\varepsilon (i{<}k)}{c}\sum _{p=0}^{k-i-1}S_{i+p,j}S_{k-p,l}\nonumber \\&+\,\frac{(-\,1)^N\delta _{kN}}{c}\sum _{p=1}^{i-1}S_{i-p,j}S_{p,l}-\frac{(-1)^N\delta _{iN}}{c}\sum _{p=1}^{k-1}S_{pj}S_{k-p,l}.\nonumber \\ \end{aligned}$$

(4.16)

Nonrelativistic Limit. The Calogero–Moser–Sutherland models appear from the above results by taking the nonrelativistic limit, when $\eta =\nu /c$ and $c\rightarrow \infty$. The Lax matrix arising from (4.7) is of the form¹²$^{,}$¹³

$$\begin{aligned} L^{\mathrm{CM}}_{ij}(z)= & {} \delta _{ij}({\dot{q}}_i+ \nu \coth (Nz))+ \nu (1-\delta _{ij}) \Big (\coth \Big (\frac{q_{i}-q_{j}}{2}\Big ) + \coth (Nz)\Big ), \nonumber \\ {\dot{q}}_i= & {} p_{i} + \nu (N-2) -\nu \sum \limits _{k \ne i}^{N} \coth \Big (\frac{q_{i}-q_{j}}{2}\Big ). \end{aligned}$$

(4.17)

Similarly, the nonrelativistic top (3.10) comes from (3.9). The gauge transformation (4.11) holds on at the level of nonrelativistic models as well [39, 46]. That is

$$\begin{aligned} \begin{array}{c} \displaystyle { L(z)=\mathrm{tr}\Big (r_{12}(z)S_2(p,q)\Big )=g(z)L^{\mathrm{CM}}(z)g^{-1}(z). } \end{array} \end{aligned}$$

(4.18)

The residue of both parts of the latter relation provides explicit change of variables, or the nonrelativistic limit of (4.15):

$$\begin{aligned}&S_{ij}(p,q)=a_i(p,q)b_j(q),\quad b_j(q)=(-1)^{j}\sigma _{j}(q), \nonumber \\&a_i(p,q)=\frac{1}{N}\sum _{n=1}^{N}\frac{\left( p_n+(i-1)\nu \right) \left( e^{-(i-1){\bar{q}}_n}+(-1)^N \delta _{iN}e^{{{\bar{q}}}_n}\right) -N\nu (-\,1)^N \delta _{iN}e^{{{\bar{q}}}_n}}{\prod \nolimits _{k:k\ne n}(e^{-{{\bar{q}}}_n}-e^{-{{\bar{q}}}_k})}.\nonumber \\ \end{aligned}$$

(4.19)

The Poisson brackets $\{S_{ij}(p,q),S_{kl}(p,q)\}$ computed via the canonical structure (4.14) reproduce (3.36) with $c_1=N$, and the value of the Casimir functions is given by the powers of the Calogero–Moser–Sutherland coupling constant

$$\begin{aligned} \begin{array}{c} \displaystyle { \mathrm{tr}(S^k)=\nu ^k. } \end{array} \end{aligned}$$

(4.20)

Thus, the Calogero–Moser–Sutherland model is gauge equivalent to the nonrelativistic top with special values of the Casimir functions corresponding to the coadjoint orbit (of $\mathrm{GL}_N$ group) of minimal dimension. Apart from the gauge transformation, we obtain explicit change of variables (in fact, a canonical map) $(p_i,q_j)\rightarrow (a_i(p,q),b_i(q))$, where $b_i$ are elementary symmetric functions. These variables are known in the quantum Calogero–Moser–Sutherland model [47, 48].