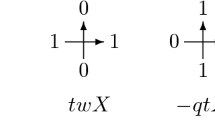Abstract
In this paper, we study transition matrices of PBW bases of the nilpotent subalgebra of quantum superalgebras associated with all possible Dynkin diagrams of type A and B in the case of rank 2 and 3, and examine relationships with three-dimensional (3D) integrability. We obtain new solutions to the Zamolodchikov tetrahedron equation via type A and the 3D reflection equation via type B, where the latter equation was proposed by Isaev and Kulish as a 3D analog of the reflection equation of Cherednik. As a by-product of our approach, the Bazhanov–Sergeev solution to the Zamolodchikov tetrahedron equation is characterized as the transition matrix for a particular case of type A, which clarifies an algebraic origin of it. Our work is inspired by the recent developments connecting transition matrices for quantum non-super algebras with intertwiners of irreducible representations of quantum coordinate rings. We also discuss the crystal limit of transition matrices, which gives a super analog of transition maps of Lusztig’s parametrizations of the canonical basis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 1.1 Background
The Zamolodchikov tetrahedron equation [46] is a three dimensional analog of the Yang–Baxter equation [1], where the latter equation serves as a cornerstone of integrable systems in two dimensions in terms of its physical applications and deeply understood algebraic aspects. Along the same line as the Yang–Baxter equation, the tetrahedron equation gives the condition of factorizations for a four-body scattering of strings, and also gives a sufficient condition for the commutativity of the associated layer-to-layer transfer matrix. Solutions to the Yang–Baxter equation are called R matrices, and it is well known that we can systematically construct R matrices through the Drinfeld-Jimbo quantum algebras [11, 19], but unlike the Yang–Baxter equation, there is no known way to obtain non-trivial solutions to the tetrahedron equation as such a systematic procedure.
Historically, one important family of solutions to the tetrahedron equation is the N-state Zamolodchikov model, which was first proposed by [47] for \(N=2\) as the first non-trivial solution and later generalized by [2, 41] for general N. From an algebraic point of view, it is known that the solutions are related to the R matrices associated with the cyclic representations of the affine quantum algebra \(U_q(A_{n-1}^{(1)})\) at roots of unity. For the history of the solutions, see the introduction of [4] and references therein.
In this paper, we focus on infinite-dimensional solutions on the Fock spaces, which are essentially different solutions from the N-state Zamolodchikov model. Our starting point is the known solution \((\mathscr {R},\mathscr {L})\) to the following tetrahedron equations:
where indices represent the tensor components on which each matrix acts non-trivially. The matrix elements of \(\mathscr {R}\in \mathrm {End}(F\otimes F\otimes F)\) and \(\mathscr {L}\in \mathrm {End}(V\otimes V\otimes F)\) will be specified in (3.2) and (3.6), where F and V are the bosonic and Fermionic Fock spaces, respectively. We call them the 3D R and 3D L.
The 3D R was first derived [21] as the intertwiner of the irreducible representations of the quantum coordinate ring \(A_q(A_2)\), where the associated tetrahedron equation (1.1) holds as the identity of the intertwiner of the irreducible representations of the quantum coordinate ring \(A_q(A_3)\) [36]. The 3D R was also independently discovered by the seminal paper [4] as explained later, and they are identified by [25]. As an amazing connection, the 3D R also gives the transition matrix of the PBW bases of the nilpotent subalgebra of the quantum algebra \(U_q^{+}(A_2)\). It is first observed by Sergeev [39], and later systematically generalized as the Kuniba–Okado–Yamada theorem [28], which states that intertwiners of irreducible representations of quantum coordinate rings agree with transition matrices of PBW bases of the nilpotent subalgebra of quantum algebras for all finite-dimensional simple Lie algebras. See also [37, 43] which proved and sophisticated this theorem from a different point of view.
On the other hand, the 3D L was obtained by a heuristic quantization of the solution to the local Yang–Baxter equation [33] by Bazhanov–Sergeev [4]. They made an ansatz that the 3D L gives an operator-valued solution to the local Yang–Baxter equation, which is equivalent to the tetrahedron equation (1.2), and solved (1.2) for \(\mathscr {R}\). It also gives an alternative derivation of the 3D R. As a remarkable result related to the 3D L, it is known that the layer-to-layer transfer matrix of size \(m\times n\) associated with the 3D L gives the spectral duality between different row-to-row transfer matrices: \(\mathfrak {sl}(m)\) spin chain of system size n and \(\mathfrak {sl}(n)\) spin chain of system size m [4]. The duality is called the rank-size duality, and later, also appeared in the context of the five-dimensional gauge theory [35].
Of course, the 3D R and 3D L are essentially three-dimensional objects, but it is known that there is an interesting connection to the R matrix. More concretely, there is a systematic way to reduce one solution to the tetrahedron equation to an infinite family of R matrices. By applying this procedure to the 3D R and 3D L, we can obtain explicit formulae of the R matrices associated with some affine quantum algebras [27]. By n-concatenation of the 3D R, we obtain the R matrices associated with the symmetric tensor representations of \(U_q(A_{n-1}^{(1)})\), and the Fock representations of \(U_q(D_{n+1}^{(2)})\), \(U_q(A_{2n}^{(2)})\) and \(U_q(C_{n}^{(1)})\). Similarly, by n-concatenation of the 3D L, we obtain the R matrices associated with the fundamental representations of \(U_q(A_{n-1}^{(1)})\), and the spin representations of \(U_q(D_{n+1}^{(2)})\), \(U_q(B_{n}^{(1)})\) and \(U_q(D_{n}^{(1)})\). Moreover, by mixing uses of some 3D R and 3D L, we also obtain the R matrices associated with the generalized quantum groups [27]. They are called matrix product solutions to the Yang–Baxter equation. For more details, see [27] and references therein.
1.2 1.2 Motivation
One of our motivations for this paper is why the 3D R and 3D L lead to such similar results, although they have totally different origins. Actually, the 3D L has been derived again in several ways after [4]. First, [25] identified the tetrahedron equation (1.2) as the set of intertwining relations of the irreducible representations of \(A_q(A_2)\), that is, the tetrahedron equation (1.2) is obtained by arranging the intertwining relations of the 3D R into the matrix form (1.2), simply by introducing the matrix \(\mathscr {L}\). See Remark 3.2 for more details of this observation. This procedure also works for the intertwining relation for \(A_q(C_2)\) [30] and even for \(A_q(G_2)\) [24], and leads to matrix product solutions to the reflection equation of Cherednik [8] and the \(G_2\) reflection equation. See Remark 3.4 for more details for type C. These are interesting connections but quite mysterious. Also, although this connection for type A gives a derivation of the tetrahedron equation (1.2), algebraic origins of the 3D L has been still unclear.
On the one hand, Sergeev gave a parallel derivation [40] for the 3D R and 3D L by using the methods called quantum geometry [3]. At first glance, it seems that they consider something like a super analog of the irreducible representations of the quantum coordinate ring \(A_q(A_2)\). See for example (56)–(59) of [40]. However, to verify it is highly non-trivial because there is no theory about irreducible representations of quantum super coordinate rings like Soibelman’s theory for the non-super case [42]. Then, the result by [40] can not be understood in terms of usual languages of quantum algebras, at least straightforwardly.
We also remark that the classical limit of the tetrahedron equation (1.2) is recently derived in relation to non-trivial transformations of a plabic network, which can be interpreted as cluster mutations [13].
1.3 1.3 Main achievements
In this paper, we give a derivation for the 3D L in terms of the PBW bases of the nilpotent subalgebra of the quantum superalgebra [45] associated with the Dynkin diagram 
. We identify the 3D L with the transition matrix of them, which clarifies a completely parallel origin for the 3D L to the 3D R. This result is just a special case of our investigations: we study transition matrices associated with all Dynkin diagrams of type A in the case of rank 2, which become parts of the tetrahedron equations. Actually, we obtain a matrix \(\mathscr {N}\in \mathrm {End}(V\otimes F\otimes V)\) by considering the case of 
, which is new and different from the 3D R and 3D L. The matrix elements of \(\mathscr {N}\) will be specified in (4.51), and we call \(\mathscr {N}\) the 3D N.
By considering the transition matrix for the case of rank 3 and attributing it to a composition of transition matrices of rank 2 in two ways, we obtain several solutions to the tetrahedron equation which the 3D R, L, and N satisfy. We study the transition matrices associated with all Dynkin diagrams of type A in the case of rank 3, where 
and 
can be easily attribnuted to 
and 
, respectively, so we consider 6 Dynkin diagrams in total. The cases for 
and 
reproduce the known tetrahedron equations (1.1) and (1.2), respectively. For the case of 
, we obtain the following equation:
This suggests the 3D N gives a new solution to the tetrahedron equation. The remaining 3 cases also give the tetrahedron like equations, but actually they are the tetrahedron equations up to sign factors. Further investigations should be done as to whether we can attribute them to the usual tetrahedron equations. See Remark 3.3 related to this issue.
We can generalize these results to the case of type B. For type B, the associated equation is the 3D reflection equation [18], which is proposed by Isaev and Kulish as a three-dimensional analog of the reflection equation of Cherednik [8]. They also call the equation the tetrahedron reflection equation. Actually, they obtained the equation as the associativity condition for the 3D boundary Zamolodchikov algebra [18, (9)], just as the tetrahedron equation is obtained as the associativity condition for the 3D Zamolodchikov algebra [46]. Physically, the 3D reflection equation gives the condition for factorizations for a three-body scattering of strings with boundary reflections, along the same line as the tetrahedron equation.
Essentially, there are only two known non-trivial solutions to the 3D reflection equation [25, 26]. Here, we present one of the equations:
where \(\mathscr {R}\) is the 3D R and the matrix elements of \(\mathscr {J}\in \mathrm {End}(F\otimes F\otimes F\otimes F)\) will be specified in (3.21). We call \(\mathscr {J}\) the 3D J. The 3D J was first derived as the intertwiner of the irreducible representations of the quantum coordinate ring \(A_q(B_2)\), where the associated 3D reflection equation (1.4) holds as the identity of the intertwiner of the irreducible representations of the quantum coordinate ring \(A_q(B_3)\) [26]. As an immediate corollary of the Kuniba–Okado–Yamada theorem, we find the 3D J also gives the transition matrix of the PBW bases of the nilpotent subalgebra of the quantum algebra \(U_q^{+}(B_2)\). Our result for type B gives new solutions to the 3D reflection equation, which generalizes the solution (1.4) to the family of solutions (5.186). Actually, we introduce three analogs of the 3D J; we call them the 3D X, Y and Z. We emphasize that our result also gives some explicit formula of transition matrices for type B.
Our idea comes from trying to interpret Sergeev’s result [40] on the side of PBW bases through the Kuniba–Okado–Yamada theorem although the theorem has not been established for the super case. Note however our proofs do not need any result for quantum coordinate rings. The derivation of the tetrahedron and 3D reflection equation is done only using higher-order relations for quantum superalgebras.
Finally, we discuss the behavior of transition matrices at \(q=0\), which is known as the crystal limit [22]. In the crystal limit, transition matrices of PBW bases give so-called transition maps of Lusztig’s parametrizations of the canonical basis because PBW bases correspond to the canonical basis in that case [5, 32]. Then, if we take the limit for super cases, it is expected we can obtain a super analog of transition maps. In this paper, we show that we can take normalizations for transition matrices so that such non-trivial limits exist, and obtain explicit formulae for almost all cases. In contrast to non-super cases, non-trivial elements of transition matrices take not only 0, 1 but also \(-1\) in the crystal limit, and they define non-trivial bijections on mixed spaces of \(\{0,1\}\) and \(\mathbb {Z}_{\ge 0}\).
1.4 1.4 Outline
The ourline of this paper is as follows. In Sect. 2, we briefly review basic facts about finite-dimensional Lie superalgebras of type A and B. Then, we introduce quantum superalgebras and their PBW theorem by [45]. In Sect. 3, we summarize the 3D operators which give solutions to the tetrahedron and 3D reflection equations. Sections 4 and 5 are main parts of this paper. They can be read almost independently. In Sect. 4, we consider transition matrices of PBW bases of the nilpotent subalgebra of quantum superalgebras associated with all possible Dynkin diagrams of type A in the case of rank 2 and 3, and we obtain several solutions to the tetrahedron equation. In Sect. 4.1, we introduce some notations to briefly describe the PBW bases of rank 3 and higher-order relations for them, which are used in Sect. 4.3. In Sects. 4.2 and 4.3, we study transition matrices of rank 2 and 3, respectively. Section 5 is type B version of Sect. 4, where the associated equation is the 3D reflection equaion. Finally, in Sect. 6, we discuss the crystal limit of transition matrices. “Appendix A” is devoted to the proof of Theorem 5.12. In “Appendix B”, we derive recurrence equations for the 3D Z, which is the transition matrix associated with 
.
2 Quantum Superalgebras of Type A and B
2.1 Root data of finite-dimensional Lie superalgebras
In this paper, we consider quantum superalgebras associated with finite-dimensional Lie superalgebras \(\mathfrak {sl}(m|n)\) and \(\mathfrak {osp}(2m+1|2n)\) [7, 12, 20, 49]. Here, m, n are non-negative integers and we assume \(m+n\ge 2\). We call \(\mathfrak {sl}(m|n)\) type A and \(\mathfrak {osp}(2m+1|2n)\) type B, respectively. Let \(\mathfrak {g}(m|n)\) denote \(\mathfrak {sl}(m|n)\) or \(\mathfrak {osp}(2m+1|2n)\). If we set \(n=0\), \(\mathfrak {g}(m)=\mathfrak {g}(m|0)\) is reduced to finite-dimensional simple Lie algebras. To avoid confusion, we also call the finite-dimensional simple Lie algebras the finite-dimensional simple non-super Lie algebras. In this case, we simply write \(\mathfrak {sl}(m|0)\) and \(\mathfrak {osp}(2m+1|0)\) by \(\mathfrak {sl}(m)\) and \(\mathfrak {so}(2m+1)\), respectively. In this section, we describe root data of \(\mathfrak {g}(m|n)\). Here, we use a similar setup to [44].
We set \(N=m+n\). Let \(\mathscr {E}(m|n)_{\mathbb {R}}\) be the N-dimensional real vector space with a non-degenerate symmetric bilinear form \((\cdot ,\cdot ):\mathscr {E}(m|n)_{\mathbb {R}}\times \mathscr {E}(m|n)_{\mathbb {R}}\rightarrow \mathbb {R}\). We use \(\epsilon _i{\ }(i=1,\ldots ,m)\) and \(\delta _i{\ }(i=1,\ldots ,n)\) as a basis of \(\mathscr {E}(m|n)_{\mathbb {R}}\) with a non-degenerate symmetric bilinear form given by
where \(\theta =0,1\) which is specified above Example 2.1, and \(\delta _{i,j}\) is the Kronecker delta. Let \(\bar{\epsilon }(m|n)=(\bar{\epsilon }_1,\ldots ,\bar{\epsilon }_{N})\) denote an ordered basis of \(\mathscr {E}(m|n)_{\mathbb {R}}\) which is a permutation of \(\epsilon _i{\ }(i=1,\ldots ,m)\) and \(\delta _i{\ }(i=1,\ldots ,n)\). Without loss of generality, we only consider cases when \(\epsilon _{i}\) appears before \(\epsilon _{i+1}\) and \(\delta _{i}\) appears before \(\delta _{i+1}\) in \(\bar{\epsilon }(m|n)\) for all i, which is called admissible.
Let \(\Phi \) be the set of roots of \(\mathfrak {g}(m|n)\) and \(\Pi =\{\alpha _1,\ldots ,\alpha _{r}\}\) be the set of simple roots of \(\mathfrak {g}(m|n)\), where r is the rank of \(\mathfrak {g}(m|n)\). Here, \(r=N-1\) for \(\mathfrak {sl}(m|n)\) and \(r=N\) for \(\mathfrak {osp}(2m+1|2n)\). We write the set of labels by \(I=\{1,\ldots ,r\}\). We call \(\Phi \) and \(\Pi \) the root system and fundamental system of \(\mathfrak {g}(m|n)\), respectively. When \(\bar{\epsilon }(m|n)\) is given, the fundamental system \(\Pi \) is realized as Table 1. We write the positve and negative part of the root lattice of \(\mathfrak {g}(m|n)\) by \(Q^{\pm }=\pm \sum _{i=1}^{r}\mathbb {Z}_{\ge 0}\alpha _{i}\backslash \{0\}\) and the positive and negative part of the root system by \(\Phi ^{\pm }=\Phi \cap Q^{\pm }\), which will be identified in Table 2 for each case. We also set the weight lattice of \(\mathfrak {g}(m|n)\) by \(\mathscr {E}(m|n)_{\mathbb {Z}}=\sum _{i=1}^{m}\mathbb {Z}\epsilon _{i}\oplus \sum _{i=1}^{n}\mathbb {Z}\delta _{i}\).
For \(\lambda =\sum _{i=1}^{m}a_{i}\epsilon _{i}+\sum _{i=1}^{n}b_{i}\delta _{i}\in \mathscr {E}(m|n)_{\mathbb {Z}}\), we define the parity \(p:\mathscr {E}(m|n)_{\mathbb {Z}}\rightarrow \{0,1\}\) of \(\lambda \) as \(p(\lambda )=\sum _{i=1}^{n}b_i{\ }(\mathrm {mod}{\ }2)\), and this induces the parity of elements of \(\Phi \) via its realization. We call \(\lambda \in \mathscr {E}(m|n)_{\mathbb {Z}}\) is even if \(p(\lambda )=0\) and odd if \(p(\lambda )=1\). We set the set of indices of odd simple roots by \(\tau \subset I\). Then, the positive part of the root system \(\Phi ^{+}\) is given in Table 2. We set the set of reduced roots by \(\tilde{\Phi }=\{\alpha \in \Phi \mid \alpha /2\notin \Phi \}\) and the positive and negative part of it by \(\tilde{\Phi }^{\pm }=\tilde{\Phi }\cap Q^{\pm }\).
For \(\alpha \in \Phi \), if \(p(\alpha )=1\) and \((\alpha ,\alpha )=0\), we call \(\alpha \) the isotropic odd root. On the one hand, if \(p(\alpha )=1\) and \((\alpha ,\alpha )\ne 0\), we call \(\alpha \) the anisotropic odd root. The set of even roots, isotropic odd roots and anisotropic odd roots are denoted by \(\Phi _{\mathrm {even}}\), \(\Phi _{\mathrm {iso}}\) and \(\Phi _{\mathrm {aniso}}\subset \Phi \), respectively. Also, the set of the positive and negative part of even roots, isotropic odd roots and anisotropic odd roots are denoted by \(\Phi ^{\pm }_{\mathrm {even}}\), \(\Phi ^{\pm }_{\mathrm {iso}}\) and \(\Phi ^{\pm }_{\mathrm {aniso}}\subset \Phi ^{\pm }\), respectively. We also set the reduced version of them by \(\tilde{\Phi }^{\pm }_{\mathrm {even}}=\Phi ^{\pm }_{\mathrm {even}}\cap \tilde{\Phi }\), \(\tilde{\Phi }^{\pm }_{\mathrm {iso}}=\Phi ^{\pm }_{\mathrm {iso}}\) and \(\tilde{\Phi }^{\pm }_{\mathrm {aniso}}=\Phi ^{\pm }_{\mathrm {aniso}}\).
2.2 Cartan matrices, Dynkin diagrams and Weyl groups
Let \((a_{ij})_{i,j\in I}\), \((d_{i})_{i\in I}\) be the Cartan matrix and the symmetrizing matrix of \(\mathfrak {g}(m|n)\). Here, \(d_i\) is given by \((\alpha _i,\alpha _i)/2\) for \(\alpha _{i}\in \tilde{\Phi }^{+}_{\mathrm {even}}\cup \tilde{\Phi }^{+}_{\mathrm {aniso}}\) and 1 for \(\alpha _{i}\in \tilde{\Phi }^{+}_{\mathrm {iso}}\). Also, \(a_{ij}\) is given by \(a_{ij}=(\alpha _i,\alpha _j)/d_i\). We often write \(A=(a_{ij})\) and \(D=\mathrm {diag}(d_1,\ldots ,d_r)\), and the symmetrized Catran matrix by \(DA=(d_{i}a_{ij})\). We call the pair (A, p) the Cartan data of \(\mathfrak {g}(m|n)\). For later use, we also define \(d_{\alpha }\) by \((\alpha ,\alpha )/2\) for \(\alpha \in \Phi _{\mathrm {even}}\cup \Phi _{\mathrm {aniso}}\) and 1 for \(\alpha \in \Phi _{\mathrm {iso}}\). Let \({\mathfrak {h}}=\sum _{i=1}^{r}\mathbb {C}h_i\) be the Cartan subalgebra of \(\mathfrak {g}(m|n)\), where \(\{h_i\}_{i\in I}\) is chosen as \(\alpha _j(h_i)=a_{ij}\). We call \(\{h_i\}_{i\in I}\) the set of simple coroots of \(\mathfrak {g}(m|n)\).
The Cartan data can be diagrammatically represented by the Dynkin diagram. The Dynkin diagram associated with (A, p) is defined as follows. First, we set r dots and decorate the i-th dot by 
for \(\alpha _i\in \tilde{\Phi }^{+}_{\mathrm {even}}\), 
for \(\alpha _i\in \tilde{\Phi }^{+}_{\mathrm {iso}}\) and 
for \(\alpha _i\in \tilde{\Phi }^{+}_{\mathrm {aniso}}\), respectively. We also use 
representing 
or 
. Then, for every pair of different numbers (i, j), we connect them with \(|a_{ij}|\) lines if \(a_{ij}\ne 0\). Also, if \(|a_{ij}|\ge 2\), these lines are equipped with an arrow pointing from the j-th dot to the i-th dot. All possible Dynkin diagrams of \(\mathfrak {g}(m|n)\) are given in Table 3, where \(\bar{\epsilon }_{N}=\epsilon _{m}\) for the first Dynkin diagram of \(\mathfrak {osp}(2m+1|2n)\) and \(\bar{\epsilon }_{N}=\delta _{n}\) for the second Dynkin diagram of \(\mathfrak {osp}(2m+1|2n)\).
Here, we specify the value of \(\theta =0,1\) in (2.1). If \(\min \{(\alpha _{i},\alpha _{j})\mid i\ne j\}<0\) for both values of \(\theta \), we choose \(\theta \) so that \((\bar{\epsilon }_1,\bar{\epsilon }_1)=1\) holds. If not, we choose \(\theta \) so that \(\min \{(\alpha _{i},\alpha _{j})\mid i\ne j\}<0\) is satisfied.
Example 2.1
For the case 
, we have \(DA=\begin{pmatrix}0&{}-1&{}0\\ -1&{}2&{}-1\\ 0&{}-1&{}1\end{pmatrix}\) for \(\theta =0\) and \(DA=\begin{pmatrix}0&{}1&{}0\\ 1&{}-2&{}1\\ 0&{}1&{}-1\end{pmatrix}\) for \(\theta =1\). We then choose \(\theta =0\) for this case.
For more examples, see Sects. 4 and 5.
Let \(W(\mathfrak {g}(m|n))\) be the Weyl group of \(\mathfrak {g}(m|n)\) which is generated by reflections \(s_{\alpha }{\ }(\alpha \in \Phi _{\mathrm {even}}\cup \Phi _{\mathrm {aniso}})\) which are associated with even and anisotropic roots. The action of them is given by
Under actions of \(W(\mathfrak {g}(m|n))\), the root system is invariant. The image of the fundamental system is a different one, but it gives the same Cartan data. For the finite-dimensional simple non-super Lie algebras, it is known that all possible choice of the fundamental system is conjugate via the Weyl group actions [16, §10.3. Theorem]. Then, the Dynkin diagrams one-to-one correspond to the finite-dimensional simple non-super Lie algebras. For non-super case, relations of \(W(\mathfrak {g}(m))\) are given by \(s_i^2=1\), \((s_is_j)^{m_{ij}}=1{\ }(i\ne j)\) where \(m_{ij}=2,3,4\) for \(a_{ij}a_{ji}=0,1,2\), respectively. Here, we write \(s_{i}=s_{\alpha _i}\).
For general finite-dimensional Lie superalgebras, however, the fundamental systems are not always conjugate via the Weyl group actions. It is known that by adding some elements and extending the Weyl group \(W(\mathfrak {g}(m|n))\), all fundamental systems become conjugate [31, Appendix II. Theorem]. The elements are called odd reflections, and we call the extended Weyl group the Weyl supergroup denoted by \(SW(\mathfrak {g}(m|n))\). Formally, odd reflections are reflections associated with odd roots, and the action of the elements of the Weyl supergroup is given by
where \(\alpha ,\beta \in \Phi \). Similar to usual reflections, the root system is invariant under actions of odd reflections, but the image of the fundamental system gives different Cartan data. Therefore, the Dynkin diagrams do not correspond to the finite-dimensional Lie superalgebras but rather their fundamental systems.
The standard choice of the fundamental system of \(\mathfrak {g}(m|n)\) is called distinguished, where the associated Dynkin diagrams have only one odd root. The realizations and the corresponding Dynkin diagrams are given in Table 4.
In this paper, we focus on the nilpotent subalgebra of quantum superalgebras, rather than the whole algebras. Since the nilpotent subalgebra depends on the choice of the fundamental system of \(\mathfrak {g}(m|n)\), in addition to the distinguished Dynkin diagrams, we also consider non-distinguished ones as given in Table 3.
2.3 Quantum superalgebras
Throughout this paper, we assume q is generic. We set \(q_i=q^{d_i}\) and \(v_{i}=q^{(\bar{\epsilon }_i,\bar{\epsilon }_i)}{\ }(i\in I)\). We use a variant of q-number and its factorial defined by
where \(k,m\in \mathbb {Z}_{\ge 0}\) and \(\pi =\pm 1\) [10]. We promise \([0]_{q,\pi }!=1\). For simplicity, we write \([k]_{q,1}=[k]_{q}\) and \([m]_{q,1}!=[m]_{q}!\) for \(\pi =1\). The quantum superalgebra \(U_q(\mathfrak {g}(m|n))\) associated with the Cartan data (A, p) is an associative algebra over \(\mathbb {C}\) generated by \(\{e_i,f_i,k_i=q_{i}^{h_i}\mid i\in I\}\) satisfying the following relations [6, 45]:
where we set \(e_{i}^{(\nu )}=e_{i}^{\nu }/[\nu ]_{q_{i},(-1)^{p(\alpha _{i})}}!\), \(f_{i}^{(\nu )}=f_{i}^{\nu }/[\nu ]_{q_{i},(-1)^{p(\alpha _{i})}}!\), and so-called additional relations for the case when the associated Dynkin diagram has the subdiagram 
or 
or 
:
where \(\phi _i,\varphi _i\) are given by
For reader’s convenience, we list (2.7) for each case which appears in this paper:
-
(1)
\(|a_{ij}|=1\) and \(\alpha _i\in \tilde{\Phi }^{+}_{\mathrm {even}}\):
$$\begin{aligned} e_{i}^{2}e_{j}-(q+q^{-1})e_{i}e_{j}e_{i}+e_{j}e_{i}^2=0 , \end{aligned}$$(2.13) -
(2)
\(|a_{ij}|=2\) and \(\alpha _i\in \tilde{\Phi }^{+}_{\mathrm {even}}\):
$$\begin{aligned} e_{i}^3e_{j}-(q+1+q^{-1})e_{i}^2e_{j}e_{i}+(q+1+q^{-1})e_{i}e_{j}e_{i}^2-e_{j}e_{i}^3=0 , \end{aligned}$$(2.14) -
(3)
\(|a_{ij}|=2\) and \(\alpha _i\in \tilde{\Phi }^{+}_{\mathrm {aniso}}\), \(\alpha _j\in \tilde{\Phi }^{+}_{\mathrm {even}}\):
$$\begin{aligned} e_{i}^3e_{j}+(1-q-q^{-1})e_{i}^2e_{j}e_{i}+(1-q-q^{-1})e_{i}e_{j}e_{i}^2+e_{j}e_{i}^3=0 , \end{aligned}$$(2.15) -
(4)
\(|a_{ij}|=2\) and \(\alpha _i\in \tilde{\Phi }^{+}_{\mathrm {aniso}}\), \(\alpha _j\in \tilde{\Phi }^{+}_{\mathrm {iso}}\):
$$\begin{aligned} e_{i}^3e_{j}-(1-q-q^{-1})e_{i}^2e_{j}e_{i}+(1-q-q^{-1})e_{i}e_{j}e_{i}^2-e_{j}e_{i}^3=0 , \end{aligned}$$(2.16)
where we always assume \(i\ne j\).
In this paper, we focus on \(U_q^{+}(\mathfrak {g}(m|n))\) which is the nilpotent subalgebra of \(U_q(\mathfrak {g}(m|n))\) generated by \(\{e_{i}\}_{i\in I}\). We represent \(U_q^{+}(\mathfrak {g}(m|n))\) by the Dynkin diagram associated with the Cartan data (A, p). We have the root space decomposition of \(U_q^{+}(\mathfrak {g}(m|n))=\bigoplus _{\alpha \in Q^{+}}U_q^{+}(\mathfrak {g}(m|n))_{\alpha }\) where each root space are given by \(U_q^{+}(\mathfrak {g}(m|n))_{\alpha }=\{g\mid k_ig=q_{i}^{\alpha (h_{i})}gk_{i}{\ }(i\in I)\}\). For \(x\in U_q^{+}(\mathfrak {g}(m|n))_{\alpha },{\ }y\in U_q^{+}(\mathfrak {g}(m|n))_{\beta }\), we define the q-commutator \([\cdot ,\cdot ]_{q}\) by
and for simplicity we write \([\cdot ,\cdot ]_{1}=[\cdot ,\cdot ]\) for \(q=1\). By using the q-commutator, the Serre relation (2.7) and the additional relation (2.10) are simply written as follows:
For later use, let \(\chi :U_q(\mathfrak {g}(m|n))\rightarrow U_q(\mathfrak {g}(m|n))\) be the anti-algebra automorphism given by
Then, \(\chi \) also gives the anti-algebra automorphism on \(U_q^{+}(\mathfrak {g}(m|n))\).
2.4 PBW bases of the nilpotent subalgebra of quantum superalgebras
We begin with non-super cases. In that case, we have \(\Phi ^{+}=\Phi ^{+}_{\mathrm {even}}\). Let \(w_0\) be the longest element of \(W(\mathfrak {g}(m))\). When a reduced expression of \(w_0=s_{i_1}\cdots s_{i_{l}}\) is given, we set \(\beta _{t}{\ }(t=1,\ldots ,l)\) by
where we set \(l=|\Phi ^{+}|\). Then, it is known that we have \(\beta _{t}\in \Phi ^{+}{\ }(t=1,\ldots ,l)\), \(\beta _{i}\ne \beta _{j}{\ }(i\ne j)\) and \(\Phi ^{+}=\{\beta _{t}\mid 1\le t\le l\}\) [17, P.25].
It is also known that there exists a quantum analog of this procedure. Let \(T_i:U_q(\mathfrak {g}(m))\rightarrow U_q(\mathfrak {g}(m)){\ }(i\in I)\) be the algebra automorphism given by
Here, \(T_i\) is known as the so-called Lusztig’s braid group action on \(U_q(\mathfrak {g}(m))\) [32]. Actually, it is known that \(\{T_i\}_{i\in I}\) satisfy the braid group relations. We set \(e_{\beta _{t}}{\ }(t=1,\ldots ,l)\) by
where \(\beta _{t}\) is given by (2.21). Then, it is known that we have \(e_{\beta _{t}}\in U_q^{+}(\mathfrak {g}(m))_{\beta _{t}}{\ }(t=1,\ldots ,l)\) and \(e_{\beta _{i}}\ne e_{\beta _{j}}{\ }(i\ne j)\). Also, it gives a PBW basis of \(U_q^{+}(\mathfrak {g}(m))\), which depends on the choice of reduced expressions of \(w_0\) [32]:
Theorem 2.2
For \(A=(a_1,\ldots ,a_{l})\in (\mathbb {Z}_{\ge 0})^{l}\), we set
where we normalize \(e_{\beta _{t}}^{(a_{t})}=e_{\beta _{t}}^{a_{t}}/[a_t]_{p_t}!\), \(p_t=q^{d_{\beta _{t}}}\). Then, \(\{E^{A}\mid A\in (\mathbb {Z}_{\ge 0})^{l}\}\) is a basis of \(U_q^{+}(\mathfrak {g}(m))\).
For super cases, it is known that there is a naive construction of a PBW basis without using some maps like the Lusztig’s braid group action [23, 45]. We note that a super analog of Lusztig’s braid group action was introduced in the context of the so-called Weyl groupoid [14, 15].
Let us explain the construction by [45]. We define two partial orders < on \(\tilde{\Phi }^{+}\) as follows. For \(\gamma =\sum _{i=1}^{r}c_i\alpha _i\in \tilde{\Phi }^{+}\), we define the integers \(\mathrm {ht}(\gamma ),g(\gamma ),c_{\gamma }\in \mathbb {N}\) by \(\mathrm {ht}(\gamma )=\sum _{i=1}^{r}c_i\), \(g(\gamma )=\min \{i\mid c_i\ne 0\}\) and \(c_{\gamma }=c_{g(\gamma )}\). Then, for \(\alpha ,\beta \in \tilde{\Phi }^{+}\), we set two partial orders \(O_1,O_2\) by
Note that \(O_1\) is the same order as [45]. By using them, we define quantum root vectors as follows:
Definition 2.3
For every \(\beta \in \tilde{\Phi }^{+}\), we define the elements \(e_{\beta }\in U_q^{+}(\mathfrak {g}(m|n))_{\beta }\) as follows:
-
(i)
If \(\beta =\alpha _{i}\), we set \(e_{\beta }=e_{i}\).
-
(ii)
If \(\beta =\alpha +\alpha _{i}\) where \(\alpha \in \tilde{\Phi }^{+}\) and \(g(\alpha )<i\), we define \(e_{\beta }\) depending on the partial order \(O_i\). We set \(e'_{\beta }=[e_{i},e_{\alpha }]_{q}\) for \(O_1\), and \(e'_{\beta }=[e_{\alpha },e_{i}]_{q}\) for \(O_2\). Then, we set \(e_{\beta }=e'_{\beta }/(q^{1/2}+q^{-1/2})\) for the case \(\mathfrak {g}(m|n)=\mathfrak {osp}(2m+1|2n)\), \(i=r\) and \(\alpha =\bar{\epsilon }_{j}{\ }(1\le j\le r-1)\). We set \(e_{\beta }=e'_{\beta }\) otherwise.
We note that the above normalization factor \(q^{1/2}+q^{-1/2}\) naturally appears from the Lusztig’s braid group action for non-super cases.
Then, the quantum root vectors give PBW bases of \(U_q^{+}(\mathfrak {g}(m|n))\):
Theorem 2.4
Let \(\beta _t{\ }(t=1,\ldots ,l)\) denote the reduced roots, which satisfy \(\beta _1<\cdots <\beta _{l}\) under the order \(O_i\). Here, \(l=|\tilde{\Phi }^{+}|\). For \(A=(a_1,\ldots ,a_{l})\) where \(a_{t}\in \mathbb {Z}_{\ge 0}\) for \(\beta _{t}\in \tilde{\Phi }^{+}_{\mathrm {even}}\cup \tilde{\Phi }^{+}_{\mathrm {aniso}}\) and \(a_{t}\in \{0,1\}\) for \(\beta _{t}\in \tilde{\Phi }^{+}_{\mathrm {iso}}\), we set
where we normalize \(e_{\beta _{t}}^{(a_{t})}=e_{\beta _{t}}^{a_{t}}/[a_t]_{p_t,(-1)^{p(\beta _{t})}}!\), \(p_t=q^{d_{\beta _{t}}}\). Then
is a basis of \(U_q^{+}(\mathfrak {g}(m|n))\).
Proof
We attribute the statement to [45]. First, we consider the case when the order is given by \(O_1\). In [45], the order among the elements of \(\tilde{\Phi }^{+}\) is the same as \(O_1\), but the quantum root vectors are defined by \(e^{\mathrm {Yam}}_{\beta }=[e_{\alpha },e_{i}]_q\) instead of \(e_{\beta }=[e_{i},e_{\alpha }]_q\) as Definition 2.3. However, \(e_{\beta }\) and \(e^{\mathrm {Yam}}_{\beta }\) satisfy the following simple relation:
Then, the only differences between our construction and [45] are overall factors and its q-dependence. Since the relations of \(U_q(\mathfrak {g}(m|n))\) are invariant under \(q\rightarrow q^{-1}\), by the Proposition 10.4.1 of [45], we find that (2.30) gives a PBS basis of \(U_{q^{-1}}^{+}(\mathfrak {g}(m|n))\). Then, under the order \(O_1\), (2.30) gives a PBW basis of \(U_q^{+}(\mathfrak {g}(m|n))\).
The case when the order is given by \(O_2\) is attributed to the case of \(O_1\). Actually, \(E_{2}^{A^{\mathrm {op}}}=\chi (E_{1}^{A})\) holds for every A, where \(A^{\mathrm {op}}\) is the reverse order of A. This shows (2.30) under the order \(O_2\) gives a PBW basis of \(U_q^{+}(\mathfrak {g}(m|n))\) because \(\chi \) is an automorphism on \(U_q^{+}(\mathfrak {g}(m|n))\). \(\square \)
Remark 2.5
The construction by [45] can be considered as a natural analog of one of Theorem 2.2 as follows. For non-super cases, we call an order < among the elements of \(\Phi ^{+}\) normal (or convex) if, for \(\alpha \in \Phi ^{+}\) which is written by \(\alpha =\beta +\gamma {\ }(\beta ,\gamma \in \Phi ^{+})\), the order among \(\alpha ,\beta ,\gamma \) satisfies \(\beta<\alpha <\gamma \) or \(\gamma<\alpha <\beta \). Then, it is known that there exists a one-to-one correspondence between orders induced by reduced expressions of \(w_0\) like (2.21) and normal orders [50, §3 Proposition 2]. The normal order can be defined in a similar way for super cases, and the orders (2.27) and (2.28) actually satisfy the condition of the normal order.
Let \(\gamma ^{A}_{B}\) and \(\tilde{\gamma }^{A}_{B}\) be the transition matrices given by
where \(X^{\mathrm {op}}=(x_l,\ldots ,x_1)\) is the reverse order of \(X=(x_1,\ldots ,x_l)\). They are one of the main objects of this paper. By using \(E_2^{X^{\mathrm {op}}}=\chi (E_1^{X})\), we obtain the following relation:
We then only consider \(\gamma _{B}^{A}\) below.
2.5 Technical lemmas for higher-order relations
In this section, we introduce some technical lemma used to prove higher-order relations in the later sections. First, the q-commutator enjoy the following Jacobi like identity [45, (4.4.2)].
Lemma 2.6
For \(x\in U_q^{+}(\mathfrak {g}(m|n))_{\alpha },{\ }y\in U_q^{+}(\mathfrak {g}(m|n))_{\beta },{\ }z\in U_q^{+}(\mathfrak {g}(m|n))_{\gamma }\), we have
Proof
By writing down the definitions, we get
We then obtain the desired results. \(\square \)
Corollary 2.7
We set \(x\in U_q^{+}(\mathfrak {g}(m|n))_{\alpha },{\ }y\in U_q^{+}(\mathfrak {g}(m|n))_{\beta },{\ }z\in U_q^{+}(\mathfrak {g}(m|n))_{\gamma }\).
-
(1)
If \([x,z]_q=0\), we have \([[x,y]_{q},z]_{q}=[x,[y,z]_{q}]_{q}\).
-
(2)
If \([y,z]=0\) and \((\beta ,\gamma )=0\), we have \([[x,y]_{q},z]_{q}=(-1)^{p(\beta )p(\gamma )}[[x,z]_{q},y]_{q}\).
By using Corollary 2.7(2) for \(y=z=e_{i}{\ }(\alpha _i\in \tilde{\Phi }^{+}_{\mathrm {iso}})\), we obtain \([[x,e_{i}]_{q},e_{i}]_{q}=0\). This suggests the Serre relation (2.18) actually holds even when \(\alpha _{i}\in \tilde{\Phi }^{+}_{\mathrm {iso}}\):
Corollary 2.8
We set \(e_{i},e_{j}\) satisfying \(a_{ij}\ne 0\) and \(i\ne j\). Then, we have
We also use the following relations for quantum root vectors. Lemma 2.9 is given in Lemma 5.2.1.(iii) and Remark 5.2.2.(i) of [45].
Lemma 2.9
We consider the quantum root vectors \(e_{\alpha }\) under the order \(O_1\).
-
(1)
For \(\alpha \in \tilde{\Phi }^{+}_{\mathrm {iso}}\), we have \(e_{\alpha }^{2}=0\).
-
(2)
Let \(\alpha \in \tilde{\Phi }^{+}\) satisfy \(c_{\alpha }=1\), where \(c_{\alpha }\) is given by the above of (2.27). Take \(\alpha _{i}\) satisfying \(g(\alpha )<i\) and \(\alpha +\alpha _{i}\notin \tilde{\Phi }^{+}\). We then have
$$\begin{aligned}{}[e_{\alpha },e_{i}]_{q}=0 . \end{aligned}$$(2.39)
A graphical representation of the tetrahedron equation
3 Tetrahedron Equation and 3D Reflection Equation
3.1 Tetrahedron equation
In this section, we summarize solutions to the tetrahedron and 3D reflection equation, which are related to transition matrices of PBW bases of the nilpotent subalgebra of quantum non-super algebras. For the history of them, see Sect. 1. Here, we consider the tetrahedron equation [46], which is a three dimensional analog of the Yang–Baxter equation [1]. The equation is defined on the tensor product of six linear spaces, and pictorially represented as Fig. 1, where \(V_i\) are some linear spaces, specified below.
In this paper, we focus on infinite-dimensional solutions on the Fock spaces. Let \(F=\bigoplus _{m=0,1,2,\ldots }\mathbb {C}|m\rangle \) be the bosonic Fock space. We set \(\mathscr {R}(q)\in \mathrm {End}(F\otimes F\otimes F)\) [21]Footnote 1 by
where we use \(\delta _{x}^{y}=\delta _{x,y}\) and the q-factorial and q-binomial:
Summations in (3.1) are actually finite due to \(\delta _{i+j}^{a+b}\delta _{j+k}^{b+c}\) in (3.2). This is also the same for other 3D operators we will introduce later. For simplicity, we also use the abbreviated notation \(\mathscr {R}=\mathscr {R}(q)\). Then, the matrix \(\mathscr {R}\) satisfies the following tetrahedron equation without a spectral parameter:
where indices represent the tensor components on which each matrix acts non-trivially. We simply call \(\mathscr {R}\) the 3D R. The 3D R gives the transition matrix of the PBW bases of the nilpotent subalgebra of the quantum algebra \(U_q^{+}(\mathfrak {sl}(3))\) associated with the Dynkin diagram 
. See Theorem 4.3 for a more detailed statement.
On the one hand, it is known that there is another solution on the Fock spaces [4]. Let \(V=\bigoplus _{m=0,1}\mathbb {C}u_m\) be the fermionic Fock space. We set \(\mathscr {L}(q)\in \mathrm {End}(V\otimes V\otimes F)\) by
where \(\mathscr {L}(q)_{i,j,k}^{a,b,c}=0\) other than (3.6). For simplicity, we also use the abbreviated notation \(\mathscr {L}=\mathscr {L}(q)\). The matrix \(\mathscr {L}\) together with the 3D R satisfies the following tetrahedron equation [4]:
We simply call \(\mathscr {L}\) the 3D L. Although the original tetrahedron equation obtained in [4] involves some parameters, the above equation (3.7) is equivalent to it because they are actually cancelled out as remarked in [4]. Actually, our 3D L concides with the original one up to a gauge transformation by some diagonal matrix.
Unlike the 3D R, the 3D L has lacked an algebraic origin in terms of established quantum algebras although they exhibit quite parallel results for their reduction to matrix product solutions to the Yang–Baxter equation as we explained in Sect. 1. In Theorem 4.4, we will derive the 3D L as the transition matrix of the PBW bases of the nilpotent subalgebra of the quantum superalgebra \(U_q^{+}(\mathfrak {sl}(2|1))\) associated with the Dynkin diagram 
, which clarifies a parallel origin for the 3D L to the 3D R.
As a relation for them, the following lemma is used for the proof of Theorem 4.4:
Lemma 3.1
For later use, in addition to the 3D R and 3D L, we define \(\mathscr {M}(q)\in \mathrm {End}(F\otimes V\otimes V)\) by
We simply call \(\mathscr {M}(q)\) the 3D M. For simplicity, we also use the abbreviated notation \(\mathscr {M}=\mathscr {M}(q)\).
Remark 3.2
As we explained in Sect. 1, the tetraehdron equation (3.7) was derived again in several ways after [4]. Here, we explain the details of the derivation by [25]. The q-boson algebra \(\mathcal {B}_q\) is an associative algebra over \(\mathbb {C}\) generated by \(\{{\mathbf {a}}^{\pm },{\mathbf {k}}^{\pm 1}\}\) satisfying the following relations:
It has a representation on F as follows:
Then, the intertwining relations of the 3D R are given by
As we explained in Sect. 1, the 3D R is uniquely characterized by (3.13) up to the normalization. Equation (3.2) is obtained by choosing \(\mathscr {R}(|0\rangle \otimes |0\rangle \otimes |0\rangle )=|0\rangle \otimes |0\rangle \otimes |0\rangle \). On the other hand, matrix elements of the 3D L can be expressed by using \(\mathscr {L}_{i,j}^{a,b}\in \mathcal {B}_q{\ }(i,j,a,b\in \{0,1\})\) defined by
where \(\mathscr {L}_{i,j}^{a,b}=0\) other than (3.15). Therefore, we can consider the 3D L as an operator-valued \(4\times 4\) matrix, and the tetrahedron equation (3.7) as an operator-valued \(8\times 8\) matrix. The key observation of [25] is each matrix element of the operator-valued equation (3.7) exactly corresponds to an intertwing relation of (3.13). That is, the tetrahedron equation (3.7) is equivalent to the set of intertwining relations of the irreducible representations of \(A_q(A_2)\). This is an interesting connection but quite mysterious. Also, this connection gives a derivation of the tetrahedron equation (3.7) but the algebraic origin of 3D L has been unclear.
Remark 3.3
There is another known solution to the tetrahedron equation which the 3D L satisfies. We set \(\tilde{\mathscr {L}}\in \mathrm {End}(F\otimes V\otimes V)\)
Then, the matrix \(\tilde{\mathscr {L}}\) together with the 3D L satisfies the following tetrahedron equation:
The equation (3.18) was first presented by [4, 38] and obtained again by quantum geometry settings [3, 40]. It plays an important role to show the commutativity of the layer-to-layer transfer matrix associated with the 3D L [38]. Later, we derive an equation (4.111) which involves only “the 3D L like objects” as (3.18). Actually, it resembles equation (3.18), but involves nonlocal sign factors, so we can not write it as a matrix equation like (3.18). We do not deal with this issue in this paper, but it is an interesting question whether we can attribute (3.18) to Corollary 4.18 or not.
3.2 3D reflection equation
We then proceed to explanations of the 3D reflection equation [18], which is a boundary analog of the tetrahedron equation. The equation is defined on the tensor product of nine linear spaces. The diagram of the 3D reflection equation is obtained in [26, Figure 1].
Essentially, there are only two known non-trivial solutions to the 3D reflection equation [25, 26]. We use the following notation:
We set \(\mathscr {J}(q)\in \mathrm {End}(F\otimes F\otimes F\otimes F)\) by
where \(\mathscr {J}(q)_{i,0,k,l}^{a,0,c,d}\) is given by
and \(\psi _1,\psi _2\) are given by
For simplicity, we also use the abbreviated notation \(\mathscr {J}=\mathscr {J}(q)\). We also set \(\mathscr {K}(q)\in \mathrm {End}(F\otimes F\otimes F\otimes F)\) by
For simplicity, we also use the abbreviated notation \(\mathscr {K}=\mathscr {K}(q)\). Then, the matrix \(\mathscr {J},\mathscr {K}\) together with 3D R satisfies the following 3D reflection equations:
We simply call \(\mathscr {J},{\ }\mathscr {K}\) the 3D J and 3D K, respectively.
The origin of the 3D K is quite similar to the 3D J as we explained in Sect. 1. That is, the 3D K gives the intertwiner of the irreducible representations of the quantum coordinate ring \(A_q(C_2)\), where the associated 3D reflection equation (3.28) holds as the identity of the intertwiner of the irreducible representations of the quantum coordinate ring \(A_q(C_3)\) [25]. As an immediate corollary of the Kuniba–Okado–Yamada theorem, we can see the 3D J also gives the transition matrix of the PBW bases of the nilpotent subalgebra of the quantum algebra \(U_q^{+}(C_2)\).
Although the 3D K itself also appears by considering \(U_q^{+}(B_2)\) up to q-dependence (see Theorems 5.11 and (2.34)), it is worth to emphasize that (3.28) does not follow from discussions only using type B, that is, it is essentially type C object different from (3.27). In this paper, we focus on the PBW basis for type B, and will give new solutions to the 3D reflection equation, which generalize the solution (3.27) to the family of solutions (5.186).
Remark 3.4
Although the 3D R, J and K have similar origins as we mentioned above, unlike the 3D R, the 3D J and 3D K themselves do not give matrix product solutions to the reflection equation because the 3D boundary Zamolodchikov algebra and its associativity condition, i.e. the 3D reflection equation, take different forms. Nevertheless, it is known that we can obtain matrix product solutions to the reflection equation by arranging the intertwining relations of 3D K into a matrix equation [30]:
where \(\mathscr {L}\) is the 3D L with \(q\rightarrow q^2\) and we introduce a matrix \(\mathscr {G}\), which gives K-matrices in the reflection equation. Interestingly, this procedure is exactly in the same way as we explained in Remark 3.2. The equation (3.29) is called the quantized reflection equation [30]. By reducing the equation (3.29), we get the solutions to the reflection equation associated with the fundamental representations of \(U_q(A_{n-1}^{(1)})\), and the spin representations of \(U_q(D_{n+1}^{(2)})\), \(U_q(B_{n}^{(1)})\) and \(U_q(D_{n}^{(1)})\) [30]. See [30] for more details. Later, the K-matrices are characterized as the interwiners of some coideal subalgebras of the quantum algebras [29].
4 PBW Bases of Type A and Tetrahedron Equation
4.1 PBW bases of type A
In this section, we focus on quantum superalgebras of type A in the case of rank 2 and 3. Here, we introduce some notations to briefly describe the PBW bases of the nilpotent subalgebra of them, and show higher-order relations for them. For the case of type A, there are no anisotropic odd roots. We then simply write \(\tilde{\Phi }^{+}_{\mathrm {even}}\cup \tilde{\Phi }^{+}_{\mathrm {aniso}}\) by \(\tilde{\Phi }^{+}_{\mathrm {even}}\). We set \(e_{ij},e_{(ij)k},e_{i(jk)}\in U_q^{+}(\mathfrak {sl}(m|n))\) by
where \(i,j,k\in I\). By considering Corollary 2.7(1), we simply write \(e_{ijk}=e_{(ij)k}\) for the case \((\alpha _i,\alpha _k)=0\). We have the following higher-order relations for them:
Proposition 4.1
Proof
(4.2) is obtained from Corollary 2.7(2) because \([e_{i-1},e_{i+1}]=0\) and \((\alpha _{i-1},\alpha _{i+1})=0\). (4.3) and (4.4) are obtained by \([e_{i-1,i},e_{i+1,i}]=[e_{i-1,i,i+1},e_{i}]=0\) where we used Corollary 2.7(1) and Lemma 2.9(2). (4.9) is a cororally of Lemma 2.9(1).
For (4.5)–(4.8), we only consider (4.5) and (4.6). The remaining relations (4.7) and (4.8) can be proved in the same way. By using the q-commutator, the left hand side of (4.5) can be written as \([[e_{i+1,i+2},e_{i}]_{q},e_{i}]_{q}\). Then we have
where we used Corollary 2.7(2) and the Serre relation (2.18). Similarly, the left hand side of (4.6) can be written as \([e_{i+1,i+2},[e_{i+1,i+2},e_{i}]_{q}]_{q}\). Then we have
where we first used (4.2) and then Corollary 2.7(1), Corollary 2.8 and (4.13). \(\square \)
Proposition 4.2
Proof
By applying the anti-algebra automorphism \(\chi \) given by (2.20) on (4.2)–(4.9), we obtain the desired results. \(\square \)
By writing down quantum root vectors given by Definition 2.3 for the case of rank 2, we find they are given by
where \(\beta _{t}{\ }(t=1,\ldots ,3)\) are the same as Theorem 2.4. For non-super case, (4.20) and (4.21) concide with quantum root vectors given by (2.25) with the reduced expressions \(w_0=s_{1}s_{2}s_{1},s_{2}s_{1}s_{2}\) of the longest element of the Weyl group, respectively.
Similarly, by writing down quantum root vectors given by Definition 2.3 for the case of rank 3, we find they are given by
where \(\beta _{t}{\ }(t=1,\ldots ,6)\) are the same as Theorem 2.4. For non-super case, (4.22) and (4.23) concide with quantum root vectors given by (2.25) with the reduced expressions \(w_0=s_{1}s_{2}s_{3}s_{1}s_{2}s_{1},s_{3}s_{2}s_{3}s_{1}s_{2}s_{3}\) of the longest element of the Weyl group, respectively.
4.2 Transition matrices of PBW bases of type A of rank 2
In this section, we consider transition matrices of the PBW bases of \(U_q^{+}(\mathfrak {sl}(m|n))\) of rank 2, so \(m+n=3\). All possible Dynkin diagrams associated with admissible realizations are given in Table 5. In Table 5, \((\Pi ,p)\) associated with same Dynkin diagrams are exactly same. We then only consider quantum superalgebras associated with the following Dynkin diagrams given by (4.24)
where they are distinguished except (IV), in the sense defined in Sect. 2.2. For the case of rank 2, quantum root vecotrs are given by (4.20) and (4.21), so the transition matrix in (2.32) is given as follows:
where the domain of indices is specified below. Hereafter, we consider each case. Sometimes, we abbreviate simple roots for Dynkin diagrams, but we always assume that they are given as (4.24).
4.2.1 The case (I) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Then, indices are specified as \(i,j,k,a,b,c\in \mathbb {Z}_{\ge 0}\) for (4.25). The transition matrix in (4.25) is explicitly given as the consequence of the Kuniba–Okado–Yamada theorem [28]:
Theorem 4.3
[28, 39]. For the quantum superalgebra associated with 
, the transition matrix in (4.25) is given by
where \(\mathscr {R}\) is the 3D R given by (3.2).
4.2.2 The case (II)
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Then, indices are specified as \(i,j,a,b\in \{0,1\},{\ }k,c\in \mathbb {Z}_{\ge 0}\) for (4.25). The transition matrix in (4.25) is explicitly given as follows:
Theorem 4.4
For the quantum superalgebra associated with 
, the transition matrix in (4.25) is given by
where \(\mathscr {L}\) is the 3D L given by (3.6).
Proof
Multiplying both sides of (4.25) by \(k_2\) from left and \(k_2^{-1}\) from right, also using the relation (2.5), we obtain
On the other hand, \(\gamma _{i,j,k}^{a,b,c}=q^{b+c-j-k}\gamma _{i,j,k}^{a,b,c}\) holds becasuse \(\{e_{1}^{(k)}e_{21}^{(j)}e_{2}^{(i)}\}\) are linearly independent by Theorem 2.4. This means, if \(\gamma _{i,j,k}^{a,b,c}\ne 0\), \(b+c=j+k\) holds. Similarly, multiplying both sides of (4.25) by \(k_1\) from left and \(k_1^{-1}\) from right, also using the relation (2.5), we obtain \(-a+b+2c=-i+j+2k\) if \(\gamma _{i,j,k}^{a,b,c}\ne 0\). Combining them, we eventually obtain the following weight conservation:
Next, we consider (4.25) for the cases \((a,b)=(0,0),(0,1),(1,0)\). For these case, the degreee of \(e_2\) is at most 1 in both sides of (4.25) thanks to the weight conservation (4.35). Now, the relations \(e_1,e_2\) satisfy are
Therefore, the only relation one can apply on both sides of (4.25) is the first relation of (4.36) for the cases \((a,b)=(0,0),(0,1),(1,0)\). The first relation of (4.36) is the same as one of the case (I) 
, so by Lemma 3.1, we obtain \(\gamma _{i,j,k}^{a,b,c}=\mathscr {L}_{i,j,k}^{a,b,c}\) for the cases \((a,b)=(0,0),(0,1),(1,0)\) and \(i+j=a+b,{\ }j+k=b+c\) are satisfied.
Eventually, it is sufficient to show that (4.25) for the cases \((a,b)=(1,1)\)
holds for \(\gamma _{1,1,c}^{1,1,c}=\mathscr {L}_{1,1,c}^{1,1,c}=1\), where we used the weight conservation (4.35) and \(e_{2}^2=0\), and multiplied both sides by \([c]_{q}!\). Actually, we can prove (4.37) by induction as follows. When \(c=0\), (4.37) trivially holds for \(\gamma _{1,1,0}^{1,1,0}=1\). Let us suppose (4.37) is true for \(c=n\) with \(\gamma _{1,1,n}^{1,1,n}=1\). Then, we obtain
where we used (4.36). Thus, (4.37) holds for \(c=n+1\) with \(\gamma _{1,1,n+1}^{1,1,n+1}=1\). To sum up the above discussion, we then obtain \(\gamma _{i,j,k}^{a,b,c}=\mathscr {L}_{i,j,k}^{a,b,c}\). \(\square \)
Corollary 4.5
Proof
By using (4.25) and (2.34), we obtain
Here, we omit the domain of indices but it is easily specified. Since \(\{e_{2}^{(a)}e_{12}^{(b)}e_{1}^{(c)}\}\) are linearly independent by Theorem 2.4, we obtain
This finishes the proof. \(\square \)
4.2.3 The case (III) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Then, indices are specified as \(j,k,b,c\in \{0,1\},{\ }i,a\in \mathbb {Z}_{\ge 0}\) for (4.25). The transition matrix in (4.25) is explicitly given as follows:
Corollary 4.6
For the quantum superalgebra associated with 
, the transition matrix in (4.25) is given by
where \(\mathscr {M}\) are the 3D M given by (3.10).
Proof
\(h:U_q^{+}(\mathfrak {sl}(2|1))\rightarrow U_q^{+}(\mathfrak {sl}(1|2))\) defined by \(e_{1}\mapsto e_{2}\), \(e_{2}\mapsto e_{1}\) gives an algebra homomorphism, where the former algebra is associated with 
and the latter is associated with 
. Then, by Theorem 4.4 and (2.34), it is easy to see that the statement holds. \(\square \)
4.2.4 The case (IV)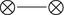 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Then, indices are specified as \(i,k,a,c\in \{0,1\},{\ }j,b\in \mathbb {Z}_{\ge 0}\) for (4.25). We set \(\mathscr {N}(q)\in \mathrm {End}(V\otimes F\otimes V)\) by
where \(\mathscr {N}_{i,j,k}^{a,b,c}=0\) other than (4.51). For simplicity, we also use the abbreviated notation \(\mathscr {N}=\mathscr {N}(q)\). We simply call \(\mathscr {N}\) the 3D N. Then, the transition matrix in (4.25) is explicitly given as follows:
Theorem 4.7
For the quantum superalgebra associated with 
, the transition matrix in (4.25) is given by
where \(\mathscr {N}\) is the 3D N given by (4.51).
Proof
By the same discussion as (4.35), we obtain the following weight conservation:
Now, the relations \(e_1,e_2\) satisfy are \(e_{1}^2=e_{2}^2=0\) and \(e_{12},e_{21}\) are given by \(e_{12}=e_{1}e_{2}+qe_{2}e_{1}\), \(e_{21}=e_{2}e_{1}+qe_{1}e_{2}\). We introduce the following notation:
We then explicitly write down \(e_{12}^b,e_{21}^{j}\) as
Actually, they are easily shown by induction. Hereafter, we consider each case for values of (a, c) in (4.25).
-
(i)
For the case \((a,c)=(0,0)\), by the weight conservation (4.53), (4.25) is explicitly written down as
$$\begin{aligned} \frac{\mu _1(b)+q^{b}\mu _2(b)}{[b]_{q}!} = \gamma _{0,b,0}^{0,b,0} \frac{\mu _2(b)+q^{b}\mu _1(b)}{[b]_{q}!} +\gamma _{1,b-1,1}^{0,b,0} \frac{\mu _1(b)}{[b-1]_{q}!} , \end{aligned}$$(4.56)where we use (4.55) and \(e_{1}^2=e_{2}^2=0\). By comparing coefficients of each monomial \(\mu _{1}(b),\mu _{2}(b)\), we obtain
$$\begin{aligned} \frac{1}{[b]_{q}!} =\gamma _{0,b,0}^{0,b,0}\frac{q^{b}}{[b]_{q}!}+\gamma _{1,b-1,1}^{0,b,0}\frac{1}{[b-1]_{q}!} ,\quad \frac{q^{b}}{[b]_{q}!} =\gamma _{0,b,0}^{0,b,0}\frac{1}{[b]_{q}!} . \end{aligned}$$(4.57)It is easy to see that \(\gamma _{0,b,0}^{0,b,0}=\mathscr {N}_{0,b,0}^{0,b,0}\) and \(\gamma _{1,b-1,1}^{0,b,0}=\mathscr {N}_{1,b-1,1}^{0,b,0}\) give the solution of (4.57).
-
(ii)
For the case \((a,c)=(0,1)\), by the weight conservation (4.53), (4.25) is explicitly written down as
$$\begin{aligned} \mu _{1}(b)e_{1} =\gamma _{0,b,1}^{0,b,1} e_{1}\mu _{2}(b) , \end{aligned}$$(4.58)where we used (4.55) and \(e_{1}^2=e_{2}^2=0\). We then obtain \(\gamma _{0,b,1}^{0,b,1}=1=\mathscr {N}_{0,b,1}^{0,b,1}\) because \(\mu _{1}(b)e_{1}=e_{1}\mu _{2}(b)\).
-
(iii)
For the case \((a,c)=(1,0)\), by the weight conservation (4.53), (4.25) is explicitly written down as
$$\begin{aligned} e_{2}\mu _{1}(b) =\gamma _{1,b,0}^{1,b,0} \mu _{2}(b)e_{2} , \end{aligned}$$(4.59)where we used (4.55) and \(e_{1}^2=e_{2}^2=0\). We then obtain \(\gamma _{1,b,0}^{1,b,0}=1=\mathscr {N}_{1,b,0}^{1,b,0}\) because \(e_{2}\mu _{1}(b)=\mu _{2}(b)e_{2}\).
-
(iv)
For the case \((a,c)=(1,1)\), by the weight conservation (4.53), (4.25) is explicitly written down as
$$\begin{aligned} \frac{\mu _2(b+1)}{[b]_{q}!} = \gamma _{1,b,1}^{1,b,1} \frac{\mu _1(b+1)}{[b]_{q}!} +\gamma _{0,b+1,0}^{1,b,1} \frac{\mu _2(b+1)+q^{b+1}\mu _1(b+1)}{[b+1]_{q}!} , \end{aligned}$$(4.60)where we used (4.55) and \(e_{1}^2=e_{2}^2=0\). Similarly to the case (i), it is easy to see that \(\gamma _{1,b,1}^{1,b,1}=\mathscr {N}_{1,b,1}^{1,b,1}\) and \(\gamma _{0,b+1,0}^{1,b,1}=\mathscr {N}_{0,b+1,0}^{1,b,1}\) give the solution of (4.60).
\(\square \)
Corollary 4.8
Proof
This is shown exactly in the same way as Corollary 4.5. \(\square \)
Remark 4.9
We find that the matrix elements of the 3D L and 3D N satisfy the following relation:
It is naturally thought that (4.62) originates from the fact that both 
and 
give the Dynkin diagrams of \(\mathfrak {sl}(2|1)\) as Table 5. However, the origin of the relation (4.62) in terms of the PBW basis is unknown to us. We do not deal with this issue in this paper, but it is interesting whether, in general, transition matrices associated with a pair of Cartan data mapped to each other via odd reflections are attributed to each other or not. For example, we will also establish a relation between transition matrices associated with such pair of Cartan data for type B. See (5.131).
4.3 Transition matrices of PBW bases of type A of rank 3 and tetrahedron equation
In this section, we consider the transition matrix of the PBW bases of \(U_q^{+}(\mathfrak {sl}(m|n))\) of rank 3, so \(m+n=4\). All possible Dynkin diagrams associated with admissible realizations are given in Table 6. In Table 6, \((\Pi ,p)\) associated with same Dynkin diagrams are exactly same. We then only consider the quantum superalgebras associated with the following Dynkin diagrams given by (4.63):
where (I), (II) and (IV) are distinguished, in the sense defined in Sect. 2.2. Here, we omit the following Dynkin diagrams given by (4.64), because the cases of (VII) and (VIII) are easily attributed to ones of (II) and (III), respectively.
For the case of rank 3, quantum root vectors are given by (4.22) and (4.23), so the transition matrix in (2.32) is given as follows:
where the domain of indices is specified below. In order to attribute the transition matrix in (4.65) to a composition of transition matrices of rank 2, we exploit the following transition matrices \(\Gamma ^{(x)}\):
where the domain of indices will be specified and explicit formulae of \(\Gamma ^{(x)}\) are given for each case in (4.63).
Then, by using \(\Gamma ^{(x)}\), (4.2)–(4.4) and (4.12)–(4.14), we can construct the transition matrix in (4.65) in two ways. The first way is given by
where summations are taken on \(i_k,x_k{\ }(k=1,\ldots ,6)\) and we set
We have put the underlines to the parts to be rewritten. The details of the above procedure are as follows. For (4.72), we used (4.67). For (4.73), we used (4.70). For (4.74), we used (4.2), (4.3) and \([e_1,e_3]=0\). For (4.75), we used (4.69). For (4.76), we used (4.66). For (4.77), we used (4.14).
Similarly, the second way is given by
where summations are taken on \(i_k,x_k{\ }(k=1,\ldots ,6)\). Again, we have put the underlines to the parts to be rewritten. The details of the above procedure are as follows. For (4.80), we used (4.4). For (4.81), we used (4.66). For (4.82), we used (4.68). For (4.83), we used (4.12), (4.13) and \([e_1,e_3]=0\). For (4.84), we used (4.71). For (4.85), we used (4.67).
Now, \(\{e_{1}^{(i_6)}e_{21}^{(i_5)}e_{321}^{(i_4)}e_{2}^{(i_3)}e_{23}^{(i_2)}e_3^{(i_1)}\}\) are linearly independent by Theorem 2.4. Then, by comparing (4.78) and (4.86), we obtain the following result:
Theorem 4.10
As the identity of transition matrices of quantum superalgebras of type A, we have
where summations are taken on \(x_k{\ }(k=1,\ldots ,6)\).
The above equation (4.87) generally involve nonlocal sign factors. In (4.63), we have \(\rho _1=\rho _2=\rho _3=0\) for (I), (II) and (III). In that case, (4.87) exactly gives the tetrahedron equation. Hereafter, we specialize Theorem 4.10 for each case given in (4.63).
4.3.1 The case (I) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Now, \(\Gamma ^{(x)}\) defined by (4.66)–(4.71) are specified as follows:
Lemma 4.11
For the quantum superalgebra associated with 
, we have (4.66)–(4.71) where \(\Gamma ^{(x)}\) are given by
Proof
\(\Gamma ^{(2|1)}\), \(\Gamma ^{(3|2)}\) are direct consquences of Theorem 4.3. \(\Gamma ^{(23|1)}\) is obtained by (4.5), (4.6) and Theorem 4.3. Actually, \(e_1,e_{23}\) satisfy the exactly same relations of \(e_1,e_2\) of \(U_q^{+}(\mathfrak {sl}(3))\) associated with 
, so \(h:U_q^{+}(\mathfrak {sl}(3))\rightarrow U_q^{+}(\mathfrak {sl}(4))\) defined by \(e_{1}\mapsto e_{1}\), \(e_{2}\mapsto e_{23}\) gives an algebra homomorphism. Also, \(d_{\alpha _2+\alpha _3}=d_{\alpha _2}\) and \(d_{\alpha _1+\alpha _2+\alpha _3}=d_{\alpha _1+\alpha _2}\) are satisfied where the left hand sides are for \(U_q^{+}(\mathfrak {sl}(4))\) and the right hand sides are for \(U_q^{+}(\mathfrak {sl}(3))\), so \([m]_{q^{d_{\alpha _2+\alpha _3}}}!=[m]_{q^{d_{\alpha _2}}}!\) and \([m]_{q^{d_{\alpha _1+\alpha _2+\alpha _3}}}!=[m]_{q^{d_{\alpha _1+\alpha _2}}}!\) hold. Therefore, by applying h on (4.25) for the case 
, we obtain
This is exactly (4.68) for \(\Gamma ^{(23|1)}=\mathscr {R}\). The remaining cases can be shown exacly in the same way. \(\square \)
The phase factors given by (4.79) are now \(\rho _1=\rho _2=\rho _3=0\). Then, (4.87) is specialized as follows:
where all indices are defined on \(\mathbb {Z}_{\ge 0}\). This is exactly the tetrahedron equation (3.4):
We then get the following result:
Corollary 4.12
The tetrahedron equation (3.4) is characterized as the identity of the transition matrices of the quantum superalgebra associated with 
.
We note that although Corollary 4.12 is a corollary of the Kuniba–Okado–Yamada theorem [28], the above calculation gives a direct derivation of the tetrahedron equation (3.4) without using any results for quantum coordinate rings. This is a key for the generalization of earlier results to super cases.
4.3.2 The case (II) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 4.11, by using Proposition 4.1 and 4.2, we can show the following lemma:
Lemma 4.13
For the quantum superalgebra associated with 
, we have (4.66)–(4.71) where \(\Gamma ^{(x)}\) are given by
The phase factors given by (4.79) are now \(\rho _1=\rho _2=\rho _3=0\). Then, (4.87) is specialized as follows:
where \(o_k,i_k,x_k\in \{0,1\}{\ }(k=1,2,4)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). This is exactly the tetrahedron equation (3.7):
We then get the following result:
Corollary 4.14
The tetrahedron equation (3.7) is characterized as the identity of the transition matrices of the quantum superalgebra associated with 
.
4.3.3 The case (III) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 4.11, by using Propositions 4.1 and 4.2, we can show the following lemma:
Lemma 4.15
For the quantum superalgebra associated with 
, we have (4.66)–(4.71) where \(\Gamma ^{(x)}\) are given by
The phase factors given by (4.79) are now \(\rho _1=\rho _2=\rho _3=0\). Then, (4.87) is specialized as follows:
where \(o_k,i_k,x_k\in \{0,1\}{\ }(k=1,3,5)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result, which gives a new solution to the tetrahedron equation.
Corollary 4.16
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the tetrahedron equation given by
4.3.4 The case (IV) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 4.11, by using Propositions 4.1 and 4.2, we can show the following lemma:
Lemma 4.17
For the quantum superalgebra associated with 
, we have (4.66)–(4.71) where \(\Gamma ^{(x)}\) are given by
The phase factors given by (4.79) are now \(\rho _1=0\), \(\rho _2=\rho _3=1\). Then, (4.87) is specialized as follows:
where \(o_k,i_k,x_k\in \{0,1\}{\ }(k=2,3,4,5)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). As we explained in Remark 3.3, this equation resembles the tetrahedron equation (3.18), but we can not eliminate the sign factors at present. Anyway, we then get the following result:
Corollary 4.18
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the tetrahedron equation up to sign factors given by (4.111).
4.3.5 The case (V) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 4.11, by using Propositions 4.1 and 4.2, we can show the following lemma:
Lemma 4.19
For the quantum superalgebra associated with 
, we have (4.66)–(4.71) where \(\Gamma ^{(x)}\) are given by
The phase factors given by (4.79) are now \(\rho _1=\rho _2=1\), \(\rho _3=0\). Then, (4.87) is specialized as follows:
where \(o_k,i_k,x_k\in \{0,1\}{\ }(k=1,2,5,6)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result:
Corollary 4.20
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the tetrahedron equation up to sign factors given by (4.116).
4.3.6 The case (VI) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 4.11, by using Propositions 4.1 and 4.2, we can show the following lemma:
Lemma 4.21
For the quantum superalgebra associated with 
, we have (4.66)–(4.71) where \(\Gamma ^{(x)}\) are given by
The phase factors given by (4.79) are now \(\rho _1=\rho _3=1\), \(\rho _2=0\). Then, (4.87) is specialized as follows:
where \(o_k,i_k,x_k\in \{0,1\}{\ }(k=1,3,4,6)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result:
Corollary 4.22
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the tetrahedron equation up to sign factors given by (4.121).
5 PBW Bases of Type B and 3D Reflection Equation
5.1 PBW bases of type B of rank 2 and 3
In this section, we focus on quantum superalgebras of type B in the case of rank 2 and 3. Here, we introduce some notations to briefly describe the PBW bases of the nilpotent subalgebra of them, and show higher-order relations for them. We define \(e'_{ij},e'_{(ij)k},e'_{i(jk)}\in U_q^{+}(\mathfrak {osp}(2m+1|2n))\) in the same way as (4.1). Let us recall the normalization \(e'_{\beta }\mapsto e_{\beta }\) given in Definition 2.3(ii). Corresponding to the normalization, we use a simplified rule as follows, which is enough to our description. We set \(e_{x}=e'_{x}/(q^{1/2}+q^{-1/2}){\ }(x=ij,(ij)k,i(jk))\) for the case x involves the letter “r” twice where r is the rank of \(U_q^{+}(\mathfrak {osp}(2m+1|2n))\) defined in Sect. 2.1, and we set \(e_{x}=e'_{x}{\ }(x=ij,(ij)k,i(jk))\) otherwise. By considering Corollary 2.7(1), we simply write \(e_{ijk}=e_{(ij)k}\) for the case \((\alpha _i,\alpha _k)=0\).
Example 5.1
The indices of the element \(e'_{(12)2}\in U_q^{+}(\mathfrak {osp}(2m+1|2n))\) for rank \(r=m+n=2\) involve the letter “2” twice. We then set \(e_{(12)2}=e'_{(12)2}/(q^{1/2}+q^{-1/2})\).
We also define elements with more q-commutators as well. For example, we define \(e'_{((jk)k)(ji)}\in U_q^{+}(\mathfrak {osp}(2m+1|2n))\) by
Then, we similarly set \(e_{x}=e'_{x}/(q^{1/2}+q^{-1/2})\) for the case x involves two letters “r”, and we set \(e_{x}=e'_{x}\) otherwise. These elements satisfy the following higher-order relations, where we only consider the case of rank 3, which is enough for our purpose in Sect. 5.3.
Proposition 5.2
For the case of rank 3, we have
Proof
(5.2) is obtained by Corollary 2.7(2) because \([e_{1},e_{3}]=0\) and \((\alpha _{1},\alpha _{3})=0\). (5.3) is obtained by Corollary 2.7(1). (5.4) is obtained by
where we used Corollary 2.7(2). For (5.7), it is sufficient to show \(e_{(12)(3(32))}=e_{(((12)3)3)2}\) by considering the anti-algebra automorphism \(\chi \) given by (2.20). Actually, we have \(e_{(12)(3(32))}=e_{((12)3)(32)}=e_{(((12)3)3)2}\) where we used Corollary 2.7(1), (5.12) and Lemma 2.9(2). (5.5) and (5.6) are shown in the same way. Here, we only present the proof for (5.5). We can calculate the left hand side of (5.5) as
where we used Lemma 2.6 and (5.11). One can see \((\alpha _1+\alpha _2+\alpha _3,\alpha _2)=(\bar{\epsilon }_1,\bar{\epsilon }_2-\bar{\epsilon }_3)=0\) and \((\alpha _1+\alpha _2,\alpha _2)=(\bar{\epsilon }_3,\bar{\epsilon }_3)=-(\alpha _1+\alpha _2+2\alpha _3,\alpha _2)\). Then, the right hand side of (5.10) is exactly the right hand side of (5.5). \(\square \)
Here, we cite a lemma from [45, Lemma 6.3.1(i)] used below.
Lemma 5.3
For \(1\le i\le r-1\), \([e_{\bar{\epsilon }_{i}},e_{\bar{\epsilon }_{i}+\bar{\epsilon }_{r}}]_{q}=0\). Especially, if \(r=3\), this gives \([e_{123},e_{((12)3)3}]_{q}=0\) for \(i=1\) and \([e_{23},e_{(23)3}]_{q}=0\) for \(i=2\).
Proposition 5.4
For the case of rank 3, we have
Proof
(5.11) and (5.12) are obtained exactly in the same way as (4.3) and (4.4), where we use the anti-algebra automorphism \(\chi \) given by (2.20). (5.13) is obtained by \([e_{((12)3)3},e_{23}]=[e_{(((12)3)3)2},e_{3}]=0\) where we used Corollary 2.7(1) and Lemma 2.9(2). (5.14) is obtained by
where we used Lemma 2.6. This is actually equal to 0 by Lemma 5.3 for \(i=2\), (5.3) and (5.13). (5.15) is obtained by
where we used (5.7) and Lemma 2.9(2). \(\square \)
Proposition 5.5
For the case of rank 3, we have
Proof
The proof of this proposition will be presented together with the next proposition. \(\square \)
Proposition 5.6
For the case of rank 3, we have
Proof
(5.28), (5.29) and (5.30) are cororallies of Lemma 2.9(1). (5.20) and (5.32) can be written together as \([[[e_{21},e_{3}]_{q},e_{3}]_{q},e_{3}]_{q}\). Then, (5.18), (5.20), (5.32) and (5.22) are obtained exactly in the same way as (4.5). (5.21) and (5.23) are obtained in the same way as (4.6), where we use (5.14) for (5.23). The left hand side of (5.24) can be written as \([[e_{((12)3)3},e_{2}]_{q},e_{2}]_{q}=[e_{(((12)3)3)2},e_{2}]_{q}\). This is equal to 0 by Lemma 2.9.
(5.19) and (5.31) can be written together as \([[[e_{1},e_{23}]_{q},e_{23}]_{q},e_{23}]_{q}\). Then, we have
where we used (5.5), Corollary 2.7(1), Corollary 2.8 and Lemma 2.9(2).
The left hand side of (5.25) can be written as \([e_{2(((12)3)3)},e_{((12)3)3}]_{q}\). Then we have
where we used (5.5), Corollary 2.7(1), Lemma 5.3 for \(i=1\), (5.3), Lemma 5.3 for \(i=2\) and (5.14).
The left hand side of (5.26) can be written as \([e_{21},e_{(21)((23)3)}]_{q}\). Then we have
where we used (5.6) and Lemma 2.6. This is actually equal to 0 because we have \([e_{21},e_{23}]_{q}=0\) by (5.12) and \([e_{21},e_{(23)1}]_{q}=[[e_{21},e_{23}]_{q},e_{1}]_{q}=0\) by Corollary 2.7(1), Corollary 2.8 and (5.12).
We prove (5.62) instead of (5.27). The left hand side of (5.62) can be written as \([[e_{12},e_{3(32)}]_{q},e_{3(32)}]_{q}\). Here, we have \([e_{12},e_{3(32)}]_{q}=[e_{123},e_{32}]_{q}/(q^{1/2}+q^{-1/2})=e_{(((12)3)3)2}\) where we used Corollary 2.7(1), (5.49) and (5.11). Then, it is sufficient to show \([e_{(((12)3)3)2},e_{3(32)}]_{q}=0\). This actually holds by repeated use of Lemma 2.6 and Lemma 2.9(2). \(\square \)
Also, by applying the anti-algebra automorphism \(\chi \) given by (2.20) on the above propositions, we obtain the following relations:
Proposition 5.7
For the case of rank 3, we have
Proposition 5.8
For the case of rank 3, we have
Proposition 5.9
For the case of rank 3, we have
Proposition 5.10
For the case of rank 3, we have
By writing down quantum root vectors given by Definition 2.3 for the case of rank 2, we find they are given by
where \(\beta _{t}{\ }(t=1,\ldots ,4)\) are the same as Theorem 2.4. For non-super case, (5.68) and (5.69) concide with quantum root vectors given by (2.25) with the reduced expressions \(w_0=s_{1}s_{2}s_{1}s_{2},s_{2}s_{1}s_{2}s_{1}\) of the longest element of the Weyl group, respectively.
Similarly, by writing down quantum root vectors given by Definition 2.3 for the case of rank 3, we find they are given by
where \(\beta _{t}{\ }(t=1,\ldots ,9)\) are the same as Theorem 2.4. For non-super case, (5.70) and (5.71) concide with quantum root vectors given by (2.25) with the reduced expressions \(w_0=s_{1}s_{2}s_{3}s_{2}s_{1}s_{2}s_{3}s_{2}s_{3}\), \(s_{3}s_{2}s_{3}s_{2}s_{1}s_{2}s_{3}s_{2}s_{1}\) of the longest element of the Weyl group, respectively.
5.2 Transition matrices of PBW bases of type B of rank 2
In this section, we consider transition matrices of the PBW bases of \(U_q^{+}(\mathfrak {osp}(2m+1|2n))\) of rank 2, so \(m+n=2\). All possible Dynkin diagrams associated with admissible realizations are given in Table 7, where they are distinguished except 
, in the sense defined in Sect. 2.2.
For the case of rank 2, quantum root vecotrs are given by (5.68),(5.69), so the transition matrix (2.32) is given as follows:
where the domain of indices is specified below. Hereafter, we consider each case. Sometimes, we abbreviate simple roots for Dynkin diagrams, but we always assume that they are given as Table 7.
5.2.1 The case (I) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Then, indices are specified as \(i,j,k,l,a,b,c,d\in \mathbb {Z}_{\ge 0}\) for (5.72). The transition matrix in (5.72) is explicitly given as the consequence of the Kuniba–Okado–Yamada theorem [28]:
Theorem 5.11
[26, 28] For the quantum superalgebra associated with 
, the transition matrix in (5.72) is given by
where \(\mathscr {J}\) is the 3D J given by (3.21).
5.2.2 The case (II) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Then, indices are specified as \(i,k,a,c\in \mathbb {Z}_{\ge 0},{\ }j,l,b,d\in \{0,1\}\) for (5.72). We set \(\mathscr {X}(q)\in \mathrm {End}(F\otimes V\otimes F\otimes V)\) by
For simplicity, we also use the abbreviated notation \(\mathscr {X}=\mathscr {X}(q)\). We simply call \(\mathscr {X}\) the 3D X. Then, the transition matrix in (5.72) is explicitly given as follows:
Theorem 5.12
For the quantum superalgebra associated with 
, the transition matrix in (5.72) is given by
where \(\mathscr {X}\) is the 3D X given by (5.83)–(5.98).
The proof of Theorem 5.12 is available in “Appendix A”.
Corollary 5.13
Proof
This is shown exactly in the same way as Corollary 4.5. \(\square \)
5.2.3 The case (III) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Then, indices are specified as \(i,k,a,c\in \mathbb {Z}_{\ge 0},{\ }j,l,b,d\in \{0,1\}\) for (5.72). We set \(\mathscr {Y}(q)\in \mathrm {End}(F\otimes V\otimes F\otimes V)\) by
For simplicity, we also use the abbreviated notation \(\mathscr {Y}=\mathscr {Y}(q)\). We simply call \(\mathscr {Y}\) the 3D Y. Then, the transition matrix in (5.72) is explicitly given as follows:
Theorem 5.14
For the quantum superalgebra associated with 
, the transition matrix in (5.72) is given by
where \(\mathscr {Y}\) is the 3D Y given by (5.106)–(5.121).
Proof
The relations \(e_1,e_2\) satisfy are
Also, the quantum root vectors are given by
On the other hand, for the case (II) 
, the relations for the generators are
where we write the generators by \(\tilde{e}_{i}\) instead of \(e_{i}\) to avoid confusion. Also, the quantum root vectors for the case (II) 
are given by
Apparently, (5.126), (5.127) and the numerators of (5.128) correspond to (5.123), (5.124) and the numerators of (5.125) with a replacement \(q\rightarrow -q\).
Here, (5.72) for the case (II) 
and (III) 
are explicitly written as follows:
Comparing (5.129) with \(q\rightarrow -q\) and (5.130), we obtain the following relation:
where we used
We then obtain the desired result by direct calculations. We note that (5.132) involves \((-1)^{1/2}\), but no matrix elements of the 3D Y involve it. \(\square \)
Corollary 5.15
Proof
This is shown exactly in the same way as Corollary 4.5. \(\square \)
5.2.4 The case (IV) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Then, the indices are specified as \(i,j,k,l,a,b,c,d\in \mathbb {Z}_{\ge 0}\) for (5.72). We write matrix elements of the transition matrix in (5.72) by
For simplicity, we also use the abbreviated notation \(\mathscr {Z}=\mathscr {Z}(q)\). We simply call \(\mathscr {Z}\) the 3D Z.
At present, an explict formula for the 3D Z is yet to be constructed. In “Appendix B”, we present recurrence equations for the 3D Z. We can calculate any matrix elements of the 3D Z by using a computer program via these equations.
Example 5.16
The following is the list of all the non-zero elements of \(\mathscr {Z}_{0,1,1,2}^{a,b,c,d}\):
5.3 Transition matrices of PBW bases of type B of rank 3 and 3D reflection equation
In this section, we condider the transition matrices of the PBW bases of \(U_q^{+}(\mathfrak {osp}(2m+1|2n))\) of rank 3, so \(m+n=3\). All possible Dynkin diagrams associated with admissible realizations are given in Table 8.
For the case of rank 3, quantum root vectors are given by (5.70) and (5.71), so the transition matrix in (2.32) is given as follows:
where the domain of indices is specified below. In order to attribute the transition matrix in (5.148) to a composition of transition matrices of rank 2, we exploit the following transition matrices \(\Theta ^{(x)}\) and \(\Xi ^{(y)}\):
where the domain of indices will be specified. For each case in Table 8, \(\Theta ^{(x)}\) and \(\Xi ^{(y)}\) are identified with the 3D operators we have already introduced.
Then, by using \(\Theta ^{(x)},\Xi ^{(y)}\), Propositions 5.2, 5.4 and Propositions 5.7, 5.8, we can construct the transition matrix in (5.148) in two ways. The first way is given by
where summations are taken on \(i_k,x_k\,(k=1,\ldots ,9)\), \(y_k\,(k=2,4,5,6,8,9)\). We have put the underlines to the parts to be rewritten. We used \(\rho _1,\rho _2,\rho _3\) given by (4.79) and we have also set
We note that \(\eta _1\), \(\eta _2\) and \(\eta _3\) are actually equal to \(\rho _1\), \(\rho _2\) and \(\rho _3\), respectively because the parts whose coefficients are 2 do not contribute the parity. We exploit both of them for a better understanding. The details of the above procedure are as follows. For (5.161), we used (5.150). For (5.162), we used (5.13) and (5.11). For (5.163), we used (5.149) and (5.4). For (5.164), we used (5.159) and (5.3). For (5.165), we used (5.152). For (5.166), we used \([e_1,e_3]=0\), (5.6), (5.12) and (5.14). For (5.167), we used (5.2), (5.4) and (5.154). For (5.168), we used (5.157). For (5.169), we used (5.15). For (5.170), we used (5.156). For (5.171), we used (5.7).
Similarly, the second way is given by
where summations are taken on \(i_k,x_k{\ }(k=1,\ldots ,9)\), \(y_k{\ }(k=2,4,5,6,8,9)\). Again, we have put the underlines to the parts to be rewritten. The details of the above procedure are as follows. For (5.174), we used (5.156). For (5.175), we used (5.47) and (5.52). For (5.176), we used (5.158) and (5.47). For (5.177), we used (5.155). For (5.178), we used \([e_1,e_3]=0\), (5.42), (5.44), (5.49) and (5.51). For (5.179), we used (5.153), (5.42) and (5.46). For (5.180), we used (5.160). For (5.181), we used (5.149). For (5.182), we used (5.42), (5.43) and (5.45), (5.48) and (5.50). For (5.183), we used (5.151). For (5.184), we used (5.43).
Now, \(\{e_{1}^{(i_9)}e_{21}^{(i_8)}e_{321}^{(i_7)}e_{3(3(21))}^{(i_6)}e_{2(3(3(21)))}^{(i_5)}e_{2}^{(i_4)}e_{32}^{(i_3)}e_{3(32)}^{(i_2)}e_{3}^{(i_1)}\}\) are linearly independent by Theorem 2.4. Then, by comparing (5.172) and (5.185), we obtain the following result:
Theorem 5.17
As the identity of transition matrices of quantum superalgebras associated with type B, we have
where summations are taken on \(x_k{\ }(k=1,\ldots ,9)\) and \(y_k{\ }(k=2,4,5,6,8,9)\).
The above equation (5.186) generally involves nonlocal sign factors. Here, we group the Dynkin diagrams given by Table 8 into the two families. In Table 8, we have \(\rho _1=\rho _2=\rho _3=\eta _1=\eta _2=\eta _3=0\) for the following Dynkin diagrams given by (5.187):
where (I) (II) and (IV) are distinguished, in the sense defined in Sect. 2.2. For each case of (5.187), (5.186) exactly gives the 3D reflection equation. On the other hand, there are non-trivial nonlocal sign factors for the following Dynkin diagrams given by (5.188):
where (VI) is distinguished. Then, as we will see later, the associated equations are the 3D reflection equation up to sign factors. Hereafter, we specialize Theorem 5.17 for each case given in (5.187) and (5.188).
5.3.1 The case (I) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Now, \(\Theta ^{(x)},\Xi ^{(y)}\) defined by (5.149)–(5.160) are specified as follows:
Lemma 5.18
For the quantum superalgebra associated with 
, we have (5.149)– (5.160) where \(\Theta ^{(x)},\Xi ^{(y)}\) are given by
Proof
\(\Theta ^{(2|1)}\) and \(\Xi ^{(y)}\) can be obtained in the same way as Lemma 4.11 via the propositions given in Sect. 5.1. The remaining cases are also obtained almost in the same way, but we have to care the normalization factor \(q^{1/2}+q^{-1/2}\) of quantum root vectors, which is given by the begining of Sect. 5.1. Here, we only present the proof for \(\Theta ^{(233|1)}\). Similarly to Lemma 4.11, by considering (5.22) and (5.23), \(h:U_q^{+}(\mathfrak {sl}(3))\rightarrow U_q^{+}(\mathfrak {so}(5))\) defined by \(e_1\mapsto e_{1}\), \(e_{2}\mapsto e_{(23)3}\) gives an algebra homomorphism. Also, \(d_{\alpha _2+2\alpha _3}=d_{\alpha _2}\) is satisfied where the left hand side is for \(U_q^{+}(\mathfrak {so}(5))\) and the right hand side is for \(U_q^{+}(\mathfrak {sl}(3))\), so \([m]_{q^{d_{\alpha _2+\alpha _3}}}!=[m]_{q^{d_{\alpha _2}}}\)! holds. Therefore, by applying h on (4.25) for the case 
, we obtain
The 3D R satisfies the weight conservation law: \(\mathscr {R}_{i,j,k}^{a,b,c}=0\) if \(i+j\ne a+b\) or \(j+k\ne b+c\). We then obtain (5.152) for \(\Theta ^{(233|1)}=\mathscr {R}\). \(\square \)
The phase factors given by (4.79) and (5.173) are now \(\rho _1=\rho _2=\rho _3=0\) and \(\eta _1=\eta _2=\eta _3=0\). Then, (5.186) is specialized as follows:
where all indices are defined on \(\mathbb {Z}_{\ge 0}\). This is exactly the 3D reflection equation (3.27):
We then get the following result:
Corollary 5.19
The 3D reflection equation (3.27) is characterized as the identity of the transition matrices of the quantum superalgebra associated with 
.
We note that although Corollary 5.19 is a corollary of the Kuniba–Okado–Yamada theorem [28], the above calculation gives a direct derivation of the 3D reflection equation (3.27) without using any results for quantum coordinate rings.
5.3.2 The case (II) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 5.18, by using the propositions given in Sect. 5.1, we can show the following lemma:
Lemma 5.20
For the quantum superalgebra associated with 
, we have (5.149)–(5.160) where \(\Theta ^{(x)},\Xi ^{(y)}\) are given by
The phase factors given by (4.79) and (5.173) are now \(\rho _1=\rho _2=\rho _3=0\) and \(\eta _1=\eta _2=\eta _3=0\). Then, (5.186) is specialized as follows:
where \(o_k,i_k,x_k,y_k\in \{0,1\}{\ }(k=5,6,8,9)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result, which gives a new solution to the 3D reflection equation.
Corollary 5.21
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the 3D reflection equation given by
5.3.3 The case (III) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 5.18, by using the propositions given in Sect. 5.1, we can show the following lemma:
Lemma 5.22
For the quantum superalgebra associated with 
, we have (5.149)–(5.160) where \(\Theta ^{(x)},\Xi ^{(y)}\) are given by
The phase factors given by (4.79) and (5.173) are now \(\rho _1=\rho _2=\rho _3=0\) and \(\eta _1=\eta _2=\eta _3=0\). Then, (5.186) is specialized as follows:
where \(o_k,i_k,x_k,y_k\in \{0,1\}{\ }(k=2,4,5,9)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result, which gives a new solution to the 3D reflection equation.
Corollary 5.23
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the 3D reflection equation given by
5.3.4 The case (IV) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 5.18, by using the propositions given in Sect. 5.1, we can show the following lemma:
Lemma 5.24
For the quantum superalgebra associated with 
, we have (5.149)–(5.160) where \(\Theta ^{(x)},\Xi ^{(y)}\) are given by
The phase factors given by (4.79) and (5.173) are now \(\rho _1=\rho _2=\rho _3=0\) and \(\eta _1=\eta _2=\eta _3=0\). Then, (5.186) is specialized as follows:
where all the indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result, which gives a new solution to the 3D reflection equation.
Corollary 5.25
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the 3D reflection equation given by
5.3.5 The case (V) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 5.18, by using the propositions given in Sect. 5.1, we can show the following lemma:
Lemma 5.26
For the quantum superalgebra associated with 
, we have (5.149)–(5.160) where \(\Theta ^{(x)},\Xi ^{(y)}\) are given by
The phase factors given by (4.79) and (5.173) are now \(\rho _1=\rho _2=\rho _3=0\) and \(\eta _1=\eta _2=\eta _3=0\). Then, (5.186) is specialized as follows:
where \(o_k,i_k,x_k,y_k\in \{0,1\}{\ }(k=2,4,6,8)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result, which gives a new solution to the 3D reflection equation.
Corollary 5.27
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the 3D reflection equation given by
5.3.6 The case (VI) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 5.18, by using the propositions given in Sect. 5.1, we can show the following lemma:
Lemma 5.28
For the quantum superalgebra associated with 
, we have (5.149)–(5.160) where \(\Theta ^{(x)},\Xi ^{(y)}\) are given by
The phase factors given by (4.79) and (5.173) are now \(\rho _1=\eta _1=0\) and \(\rho _2=\rho _3=\eta _2=\eta _3=1\). Then, (5.186) is specialized as follows:
where \(o_k,i_k,x_k,y_k\in \{0,1\}{\ }(k=2,4,6,8)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result:
Corollary 5.29
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the 3D reflection equation up to sign factors given by (5.231).
5.3.7 The case (VII) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 5.18, by using the propositions given in Sect. 5.1, we can show the following lemma:
Lemma 5.30
For the quantum superalgebra associated with 
, we have (5.149)–(5.160) where \(\Theta ^{(x)},\Xi ^{(y)}\) are given by
The phase factors given by (4.79) and (5.173) are now \(\rho _3=\eta _3=0\) and \(\rho _1=\rho _2=\eta _1=\eta _2=1\). Then, (5.186) is specialized as follows:
where \(o_k,i_k,x_k,y_k\in \{0,1\}{\ }(k=5,6,8,9)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result:
Corollary 5.31
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the 3D reflection equation up to sign factors given by (5.237).
5.3.8 The case (VIII) 
In this case, the corresponding symmetrized Cartan matrix is given by
and the corresponding positive roots are given by
Similarly to Lemma 5.18, by using the propositions given in Sect. 5.1, we can show the following lemma:
Lemma 5.32
For the quantum superalgebra associated with 
, we have (5.149)–(5.160) where \(\Theta ^{(x)},\Xi ^{(y)}\) are given by
The phase factors given by (4.79) and (5.173) are now \(\rho _2=\eta _2=0\) and \(\rho _1=\rho _3=\eta _1=\eta _3=1\). Then, (5.186) is specialized as follows:
where \(o_k,i_k,x_k,y_k\in \{0,1\}{\ }(k=2,4,5,9)\) and the other indices are defined on \(\mathbb {Z}_{\ge 0}\). We then get the following result:
Corollary 5.33
As the identity of the transition matrices of the quantum superalgebra associated with 
, we have the 3D reflection equation up to sign factors given by (5.243).
6 Crystal Limit
6.1 Crystal limit of transition matrices of rank 2
In this section, we consider some transition matrices obtained in Sects. 4 and 5 at \(q=0\), which is known as the crystal limit [22]. First, we note that the crystal limit of transition matrices for non-super cases reproduces so-called transition maps of Lusztig’s parametrizations of the canonical basis [5, 32]. For type A and B, we set the crystal limits of the 3D R and 3D J by
Then, these elements are explicitly given as follows [5]:
where \(x_1=\min (i+2\min (j,l),k+2l)\), \(x_2=\min (i+\min (j,l),k+l)\). (6.2) and (6.3) follow from the fact that diagonal elements of transition matrices from PBW bases to the canonical basis is 1 and off-diagonal elements are in \(q\mathbb {Z}[q]\). They define the non-trivial bijections on \((\mathbb {Z}_{\ge 0})^{3}\) and \((\mathbb {Z}_{\ge 0})^{4}\), respectively. There also exists the crystal limit of the tetrahedron equation (3.7) and the 3D reflection equation themselves, so they gives the combinatorial solutions to them. See also related results given in [25].
Here, we present a super analog of these results. Let us begin with the case of type A of rank 2. We set the crystal limits of the 3D L, M and N by
We note that the normalization change in (6.6) corresponds to use unnormalized PBW bases for 
. This is consistent with earlier observations given in [9, Section 5.3]. Then, we have the following results by direct calculations:
Proposition 6.1
The crystal limit of the 3D L defines a non-trivial bijection on \(\{0,1\}^{2}\times \mathbb {Z}_{\ge 0}\). The elements are given by
where \(\mathcal {L}_{i,j,k}^{a,b,c}=0\) other than (6.7).
Corollary 6.2
The crystal limit of the 3D M defines a non-trivial bijection on \(\mathbb {Z}_{\ge 0}\times \{0,1\}^{2}\). The elements are given by \(\mathcal {M}_{i,j,k}^{a,b,c}=\mathcal {L}_{k,j,i}^{c,b,a}\).
Proposition 6.3
The crystal limit of the 3D N defines a non-trivial bijection on \(\{0,1\}\times \mathbb {Z}_{\ge 0}\times \{0,1\}\). The elements are given by
where \(\mathcal {N}_{i,j,k}^{a,b,c}=0\) other than (6.8).
Next, we proceed to the case of type B of rank 2. We set the crystal limits of the 3D X and 3D Y by
We note that the normalization changes in (6.9) and (6.10) correspond to use partially unnormalized PBW bases for 
and 
, respectively. Then, we have the following results by direct calculations:
Proposition 6.4
The crystal limit of the 3D X defines a non-trivial bijection on \(\mathbb {Z}_{\ge 0}\times \{0,1\}\times \mathbb {Z}_{\ge 0}\times \{0,1\}\). The matrix elements are given by
where \(\mathcal {X}_{i,j,k,l}^{a,b,c,d}=0\) otherwise, and we used \(\theta \) defined by \(\theta (\mathrm {true})=1\) and \(\theta (\mathrm {false})=0\).
Proposition 6.5
The crystal limit of the 3D Y defines a non-trivial bijection on \(\mathbb {Z}_{\ge 0}\times \{0,1\}\times \mathbb {Z}_{\ge 0}\times \{0,1\}\). The matrix elements are given by
where \(\mathcal {Y}_{i,j,k,l}^{a,b,c,d}=0\) otherwise, and we used \(\theta \) defined by \(\theta (\mathrm {true})=1\) and \(\theta (\mathrm {false})=0\).
Here, the bijections obtained by the crystal limit of the 3D X and 3D Y are actually same, but have different sign factors. Actually, \(\mathcal {Y}_{i,j,k,l}^{a,b,c,d}\) takes not only 0, 1 but also \(-1\). This is a new aspect not arising for non-super cases.
We can also observe the crystal limit of the 3D Z although we do not have an explicit formula for it. We set the crystal limit of the 3D Z by
Supported by computer experiments, we conjecture the crystal limit of the 3D Z also defines a non-trivial bijection on \((\mathbb {Z}_{\ge 0})^{4}\). For example, the list of all the non-zero elements of \(\mathscr {Z}_{0,1,1,2}^{a,b,c,d}\) is given in Example 5.16. The crystal limit of them gives \(\mathcal {Z}_{0,1,1,2}^{a,b,c,d}=\delta _{a,1}\delta _{b,1}\delta _{c,0}\delta _{d,3}\). We note that the negative factor also appears for the 3D Z. For example, the following is the list of all the non-zero elements of \(\mathscr {Z}_{2,0,1,0}^{a,b,c,d}\):
The crystal limit of them gives \(\mathcal {Z}_{2,0,1,0}^{a,b,c,d}=-\delta _{a,2}\delta _{b,0}\delta _{c,1}\delta _{d,0}\).
The above results give a super analog of Lusztig’s parametrizations of the canonical basis. To the best of my knowledge, there is no such a study considering transition maps for super cases at present. We note that there are some earlier results attempting to construct the canonical basis from PBW bases for super cases recently [9, 10] although they mainly deal with the distinguished Dynkin diagrams and the canonical basis not depending on reduced expressions has obtained only for 
. As we considered for the 3D N, it seems our results are consistent with them. On the other hand, further investigations should be done for negative factors, which is also remarked in [10, Remark 7.10].
6.2 Crystal limit of transition matrices of rank 3
Here, we remark for the case of rank 3. In contrast to the case of rank 2, we can not take the crystal limit for all cases. For example, we obtained the tetrahedron equation for 
given by (4.106):
This equation is not consistent with the crystal limits introduced in the previous section because of their staggered q-dependence of the components.
Among the Dynkin diagrams dealt with Sects. 4.3 and 5.3, we can take the limit for the following cases:
where we omit the non-super cases. Actually, by setting the normalization factors appropriately, we obtain solutions to the tetrahedron and 3D reflection equations which are compositions of bijections. Such solutions are often called set-theoretical or combinatorial, here we use the latter term.
Corollary 6.6
We have the combinatorial solution to the tetrahedron equation given by
and the combinatorial solution up to sign factors given by
where summations are taken on \(x_k{\ }(k=1,\ldots ,6)\).
Corollary 6.7
We have the combinatorial solution to the 3D reflection equation given by
Conjecture 6.8
We have the combinatorial solution to the 3D reflection equation given by
and the combinatorial solution up to sign factors given by
where summations are taken on \(x_k{\ }(k=1,\ldots ,9)\) and \(y_k{\ }(k=2,4,5,6,8,9)\).
7 Concluding Remarks
In this paper, we studied transition matrices of PBW bases of the nilpotent subalgebra of quantum superalgebras of type A and B in the case of rank 2 and 3, and obtained explicit formulae for many cases. By considering the case of rank 3, we obtained the “mother” solution to the tetrahedron equation (4.87) and 3D reflection equation (5.186) as identities of transition matrices attributed to compositions of transition matrices of rank 2 in two ways. Then, we reduced them to special cases and obtained several solutions to the tetrahedron and 3D reflection equation. The parts of them are summarized as the following table:
Type A:
Type B:
It is important that our proofs exploit higher-order relations for quantum superalgebras given in Sects. 4.1 and 5.1, and did not use any result for quantum coordinate rings.
For the case of 
, our approach exactly reproduced matrix elements of the 3D L (3.6), and the associated tetrahedron equation (3.7) for 
. That is one of the remarkable result of this paper. It was known that the 3D L also satisfies another tetrahedron equation (3.18). We obtained the similar equation (4.111) for 
, but it involves nonlocal sign factors, so we can not write it as a matrix equation at present, in the sense explained in Remark 3.3. It is open whether we can attribute (3.18) to (4.111). If we can, it is also interesting whether the procedure “eliminating nonlocal sign factors” can be applied to other tetrahedron equations (4.116) and (4.121), and the 3D reflection equations (5.231), (5.237) and (5.243) for the case of type B.
We further obtained the new solution to the tetrahedron equation by considering 
, which we call the 3D N (4.51). The associated equation (4.106) was obtained by considering 
. We found matrix elements of the 3D N are related to ones of the 3D L as (4.62). It is interesting whether, in general, transition matrices associated with a pair of Cartan data mapped to each other via odd reflections are attributed to each other or not.
Our framework also can be applied to the case of type B. We derived the new solutions to the 3D reflection equation (5.204), (5.211), (5.218) and (5.225). As parts of the equations, we introduced the 3D X, Y and Z and obtained explicit formulae for the 3D X and 3D Y given by (5.83)–(5.98) and (5.106)–(5.121), respectively. Although we did not for the 3D Z, we can calculate any matrix elements by recurrence equations like Example 5.16. We hope to report an explicit formula for the 3D Z in a future publication.
We also discussed the crystal limit of transition matrices for super cases, and obtained a super analog of transition maps of Lusztig’s parametrizations of the canonical basis. We hope that our result gives a new insight into recent studies for a super analog of the canonical basis [9, 10]. It is also an interesting question whether a geometric lifting [5] for them exists or not.
Our result stimulates to challenge whether the Kuniba–Okado–Yamada theorem can be generalized to the case of quantum superalgebras, or not. This question is quite interesting but needs hard works because there is no theory about irreducible representations of quantum super coordinate rings like Soibelman’s theory for the non-super case [42]. To construct a super version of Soibelman’s theory, it seems that the Weyl groupoid plays important roles [15]. More concretely, as we mentioned in Sect. 1, [40] seems to give a related result. We hope to report this issue in a future publication.
Notes
The formula given in [21] involves misprints unfortunately.
References
Baxter, R.J.: Exactly Solved Models in Statistical Mechanics. Dover, Mineola (2007)
Bazhanov, V.V., Baxter, R.J.: New solvable lattice models in three dimensions. J. Stat. Phys. 69, 453–485 (1992)
Bazhanov, V.V., Mangazeev, V.V., Sergeev, S.M.: Quantum geometry of 3-dimensional lattices and tetrahedron equation. In: XVIth International Congress on Mathematical Physics. World Scientific Publishing, Hackensack, pp. 23–44 (2010)
Bazhanov, V.V., Sergeev, S.M.: Zamolodchikov’s tetrahedron equation and hidden structure of quantum groups. J. Phys. A Math. Theor. 39, 3295 (2006)
Berenstein, A., Zelevinsky, A.: Tensor product multiplicities, canonical bases and totally positive varieties. Invent. Math. 143, 77–128 (2001)
Chaichian, M., Kulish, P.: Quantum Lie superalgebras and \(q\)-oscillators. Phys. Lett. B 234, 72–80 (1990)
Cheng, S.J., Wang, W.: Dualities and Representations of Lie Superalgebras, Graduate Studies in Mathematics, vol. 144. American Mathematical Society, Providence (2012)
Cherednik, I.V.: Factorizing particles on a half-line and root systems. Theor. Math. Phys. 61, 35–44 (1984)
Clark, S.: Canonical bases for the quantum enveloping algebra of \(gl(m|1)\) and its modules. arXiv:1605.04266v1
Clark, S., Hill, D., Wang, W.: Quantum shuffles and quantum supergroups of basic type. Quantum Topol. 7, 553–638 (2016)
Drinfeld, V.G.: Quantum groups. Proc. ICM 1(2), 798–820 (1986)
Frappat, L., Sciarrino, A., Sorba, P.: Structure of basic Lie superalgebras and of their affine extensions. Commun. Math. Phys. 121, 457–500 (1989)
Gavrylenko, P., Semenyakin, M., Zenkevich, Y.: Solution of tetrahedron equation and cluster algebras. arXiv:2010.15871v1
Heckenberger, I.: Lusztig isomorphisms for Drinfel’d doubles of bosonizations of Nichols algebras of diagonal type. J. Algebra 323, 2130–2180 (2010)
Heckenberger, I., Yamane, H.: A generalization of Coxeter groups, root systems, and Matsumoto’s theorem. Math. Z. 259, 255–276 (2008)
Humphreys, J.E.: Introduction to Lie Algebras and Representation Theory, Graduate Texts in Mathematics, vol. 9. Springer, New York (1972)
Humphreys, J.E.: Reflection Groups and Coxeter Groups. Cambridge University Press, Cambridge (1990)
Isaev, A.P., Kulish, P.P.: Tetrahedron reflection equations. Mod. Phys. Lett. A 12, 427–437 (1997)
Jimbo, M.: A \(q\)-analogue of \(U(\mathfrak{gl}(N+1))\), Hecke algebra, and the Yang–Baxter equation. Lett. Math. Phys. 11, 247–252 (1986)
Kac, V.G.: Lie superalgebras. Adv. Math. 26, 8–96 (1977)
Kapranov, M.M., Voevodsky, V.A.: 2-categories and Zamolodchikov tetrahedra equations. Proc. Sympos. Pure Math. 56, 177–259 (1994)
Kashiwara, M.: On crystal bases of the \(Q\)-analogue of universal enveloping algebras. Duke Math. J. 63, 465–516 (1991)
Khoroshkin, S., Tolstoy, V.N.: Universal \(R\)-matrix for quantized (super)algebras. Commun. Math. Phys. 141, 599–617 (1991)
Kuniba, A.: Matrix product solutions to the \(G_2\) reflection equation. J. Integrable Syst. 3, xyy008 (2018)
Kuniba, A., Okado, M.: Tetrahedron and 3D reflection equations from quantized algebra of functions. J. Phys. A Math. Theor. 45, 465206 (2012)
Kuniba, A., Okado, M.: A solution of the 3D reflection equation from quantized algebra of functions of type B. In: Symmetries and Groups in Contemporary Physics, Nankai Series in Pure, Applied Mathematics and Theoretical Physics, pp. 181–190 (2013)
Kuniba, A., Okado, M., Sergeev, S.: Tetrahedron equation and generalized quantum groups. J. Phys. A Math. Theor. 48, 304001 (2015)
Kuniba, A., Okado, M., Yamada, Y.: A common structure in PBW bases of the nilpotent subalgebra of \(U_q({g})\) and quantized algebra of functions. SIGMA Symmetry Integr. Geom. Methods Appl. 9:049 (2013)
Kuniba, A., Okado, M., Yoneyama, A.: Reflection \({K}\) matrices associated with an Onsager coideal of \({U}_p({A}_{n-1}^{(1)})\),\({U}_p({B}_n^{(1)})\),\({U}_p({D}_n^{(1)})\) and \({U}_p({D}_{n+1}^{(2)})\). J. Phys. A Math. Theor. 52, 375202 (2019)
Kuniba, A., Pasquier, V.: Matrix product solutions to the reflection equation from three dimensional integrability. J. Phys. A Math. Theor. 51, 255204 (2018)
Leites, D., Saveliev, M., Serganova, V.: Embeddings of Lie superalgebra \(osp(1,2)\) and nonlinear symmetric equations. In: Group Theoretical Methods in Physics, Proceedings of the Third Yurmala Seminar, Yurmala (1985)
Lusztig, G.: Canonical bases arising from quantized enveloping algebras. J. Am. Math. Soc. 3, 447–498 (1990)
Maillet, J.M., Nijhoff, F.W.: Integrability for multidimensional lattice models. Phys. Lett. B 224, 389–396 (1989)
Manin, Y.I.: Multiparametric quantum deformation of the general linear supergroup. Commun. Math. Phys. 123, 163–175 (1989)
Mironov, A., Morozov, A., Runov, B., Zenkevich, Y., Zotov, A.: Spectral dualities in XXZ spin chains and five dimensional gauge theories. JHEP 12, 034 (2013)
Reshetikhin, N.Y., Takhtadzhyan, L.A., Faddeev, L.D.: Quantization of Lie groups and Lie algebras. Leningrad Math. J. 1, 193–225 (1990)
Saito, Y.: Quantized coordinate rings, PBW-type bases and \(q\)-boson algebras. J. Algebra 453, 456–491 (2016)
Sergeev, S.M.: Quantum curve in \(q\)-oscillator model. Int. J. Math. Math. Sci. 2006, 92064 (2006)
Sergeev, S.M.: Tetrahedron equations and nilpotent subalgebras of \({\mathscr {U}}_q(sl_n)\). Lett. Math. Phys. 83, 231–235 (2008)
Sergeev, S.M.: Supertetrahedra and superalgebras. J. Math. Phys. 50, 083519 (2009)
Sergeev, S.M., Mangazeev, V.V., Stroganov, Y.G.: The vertex formulation of the Bazhanov–Baxter model. J. Stat. Phys. 82, 31–49 (1996)
Soibelman, Y.S.: Selected topics in quantum groups. Int. J. Mod. Phys. A 7(Suppl. 1B), 859–887 (1992)
Tanisaki, T.: Modules over quantized coordinate algebras and PBW-bases. J. Math. Soc. Jpn. 69, 1105–1156 (2017)
Xu, Y., Zhang, R.B.: Quantum correspondences of affine Lie superalgebras. arXiv:1607.01142v3
Yamane, H.: Quantized enveloping algebras associated with simple Lie superalgebras and their universal \(R\)-matrices. Publ. RIMS Kyoto Univ. 30, 15–84 (1994)
Zamalodchikov, A.B.: Tetrahedra equations and integrable systems in three-dimensional space. Sov. Phys. JETP 52, 325–336 (1980)
Zamolodchikov, A.B.: Tetrahedron equations and the relativistic \(S\)-matrix of straight-strings in \(2+1\)-dimensions. Commun. Math. Phys. 79, 489–505 (1981)
Zhang, R.B.: Structure and representations of the quantum general linear supergroup. Commun. Math. Phys. 195, 525–547 (1998)
Zhang, R.B.: Serre presentations of Lie superalgebras. In: Advances in Lie Superalgebras, Springer INdAM Series, vol. 7, pp. 235–280 (2014)
Zhelobenko, D.P.: Extremal cocycles of Weyl groups. Funct. Anal. Appl. 21 (1987)
Acknowledgements
The author thanks Atsuo Kuniba and Masato Okado for helpful comments and discussions. Special thanks are due to Atsuo Kuniba for the encouragement to complete this project.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by J. Gier.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Proof of Theorem 5.12
By considering (2.34), it is sufficient to prove \(\tilde{\gamma }_{i,j,k,l}^{a,b,c,d}=\mathscr {X}_{l,k,j,i}^{d,c,b,a}\). Our proof is motivated by the proof of Proposition 2. of [28]. If we obtain an explicit formula for \(X_{i,j,k,l}^{a,b,c,d}\) defined by
we can obtain \(\tilde{\gamma }_{i,j,k,l}^{a,b,c,d}\) by
Then, in order to prove \(\tilde{\gamma }_{i,j,k,l}^{a,b,c,d}=\mathscr {X}_{l,k,j,i}^{d,c,b,a}\), it is sufficient to show \(X_{i,j,k,l}^{a,b,c,d}\) is given by
1.1 A.1. Recurrence Equations
Our strategy to derive (A.3)–(A.10) is using recurrence equations for \(X\). For simplicity, we write \(b_1=e_{1},{\ }b_2=e_{21},{\ }b_3=e_{2(21)},{\ }b_4=e_{2}\) and \(F_1^{i,j,k,l}=b_1^{i}b_2^{j}b_3^{k}b_4^{l}\), \(F_2^{l,k,j,i}=\chi (F_1^{i,j,k,l})\). Then, (A.1) with \(q\rightarrow q^{-1}\) is represented by
The elements \(b_i\) satisfy the following relations:
We can easily prove the following relations for \(n\in \mathbb {N}\) by induction.
Then, the left multiplication of \(b_1,b_2,b_4\) on \(F_1^{a,b,c,d}\) and \(F_2^{l,k,j,i}\) are given by
where the left multiplication of \(b_2\) on \(F_2^{l,k,j,i}\) can be calculated only using the right multiplication of \(b_1,b_4\) on \(F_1^{i,j,k,l}\) via \(b_2F_2^{l,k,j,i}=\chi (F_1^{i,j,k,l}(b_1b_4-qb_4b_1))\). By considering the left multiplication of \(b_1,b_2,b_4\) on (A.11), we obtain the following recurrence equations:
1.2 A.2. 1-parameter family
We first construct the 1-parameter family for \(X_{i,j,k,l}^{a,b,c,d}\) by using (A.29), which has generic j, b and takes as small as possible l, d for each \(i,k,a,c\in \{0,1\}\). By the same discussion as (4.35), we obtain the following weight conservation:
-
(1)
For the case \((i,k,a,c)=(0,0,0,0)\), the non-trivial case for (A.29) is \(j=b+1,l=d\) by (A.31). Then, if we set \(d=0\), (A.29) gives
$$\begin{aligned} X_{0,b+1,0,0}^{0,b+1,0,0} =-qX_{0,b,0,0}^{0,b,0,0} =(-q)^{b+1}X_{0,0,0,0}^{0,0,0,0} . \end{aligned}$$(A.31)It is easy to verify \(X_{0,0,0,0}^{0,0,0,0}=1\), so we obtain
$$\begin{aligned} X_{0,b,0,0}^{0,b,0,0} =(-q)^{b} . \end{aligned}$$(A.32)Later, we use the case \(d=1\). By setting \(d=1\), (A.29) gives
$$\begin{aligned} X_{0,b+1,0,1}^{0,b+1,0,1} =-q^{1/2}(1-q^2)X_{0,b-1,1,0}^{0,b,0,1} +(1-q-q^2)X_{0,b,0,1}^{0,b,0,1} . \end{aligned}$$(A.33) -
(2)
For the case \((i,k,a,c)=(0,1,0,0)\), the non-trivial case for (A.29) is \(j=b,l=d-1\) by (A.31). Then, if we set \(d=1\), (A.29) gives
$$\begin{aligned} X_{0,b,1,0}^{0,b+1,0,1}&=q^2X_{0,b-1,1,0}^{0,b,0,1} -q^{1/2}(1+q)X_{0,b,0,1}^{0,b,0,1} \end{aligned}$$(A.34)$$\begin{aligned}&=q^2\left[ q^2X_{0,b-2,1,0}^{0,b-1,0,1} -q^{1/2}(1+q)X_{0,b-1,0,1}^{0,b-1,0,1} \right] \nonumber \\&\quad -q^{1/2}(1+q)\left[ -q^{1/2}(1-q^2)X_{0,b-2,1,0}^{0,b-1,0,1} +(1-q-q^2)X_{0,b-1,0,1}^{0,b-1,0,1} \right] \end{aligned}$$(A.35)$$\begin{aligned}&=q(1+q-q^2)X_{0,b-2,1,0}^{0,b-1,0,1} -q^{1/2}(1-q^2)X_{0,b-1,0,1}^{0,b-1,0,1} \end{aligned}$$(A.36)$$\begin{aligned}&=q(1-(-q)^{b-1}-(-q)^{b})X_{0,0,1,0}^{0,1,0,1} -q^{1/2}(1-(-q)^b)X_{0,1,0,1}^{0,1,0,1} , \end{aligned}$$(A.37)where we use (A.34). It is easy to verify \(X_{0,0,1,0}^{0,1,0,1}=-q^{1/2}(1+q)\), \(X_{0,1,0,1}^{0,1,0,1}=1-q-q^2\), so we obtain
$$\begin{aligned} X_{0,b,1,0}^{0,b+1,0,1}&=-q^{3/2}(1+q)(1-(-q)^{b-1}-(-q)^{b})-q^{1/2}(1-(-q)^b)(1-q-q^2) \end{aligned}$$(A.38)$$\begin{aligned}&=-q^{1/2}(1-(-q)^{b+1}) . \end{aligned}$$(A.39)
Similarly, we can derive the following formulae for other \(i,k,a,c\in \{0,1\}\):
1.3 A.3. 2-parameter family
Next, we lift the 1-parameter family to the 2-parameter family by using (A.30) and (A.28), which has generic j, k, b, d for each \(i,k,a,c\in \{0,1\}\).
-
(I)
For the case \((a,c)=(0,1)\), (A.30) gives
$$\begin{aligned} X_{i,j,k,l}^{0,b,1,d+1} =qX_{i,j,k,l-1}^{0,b,1,d} =q^{\alpha +1}X_{i,j,k,l-\alpha -1}^{0,b,1,d-\alpha } , \end{aligned}$$(A.47)where \(\alpha \) is specified below.
-
(i)
For the case \((i,k)=(0,0)\), the non-trivial case for (A.48) is \(j=b+1,l=d+2\) by (A.31). In that case, (A.48) gives
$$\begin{aligned} X_{0,b+1,0,d+2}^{0,b,1,d+1}&=q^{d+1}X_{0,b+1,0,1}^{0,b,1,0} , \end{aligned}$$(A.48)$$\begin{aligned} \therefore X_{0,b+1,0,d+1}^{0,b,1,d}&=-q^{d+1/2}(1-q) . \end{aligned}$$(A.49) -
(ii)
For the case \((i,k)=(0,1)\), the non-trivial case for (A.48) is \(j=b,l=d+1\) by (A.31). In that case, (A.48) gives
$$\begin{aligned} X_{0,b,1,d+1}^{0,b,1,d+1}&=q^{d+1}X_{0,b,1,0}^{0,b,1,0} , \end{aligned}$$(A.50)$$\begin{aligned} \therefore X_{0,b,1,d}^{0,b,1,d}&=q^{d+1} . \end{aligned}$$(A.51) -
(iii)
For the case \((i,k)=(1,0)\), the non-trivial case for (A.48) is \(j=b,l=d+3\) by (A.31). In that case, (A.48) gives
$$\begin{aligned} X_{1,b,0,d+3}^{0,b,1,d+1}&=q^{d+1}X_{1,b,0,2}^{0,b,1,0} , \end{aligned}$$(A.52)$$\begin{aligned} \therefore X_{1,b,0,d+2}^{0,b,1,d}&=q^{d+1/2}(1-q)^2 . \end{aligned}$$(A.53) -
(iv)
For the case \((i,k)=(1,1)\), the non-trivial case for (A.48) is \(j=b-1,l=d+2\) by (A.31). In that case, (A.48) gives
$$\begin{aligned} X_{1,b-1,1,d+2}^{0,b,1,d+1}&=q^{d+1}X_{1,b-1,1,1}^{0,b,1,0} , \end{aligned}$$(A.54)$$\begin{aligned} \therefore X_{1,b,1,d+1}^{0,b+1,1,d}&=-q^{d+1}(1-q)(1-(-q)^{b+1}) . \end{aligned}$$(A.55)
-
(i)
-
(II)
For the case \((a,c)=(0,0)\), (A.30) gives
$$\begin{aligned} X_{i,j,k,l}^{0,b,0,d+1}&=X_{i,j,k,l-\alpha -1}^{0,b,0,d-\alpha } -q^{-1/2}(1-(-1)^bq^b)\frac{1-q^{\alpha +1}}{1-q}X_{i,j,k,l-\alpha }^{0,b-1,1,d-\alpha } , \end{aligned}$$(A.56)where \(\alpha \) is specified below.
-
(i)
For the case \((i,k)=(0,0)\), the non-trivial case for (A.57) is \(j=b,l=d+1\) by (A.31). In that case, (A.57) gives
$$\begin{aligned} X_{0,b,0,d+1}^{0,b,0,d+1}&=X_{0,b,0,0}^{0,b,0,0} -q^{-1/2}(1-(-1)^bq^b)\frac{1-q^{d+1}}{1-q}X_{0,b,0,1}^{0,b-1,1,0} , \end{aligned}$$(A.57)$$\begin{aligned} \therefore X_{0,b,0,d}^{0,b,0,d}&=(-q)^{b} +(1-(-q)^b)(1-q^{d}) \end{aligned}$$(A.58)$$\begin{aligned}&=1-(1-(-q)^{b})q^d . \end{aligned}$$(A.59) -
(ii)
For the case \((i,k)=(0,1)\), the non-trivial case for (A.57) is \(j=b-1,l=d\) by (A.31). In that case, (A.57) gives
$$\begin{aligned} X_{0,b-1,1,d}^{0,b,0,d+1}&=X_{0,b-1,1,0}^{0,b,0,1} -q^{-1/2}(1-(-1)^bq^b)\frac{1-q^{d}}{1-q}X_{0,b-1,1,1}^{0,b-1,1,1} \end{aligned}$$(A.60)$$\begin{aligned}&=X_{0,b-1,1,0}^{0,b,0,1} -q^{1/2}(1-(-1)^bq^b)\frac{1-q^{d}}{1-q}X_{0,b-1,1,0}^{0,b-1,1,0} , \end{aligned}$$(A.61)$$\begin{aligned} \therefore X_{0,b,1,d}^{0,b+1,0,d+1}&=-q^{1/2}(1-(-q)^{b+1}) -q^{3/2}(1-(-q)^{b+1})\frac{1-q^{d}}{1-q} \end{aligned}$$(A.62)$$\begin{aligned}&= -\frac{q^{1/2}(1-(-q)^{b+1})(1-q^{d+1})}{1-q} . \end{aligned}$$(A.63) -
(iii)
For the case \((i,k)=(1,0)\), the non-trivial case for (A.57) is \(j=b-1,l=d+2\) by (A.31). In that case, (A.57) gives
$$\begin{aligned} X_{1,b-1,0,d+2}^{0,b,0,d+1}&=X_{1,b-1,0,1}^{0,b,0,0} -q^{-1/2}(1-(-1)^bq^b)\frac{1-q^{d+1}}{1-q}X_{1,b-1,0,2}^{0,b-1,1,0} , \end{aligned}$$(A.64)$$\begin{aligned} \therefore X_{1,b,0,d+1}^{0,b+1,0,d}&=(1-q)(1-(-q)^{b+1}) -(1-q)(1-(-q)^{b+1})(1-q^{d}) \end{aligned}$$(A.65)$$\begin{aligned}&=q^d(1-q)(1-(-q)^{b+1}) . \end{aligned}$$(A.66) -
(iv)
For the case \((i,k)=(1,1)\), the non-trivial case for (A.57) is \(j=b-2,l=d+1\) by (A.31). In that case, (A.57) gives
$$\begin{aligned} X_{1,b-2,1,d+1}^{0,b,0,d+1} =&X_{1,b-2,1,0}^{0,b,0,0} -q^{-1/2}(1-(-1)^bq^b)\frac{1-q^{d+1}}{1-q}X_{1,b-2,1,1}^{0,b-1,1,0} , \end{aligned}$$(A.67)$$\begin{aligned} \therefore X_{1,b,1,d}^{0,b+2,0,d}&=-q^{1/2}(1-(-q)^{b+1})(1-(-q)^{b+2}) \nonumber \\&\quad +q^{1/2}(1-(-q)^{b+1})(1-(-q)^{b+2})(1-q^{d}) \end{aligned}$$(A.68)$$\begin{aligned}&=-q^{d+1/2}(1-(-q)^{b+1})(1-(-q)^{b+2}) . \end{aligned}$$(A.69)
-
(i)
Similarly to (II), we can derive the following formulae for \((a,c)=(1,1)\):
Finally, we consider the case \((a,c)=(1,0)\). (A.28) with \((a,c)=(0,0)\) gives
-
(i)
For the case \((i,k)=(0,0)\), the non-trivial case for (A.73) is \(j=b+1,l=d-1\) by (A.31). In that case, (A.73) gives
$$\begin{aligned} X_{0,b+1,0,d-1}^{1,b,0,d}&=-q^{d-1/2}X_{0,b-1,1,d-1}^{0,b,0,d} +\frac{1-q^{d}}{1-q}X_{0,b,0,d}^{0,b,0,d} \end{aligned}$$(A.73)$$\begin{aligned}&=-q^{d-1/2} \left( -\frac{q^{1/2}(1-(-q)^{b})(1-q^d)}{1-q} \right) \nonumber \\&\quad +\frac{1-q^{d}}{1-q} \left( 1-(1-(-q)^{b})q^{d} \right) \end{aligned}$$(A.74)$$\begin{aligned}&=\frac{1-q^d}{1-q} , \end{aligned}$$(A.75)$$\begin{aligned} \therefore X_{0,b+1,0,d}^{1,b,0,d+1} =&\frac{1-q^{d+1}}{1-q} . \end{aligned}$$(A.76) -
(ii)
For the case \((i,k)=(0,1)\), the non-trivial case for (A.73) is \(j=b,l=d-2\) by (A.31). In that case, (A.73) gives
$$\begin{aligned} X_{0,b,1,d-2}^{1,b,0,d}&=-q\frac{1-q^{d-1}}{1-q}X_{0,b-1,1,d-1}^{0,b,0,d}\nonumber \\&\quad +\frac{(1+q)(1-q^{d-1})(1-q^{d})}{(1-q)(1-q^2)}q^{-d+3/2}X_{0,b,0,d}^{0,b,0,d} \end{aligned}$$(A.77)$$\begin{aligned}&=-q\frac{1-q^{d-1}}{1-q} \left( -\frac{q^{1/2}(1-(-q)^{b})(1-q^d)}{1-q} \right) \nonumber \\&\quad +\frac{(1+q)(1-q^{d-1})(1-q^{d})}{(1-q)(1-q^2)}q^{-d+3/2} \left( 1-(1-(-q)^{b})q^{d} \right) \end{aligned}$$(A.78)$$\begin{aligned}&= \frac{q^{-d+3/2}(1-q^{d-1})(1-q^{d})}{(1-q)^2} , \end{aligned}$$(A.79)$$\begin{aligned} \therefore X_{0,b,1,d}^{1,b,0,d+2}&=\frac{q^{-d-1/2}(1-q^{d+1})(1-q^{d+2})}{(1-q)^2} . \end{aligned}$$(A.80) -
(iii)
For the case \((i,k)=(1,0)\), the non-trivial case for (A.73) is \(j=b,l=d\) by (A.31). In that case, (A.73) gives
$$\begin{aligned} X_{1,b,0,d}^{1,b,0,d}&=(-1)^{b}q^{b+d}X_{0,b,0,d}^{0,b,0,d} -q^{d+1/2}X_{1,b-2,1,d}^{0,b,0,d} +\frac{1-q^{d+1}}{1-q}X_{1,b-1,0,d+1}^{0,b,0,d} \end{aligned}$$(A.81)$$\begin{aligned}&= (-q)^{b}q^{d} \left( 1-(1-(-q)^{b})q^{d} \right) \nonumber \\&\quad -q^{d+1/2} \left( -q^{d+1/2}(1-(-q)^{b-1})(1-(-q)^{b}) \right) \nonumber \\&\quad +\frac{1-q^{d+1}}{1-q} \left( q^{d}(1-q)(1-(-q)^{b}) \right) \end{aligned}$$(A.82)$$\begin{aligned}&=q^d . \end{aligned}$$(A.83) -
(iv)
For the case \((i,k)=(1,1)\), the non-trivial case for (A.73) is \(j=b-1,l=d-1\) by (A.31). In that case, (A.73) gives
$$\begin{aligned} X_{1,b-1,1,d-1}^{1,b,0,d}&=(-q)^{b}q^{d}X_{0,b-1,1,d-1}^{0,b,0,d} -q\frac{1-q^{d}}{1-q}X_{1,b-2,1,d}^{0,b,0,d} \nonumber \\&\quad +\frac{(1+q)(1-q^{d})(1-q^{d+1})}{(1-q)(1-q^2)}q^{-d+1/2}X_{1,b-1,0,d+1}^{0,b,0,d} \end{aligned}$$(A.84)$$\begin{aligned}&=(-q)^{b}q^{d} \left( -\frac{q^{1/2}(1-(-q)^{b})(1-q^d)}{1-q} \right) \nonumber \\&\quad -q\frac{1-q^{d}}{1-q} \left( -q^{d+1/2}(1-(-q)^{b-1})(1-(-q)^{b}) \right) \nonumber \\&\quad +\frac{(1+q)(1-q^{d})(1-q^{d+1})}{(1-q)(1-q^2)}q^{-d+1/2} \left( q^{d}(1-q)(1-(-q)^{b}) \right) \end{aligned}$$(A.85)$$\begin{aligned}&=\frac{q^{1/2}(1-(-q)^{b})(1-q^{d})}{1-q} , \end{aligned}$$(A.86)$$\begin{aligned} \therefore X_{1,b,1,d}^{1,b+1,0,d+1}&=\frac{q^{1/2}(1-(-q)^{b+1})(1-q^{d+1})}{1-q} . \end{aligned}$$(A.87)
Therefore, (A.50), (A.52), (A.54), (A.56), (A.60), (A.64), (A.67), (A.70), (A.71), (A.72), (A.77), (A.81), (A.84) and (A.88) exactly correspond to (A.3)–((A.10)).
Appendix B. Recurrence Equations for the 3D Z
In order to calculate matrix elements of the 3D Z, it is sufficient to calculate \(\tilde{\gamma }_{i,j,k,l}^{a,b,c,d}\) by the relation (2.34). If we obtain a formula for \(Z\) defined by
we can obtain \(\tilde{\gamma }_{i,j,k,l}^{a,b,c,d}\) by
Then, it is sufficient to calculate \(Z_{i,j,k,l}^{a,b,c,d}\). In this section, we derive recurrence equations for \(Z\). By the same discussion as (4.35), we obtain the following weight conservation:
For simplicity, we write \(b_1=e_{1},{\ }b_2=e_{21},{\ }b_3=e_{2(21)},{\ }b_4=e_{2}\) and \(F_1^{i,j,k,l}=b_1^{i}b_2^{j}b_3^{k}b_4^{l}\), \(F_2^{l,k,j,i}=\chi (F_1^{i,j,k,l})\), where \(\chi \) is the anti-algebra automorphism given by (2.20). Then, (B.1) is represented by
The elements \(b_i\) satisfy the following relations:
We can easily prove the following relations for \(n\in \mathbb {N}\) by induction.
Then, the left multiplication of \(b_2,b_3,b_4\) on \(F_1^{a,b,c,d}\) are given by
and the right multiplication of \(b_1,b_4\) on \(F_1^{i,j,k,l}\) are given by
Calculating \(F_1^{i,j,k,l}(b_1b_4-qb_4b_1)\) and \(F_1^{i,j,k,l}(b_1b_4^2+(1-q)b_4b_1b_4-qb_4^2b_1)/(q^{1/2}+q^{-1/2})\), then by using \(\chi \), we get
By considering the left multiplication of \(b_2,b_3,b_4\) on (B.4), we obtain the following recurrence equations:
which (B.24) holds for \(b\ge 1\), (B.25) holds for \(c\ge 1\) and (B.26) holds for \(d\ge 1\).
We can calculate \(Z_{i,j,k,l}^{a,b,c,d}\) by using the above reccurence equations (B.24)–(B.26) as follows. First, we can reduce \(Z_{i,j,k,l}^{a,b,c,d}\) to the case of \(d=0\) by using (B.26). Second, we can reduce \(Z_{i,j,k,l}^{a,b,c,0}\) to the case of \(c=0\) by using (B.25) keeping \(d=0\). Finally, we can reduce \(Z_{i,j,k,l}^{a,b,0,0}\) to the case of \(b=0\) by using (B.24) keeping \(c=d=0\). Then, by considering the weight conservation (B.3), we find \(Z_{i,j,k,l}^{i,0,0,0}\ne 0\) for \(j=k=l=0\) and \(a=i\). In that case, we can easily obtain \(Z_{i,0,0,0}^{i,0,0,0}=1\) by (B.1). Therefore, we can obtain any matrix elements of \(Z\) by the above procedure. See Example 5.16 for the cases of \((i,j,k,l)=(0,1,1,2)\).
Rights and permissions
About this article
Cite this article
Yoneyama, A. Tetrahedron and 3D Reflection Equation from PBW Bases of the Nilpotent Subalgebra of Quantum Superalgebras. Commun. Math. Phys. 387, 481–550 (2021). https://doi.org/10.1007/s00220-021-04098-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-04098-8