On a strengthening of the Blaschke–Leichtweiss theorem

Abstract

The Blaschke–Leichtweiss theorem (Leichtweiss in Abh Math Semin Univ Hambg 75:257–284, 2005) states that the smallest area convex domain of constant width w in the 2-dimensional spherical space ${\mathbb {S}}^2$ is the spherical Reuleaux triangle for all $0<w\le \frac{\pi }{2}$. In this paper we extend this result to the family of wide r-disk domains of ${\mathbb {S}}^2$, where $0<r\le \frac{\pi }{2}$. Here a wide r-disk domain is an intersection of spherical disks of radius r with centers contained in their intersection. This gives a new and elementary proof of the Blaschke–Leichtweiss theorem. Furthermore, we investigate the higher dimensional analogue of wide r-disk domains called wide r-ball bodies. In particular, we determine their minimum spherical width (resp., inradius) in the spherical d-space ${\mathbb {S}}^d$ for all $d\ge 2$. Also, it is shown that any minimum volume wide r-ball body is of constant width r in ${\mathbb {S}}^d$, $d\ge 2$.

1 Introduction

1.1 On the definition of convex bodies of constant width in spherical space

Let ${\mathbb {S}}^d=\{\textbf{x}\in {\mathbb {E}}^{d+1} \ |\ \Vert \textbf{x}\Vert =\sqrt{\langle \textbf{x},\textbf{x}\rangle }=1\}$ be the unit sphere centered at the origin $\textbf{o}$ in the $(d+1)$-dimensional Euclidean space ${\mathbb {E}}^{d+1}$, where $\Vert \cdot \Vert$ and $\langle \cdot , \cdot \rangle$ denote the canonical Euclidean norm and the canonical inner product in ${\mathbb {E}}^{d+1}$, $d\ge 2$. A $(d-1)$-dimensional great sphere of ${\mathbb {S}}^d$ is an intersection of ${\mathbb {S}}^d$ with a hyperplane of ${\mathbb {E}}^{d+1}$ passing through $\textbf{o}$ (i.e., with a d-dimensional linear subspace of ${\mathbb {E}}^{d+1}$). In particular, an intersection of ${\mathbb {S}}^d$ with a 2-dimensional linear subspace in ${\mathbb {E}}^{d+1}$ is called a great circle of ${\mathbb {S}}^d$. Two points are called antipodes if they can be obtained as an intersection of ${\mathbb {S}}^d$ with a line through $\textbf{o}$ in ${\mathbb {E}}^{d+1}$. If $\text{\AA },\textbf{b}\in {\mathbb {S}}^d$ are two points that are not antipodes, then we label the (uniquely determined) shortest geodesic arc of ${\mathbb {S}}^d$ connecting $\textbf{a}$ and $\textbf{b}$ by $\textbf{a}\textbf{b}$. In other words, $\textbf{a}\textbf{b}$ is the shorter circular arc with endpoints $\textbf{a}$ and $\textbf{b}$ of the great circle $\widehat{\textbf{a}\textbf{b}}$ that passes through $\textbf{a}$ and $\textbf{b}$. The length of $\textbf{a}\textbf{b}$ is called the spherical distance between $\textbf{a}$ and $\textbf{b}$ and it is labelled by $\textrm{dist}_s (\textbf{a},\textbf{b})$. Clearly, $0<\textrm{dist}_s (\textbf{a},\textbf{b})<\pi$. If $\textbf{a},\textbf{b}\in {\mathbb {S}}^d$ are antipodes, then we set $\textrm{dist}_s (\textbf{a},\textbf{b})=\pi$. Let $\textbf{x}\in {\mathbb {S}}^d$ and $r\in (0,\frac{\pi }{2}]$. Then the set

$$\begin{aligned}{} & {} \textbf{B}_s^d[\textbf{x}, r]:=\{\textbf{y}\in {\mathbb {S}}^d\ |\ \textrm{dist}_s (\textbf{x},\textbf{y})\le r\}\ (\mathrm{resp.,}\ \textbf{B}_s^d(\textbf{x}, r):=\\{} & {} \quad \{\textbf{y}\in {\mathbb {S}}^d\ |\ \textrm{dist}_s (\textbf{x},\textbf{y})< r\}) \end{aligned}$$

is called the d-dimensional closed (resp., open) spherical ball, or shorter the d-dimensional closed (resp., open) ball, centered at $\textbf{x}$ having (spherical) radius r in ${\mathbb {S}}^d$. In particular, $\textbf{B}_s^d[\textbf{x}, \frac{\pi }{2}]$ (resp., $\textbf{B}_s^d(\textbf{x}, \frac{\pi }{2})$) is called the closed (resp., open) hemisphere of ${\mathbb {S}}^d$ with center $\textbf{x}$. Moreover, $\textbf{B}_s^2[\textbf{x}, r]$ (resp., $\textbf{B}_s^2(\textbf{x}, r)$) is called the closed (resp., open) disk with center $\textbf{x}$ and (spherical) radius r in ${\mathbb {S}}^2$. Now, the boundary of $\textbf{B}_s^d[\textbf{x},r]$ (resp., $\textbf{B}_s^d(\textbf{x}, r)$) in ${\mathbb {S}}^d$ is called the $(d-1)$-dimensional sphere $S_s^{d-1}(\textbf{x}, r)$ with center $\textbf{x}$ and (spherical) radius r in ${\mathbb {S}}^d$. As a special case, the boundary of the disk $\textbf{B}_s^2[\textbf{x}, r]$ (resp., $\textbf{B}_s^2(\textbf{x}, r)$) in ${\mathbb {S}}^2$ is called the circle with center $\textbf{x}$ and of (spherical) radius r and it is labelled by $S_s^1(\textbf{x}, r)$. We introduce the following additional notations. For a set $X\subseteq {\mathbb {S}}^d$ and $r\in (0,\frac{\pi }{2}]$ let

$$\begin{aligned} \textbf{B}_s^d[X, r]:= \bigcap _{\textbf{x}\in X}{} \textbf{B}_s^d[\textbf{x}, r]\ \textrm{and}\ \textbf{B}_s^d(X, r):= \bigcap _{\textbf{x}\in X}{} \textbf{B}_s^d(\textbf{x}, r). \end{aligned}$$

Another basic concept is spherical convexity: we say that $Q\subset {\mathbb {S}}^d$ is spherically convex if it has no antipodes and for any two points $\textbf{x},\textbf{y}\in Q$ we have $\textbf{x}\textbf{y}\subseteq Q$. (It follows that there exists $\textbf{q}\in {\mathbb {S}}^d$ such that $Q\subseteq \textbf{B}_s^d(\textbf{q}, \frac{\pi }{2})$ with $\textbf{B}_s^d(\textbf{x}, \frac{\pi }{2})$ being spherically convex.) As the intersection of spherically convex sets is spherically convex therefore if $X\subset \textbf{B}_s^d(\textbf{x}, \frac{\pi }{2})$, then we define the spherical convex hull $\textrm{conv}_sX$ of X as the intersection of spherically convex sets containing X. By a convex body in ${\mathbb {S}}^d$ (resp., a convex domain in ${\mathbb {S}}^2$) we mean a closed spherically convex set with non-empty interior in ${\mathbb {S}}^d$ (resp., in ${\mathbb {S}}^2$). Let ${\mathcal {K}}_s^d, d\ge 2$ denote the family of convex bodies in ${\mathbb {S}}^d$. If $Q\subseteq {\mathbb {S}}^d, d\ge 2$, then its spherical diameter is $\textrm{diam}_s(Q):=\sup \{\textrm{dist}_s(\textbf{x},\textbf{y})\ |\ \textbf{x},\textbf{y}\in Q\}$. The following brief definition serves the purpose of our introduction as well as motivates our strengthening of the Blaschke–Leichtweiss theorem in an efficient way. On the other hand, we call the attention of the interested reader to some equivalent definitions that are discussed in the articles [5, 12, 18, 22,23,24,25, 28] and are surveyed in [26].

Definition 1.1

Let $\textbf{K}\subset {\mathbb {S}}^d, d\ge 2$ be a closed set with spherical diameter $0<w:=\textrm{diam}_s(\textbf{K})\le \frac{\pi }{2}$. We say that $\textbf{K}$ is a convex body of constant width w in ${\mathbb {S}}^d$ if $\textbf{K}=\textbf{B}_s^d[\textbf{K}, w]$. Let ${\mathcal {K}}_s^d(w)$ denote the family of convex bodies of constant width w in ${\mathbb {S}}^d$ for $d\ge 2$ and $0<w\le \frac{\pi }{2}$.

Clearly, ${\mathcal {K}}_s^d(w)\subset {\mathcal {K}}_s^d$ for all $d\ge 2$ and $0<w\le \frac{\pi }{2}$.

1.2 The Blaschke–Leichtweiss theorem

The classical Blaschke-Lebesgue theorem states that in the Euclidean plane among all convex sets of constant width $w'>0$ the Reuleaux triangle minimizes area. Here the Reuleaux triangle is the intersection of three disks of radius $w'$ with centers at the vertices of an equilateral triangle of side length $w'$. For a survey on this theorem and its impact on extremal geometry we refer the interested reader to the recent elegant papers [20] and [21]. Very different proofs of this theorem were given by Blaschke [8], Lebesgue [27], Fujiwara [15, 16], Eggleston [14], Besicovich [2], Ghandehari [17], Campi, Colesanti, and Gronchi [10], Harrell [19], and M. Bezdek [7]. So, it is natural to ask whether any of these proofs can be extended to ${\mathbb {S}}^2$. Actually, Blaschke claimed that this can be done with his Euclidean proof (see [8], p. 505), but one had to wait until Leichtweiss did it (using some ideas of Blaschke) in [28]. So, we call the following statement the Blaschke–Leichtweiss theorem: if $\textbf{K}\in {\mathcal {K}}_s^2(w)$ with $0<w\le \frac{\pi }{2}$, then

$$\begin{aligned} \textrm{area}_s(\textbf{K})\ge \textrm{area}_s(\mathbf{\Delta }_2(w)), \end{aligned}$$

(1)

where $\textrm{area}_s(\cdot )$ refers to the spherical area of the corresponding set in ${\mathbb {S}}^2$ and $\mathbf{\Delta }_2(w)$ denotes the spherical Reuleaux triangle which is the intersection of three disks of radius w with centers at the vertices of a spherical equilateral triangle of side length w. As the only known proof of (1) is the one published in [28] which is a combination of geometric and analytic ideas presented on twenty pages, one might wonder whether there is a simpler approach. This paper intends to fill this gap by proving a stronger result (Theorem 1.3) in a new and elementary way. The Euclidean analogue of Theorem 1.3 has already been proved for disk-polygons in [7] and our proof of Theorem 1.3 presented below is an extension of the Euclidean technique of [7] to ${\mathbb {S}}^2$ combined with the properly modified spherical method of [3]. For the sake of completeness we note that in [3] the author and Blekherman proved a spherical analogue of Pál’s theorem stating that the minimal spherical area convex domain of given minimal spherical width $\omega$ is a regular spherical triangle for all $0<\omega \le \frac{\pi }{2}$.

1.3 The Blaschke–Leichtweiss theorem extended: minimizing the area of wide r-disk domains in ${\mathbb {S}}^2$

The following definition introduces wide r-disk domains in ${\mathbb {S}}^2$ the spherical areas of which we wish to minimize for given $0<r\le \frac{\pi }{2}$.

Definition 1.2

Let $0<r\le \frac{\pi }{2}$ be given and let $\emptyset \ne X$ be a closed subset of ${\mathbb {S}}^2$ with $\textrm{diam}_s(X)\le r$. Then $\textbf{B}_s^2[X, r]$ is called the wide r-disk domain generated by X in ${\mathbb {S}}^2$. The family of wide r-disk domains of ${\mathbb {S}}^2$ is labelled by ${\mathcal {B}}^2_{s,\textrm{wide}}(r)$.

Now, (1) can be generalized as follows.

Theorem 1.3

Let $0<r\le \frac{\pi }{2}$ and $\textbf{D}\in {\mathcal {B}}^2_{s, \textrm{wide}}(r)$. Then $\textrm{area}_s(\textbf{D})\ge \textrm{area}_s(\mathbf{\Delta }_2(r))$.

As $\mathbf{\Delta }_2(r)\in {\mathcal {K}}_s^2(r)\subset {\mathcal {B}}^2_{s, \textrm{wide}}(r)$ holds for all $0<r\le \frac{\pi }{2}$ therefore (1) follows from Theorem 1.3 in a straightforward way. We note that our method of proving Theorem 1.3 is completely different from the ideas and techniques used in [28].

The rest of the paper is organized as follows. Section 3 gives a proof of Theorem 1.3 via successive area decreasing cuts and symmetrization. That proof is based on some extremal properties of wide r-disk domains, which are discussed in Sect. 2. Furthermore, Sect. 2 investigates the higher dimensional analogue of wide r-disk domains called wide r-ball bodies for $0<r\le \frac{\pi }{2}$. In particular, we determine their minimum spherical width (resp., inradius) in ${\mathbb {S}}^d$, $d\ge 2$. Also, it is shown that any minimum volume wide r-ball body is of constant width r in ${\mathbb {S}}^d$, $d\ge 2$.

2 On minimizing the inradius, width, and volume of wide r-ball bodies in ${\mathbb {S}}^d$ for $d\ge 2$ and $0<r\le \frac{\pi }{2}$

It is natural to extend Definition 1.2 to ${\mathbb {S}}^d$ thereby introducing the family of wide r-ball bodies (resp., wide r-ball polyhedra) in ${\mathbb {S}}^d$ as follows.

Definition 2.1

Let $0<r\le \frac{\pi }{2}$ be given and let $\emptyset \ne X$ be a closed subset of ${\mathbb {S}}^d$, $d\ge 2$ with $\textrm{diam}_s(X)\le r$. Then $\textbf{B}_s^d[X, r]$ is called a wide r-ball body generated by X in ${\mathbb {S}}^d$. The family of wide r-ball bodies of ${\mathbb {S}}^d$ is labelled by ${\mathcal {B}}^d_{s,\textrm{wide}}(r)$. If $X\subset {\mathbb {S}}^d$ with $0<\textrm{card}(X)<+\infty$ and $\textrm{diam}_s(X)\le r$, then $\textbf{B}_s^d[X, r]$ is called a wide r-ball polyhedron generated by X in ${\mathbb {S}}^d$. The family of wide r-ball polyhedra of ${\mathbb {S}}^d$ is labelled by ${\mathcal {P}}^d_{s, \textrm{wide}}(r)$.

We leave the straightforward proof of the following claim (using Definition 2.1) to the reader.

Proposition 2.2

Every wide r-ball body $\textbf{B}_s^d[X, r]\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)$, $d\ge 2$, $0<r\le \frac{\pi }{2}$ can be approximated (in the Hausdorff sense) arbitrarily close by a suitable wide r-ball polyhedron and therefore there exists a sequence $\textbf{P}_n\in {\mathcal {P}}^d_{s, \textrm{wide}}(r)$, $n=1,2,\dots$ such that $\lim _{n\rightarrow +\infty }\textrm{vol}_s(\textbf{P}_n)=\textrm{vol}_s(\textbf{B}_s^d[X, r])$, where $\textrm{vol}_s(\cdot )$ stands for the d-dimensional spherical volume of the corresponding set in ${\mathbb {S}}^d$.

Although the question of finding an extension of Theorem 1.3 to ${\mathbb {S}}^d$ for $d\ge 3$ seems to be a natural one, it is a considerably more difficult problem than it appears at first sight. Based on Proposition 2.2 we can phrase it as follows.

Problem 2.3

Find

$$\begin{aligned}{} & {} c_{BL}(r, d):=\inf \{\textrm{vol}_s(\textbf{B}_s^d[X, r])\ |\ \textbf{B}_s^d[X, r]\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)\}\\{} & {} \quad =\inf \{\textrm{vol}_s(\textbf{P}_s^d[X, r])\ |\ \textbf{P}_s^d[X, r]\in {\mathcal {P}}^d_{s, \textrm{wide}}(r)\} \end{aligned}$$

for given $0<r\le \frac{\pi }{2}$ and $d\ge 3$.

Proposition 2.5 can be used to lower bound $c_{BL}(r, d)$ with the spherical volume of a properly chosen ball.

Definition 2.4

The smallest ball (resp., the largest ball) containing (resp., contained in) the convex body $\textbf{K}\in {\mathcal {K}}_s^d$, $d\ge 2$ is called the circumscribed (resp., inscribed) ball of $\textbf{K}$ whose radius $R_\textrm{cr}(\textbf{K})$ (resp., $R_\textrm{in}(\textbf{K})$) is called the circumradius (resp., inradius) of $\textbf{K}$.

Proposition 2.5

Let $\textbf{B}_s^d[X, r]\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)$ with $d\ge 2$ and $0<r\le \frac{\pi }{2}$. Then

$$\begin{aligned} R_\textrm{in}(\textbf{B}_s^d[X, r]) \ge R_\textrm{in}(\mathbf{\Delta }_d(r)), \end{aligned}$$

where $\mathbf{\Delta }_d(r)\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)$ denotes the intersection of $d+1$ closed balls of radii r centered at the vertices of a regular spherical d-simplex of edge length r in ${\mathbb {S}}^d$.

Proof

As $\textbf{B}_s^d[X, r]\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)$ therefore $\textrm{diam}_s(X)\le r$. This and the spherical Jung theorem [13] imply that there exists $\textbf{x}_0\in {\mathbb {S}}^d$ such that $X\subset \textbf{B}_s^d[\textbf{x}_0, R_\textrm{cr}(\mathbf{\Delta }_d(r))]$. It follows that

$$\begin{aligned} \textbf{B}_s^d[\textbf{x}_0,R_\textrm{in}(\mathbf{\Delta }_d(r))]=\textbf{B}_s^d[\textbf{x}_0, r-R_\textrm{cr}(\mathbf{\Delta }_d(r))]\subset \textbf{B}_s^d[X, r] \end{aligned}$$

and therefore $R_\textrm{in}(\textbf{B}_s^d[X, r]) \ge R_\textrm{in}(\mathbf{\Delta }_d(r))$, finishing the proof of Proposition 2.5. $\square$

For more details on the concepts introduced in Definitions 2.6, 2.7, and 2.8, we refer the interested reader to the recent paper of Lassak [22]. As usual, we say that the $(d-1)$-dimensional great sphere $C_s^{d-1}(\textbf{x}, \frac{\pi }{2})$ is a supporting $(d-1)$-dimensional great sphere of $\textbf{K}\in {\mathcal {K}}_s^d$ if $C_s^{d-1}(\textbf{x}, \frac{\pi }{2})\cap \textbf{K}\ne \emptyset$ and $\textbf{K}\subset \textbf{B}_s^d[\textbf{x},\frac{\pi }{2}]$, in which case $\textbf{B}_s^d[\textbf{x},\frac{\pi }{2}]$ is called a closed supporting hemisphere of $\textbf{K}$. One can show that through each boundary point of $\textbf{K}$ there exists at least one supporting $(d-1)$-dimensional great sphere of $\textbf{K}$ moreover, $\textbf{K}$ is the intersection of its closed supporting hemispheres. Two hemispheres of ${\mathbb {S}}^d$ are called opposite if the their centers are antipodes.

Definition 2.6

The intersection of two distinct closed hemispheres of ${\mathbb {S}}^d$ which are not opposite is called a lune of ${\mathbb {S}}^d$. Let ${\mathcal {L}}_s^d$ denote the family of lunes in ${\mathbb {S}}^d$.

Every lune of ${\mathbb {S}}^d$ is bounded by two $(d-1)$-dimensional hemispheres (lying on two distinct $(d-1)$-dimensional great spheres of ${\mathbb {S}}^d$) sharing pairs of antipodes in common, which are called the vertices of the lune.

Definition 2.7

The angular measure of the angle formed by the two $(d-1)$-dimensional hemispheres bounding the lune $\textbf{L}\in {\mathcal {L}}_s^d$ (which is equal to spherical distance of the centers of the two $(d-1)$-dimensional hemispheres bounding $\textbf{L}$) is called the spherical width of the given lune labelled by $\textrm{width}_s(\textbf{L})$.

Definition 2.8

For every closed supporting hemisphere $\textbf{H}$ of the convex body $\textbf{K}\in {\mathcal {K}}_s^d$ there exists a closed supporting hemisphere $\textbf{H}'$ of $\textbf{K}$ such that the lune $\textbf{H}\cap \textbf{H}'$ has minimal width for given $\textbf{H}$ and $\textbf{K}$. We call $\textrm{width}_s(\textbf{H}\cap \textbf{H}')$ the width of $\textbf{K}$ determined by $\textbf{H}$ and label it by $\textrm{width}_\textbf{H}(\textbf{K})$. Finally, the minimal spherical width (also called thickness) $\textrm{width}_s(\textbf{K})$ of $\textbf{K}$ is the smallest spherical width of the lunes that contain $\textbf{K}$, i.e., $\textrm{width}_s(\textbf{K})=\min \{\textrm{width}_\textbf{H}(\textbf{K})\ |\ \textbf{H}\ { is\ a \ closed} {supporting\ hemisphere\ of}\ \textbf{K}\}$.

Next, we recall the following claim from [22] (Claim 2), which is often applicable.

Sublemma 2.9

Let $\textbf{K}\in {\mathcal {K}}_s^d$. If $\textbf{L}\in {\mathcal {L}}_s^d$ contains $\textbf{K}$ and $\textrm{width}_s(\textbf{K}){=}\textrm{width}_s(\textbf{L})$, then both centers of the $(d-1)$-dimensional hemispheres bounding $\textbf{L}$ belong to $\textbf{K}$.

Remark 2.10

We note that Definition 2.8 supports to say that the convex body $\textbf{K}\in {\mathcal {K}}_s^d$ is of constant width $0<w\le \frac{\pi }{2}$ in ${\mathbb {S}}^d$ if the width of $\textbf{K}$ with respect to any supporting hemisphere is equal to w. Theorem 2 of [25] proves that this definition of constant width is equivalent to the one under Definition 1.1, i.e., $\textbf{K}\in {\mathcal {K}}_s^d(w)$ for $d\ge 2$ and $0<w\le \frac{\pi }{2}$ if and only if $\textrm{width}_s(\textbf{K})=\textrm{diam}_s(\textbf{K}) =w$ holds for $\textbf{K}\in {\mathcal {K}}_s^d$.

Now, we are ready to prove the following close relative of Proposition 2.5.

Proposition 2.11

Let $\textbf{B}_s^d[X, r]\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)$ with $d\ge 2$ and $0<r\le \frac{\pi }{2}$. Then

$$\begin{aligned} \textrm{width}_s(\textbf{B}_s^d[X, r]) \ge \textrm{width}_s(\mathbf{\Delta }_d(r))=r. \end{aligned}$$

Proof

It will be convenient to use the following notion (resp., notation) from [6].

Definition 2.12

For a set $X\subseteq {\mathbb {S}}^d$, $d\ge 2$ and $0<r\le \frac{\pi }{2}$ let the r-dual set $X^r$ of X be defined by $X^r:=\textbf{B}_s^d[X, r]$. If the spherical interior $\textrm{int}_s(X^r)\ne \emptyset$, then we call $X^r$ the r-dual body of X.

r-dual sets satisfy some basic identities such as $((X^r)^r)^r=X^r$ and $(X\cup Y)^r=X^r\cap Y^r$, which hold for any $X\subseteq {\mathbb {S}}^d$ and $Y\subseteq {\mathbb {S}}^d$. Clearly, also monotonicity holds namely, $X\subseteq Y\subseteq {\mathbb {S}}^d$ implies $Y^r\subseteq X^r$. Thus, there is a good deal of similarity between r-dual sets and spherical polar sets in ${\mathbb {S}}^d$. For more details see [6]. The following statement is a spherical analogue of Lemma 3.1 in [4].

Sublemma 2.13

Let $\textbf{H}$ be a closed supporting hemisphere of the r-dual body $X^r$ of $X\subset {\mathbb {S}}^d$ bounded by the $(d-1)$-dimensional great sphere H in ${\mathbb {S}}^d$ such that $\textbf{H}$ and H support $X^r$ at the boundary point $\textbf{x}\in H\cap \textrm{bd}(X^r)$, where $d\ge 2$, and $0<r\le \frac{\pi }{2}$. Then the d-dimensional closed ball of radius r of ${\mathbb {S}}^d$ that is tangent to H at $\textbf{x}$ and lies in $\textbf{H}$ contains the r-dual body $X^r$.

Proof

(The following proof is the spherical analogue of the Euclidean proof of Lemma 3.1 of [4].) Let $\textbf{B}_s^d[\textbf{c}, r]$ be the d-dimensional closed ball of radius r of ${\mathbb {S}}^d$ that is tangent to H at $\textbf{x}$ and lies in $\textbf{H}$. Assume that $X^r$ is not contained in $\textbf{B}_s^d[\textbf{c}, r]$, i.e., let $\textbf{y}\in X^r\setminus \textbf{B}_s^d[\textbf{c}, r]$. Then by taking the intersection of the configuration with the 2-dimensional spherical plane spanned by $\textbf{x}, \textbf{y}$, and $\textbf{c}$ we see that there is a shorter circular arc of radius r connecting $\textbf{x}$ and $\textbf{y}$ that is not contained in $\textbf{B}_s^d[\textbf{c}, r]$ and therefore it is not supported by neither H nor $\textbf{H}$. On the other hand, as $\textbf{x},\textbf{y}\in X^r$ therefore any such arc must be contained in $X^r$ and must be supported by H as well as $\textbf{H}$, a contradiction. $\square$

Now, let $X^r=\textbf{B}_s^d[X, r]\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)$ with $d\ge 2$ and $0<r\le \frac{\pi }{2}$. Sublemma 2.9 implies that there exists $\textbf{L}\in {\mathcal {L}}_s^d$ such that $X^r\subseteq \textbf{L}:=\textbf{B}_s^d[\textbf{x}, \frac{\pi }{2}]\cap \textbf{B}_s^d[\textbf{y}, \frac{\pi }{2}]$ and $\textbf{x}'\in S_s^{d-1}(\textbf{x}, \frac{\pi }{2})\cap X^r$ is the center of the $(d-1)$-dimensional hemisphere $S_s^{d-1}(\textbf{x}, \frac{\pi }{2})\cap \textbf{B}_s^d[\textbf{y}, \frac{\pi }{2}]$ and $\textbf{y}'\in S_s^{d-1}(\textbf{y}, \frac{\pi }{2})\cap X^r$ is the center of the $(d-1)$-dimensional hemisphere $S_s^{d-1}(\textbf{y}, \frac{\pi }{2})\cap \textbf{B}_s^d[\textbf{x}, \frac{\pi }{2}]$ satisfying $\textrm{width}_s(X^r)=\textrm{width}_s(\textbf{L})=\textrm{dist}_s(\textbf{x}',\textbf{y}')$. It follows from Sublemma 2.13 in a straightforward way that there exists $\textbf{B}_s^d[\textbf{x}'', r]$ (resp., $\textbf{B}_s^d[\textbf{y}'', r]$) such that $X^r\subseteq \textbf{B}_s^d[\textbf{x}'', r]\subseteq \textbf{B}_s^d[\textbf{x}, \frac{\pi }{2}]$ (resp., $X^r\subseteq \textbf{B}_s^d[\textbf{y}'', r]\subseteq \textbf{B}_s^d[\textbf{y}, \frac{\pi }{2}]$) and $\textbf{B}_s^d[\textbf{x}'', r]$ (resp., $\textbf{B}_s^d[\textbf{y}'', r]$) is tangent to $S_s^{d-1}(\textbf{x}, \frac{\pi }{2})$ (resp., $S_s^{d-1}(\textbf{y}, \frac{\pi }{2})$) at $\textbf{x}'$ (resp., $\textbf{y}'$) with $\textbf{x}''\in ({X^r})^{r}$ (resp., $\textbf{y}''\in ({X^r})^{r}$). By construction

$$\begin{aligned} 2r-\textrm{width}_s(X^r)=2r-\textrm{dist}_s(\textbf{x}',\textbf{y}')=\textrm{dist}_s(\textbf{x}'',\textbf{y}'')\le \textrm{diam}_s\left( (X^r)^{r}\right) \end{aligned}$$

and therefore

$$\begin{aligned} 2r\le \textrm{width}_s(X^r)+\textrm{diam}_s(({X^r})^{r}). \end{aligned}$$

(2)

Sublemma 2.14

Let $0<r\le \frac{\pi }{2}$ be given and let $\emptyset \ne X$ be a closed subset of ${\mathbb {S}}^d$, $d\ge 2$ with $\textrm{diam}_s(X)\le r$. Then

$$\begin{aligned} \textrm{diam}_s\left( (X^r)^{r}\right) \le r. \end{aligned}$$

(3)

Proof

Recall ([12] or [25]) that a closed set $Y\subset {\mathbb {S}}^d$ is called a complete set if $\textrm{diam}_s(Y\cup \{\textbf{y}\})>\textrm{diam}_s (Y)$ holds for all $\textbf{y}\in {\mathbb {S}}^d\setminus Y$. It is easy to prove the following claim (see Lemma 1 of [25]): if Y is a complete set with $\textrm{diam}(Y)\le \frac{\pi }{2}$, then $Y= Y^{\textrm{diam}_s(Y)}\in {\mathcal {K}}_s^d(\textrm{diam}_s (Y))\subset {\mathcal {K}}_s^d$. Furthermore, it is well know (see Theorem 1 of [12] or Theorem 1 of [25]) that each set of diameter $\delta \in (0, \pi )$ in ${\mathbb {S}}^d$ is a subset of a complete set of diameter $\delta$ in ${\mathbb {S}}^d$. Thus, there exists a complete set $Y\subset {\mathbb {S}}^d$ such that $X\subseteq Y$ with $\textrm{diam}_s(X)\le \textrm{diam}_s(Y)=r$. By the monotonicity of the r-dual operation it follows that $(X^r)^r\subseteq (Y^r)^r=Y$ and so, $\textrm{diam}_s\left( (X^r)^{r}\right) \le \textrm{diam}_s(Y)=r$. $\square$

Thus, (2) and (3) yield $r\le \textrm{width}_s(X^r)$, finishing the proof of Proposition 2.11. $\square$

In fact, $c_{BL}(r, d)$ is equal to the minimum of the volumes of convex bodies of constant width r in ${\mathbb {S}}^d$ as stated in Proposition 2.15. This can be proved as follows. Let $0<r\le \frac{\pi }{2}$ be given and let $\emptyset \ne X$ be a closed subset of ${\mathbb {S}}^d$, $d\ge 2$ with $\textrm{diam}_s(X)\le r$. Then the proof of Sublemma 2.14 shows the existence of a complete set $Y\subset {\mathbb {S}}^d$ such that $X\subseteq Y$ with $\textrm{diam}_s(X)\le \textrm{diam}_s(Y)=r$. As $Y^r=Y$ therefore Y is a convex body of constant width r, i.e., $Y\in {\mathcal {K}}_s^d(r)$. Moreover, the monotonicity of the r-dual operation implies that $Y=Y^r\subseteq X^r$, where $X^r=\textbf{B}_s^d[X, r]\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)$. Finally, Blaschke’s selection theorem applied to ${\mathcal {K}}_s^d(r)$ [29] yields

Proposition 2.15

Every wide r-ball-body $\textbf{B}_s^d[X, r]\in {\mathcal {B}}^d_{s, \textrm{wide}}(r)$ contains a convex body of constant width r, i.e., there exists $Y=\textbf{B}_s^d[Y, r]\in {\mathcal {K}}_{s}^d(r)$ such that $Y\subseteq \textbf{B}_s^d[X, r]$, where $0<r\le \frac{\pi }{2}$ and $d\ge 2$. Thus,

$$\begin{aligned} c_{BL}(r, d)=\min \{\textrm{vol}_s(\textbf{K})\ |\ \textbf{K}\in {\mathcal {K}}_{s}^d(r)\} \end{aligned}$$

holds for all $0<r\le \frac{\pi }{2}$ and $d\ge 2$.

In connection with Proposition 2.15 it is natural to look for the spherical analogue of Schramm’s lower bound [30] for the volume of convex bodies of constant width in ${\mathbb {E}}^d$. This has been done by Schramm [31] for $c_{BL}\left( \frac{\pi }{2}, d\right) =\min \left\{ \textrm{vol}(\textbf{K})\ |\ \textbf{K}\in {\mathcal {K}}_{s}^d\left( \frac{\pi }{2}\right) \right\}$ as follows.

Remark 2.16

Proposition 9 of [31] implies that

$$\begin{aligned} c_{BL}\left( \frac{\pi }{2}, d\right) \ge \sqrt{ \frac{8^d}{2\pi (d+1)(d+4)^d} }\textrm{vol}_s\left( {\Delta }_d\left( \frac{\pi }{2}\right) \right) , \end{aligned}$$

where $\textrm{vol}_s({\mathbb {S}}^d)=(d+1)\omega _{d+1}=\frac{(d+1)\pi ^{\frac{d+1}{2}}}{\Gamma (\frac{d+3}{2})}$, $\textrm{vol}_s\left( {\Delta }_d\left( \frac{\pi }{2}\right) \right) =\frac{(d+1)\omega _{d+1}}{2^{d+1}}$ and $d\ge 3$.

It seems reasonable to hope for the following strengthening of the estimate of Remark 2.16 (resp., of Conjecture 1.6 from [5]).

Conjecture 2.17

$c_{BL}(\frac{\pi }{2}, d)=\textrm{vol}_s({\Delta }_d(\frac{\pi }{2}))$, i.e., if $\textbf{K}\in {\mathcal {K}}_s^d(\frac{\pi }{2})$, then $\textrm{vol}_s(\textbf{K})\ge \textrm{vol}_s({\Delta }_d(\frac{\pi }{2}))$ for all $d\ge 3$.

3 Proof of Theorem 1.3

Let $0<r\le \frac{\pi }{2}$ and $\textbf{D}\in {\mathcal {B}}^2_{s, \textrm{wide}}(r)$. Our goal is to show that $\textrm{area}_s(\textbf{D})\ge \textrm{area}_s(\mathbf{\Delta }_2(r))$. Let $\textbf{C}_\textrm{in}$ be the inscribed disk of $\textbf{D}$ with center $\textbf{c}$ having radius $R_\textrm{in}$. We may assume that $2R_\textrm{in}< r$. Namely, if $r\le 2R_\textrm{in}$, then $\textbf{D}$ contains a disk of diameter r and so, it follows via the spherical isodiametric inequality [9] that $\textrm{area}_s(\textbf{D})\ge \textrm{area}_s(\mathbf{\Delta }_2(r))$.

Next, one of the following two cases must occur: either the boundaries of $\textbf{D}$ and $\textbf{C}_\textrm{in}$ have two points in common such that the shorter great circular arc connecting them is a diameter of $\textbf{C}_\textrm{in}$ or the boundaries of $\textbf{D}$ and $\textbf{C}_\textrm{in}$ have three points in common such that $\textbf{c}$ is in the interior of the triangle that is the spherical convex hull of these three points. In the first case, Sublemma 2.13 implies that $\textbf{D}$ contains a disk of diameter r and so, as above we get that $\textrm{area}_s(\textbf{D})\ge \textrm{area}_s(\mathbf{\Delta }_2(r))$.

Fig. 1

Cap $\textbf{C}_1$ of the cap-domain $\textbf{C}:=\textbf{C}_1\cup \textbf{C}_2\cup \textbf{C}_3\cup \textbf{C}_\textrm{in}$ in the hemisphere of ${\mathbb {S}}^2$ with center $\textbf{c}$

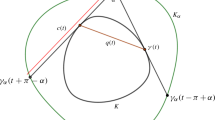
In the second case, let the three selected points in common of the boundaries of $\textbf{D}$ and $\textbf{C}_\textrm{in}$ be $\textbf{a}_1$, $\textbf{a}_2$, and $\textbf{a}_3$ and let the supporting great circles to $\textbf{C}_\textrm{in}$ at these points be $L_1$, $L_2$, and $L_3$ respectively (Fig. 1). Note that $L_1$, $L_2$, and $L_3$ are also supporting great circles to $\textbf{D}$ and thus, $\textbf{D}$ lies in one of the spherical triangles determined by $L_1$, $L_2$, and $L_3$. Let us label this spherical triangle by $\triangle \textbf{n}_1\textbf{n}_2\textbf{n}_3$ having the vertices $\textbf{n}_1$, $\textbf{n}_2$, and $\textbf{n}_3$ such that $\textbf{n}_1$ is not on $L_1$ (i.e., $\textbf{n}_1$ is “opposite” to $L_1$ ), $\textbf{n}_2$ is not on $L_2$, and $\textbf{n}_3$ is not on $L_3$. Now, let $\textbf{p}_1$ be the point on the same side of $L_1$ as $\textbf{D}$ such that $\textbf{p}_1\textbf{a}_1$ is of length r and is perpendicular to $L_1$ at $\textbf{a}_1$. Let $M_1$ be the great circle perpendicular to $\textbf{p}_1\textbf{a}_1$ at $\textbf{p}_1$. Note that the angle between $L_1$ and $M_1$ is r. By Proposition 2.11, $M_1$ must contain a point of $\textbf{D}$. Let this point be $\textbf{q}_1$. Since $0<r\le \frac{\pi }{2}$ we have that

$$\begin{aligned} \textrm{dist}_s(\textbf{q}_1,\textbf{c})\ge \textrm{dist}_s(\textbf{p}_1,\textbf{c})=r-R_\textrm{in}>R_\textrm{in}. \end{aligned}$$

(4)

Let $\textbf{t}_{11}$ and $\textbf{t}_{12}$ be the two points in common of the boundary of $\textbf{C}_\textrm{in}$ with the two circles of radius r passing through $\textbf{q}_1$ that are tangent to $\textbf{C}_\textrm{in}$ and whose disks of radius r contain $\textbf{C}_\textrm{in}$. Here the shorter circular arc of radius r connecting $\textbf{q}_1$ and $\textbf{t}_{11}$ (resp., $\textbf{t}_{12}$) and sitting on the corresponding circle of radius r just introduced, is labeled by $(\textbf{q}_1\textbf{t}_{11})_r$ (resp., $(\textbf{q}_1\textbf{t}_{12})_r$). The circular arcs $(\textbf{q}_1\textbf{t}_{11})_r$ and $(\textbf{q}_1\textbf{t}_{12})_r$ have equal lengths moreover, the cap $\textbf{C}_1$ bounded by $(\textbf{q}_1\textbf{t}_{11})_r$ and $(\textbf{q}_1\textbf{t}_{12})_r$ and the shorter circular arc of radius $R_\textrm{in}$ connecting $\textbf{t}_{11}$ and $\textbf{t}_{12}$ on the boundary of $\textbf{C}_\textrm{in}$ lies in $\textbf{D}$ and therefore it lies also in the spherical triangle $\triangle \textbf{n}_1\textbf{a}_2\textbf{a}_3\subset \triangle \textbf{n}_1\textbf{n}_2\textbf{n}_3$. (Here we have used the property of $\textbf{D}$ that if we choose two points in $\textbf{D}$, then any shorter circular arc of radius $r'$ with $r\le r'\le \frac{\pi }{2}$ connecting the two points lies in $\textbf{D}$.) We can perform the same procedure for the points $\textbf{a}_2$ and $\textbf{a}_3$, producing the caps $\textbf{C}_2$ and $\textbf{C}_3$. By construction the caps $\textbf{C}_1$, $\textbf{C}_2$, and $\textbf{C}_3$ are non-overlapping and the cap-domain $\textbf{C}:=\textbf{C}_1\cup \textbf{C}_2\cup \textbf{C}_3\cup \textbf{C}_\textrm{in}$ is a subset of $\textbf{D}$ and therefore

$$\begin{aligned} \textrm{area}_s(\textbf{D})\ge \textrm{area}_s(\textbf{C}). \end{aligned}$$

(5)

Fig. 2

The cap-domain $\textbf{C}^*:=\textbf{C}_1^*\cup \textbf{C}_2^*\cup \textbf{C}_3^*\cup \textbf{C}_\textrm{in}$ compared to $\textbf{D}^*$ via dissection and symmetry

Let $\textbf{D}^*:=\mathbf{\Delta }_2(r)$ with vertices $\textbf{b}_1$, $\textbf{b}_2$, and $\textbf{b}_3$ such that its center is $\textbf{c}$ (Fig. 2). If $R_\textrm{in}^*$ denotes the inradius of $\textbf{D}^*$, then $\textrm{dist}_s(\textbf{b}_1,\textbf{c})=\textrm{dist}_s(\textbf{b}_2,\textbf{c})=\textrm{dist}_s(\textbf{b}_3,\textbf{c})=r-R_\textrm{in}^*$. Clearly, Proposition 2.5 yields that $r-R_\textrm{in}^*\ge r-R_\textrm{in}$. Thus, let $\textbf{c}_i$ be the point on the great circular arc $\textbf{b}_i\textbf{c}$ such that $\textrm{dist}_s(\textbf{c}_i,\textbf{c})=r-R_\textrm{in}$, $1\le i\le 3$. Let $\textbf{t}_{11}^*$ and $\textbf{t}_{12}^*$ be the two points in common of the boundary of $\textbf{C}_\textrm{in}$ with the two circles of radius r passing through $\textbf{c}_1$ that are tangent to $\textbf{C}_\textrm{in}$ and whose disks of radius r contain $\textbf{C}_\textrm{in}$. Here the shorter circular arc of radius r connecting $\textbf{c}_1$ and $\textbf{t}_{11}^*$ (resp., $\textbf{t}_{12}^*$) and sitting on the corresponding circle of radius r just introduced, is labeled by $(\textbf{c}_1\textbf{t}_{11}^*)_r$ (resp., $(\textbf{c}_1\textbf{t}_{12}^*)_r$). The circular arcs $(\textbf{c}_1\textbf{t}_{11}^*)_r$ and $(\textbf{c}_1\textbf{t}_{12}^*)_r$ have equal lengths. Moreover, let the cap $\textbf{C}_1^*$ be the domain bounded by $(\textbf{c}_1\textbf{t}_{11}^*)_r$ and $(\textbf{c}_1\textbf{t}_{12}^*)_r$ and the shorter circular arc of radius $R_\textrm{in}$ connecting $\textbf{t}_{11}^*$ and $\textbf{t}_{12}^*$ on the boundary of $\textbf{C}_\textrm{in}$. From (4) it follows that $\textrm{area}_s(\textbf{C}_1)\ge \textrm{area}_s(\textbf{C}_1^*)$. Similarly, we can define the caps $\textbf{C}_2^*$ and $\textbf{C}_3^*$ with vertices $\textbf{c}_2$ and $\textbf{c}_3$ for which $\textrm{area}_s(\textbf{C}_2)\ge \textrm{area}_s(\textbf{C}_2^*)$ and $\textrm{area}_s(\textbf{C}_3)\ge \textrm{area}_s(\textbf{C}_3^*)$. By construction the caps $\textbf{C}_1^*$, $\textbf{C}_2^*$, and $\textbf{C}_3^*$ are non-overlapping and therefore the cap-domain $\textbf{C}^*:=\textbf{C}_1^*\cup \textbf{C}_2^*\cup \textbf{C}_3^*\cup \textbf{C}_\textrm{in}$ satisfies the inequality

$$\begin{aligned} \textrm{area}_s(\textbf{C})\ge \textrm{area}_s(\textbf{C}^*). \end{aligned}$$

(6)

Based on (5) and (6) we finish the proof of Theorem 1.3 by showing the inequality

$$\begin{aligned} \textrm{area}_s(\textbf{C}^*)\ge \textrm{area}_s(\textbf{D}^*). \end{aligned}$$

(7)

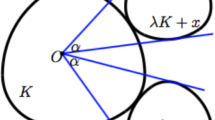
Let $\textbf{b}_{12}$ be the midpoint of $(\textbf{b}_1\textbf{b}_2)_r$, which is the shorter circular arc of radius r connecting $\textbf{b}_1$ and $\textbf{b}_2$ on the boundary of $\textbf{D}^*$ (Fig. 2). Moreover, let $\textbf{b}_3^*:=\widehat{\textbf{c}\textbf{b}_3}\cap (S_s^1(\textbf{c}, R_\textrm{in})\setminus \textbf{c}\textbf{b}_3)$. From this it follows that $\textrm{dist}_s(\textbf{b}_1,\textbf{c}_1)=\textrm{dist}_s(\textbf{b}_{12},\textbf{b}_3^*)=R_\textrm{in}-R_\textrm{in}^*$. Let $\textbf{f}:=(\textbf{b}_1\textbf{b}_{12})_r\cap (\textbf{c}_1\textbf{b}_3^*)_r$, where $(\textbf{b}_1\textbf{b}_{12})_r$ (resp., $(\textbf{c}_1\textbf{b}_3^*)_r$) is the shorter circular arc of radius r connecting $\textbf{b}_1$ and $\textbf{b}_{12}$ (resp., $\textbf{c}_1$ and $\textbf{b}_3^*$) such that $(\textbf{b}_1\textbf{b}_{12})_r$ lies on the boundary of $\textbf{D}^*$ (resp., the disk $\textbf{B}_s^2[\textbf{c}', r]$ containing $(\textbf{c}_1\textbf{b}_3^*)_r$ on its boundary contains $\textbf{b}_3$ (resp., $\textbf{b}_1$) in its interior (resp., exterior)). We note that by construction

$$\begin{aligned} (\textbf{c}_1\textbf{b}_3^*)_r\subset \textbf{C}^* . \end{aligned}$$

(8)

Sublemma 3.1

Let $\textbf{u}:=\widehat{\textbf{b}_3\textbf{c}'}\cap (S_s^1(\textbf{b}_3, r)\setminus \textbf{B}_s^2[\textbf{c}', r])$ and $\textbf{v}:=\widehat{\textbf{b}_3\textbf{c}'}\cap (S_s^1(\textbf{c}', r)\setminus \textbf{B}_s^2[\textbf{b}_3, r])$ (Fig. 3). Furthermore, let $(\textbf{f}{} \textbf{v})_r$ be the shorter circular arc of $S_s^1(\textbf{c}', r)$ connecting $\textbf{f}$ and $\textbf{v}$ and let $\textbf{x}\in (\textbf{f}{} \textbf{v})_r$ be a point moving from $\textbf{f}$ to $\textbf{v}$. Then the point of $\textbf{B}_s^2[\textbf{b}_3, r])$ closest to $\textbf{x}$ is $\textbf{y}:=\textbf{b}_3\textbf{x}\cap S_s^1(\textbf{b}_3, r)$ and $\textrm{dist}_s (\textbf{x},\textbf{y})$ is a strictly increasing function of the length of $(\textbf{f}\textbf{x})_r$, where $(\textbf{f}\textbf{x})_r$ denotes the shorter circular arc of $S_s^1(\textbf{c}', r)$ connecting $\textbf{f}$ and $\textbf{x}$.

Fig. 3

Cauchy’s Arm Lemma applied to $\triangle \textbf{b}_3\textbf{c}'\textbf{x}$ in ${\mathbb {S}}^2$

Proof

Clearly, the point of $\textbf{B}_s^2[\textbf{b}_3, r]$ closest to $\textbf{x}$ must have the property that the great circle passing through it and tangent to $\textbf{B}_s^2[\textbf{b}_3, r]$ is orthogonal to the great circular arc connecting that point to $\textbf{x}$. It follows that the closest point is $\textbf{y}=\textbf{b}_3\textbf{x}\cap S_s^1(\textbf{b}_3, r)$. On the other hand, notice that as $\textbf{x}\in (\textbf{f}{} \textbf{v})_r$ moves from $\textbf{f}$ to $\textbf{v}$ the angle $\angle \textbf{b}_3\textbf{c}'\textbf{x}$ at the vertex $\textbf{c}'$ of the spherical triangle $\triangle \textbf{b}_3\textbf{c}'\textbf{x}$ (bounded by the great circular arcs $\textbf{b}_3\textbf{c}', \textbf{c}'\textbf{x}$ and $\textbf{b}_3\textbf{x}$) strictly increases and so, the spherical version of Cauchy’s Arm Lemma (see [1] or [11], p. 228) implies that $\textrm{dist}_s (\textbf{b}_3,\textbf{x})$ strictly increases and therefore also $\textrm{dist}_s (\textbf{x},\textbf{y})=\textrm{dist}_s (\textbf{b}_3,\textbf{x})-r$ strictly increases. $\square$

Next, we note that the spherical distance of $\textbf{b}_3^*$ (resp., $\textbf{b}_1$) to $\textbf{B}_s^2[\textbf{b}_3, r]$ (resp., $\textbf{B}_s^2[\textbf{c}', r]$) is equal to $\textrm{dist}_s(\textbf{b}_3^*, \textbf{b}_{12})=R_\textrm{in}-R_\textrm{in}^*$ (resp., is at most $\textrm{dist}_s(\textbf{b}_1,\textbf{c}_1)=R_\textrm{in}-R_\textrm{in}^*$). Hence, Sublemma 3.1 implies that the length of $(\textbf{b}_1\textbf{f})_r$ (resp., $(\textbf{c}_1\textbf{f})_r$) is at most as large as the length of $(\textbf{b}_3^*\textbf{f})_r$ (resp., $(\textbf{b}_{12}{} \textbf{f})_r$), where $(\textbf{b}_1\textbf{f})_r$, $(\textbf{c}_1\textbf{f})_r$, $(\textbf{b}_3^*\textbf{f})_r$, and $(\textbf{b}_{12}{} \textbf{f})_r$ are circular arcs of radius r with endpoints indicated such that $(\textbf{b}_1\textbf{f})_r\subset (\textbf{b}_1\textbf{b}_{12})_r$, $(\textbf{c}_1\textbf{f})_r\subset (\textbf{c}_1\textbf{b}_3^*)_r$, $(\textbf{b}_3^*\textbf{f})_r\subset (\textbf{c}_1\textbf{b}_3^*)_r$, and $(\textbf{b}_{12}{} \textbf{f})_r\subset (\textbf{b}_1\textbf{b}_{12})_r$. It follows that the triangular shape region $\widehat{\triangle }\textbf{b}_1\textbf{c}_1\textbf{f}$ bounded by $(\textbf{b}_1\textbf{f})_r, \textbf{b}_1\textbf{c}_1$, and $(\textbf{c}_1\textbf{f})_r$ has an isometric copy contained in the triangle shape region $\widehat{\triangle }\textbf{b}_3^*\textbf{b}_{12}\textbf{f}$ bounded by $(\textbf{b}_3^*\textbf{f})_r, \textbf{b}_3^*\textbf{b}_{12}$, and $(\textbf{b}_{12}{} \textbf{f})_r$. This implies that

$$\begin{aligned} \textrm{area}_s(\widehat{\triangle }\textbf{b}_1\textbf{c}_1\textbf{f})\le \textrm{area}_s(\widehat{\triangle }\textbf{b}_3^*\textbf{b}_{12}{} \textbf{f}). \end{aligned}$$

(9)

Thus, using (8), (9), and the symmetries of $\textbf{D}^*$ and $\textbf{C}^*$ we get that

$$\begin{aligned} \frac{1}{6}\textrm{area}_s(\textbf{D}^*\setminus \textbf{C}^*)\le \textrm{area}_s(\widehat{\triangle }\textbf{b}_1\textbf{c}_1\textbf{f})\le \textrm{area}_s(\widehat{\triangle }\textbf{b}_3^*\textbf{b}_{12}{} \textbf{f})\le \frac{1}{6}\textrm{area}_s(\textbf{C}^*\setminus \textbf{D}^*).\nonumber \\ \end{aligned}$$

(10)

Hence, (7) follows, finishing the proof of Theorem 1.3.