Introduction

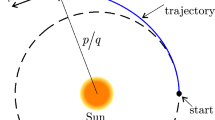
The interstellar probe mission is to place a spacecraft on a heliocentric escape trajectory that will reach 100 to 1,000 Astronomical Units (AU) in a reasonable mission time [1]. Investigation of the heliopause and outer solar system will benefit the understanding of the nature of the interstellar medium, and its implication for the origin and evolution of matter in the Galaxy. With the long-term mission flying of Voyager spacecraft and the launch of New Horizons in 2006, the concept and mission design of the interstellar probe mission are being reconsidered by the science community. With the first successful flying of sailcraft IKAROS [2] launched by Japan and the recent Nano-Sail D launched by NASA, solar sailing is now seen as one of the most potential propulsion systems for the deep space exploration missions. Compared to the velocity of 3 AU per year (AU/Y) for the Voyager spacecraft, a cruise speed of more than 10 AU/Y for relatively mid performance solar sails is attractive for most scientists [3]. Using a short inner-loop about the Sun solar sails can dramatically accelerate the sailcraft to cruise speeds. The state of art of the sail technologies still cannot make such an innovative mission realistic. Looking further ahead, it is important and significant that feasibility of the potential future mission should be estimated and discussed along with the critical technologies.

Since solar sails consume no fuel the optimization performance index is usually minimization of mission time or maximization of the required sail acceleration. Generally, in many cases, these two conditions are equivalent [4, 5]. For estimating future solar sail technology requirements, many scientists investigated the feasibility of interstellar probe missions using a time-optimal control model. With a reasonable assumption of a jettison point at 5 AU, a parametric study to 100, 250 and 1,000 AU was conducted by Sauer [1] using a single solar flyby with respect to highly different characteristic accelerations. Shortly after, Dachwald [6] restudied the problem by using relatively low performance solar sails (generally, solar sails with an acceleration greater than 3 mm/s2 are referred to as high performance sails [7]). The temperature limit and different sail models were taken into account in his paper to give a more accurate estimation of such missions. However, to the authors’ knowledge, the objective functions presented in all previous analyses only involved the final time at the jettison point to estimate the minimum time of the whole mission. Therefore, the results are not global-time-optimal solutions and could be improved. Meanwhile, although examining each flyby trajectory for a number of values of escape energy would be prohibitive [1], the influence of the departure point from the Earth orbit with zero hyperbolic excess velocity (C 3 = 0 km2/s2) for such a long duration mission should also be taken into consideration.

For the investigation of interstellar missions a new objective function that minimizes the mission time for a given characteristic sail acceleration is proposed. An important contribution is identifying the advantages of the new objective function that leads to an improved time-optimal solution within the current assumptions. The optimal control model in the Heliocentric Inertial Frame is presented in non-dimensional units. An indirect method is adopted to calculate the optimal control laws that minimize the mission time. As it is difficult to obtain the appropriate initial values of the adjoint variables that yield the optimal control law, a technique of scaling the adjoint variables is introduced in the optimal control model. After derivation of the optimal control framework, a detailed comparison between the current work of this paper and Sauer’s result is given in the discussion of numerical simulations. Regardless of the geocentric escape trajectory, the departure point of the sailcraft from the Earth orbit is considered for the 100 AU demonstration mission. Unlike rendezvous missions the jettison direction of the interstellar probe is not specified and is determined from the optimization routine. The above discussions are for a relatively mid performance solar sail to reach 100 AU in a reasonable mission time. The last involved case illustrates a 250 AU interstellar mission with a sail of lightness number 0.75. There is an interesting discovery that the angular momentum reversal trajectory [8, 9] is a local optimal solution for such missions. Hence, it is unnecessary to reverse the angular momentum for the spacecraft to gain high energy in the optimized sail orientation. This result is consistent with Sauer’s and gives a clear vision about the two types of solar escape trajectories in the optimal control model. The angular momentum reversal mode addressed in Ref. [8] is an alternative for escaping the solar system with the advantage of fixed sail orientation in the whole heliocentric escape trajectory. It was rarely proposed as stated in Ref. [9] due to the use of high performance sails. The discussion and framework presented in this paper will provide a good estimate for the future mission design and a new understanding of the single solar flyby.

Optimal Control Model for an Ideal Solar Sail

In this analysis the solar sail is modeled as a perfectly reflecting plane surface. The effect of solar wind and the wrinkle of the sail are not considered. The sail lightness number β is used to describe the solar radiation pressure acceleration, and it is expressed as

$$ {\mathbf{f}}_s=\beta \frac{\mu}{r^2}{ \cos}^2\alpha \mathbf{n} $$
(1)

In the above equation β = 1 corresponds to a sail acceleration 5.93 mm/s2 at 1 AU away from the Sun. The parameter μ is the solar gravitational constant and n is the sail normal vector aligned with the direction of the sail force. The variable r is the sail distance away from the Sun, α is the angle between the sail force vector and the sunlight direction and is called the “cone angle”. In the two-body frame all perturbation forces are neglected and only the solar gravity and solar radiation pressure force exert on the sail. For convenience, the dynamic equations of motion with non-dimensional units are introduced in the ecliptic inertial frame. The distance unit is taken as the mean Earth-Sun distance (1 AU), while the time unit is selected to fulfill the condition that the solar gravitational constant is unitary. With such a choice, the equations of motion then become

$$ \left\{\begin{array}{l}\dot{\mathbf{R}}=\mathbf{V}\\ {}\dot{\mathbf{V}}=-\frac{1}{R^3}\mathbf{R}+\beta \frac{1}{R^4}{\left(\mathbf{R}\cdot \mathbf{n}\right)}^2\mathbf{n}\end{array}\right. $$
(2)

where R and V are the position and velocity vectors of the sailcraft, respectively. Before the journey of an interplanetary orbit the sailcraft must escape the Earth’s gravity. In principle the Earth escape trajectory can be attained using several modes of propulsion before sail deployment or the sail can be used to escape the Earth. The interplanetary transfer orbit does not include the geocentric orbit and all trajectories calculated in this paper assume direct insertion of the sail from Earth orbit at zero hyperbolic excess speed (C 3 = 0 km2/s2). Considering the possible influence of the departure time for the interstellar mission, the departure time will now be investigated. The initial conditions specified with respect to the ecliptic inertial frame are

$$ {\Psi}_0\left[{t}_0,\mathbf{R}\left({t}_0\right),\mathbf{V}\left({t}_0\right)\right]=\left[\begin{array}{c}\hfill {\mathbf{R}}_0-{\mathbf{R}}_{\boldsymbol{e}}\left({t}_0\right)\hfill \\ {}\hfill {\mathbf{V}}_0-{\mathbf{V}}_e\left({t}_0\right)\hfill \end{array}\right]=\mathbf{0} $$
(3)

where R 0 and V 0 are the position and velocity vectors of the sailcraft at the initial time, respectively; R e(t 0) and V e(t 0) are the Earth’s position and velocity vectors.

Within a single solar photonic assist the sail trajectory consists of three main phases. First, the sailcraft should lower its orbit perihelion by varying the sail attitude. Generally, the perihelion of the trajectory always has some constraints due to the thermal limits [10] of the sail film. Second, it goes back approaching the Sun before arriving at its perihelion. Third, as perihelion is reached, the sail is turned to a Sun-facing attitude and is rapidly accelerated to its cruise speed [3]. According to the dynamic characteristic of the trajectory there will be an inner constraint, which is handled as

$$ {\Psi}_1\left[{t}_1,\mathbf{R}\left({t}_1\right),\mathbf{V}\left({t}_1\right)\right]=\left[\begin{array}{c}\hfill \left\Vert {\mathbf{R}}_1\right\Vert -{r}_p\hfill \\ {}\hfill {\mathbf{V}}_1^{\mathrm{T}}{\mathbf{R}}_1\hfill \end{array}\right]=0 $$
(4)

where t 1 is the time of perihelion passage; r p is the value of the limited perihelion; R 1 and V 1 are the position and velocity vectors of the sailcraft at perihelion, respectively.

After perihelion the sailcraft rapidly accelerates to a high speed within a short duration. Note that at a distance of about 5 to 10 AU away from the Sun the net acceleration on the sail is very small, the orbit speed decreases very slowly as the sailcraft maneuvers farther from the Sun. The final branch of the interstellar trajectory can be approximated by a straight line. Strictly speaking, there is no cruise speed to a far distant target. A pseudo-cruise speed can be reasonably adopted to reduce the simulation effort. Throughout this paper the interstellar trajectories are all assumed jettisoned at the lesser distance of 5 AU, an assumption that was adopted in previous studies [1, 11] to guarantee the acquisition of science data without possible interference from the sail. The final constraints of the sail can be written as

$$ {\Psi}_f\left[{t}_f,\mathbf{R}\left({t}_f\right),\mathbf{V}\left({t}_f\right)\right]=\left\Vert {\mathbf{R}}_f\right\Vert -{r}_f=0 $$
(5)

where R f is the sail position vector at the jettison point, and r f is the value of the distance between the sail jettison point and the Sun.

Generally, the performance index in the trajectory optimization is to minimize flight time for a given quality sail. Particularly, the flight time of an interstellar mission is one of the most important issues. Therefore, the real objective function of the minimum time interplanetary transfer problem is given by

$$ J=-{\lambda}_0{\displaystyle {\int}_0^T\mathrm{d} t} $$
(6)

where T is the flight time to reach the required interstellar distance S r , such as the heliopause. The global calculation from the starting point to S r is usually difficult and somewhat unnecessary. As was stated before in Eq. 5, under the reasonable assumption of a jettison point at r f , the function (6) can be transformed to an approximation form

$$ J\approx -{\lambda}_0\left({\displaystyle {\int}_0^{t_f}\mathrm{d} t}+\frac{S_r-{r}_f}{\left\Vert {\mathbf{V}}_f\right\Vert}\right)=-{\lambda}_0{\displaystyle {\int}_0^{t_f}\mathrm{d} t}-{\lambda}_0\frac{S_r-{r}_f}{\left\Vert {\mathbf{V}}_f\right\Vert } $$
(7)

where ||V f || is the magnitude of the sail final speed at the jettison point; λ0 is a positive constant. Obviously, the value of the jettison speed will influence the flight time related to S r . An objective function adopted by previous studies [1] is to use only the first term on the right side of Eq. 7

$$ {J}_1=-{\lambda}_0{\displaystyle {\int}_0^{t_f}\mathrm{d} t} $$
(8)

From Eq. 7, another objective function obtained by approximation of the second right term is equivalently written as

$$ {J}_2\approx {\lambda}_0\left\Vert {\mathbf{V}}_f\right\Vert $$
(9)

Actually, Eq. 8 yields the minimum time transfer to the jettison point after sail deployment, while Eq. 9 corresponds to the maximum of jettison velocity at the jettison point. As both of these objective functions are an approximation of Eq. 7, the solutions obtained under such functions cannot be the global time-optimal solutions. Therefore, a new objective function is introduced in this paper as following

$$ {J}_3={\lambda}_0\left(1-\varepsilon \right)\left\Vert {\mathbf{V}}_f\right\Vert -{\lambda}_0\varepsilon {\displaystyle {\int}_0^{t_f}\mathrm{d} t} $$
(10)

where the scale parameter ε is in the interval [0, 1]. It is interesting that the objective function J 3 can be separated into another two functions with a different value of ε, e.g. J 1 with ε = 1 and J 2 with ε = 0. The flight time among different objective functions will be described in detail through numerical simulations. The objective function J 3 will be adopted in the following derivation of equations.

The Hamiltonian of the system is defined as

$$ H=-\varepsilon {\lambda}_0+{\boldsymbol{\lambda}}_{\mathrm{R}}(t)\cdot \mathbf{V}+{\boldsymbol{\lambda}}_{\mathrm{V}}(t)\cdot \left[-\frac{1}{R^3}\mathbf{R}+\beta \frac{1}{R^4}{\left(\mathbf{R}\cdot \mathbf{n}\right)}^2\mathbf{n}\right] $$
(11)

where λ R (t) and λ V (t) are the adjoint variables for position and velocity. The velocity adjoint is also referred to as the “primer vector” and defines the optimal direction for the solar radiation force vector. The time derivative of the adjoint variables from the Euler-Lagrange equations is

$$ \left\{\begin{array}{l}{\dot{\boldsymbol{\lambda}}}_{\mathrm{R}}=-\frac{\partial H}{\partial \mathbf{R}}=\frac{1}{R^3}{\boldsymbol{\lambda}}_{\mathrm{V}}-\frac{3}{R^5}\left(\mathbf{R}\cdot {\boldsymbol{\lambda}}_{\mathrm{V}}\right)\mathbf{R}-2\beta \frac{1}{R^4}\left(\mathbf{R}\cdot \mathbf{n}\right)\left(\mathbf{n}\cdot {\boldsymbol{\lambda}}_{\mathrm{V}}\right)\left[\mathbf{n}-\frac{2\left(\mathbf{R}\cdot \mathbf{n}\right)\mathbf{R}}{R^2}\right]\\ {}{\dot{\boldsymbol{\lambda}}}_{\mathrm{V}}=-\frac{\partial H}{\partial \mathbf{V}}=-{\boldsymbol{\lambda}}_{\mathrm{R}}\end{array}\right. $$
(12)

The optimal values of the control variables are obtained by invoking the Pontryagin maximum principle [12] by maximizing H at any time. Under the necessary condition, the orientation of the sail force vector will be defined as

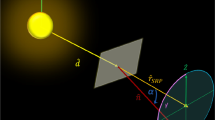
$$ \mathbf{n}(t)= \arg \max H\left( t,\mathbf{n},\boldsymbol{\lambda} \right) $$
(13)

In order to maximize the Hamiltonian the solar radiation pressure force vector must lie in the plane defined by the position vector and primer vector such that

$$ \mathbf{n}=\left\{\begin{array}{l}\frac{ \sin \left(\tilde{\alpha}-\alpha \right)}{ \sin \tilde{\alpha}}\frac{\mathbf{R}}{\left\Vert \mathbf{R}\right\Vert }+\frac{ \sin \alpha}{ \sin \tilde{\alpha}}\frac{{\boldsymbol{\lambda}}_{\mathrm{V}}}{\left\Vert {\boldsymbol{\lambda}}_{\mathrm{V}}\right\Vert } if\tilde{\alpha}\in \left(0,\pi \right)\\ {}\frac{\mathbf{R}}{\left\Vert \mathbf{R}\right\Vert } if\tilde{\alpha}=0\end{array}\right. $$
(14)

In the above function α is the cone angle of the primer vector. A special case should be pointed out that α = π indicates α = π/2, corresponding to no sail acceleration. In fact, the optimal control of the sail is a kind of locally optimal problem [13], which is different from the continuous low-thrust propulsion system. The reason why λ V is referred to as the primer vector is that one should align the direction of the low-thrust along the primer vector to maximize the Hamiltonian [14]. However, such an optimal control law is not suitable for the solar sail. Maximizing the Hamiltonian means adjusting the sail attitude to maximize the projection of the normal vector along the primer vector. The relationship between the sail normal vector and the primer vector is illustrated in Fig. 1, where e is a unit vector perpendicular to the radial direction.

Fig. 1
figure 1

Description of the sail optimal control law

Full size image

The transversality conditions indicate that when the initial boundary state is fixed, the corresponding adjoints are free. When the former is free the latter is zero [12]. According to the baselines the corresponding final adjoints satisfy

$$ \begin{array}{l}{\boldsymbol{\lambda}}_{\boldsymbol{R}}\left({t}_f\right)={\gamma}_3\cdot \frac{\partial {\Psi}_f}{\partial \mathbf{R}\left({t}_f\right)}={\gamma}_3\frac{{\mathbf{R}}_f}{\left\Vert {\boldsymbol{R}}_f\right\Vert}\\ {}{\boldsymbol{\lambda}}_{\boldsymbol{V}}\left({t}_f\right)={\lambda}_0\cdot \frac{\partial \varphi}{\partial \mathbf{V}\left({t}_f\right)}={\lambda}_0\left(1-\varepsilon \right)\frac{{\mathbf{V}}_f}{\left\Vert {\mathbf{V}}_f\right\Vert}\end{array} $$
(15)

Remember that there is an inner constraint at the perihelion during the interplanetary transfer. The adjoints at t 1 are

$$ \begin{array}{l}{\boldsymbol{\lambda}}_R\left({t}_1^{+}\right)={\boldsymbol{\lambda}}_R\left({t}_1^{-}\right)-{\gamma}_1\frac{{\mathbf{R}}_1}{\left\Vert {\mathbf{R}}_1\right\Vert }-{\gamma}_2{\mathbf{V}}_1\\ {}{\boldsymbol{\lambda}}_V\left({t}_1^{+}\right)={\boldsymbol{\lambda}}_V\left({t}_1^{-}\right)-{\gamma}_2{\mathbf{R}}_1\end{array} $$
(16)

The superscript ‘–’ and ‘+’ are the moments just before and after a point, that is the perihelion point here. The stationary condition relevant to the perihelion date is

$$ H\left({t}_1^{-}\right)- H\left({t}_1^{+}\right)=0 $$
(17)

The final stationary condition is given by

$$ H\left({t}_f\right)=-{\lambda}_0\frac{\partial \varphi}{\partial {t}_f}-{\gamma}_f\frac{\partial {\varPsi}_f}{\partial {t}_f}=0 $$
(18)

where γ = [γ 1, γ 2, γ 3] and γ f are Lagrange multipliers related to the perihelion and final time constraints. The sailcraft departs from the Earth orbit with zero hyperbolic excess speed. The solar planets are assumed to evolve in Keplerian orbits and their orbital elements are listed in Table 1.

Table 1 Mean orbital elements of Earth and Mars at perihelion
Full size table

In this paper the minimum time control history is obtained by using an indirect method. Since the equations of the adjoint variables are homogeneous, a solution to the equations multiplied by a factor will also be a feasible solution. Take the Hamiltonian to be scaled to match the transversality conditions, which can be achieved through adjusting the positive constant λ0. After normalization the adjoint variables and λ0 can be fixed in a unit sphere and obtained by a combination of trigonometric functions with nine angles [15].

$$ \left\{\begin{array}{l}{\boldsymbol{\lambda}}_{\mathrm{R}}\left({t}_0\right)= \cos {\alpha}_0 \cos {\alpha}_1 \cos {\alpha}_2{\left[ \cos {\alpha}_3 \cos {\alpha}_4, \cos {\alpha}_3 \sin {\alpha}_4, \sin {\alpha}_3\right]}^{\mathrm{T}}\\ {}{\boldsymbol{\lambda}}_{\mathrm{V}}\left({t}_0\right)= \cos {\alpha}_0 \cos {\alpha}_1 \sin {\alpha}_2{\left[ \cos {\alpha}_5 \cos {\alpha}_6, \cos {\alpha}_5 \sin {\alpha}_6, \sin {\alpha}_5\right]}^{\mathrm{T}}\ \\ {}\boldsymbol{\gamma} = \cos {\alpha}_0 \sin {\alpha}_1{\left[ \cos {\alpha}_7 \cos {\alpha}_8, \cos {\alpha}_7 \sin {\alpha}_8, \sin {\alpha}_7\right]}^{\mathrm{T}}\\ {}{\lambda}_0= \sin {\alpha}_0,{\alpha}_{0,1,2}\in \left(0,\frac{\pi}{2}\right),\kern0.5em {\alpha}_{3,5,7}\in \left(-\frac{\pi}{2},\frac{\pi}{2}\right),\kern0.5em {\alpha}_{4,6,8}\in \left(0,2\pi \right)\end{array}\right. $$
(19)

With such a technique the concerned optimal control problem is transformed to the solution of a set of algebraic equations. Importantly, the related variables in the normalization should satisfy the following equation

$$ \sqrt{\lambda_0^2+{\boldsymbol{\lambda}}_{\boldsymbol{R}}^{\mathrm{T}}\left({t}_0\right){\boldsymbol{\lambda}}_{\boldsymbol{R}}\left({t}_0\right)+{\boldsymbol{\lambda}}_{\boldsymbol{V}}^{\mathrm{T}}\left({t}_0\right){\boldsymbol{\lambda}}_{\boldsymbol{V}}\left({t}_0\right)+{\gamma}_1^2+{\gamma}_2^2+{\gamma}_3^2}=1 $$
(20)

There are 12 free variables, that include the perihelion time t 1, the jettison time t f , initial values of the adjoint variables λ R (t 0) and λ V (t 0), and λ 0 and γ. The number of equations with variables constraints, transversality conditions and stationary conditions are also 12, listed as Eqs. 4, 5, 15, 17, 18 and Eq. 20. There are 12 free parameters with 12 equations which yield a multi-point boundary value problem.

For the indirect method, the initial values of the adjoint variables need to be guessed by some method to obtain the optimal control law. Due to difficulties with the guess work many papers [16–18] try to give effective methods for obtaining the initial values. Since the equations of the adjoint variables are homogeneous, the scaling of the adjoint variables makes the optimization easier than before. With the above transformation it will be easy to obtain the required solutions of the optimization.

In our current simulation, a conversion of a Fortran program available in the MinPack-1 suite to the C++ language is used to solve the problem [15]. The dynamical equations are integrated in double precision using a seventh (eighth) order Runge–Kutta-Fehlberg method (RKF7(8)) with an adaptive step size in the absolute and relative errors of 10−8. The angles to generate the initial adjoints in Eq. 19 and the required flight times are obtained by random guesses between −1 to 1 multiplied by their boundary values. On rare occasions involving “bad” guesses for the initial adjoints, the pathological condition λ 0 = 0 is encountered with a solution that is feasible, but not necessarily optimal. Nevertheless, such cases can easily by eliminated by a slight modification of the initial guesses.

Numerical Results and Discussions

After derivation of the time optimal control model with the new objective function, the results of mission analyses are presented in this section by varying the scale parameter ε. The first scenario is a mission to 100 AU with a relatively mid performance solar sail of 2.4 mm/s2, the same as Sauer’s [1]. A comparison between Sauer’s result and this current work is made via numerical simulations. The following concerned problem is the deployment point of the sail from the Earth orbit. Although the launch window is not an issue for a sailcraft, the departure point may possibly influence the flight time of the interstellar mission. Finally, an investigation for a more distant 250 AU mission is also conducted by using a relatively high performance solar sail. There is an interesting discovery that the angular momentum reversal trajectory (referred as “reversal flyby”) is a local-optimal solution, this has not been addressed previously. The differences between two typical flybys are shown to give a better understanding of such trajectories.

Interstellar Probe Mission of 100 AU

The scenario of an interstellar mission to 100 AU is studied first and compared with existing research work accomplished by Sauer [1] ten years ago. The demonstrated mission of Ref. [3] allows the solar sail to pass no closer than 0.3 AU to the Sun with an acceleration of 2.4 mm/s2 (lightness number of 0.4047) to reach 100 AU in 10 years. His result based on the optimal control model shows that the jettison speed at 5 AU is 10.9 AU per year (AU/Y) and the flight time to 100 AU is 10 years. In this paper, seven sample trajectories with the new objective function J 3 for the 100 AU mission are shown in Fig. 2 with the same perihelion distance of 0.3 AU. All these trajectories depart from the perihelion of the Earth orbit assuming no constraints on the jettison direction. The optimal trajectories are all in the ecliptic plane in a 3D dynamic model. The corresponding trajectory parameters with different ε are listed in Table 2. Actually, the case of ε = 1 corresponds to the time optimal transfer to 5 AU and the case of ε = 0 corresponds to the optimal trajectory with maximum jettison velocity due to no fuel consumption of a sailcraft. However, both of them are definitely not time optimal solutions to 100 AU. The jettison points at 5 AU cover a wide range about 54° from the time optimal solution to the maximum velocity solution with the same departure point. The 5 AU circular orbit plotted with dash points every π/50 demonstrates clearly the situation. It can be seen from Fig. 2 that the trajectory most similar to Sauer’s result is the ε = 0.024 trajectory in which the sailcraft goes beyond the Mars orbit before approaching the Sun. However, one would expect similar trajectories are produced from the same objective function (ε = 1). Such a difference may result from the constraint of its perihelion distance, that is, the fixed 0.3 AU distance is adopted in the current simulations while in Sauer’s work it was set for the sailcraft to pass no closer than 0.3 AU. The jettison speed with ε = 0.024 is about 11.755 AU/Y, which is approximately 1 AU/Y more than Sauer’s 10.9 AU/Y. The 10.9 AU/Y jettison speed corresponds to the case ε = 0.1 in this simulation while its flight time is about 9.7 years to 100 AU. Therefore, there should be a choice of the value of ε for different missions to pursue the minimum time solutions. The best time optimal solution of 100 AU mission here is 9.546 years with a jettison speed about 11.33 AU/Y. It should be noted that some other value of ε could result in a better solution in terms of flight time and jettison velocity. Since it is difficult to obtain the best value of ε by enumeration, a better solution may be found by optimizing ε with an outer-loop solver, while an inner-loop optimizer would compute the optimal sail angles. Such an approach may be performed in future research.

Fig. 2
figure 2

Interstellar Probe trajectories with different ε

Full size image
Table 2 Trajectory parameter variations with respect to ε
Full size table

For such a 10 year mission, the mission time was reduced 5 %. With a higher quality sail and a greater mission distance there may be a noticeable difference in mission time. Even for this mission there will be a five year mission gap between the cases ε = 1.0 and ε = 0.01 to 500 AU. According to the simulations, in the 5 AU time optimal solution given in Table 2, the sailcraft maneuvers to its aphelion of 1.02 AU and then approaches the perihelion at 0.3 AU to escape the solar system with a jettison speed of 10.6 AU/Y in about 0.957 year. For the near-energy optimal solution the sailcraft takes about 4.67 years to achieve the jettison point with flying far beyond the Mars orbit with an aphelion of 4.84 AU. It should be noted that the case with the strict value of ε = 0 is not given in Table 2. Comparison between the case ε = 0.004 and ε = 0.001 indicates that a growth of only 0.2 AU/Y of jettison speed needs more than a 1.4 year mission time before jettison. Therefore, the truly optimal solution of maximum jettison velocity may not be practical in the mission design. The variation of the trajectories is slight within the interval ε ∈ [0.1, 1.0] & [0.0, 0.001] while major in (0.001, 0.1). A higher jettison speed can reduce the flight time of the pseudo-cruise phase, but with a cost of a longer flight time before its perihelion (because the trajectories of different cases between the perihelion and the jettison point for the sailcraft are nearly the same). Consequently, the value of ε should be determined by the mission distance and the sail lightness number.

The optimal sail orientations for the above trajectories are given in Fig. 3. Due to the numerous trajectories with different ε, only two scenarios with ε = 1.0 and ε = 0.044 are given with their optimal control angles as demonstrated missions. Figure 3 shows that the whole variation trend for these two cases is similar to each other with a jumping of sail clock angle from π to 0 occurring at the point where the sail cone angle arrives at its maximum value of π/2. When the jettison point is approached the sail is slewed to a Sun-facing attitude and is rapidly accelerated to its cruise speed, which is consistent with the anticipated solution.

Fig. 3
figure 3

Optimal sail orientations for the trajectories with different ε

Full size image

In order to illustrate the effectiveness of the strategy with objective function J 3, a comparison is given in Table 3. The time optimal results are interpolated from Sauer’s published paper [1]. There may be some marginal error greater or less than the real result obtained by Sauer. The interpolated result used by Scheeres [19] is also listed in Table 3 as a proof. It should be noted that the initial orbit of Scheeres’ mission trajectory is 1 AU circular orbit while Sauer’s is the real Earth orbit. Through comparison it can be found that the mission time in J 3 will be 0.2 to more than 1.0 year less than Sauer’s. As the sail lightness number increases the difference of mission time between the J 3 result and Sauer’s becomes less and less. Such a trend indicates that with a higher quality sail there is no need to go beyond the 1 AU orbit to gain high energy; the results in J 3 and in J 1 become close to each other. The corresponding value of ε to the J 3 result is also listed in Table 3 to provide a reference to the designers. With the same perihelion the value of ε will grow as the sail lightness number increases. For a given sail lightness number the value of ε will decrease as the minimum solar distance away from the Sun (referred as “perihelion” in Table 3) increases. Such regularities revealed in this paper will benefit the designers in applying J 3 to the real mission design.

Table 3 Mission time to 100 AU (comparison with Sauer)
Full size table

Departure Point from Earth Orbit

Without requirements on the jettison direction, the departure point of the sailcraft can be from any position in the Earth orbit regardless of the geocentric escape phase. Many works on the topic of optimal control problem for solar sails have been published with respect to the rendezvous problem [20], transferring to predetermined mission orbits [21], and the escape trajectories [22]. Generally the departure time, also named “launch window,” influences the mission time greatly for the two former cases. Therefore, the departure time is usually free and obtained by finding the minimum transfer time. In contrast to the other two typical missions the influence of the departure time for the interstellar mission is discussed in this part. As an illustration a sail of 2.4 mm/s2 will still be used to reach 100 AU with a perihelion of 0.3 AU. Taking the objective function into account two particular points of the Earth orbit will be given full consideration, the perihelion and aphelion, respectively. The reason for this option is that the orbital energy of all other points in the Earth orbit is between the two points. In order for the result to be comprehensive, four groups of simulation results are given in Table 4. With the same value of the parameter ε the parameters of the mission orbit are listed, including the aphelion of the mission orbit, the total mission time to 100 AU, the jettison speed and the transfer time before jettison, etc. Table 4 shows that the jettison speed of starting from the Earth perihelion is only slightly more than from the aphelion, which is the same as the situation of the total mission time to 100 AU. The above discussion indicates that there is no need to optimize the departure time. Starting from the Earth perihelion will always be a preferable option for the interstellar missions.

Table 4 Comparison between different departure points
Full size table

Locally Optimal Solution of the Interstellar Mission

A relatively mid performance solar sail can enable the sailcraft to reach 100 AU in 10 years. Using such a sail the interstellar mission to 250 AU will take more than 22 years as shown in Table 2. Therefore, for future engineering there will be a higher requirement on the sail quality to reach 250 AU in a reasonable mission time. A sail of 4.4475 mm/s2 (lightness number of 0.75) will be adopted to give a clear vision about the influence of the sail quality. In terms of the minimum distance away from the Sun, single solar photonic assisted trajectories with different perihelion will also be discussed for such a sail. The simulation results with objective function J 3 of ε = 1 with different perihelion are shown in Fig. 4. Interestingly, there are two extreme points for each perihelion with such a relatively high performance solar sail. Detailed data about the trajectories are listed in Table 5. It can be seen clearly that one of the results is the direct flyby trajectory leading to the globally optimal result, which is the same as Sauer’s optimized result. The other locally optimal result is the trajectory in angular momentum reversal. Note that the current control history of the sail orientations is totally different from that obtained by Vulpetti [8]. The appearance of the unanticipated reversal flyby is due to the different guesses of the jettison time in the form of (t f  = t a  + t b *x t ). The parameters t a and t b are constants based on the problem while x t is an initial guess between zero and one. When the maximum boundary value of the jettison time t f exceeds the flight time of the reversal trajectory, it is possible to obtain the reversal trajectory, but it is not guaranteed. From Table 5, the optimal trajectory in direct flyby is superior to the reversal trajectory in the aspects of mission time to 250 AU and jettison speed at 5 AU. This result coincides with Sauer’s finding that there is no need to reverse the angular momentum vector with optimized sail orientation for a solar system escape. It indicates that the advantage of the reversal trajectory is not in the optimized trajectory. As is known, the attitude control of the solar sail is very difficult [23], especially a large sail. The best way to obtain a high speed with a fixed cone angle to escape the solar system with a high performance solar sail is to adopt the reversal trajectory. It is easy to understand that with the increasing perihelion distance the flight time of the interstellar mission will be longer. The direct flyby trajectories do not need to go beyond 1 AU before passing inside the Earth orbit. Within such a framework, the interstellar mission in other sail accelerations can also be solved.

Fig. 4
figure 4

Interstellar probe trajectories with lightness number 0.75 in J 1

Full size image
Table 5 Optimal results in J 3 of ε = 1with sail lightness number 0.75
Full size table

Conclusions

Time optimal interstellar probe trajectories have been investigated by using an ideally reflecting solar sail. An indirect method has been applied to calculate the optimal control model in the two-body dynamic system. Under the reasonable assumption of jettison at 5 AU, a new objective function is presented to search for the time optimal solutions. As the values of the initial adjoint variables are very sensitive, normalization of these variables so that they are restricted to a unit hyper sphere makes the optimization much easier than before. An interstellar mission to 100 AU with a sail of 2.4 mm/s2 is studied by varying the scale parameter of the new objective function. A comparison of the current simulation and Sauer’s result under the same condition shows that the method in this paper will result in an improved time optimal solution. In contrast to the rendezvous problem, departure from the Earth perihelion is always a preferable option assuming no constraints on the jettison direction. Another contribution of this paper is an interesting discovery that the angular momentum reversal trajectory is a local optimal solution to such an interstellar mission. The simulation results show that the direct flyby is superior to the reversal flyby if only to escape the solar system in terms of the mission time. A reversal flyby takes more time than a corresponding direct flyby. It is confirmed that there is no need to reverse the angular momentum in the optimized sail orientations. A precursor mission to 250 AU is also discussed by using a relatively high performance solar sail.