1 Introduction

A solar sail is a propellantless propulsive system that exploits the solar radiation pressure to produce thrust [1, 2], whose magnitude scales with the inverse square heliocentric distance and is proportional to the reflective area exposed to sunlight. The trajectory design of a solar sail-based mission is a rather complex task, which is usually addressed by solving an optimal control problem. Since the solar sail does not require any propellant to generate thrust, the solution of such a problem is the steering law that minimizes the required flight time to reach a target position on the final orbit [3]. In this context, interesting approaches used for solar sail-based transfers are offered by multiple shooting methods [4,5,6,7] and shape-based methods [8, 9]. The former look for the optimal control law by maximizing the Hamiltonian of the system at each time instant, in accordance with Pontryagin’s maximum principle. However, this method requires the adjoint variables to be included in the system dynamics, although their initial guess may be a difficult task. On the other hand, shape-based methods pose a constraint on the trajectory shape, thus limiting the flexibility of this procedure.

The analysis proposed in this paper uses a different approach. The transfer trajectory is splitted into several arcs, and a piecewise-constant sail attitude is used, in analogy with Refs. [10, 11]. Under such an assumption, the problem of finding the optimal control law amounts to determining the sail attitude in each arc and the time instants at which the attitude is (instantaneously) modified, so that the flight time is minimized. This idea has been exploited in the past, for example in Ref. [10] where a locally optimal steering law was employed, while in Ref. [11], the authors applied the hypothesis of piecewise-constant attitude to a classical multiple shooting method. In this work, we look for an optimal (albeit simplified) control law, which is calculated in two steps. The first step exploits a genetic algorithm to perform a global search of possible solutions of the optimal control problem, while the second step involves a gradient-based method that uses the output of the genetic algorithm as its first guess and converges towards the optimal solution.

The optimization algorithm described so far is tested in this work by analyzing two mission scenarios involving the exploration of outer regions of the Solar System. In this regard, several works in literature have shown that a solar sail is a very promising option for reaching large heliocentric distances within a reasonable flight time [5, 12, 13]. This result is usually achieved by means of a solar photonic assist, that is, a maneuver that requires a close passage to the Sun, to exploit the increase of both the solar radiation pressure and the Sun’s gravity, thus enormously increasing the spacecraft orbital energy [5, 14, 15]. The heliocentric trajectory after a solar photonic assist is almost rectilinear with a large velocity, so that the spacecraft is capable of quickly moving towards the outer Solar System region.

This paper is organized as follows. First, the mathematical model used to describe the solar sail-based spacecraft dynamics is introduced, along with the adopted thrust model. Then, the optimal control problem is formulated. The algorithm is tested in two outer Solar System exploration scenarios, in analogy with Refs. [5, 12, 13], and the results of numerical simulations are presented and discussed. Finally, the Conclusion section resumes the main outcomes of this analysis.

2 Mathematical Model

We consider a solar sail-based spacecraft that is subjected to the solar radiation pressure and the Sun’s gravity only. Assuming a two-dimensional (heliocentric) scenario, the spacecraft state vector \(\varvec{x}\) can be written as

$$\begin{aligned} \varvec{x} \triangleq [p, \, f, \, g, \, L]^{\text {T}}, \end{aligned}$$
(1)

where \(\{p, \, f, \, g, \, L \}\) are the four modified equinoctial orbital elements (MEOEs) [16, 17] that describe the spacecraft motion along the reference plane. The relationship between MEOEs and classical (osculating) orbital elements \(\{a,\,e,\,\omega ,\nu \}\) are

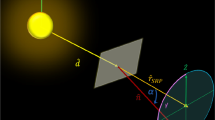
$$\begin{aligned} p = a\,(1-e^2) \qquad f = e \, \sin {\omega } \qquad g = e \, \cos {\omega } \qquad L = \nu +\omega , \end{aligned}$$
(2)

where the argument of pericenter \(\omega\) coincides with the angle between a generic fixed direction along the reference plane and the osculating orbit apse line at pericenter. When the spacecraft is only subjected to the gravitational acceleration of the primary body, the angle L changes with time while the elements \(\{p, \, f, \, g\}\) are constants of motion. However, when the solar sail is deployed, the solar radiation pressure generates a propulsive acceleration vector \(\varvec{a} \triangleq [a_\mathrm{r}, \, a_\mathrm{t}]^{\text {T}}\) whose components \(a_r\) and \(a_t\) are aligned with the radial (i.e., Sun-spacecraft) and circumferential directions, respectively; see Fig. 1.

Fig. 1
figure 1

Reference frame and propulsive acceleration components

Full size image

Assuming an ideal force model [1], that is, a solar sail thrust model in which each photon impinging on the reflective surface is specularly reflected, the components of the propulsive acceleration vector \(\varvec{a}\) can be written as [2]

$$\begin{aligned} \begin{bmatrix} a_\mathrm{r} \\ a_\mathrm{t} \end{bmatrix} = a_\mathrm{c} \frac{r_\oplus ^2}{(p/q)^2} \begin{bmatrix} \cos ^3{\alpha } \\ \cos ^2{\alpha }\sin {\alpha } \end{bmatrix} \end{aligned},$$
(3)

where \(q \triangleq 1 + f\,\cos L + g \, \sin L\) is an auxiliary variable (note that the ratio p/q coincides with the Sun-spacecraft distance), \(r_\oplus \triangleq 1 \text {au}\) is the reference distance, and \(\alpha \in [-\pi /2, \, \pi /2]\) rad is the sail pitch angle, that is, the angle between the Sun-spacecraft line and the direction of vector \(\varvec{a}\). In particular, the pitch angle \(\alpha\) is the classical control parameter of a solar sail in a two-dimensional mission scenario; see Fig. 2. Note that in Fig. 2 the propulsive acceleration components \(\{a_r, \, a_t \}\) are normalized with respect to the maximum propulsive acceleration \(a_{\max }\) that a solar sail can generate at a given heliocentric distance.

Fig. 2
figure 2

Dimensionless component of propulsive acceleration as functions of the pitch angle \(\alpha\)

Full size image

Other more accurate (and more complex) thrust models [18] exist, which take into account the optical properties of the reflective film [19], the degradation of the sail surface [20,21,22,23], the sail billowing [2, 24], the presence of wrinkles [25, 26], diffractive effects [27], and the uncertainties associated with the reflective film characterization [28,29,30]. However, the ideal force model has been chosen here to allow the results obtained in this analysis to be compared with a large amount of literature results [5, 12, 13]. In Eq. (3), the (performance) parameter \(a_c\) is the sail characteristic acceleration, which denotes the maximum propulsive acceleration magnitude at the reference heliocentric distance, that is, when \((p/q) = r_\oplus\).

Taking into account Eq. (3), the time variation of the state vector \(\varvec{x}\) defined in Eq. (1) is provided by the well-known Gauss variational equations, which can be written in matrix form as [31]

$$\begin{aligned} \varvec{\dot{x}} = \mathbb {A} \, \varvec{a} + \varvec{b}, \end{aligned}$$
(4)

where \(\mathbb {A}\) is the state matrix given by

$$\begin{aligned} \mathbb {A} \triangleq \frac{1}{q} \, \sqrt{\frac{\mu _{\odot }}{p}} \begin{bmatrix} 0 &{} 2\,p \\ q\,\sin L &{} (q+1) \cos L + f \\ -q\,\cos L &{} (q+1) \sin L + g \\ 0 &{} 0 \end{bmatrix}, \end{aligned}$$
(5)

and \(\varvec{b}\) is an auxiliary vector defined as

$$\begin{aligned} \varvec{b} \triangleq \left[ 0, \, 0,\, 0, \, \sqrt{\frac{\mu _{\odot }}{p^3}} \, q^2\right] ^{\text {T}}, \end{aligned}$$
(6)

in which \(\mu _{\odot }\) is the Sun’s gravitational parameter.

2.1 Optimal Control Problem Formulation

The analysis discussed in this paper is focused on optimal, solar sail-based, outer Solar System exploration scenarios, in which the time variation of the pitch angle is designed to minimize the flight time required to transfer the spacecraft from an initial (i.e., at time \(t_0 \triangleq 0\)) given state

$$\begin{aligned} \varvec{x}(t_0) = \varvec{x}_0 \triangleq [p_0, \, f_0, \, g_0, \, L_0]^{\text {T}}, \end{aligned}$$
(7)

to a given (target) heliocentric distance \(r_{\text {obj}}\). This amounts to enforcing, at the final (unknown) time \(t_f >t_0\), the constraint

$$\begin{aligned} \frac{p(t_{f})}{q(t_{f})} \equiv \frac{p_{f}}{1+f_{f}\,\cos L_{f} + g \, \sin L_{f}} = r_{\text {obj}}. \end{aligned}$$
(8)

In Eqs. (7)–(8), the subscript 0 (or f) denotes the initial (or final) value of the spacecraft MEOEs.

When dealing with solar sail (or other advanced propellantless propulsion systems such as, for example, the electric solar wind sail [32,33,34,35]) transfers to the outer Solar System, a constraint on the transfer trajectory [5, 10, 15] must be typically enforced to avoid the spacecraft from passing too close to the Sun. Indeed, as previously discussed, a trajectory with one (or more) solar photonic assists [12] could represent the solution of the optimal control problem, but the intense thermal load due to solar radiation could cause a severe damage to the scientific instrumentation, thus jeopardizing the mission success. For that reason, each state of the system during the transfer must satisfy the following inequality constraint

$$\begin{aligned} \frac{p(t)}{q(t)} \equiv \frac{p(t)}{1+f(t)\,\cos L(t) + g(t)\, \sin L(t)} \ge r_{\text {min}}, \end{aligned}$$
(9)

where \(r_{\text {min}}\) is the minimum heliocentric distance imposed by thermal load constraints; see Fig. 3.

Fig. 3
figure 3

Conceptual sketch of the solar photonic assist to reach a target distance

Full size image

The optimal trajectory is obtained by solving an optimal control problem, in which the control angle \(\alpha = \alpha (t)\) with \(t \in [0, \, t_{f}]\) is designed to reach the target condition of Eq. (8) from the initial state provided by Eq. (7) by minimizing the performance index \(J \triangleq t_{f}\) and satisfying the inequality constraint given by Eq. (9). In this paper, a simplified approach to the trajectory optimization is adopted, to reduce the computational effort in solving this advanced mission scenario. As stated, the whole transfer trajectory is divided into N arcs and the sail attitude is kept constant along each arc, as proposed in Ref. [11]. Under those assumptions, consider the generic i-th arc (with \(i \in [1, \, N]\)), and let the (constant) pitch angle during the i-th arc be denoted as \(\alpha _i\). The propulsive acceleration vector in the i-th arc \(\varvec{a}_i\) is found by substituting the value \(\alpha = \alpha _i\) into Eq. (3), and the dynamics of the system is calculated by integrating Eq. (4) with \(\varvec{a} = \varvec{a}_i\) and using the terminal values at the \((i-1)\)-th arc as the initial conditions (i.e., the initial values of the MEOEs). At a generic time instant \(t_i\), when the i-th arc is terminated, the pitch angle is suddenly switched to a new value \(\alpha _{i+1}\), and the procedure is repeated. With this approach, the number of control variables involved in the optimal control problem is equal to \(2 \, N\), and the vector of controls \(\varvec{u}\) is given by

$$\begin{aligned} \varvec{u} = \left[ \alpha _1, \, \alpha _2, \dots , \alpha _i, \dots , \alpha _{N-1}, \, \alpha _N, \, t_1, \, t_2, \dots , t_i, \dots , \, t_{N-1}, t_N \right] ^{\text {T}}, \end{aligned}$$
(10)

where the end of the N-th arc coincides with the end of the transfer trajectory, that is, \(t_N \equiv t_f\), which is the performance index to be minimized. In other terms, solving the simplified optimal control model amounts to finding the vector \(\varvec{u}\) that minimizes the final time \(t_f\) and generates a transfer trajectory complying with the minimum heliocentric distance inequality constraint given by Eq. (9) and with the terminal condition equality constraint given by Eq. (8).

The solution of this optimal control problem is found in two steps. The first step exploits a genetic algorithm to perform a global search of the possible solutions by means of MATLAB built-in Augmented Lagrangian Genetic Algorithm function, which allows equality and inequality constraints to be enforced. The settings of the genetic algorithm used in this analysis are as follows. The total population is set to 20 individuals, the crossover fraction is 0.8, while the mutation fraction is 0.2, and 2 individuals are preserved through each iteration. The bounds for the control variables are \(\alpha _i \in [-\pi /2, \, \pi /2]\) rad, \(t_i/t_f \in [0, \, 1]\), while the range for \(t_f\) is specifically selected for each case. The second step involves a gradient-based method that uses the solution provided by the genetic algorithm as a first guess, and converges towards the optimal (i.e., minimum flight time) solution. This step exploits MATLAB built-in function fmincon, which also allows equality and inequality constraints to be enforced in a straightforward way.

3 Numerical Simulations

The optimization procedure discussed in the previous section has been simulated in a couple of mission scenarios in which the initial state is consistent with a spacecraft that leaves Earth’s sphere of influence with zero excess velocity (neglecting the Earth’s orbital eccentricity), that is, \(\varvec{x}_0 = [1 \text {au}, \, 0, \, 0, \, 0]^{\text {T}}\); see Eq. (7). Different values of minimum heliocentric distance have been used in the numerical simulations, i.e., \(r_{\text {min}} = \{0.2, \, 0.3, \, 0.4 \} \text {au}\), in analogy with previous works [5, 12, 13] and in accordance with classical solar sail thermal analyses [36]. The numbers of arcs used in the simulations are comprised in the range \(N \in [2, \, 6]\), while the values of characteristic acceleration used in the simulations are \(a_c \in \{1, \, 2, \, 3, \, 4, \, 5 \}\) mm/s\(^{2}\). All the numerical simulations are run on an Intel core-i7 processor, and the computational times are all on the order of 2–5 min for the genetic algorithm, and about 20–30 s for the gradient-based method. Each test case has been run 30 times, and the best solutions are reported in the remainder of this section.

Fig. 4
figure 4

Minimum flight times \(t_\mathrm{f}\) as functions of number of arcs N, characteristic acceleration \(a_\mathrm{c}\), and minimum heliocentric distance \(r_{\text {min}}\) for a simplified Neptune’s flyby scenario (\(r_{\text {obj}} = 30\text { au})\)

Full size image

In analogy with Ref. [12], the first analyzed optimal trajectory is consistent with a (simplified) Neptune flyby mission scenario, which is obtained by setting the target heliocentric distance equal to Neptune’s orbital radius, i.e., \(r_{\text {obj}} = 30\text {au}\) in Eq. (8). Note that this approach does not take into account planetary ephemeris, Neptune’s orbital eccentricity, and the gravitational perturbation due to other planets. The optimal flight times for different values of the characteristic acceleration \(a_c\), number of arcs N, and minimum heliocentric distance \(r_{\text {min}}\) are plotted in Fig. 4. Some important observations can be derived from Fig. 4. First, it may be observed that increasing the minimum heliocentric distance causes a significant increase of the minimum flight times, as it may be observed by comparing the flight times of Fig. 4a with those of Fig. 4c. Accordingly, if technological progress helps to relax the constraint on the minimum Sun-spacecraft distance, the flight times will be significantly affected. Figure 4 also highlights that, even with a simplified control law and assuming a medium-term solar sail, Neptune’s orbit can be reached within a reasonable flight time of 6–8 years, and these values further decrease for medium- and high-performance solar sails. For comparison, consider that the only probe that reached Neptune so far is Voyager 2 [37], which performed a Neptune flyby after a flight time of 12 years and three flybys with Jupiter, Saturn, and Uranus. Moreover, the improvements in terms of optimal flight times obtained by increasing the number of arcs are relevant for \(N< 4\), but become practically negligible for \(N \ge 5\), so that the minimum flight times obtained for \(N=6\) can be considered close to that estimated by our proposed (simplified) approach, with the only possible exception of lower values of the characteristic acceleration. The obtained flight times are very close (and sometimes even smaller) to those found by Dachwald with an elegant optimization algorithm based on the concept of evolutionary neurocontrol [12]. The reason for this interesting result is that Neptune’s ephemeris are taken into account in Ref. [12]. In general, the simplified control law provides a very accurate estimation of the required time for performing a Neptune flyby with a solar sail-based spacecraft. Note that a solution was not found for \(a_\mathrm{c} = 1\) mm/s\(^{2}\) and \(N \le 3\), because with this (small) value of the characteristic acceleration at least two photonic assists are required to reach the target distance, as it may be observed in Fig. 5a. Each photonic assist requires the pitch angle to be first kept at a negative value to move the osculating orbit perihelion closer to the Sun, and then at a positive value to increase the orbital energy due to the combined effect of the increased solar radiation pressure and the Sun’s close encounter; see Fig. 5b. Therefore, when two photonic assists are required, the minimum feasible value of arcs is \(N=4\). On the other hand, if \(a_\mathrm{c} \ge 2\) mm/s\({^2}\) just one photonic assist is sufficient for reaching the target; see Fig. 5c, d. In particular, the pitch angle changes required by a solar photonic assist are aimed to minimizing the spacecraft angular momentum, to obtain an escape trajectory that is nearly rectilinear.

Fig. 5
figure 5

Minimum-time trajectories (grey dots = pitch angle switches) and optimal (simplified) control laws for Neptune’s flyby scenarios (\(r_{\text {obj}} = 30 \text {au})\) for \(N=4\), \(r_{\text {min}} = 0.3 \text {au}\), and \(a_c = \{1, \, 2 \}\) mm/s\(^{2}\)

Full size image

The second mission scenario consists in an escape from the Solar System. Such a mission should aim at exploring the external regions of the Solar System and the interstellar medium, and for this reason a target heliocentric distance \(r_{\text {obj}} = 100 \text {au}\) is selected. The minimum flight times obtained with the simplified control law are plotted in Fig. 6 as functions of \(a_\mathrm{c}\), N and \(r_{\text {min}}\).

Fig. 6
figure 6

Minimum flight times \(t_\mathrm{f}\) as functions of number of arcs N, characteristic acceleration \(a_\mathrm{c}\), and minimum heliocentric distance \(r_{\text {min}}\) for Solar System escape scenario (\(r_{\text {obj}} = 100 \text {au})\)

Full size image

Similar to the Neptune flyby case, the minimum heliocentric distance constraint significantly affects the flight time, and the results obtained for \(N \ge 5\) are close to the minimum value obtained with this simplified procedure. The results of Fig. 6 for \(N=6\) are very close to those obtained by Sauer [5] and Zeng [13] for medium- or high- performance solar sails, i.e., \(a_\mathrm{c} \ge 2\) mm/s\(^{2}\). Notably, when \(a_\mathrm{c} = 1\) mm/s\(^{2}\), the (simplified) proposed control law outperforms literature results. This may be caused by the fact that our algorithm provides a transfer trajectory with two solar photonic assists for this value of \(a_c\), as previously discussed, whereas in Refs. [5, 13] all of the plotted solutions exploit just one photonic assist.

4 Conclusion

This paper has discussed a simplified optimal control law for a solar sail-based spacecraft in a mission towards the outer regions of the Solar System. The proposed mathematical model allows an accurate estimation of the minimum-time trajectory to be found with a reasonable computational time and without requiring an initial guess of the co-state variables. The simplified control law is based on the idea of dividing the whole transfer trajectory into a certain number of arcs, and keeping the sail attitude constant through each arc. The algorithm has been tested in two mission scenarios, and the numerical results suggest that a solar sail with medium-term technology may outperform conventional thrusters in terms of mission flight time. A comparison with existing literature shows that the simplified control law discussed in this analysis is able to give results similar to those obtained with more complex techniques with just a few number of arcs.