EOQ Model Under Discounted Partial Advance—Partial Trade Credit Policy with Price-Dependent Demand

Abstract

The aim of this article is to investigate an inventory model with discounted partial advance payment in a single supplier–single retailer supply chain in the presence of credit period when the demand rate is price sensitive. The lengths of the credit period, advance period, as well as rate of discount on advance payment, are specified by the supplier. Conditions for unique optimal values of the decision variables, namely, the retailer’s selling price and cycle length are obtained. Optimal values of the decision variables are determined iteratively. An algorithm is developed and a numerical example is presented to demonstrate the solution algorithm. Sensitivity analysis is conducted. It is observed that optimal cycle time is affected by the two interest rates. Optimal net profit is affected by the demand rate and the discount factor. Both, the optimal cycle time, as well as the optimal net profit is affected by the supplier’s selling price and the proportion of units for which the advance payment is made. Optimal retailer’s selling price is significantly affected by the discount factor, supplier’s selling price, price elasticity of the demand function as well as the proportion of units for which advance payment is made. We also observe that the retailer’s net profit does not decrease significantly on increasing the advance period.

13.1 Introduction

In the competitive situation prevailing in the market, a major effort is required by suppliers to provide facilities which would, in turn, attract orders from retailers. One such facility popular in a supplier–retailer contract is to offer goods on credit for some interest-free period—generally termed as the trade credit period or permissible delay in payment. The retailer may pay the entire amount or a part of it to the supplier at the end of the credit period. Once the credit period is over, interest is charged by the supplier on the remaining dues.

The benefits of trade credit policy in the context of marketing are identified as leading to increased sales and as a tool to attract new retailers who deem credit policy as a kind of price reduction. Another advantage is that due to trade credit, an established retailer may pay more promptly resulting in a reduction in the outstanding sales dues. Trade credit provides financial support to the retailer along with providing a certification of quality from the supplier.

During the last few decades, many inventory models have been developed considering the trade credit facility. Goyal [8], Teng [27], Chang et al. [3], Sarkar [22], Chen and Teng [5], Taleizadeh et al. [26], Tiwari et al. [30], Jaggi et al. [14] and many others have considered trade credit when the demand is constant.

In practice, quite often, the end customer demand at the retailer is price-sensitive. In such a situation, decisions regarding setting the retailer’s selling price and order quantity are to be made by the retailer. Price-sensitive demand without trade credit has been considered by many authors, e.g., Banerjee and Sharma [2]. For an inventory model under trade credit contract with price-sensitive demand, optimal pricing policies were obtained by Hwang and Shinn [13]. Under cooperative and noncooperative structures, Abad and Jaggi [1] developed a model with price-dependent demand to obtain the retailer’s optimal unit price and replenishment cycle as well as the seller’s optimal selling price and credit period. Teng et al. [28] found the optimal selling price and replenishment policies considering a model with price-sensitive demand for deteriorating items. They concluded that under trade credit, the cycle time, and order quantity will decrease. Price-sensitive demands for integrated inventory models that involve trade credit have also been developed by Ouyang et al. [21], Chen and Kang [4] and Chung and Liao [6].

Ho et al. [12], Shah et al. [23] analyze the decision policy when the buyer receives a cash discount if he pays any fraction of purchase cost within a shorter allowable credit period and then clears the remaining balance in the long credit period. Such a policy is called a two-part permissible delay.

Some more realistic models have considered revenue earned through sales as well as interest earned during the credit period and even later for price-sensitive demand [15, 16, 19, 20, etc.].

Retailers are generally in search of long credit periods for the purchase of their goods, whereas this tendency may lead to financial complications for small suppliers and hence to supply crunch for the retailer. Hence, sometimes, it may be worthwhile for the supplier to demand advance payment. Zhang et al. [32] stated that advance payment is a known practice in the Chinese automobile and steel industries. Maiti et al. [18] observed that in the bricks and tiles factories in India, sometimes a price discount on advance payment is offered to the retailer if made at his own discretion.

In inventory literature, very little consideration has been given to the advance payment and its influences on inventory decisions. Maiti et al. [18] developed a stochastic inventory model with advance payment. They assumed that the retailer’s procurement price depended on the fraction of the advance payment. Their model was extended by Gupta et al. [9]. However, these two papers do not consider trade credit policy. Both advance payment and trade credit were considered by Thangam [29] for constant demand. Full advance and partial advance partial credit were incorporated by Zhang et al. [32] for constant demand. They conclude that in both the payment policies, length of the period of advance payment does not affect the retailer’s optimal policy.

Taleizadeh [25] studied a lot sizing model without credit period under price-dependent demand with advance payment policy when the equal installments of the advance payment of the purchase cost are specified by the supplier. For constant demand, Wu et al. [31] studied the model when the seller requires an advance-cash-credit (ACC) payment.

From the above-detailed literature review, we find that till now, very few papers have considered advance payments. Out of these few papers, some have not considered trade credit [18, 24] while others, who have considered advance payment, as well as trade credit, have regarded demand to be constant [17, 31, 32, 33] or time dependent [7]. Although Diabat et al. have considered both advance payment as well as delayed payment, the two are for different echelons in the supply chain with upstream advance payment and downstream delayed payment.

In the present paper, we consider iso-elastic price-dependent demand with partial advance payment before the supply is received when the credit period is also allowed. The aim of this article is to study an optimal inventory model that considers ordering and pricing decisions under discounted partial advance and partial credit period when the customer demand is an iso-elastic function of the retailer’s selling price. We obtain the optimal price and optimal length of replenishment cycle when shortages are not allowed. We also examine how the variations in the model parameters affect the optimal solution.

The rest of this paper is organized as follows: Sect. 13.2 presents the assumptions and notations. Section 13.3 explains the working of the model, Numerical example is given in Sect. 13.4 along with algorithm, sensitivity analysis and managerial insights. In Sect. 13.5, we present the conclusions.

13.2 Notations and Assumptions

The following notations are used in this paper:

D:

demand dependent on retailer’s price rate per unit. D = α P ^-β_R , α, β > 1.

h:

unit inventory holding cost per unit time.

A:

ordering cost per order.

I₁:

the interest rate paid per unit time to supplier by retailer.

I_PR:

the interest rate per unit time to be paid by retailer to financer for loan.

I_ER:

the interest rate earned per unit time by retailer.

t₀:

epoch of advance payment

M_A:

the retailer’s advance period stipulated by the supplier.

M_R:

the credit period provided by the supplier to the retailer.

Net:

the retailer’s net profit per unit time.

A₁:

proportion of Q for which an advance payment is made by the retailer at epoch M_A.

A₂:

proportion of Q for which payment is paid by the retailer at epoch M_R. 0 ≤ A₁ + A₂ ≤ 1.

ρ:

discount factor for advance booking, 0 < ρ < 1. The discount percent is 100(1–ρ).

T:

the retailer’s inventory cycle length (Decision variable)

P_S:

supplier’s unit selling price.

P_R:

retailer’s unit selling price $( {\text{P}}_{\text{R}} > {\text{P}}_{\text{S}} )$. (Decision variable)

Q:

the retailer’s order quantity per cycle (Decision variable). Q = DT

* With any decision variable indicates its optimal value.

Assumptions

The model is developed with the following underlying assumptions:

• 1. The supplier provides a fixed credit period M_R to the retailer for settling the accounts.

• 2. The end consumer market demand rate declines with an increase in the retailer’s selling price, D(P_R) = αP ^-β_R , where α > 0 and β being, respectively, the scaling factor and the index of price elasticity. For notational simplicity, we will be interchangeably using D(P_R) and D in this work.

• 3. The retailer starts selling the goods as soon as he receives it.

• 4. The earnings accumulated by the retailer is withdrawn only at epoch T, or later.

• 5. For the payments made to supplier at t₀ and M_R, the retailer has to take loan from the financial institution like banks—which we call financer, while for the payment made at epoch T, the retailer uses a part of the earnings accumulated till time T.

• 6. Shortages are not allowed.

• 7. Replenishment rate and time horizon are infinite.

13.3 The Model

The model is developed with the stated advance period under trade credit with a price-dependent demand so as to maximize net profit for the retailer. The retailer orders for Q units of inventory at epoch t₀, which is M_A time units before the beginning of the selling season. The ordered units arrive at the beginning of the selling season. The payments for the ordered units are made by the retailer in three parts:

• 1. An advance payment at epoch t₀ for proportion A₁ of Q units is made at the discounted rate ρP_S. 0 ≤ A₁ ≤ 1.

• 2. For the remaining quantity, payment has to be made depending on the following two cases.

Case I: M_R ≤ T

In this case, a payment at the rate P_S for proportion A₂ of Q units is made at the epoch M_R. No interest is paid to the supplier for this delayed payment under the credit policy. 0 ≤ A₁ + A₂ ≤ 1. Payment for the remaining proportion 1 – (A₁ + A₂) of Q units at the rate P_S along with interest charged by the supplier from M_R to T at the rate I₁. is made at epoch T.

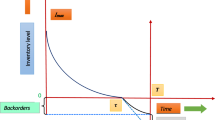
The payments at t₀ and M_R are made by taking a loan from financer. The retailer starts selling his goods from the beginning of the selling period. The sales earnings up to Tare invested as they accumulate and interest is earned on it at the rate I_ER. When the selling period ends, the payment to the supplier and loan repayment and payment of interest for the loan to the financer will be made by the retailer from the sales as well as interest earnings up to T (Fig. 13.1a).

Fig. 13.1

a Time Inventory Graph when M_R ≤ T.

Case II: M_R > T

In this case, a payment for the remaining proportion (1 – A₁) of Q units is made at the rate P_S at epoch M_R so as to take advantage of the credit period. No interest is to be paid for this payment, the credit period M_R being larger than the cycle length T, and no loan is to be taken by the retailer for the payment. Repayment the loan taken from the financer at t₀ and interest on it is to be repaid to the financer at epoch T, i.e., when the selling period ends (Fig. 13.1b).

Fig. 13.1

b Time Inventory Graph when M_R > T

13.3.1 Computation of Net

The retailer’s net profit for the cycle is given by

Net = Total revenue earned – (Ordering cost + Stock holding cost + Purchase cost + Interest paid) where

Total revenue earned = Sales revenue + Interest earned

Ordering cost is A

Stock holding cost is $\frac{{{\text{h}}\left( {{\text{DT}}^{2} } \right)}}{2}$

The total revenue earned, interest earned, interest paid and net profit per unit time for Case I and Case II are as follows:

Case I: M_R ≤ T

The total purchasing cost paid at epoch M_A, M_R and T of quantity (A₁Q), (A₂Q) and (1 – (A₁ + A₂))Q, respectively, is

$$ \left( {\uprho{\text{P}}_{\text{S}} } \right)\left( {{\text{A}}_{1} {\text{Q}}} \right) + {\text{P}}_{\text{S}} \left( {{\text{A}}_{2} {\text{Q}}} \right) + {\text{P}}_{\text{S}} \left( {1 - \left( {{\text{A}}_{1} + {\text{A}}_{2} } \right)} \right){\text{Q}} $$

The interest paid by the retailer till T, for the loan taken at the epochs t₀ and M_R, is $\left( {{{\text{T + M}}}_{{\text{A}} }} \right)\left( {{\text{A}}_{1} {\text{Q}}} \right)(\uprho{{\text{P}}}_{{\text{S}}} ){{\text{I}}}_{{\text{PR}}} + \left( {{{\text{T}}} - {{\text{M}}}_{{\text{R}}} } \right)\left( {{{\text{A}}_{2}} {{\text{Q}}}} \right){{\text{P}}}_{{\text{S}}} {{\text{I}}}_{{\text{PR}}}$

The interest paid by the retailer to the supplier for the amount paid at T is $\left( {{{\text{T - M}}}_{{\text{R}} }} \right)(\left( {1 - \left( {{{\text{A}}}_{{1}} + {{\text{A}}}_{{2}} } \right)){{\text{Q}}}} \right){{\text{P}}}_{{\text{S}}} {{\text{I}}}_{{1}}$

Total revenue earned by the retailer is

$$ {\text{P}}_{\text{R}} \left( {\text{DT}} \right) + \frac{{{\text{P}}_{\text{R}} ({\text{DT}}){\text{I}}_{\text{ER}} {\text{T}}}}{2} $$

Hence, the net profit per unit time of the retailer is

$$ \begin{aligned} {{\text{Net}}}\,1 & = {{\text{P}}}_{{\text{R}}} {{\text{D}}}\left( {1 + \frac{1}{2}{{\text{I}}}_{{\text{ER}}} {{\text{T}}}} \right) - \frac{\text{A}}{{\text{T}}} - \frac{\text{hDT}}{{2}} - {{\text{P}}}_{{\text{S}}} {{\text{D}}}\left[ {\left( {{1 - {{\text{A}}}_{1} }} \right)\left( {{1 + {{\text{I}}}}_{{1}} \left( {{{\text{T}}} - {{\text{M}}}_{{\text{R}}} } \right)} \right)} \right. \\ & \quad \left. { - {{\text{A}}}_{{2}} \left( {{{\text{I}}}_{{1}} - {{\text{I}}}_{{\text{PR}}} } \right)\left( {{{\text{T}}} - {{\text{M}}}_{{\text{R}} }} \right) + {{\text{A}}}_{{1}}\uprho\left( {1 + {{\text{I}}}_{{\text{PR}}} \left( {{{\text{T}}} + {{\text{M}}}_{{\text{A}} }} \right)} \right)} \right] \\ \end{aligned} $$

(13.1)

Case II: M_R > T

The total purchasing cost paid at epoch M_A and T of quantity(A₁Q) and (1 – A₁)Q, respectively, is

$$ \left( {\uprho{\text{P}}_{\text{S}} } \right)\left( {{\text{A}}_{1} {\text{Q}}} \right) + {\text{P}}_{\text{S}} \left( {1 - {\text{A}}_{1} } \right){\text{Q}} $$

The interest paid by the retailer till T to the financer for the amount paid at the epoch t₀ is

$$ \left( {{\text{T + M}}_{\text{A}} } \right)\left( {{\text{A}}_{1} {\text{Q}}} \right)(\uprho{\text{P}}_{\text{S}} ){\text{I}}_{\text{PR}} $$

Total revenue earned by the retailer is

$$ {\text{P}}_{\text{R}} \left( {\text{DT}} \right) + \frac{{{\text{P}}_{\text{R}} ({\text{DT}}){\text{I}}_{\text{ER}} {\text{T}}}}{2} + {\text{P}}_{\text{R}} \left( {\text{DT}} \right)\left( {{\text{M}}_{\text{R}} - {\text{T}}} \right){\text{I}}_{\text{ER}} $$

Hence, the net profit per unit time of the retailer is

$$ {{\text{Net}}}\,2 = {{\text{P}}}_{{\text{R}}} {{\text{D}}}\left[ {1 + {{\text{I}}}_{{\text{ER}}} \left( {{{\text{M}}}_{{\text{R}}} - \frac{{\text{T}}}{{2}}} \right)} \right] - \frac{\text{A}}{{\text{T}}} - \frac{\text{hDT}}{{2}} - {{\text{P}}}_{{\text{S}}} {{\text{D}}}\{ {{\text{A}}}_{{1}} [1 -\uprho\{ 1 + {{\text{I}}}_{{\text{PR}}} \left( {{{\text{M}}}_{{\text{A}}} + {{\text{T}}}} \right)\} ] - 1\} $$

(13.2)

The overall net profit per unit time is

$$ {\text{Net}} = \left\{ {\begin{array}{*{20}l} {{\text{Net}}1; {\text{ for M}}_{\text{R}} \le {\text{T}}} \hfill \\ {{\text{Net}}2; {\text{ for M}}_{\text{R}} > {\text{T}}} \hfill \\ \end{array} } \right. $$

(13.3)

13.3.2 Analysis

Using assumption 3 and Q = DT, it is apparent that Net is a function of decision variables P_R and T. In order to obtain the optimal values of the decision variables analysis of the net profit function for Case I and Case II are presented:

13.3.2.1 Necessary Conditions

The first-order (necessary) conditions for maximization of Netj with respect to T and P_R are

$$ \frac{{\partial {\text{Netj(T, P}}_{\text{R}} )}}{{\partial {\text{T}}}} = 0\quad \quad \frac{{\partial {\text{Netj(T, P}}_{\text{R}} )}}{{\partial {\text{P}}_{\text{R}} }} = 0;\quad \quad {\text{j}} = 1,2. $$

Differentiating (1) with respect to T and P_R, we get, respectively

$$ \frac{{\partial {{\text{Net1(T, P}}}_{{\text{R}}} )}}{{\partial {{\text{T}}}}} =\upalpha\,{{\text{P}}}_{{\text{R}}}^{{ {-\upbeta}}} \left\{ {\frac{{{{\text{I}}}_{{\text{ER}}} {{\text{P}}}_{{\text{R}}} }}{{2}} - \frac{\text{h}}{{2}} - {{\text{P}}}_{{\text{S}}} \left[ {\left( {1 - {{\text{A}}}_{{1}} } \right){{\text{I}}}_{{1}} - {{\text{A}}}_{{2}} \left( {{{\text{I}}}_{{1}} - {{\text{I}}}_{{\text{PR}}} } \right) + {{\text{A}}}_{{1}} {{\text{I}}}_{{\text{PR}}}\uprho} \right]} \right\} + \frac{\text{A}}{{{{\text{T}}}^{{2}} }} $$

(13.4)

and

$$ \frac{{\partial {\text{Net1(T, P}}_{\text{R}} )}}{{\partial {\text{P}}_{\text{R}} }} = \frac{1}{2}\upalpha{\text{P}}_{\text{R}}^{{ - \left( {\upbeta + 1} \right)}} {\text{R}}1 $$

(13.5)

where

$$ \begin{aligned} {\text{R}}1 & = - {\text{P}}_{\text{R}} \left( {2 + {\text{I}}_{\text{ER}} {\text{T}}} \right)\left( {\upbeta - 1} \right) \\ & \quad +\upbeta\left[ {\text{hT}} \right. \\ & \quad + 2{\text{P}}_{\text{S}} \left\{ {\left( {1 - {\text{A}}_{1} } \right)\left( {1 + {\text{I}}_{1} \left( {{\text{T}} - {\text{M}}_{\text{R}} } \right)} \right)} \right. - {\text{A}}_{2} \left( {{\text{I}}_{1} - {\text{I}}_{\text{PR}} } \right)\left( {{\text{T}} - {\text{M}}_{\text{R}} } \right) \\ & \quad \left. {\left. { + {\text{A}}_{1}\uprho\left( {1 + {\text{I}}_{\text{PR}} \left( {{\text{M}}_{\text{A}} + {\text{T}}} \right)} \right)} \right\}} \right] \\ \end{aligned} $$

We note that RHS of (5) is zero iff R₁ = 0.

On equating (13.4) and (13.5) to zero, we get, respectively

$$ {{\text{T}}}_{{1}}^{ *} { = }\frac{{\sqrt {2{{\text{A}}}} }}{{\sqrt {\upalpha\,{{\text{P}}}_{{\text{R}}}^{{{ -\upbeta}}} \left[ {{{\text{h}}} - {{\text{I}}}_{{\text{ER}}} {{\text{P}}}_{{\text{R}}} + 2{{\text{P}}}_{{\text{S}}} \left( {\left( {1 - {{\text{A}}}_{{1}} } \right){{\text{I}}}_{{1}} - {{\text{A}}}_{{2}} \left( {{{\text{I}}}_{{1}} - {{\text{I}}}_{{\text{PR}}} } \right) + {{\text{A}}}_{{1}} {{\text{I}}}_{{\text{PR}}}\uprho} \right)} \right]} }} $$

(13.6)

And on substituting for R₁, we get

$$ {\text{P}}_{{{\text{R}}1}}^{ *} { = }\frac{{\upbeta\left[ {{\text{hT}} + 2{\text{P}}_{\text{S}} \left\{ {\left( {1 - {\text{A}}_{1} } \right)\left( {1 + {\text{I}}_{1} \left( {{\text{T}} - {\text{M}}_{\text{R}} } \right)} \right) - {\text{A}}_{2} \left( {{\text{I}}_{1} - {\text{I}}_{\text{PR}} } \right)\left( {{\text{T}} - {\text{M}}_{\text{R}} } \right) + {\text{A}}_{1}\uprho\left( {1 + {\text{I}}_{\text{PR}} \left( {{\text{M}}_{\text{A}} + {\text{T}}} \right)} \right)} \right\}} \right]}}{{\left( {2 + {\text{I}}_{\text{ER}} {\text{T}}} \right)\left( {\upbeta - 1} \right)}} $$

(13.7)

Similarly, differentiating (2) with respect to T and P_R,we get respectively

$$ \frac{{\partial {{\text{Net2(T, P}}}_{{\text{R}}} )}}{{\partial {{\text{T}}}}} =\upalpha{{\text{P}}}_{{\text{R}}}^{{ -\upbeta}} \left\{ { - \frac{{{{\text{I}}}_{{\text{ER}}} {{\text{P}}}_{{\text{R}} }}}{{2}} - \frac{\text{h}}{{2}} - {{\text{A}}}_{{1}} {{\text{I}}}_{{\text{PR}}} {{\text{P}}}_{{\text{S}}}\uprho} \right\} + \frac{\text{A}}{{{{\text{T}}}^{{2}} }} $$

(13.8)

and

$$ \frac{{\partial {\text{Net2(T, P}}_{\text{R}} )}}{{\partial {\text{P}}_{\text{R}} }} = \frac{{\upalpha }}{2}{\text{P}}_{\text{R}}^{{ - \left( {\upbeta + 1} \right)}} {\text{R}}2 $$

(13.9)

where

$$ {{\text{R}}}2 = - {{\text{P}}}_{{\text{R}}} \left( {2 + 2{{\text{I}}}_{{\text{ER}}} {{\text{M}}}_{{\text{R}}} - {{\text{I}}}_{{\text{ER}}} {{\text{T}}}} \right)\left( {\upbeta - 1} \right) +\upbeta\left[ {{{\text{hT}}} - 2{{\text{P}}}_{{\text{S}} }} \right[\{ {{\text{A}}}_{{1}} (1 -\uprho(1 + {{\text{I}}}_{{\text{PR}}} \left( {{{\text{M}}}_{{\text{A}}} + {{\text{T}}}} \right))) - 1\} ] $$

On equating (13.8) and (13.9) to zero, we get, respectively

$$ {{\text{T}}}_{{2}}^{{ *}} = \frac{{\sqrt {2A} }}{{\sqrt {\upalpha\,{{\text{P}}}_{{\text{R}}}^{{{ -\upbeta}}} \left( {h + {{\text{I}}}_{{\text{ER}}} {{\text{P}}}_{{\text{R}}} + 2{{\text{A}}}_{{1}} {{\text{I}}}_{{\text{PR}}} {{\text{P}}}_{{\text{S}}} \rho } \right)} }} $$

(13.10)

and

$$ {{{\text{P}}}}_{{{{{\text{R}}}}2}}^{{ *}} {{ = }}\frac{{\upbeta({{{\text{hT}}}} - 2{{{\text{P}}}}_{{{\text{S}}}} \left[ {{{{\text{A}}}}_{{{1}}} \left( {1 -\uprho(1 + {{{\text{I}}}}_{{{\text{PR}}}} \left( {{{{\text{M}}}}_{{{\text{A}}}} + {{{\text{T}}}}} \right))) - 1} \right]} \right)}}{{\left( 2 + 2{{{\text{I}}}}_{{{\text{ER}}}} {{{\text{M}}}}_{{{\text{R}}}} -{{{ {\text{I}}}}_{{{\text{ER}}}} {{{\text{T}}}}} \right)\left( {\upbeta - 1} \right)}} $$

(13.11)

13.3.2.2 Sufficiency Conditions

The second order (sufficiency) conditions for Netj, j = 1, 2 to be maximum with respect to T and P_R, respectively, are

(i) $\frac{{{\partial^{2} {{\text{Netj}}}}\left( {{{\text{T}}}, {{\text{P}}}_{{\text{R}}} } \right) }}{{{\partial {{\text{T}}}^{{2}} }}} < 0$, (ii) $\frac{{\partial^{2} {\text{Netj}}\left( {{\text{T}},{\text{P}}_{\text{R}} } \right)}}{{\partial {\text{P}}_{\text{R}}^{2} }} < 0$

for which, wide sufficient conditions are derived in Appendix 1

For Net j to be jointly concave with respect to both the decision variables T and P_R, we require that Netj satisfies (i) or (ii) and

(iii) $\frac{{\partial^{2} {\text{Netj}}\left( {{\text{T}},{\text{P}}_{\text{R}} } \right)}}{{\partial {\text{T}}^{2} }}\frac{{\partial^{2} {\text{Netj}}\left( {{\text{T}},{\text{P}}_{\text{R}} } \right)}}{{\partial {\text{P}}_{\text{R}}^{2} }} - \left( {\frac{{\partial^{2} {\text{Netj}}\left( {{\text{T}},{\text{P}}_{\text{R}} } \right) }}{{\partial {\text{T}}\partial {\text{P}}_{\text{R}} }}} \right)^{2} > 0$

Condition (iii) has been further discussed in Appendix 2.

13.4 Algorithm

On the basis of above theoretical results, the following solution algorithm has been developed to determine an optimal solution of the model for the given parameters α, β, A, h, I_ER, I_PR, I₁, ρ, A₁, A₂, P_S, M_A, M_R.

Step 1: Input values of all the parameters.

Step 2: We find the optimal values of T and P_R for T ≥ M_R, i.e., T ^*₁ , P ^*_R1 as follows:

• (i) Put j = 0. Select the initial value P ^*_R1 of P_R1 as P_R10 = P_S.

• (ii) Substitute P_R = P ^*_R1j in (6) and compute T ^*_1j .

  Set j = j + 1.

• (iii) Substitute T = T ^*_1j in (7) to obtainP ^*_R1j+1 .

• (iv) Repeat (ii) – (iii) till the values of T ^*_1j and P ^*_R1j stabilize, say, to T ^*₁ and P ^*_R1 , respectively.

• (v) Substitute T ^*₁ and P ^*_R1 in (1) to obtain the optimal value of Net1*

Step 3: We find the optimal values of T and P_R for T ≥ M_R, i.e., T ^*₂ , P ^*_R2 as follows:

• (i) Put j = 0. Set P_R20 = P_S a guess value of P_R2.

• (ii) Substitute P_R = P ^*_R2j in (10) and compute T ^*_2j .

  Set j = j + 1.

• (iii) Substitute T = T ^*_2j in (11) to obtainP ^*_R2j+1 .

• (iv) Repeat (ii) – (iii) till the values of T ^*_2j and P ^*_R2j stabilize, say, to T ^*₂ and P ^*_R2 , respectively.

• (v) Substitute T ^*₂ and P ^*_R2 in (2) to obtain the optimal value of Net2*

Step 4: The optimal net profit is Net* = Max (Net1*, Net2*). Stop.

13.4.1 Numerical Example

In this section, we provide a numerical example to illustrate the results satisfying both the above necessary and sufficient conditions of maximization obtained in Sect. 13.3. We apply the above algorithm to obtain optimal values of the decision variables and to conduct sensitivity analysis. We consider the following values for the input parameters in proper units.

Example: Let us take the following parameter values of the inventory system as follows:α = 1,000,000, β = 2, h = 0.65, A = 50, I_ER = 0.06, I_PR = 0.09, I₁ = 0.1, ρ = 0.4, A₁ = 0.2, A₂ = 0.4, P_S = 5, M_R = 0.08, M_A = 0.04.

Plots of Net1 and Net2 with respect to T and P_R for Case I (T ≥ M_R) and Case II (T < M_R) are presented in Fig. 13.2a and Fig. 13.2b, respectively. From the figures, it is clear that for this set of input parameters, Net is jointly Concave function of P_R and T for both the cases.

Fig. 13.2

a Net versus T and P_R for M_R ≤ T,

Fig. 13.2

b Net versus T and P_R for M_R > T

The optimal values are as follows:

Decision variable	Case I	Case II
T*	0.0908	0.0790
PR*	8.8525	8.8385
Net*	56084.2	56075.6

Case I provides a larger value of Net. Hence, the column under Case I provides the optimal set of values.

13.4.2 Sensitivity Analysis

We now study the effects of changes in the values of the system parameters α, β, h, A, I_ER, I_PR, I₁, ρ, A₁, A₂, P_S, M_R, M_A on the optimal values of retailer’s price, cycle length and net profit.

The sensitivity analysis is performed by changing each of the parameters by +50%, +25%, −25%, and −50% taking one parameter at a time and keeping the values of the remaining parameters unchanged.

The results for the cost parameters and other parameters of the model are presented in Table 13.1 and Table 13.2, respectively.

Table 13.1 Sensitivity analysis of the optimal solution with change in cost parameters

Table 13.2 Sensitivity analysis of the optimal solution with respect to model parameters

Table 13.1 shows the change in optimal values of the decision variables and the optimum net profit with changes in the cost parameters. We observe that increase in P_s by 50% results in increase in T* by almost 40%, increase in P_R* by almost 50% and decrease in Net* by 33%. Increase in I_ER by 50% results in about 18% increase in T* whereas surprisingly, this does not significantly affect the net profit. A 50% decrease in I_PR andI₁ results in almost 14% and 13% increase in T*, respectively. Increase in ρ by 50% results in increase in optimal cycle time by 4% and the retailers’ selling price by about 5% and net profit decreases by 4.40%. Increase in A by 50% results in about 23% increases in T*. A 50% decrease in h results in about 23% increase in T*.

Table 13.2 shows the change in optimal values of the decision variables and the optimum net profit with changes in the model parameters, where the significant changes are written in bold characters. It is seen that increase in the credit period M_R by 25% results in decline in T* and hence, Case II becoming optimal, i.e., the inventory ordered should be such that it is sold off before the end of the credit period.

The parameters α and β are major factors that affect—the optimal values of the cycle time, retailer’s price, as well as the net profit. A 25% increase/decrease in the value of α result in a proportionate increase/decrease in the value of net profit. A 25% decrease in α results in about 16% increase in the optimal cycle length, while 50% increase in β results in 84% increase in the optimal cycle length.

The results of sensitivity analysis presented above are also shown below graphically in order to enable a quicker comprehension (Fig 13.3a,b,c).

Fig. 13.3

a Significant change in T* with change in parameters

Fig. 13.3

b Significant change in P_R* with change in parameters

Fig. 13.3

c Significant change in Net* with change in parameters

13.4.3 Managerial Insights

We find that among cost factors, increasing supplier’s selling price results in a significant increase in the optimal cycle time, but a drastic decrease in the optimum profit. Other factors that result in a significant change in optimal time are the rates of interest to be paid by and earned by the retailer, ordering cost, discount factors well as the holding cost. However, other than the supplier’s price, net profit is not significantly affected by cost factors. Hence supplier’s price must be negotiable to attain a profitable level for the retailer. Increase in the proportion of advance payment will result in decline in optimal value of the retailer’s selling price and hence increase in end customer demand. Thus, an increase in the proportion of order quantity obtained at discounted price and increase in revenue earned due to increased demand together lead to an increase in the net profit rate of the retailer. Further, an advantage of increasing A₁ is that it will contribute to increase in supplier’s corpus fund. A completely opposite effect is seen when the discount factor is increased. The retailer’s net profit is significantly affected by both the demand parameters. Hence, the demand rate must be estimated with care. Increase in duration of advance payment by the supplier will not result in a reduction in the retailer’s net profit as in Zhang [18].

13.5 Conclusion and Future Scope

In this paper, we have discussed a payment policy for supply chains with permissible delay in payment and partial advance payment at a discounted price where the retailer’s selling price is a decision variable. Iso-elastic price-dependent demand function has been considered and useful managerial insights are obtained from sensitivity analysis.

In future, other types of price-dependent demand functions may be explored for other real-life problems. Further, being an important determinant of the retailer’s payment policy, discount may be optimally determined using procedure similar to Gupta et al. [10] for constant demand and Gupta et al. [11] for iso-elastic demand.

This research did not receive any specific grant from funding agencies in the public, commercial, or nonprofit sectors.

Appendices

Appendix 1 (Sufficiency Conditions)

For Case I (T ≥ M_R), the second-order derivatives with respect to T and P_R are given by differentiating (4) and (5), respectively, i.e.,

$$ \frac{{\partial^{2} {\text{Net}}1\left( {{\text{T}},{\text{P}}_{\text{R}} } \right) }}{{\partial {\text{T}}^{2} }} = - \frac{{2{\text{A}}}}{{{\text{T}}^{3} }} < 0 $$

$$ \frac{{\partial^{2} {\text{Net}}1\left( {{\text{T}},{\text{P}}_{\text{R}} } \right)}}{{\partial {\text{P}}_{\text{R}}^{2} }} = - \frac{\upalpha}{2}{\text{P}}_{\text{R}}^{{ - \left( {\upbeta + 1} \right)}} \left[ {{\text{P}}_{\text{R}}^{ - 1} \left( {\upbeta + 1} \right)\left( {{\text{R}}1} \right) + \left( {\upbeta - 1} \right)\left( {2 + {\text{I}}_{\text{ER}} {\text{T}}} \right)} \right] $$

At P_R* since $\frac{\partial Net1}{{\partial P_{R} }} = 0$, we have R₁ = 0.

Since R1 = 0,

$$ \frac{{\partial^{2} {\text{Net}}1\left( {{\text{T}}, {\text{P}}_{\text{R}} } \right)}}{{\partial {\text{P}}_{\text{R}}^{2} }}\left\langle {0\,{\text{If}}\,\upbeta - 1} \right\rangle 0,\,{\text{i}}.{\text{e}}.,\,\upbeta > 1. $$

For Case II (T < M_R), the second-order derivatives with respect to T and P_R are given by differentiating (8) and (9), respectively, i.e.,

$$ \begin{aligned} \frac{{\partial^{2} {{\text{Net}}}2\left( {{{\text{T}}}, {{\text{P}}}_{{\text{R}}} } \right) }}{{\partial {{\text{T}}}^{{2}} }} & = - \frac{{2{{\text{A}}}}}{{{{\text{T}}}^{{3}} }} < 0 \\ \frac{{\partial^{2} {{\text{Net}}}2\left( {{{\text{T}}}, {{\text{P}}}_{{\text{R}}} } \right)}}{{\partial {{\text{P}}}_{{\text{R}}}^{{2}} }} & = - \frac{\upalpha}{2}{{\text{P}}}_{{\text{R}}}^{{ - \left( {\upbeta + 1} \right)}} [{{\text{P}}}_{{\text{R}}}^{{ - 1}} \left( {\upbeta + 1} \right)\left( {{{\text{R}}}2} \right) + \left( {\upbeta - 1} \right)\left( {2 + 2{{\text{I}}}_{{\text{ER}}} {{\text{M}}}_{{\text{R}}} - {{\text{I}}}_{{\text{ER}}} {{\text{T}}}} \right) \\ \end{aligned} $$

Since R2 = 0

$$ \frac{{\partial^{2} {\text{Net}}2\left( {{\text{T}}, {\text{P}}_{\text{R}} } \right)}}{{\partial {\text{P}}_{\text{R}}^{2} }}\left\langle {0,\,If\,\upbeta - 1} \right\rangle 0,\,{\text{i}}.{\text{e}}.,\,\upbeta > 1. $$

Appendix 2 (Determinant of the Hessian Matrix)

For Case I, T ≥ M_R, we have

$$ \frac{{\partial^{2} {\text{Net}}1\left( {{\text{T}}, {\text{P}}_{\text{R}} } \right) }}{{\partial {\text{T}}^{2} }} = - \frac{{2{\text{A}}}}{{{\text{T}}^{3} }} $$

$$ \frac{{\partial^{2} {\text{Net}}1\left( {{\text{T}},{\text{P}}_{\text{R}} } \right)}}{{\partial {\text{P}}_{\text{R}}^{2} }} = - \frac{\upalpha}{2}{\text{P}}_{\text{R}}^{{ - \left( {\upbeta + 2} \right)}} \left[ {{\text{P}}_{\text{R}}^{ - 1} \left( {\upbeta + 1} \right)\left( {{\text{R}}1} \right) + \left( {2 + {\text{I}}_{\text{ER}} {\text{T}}} \right)\left( {\upbeta - 1} \right)} \right] $$

On differentiating (5), we get

$$ \begin{aligned} \frac{{\partial^{2} {{\text{Net}}}1\left( {{{\text{T}}},{{\text{P}}}_{{\text{R}}} } \right) }}{{\partial {{\text{T}}}\partial {{\text{P}}}_{{\text{R}}} }} & = \frac{\upalpha}{2} {{\text{P}}}_{{\text{R}}}^{{ - \left( {\upbeta + 1} \right)}} \left\{ { - {{\text{P}}}_{{\text{R}}} {{\text{I}}}_{{\text{ER}}} \left( {\upbeta - 1} \right)} \right. \\ & \quad \left. { +\upbeta\left\{ {{{\text{h}}} + 2{{\text{P}}}_{{\text{S}}} \left[ {\left( {1 - {{\text{A}}}_{{1}} } \right){{\text{I}}}_{{1}} - {{\text{A}}}_{{2}} \left( {{{\text{I}}}_{{1}} - {{\text{I}}}_{{\text{PR}}} } \right) + {{\text{A}}}_{{1}}\uprho{{\text{I}}}_{{\text{PR}}} } \right]} \right\}} \right\} \\ \end{aligned} $$

The determinant of this Hessian matrix for Case I is

$$ \begin{aligned} {{\text{Hessian}}}1 & = - \frac{{2{{\text{A}}}}}{{{{\text{T}}}^{{3}} }}\left\{ { - \frac{\upalpha}{2}{{\text{P}}}_{{\text{R}}}^{{ - \left( {\upbeta + 2} \right)}} \left[ {{{\text{P}}}_{{\text{R}}}^{{ - 1}} \left( {{\upbeta + 1}} \right)\left( {{{\text{R}}}1} \right) + \left( {2 + {{\text{I}}}_{{\text{ER}}} {{\text{T}}}} \right)\left( {{\upbeta - 1}} \right)} \right]} \right\} \\ & \quad - \left[ {\frac{{\upalpha}}{{2}}\,{{\text{P}}}_{{\text{R}}}^{{ - \left( {\upbeta + 1} \right)}} \left\{ { - {{\text{P}}}_{{\text{R}}} {{\text{I}}}_{{\text{ER}}} \left( {\upbeta - 1} \right) +\upbeta\left[ {{{\text{h}}} + 2{{\text{P}}}_{{\text{S}}} \left( {\left( {1 - {{\text{A}}}_{{1}} } \right){\text{I}}_{1} - {{\text{A}}}_{{2}} \left( {{{\text{I}}}_{{1} }- {{\text{I}}}_{{\text{PR}}} } \right)} \right.} \right.} \right.} \right. \\ & \quad \left. {\left. {\left. {\left( { + {{\text{A}}}_{1}\uprho{{\text{I}}}_{{\text{PR}}} } \right)} \right]} \right\}} \right]^{2} \\ \end{aligned} $$

Since R1 = 0

$$ \begin{aligned} {{\text{Hessian}}}1 & = \frac{\text{A}}{{{{\text{T}}}^{3} }}\upalpha {{\text{P}}}_{{\text{R}}}^{{ - \left( {{\upbeta + 2}} \right)}} \left( {2 + {{\text{I}}}_{{\text{ER}}} {{\text{T}}}} \right)\left( {{\upbeta - 1}} \right) \\ & \quad - \left[ {\frac{{\upalpha}}{{2}}\,{{\text{P}}}_{{\text{R}}}^{{ - \left( {{\upbeta + 1}} \right)}} } \right.\left\{ { - {{\text{P}}}_{{\text{R}}} {{\text{I}}}_{{\text{ER}}} \left( {{\upbeta - 1}} \right) +\upbeta} \right.\left[ {{{\text{h}}} + 2{{\text{P}}}_{{\text{S}}} \left( {\left( {1 - {{\text{A}}}_{{1}} } \right){{\text{I}}}_{{1}} - {{\text{A}}}_{{2}} \left( {{{\text{I}}}_{{1}} - {{\text{I}}}_{{\text{PR}}} } \right)} \right.} \right. \\ & \quad \left. {\left. {\left. {\left. { + {{\text{A}}}_{{1}}\uprho{{\text{I}}}_{{\text{PR}}} } \right)} \right]} \right\}} \right]^{2} \\ \end{aligned} $$

i.e.,

$$ {\text{Hessian}}1 = {\text{AA}} - {\text{BB}} $$

where

$$ {\text{AA}} = \frac{\text{A}}{{{\text{T}}^{3} }}\upalpha\,{\text{P}}_{\text{R}}^{{ - \left( {\upbeta + 2} \right)}} \left( {2 + {\text{I}}_{\text{ER}} {\text{T}}} \right)\left( {\upbeta - 1} \right) > 0\,{\text{if}}\,\upbeta > 1. $$

$$ {{\text{BB}}} = \left[ {\frac{\upalpha}{2}\,{{\text{P}}}_{{\text{R}}}^{{ - \left( {\upbeta + 1} \right)}} \left\{ { - {{\text{P}}}_{{\text{R}}} {{\text{I}}}_{{\text{ER}}} \left( {\upbeta - 1} \right) +\upbeta\left[ {{{\text{h}}} + 2{{\text{P}}}_{{\text{S}}} \left( {\left( {1 - {{\text{A}}}_{1} } \right){{\text{I}}}_{1} - {{\text{A}}}_{2} \left( {{\text{I}}_{1} - {{\text{I}}}_{{\text{PR}}} } \right) + {{\text{A}}}_{1}\uprho{{\text{I}}}_{{\text{PR}}} } \right)} \right]} \right\}} \right]^{2} $$

Since $\frac{{\partial^{2} {\text{Net}}1}}{{\partial {\text{T}}^{2} }} < 0$, the condition for joint concavity of Net1 with respect to T and P_R is AA > BB.

For Case II, for T < M_R, we have

$$ \frac{{\partial^{2} {\text{Net}}2\left( {{\text{T}}, {\text{P}}_{\text{R}} } \right)}}{{\partial {\text{T}}^{2} }} = \frac{{ - 2{\text{A}}}}{{{\text{T}}^{3} }} $$

$$ \frac{{\partial^{2} {{\text{Net}}}2\left( {{\text{T}},{{\text{P}}}_{{\text{R}}} } \right)}}{{\partial {{\text{P}}}_{{\text{R}}}^{2} }} = - \frac{\alpha }{2}{{\text{P}}}_{{\text{R}}}^{{ - \left( {\beta + 1} \right)}} \left[ {{\text{P}}_{{\text{R}}}^{ - 1} \left( {\beta + 1} \right)\left( {{\text{R}}2} \right) + \left( {\beta - 1} \right)\left( {2 + 2{{\text{I}}}_{{\text{ER}}} {{\text{M}}}_{{\text{R}}} - {{\text{I}}}_{{\text{ER}}} {\text{T}}} \right)} \right] $$

On differentiating (9) with respect to T, we get

$$ \frac{{\partial^{2} {{\text{Net}}}2\left( {{\text{T}},{{\text{P}}}_{{\text{R}}} } \right)}}{{\partial {{\text{T}}}\partial {{\text{P}}}_{{\text{R}}}}} = \frac{\alpha }{2}{{\text{P}}}_{{\text{R}}}^{{ - \left( {\beta + 1} \right)}} \left[ {{\text{P}}_{{\text{R}}} {{\text{I}}}_{{\text{ER}}} \left( {\beta - 1} \right) +\upbeta\left( {{\text{h}} + 2{{\text{P}}}_{{\text{S}}} {{\text{A}}}_{1}\uprho{{\text{I}}}_{{\text{PR}}}} \right)} \right] $$

The determinant of the Hessian matrix for Case II is

$$ \begin{aligned} {{\text{Hessian}}}2 & = \frac{{ - 2{{\text{A}}}}}{{{\text{T}}^{3} }}\left\{ { - \frac{\alpha }{2}{{\text{P}}}_{{\text{R}}}^{{ - \left( {\beta + 1} \right)}} \left[ {{\text{P}}_{{\text{R}}}^{ - 1} \left( {\beta + 1} \right)\left( {{\text{R}}2} \right) + \left( {\beta - 1} \right)\left( {2 + 2{{\text{I}}}_{{\text{ER}}} {{\text{M}}}_{{\text{R}}} - {{\text{I}}}_{{\text{ER}}} {{\text{T}}}} \right)} \right]} \right\} \\ & \quad - \left\{ {\frac{\alpha }{2}{{\text{P}}}_{{\text{R}}}^{{ - \left( {\beta + 1} \right)}} \left[ {{{\text{P}}}_{{\text{R}}} {{\text{I}}}_{{\text{ER}}} \left( {\beta - 1} \right) +\upbeta\left( {{\text{h}} + 2{{\text{P}}}_{{\text{S}}} {{\text{A}}}_{1}\uprho{{\text{I}}}_{{\text{PR}}} } \right)} \right]} \right\}^{2} \\ \end{aligned} $$

Since at P_R2*, R2 = 0,

$$ \begin{aligned} {{\text{Hessian}}}\,2 & = \frac{{\text{A}}}{{{\text{T}}^{3} }}\alpha {{\text{P}}}_{{\text{R}}}^{{ - \left( {\beta + 1} \right)}} \left( {\beta - 1} \right)\left( {2 + 2{{\text{I}}}_{{\text{ER}}} {{\text{M}}}_{{\text{R}}} - {{\text{I}}}_{{\text{ER}}} {{\text{T}}}} \right) \\ & \quad - \left\{ {\frac{\alpha }{2}{{\text{P}}}_{{\text{R}}}^{{ - \left( {\beta + 1} \right)}} \left[ {{\text{P}}_{{\text{R}}} {{\text{I}}}_{{\text{ER}}} \left( {\beta - 1} \right) +\upbeta\left( {{\text{h}} + 2{\text{P}}_{{\text{S}}} {{\text{A}}}_{1}\uprho{{\text{I}}}_{{\text{PR}}} } \right)} \right]} \right\}^{2} \\ \end{aligned} $$

i.e.,

$$ {\text{Hessian}}2 = {\text{CC}} - {\text{DD}} $$

where

$$ {{\text{CC}}} = \frac{{\text{A}}}{{{\text{T}}^{3} }}\alpha {{\text{P}}}_{{\text{R}}}^{{ - \left( {\beta + 1} \right)}} \left( {\beta - 1} \right)\left( {2 + 2{{\text{I}}}_{{\text{ER}}} {{\text{M}}}_{{\text{R}}} - {{\text{I}}}_{{\text{ER}}} {{\text{T}}}} \right)$$

$$ {{\text{DD}}} = \left\{ {\frac{\alpha }{2}{{\text{P}}}_{{\text{R}}}^{{ - \left( {\beta + 1} \right)}} \left[ {{{\text{P}}}_{{\text{R}}} {{\text{I}}}_{{\text{ER}}} \left( {\beta - 1} \right) +\upbeta\left( {{\text{h}} + 2{{\text{P}}}_{{\text{S}}} {{\text{A}}}_{1}\uprho{{\text{I}}}_{{\text{PR}}}} \right)} \right]} \right\}^{2} $$

Since $\frac{{\partial^{{2}} {{\text{Net}}2}}}{{{\partial {{\text{T}}}^{{2}}}} } < 0$, the condition for concavity of Net2 is CC > DD.