The Question of Method in a Vygotskian Semiotic Approach

Abstract

In this chapter we present the main ideas of an educational Vygotskian semiotic approach, emphasizing in particular some crucial questions about its methods of inquiry. We resort, on the one hand, to Leont’ev’s (1978) work on activity, and, on the other hand, to Vygotsky’s cultural psychology. Considering a theory as an interrelated triplet of “components” (P, M, Q), where P stands for principles, M stands for methodology, and Q for research questions, in the first part of the chapter we present a brief sketch of the Vygotskian semiotic approach through the lenses of the aforementioned components. We refer in particular to two methodological constructs that have been built to account for multimodal sensuous actions: the semiotic node and the semiotic bundle. To illustrate the semiotic approach, in the second part of the chapter we discuss an example from a classroom activity concerning pattern generalization. This example constituted an important step in developing the semiotic approach under consideration. The example is about the role of words, gestures, and rhythm in the students’ process of objectifying (i.e., noticing or becoming aware of) mathematical relationships. We discuss how a “crude fact” that was not anticipated led to a transformation of the theory, and in particular its methods and research questions.

The critical issue, then, is method

Vygotsky 1987, p. 45

1 Introduction

Mathematics education researchers resort to procedures to describe the phenomena they investigate and also to make claims about their objects of study. Naturally, since the procedures allow researchers to argue and reach conclusions, their “appropriateness” is of paramount importance: to a large extent, the cogency of an investigation depends on the persuasiveness of the procedures.

One of the most vigorous debates in the history of mathematics education has consequently been the one revolving around the nature of these procedures. Should we understand these procedures in the sense of the natural sciences? Or should we rather understand them in the sense of the social sciences? The choice is not simple. It entails adopting a view of the nature of the phenomena dealt with. In other words, the question about the nature of the procedures goes beyond the procedures themselves.

In the first case, procedures are generally understood as based on, or following, models of scientific practice. The testing of the models—e.g., models of didactical situations—and replicability of results become central questions. Naturally, within this approach, it is assumed that educational phenomena are amenable to be modeled. That is, there are some regularities that remain constant in the observed phenomena; furthermore these regularities can be grasped (even if only approximately) if the proper tools are employed. In this case, one of the tasks of mathematics education is to grasp such regularities (Brousseau 2005).

In the second case, procedures are not understood as models. This is the view that the social sciences—at least in some of their recent trends (e.g., Atkinson and Hammersley 1994; Shweder and LeVine 1984)—tend to adopt. The nature of the social phenomena is considered to be non-amenable to be modeled or factored out in terms of controllable variables. Deeply sensitive to their context (social, cultural, historical, etc.), social phenomena (which includes educational phenomena, e.g., teaching and learning) are assumed to be messy by nature. You may try to remove the redundant, the apparently unnecessary, the fuzzy, and what will remain will still be redundant and fuzzy, not because you did not do your job well, but because it is the phenomenon’s real nature.

By virtue of their radical differences, both research paradigms convey different ideas of the searchable and have recourse to different procedures or methods. The semiotic approach that we discuss in this chapter belongs to the social science paradigm. As such, it conceives of the educational phenomena as messy and context sensitive. Its claims are not backed up by some immutable laws whose existence is asserted by a confrontation of the laws and empirical facts. Rather, general assertions are sustained by actual references that may guide further action through a reflective stance.

The focus of the semiotic approach that we discuss in this paper is on the phenomenon of teaching and learning—a phenomenon embedded in the idea of classroom activity.

In the sense that the semiotic approach does not aim to uncover hidden laws behind teachers’ and students’ actions, the approach could be said to be interpretative. But it is more than that. We do not register the educational phenomenon in order to offer plausible interpretations of it. Although we provide interpretations, we also design the classroom activities, and by designing them, we alter and transform the manners in which teaching and learning co-occur.

In this chapter, we present the main ideas of our semiotic approach, emphasizing in particular some crucial questions about our methods of inquiry. In Sect. 7.2 we discuss the concept of method as a central problem of scientific inquiry. We draw on Vygotsky’s idea of method—an idea that tormented him throughout his short life and to which he continuously returned as he moved progressively away from the influence of reflexology and instrumentation to a more encompassing view of humans and the human mind. In Sects. 7.3 and 7.4 we present the theoretical underpinnings of our semiotic methodology, which we illustrate in Sect. 7.5 through a classroom example.

2 Method as the Central Problem of Scientific Inquiry

In trying to provide scientific accounts of human phenomena, a method of enquiry has to be devised. “Finding a method,” Vygotsky (1993) says, “is one of the most important tasks of the researcher” (p. 27). Now, it would be a mistake to think that methods precede the inquiry or research that they are supposed to support. In general, a method “is simultaneously a prerequisite and product, a tool and a result of the research” (Vygotsky 1993, p. 27).

This concept of method, as simple as it may appear, only makes sense within a theoretical general view of what is studied and how it can be studied. For Vygotsky, who followed Marx’s Hegelian view of reality, both the object of study (reality) and the manner in which it can be studied are always in motion. They come to form a dialectical unity where the components affect each other in a dynamic way. It is hence unimaginable that a method could precede in its entirety the investigation, which is in itself an activity in continuous movement.

But a method is more than something that comes into existence in the course of research. Method, as Vygotsky understood it, is not the mere systematic application of a set of principles. Nor is it simply a way of doing something—a technique. Method comes from the Greek methodos, a word made up of meta—“after”—and hodos—“a traveling”—meaning hence “a following after” (Online etymology dictionary 2013). A method’s main characteristic is to be inquisitional and reflective, that is, a philosophical practice. It is in this non-instrumentalist Vygotskian sense that we understand method here and that method can be said to be at the heart of a theory.

Let us notice that the sought object in the “following after” of a method is not merely something that is there, waiting to be discovered. By asking questions—research questions—theories fabricate those objects. They also fabricate the evidence that shows the objects in accordance with the procedures that theories follow in their persuasive endeavour.

This does not mean, however, that theories fabricate their objects and methods as they wish. This would amount to a blunt and self-defeating relativism. What it does mean is that methods are rooted in theoretical principles that convey worldviews. Let us give a short example. In his Genetic Epistemology, Piaget (1970) resorts to methods that, at first sight, seem extremely simple and even merely instrumental: a few objects and a child who is required to answer some questions or to solve some problems in laboratory interviews. The design of the task and the setting into motion of the child’s activity (along with the supposedly neutral role of the observing researcher) unavoidably embodies a worldview of human intelligence and its main traits—e.g., that intelligence and its development can be accounted for in terms of problem solving procedures and their underpinning formal logical meanings. Piaget’s methods crystalize aspects of a general Western worldview: one in which, since Kant, reason appears as a regulative entity of human experience supplemented with the nineteenth century understanding of evolution. As Walkerdine (1997) notes:

In the work of Piaget, an evolutionary model was used in which scientific and mathematical reasoning were understood as the pinnacle of an evolutionary process of adaptation. The model viewed the physical world as governed by logicomathematical laws, which came to form the basis of children’s development of rationality. (p. 59)

Infused with such a worldview, Piaget’s investigative procedures turn to find traces of logical thinking behind the child’s action and utterances:

Piaget examines a child’s protocol and picks out the significant underlying propositions (which he can then order in the logical parlance of p’s and q’s); the mental action reflected in the protocol is a series of operations performed on the propositions. The individual has reached formal operations when he can systematically and exhaustively explore the relations between propositions describing a phenomenon. (Gardner 1970, p. 359)

Piaget’s tasks are designed in a way to elicit logical propositions and their combination in the child’s actions and discourse. It is in this sense that theories fabricate their objects of investigation and the evidence to sustain their claims.

We should not be led to think though that methods remain caught in their own endeavours and are blind to other possibilities. We have insisted on the fact that methods are not merely instrumental procedures to follow. Methods are part of a reflective, philosophical practice. And as such, they are prone, at least in principle, to continuously examine their results and the worldviews that they purport. There is also another source of change and transformation: since methods embody crystallization of cultural worldviews and since worldviews within a given culture are not homogeneous, methods do not go generally undisputed. Thus, anthropologist Lévi-Strauss criticized Piaget for resorting to a rather artificial methodology:

What I do ask, and I formulate this question rather naively in ethnological terms, is whether Piaget’s research techniques aren’t rather artificial in character. His experiments are set up in advance, prefabricated, which does not seem to me to be the best way to understand the mind in all its spontaneity. (Grinevald 1983, p. 84)

Let us summarize. Methods are a central element of scientific enquiry. But methods cannot be reduced to a pure instrumental sequence of steps defined in advance and to be followed blindly. Methods convey worldviews. That is, they make assumptions about what is to be known and how it can be known. And because what distinguishes a scientific inquiry from other inquiries, we suggest, is its systematic and explicit character, the scientific inquiry has to be as precise as possible about the principles it adopts. These principles wrap already the raw material to be studied with categorial substance—that is, with conceptual categories that already infuse the objects of study with scientific value and understanding. “We study [a] given particular gas not as such, but from a special viewpoint” (Vygotsky 1997, p. 318). This is why

The material of science is not raw, but logically elaborated, natural material which has been selected according to a certain feature. Physical body, movement, matter – these are all abstractions. The fact itself of naming a fact by a word means to frame this fact in a concept, to single out one of its aspects; it is an act toward understanding this fact by including it into a category of phenomena which have been empirically studied before. (Vygotsky 1997, p. 249)

In previous work (Radford 2008a), to try to better understand theories in mathematics education, and to avoid forgetting the philosophical or reflective nature of their methods, we have suggested that it may be worthwhile to think of theories as dynamic entities composed of interrelated “parts.” These parts are: (1) the principles that are assumed by the theory and that define the spectrum of what is to be known and how it can be known; (2) the methodology or method (that is, the reflective procedures through which the inquisitive endeavour is carried out); and (3) the research questions that the theory strives to answer or investigate. In short, a theory, we suggest, is a triplet T = (P, M, Q), where P stands for principles, M stands for methodology, and Q for research questions. This analytic description of theories does not mean, as the previous discussion suggests, that the different parts of the theory are independent of each other. They are interconnected and evolve in a dynamic way. Thus, a result may require a new or deeper interpretation for which new theoretical principles have to be elaborated, or it may require the development of new methodologies. A new result may also lead one to ask new research questions.

In the following section, we discuss some aspects of our semiotic approach. We start by addressing the links between semiotics and education.

3 A Vygotskian Semiotic Approach

The semiotic approach that we outline seeks to answer questions about teaching and learning. At first sight, it may seem curious to resort to semiotics to answer educational questions. Indeed, semiotics, in its different trends and developments, is not a theory of teaching, nor is it a theory of learning. Semiotics was developed in close relation to phenomenological concerns—e.g. Peirce (1958), Husserl (1970), Hegel (2009), and around questions of language—e.g., Saussure (1916). Where is the connection? Semiotics is a theory of how signs signify. It is a theory of signification. It can provide insights into the manner in which educational practices work, for as Walkerdine (1997) noted, “All practices are produced through the exchange of signs and are both material and discursive” (p. 63).

As a cursory glimpse at a classroom would show, there is indeed a tremendous array of signs (some of them written and oral, but also embodied signs such as gestures and body posture) and artifacts in circulation in a teaching and learning activity. And this would be even more evident in a mathematics classroom, where recourse to concrete objects (e.g., plastic geometric shapes, blocks, etc.) is often made.

Since semiotics is not a theory of knowing or a theory of learning, to be successfully used in education, semiotics has to be integrated into an educational theory. This integration cannot be a mere juxtaposition of semiotic concepts and educational ones (Radford 2013a). Since theories are based in theoretical principles and specific methodologies, there is a limit to the integration that can be achieved—for a typology, see Prediger et al. (2008). This integration depends strongly on the compatibility of the principles of the theories (Radford 2008a).

The problem of integration of theories does not concern mathematics education only. Vygotsky criticized the efforts made by Luria and other Russian scholars who were attempting to combine Freud’s work and Marxist psychology and the contradictions that such an endeavour caused. As a result of a direct fusing of these theories, a series of contradictions appeared. Since these contradictions were unavoidable, they were merely excluded, leading to a strange situation that Vygotsky (1997) summarizes as follows:

Very flagrant, sharp contradictions which strike the eye are removed in a very elementary way: they are simply excluded from the system, are declared to be exaggerations, etc. Thus, Freudian theory is de-sexualized as pansexualism obviously does not square with Marx’s philosophy. No problem, we are told – we will accept Freudian theory without the doctrine of sexuality. But this doctrine forms the very nerve, soul, center of the whole system. Can we accept a system without its center? After all, Freudian theory without the doctrine of the sexual nature of the unconscious is like Christianity without Christ or Buddhism with Allah. (p. 261)

The integration of education and semiotics requires us to be careful so that we do not denaturalize the theories we try to connect. In our case, we resort, on the one hand, to Leont’ev’s (1978) Hegelian phenomenological account of knowledge and knowing, and on the other hand, to Vygotsky’s cultural psychology. The former provides us with a historical conception of signification from which learning can be defined as a social semiotic process that is always in the making, unsettled and unsettleable. The latter provides us with a psychological account of signs. In contradistinction to Saussure’s (1916) and Peirce’s (1958) semiotics, Vygotsky’s semiotics does not resort to a representational idea of signs. His concept of sign is rather located within his work in special education: a sign is an auxiliary means to organize our behavior. Signs are tools of reflection that allows individuals to plan action. Thus the knot in the handkerchief serves the purpose of a recall that moves the individual into action. The Vygotskian concept of sign provides us with clues to understand the actual processes of teaching and learning.

What follows is a succinct account of the main ideas of the resulting semiotic approach to mathematics teaching and learning.

3.1 Knowledge

Grosso modo, there are two main philosophical traditions that have inspired theories of knowledge in the Western World. The first one is the rationalist tradition, epitomized by Kant, in which knowledge is considered to be the result of the doings and meditations of a subject whose mind obeys logical drives—either already there (“within our own soul,” as Leibniz (1949, p. 15) used to say) or developmentally (as in Piaget’s (1970) Genetic Epistemology). The second tradition is the dialectical-materialist one developed by Hegel and Marx, where knowledge is not the result of logical drives but the result of individuals’ sensuous reflections and material deeds in cultural, historical, and political contexts. In opposition to the rationalist tradition, in the dialectical-materialist view knowledge is not something that we represent. Actually, knowledge cannot be represented, for knowledge is always in motion. Knowledge is pure possibility. It is constituted of culturally and historically encoded forms of reflection and action that, instead of lending themselves to representation, are sources for action (Radford 2013b). Numbers, for instance, are not things or essences to be represented. They are possibilities for action (e.g., to count or to carry out complex calculations).

As pure possibility, knowledge cannot be an object of consciousness. To become an object of consciousness and thought, knowledge has to be set into motion. Knowledge has to be filled up with concrete determinations. And this can only happen through activity—sensuous and material activity. This is what students and teachers do when they participate in classroom activity.

Let us refer to a short example to illustrate these ideas. The example is about pattern generalization.

Pattern generalization is a cultural activity at the heart of many ancient civilizations. The Pythagoreans and the Babylonians, for instance, practiced it, where it started as an endeavour motivated to answer concrete counting processes or sense-making investigations. These endeavours became encoded ways of reflecting and acting that were refined in the course of cultural history (Diophantus, Fermat, etc.).

In contemporary curricula, in particular in the English-speaking countries, pattern generalization appears often as a road to algebra. It is within this pedagogical intention that we have resorted to it.

As an object of knowledge, pattern generalization is not something to be represented. It is something to be known. However, from the students’ viewpoint, pattern generalization (in fact all mathematical content to be known) appears, first, as pure possibility (a possibility to do something, to solve some problems or to argue about something). And in order for it to be known, it has to be set into motion. Knowledge has to evolve and to appear in concrete practice. By being filled up with some conceptual content, what appears is not knowledge in its entirety, but a concrete instance of it. Hegel (2009) called it the singular. We have, then: (1) the general, which is knowledge as such (in this case pattern generalization), (2) the activity through which knowledge is brought forward or actualized, and (3) knowledge in motion, filled up with conceptual content, that is, the singular. Figure 7.1 provides a diagram of these three elements.

Fig. 7.1

The singular as knowledge actualized in activity

What Fig. 7.1 expresses is the mediated nature of knowledge. We do not have access to knowledge but through mediation. As pure possibility, knowledge cannot be fully accounted for by any one of its instances (the singulars). Not even the most perfect triangle reveals the depth of the concept of triangle, not because we will always make unnoticeable mistakes in drawing a triangle or because there would be triangles with other shapes different from the one we drew. The reason is this: The concept of triangle cannot be revealed in its representation, because the concept is not representable. The concept is knowledge, that is possibility, and as such cannot be represented; it can only be actualized in the activity that fills it up with particular conceptual content.

The singular as actualization of knowledge in activity should not be seen as something static or as an end point, but as an event. It is rather an “unfinished and inherently open-ended event” (Roth 2013). It is a process—a semiotic process through and through. Not only because in the activity that actualizes knowledge and transforms it into an event students and teachers resort to discursive, embodied, and material signs and artifacts, but, overall (and indeed this is the real reason), because in mobilizing signs students and teachers engage in processes of signification. The singular is a semiotic event.

From a semiotic viewpoint, there is something extremely important to understand about the activity that actualizes knowledge. This activity is, essentially, an activity of signification. In fact, the activity through which knowledge is actualized is an activity of conflicting significations. The teacher is aware of the aim of the activity. In our example, the aim (or in Leont’ev’s terminology, the object of the activity) is to make the students aware of the historically and culturally constituted way of thinking and reflecting about pattern generalization. Before engaging in the activity, the students do not know about such a way of reflecting and thinking—at least not in all the scientific-cultural curricular details. If the students knew, there would not be learning on the horizon. The activity would be an exercise activity—i.e., practicing something already known. The epistemological asymmetry that underpins teaching and learning activity (Roth and Radford 2011) infuses the activity with its inherent contradictions. The idea of contradiction has to be understood here in its dialectical sense, namely as precisely what drives the activity further.

3.2 Learning

Now, the fact that the students do not know yet the aim of the activity (e.g., how to generalize a pattern algebraically) does not mean that they cannot engage in the activity. In fact, they resort to what they already know. This is why it is not surprising that, when students engage in algebraic pattern activity, they resort to arithmetic generalizations.

The conflicting significations that are at the heart of the activity can be formulated in the following terms. The aim of the activity (knowing how to generalize patterns algebraically) is dynamically and variously refracted in the students’ and teachers’ consciousness as the activity unfolds. The conflicting significations move (in a dialectical sense), creating tensions that, at moments, may be partially resolved or intensified. Attenuated or not, these tensions do not disappear. They constitute mobile wholes made up of different perspectives and positions that each participant of the activity brings in.

The attuning of inter-subjective perspectives is the requisite for learning to occur. It does not mean that teachers and students have to agree on, say, the manner in which a pattern can be generalized. Attuning refers also to matters of deep disagreement and unresolved tensions.

In previous work we have suggested that learning can be studied through processes of objectification, that is “those processes through which students gradually become acquainted with historically constituted cultural meanings and forms of reasoning and action” (Radford 2010, p. 3). In light of the previous discussion we want to stress that acquaintance does not mean agreement. It means understanding—a socially responsible and conceptually articulated understanding of something even if we do not agree with it.

4 The Methodology of Our Semiotic Approach

We are now in a position to describe the chief elements of our methodology. Because knowledge is pure possibility, for it to become the object of students’ consciousness, it has to be set into motion through activity. The first problem is hence the design of the activity.

We spend a great deal of time working with teachers designing teaching-learning activities. The curricular goals are taken as the basis of the activities. They are very general—e.g., to think algebraically about pattern generalization, to solve equations algebraically, to think probabilistically, to argue and prove, etc.

These aims are general and need more specification. The specification depends on the curricular requirements. In our research with young and adolescent students about pattern generalization, some of the specifications refer to a focus on functional relationships between variables in figural sequences and the building of formulas for remote terms—using the standard algebraic symbolism or a conjunction of other semiotic systems (Sabena et al. 2005).

The specifications shape the conceptual content of the activity through which knowledge will be instantiated. An a priori epistemological analysis (Artigue 1995) helps us structure the activity: we carefully select the questions and problems and their order in the activity. The first questions are easy, to ensure that students embark in the activity; bit by bit the questions become more and more complex, leading the students to mobilize the mathematical content in depth—for some examples see Radford and Demers (2004), and Radford et al. (2009).

Because leaning is a social phenomenon, classroom interaction is a central element of the activities we design (Radford 2011). Usually, the classroom is divided into small groups. The teacher circulates among the groups and engages in discussions with the students (Radford 2013b). Naturally, it is impossible to predict the manner in which interaction will occur. The activity that mediates and actualizes knowledge is unpredictable. Although planned, this activity is an event—something unrepeatable and always new. This is why we see the classroom as a dynamic system going through states out of which the conflicting significations arise.

The role that we ascribe to the teacher is particularly different from the one we find in most other educational approaches. Indeed, for us, the teacher is not a coach or a guide or a helper or an observer—or worse, someone who transmits knowledge. Her main role is ethical (Radford and Roth 2011). The teacher is part of the activity that mediates and actualizes knowledge. She is part of the whole ensemble of classroom consciousness trying to get attuned with each other. Much like the students, she brings to this activity her idiosyncratic way of thinking and understanding mathematics. It is out of the personal efforts of all members of the activity that the activity eventfully realizes the general in the singular.

In coming to understand others and the mathematical task at hand, teachers and students engage hence in activity. They do not engage in a purely meditative manner, but in a sensuous and material way. They resort to a wide range of semiotic systems through which they come to form their intentions and ideas against the background of culturally and historically constituted ways of thinking and acting. In the course of the objectification processes, students and teachers produce multimodal actions. Through these actions complex meanings are formed in an inter-subjective way.

Since “the method must be adequate to the subject studied” (Vygotsky 1993, p. 27), to investigate these processes of objectification and signification, we use fine-grained video-analysis.

One or more video-cameras are used to register the teacher’s and students’ small group activities and classroom discussions. Videos are fully transcribed, and complemented with written materials produced during the activity (students’ sheets, field notes by the researcher, etc.). From video and the transcript, episodes are selected, which are helpful in answering the specific research questions (Q) of the study. These episodes are carefully analysed over and over in detail, and confronted with the theoretical assumptions (P).

This kind of analysis is consonant with microethnographic methodologies (Streeck and Mehus 2005), since it “encompasses a collection of techniques and analyses tracing the moment-by-moment bodily and situated activity of subjects engaged in certain events and interactions” (Nemirovsky et al. 2012, p. 294), in which a particular attention is given to “talk, gesture, facial expression, body posture, drawing of symbols, manipulation of tools, pointing, pace, and gaze” (ibid.): they constitute semiotic resources through which the students’ and teacher’s mathematical activity develops.

Our semiotic approach also allows us to theoretically include embodied means of expression, as semiotic resources in learning processes, and to look at their relationship with the traditionally studied semiotic systems (e.g. written mathematical symbolism). In looking at the different semiotic resources in an integrated and systemic way, attention is paid to relationships, dialectics, and dynamics between them. Some of these relationships may concern different kinds of resources in the same time moment: for example, they may concern co-occurrences of words and gestures.

However, in opposition to pure semiotic approaches and microethnographic methodologies, we are not interested in the semiotic resources per se. We are interested in the manner in which teachers and students resort to the semiotic resources in processes of learning, that, as mentioned previously, we theorize as processes of objectification. The methodological problem for us is, hence, to account for the manner in which the whole range of semiotic resources are used by teachers and students in the course of the social processes of objectification through which students become aware of the cultural logic and meanings of thinking and doing mathematically.

In order to provide description and interpretation of learning as a sign-mediated activity, two methodological constructs have been developed: the concept of semiotic node and the concept of semiotic bundle.

A semiotic node is a part of the students’ and teachers’ joint activity where embodied and other signs from various semiotic systems are put to work together in processes of objectification. In other words, a semiotic node refers to segments of activity where students and teachers bring forward possible mathematical interpretations and courses of action against the backdrop of culturally and historically constituted forms of thinking and doing (Radford et al. 2003). The central idea is that mathematics learning is a reflective activity that involves consciousness. And consciousness, from the dialectical materialist viewpoint we adopt here, is intimately related to our use of semiotic systems and artifacts. In the course of the process of objectification—in particular, in those crucial moments in which the students gain an awareness and understanding of cultural mathematical meanings—“signs play different and complementary roles” (Radford 2009, p. 474). Through the concept of semiotic node we explore focal points of the activity that mediates knowledge and where episodes of objectification occur. Semiotic nodes provide us with relevant segments of the semiotic activity where learning is taking place.

In this sense, semiotic nodes are methodological tools to study learning. Through the teacher’s and students’ use of various semiotic resources, we can have, methodologically speaking, an idea of the students’ reflective learning activity and the kind of interpretations and meanings that the students produce.

The evolution of semiotic nodes provides us with a more general view of the manner in which learning is occurring. To investigate the evolution of semiotic nodes, we have introduced the concept of semiotic contraction. A semiotic contraction refers to the reorganization of semiotic resources that occurs as a result of the students’ increased consciousness of mathematical meanings and interpretations. Contraction “makes it possible to cleanse the remnants of the evolving mathematical experience in order to highlight the central elements that constitute it” (Radford 2008b, p. 94). Thus, fewer gestures may be required as the students refine their ideas and become more and more conscious of mathematical structures and ideas.

The concept of semiotic bundle offers also a synchronic and a diachronic approach to the investigation of learning. Here, the focus is in the evolution of signs. This notion has been elaborated by Arzarello (2006), Arzarello et al. (2009) in order to give account of the multimodality of mathematics learning and teaching processes. The term “multimodality” comes from neuroscientific studies that have highlighted the role of the brain’s sensory-motor system in conceptual knowledge and have proposed a multimodal model for brain functioning, instead of a modular model (Gallese and Lakoff 2005). On the other hand, “multimodality” is also used in communication design to speak of the multiple modes we use to communicate and express meanings to our interlocutors: e.g. words, sounds, figures, etc. Within this perspective, a semiotic bundle has been defined as

a system of signs […] that is produced by one or more interacting subjects and that evolves in time. Typically, a semiotic bundle is made of the signs that are produced by a student or by a group of students while solving a problem and/or discussing a mathematical question. Possibly the teacher too participates to this production and so the semiotic bundle may include also the signs produced by the teacher. (Arzarello et al. 2009, p. 100)

Focusing the attention on a wide variety of means of expression, from the standard mathematical symbols (e.g., algebraic representations) to the embodied ones (such as gestures, gazes, and so on), and considering all of them as semiotic resources in teaching and learning processes, the semiotic bundle construct widens the range of semiotic resources that are traditionally discussed in mathematics education literature (e.g., Duval 2006; Ernest 2006).

In order to clarify the notion of semiotic bundle, we can consider for instance the set of words, the set of gestures, and that of written signs (e.g. algebraic symbols) that are used in a certain mathematical activity. The three sets, which are used along the mathematical activity, constitute the semiotic bundle: the interpretation of one kind of resources (e.g. speech) can be fully done only taking into account also the other resources (gestures and written signs). In this sense, the semiotic bundle considers the semiotic resources in a unifying analysis tool. Of course, depending of the needs of analysis, each semiotic set can also be analysed in a separated way. But since different semiotic sets very often intertwine, a global view on them is necessary.

The semiotic bundle can be an analytical tool in order to detect cases of semiotic nodes, when the attention focuses on synchronic relationships between signs used to accomplish an objectification process.

Besides the synchronic view, the semiotic bundle offers the possibility of performing a diachronic analysis, that is to say of studying the evolution of semiotic resources in the passing of time, and the evolution of their mutual relationships. With this view, genetic phenomena regarding signs may be observed, when some signs are transformed into another kind of signs (e.g., of gestures giving origin to written drawing in pre-algebraic context, see Sabena et al. 2012). A diachronic view has allowed researchers in gesture studies to elaborate the notion of “catchment”. McNeill and colleagues identified a catchment when some gesture form features recur in at least two (not necessarily consecutive) gestures (McNeill 2005; McNeill et al. 2001). According to their framework, they interpreted catchments as indicating discourse cohesion, due to the recurrence of consistent visuospatial imagery in the speaker’s thinking. In our semiotic frame, catchments may be of great importance since they can give us clues about the evolutions of meanings in students’ multimodal discourses and in their objectifying processes (for an example about catchments in structuring a mathematical argument, see Arzarello and Sabena 2014).

To illustrate our methodology, in the remainder of the chapter we show an example that constituted an important step in developing our semiotic approach. It showed us that, as quoted above, a method can be “simultaneously a prerequisite and product, a tool and a result of the research” (Vygotsky 1993, p. 27).

The example is about the role of words, gestures and rhythm in objectifying (i.e., noticing or becoming aware of) mathematical relationships; the analysis has been reported previously (Sabena et al. 2005; Radford et al. 2006, 2007).

During our research activity, we did not anticipate rhythm as playing a subtle and profound semiotic role in mathematics cognition. Watching a video clip over and over within the possibilities of a low motion and frame-to-frame analysis, and focusing on students’ words and gestures, we began to notice that rhythm was playing a fundamental role as a semiotic resource in the students’ activity. This “crude fact” was theorized through the principles of the theory: we realized that rhythm was a fundamental semiotic means of knowledge objectification. That is, through an apparently unconscious recourse to rhythm, the students started perceiving, behind the mathematical signs, a general mathematical structure.

Dedicated software developed in linguistic research allowed us to carry out a pitch and prosodic analysis to confirm the role of rhythm. To be duly interpreted, the new results required a refinement of the theoretical principles. We gained a new theoretical sensitivity that allowed us to be alert to phenomena that escaped our research lenses before. The methodology of analysis also evolved, with the refinement of both the technical means (e.g. the use of the new software), and a more sensitive research eye. We call the resulting methodology a multi-semiotic methodology (Radford et al. 2006), and we illustrate it in the next section, with reference to the specific example.

5 Multi-Semiotic Analysis: An Example Concerning Pattern Generalization

To illustrate our semiotic approach, we refer to a classroom activity concerning pattern generalization as a way to approach algebraic thinking.

The data come from a 5-year longitudinal research program, and were collected during classroom lessons that are part of the regular school mathematics program in a French-Language school in Ontario. As described above, lessons are jointly designed by the teacher and our research team. The students spend substantial periods of time working together in small groups of 3 or 4, with the teacher interacting continuously with the different groups. At some points, the teacher conducts general discussions allowing the students to expose, compare, and confront their different solutions.

We focus on a classical pattern problem that Grade 9 students had to investigate in a math lesson. The problem deals with the study of an elementary sequence that is visually depicted (see Fig. 7.2). In the first part of the lesson, the students were required to continue the sequence, drawing Terms 4 and 5 and then to find out the number of circles on Terms 10 and 100. In the second part, the students were asked to write a message explaining how to calculate the number of circles in any term and, in the third part, to write an algebraic formula.

Fig. 7.2

The three first terms of the sequence

We provide a multi-semiotic microanalysis of the work done on the first and in the second part of the math lesson by one group of students formed by Jay, Mimi, and Rita. Referring to the first part, we illustrate in particular how words and gestures play a crucial role in allowing the students to perceive the terms as divided into two rows. In the course of the students’ joint activity, knowledge as pure possibility becomes actualized in the form of a factual generalization (Radford 2003), i.e. a generalization of actions in the form of an operational schema that applies to any concrete term, regardless of its position in the sequence. Referring to the second part, we show how rhythm serves as a subtle semiotic device that helps the students notice a regularity that proved to be crucial to convey a sensuous meaning of mathematical generality.

5.1 Words-Gesture Combinations in the Production of a Factual Generalization

At the beginning of the activity, the students count the number of circles in the terms, and realize that it increases by two each time. Then, in order to draw Term 4, they use gestures and speech through which they identify the two rows of the terms and their numerosity as key-elements in the problem solution:

1. Rita:

You have five here… (pointing to Term 3 on the sheet)

2. Mimi:

So, yeah, you have five on top (she points to the sheet, placing her hand in a horizontal position, in the space in which Jay is beginning to draw Term 4; see Fig. 7.3) and six on the… (she points again to the sheet, placing her hand a bit lower)

Fig. 7.3

Mimi’s first gesture on line 2

3. Jay:

Why are you putting…? Oh yeah, yeah, there will be eleven, I think (He starts drawing Term 4)

4. Rita:

Yep

5. Mimi:

But you must go six on the bottom … (Jay has just finished drawing the first row of circles) and five on the top (Jay finishes drawing the second row)

Although Jay materially undertakes the task of drawing Terms 4 and 5, each student is engaged in the action. In line 1, Rita is not merely informing her group-mates that Term 4 contains a row of five circles. In fact, through a deictic gesture she is suggesting a qualitative and quantitative way to apprehend the next terms. Pointing to a specific part of Term 3, which is given on the sheet, but referring in her speech to Term 4, Rita provides a link between the two terms. Through gesture and speech she is suggesting a specific way to build Term 4. This is an example of a process of perceptual semiosis: a process in which perception is continuously refined through signs.

This grasping of the term is easily adopted by Mimi, and properly described through the spatial deictics “top” and “bottom” (lines 2 and 5). It amounts to shifting from blunt counting to a scheme of counting. This scheme is the first step in the process through which knowledge as pure possibility is endowed with concrete determinations. From something fuzzy and general, knowledge becomes shaped, refined, and specified. It does not become a thing or an object (as in other accounts of objectification). The schema is possibility transformed into action, the result being an open event itself in movement and open to further transformation. In dialectical logic, the schema is an example of the ascent from the abstract to the concrete (Radford 2013b).

In line 2, Mimi’s words are accompanied by two corresponding deictic gestures, which allow her to participate in the drawing process and depict the spatial position of the rows in an iconic way. In line 5, Mimi does not make any gestures; rather, her words are perfectly synchronized with Jay’s action, almost directing him in the action of drawing: in fact, to complete her sentence with the description of the second row, Mimi waits until Jay finishes drawing the first row of circles.

The gesture-speech combination referring to the spatial location “top” and “bottom” is soon after enacted by Jay to explain why he thinks that Term 10 will have 23 chips and Term 100 will have 203 chips:

6. Jay:

Ok. Term 4 has five on top, right? (with his pencil, he points to the top row of Term 4, moving his pencil from the left to the right, Fig. 7.4, left)

Fig. 7.4

Left, Jay’s moving gesture (line 6). Right, Jays’ second gesture (line 8)

7. Mimi:

Yeah…

8. Jay:

…and it has six on the bottom (he points to the bottom row using a similar gesture as in line 7, Fig. 7.4, right).

9. Mimi:

(pointing to the circles while counting) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. (Pause) […] Oh yeah. Term 10 would have …

10. Jay:

10 there would be like …

11. Mimi:

There would be eleven (Fig. 7.5, left: she is making a quick gesture that points to the air. Jay is placing his hand in a horizontal position) and there would be ten (Fig. 7.5, right: she is making the same quick gesture but higher up. Jay is shifting his hand lower down) right?

Fig. 7.5

Synchronization between the two students’ gestures

12. Jay:

Eleven (Fig. 7.6: similar gesture but more evident, with the whole hand) and twelve (same gesture but lower).

Fig. 7.6

Synchronization between the students’ gestures

13. Mimi:

Eleven and twelve. So it would make twenty-three, yeah.

14. Jay:

100 would have one-hundred and one and one-hundred and two (Fig. 7.7: same gestures as the previous ones, but in the space in front of his face).

Fig. 7.7

Synchronization between gestures

15. Mimi:

Ok. Cool. Got it now. I just wanted to know how you got that.

As we can see in the transcript and related pictures, both Jay and Mimi enact the same gesture-speech combination at different times. The repeated enactment, which shows a gesture catchment, allows the students to shift from the given drawings (representing Terms 3 and 4) to imagined ones (referring to Terms 10 and 100). This shifting is carried out while preserving a certain schema in the grasping of the term, as an important means for accomplishing a factual generalization of the pattern (which can be a first step in the algebraic generalization process).

In Jay’s first utterance (lines 6 and 8), the deictic gestures appear endowed with a dynamic feature that clearly depicts the geometric grasping of the term as made up of two horizontal rows. Its goal is to clear away any ambiguity about the referent of the discourse, in order to explain a strategy. Term 4 is perceptively present on the scene, and indeed materially touched by Jay through his pencil. Talking about Term 10, Mimi (line 11) performs two gestures that keep certain specific aspects of those of Jay, that is, one gesture for each row, and the vertical shift. But now, because the referred term is not available in the perceptual field, the gestures are made in the air. Also Jay’s last gestures (line 13), referring to Term 100, appear in the air in the space in front of him, as if pointing to the rows of a non visible term. Indeed, if we pay attention to the position of his hands when he refers to the different terms, we can notice a progressive detachment from the sheet (Fig. 7.8).

Fig. 7.8

The detachment of gestures

Furthermore, from the micro-analysis of the video, carried out with slow motion devices, we can detect that Jay is following Mimi’s argument so closely that his gestures appear perfectly synchronous with his mate’s words and gestures (see line 11 and Fig. 7.5).

The previous episodes show key instances of a process of objectification through which the students become aware of a culturally and historically constituted manner of thinking about sequences. More specifically, through a sensuous coordination of gestures and speech, the students make apparent key traits of Term 100—a term that is not directly perceivable. The tight coordination between gestures and speech takes place in a particular segment of the students’ mathematical activity, leading to the objectification of knowledge: it constitutes a semiotic node. In the considered episode, gestures play a specific role in the knowledge objectification: the indexicality of the repeated gestures undergoes a gradual shift from an existential signification (referring to Terms 3 and 4, materially present on the sheet) to an imaginative mode of signification (referring to Terms 10 and 100).

Notice that the objectifying gestures undergo a process of simplification that involves the loss of movement (along the rows of the term) and a shortening of their duration. A progressive simplification is also evident in the uttered words: from line ten onward, the deictic terms disappear, leaving barely numerical semantic content, organized by the conjunction “and”. Even if Terms 10 and 100 are not materially present, the students can imagine them very precisely and would be able to draw them; but, having reached a certain stage in the process of objectification, they do not need to specify all the details, and the reference to the form of the term can smoothly remain implicit in their speech. We have referred to this simplification of the students’ semiotic activity as a semiotic contraction (Radford 2008b).

5.2 Words, Gesture and Rhythm: Refining the Generalization

The genesis of algebraic generalizations entails the awareness that something stays the same and that something else changes. In order to perceive the general, the students have to make choices: they have to bring to the fore some aspects of the terms (emphasis) and leave some other aspects behind (de-emphasis). In this striving, all the resources at students’ disposal may be of great help—even rhythm, with its combination of sound and silence. While we were conducting our video-analysis of the second part of the activity, and were focusing on words and gestures, rhythm came unexpectedly to the fore as another important semiotic means of objectification.

Rhythm creates the expectation of a forthcoming event (You 1994) and constitutes a crucial semiotic device in making apparent the perception of an order that goes beyond the particular terms. It emerged in a moment in which the students were stuck in discussing Mimi’s hypothesis that to find out the number of circles in any term of the sequence you need to add three to the number of the term. Since Joy refuses this hypothesis, on the base that it does not hold for Term 100 (where there are 203 chips), Mimi said:

16a. Mimi:

You know what I mean? Like… for Term 1 (pointing gesture to Term 1) you will add like (making another gesture, see Fig. 7.9)…

Fig. 7.9

Gestures in line 16a

To explore the role that digit 3 may play, in line 16a Mimi makes two gestures, each one coordinated with word-expressions of differing values. The first couple gesture/word has an indexical-associative meaning: it indicates the first circle on the top of the first row and associates it with Fig. 7.1 (see Fig. 7.9, left bottom). The second couple achieves a meaningful link between digit 3 and three “remarkable” circles in the term. The resulting geometric-numeric link is linguistically specified in additive terms (“you will add”) (see Fig. 7.9, right bottom).

Although Mimi has not mentioned or pointed to the first circle on the bottom row, the circle has been noticed. That is, although the first circle of the bottom has remained outside the realms of word and gesture, it has fallen into the realm of vision. Indeed, right after finishing her previous utterance, Mimi starts with a decisive “OK!” that announces the recapitulation of what has been said and the opening up towards a deeper level of objectification, a level where all the circles of the terms will become objects of discourse, gesture and vision. She says:

16b. Mimi:

OK! It would be like one (indexical gesture on Term 1), one (indexical gesture on Term 1), plus three (grouping gesture); this (making the same set of gestures but now on Term 2) would be two, two, plus three; this (making the same set of gestures but now on Term 3) would be three, three, plus three.

Making two indexical gestures and one “grouping gesture” that surrounds the three last circles on Term 1, Mimi renders a specific configuration apparent to herself and to her group-mates. This set of three gestures is repeated as she moves to Term 2 and Term 3. The gestures are accompanied by the same sentence structure (see Fig. 7.10). Through a coordination of gestures and words, Mimi thereby objectifies (i.e., notices) a general structure in a dynamic way and moves from particular terms towards a grasping of the general term of the sequence. Notice that, in our interpretation, gestures and words are not uttered once the idea has been formed. On the contrary, the idea is taking place while Mimi is gesturing and talking. We move away here from rationalist interpretations where gestures and words would appear and be used after the idea is formed. In other words, communication does not follow understanding and interpretation. Mimi is talking here to her teammates and to herself, at the same time.

Fig. 7.10

On the left, Mimi making the (first) indexical gesture on Term 1. On the right, the new spatial perception of the terms as a result of the process of knowledge objectification

In the course of our data analysis, a closer attention to the previous passage suggested that the coming into existence of the refined students’ schema is much more than a matter of coordinating word and gesture. There was another important element, concerning the rhythmical way in which words and gestures were performed.

After listening to the audio recording, to get a better idea of the manner in which the students emphasize and de-emphasize the various features of the terms through rhythm, we conducted a prosodic analysis of Mimi’s key utterance in line 16b (“one plus one plus three” etc.). Prosody refers to all those vocal features to which speakers resort in order to mark, in a distinctive way, the ideas conveyed in conversation. Typical prosodic elements include intonation, prominence (as indicated by the duration of words) and perceived pitch.

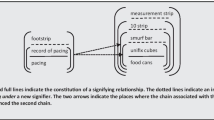
Our prosodic investigation was carried out using Praat (www.praat.org)—a software devoted to voice analysis. Our prosodic analysis focused on the temporal distribution of words and word intensity. In the top part of Fig. 7.11, the waveform shows a visual distribution of words in time; the curve at the bottom shows the intensity of uttered words (measured in dB).

Fig. 7.11

Prosodic analysis of Mimi’s utterance conducted with Praat

The waveform allows us to neatly differentiate two kinds of rhythms: within and between terms. The first type of rhythm, generated through word intensity and pauses between words, helps the students to make apparent a structure within each term. In conjunction with words and gestures (the hand performing the same kind of gesture on each term), this rhythm organizes the way of counting. The other type of rhythm appears as a result of generated “transitions” between the counting processes carried out by Mimi when she goes from one term to the next. To generate these transitions, at the lexical level, Mimi uses the same expression, namely “this would be”, the semantic value of which indicates the hypothetical nature of the emerging counting schema. At the temporal level, this expression allows Mimi to accomplish a separation between the counted terms. At the kinesthetic level, the transition corresponds to the shifting of the hand from one term to the next. Figure 7.12 provides us with a precise idea of the within and between terms’ rhythm.

Fig. 7.12

Intensity and time data of Mimi’s utterance, as derived from Praat prosodic analysis. Rows 1 and 2 show the intensity (dB) and time position of words (s), both measured at the middle of the duration of the word. Row 3 gives the elapsed time between consecutive words. Row 4 gives the total time of the speech segments

Using a matrix system of reference a_ij for the terms of Fig. 7.12, the data in row 3 indicate that a₃₃ < a₃₂, a₃₈ < a₃₇, a₃₁₃ < a₃₁₂, i.e. the data show that the time elapsed between the additive preposition “plus” and the uttered number prior to it is consistently shorter than the elapsed time between the two uttered numbers before “plus”. Thus, while the elapsed time between the second “one” and “plus” is 0.360 s (a₃₃), the elapsed time between “one” and “one” is 0.508 s (a₃₂). It is also interesting to note that, in the case of Terms 1 and 2, the elapsed time between “plus” and the following word is shorter than the time between “plus” and the uttered number before it (i.e. a₃₄ < a₃₃, a₃₉ < a₃₈). The rhythmic distribution of words hence suggests that the preposition “plus” does not merely play the role of an arithmetic operation. By emphasizing and de-emphasizing aspects of the terms, it plays a key prosodic role in the constitution of the counting schema.

Note that the temporal distribution of words of the two first speech segments (0.157 ≤ t ≤ 1.348; 2.161 ≤ t ≤ 3.463) is quite similar to that of the third speech segment (4.793 ≤ t ≤ 5.633). However, the data indicate that the duration of the latter (0.840 s) is shorter than the duration of the former (i.e. 1.191 and 1.302; see row 5).

The students did not need to go beyond Term 3 to come up with the refined counting schema. One of the reasons for this may be that the generalized structure was recognized during the investigation of the two first terms and the third term hence played the role of verification.

The previous data help us understand the students’ mechanisms of emphasizing and de-emphasizing features of the terms. The prosodic analysis sheds light on the articulated ways in which rhythm is used as a semiotic device in the students’ phenomenological apprehension of the general. This is why it may be worthwhile to think of algebraic generalization as a process similar to the creation of a sculpture or of a painting. Some elements are brought to the fore; others are left in the back. Both are important, for it is through their contrast that one notices what has to be noticed. Rhythm accentuates this contrast in the students’ semiotic activity. It heightens the constant and the variable as well as their relationships in the act of generalization.

6 Concluding Remarks

In this chapter we discussed some aspects of the methodology of our semiotic approach. Drawing on Vygotsky’s idea of method we argued that a method is not an instrument or a mere sequence of actions to be followed. A method is rather a reflexive and critical endeavour—a philosophical practice. As such a method conveys a worldview that provides ideas about the entities or phenomena that can be investigated and how they can be investigated. These ideas are translated into theoretical principles in a particular language and meanings through which research questions can be expressed. This is why methods work in tandem with theoretical principles and research questions and that a theory can be considered as an interrelated triplet of “parts”: (P, M, Q), where P stands for principles, M stands for methodology, and Q for research questions.

The principles P should clarify our assumptions and ideas about knowledge and learning. We presented a succinct sketch of them in the first part of the chapter. Following Hegel’s dialectical materialism, we suggested that, from the students’ viewpoint, knowledge appears as pure possibility. However, for knowledge to become an object of consciousness and thought, it has to be set in motion and filled up with conceptual determinations. This is what teaching-learning activity does. In the course of the activity (in Leont’ev’s (1978) sense), knowledge becomes actualized or realized. However, knowledge’s actualization is not a thing. Its actualization is an event.

In the example that we discussed in the chapter, knowledge is the pure possibility of thinking, reflecting, and solving pattern generalization problems in a cultural and historical manner that has been refined through centuries by previous generations.

From the students’ viewpoint, the algebraic manner of thinking about patterns is there, as pure possibility. It becomes actualized as the students engage in sensuous, material activity. In the course of the activity through which knowledge is actualized, knowledge reveals itself and can become an object of consciousness and thought. In our example, its sensuous and material revelation occurred through the formation of a schema. Let us insist on the idea that the schema is not an objectified thing, but an event: the schema is possibility transformed into action, the result being an open event itself in movement and open to further transformation.

Within this context, the account of learning rests on the account of how knowledge is transformed from pure possibility into an object of consciousness. The method is the critical and reflexive endeavour through which this transformation is investigated. Because the activity that mediates and actualizes knowledge into a singular event is an intersubjective, sensuous, and material activity, we trace all signs that intervene in the activity—traditional written signs, but also corporeal signs, such as gestures and posture (e.g. position of the hands and the fingers).

Through fine-grained semiotic analyses we accounted for the manner in which signs signified in the mediating activity. We discussed how we became conscious of the importance of rhythm in mathematics cognition, and how a “crude fact” led to a transformation of our theory, and in particular its methods and research questions. We mentioned in particular two methodological constructs that have been built to help us disentangle the intricacies of multimodal sensuous actions: the semiotic node and the semiotic bundle. The former provides us with a synchronic tool to focus on the manner in which students endow with meaning their actions in coming to discern mathematical relationships and structures in their work. The latter provides us with a diachronic tool to follow the evolution of signs’ interrelationships in the course of the activity. For instance, if we carefully analyse the excerpts presented here by looking at the diachronic evolution of the semiotic bundle, we can observe how the catchment develops and how meanings are emerging along with the evolution. This evolution signals the key moments of the students’ objectification process in the pattern generalization activity.