Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Many internal organs such as stomach, intestine, bronchia, urinary bladder, uterus, airways, or blood vessels are composed by multiple layers of spindle-shaped smooth muscle cells (SMCs). Focusing on vessel mechanics, vascular smooth muscle cells are the key component in the vascular system regulating the diameter of vessels, triggered by various neural, chemical and mechanical signals. Human arteries are comprised of three distinct layers, the intima, the media, and the adventitia, in which the proportion and structure of each varies with size and function of the particular artery.

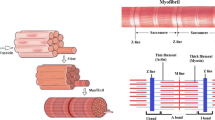
From the mechanical perspective, the media is the most significant layer in human healthy arteries. It is the middle layer and is characterized by a complex three-dimensional network of smooth muscle cells embedded in a matrix of elastin and collagen fibers (Fritsch and Kuehnel, 2007). However, this architecture gives the media high passive strength and the ability to resists loads in multiple directions. Due to the existence of SMCs inside the media it is of particular interest related to smooth muscle (SM) activation, too. Focusing at cell level, SM contraction is rooted on one basic unit, the SMC, see Fig. 5.1(b). These spindle-shaped cells contains a single centrally positioned elongated nucleus and vary notably in size, from 30 μm length in walls of small vessels to 200 μm length and 5 μm width in the intestine, see Rhoades and Bell (2008). They are characterized by a fusiform shape. In the mid-region they are thickest and tapered at each end. SMs are built up of layers of cells (Fig. 5.1(a)) that are linked together by various junctional contacts that serve as points of cell to cell communication and mechanical linkages (dense plaque). The mechanical contraction is caused by contractile units which consist of two filaments: actin and myosin, see Fig. 5.1(c). These filaments are present in large numbers and roughly aligned with the long axis of the cell, see, e.g., Kuo and Seow (2004) and Seow and Paré (2007). They are loosely associated into thin myofibrils. These myofibrils consist of a centrally located myosin filament surrounded by multiple actin filaments. In electron micrographs (e.g., Bond and Somlyo, 1982; Hodgkinson et al., 1995; Herrera et al., 2005) numerous dense staining regions, known as dense bodies (Fig. 5.1(d)), can be identified scattered throughout the cytoplasm of the cell. In common with the Z-discs of skeletal muscles, these dense bodies contain the actin-binding protein α-actinin and appear to serve as anchorage points for actin filaments of myofibrils. Their association with the system of internal intermediate filaments essential serve to integrate contractions over the entire cell and allow the very high degree of shortening achieved by these cells. When actin filaments run into the cell membrane, they connect the dense bodies and dense plaques. Based on the coupling by pairs of opposed adjacent dense bodies located on neighboring cells force transmission is accomplished across cell boundary. Thus, it appears that SMs are composed on a huge number of contractile units in series as well as in parallel.

Fig. 5.1
figure 1

Structural and geometrical characteristics of smooth muscles: (a) layers of smooth muscle cells; (b) isolated smooth muscle cell; (c) single, relaxed unit (myosin heads in skew position); (d) same contracted unit (myosin heads in vertical position)

Full size image

In comparison to experimental investigations there exist only a few approaches describing parts of the biochemical-mechanical process in SM activation by means of mathematical models. Looking at this type of models it stands out that a huge number of these models is realized in a one-dimensional framework, see, e.g., Fay and Delise (1973), Gestrelius and Borgström (1986), Lee and Schmid-Schönbein (1996a,b), Miftakhov and Abdusheva (1996), Rachev and Hayashi (1999), Yang et al. (2003a,b), Zulliger et al. (2004), Herrera et al. (2005), Bates and Lauzon (2007), Bursztyn et al. (2007), Stålhand et al. (2008) and Murtada et al. (2010). All these models have the main restriction that they are implemented in form of so-called stand-alone programmes. Hence, only limited estimations are possible as the chemomechanical behaviors of smooth muscles significantly depend on their geometry undergoing large deformations it is essential to take a three-dimensional modeling approach into account. However, to the authors knowledge, there only exists one three-dimensional coupled chemomechanical modeling approach presenting three-dimensional boundary-value problems, see Schmitz and Böl (2011). Herein, steady state characteristics of the calcium concentration are presented, only.

The present contribution concentrated on the development of a three-dimensional chemomechanical SM model including dynamic behavior of the calcium concentration. Section 5.2 introduces the governing equations of a coupled boundary-value problem for SM chemomechanics. Before the manuscript is concluded with Sect. 5.4, Sect. 5.3 shows illustrative numerical examples.

2 Field Equations of Smooth Muscle Chemomechanics

2.1 Kinematics

As this work focuses on the modeling of vascular smooth muscle tissue, an anisotropic material with outstanding directions for collagen bundles and SMC layers has to be considered. Collagen bundles as well as SMC layers are aligned tangentially with the wall of the vessel (Herlihy and Murphy, 1973; Walmsley and Murphy, 1987; Dahl et al., 2007) accomplished by the angle Φ, see Fig. 1 in Schmitz and Böl (2011). The in-wall dispersions Θ c/s (c = collagen and s = SM layer) leading to arbitrary direction vectors which are able to describe the collagen and SMC orientations in the reference configuration using so-called unit direction vectors

$$ \mathbf{M}_{\mathrm{c}/\mathrm{s}} = \left ( \begin{array}{c} \cos\varTheta_{\mathrm{c}/\mathrm{s}} \cos\varPhi\\ \cos\varTheta_{\mathrm{c}/\mathrm{s}} \sin\varPhi\\ \sin\varTheta_{\mathrm{c}/\mathrm{s}} \end{array} \right ). $$
(5.1)

Consequently, the structural tensors

$$ \mathbf{Z}_{\mathrm{c}/\mathrm{s}} = \mathbf{M}_{\mathrm{c}/\mathrm{s}} \otimes\mathbf{M}_{\mathrm{c}/\mathrm{s}} $$
(5.2)

can be constructed by means of the dyadic product including the directional information of a certain SMC layer M s or collagen fiber bundle M c. This allows the computation of corresponding stretches

$$ \lambda_{\mathrm{c}/\mathrm{s}}^2= I_{4,\mathrm{c}/\mathrm{s}} = \mathbf{C}: \mathbf{Z}_{\mathrm{c}/\mathrm{s}}, $$
(5.3)

where the fourth invariant I 4,c/s can be expressed as scalar product of the right Cauchy-Green tensor C and Z c/s.

2.2 Balance Equations

Using classical non-linear continuum mechanics, a coupled problem of chemomechanical SM contraction is formulated in terms of two primary field variables, namely the placement φ(X,t) and the calcium concentration c(X,t). Consequently, a chemomechanical state of a material point X at the time t is defined as

(5.4)

Spatial as well as temporal evolution of the primary field variables are governed by two basic field equations: the balance of linear momentum and the diffusion-type equation of excitation through calcium.

The balance of linear momentum in spatial form

(5.5)

describes the quasi-static stress equilibrium. Herein \(\bar{\mathbf{b}}\) is the given spatial body force per unit reference volume. The operator div[•] indicates the divergence with respect to the spatial coordinates x, and σ denotes the Cauchy stress tensor given as

$$ \boldsymbol{\sigma}= 2J^{-1}\mathbf{F} \frac{{\partial\varPsi (\boldsymbol{\varphi})}}{\partial\mathbf{C}}{\mathbf{F}}^{\mathrm{T}}, $$
(5.6)

depending on the deformation measures C and F as well as on a strain-energy function Ψ(φ), see Sect. 5.2.3. The mechanical problem is completed by essential and natural boundary conditions,

(5.7)

The surface stress traction vector \(\bar{\mathbf{t}}\), defined on , is related to the Cauchy stress tensor σ via the Cauchy stress theorem \(\bar {\mathbf{t}}:= \boldsymbol{\sigma} \mathbf{n}\), where the outward surface normal is specified as n.

The second field equation describes the calcium concentration inside the SM tissue. The well-known Fick’s second law

(5.8)

predicts how diffusion causes the concentration field c to change with time. Herein, the diffusion flux vector

$$ \mathbf{q}= - \mathbf{d}(\boldsymbol{\varphi}) \nabla_x c $$
(5.9)

relates to the calcium concentration gradient ∇ x c via the deformation dependent, anisotropic diffusion tensor d(φ). Based on the microstructure of SM tissue the diffusion tensor

$$ \mathbf{d}(\boldsymbol{\varphi}) = d_{\mathrm{iso}} \mathbf{I}+ \frac {d_{\mathrm{aniso}}}{n}\sum_{i=1}^n \mathbf{Z}_i^{\mathrm{R}} $$
(5.10)

is additively decomposed into an isotropic (related to the elastin and matrix material) and an anisotropic part (related to the collagen fibers in SMCs) including the appropriate diffusion coefficients d iso and d aniso, respectively. The number of considered directions inside the SM tissue is controlled by n and I denotes the identity tensor. Further,

$$ \mathbf{Z}_{i}^{\mathrm{R}} = { \mathbf{R}} {\mathbf{Z}}_{i}{\mathbf {R}}^{\mathrm{T}}= \frac{{\mathbf{F}} {\mathbf{M}}_{i}}{|\mathbf{FM}_{i}|}\otimes \frac{\mathbf{FM}_{i}}{|\mathbf{FM}_{i}|} $$
(5.11)

are the rotated structural tensors without the stretch component U of the deformation gradient F=RU, whereby R is the rotation tensor.

Analogously to the momentum balance, the calcium field equation also uses corresponding essential and natural boundary conditions

(5.12)

The diffusion surface flux term \({\bar{q}}\) is related to the spatial flux vector through the Cauchy-type formula \({\bar{q}}:=\mathbf{q}\cdot\mathbf{n}\).

2.3 An Active Artery Model

In this section we give a short review over the governing constitutive equations for the active artery model. Thus, the used strain-energy function for the media layer

$$ \varPsi (\boldsymbol{\varphi} ) = \varPsi_{\mathrm{e}} + \varPsi_{\mathrm{c}} + \varPsi_{\mathrm{s}} $$
(5.13)

is additively decomposed in the three components: the load-bearing proteins elastin (Ψ e) and collagen (Ψ c) and the active, contractile SMCs (Ψ s).

2.3.1 Elastin

The first component of the strain-energy function Ψ e stays for elastin, a protein used to build up load-bearing structures in creature tissue. As flexible elastin molecules are randomly arranged in a three-dimensional network, the isotropic neo-Hookean material model

$$ {\varPsi}_{\mathrm{e}} = \frac{\mu_{\mathrm{e}}}{2} (I_1 - 3 ) $$
(5.14)

has been chosen to mirror such characteristics. Herein, the shear modulus μ e as single material parameter seems sufficient. Further, the first invariant \(I_{1}=\operatorname{tr} \mathbf{C}\) is defined as the trace of C.

2.3.2 Collagen

The second main connective tissue component in arteries, collagen (Ψ c), dominates their mechanical behavior by a stress-stretch relation of exponential type along the fiber direction. Experimental observations by, e.g., Dahl et al. (2007) indicate that collagen fibers are preferably aligned with the vessels longitudinal axis, helically and circumferentially. Thus, the dispersion of the collagen fibers by incorporation angles Θ c,i has been measured. In doing so, the relative frequency f c has been regarded to fulfill the relation \(\sum_{i=1}^{n_{\mathrm{c}}} f_{\mathrm{c},i} = 1\) with n c being the number of different directions i. For the modeling of such material characteristics, the used strain energy is weighted in every incorporated direction with the corresponding, measured collagen fraction f c,i and can be written as

$$ {\varPsi}_{\mathrm{c}} = \sum_{i=1}^{n_{\mathrm{c}}} f_{\mathrm{c},i} \varPsi_{\mathrm{c},i}. $$
(5.15)

Herein, the strain-energy functions

$$ {\varPsi}_{\mathrm{c},i} = \begin{cases} \frac{c_1}{2 c_2} \exp [ c_2 ( \lambda_{\mathrm{c},i}^2 - 1 )^2 ] & \mbox{if}\ \lambda_{\mathrm{c},i} \ge1,\\ 0 & \text{else}, \end{cases} $$
(5.16)

depend on two material constants, c 1 and c 2, see Holzapfel et al. (2000).

2.3.3 Smooth Muscle Cells

The third component in arteries are mainly circumferentially oriented SMCs. However, it stands out that there is a certain stretch at which the generated force reaches a maximum value, see Schmitz and Böl (2011). Having those experimentally obtained force-stretch characteristics in mind, the strain-energy function of a single SMC or a layer of SMCs reads

$$ \varPsi_{\mathrm{s}} = \sum _{j=1}^{n_{\mathrm{s}}} f_{\mathrm{s},j} \varPsi_{\mathrm{s},j}. $$
(5.17)

According to the findings of Walmsley and Murphy (1987) the active strain-energy function has been weighted with the SMC volume fractions f s,j in every incorporated direction j. Further, n s denotes the number of considered directions and the direction dependent strain-energy functions

(5.18)

Herein, s 1 is a stress-like material parameter and s 2 is a dimensionless constant. Further, λ s specifies the SMC stretch and λ max defines the stretch at which the generated stress

$$ P_{\max} = \kappa (n_{\mathrm{C}} + n_{\mathrm{D}} ), $$
(5.19)

depending on the parameter κ, reaches its maximum. The whole contraction process is triggered by the chemical degree of activation (n C+n D) provided by Hai and Murphy (1988), describing the time and calcium dependent contraction kinetics. This model is described by the differential equation system

$$ \left [ \begin{array}{l} {\dot{n}}_{\mathrm{A}}\\ {\dot{n}}_{\mathrm{B}}\\ {\dot{n}}_{\mathrm{C}}\\ {\dot{n}}_{\mathrm{D}} \end{array} \right ] = \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -k_1 & k_2 & 0 & k_7 \\ k_1 & -(k_2 + k_3) & k_4 & 0 \\ 0 & k_3 & -(k_4 + k_5) & k_6 \\ 0 & 0 & k_5 & -(k_6 + k_7) \end{array} \right ] \left [ \begin{array}{c} n_{\mathrm{A}}\\ n_{\mathrm{B}}\\ n_{\mathrm{C}}\\ n_{\mathrm{D}} \end{array} \right ], $$
(5.20)

composed of four first order differential equations in time for four chemical states n A, n B, n C, and n D. As these are fractions, n A+n B+n C+n D=1 has to be hold. The first two, n A and n B, represent non-force generating states whereas the last two, n C and n D, are related to generated force and thus, be mechanically significant. Further the rate constant have been used as published in Schmitz and Böl (2011), in doing so k 1=k 6 and k 2=k 5. SMC contraction is triggered by an increase in intracellular calcium which is controlled by the calcium-dependent rate constants k 1 and k 6. Thus, a simple relation is given by

$$ k_1 = k_6=\frac{ (\alpha [\mathrm{Ca}^{2+} ] )^2}{ (\alpha [\mathrm{Ca}^{2+} ] )^2+{ K}^2_{\mathrm{CaCaM}}}, $$
(5.21)

where α>0 is a positive constant, [Ca2+] characterizes the calcium concentration, and K CaCaM denotes the half-activation constant for the calcium-calmodium complex [CaCaM]. In this approach the rate parameters k i have to be identified by experimental data (Hai and Murphy, 1988; Yang et al., 2003a,b).

3 Numerical Examples

This section aims to study how the chemical excitation affects the mechanical behavior at muscle level. In doing so, we first validate the presented modeling approach with experiments by Herlihy and Murphy (1973) before in a second step the dependence of the chemical activation on the contraction characteristics has been studied. If not otherwise specified, the material parameters listed in Tables 5.1 (mechanical parameters) and 5.2 (parameters for the calcium diffusion) are used for the following simulations.

Table 5.1 Material parameters for porcine carotid artery tissue. As the media and the adventitia exhibit a certain amount of elastin and collagen, the mechanical behavior of these two constituent is described by Eqs. (5.14) and (5.16), respectively. In order to distinct between the appropriate material parameters, upper indexes have been used, med=media and adv=adventitia
Full size table
Table 5.2 Material parameters needed for the calcium diffusion inside the SM tissue
Full size table

3.1 Model Validation

For the model validation active and passive tension experiment performed on porcine medial strips (Herlihy and Murphy, 1973) have been used, see Fig. 5.2(a). Following the experimental protocol, the porcine strips have been completely activated so that a temporally converged contraction process is existent. Two main orientations (Θ s,1/2=±4.5∘) of SMC layers with equal SMC fractions (f s,1/2=0.5) have been measured. Strips with dimensions h/w/t=8.0/1.3/1.0 mm have been dissected along the SMCs alignment, namely Θ strip=85.5°. According to the experimental boundary conditions in Herlihy and Murphy (1973) we approximate them by fixing both ends of the strip in all directions. For the collagen dispersion of porcine, medial tissue experimental data by Dahl et al. (2007) have been used. The values for the rate constants of the chemical model have been taken from Hai and Murphy (1988) as these are rooted on data obtained by Singer and Murphy (1987) investigating swine tissue as well. Hence, a consistent parameter set is created, see Table 5.1.

Fig. 5.2
figure 2

Model validation using experimental data by Herlihy and Murphy (1973) obtained from medial strips (Θ strip=85.5∘): (a) force-stretch response from experiment and model and (b) results of the finite element simulation. Deformed shape and von Mises stress distribution at λ strip=1.2

Full size image

Figure 5.2(a) indicates that the proposed model accurately captures the force-stretch behavior. As the tissue strip is aligned with the loading direction in the strips long axis high stress values can be identified, see Fig. 5.2(b).

3.2 Muscle Tissue Strip

In order to show the ability of the model a three-dimensional tissues example, dissected from vessels is used, see Fig. 5.3. The strip is characterized by two layers, the contractible media (t m=0.1 mm, light grey) and the adventitia (t a=0.1 mm, dark grey). In the proposed example we are interested in the tissue response when a completely deactivated strip with an extracellular calcium concentration being initially zero is exposed to an environment with an external calcium concentration of [Ca2+]=500 mMol. This example is closely related to the experimental work of Arner (1982).

Fig. 5.3
figure 3

Porcine tissue strip dissected from an artery. The strip has the dimensions l/w/t a/t m=3.0/3.0/0.1/0.1 mm

Full size image

In order to analyze the contraction process the main variables, i.e. the calcium concentration [Ca2+], the chemical concentrations (n C+n D), and the equivalent von Mises stress σ vM have been tracked during contraction. In doing so, Fig. 5.4 illustrated the results for four discrete time steps t=10/30/80/250 s. Focusing on the calcium concentration (first line) a converged state is achieved in dependence on the choice of the diffusion coefficients, here this situation occurs at time t=80 s. The chemical states (n C+n D) in the second line display a small delay with respect to the calcium concentration, see, e.g., at time t=30 s. Also here, the converged state arises after 80 seconds. In the third line the distribution of the equivalent von Mises stress is illustrated. Small stresses can be detected for the first time step (10 s). As the media differs from the adventitia by a higher stiffness also the stress values a higher. This is impressively documented at time t=30 s where the maximum stress is achieved. The stress increases continuously until at 80 seconds a decrease can be observed. During further activation the stress again increases. Focusing on the overall deformation of the strip a clear bending deformation can be seen that continuously increases. This bending arises from the fact that the layers are aligned asymmetrical and that the media contracts, only.

Fig. 5.4
figure 4

Progress of the main variables [Ca2+], (n C+n D), and σ vM during SM contraction. For the sake of clarity the deformed strip has been cut virtually, so that the distribution of the appropriate variables can be identified

Full size image

4 Conclusion

In this work, a monolithic coupled two field approach for the chemomechanical prediction of smooth muscle contraction has been developed and implemented into the framework of the finite element method. The strain-energy function of the mechanical model consists of three parts associated with the constituents inside a SM tissue. The chemical part has been represented using the four state model by Hai and Murphy (1988) triggered by the dynamic state of the calcium concentration inside the muscle.

It has been shown that the model shows an excellent agreement with experimental data. As the model is implemented into the finite element method it is possible to study the deformation behavior of SM contraction in a three-dimensional way. In doing so, deactivated tissue strips have been virtually loaded by an external calcium concentration, leading to a diffusion of the calcium trough the strip. As two layers, the media and the adventitia, have been considered the strip’s deformation is dominated by a bending mode what seems to be a reasonable result.

We conclude by noting that such class of models in combination with the realistic three-dimensional SM geometries may provide significant contributions for the understanding, identification and treatment of SM activation.