A Bio-chemo-mechanical Model for Cell Contractility, Adhesion, Signaling, and Stress-Fiber Remodeling

Abstract

A bio-chemo-mechanical model is described that targets contractility, adhesion, signaling, and cytoskeleton formation and remodeling, where the effort in the case of the last phenomena is focused on actomyosin stress-fibers. The contractility of the cell is driven by the stress-fibers, which also determine much of the active and passive mechanics that characterize the cell’s mechanical behavior. The stress-fibers attach to adhesion proteins that connect the cell to an extracellular matrix or to a substrate, and apply contractile force through them. This in turn generates signals that can trigger cytoskeleton formation and remodeling. The signals can also arise from external sources such as nervous impulses and biochemical changes to the cell’s surroundings. The model is installed as a user element in a finite element code and used to simulate cell behavior in vitro, such as contraction on a compliant, smooth, flat substrate, or on a bed of compliant posts. Interactions with patterned substrates are also modeled, such as where cells have a limited area to which they can adhere, or where the cells interact with grooves. The results of these simulations are very encouraging as they are largely consistent with observed cell behavior.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

About 10 years ago we became interested in the biomechanics of eukaryotic cells, mainly due to the experiments of Chen and coworkers (Tan et al. 2003), where cells are placed on a bed of small compliant posts and, adhering to them, contract and cause bending of the posts. The post deflections can be measured, and as a result the forces being applied by the cell, typically on the scale of tens of nanonewtons, can be quantified. Many interesting phenomena emerge from such experiments, such as how cells interact with posts of various levels of stiffness, and with differing numbers of posts. These phenomena are paralleled by equivalent observations of cells on compliant, smooth, flat substrates, or on patterned substrates consisting of topography (say grooves) or limited segments to which the cell can adhere. We developed a bio-chemo-mechanical model for the cell contractility, its adhesion to its substrate whether smooth or post-like, the relevant biochemical signaling that goes on inside the cell, and the consequent activity within the cell such as cytoskeleton formation and remodeling. Our purpose in developing the model was to aid in the development of a deeper understanding of the cell behavior being observed in the experiments, and to support the development of further experimental activity. In addition, we hope that our model can be applied to situations where cell mechanics, contractility, and adhesion are known to be important in biology and medicine, such as cell motility, wound healing, development, and embryology, the behavior of stem cells, and in diseases such as cancer, congestive heart failure and cardiac recovery after infarctions where forces and stiffness are known to be relevant parameters. This hope is as yet unrealized, but we aim to continue to develop our model to bring it to a state of readiness where it may yet play such a role.

The purpose of this article is to summarize the model, originally presented in Deshpande et al. (2006, 2007), and to describe some results obtained with it. In doing so, we will describe the results of some experiments on the mechanobiology of cells that we have been able to simulate. However, we do not intend this paper to be a comprehensive review of the behavior of cells in a mechanical setting, or of their active mechanical behavior. We only describe experiments that have either guided our thinking in the development of our models or that we have simulated with some degree of success. Similarly, we will not review the broad category of models for the mechanobiology of cells and will focus only on our own work to provide a summary of it. Furthermore, much of the biochemistry that is a background to our work, and some of the mechanics, is described in the textbook of Alberts et al. (2008).

We note also that the model we describe is one currently in transition. There are certain elements of it that have a high degree of phenomenology built in to them, and our current view is that some of this should be replaced by model features that possess a more fundamental treatment of the chemistry and physics. In fact, one of us is a co-author of a recent paper that puts forward some of the ideas and treatments that bring a more fundamental approach to some aspects of the chemistry and physics of the cell behavior than has previously been embedded in our model. This paper, Vigliotti et al. (2015b), addresses the response of cells under cyclic straining in vitro on flat substrates and within 3-dimensional synthetic extracellular matrices. As a result of this new treatment, the complex and subtle differences in behavior in the relevant experiments have been rationalized, whereas the previous version was only able to simulate the results of the experiments to a low level of fidelity. Therefore, the more fundamental treatments embedded in the new version of the model, and their success in their ability to model the situation described, encourage us that they have value that can be exploited to simulate further important phenomena in the mechanobiology of cells. This development may suggest that summarizing the prior features of the model in the current article is pointless; however, many aspects of the model remain the same, and the phenomenological treatments that are used in many cases give the same results as would arise from the new, more fundamental treatment. Furthermore, at this turning point a retrospective assessment of where we are has value and is briefly summarized in this paper.

2 Relevant Cell Features

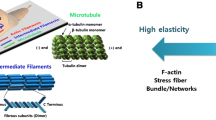
The behavior of the cell that is described by the model arises from stress-fibers, long fibrils that consist of actin protein chains entangled by myosin molecular motors. These fibrils, described in further detail by Alberts et al. (2008), are one component of the cell cytoskeleton. In addition to the stress-fibers, in the cytoskeleton there are intermediate filaments and microtubules, also fibrillar elements. However, we focus on the stress-fibers as they are the source of cell contractility, and therefore mechanically provide one of the most important contributions to the cell active behavior. The cytoskeleton lives within a lipid cell membrane that surrounds the cell, and within a hydrous cytosol that has protein monomers for the fibrillar elements of the cytoskeleton dissolved in it. In addition, there are other elements within the cell such as the endoplasmic reticulum, the mitrochondria and the golgi body that all play roles in the biochemistry of the cell. For example, the mitrochondria generate ATP, the fuel for many processes that take place within the cell, including the contractility driven by the myosin motors. Central to the cell is the nucleus where its DNA is stored and gene transcription takes place. All these features are described in more detail by Alberts et al. (2008).

Fig. 1

A cell treated to enable visualization of stress-fibers (left) and focal adhesions. In the right-hand image image the nucleus is also visible

An illustration of the geometry of stress-fibers is shown in Fig. 1, where they have been visualized in vitro by proteins that attach to them and cause fluorescence. In the left-hand image the stress-fibers can be seen and in the right-hand image the bright short streaks are focal adhesions. The latter consist of a plaque of various proteins inside the cell membrane and adjacent to it. One protein within the plaque, integrin, is transmembrane and attaches to ligands outside the cell. This anchors the focal adhesion either to the extracellular matrix or, in vitro, to a substrate that has been treated to present ligands. The other end of the integrin molecule attaches to the focal adhesion plaque, which in turn attaches to the end of one or more stress-fibers. There are usually multiple integrins associated with a given focal adhesion; indeed a focal adhesion is defined to be an attachment that encompasses many integrin proteins.

Fig. 2

A smooth muscle cell adhered to PDMS posts whose tips are coated with fibronectin. The cell has adhered to the posts, contracted, and as a result deflected the posts. The scale marker is $10\,\upmu$m. Results from Tan et al. (2003)

Fig. 3

A cell imaged for actin (green) with arrows showing the magnitude and direction of force applied to the tip of the relevant post. The arrow at bottom right is a scale indicator whose length equals 20 nN

Fig. 4

Force magnitudes applied to 25 posts by a smooth muscle cell. Shown as a function of time elapsed after up-regulation of the cell. Results from Tan et al. (2003)

Fig. 5

Cells on fibronectin patterns stained to allow visualization of fibronectin (left column), vinculin (second column from the left) and actin (second column from the right). Vinculin is a protein present in focal adhesion complexes. The column on the right is a merger of the other three columns. Results from Théry et al. (2006)

In vitro, a substrate can be treated with materials, such as fibronectin, that present ligands favored by integrins for attachment. This can be done on a flat stiff surface, and a cell in a nutrient bath adjacent to this surface will spontaneously adhere. However, the most interesting results are obtained when the substrate is compliant so that the cell is capable of deforming the substrate by its contractile apparatus. Experiments on such surfaces have shown that many types of cells are indeed contractile, and respond both biochemically and mechanically to the stiffness of the substrate, e.g., by growing a more profuse cytoskeleton that is more powerful in contraction when the stiffness is at a favorable level. The most easily quantifiable experiments in terms of mechanics are those involving cells on posts, since it is straightforward to measure the forces applied to the posts by the cells. An illustration of this set up, developed by Tan et al. (2003), is shown in Fig. 2 which is a top view of a smooth muscle cell adhered to PDMS posts having fibronectin on their tips. The posts are $3\,\upmu$m in diameter and tens of $\mu$m long, and it can be seen that the cell is capable of bending the posts, having done so by contracting. The results of an experiment visualizing the actin in the cell and showing arrows that indicate the forces applied is illustrated in Fig. 3. A temporal graph of the magnitudes of the forces applied to posts by a smooth muscle cell is given in Fig. 4. In the relevant experiment by Tan et al. (2003) the cell was at first down regulated so that it was relatively inactive, a state it was in at time zero in Fig. 4. The cell was then stimulated biochemically at time zero, with the result that it remodeled its cytoskeleton, and in doing so increased the forces generated by its contractile machinery. In this case, the post is attached to approximately 25 posts, and it can be seen that the forces applied rise as high as 100 nN and take approximately 5 min to mature. We note that some aspects of the behavior of cells on posts are influenced by the fact that only discrete areas are available for the cell to adhere to, and that the tips of the posts are all in the same plane. Therefore, the distribution of actin and the degree of contractility may be influenced by the synthetic setting that the cell is placed in. However, almost all of the phenomena observed in cells on posts are reflected by the behavior of cells in other settings, such as in 3-dimensional gels. Furthermore, we judge the response of cells on posts to be a valid set of results for guiding the development of a model and for verifying and validating it.

The significance of focal adhesions is illustrated in the results of experiments carried out by Théry et al. (2006), who formed patterned, flat, surfaces by coating fibronectin in shapes of the letters of the alphabet on a stiff substrate. They then allowed cells to adhere to the fibronectin, with results shown in Fig. 5. In these images it can be seen that the cells extend to cover almost the convex hull of the fibronectin patterns, but the cells adhere directly only to the fibronectin, as vinculin, a focal adhesion protein, is visible only where there is fibronectin available for the adhesion to bind to. Furthermore, the focal adhesions are clustered around the edges of the fibronectin patterns with highest curvature. The focal adhesions are providing the means by which the cells anchor themselves to the substrate, which they do so by binding to the fibronectin, which is an extracellular matrix protein. This illustrates the role of the focal adhesions, or focal complexes, as they can connect the cells to the adjacent extracellular matrix, thereby enabling cells to perform their functions in conjunction with nearby cells of like type.

We note that in the images of Fig. 5 there are significant areas of the cells that are not adhered directly to the fibronectin, as there are large areas where vinculin is absent. We see, therefore, that the focal adhesions form around the perimeter of the available ligands, and that actin stress-fibers are strung from one set of focal adhesions to another. Although this behavior is not universal in vivo, it is a notable aspect of the role that focal adhesions play. We note also that that there are pronounced amounts of actin visible along the unadhered edges of the cells, and that these edges are concave outwards due to contractility of the cell cytoskeleton.

3 The Model

As noted above, our model focuses on the cytoskeleton and the adhesions, but has a rudimentary representation of other features of the cell, captured by background elasticity. We use isotropic, linear infinitesimal strain elasticity, but this could be replaced by something more complicated such as viscoelasticity or nonlinear large strain elasticity. Indeed, in some versions of our model applied to some simulations, the latter is what is used for the background mechanical behavior. The stress-fiber model consists of three elements. The first is a signal that initiates the processes of interest; it could be generated by a nervous impulse, or it could be the outcome of a feedback loop that involves forces being applied to proteins within the cell. An example of the latter is that focal adhesions are known to generate signals when forces are applied to them. In the initial version of the model, the signal is very simple, given by

$$\begin{aligned} C=e^{-t_i/\theta }, \end{aligned}$$

(1)

where $t_i$ is the time elapsed since initiation of the signal and $\theta$ is its decay time. Therefore the signal rises to unity very rapidly and decays to zero as time elapses thereafter. This behavior is designed to simulate the concentration of signaling proteins and ions, with an example of the latter being Ca$^{++}$. The signal is applied simultaneously everywhere in the cell; in later versions of the model developed by Pathak et al. (2011) we have used reaction-diffusion equations to simulate signals, including the release of signaling proteins from their sources as the signal initiates, the downstream activation of further signaling proteins and the accompanying ions such as calcium. We have found that in many settings the simple signal in Eq. (1) applied simultaneously everywhere in the cell is an adequately accurate representation of the deeper complexities of the signaling process.

The second element of the model is the chemical kinetics of stress-fiber polymerization and depolymerization. This is stated as

$$\begin{aligned} \frac{\mathrm{d}\eta }{\mathrm{d}t} = (1-\eta )\frac{\bar{k}_\mathrm{f} C}{\theta } - \left( 1-\frac{T}{\eta T_\mathrm{max}}\right) \eta \frac{\bar{k}_\mathrm{b}}{\theta }, \end{aligned}$$

(2)

where at a material point in the cell $\eta$ is a scaled concentration of stress-fibers emanating from that point in a given orientation, t is time, $\bar{k}_\mathrm{f}/\theta$ is the forward rate constant for the polymerization reaction, $\bar{k}_\mathrm{b}/\theta$ is the reverse, i.e., depolymerization rate constant, T is the tension in the stress-fiber and $T_\mathrm{max}$ is a cell phenotype dependent constant. We note that the signal is embedded in the forward reaction term in Eq. (2), and therefore sets off the process of polymerization of stress-fibers from actin and myosin proteins. Furthermore, $\eta T_\mathrm{max}$ is the isometric tension in a stress-fiber at concentration $\eta$. The presence of the stress-fiber tension in the depolymerization term of Eq. (2) makes the process mechanosensitive. If the tension T reaches the isometric level, $\eta T_\mathrm{max}$, depolymerization is eliminated and a stable stress-fiber can be retained. In the absence of the term in parenthesis containing the stress-fiber tension the signal in Eq. (2), which decays to zero after its initial rise, would simply initiate polymerization that would lead to depolymerization that would sweep away the stress-fiber. Therefore, in our model stress-fibers can only be formed where they can sustain isometric tension at some level of stress-fiber concentration, which means that they must be constrained in some way to a foundation that can sustain the tension applied to it. This foundation is considered to be focal adhesions that connect the stress-fibers to the extracellular matrix or to a substrate to which the cell is affixed. In the earliest version of the model, these focal adhesions form spontaneously on demand so that they are always available to support stress-fibers that are able to attach to them. As noted above, $\eta$ is a scaled concentration equal to the number passing through unit area divided by the maximum possible number that can do so. Its value is therefore limited to $0\le \eta \le 1$.

The third element of our model is a constitutive law for the stress-fiber contraction, given by

$$\begin{aligned} \frac{T}{T_\mathrm{max}}= \left\{ \begin{array}{lcl} 0 &{} &{} \dot{\varepsilon }/\dot{\varepsilon }_0 < - \eta /\bar{k}_\mathrm{v}, \\ \eta + \bar{k}_\mathrm{v} \displaystyle \frac{\dot{\varepsilon }}{\dot{\varepsilon }_0} &{} \qquad &{} - \eta /\bar{k}_\mathrm{v} \le \dot{\varepsilon }/\dot{\varepsilon }_0 \le 0 ,\\ \eta &{} &{} \dot{\varepsilon }/\dot{\varepsilon }_0 > 0, \end{array} \right. \end{aligned}$$

(3)

where $\bar{k}_\mathrm{v}$ is a rate constant or viscosity parameter, $\dot{\varepsilon }$ is the strain-rate of the stress-fiber (positive in extension) and $\dot{\varepsilon }_0$ is a material constant. The model in Eq. (3) is justified by Hill (1938) muscle kinetics and is a simplified version of it, approximated into three linear segments instead of the usual nonlinear function. Such justification relies on the fact that the proteins in stress-fibers (myosin II and actin) are identical to those present in the sarcomeres of skeletal muscle, and therefore will possess the same dynamic constitutive response. Furthermore, stress-fiber shrinkage is a somewhat slow process, and therefore the original Hill (1938) model is assumed to be an adequate representation of their constitutive behavior.

Fig. 6

A spread cell and a representative volume element (RVE) extracted from it. The layout of the cytoskeleton is represented by stress-fibers emanating from the center of the disk in all orientations within the plane of the flat cell, which has uniform thickness h. The density of stress-fibers passing through unit area at the perimeter of the RVE is a function of position, $\phi$, around the perimeter. Similarly the concentration and distribution of stress-fibers at one point in the cell can be very different from those elsewhere in the cell

The equations above are homogenized into a 2-dimensional or 3-dimensional formulation through the construction of a representative volume element (RVE) that is used to compute the stress. We will summarize the 2-dimensional case as it is simpler and is valid for a spread cell whose thickness is very small compared to its other dimensions. A 3-dimensional formulation is given in papers such as that by Ronan et al. (2012) and Dowling et al. (2012). For the 2-dimensional formulation we consider the disk shaped region shown in Fig. 6, sometimes known as a microdisk or micropill. The layout of the cytoskeleton is represented by stress-fibers emanating from the center of the disk in all orientations within the plane of the flat cell, which has uniform thickness h. The density of stress-fibers passing through unit area at the perimeter of the RVE is a function of position, $\phi$, around the perimeter. Similarly the concentration of stress-fibers at one point in the cell can be very different from that elsewhere in the cell. We first compute the stress-fiber tension at $\phi$ according to Eq. (3) and convert it to a stress by use of

$$\begin{aligned} \sigma (\phi )=\frac{2T(\phi )}{\pi Rh}, \end{aligned}$$

(4)

where R is the radius of the RVE as shown in Fig. 6. A plane stress tensor at the material point centered within the RVE is then given by

$$\begin{aligned} \left[ \begin{array}{cc} \sigma _{11} &{} \sigma _{12}\\ \sigma _{12} &{} \sigma _{22}\end{array} \right] =\frac{1}{\pi }\int \limits ^{\pi /2}_{-\pi /2} \Bigg [ \begin{array}{cc} \sigma (\phi )\cos ^2\phi &{} \frac{1}{2}\sigma (\phi )\sin 2\phi \\ \frac{1}{2}\sigma (\phi )\sin 2\phi &{} \sigma (\phi )\sin ^2 \phi \end{array} \Bigg ] \mathrm{d}\phi . \end{aligned}$$

(5)

Note that in this formulation we have assumed that the rigid rotation of the RVE associated with the deformation is negligible and therefore no adjustment of the stress components into the current configuration is used. In our paper Deshpande et al. (2007) this adjustment is given to provide a more general case and is used throughout our numerical computations. To the stress deduced from Eq. (5) are added components to represent other elements of the cell acting in parallel to the stress-fiber cytoskeleton. For example, linear or nonlinear continuum elasticity is used to represent microtubules, intermediate filaments (i.e., other elements of the cytoskeleton are modeled as passive elements), the plasma membrane, the nucleus and other organelles within the cell. The total Cauchy stress in the cell is therefore

$$\begin{aligned} \varSigma _{ij}=\sigma _{ij}+\sigma _{ij}^\mathrm{A}, \end{aligned}$$

(6)

where $\sigma _{ij}^\mathrm{A}$ is the stress added in the manner described above. Note that the stress $\sigma _{ij}^\mathrm{A}$ is usually derived from uniform mechanical properties within the cell such as the elasticities, and therefore does not recognize spatial heterogeneities within the cell. However, in some of our 3D computations, with a more elaborate stress tensor than is given in Eq. (5), organelles such as the nucleus are identified explicitly as separate regions of the cell and given their own mechanical properties.

We have developed user materials for finite element codes such as the Abaqus software (2013) that encompass all the phenomena and formulations summarized in Eqs. (1)–(6), thereby enabling us to undertake fairly elaborate computations. Similarly, 3-dimensional user elements have been developed for the same purpose, and have been used in papers such as Ronan et al. (2012) and Dowling et al. (2012).

4 Results

The model described above has been used to simulate a number of phenomena in the response of cells to their mechanical environment. In one case, a spread cell is attached to 121 compliant microposts that are represented as springs in a square array in the numerical simulations. The cell is down regulated so that its stress-fiber cytoskeleton is minimal and its contractile stress negligible. It is then stimulated by a signal, so that stress-fibers polymerize, attach to posts through focal adhesion connections, and, by contracting, pull on the posts. The results for post deflection magnitudes, or equivalently the magnitude of forces applied to posts, are shown in Fig. 7 as a function of time elapsed after stimulation. Since the problem has twofold symmetry results for one quarter of the system are shown in Fig. 7, i.e., for the 25 posts in a given quarter that displace. Material and cell parameters can be identified to quantify the forces generated and applied to the posts by the cell activity. This will not be pursued here, but instead we will simply draw the reader’s attention to Fig. 4, which displays the equivalent experimental results of Tan et al. (2003) for a cell on 25 posts. The similarities between the results of the simulation in Fig. 7 and those for the experiments in Fig. 4 are clear. Given that a 100 nN force would deflect a post tip by 1 % of its length, and that the signal relaxation time, $\theta$, is approximately 1 min, the equivalency between the two sets of results is very close. Furthermore the experimental observation that posts around the perimeter of the cell experience greater force and displacement magnitudes than posts in the interior of the cell is present also in the results of the simulation.

Fig. 7

Simulation results for the displacement of the tips of posts to which a contractile cell is attached. The cell is at first quiescent, but is then stimulated, polymerizing a stress-fiber cytoskeleton that attaches to posts via focal adhesions, and, by pulling on the posts through contractility, displaces the tips of the posts by a magnitude U. The length of the posts is L and the result are shown as a function of time elapsed after stimulation

4.1 Influence of Substrate Stiffness on Cell Response

Having shown that the model simulates well the response of cells adhered to microposts, we now investigate the influence of post stiffness on the cell’s behavior. The motivation behind this step is the experimental observation of Lo et al. (2000), Discher et al. (2005) and others that cells generate a prominent cytoskeleton and apply relatively high contractile forces to a substrate when that substrate is stiff, but when the substrate is compliant the cytoskeleton is less well developed and the contractile forces are lower. The relevant simulations, described by Deshpande et al. (2006), are carried out for a square, spread cell that is attached to posts at each of its corners, and are implemented for an initially quiescent cell that is stimulated by a signal at time zero. As with the simulation for the cell on 121 posts, it then builds a cytoskeleton, attaches stress-fibers to posts via focal adhesions, and, by contracting the stress-fibers, pulls on the posts. Results for the post deflections and forces applied to the posts are shown in Fig. 8. The lower of the diagrams in Fig. 8 demonstrates that stiffer posts lead to higher forces being applied to the posts. The nonmonotonic response observed for the higher stiffness posts is a result of the interplay among the various time constants in the model, details of which for these computations are given in Deshpande et al. (2006). Note that the post displacements follow the opposite trend and are larger for the more compliant posts. Thus the model does not yield cell behavior that conforms to homeostasis for the post deflections, i.e., the cell deformations do not seek a fixed value of the final post deflections that is independent of the post stiffness.

Fig. 8

Simulation results for the post deflections and forces applied to corner posts by a square, spread cell. The post deflections are normalized by $50\,\upmu$m which is the edge length of the cell, and the force applied to the post is normalized by 17.5 nN, which is the largest force the stress-fibers can exert on a post. The signal decay time, $\theta$, is 720 s. The number in the box over each curve is the normalized stiffness of the posts, where the normalization factor is 0.35 nN$/\upmu$m

The source of the behavior summarized in Fig. 8 is the interaction of the post stiffness with the depolymerization of stress-fibers. A stress-fiber attached to a stiff post and pulling on it will not be able to shrink rapidly and, from Eq. (3), will generate a high tension before the post has deflected very much. As a result T in Eq. (2) will remain close to $\eta T_\mathrm{max}$ and there will not be much depolymerization. That which does occur will cease when $\eta T_\mathrm{max}$ reaches a value equal to T, and the stress-fiber network will be stabilized in isometric condition at a relatively high value of $\eta$. Thus, the stress-fiber cytoskeleton network will be relatively profuse. In turn, Eq. (3) tells us that with a relatively high value of $\eta$, the force applied by the stress-fiber to the post will be high. In contrast, when a stress-fiber is attached to a compliant post and pulls on it, the stress-fiber will be able to shrink relatively rapidly as the post deflects significantly. As a result T in Eq. (2) will fall significantly below $\eta T_\mathrm{max}$ allowing a great deal of depolymerization. Thus $\eta T_\mathrm{max}$ will equate with T at a relatively low value of $\eta$, leaving an isometric network of stress-fibers that is not very well developed. Furthermore, the result from Eq. (3) indicates that when $\eta$ is low, the isometric force generated by the stress-fiber is small, and thus the force applied to the post is relatively low. These observations regarding the extent of cytoskeleton development and the level of forces applied to the substrate are consistent with experimental observations, such as those made by Lo et al. (2000) and Discher et al. (2005).

4.2 Influence of the Number of Posts to Which a Cell Is Attached

Tan et al. (2003) carried out an experiment to investigate the behavior of smooth muscle cells when allowed to adhere to a limited number of posts. They coated fibronectin on a limited number of posts and attached cells to them where the posts elsewhere had no fibronectin, and were thus unattractive for attachment by the cells. In this way Tan et al. (2003) were able to adhere the cells to square arrays of 4, 9, 16, and 25 posts. In fact, the plot shown in Fig. 4 depicts the forces generated when the cell is attached to 25 posts. From the post deflections, Tan et al. (2003) computed the average magnitude of the forces applied to the posts, and obtained the surprising result that this value rose with the number of posts. These results are shown in Fig. 9. The reason why these results are surprising lies in the observation in Figs. 4 and 7 that the magnitude of the force applied to perimeter posts is larger, sometimes much larger, than the magnitude applied to interior posts. Thus as one introduces more interior posts by increasing the number in a square array, i.e., going from zero, to 1, 4 to 9 interior posts as the total number of posts is taken from 4 to 25, the force per post should fall if the force applied to the perimeter posts retains its magnitude as the number of posts increases. The experimental results indicate that this trend is not occurring, and that the magnitude of the forces being applied to the perimeter posts must be rising as the number of posts increases.

Fig. 9

Average magnitude of the force applied by a smooth muscle cell to posts as a function of the size of the cell. The four bar graphs correspond from left to right to cells on 4, 9, 16, and 25 posts. The dashed line is a result of one of our simulations fitted to the result for the largest cell

We have simulated this situation by placing our model cells on different numbers of posts in square arrays, going as high as 21 by 21 posts, and initiating stress-fiber polymerization by imposing a signal. The results are obtained in nondimensional form, and we have fitted one set of them to the experimental data by forcing agreement with the experimental result for the largest number of posts in Fig. 9. Although Fig. 9 is not a linear plot on the abscissa, it happens that our four results when plotted on Fig. 9 fall in a straight line, which is the dashed one shown in that figure. It can be seen that our model correctly predicts the scaling of the average force per post as the number of posts is increased. This behavior comes about in our model because a cell sitting on many posts senses a stiff environment, whereas a cell attached to only a few posts is in a compliant one. Therefore the cell responds with the same trend that is seen when it interacts with stiff posts as opposed to the same number of compliant post; the force magnitudes applied to the posts rise as the environment stiffens. Thus, in the stiff environment where the cell is sitting on many posts it responds by generating a high force per post, whereas in the compliant situation of being on a few posts causes the cell to generate lower forces per post.

As noted above, we carried out our calculations for a very large number of posts in a square array, up to 441. By that stage in some of our simulations for stiffer posts the average magnitude of the forces applied to the posts is falling as the number of posts is increased. This is an indication that the effect referred to above is occurring; namely as more interior posts are introduced, the force per post is diluted because the interior posts experience lower forces than the perimeter posts. To investigate this situation, we consider experiments by Yan et al. (2007) for fibroblasts where much smaller posts are used, so that many more can be placed under a cell of a given size. We find that our simulations for this case agree with the data, which now see a reduction in force per post as the number of posts is increased. Both the experimental data and the results of the simulations are published in McGarry et al. (2009).

Fig. 10

Experimental setup for the in vitro strain cycling of cells attached to flexible substrates. The strain cycle imposed on the substrate is also experienced by the base of the cell where it adheres to the substrate

Fig. 11

Cells that have been subjected to uniaxial cyclic straining in vitro for 6 h at 1 Hz. The cells have been stained to visualize the stress-fibers, with an increased degree of alignment associated with an increased magnitude of cyclic stretch. Results from Kaunas et al. (2005)

Fig. 12

Degree of polymerization of stress-fibers as a function of time during cyclic stretch at 1 Hz as simulated using the bio-chemo-mechanical model. The results are shown for various orientations relative to the cyclic stretch direction which is at $0^\circ$. Greater alignment is achieved at 10 % straining than at 3 % and the alignment is then transverse to the direction of cyclic stretch

4.3 Cells Subject to Cyclic Stretch

Certain types of cells in the body are subject to stretching and shortening in a cyclic manner; a prominent example is the vascular endothelial cell that lines arteries. Since an artery’s diameter expands and contracts with the cardiac cycle, these cells are subject to cyclic stretch at a frequency of approximately 1 Hz. An experimental observation is that in vivo stress-fibers align transverse to the direction of stretch, and therefore align with the blood flow direction in the artery (Zhao et al. 1995). It should be noted that fluid shear stress from the flowing blood also influences the stress-fiber orientation, but we will confine ourselves to the case where stretch dominates the resulting morphology. This situation can be reproduced in vitro by placing a cell on a flexible flat substrate and imposing a strain cycle on it, an experiment that has been been carried out by several research groups. Results from some of these efforts are summarized in the paper by Wei et al. (2008), and the experimental setup for one of them, carried out by Kaunas et al. (2005), is depicted in Fig. 10. As indicated in that graphic, in this case uniaxial strain in the plane of the substrate is imposed on the cell, so that $\varepsilon _{22}=0$. The amplitude of $\varepsilon _{11}$ during cycling is varied from zero to 10 %. Images of the cells after 6 h of cycling at 1 Hz are shown in Fig. 11, which is taken from Kaunas et al. (2005). In the case of isometric strain imposed on the cell, i.e., $\varepsilon _{11} = 0$, the distribution of stress-fibers is essentially isotropic at the end of the experiment after steady state conditions have set in, with equal numbers found in any orientation within the plane of the cell. At $\varepsilon _{11} = 10$ % the stress-fibers at the end of the experiment in steady state are almost all aligned in the direction of zero strain, i.e., parallel to the $x_2$-axis. Results from simulations carried out with our bio-chemo-mechanical model are shown in Fig. 12. The graphs show the development of stress-fiber polymerization with time during uniaxial cyclic stretch at 1 Hz, with the degree of polymerization shown in different orientations relative to the direction of cyclic stretch which is at $0^\circ$. It can be seen that by 6 h the cell is in steady state, and that 10 % straining produces a greater degree of stress-fiber alignment than 3 %. A polar plot showing the stress-fiber orientations after 6 h is also shown in Fig. 12, which brings out clearly the greater degree of alignment in the case of the larger strain. It is also clear that the stress-fibers tend to align in the nonstretching direction, just as is observed in the experiments.

In our model the phenomenon of alignment of the stress-fibers arises from the tendency for them to polymerize and depolymerize. First we note that a signal is initiated at the beginning of the stretching stage of the strain cycle, consistent with the fact that focal adhesions generate signals when tension increments are applied to them. Since the decay time for the signal is rather long compared to the period of cycling, one signal has hardly decayed before the subsequent one replaces it. As a consequence one may regard the simulations as ones in which the signal is permanently on at its maximum strength. This feature drives continued polymerization in all orientations within the cell at all times during the simulations. The different results at different orientations therefore depend solely on how depolymerization is occurring. Because isometric behavior induces a large tension in the stress-fibers, and because such a tension precludes significant depolymerization, many stress-fibers form and are preserved in the isometric, nonstretching direction in all cases. In contrast, the shortening stage of the cyclic straining leads to a lower tension in the stress-fibers, allowing depolymerization to occur. It should be noted that the stretching stage of the strain cycle is associated with a high tension in the stress-fibers so that significant depolymerization does not then occur. However, the depolymerization associated with the stage of shortening is sufficient to reduce the stress-fibers in the shortening direction, leading to the results depicted in Fig. 12.

4.4 Cells on Patterned Substrates

As noted above in Sect. 2, Théry et al. (2006) formed patterns of fibronectin in shapes of letters of the alphabet and allowed cells to adhere to them, with results that are illustrated in Fig. 5. The features of these results have been described already in Sect. 2, and will not be repeated here. To simulate these results, it was found necessary to develop a more detailed model of focal adhesions, including their growth that is coupled to the development of the stress-fiber network. For this development, described in Deshpande et al. (2008), emphasis is placed on the role of integrins. These proteins are transmembrane elements that are capable of connecting the focal adhesion plaque to ligands external to the cell, and therefore binding the cell to the extracellular matrix or to a substrate in vitro. The focal adhesion plaque is a complex aggregate of proteins, including vinculin, and attaches to stress-fibers to make the connection between the adhesion and the cytoskeleton. It is vinculin that is visualized in Fig. 5 to provide the images of the locations of the focal adhesions.

Fig. 13

The integrin protein shown in its two configurations, the bent and straight states. The gray patch at the bottom represents the membrane, in which the integrin sits

4.4.1 Focal Adhesion Model

The integrin protein has two configurations, a bent state and a straight one as shown in Fig. 13, where the gray patches at the bottom of the molecules represent the membrane in which the integrin is embedded. In the straight configuration the integrin can bind to the focal adhesion plaque and to extracellular ligands, and therefore becomes immobilized. In the bent state, interactions among the complexes of the protein preclude it from binding to any other entity. Furthermore, its embedment in the membrane involves only physical bonds, so that the bent integrin is free to move around on the membrane surface of the cell. In the bent state the energy of the protein is low, whereas it is high when the integrin is straight. However, the difference in energy between the two states is relatively low and thermal activation is capable of spontaneously converting one to another. We therefore assume thermodynamic equilibrium between integrins in the straight and bent states. The chemical potential of the bent integrins is given as

$$\begin{aligned} \chi _L=\mu _L + kT \ln \left( \frac{\xi _L}{\xi _R}\right) , \end{aligned}$$

(7)

where $\mu _L$ is the standard chemical potential or enthalpy of the protein, k is Boltzmann’s constant for the molecule, T is the absolute temperature, $\xi _L$ is the number of integrins per unit area of the membrane, and $\xi _R$ is a reference datum for such concentration. The chemical potential for the straight, bound integrins is

$$\begin{aligned} \chi _H=\mu _H+kT\ln \left( \frac{\xi _H}{\xi _R}\right) +\varPhi (\varDelta )-F\varDelta , \end{aligned}$$

(8)

where $\chi _H$, $\mu _H$, and $\xi _H$ have definitions analogous to those for the bent integrins, $\varDelta$ is the distance between the integrin and an extracellular ligand with which it is interacting, $\varPhi$ is the internal energy of that interaction and therefore a function of $\varDelta$, and $F = \mathrm{d}\varPhi /\mathrm{d}\varDelta$ is the force of attraction between the integrin and the extracellular ligand. Thus the combination $\varPhi (\varDelta )-F\varDelta$ is the potential energy of the load applied to the integrin, and installs mechanosensitivity in the chemical potential of the integrin. The description of the mechanosensitive term in Eq. (8) given above is confined to a one-dimensional picture that is adequate for flat, spread cells. In that case, the integrin and the ligand to which it is attracted lie in the same plane and the parameter $\varDelta$ is the distance within that plane between the integrin and the ligand. The function $\varPhi$ is zero when $\varDelta = 0$, with that state representing a perfect placement of the integrin and the ligand in regard to their attraction to each other. The function $\varPhi$ increases monotonically with $\varDelta$ and has a smooth minimum at $\varDelta = 0$. For example, a quadratic dependence of $\varPhi$ on $\varDelta$ is a reasonable model adjacent to $\varDelta = 0$. For larger values of $\varDelta$ the function $\varPhi$ approaches an asymptote as the interaction between the integrin and the ligand becomes insensitive to increasing distance between them. The asymptotic value of $\varPhi$ at large values of $\varDelta$, when averaged over many integrins, is analogous to a surface energy as it represents the work that must be done to create a large separation between the integrins and the ligands to which they are attracted. Furthermore, the force attracting the integrin to a ligand is zero when they are well separated. We note that the function $\varPhi$ is such that $\varPhi (\varDelta )-F\varDelta \le 0$ when the magnitude of $\varDelta$ is less than a critical value. Beyond that value, $\varPhi (\varDelta )-F\varDelta \ge 0$, and $\varPhi (\varDelta )-F\varDelta = 0$ only when $\varDelta = 0$, and at the critical separation where $\varPhi (\varDelta )-F\varDelta$ changes sign. In addition, there are complications when a given integrand is interacting with multiple ligands. Details of these and other aspects of the model are given in Deshpande et al. (2008) but will not be described here as they are not essential to an understanding of the mechanosensitive behavior that Eq. (8) induces.

We note that $\mu _H > \mu _L$. Therefore in the absence of any displacement of the integrin relative to a ligand to which it is bound, i.e., $\varDelta =0$, the equilibrium condition $\chi _H=\chi _L$ requires exponentially more low affinity, bent integrins than straight ones. However, if $\varDelta \ne 0$, but lies below the critical level so that $\varPhi (\varDelta )-F\varDelta \le 0$, equilibrium will demand an increased number of straight integrins, so that the formation of focal adhesions is favored by the application of force to them. Such behavior is observed in experiments, e.g., Chen et al. (2003). In contrast, if the integrin is pulled strongly away from its favored ligand, $\varPhi (\varDelta )-F\varDelta \ge 0$ and equilibrium will encourage the focal adhesion to disintegrate.

In our model, equilibrium between the low and high affinity integrins is augmented by a trafficking equation that moves the mobile, low affinity integrins on the membrane by diffusional mass transport. Details of the mass transport equations are given in the paper by Deshpande et al. (2008), and some enhancements are presented by Pathak et al. (2011), but this aspect of the model will not be detailed here.

4.4.2 Results from the Simulations for Cells on Patterned Substrates

The resulting focal adhesion formulation, coupled to the cytoskeleton model summarized in Eqs. (1)–(6), is used to simulate the cell behavior depicted in Fig. 5, with results, developed by Pathak et al. (2008), summarized in Figs. 14 and 15.

Fig. 14

Distribution of actin resulting from simulations of cells placed on fibronectin patterns. The shape in blue is the fibronectin patch while the cell is depicted by the color contour plot representing the concentration and orientation of stress-fibers. Red indicates a high concentration of stress-fibers while blue depicts a low concentration. The orientation of the stress-fibers is shown by the dashed lines in the color contour plot

Fig. 15

Distribution of focal adhesions resulting from simulations of cells placed on fibronectin patterns. The focal adhesions are the red zone and outline the perimeter of the fibronectin patch

As with many of our simulations, the process of development of the cytoskeleton is initiated by a signal from a condition in which the cell is down regulated, without a significant cytoskeleton and lacking adhesions. The integrins are initially distributed uniformly on the cell membrane and are predominantly low affinity bent ones, with a few straight ones in equilibrium with the bent type. After the signal is initiated, polymerization of the stress-fibers begins and evolves into an isometric steady state, with the resulting structure stabilized by the tension retained within the contractile stress-fibers. This tension in the stress-fibers is transducted to the straight integrins that bind to the stress-fibers. The force applied to the integrins encourages the formation of an ever-increasing concentration of straight ones, which are converted from the bent type. The resulting depletion of the mobile, bent type of integrin induces their diffusion on the membrane in an attempt to equalize their distribution. This has the effect of bringing a fresh supply of low affinity integrins to the locations where force is being applied to the straight ones, and enables further conversion of bent ones to the straight configuration, binding them to the stress-fibers and permitting continued growth of the focal adhesion cluster. This process continues to steady state.

As noted above, the outcomes are shown in Figs. 14 and 15, with the former depicting the distribution of actin, i.e., the stress-fibers, and the latter giving the concentration of high affinity, bound integrins, i.e., the focal adhesions. These results should be compared with Fig. 5, which shows the experimental observations of the same features. The following characteristics can be observed in both the experimental results and the outcomes of the simulations. The actin concentration is highest adjacent to the unadhered edges of the cell, i.e., in each case the cell has extended beyond the fibronectin patch to almost cover its convex hull, so that there are regions where the cell is not adhered to the substrate below it—it is at the edges of these zones that the actin concentration is greatest. The stress-fibers are aligned parallel to the nearby edge of the cell, and contractility has deformed the unadhered edge of the cell into a concave outward configuration. The curvature of these edges in the simulations agrees with that in the experiments. In both the simulations and the experiments, the focal adhesions are formed around the perimeter of the fibronectin patch, with low concentrations of bound integrins in the interior of the patch. In the experiments the focal adhesions are largely confined to the high curvature edges of the fibronectin patch, but in the simulations the focal adhesions have extended to such an extent that they completely surround the fibronectin patch. This discrepancy is the only major deficiency in the results of our simulations. However, it should be noted that during the transient process of developing the results shown in Fig. 15 the focal adhesions first appear at the high curvature edges of the fibronectin patch. Unfortunately they continue to grow until they completely surround the patch. This outcome suggests that we have too many integrins present in our simulations, providing an almost inexhaustible supply of components for the formation of focal adhesions. We believe, therefore, that if we reduced the initial supply of integrins in our simulations the growth of focal adhesions would terminate before completely surrounding the fibronectin patch. In steady state this would leave the focal adhesions clustered near the high curvature edges of the fibronectin patch, consistent with the experimental observations.

Fig. 16

A cell on a stiff elastic substrate (upper) and one on a compliant elastic substrate (lower). The colors represent the concentration of stress-fibers with red being the highest level and blue being low. The cell has a nucleus, which is the central feature in blue in each case surrounded by a small concentration of stress-fibers

4.5 Cells Adhered to Elastic Substrates

We have simulated the interaction of cells with flat, compliant substrates using a 3-dimensional extension of the model. The results of these computations are reported in Ronan et al. (2014), and an example of these is shown in Fig. 16. This figure is a color contour plot for cells adhered to elastic substrates. The upper one is a cell on a relatively stiff substrate, while the lower one sits on a more compliant substrate; however, in both cases the elastic stiffness of the substrate is low enough that the contractile tractions generated by the cell are able to distort the substrate. The red color in the contour plots indicates a high concentration of stress-fibers while the blue depicts a low concentration. It can be seen that the stiff substrate induces the cell to generate a profuse stress-fiber cytoskeleton while the more compliant substrate does not. Furthermore, the tractions applied to the stiff substrate are much higher in magnitude than those applied to the compliant substrate, a feature that correlates with the degree of stress-fiber development. Furthermore, results of Ronan et al. (2014) not depicted here show that the focal adhesion at the edge of the cell on the stiff substrate is much larger than that at the edge of the cell on the compliant substrate. These outcomes of the model in which a stiff substrate induces a greater degree of cytoskeleton polymerization, higher contractile tractions and larger focal adhesions are consistent with experimental observations, such as those of Engler et al. (2006). We note also that the contractility of the cytoskeleton of the cell on the stiff substrate applies a higher pressure to the nucleus of that cell than when the cell is on a compliant substrate. This raises the possibility of the mechanics of the cell playing a role in the biochemistry and genetic regulatory mechanisms that take place in the nucleus.

Fig. 17

A cell being sheared by a probe being moved horizontally relative to the substrate to which the cell is adhered. The colors in the cell represent the concentration of stress-fibers, which remodel during deformation of the cell. Red indicates a high concentration of stress-fibers while blue depicts a low concentration

4.6 Cells Subject to Shearing Deformations

The 3-dimensional formulation of the cell model has also been used to study the response of chondrocyte cells being sheared, where these results are fully described in the paper by Dowling et al. (2012). A schematic of the experimental setup is shown in Fig. 17 with a simulated cell shown being deformed by the probe. The cell is adhered to the substrate and the concentration of stress-fibers within it at the stage of the simulation depicted is shown as a color contour plot with the red color indicating a high concentration of stress-fibers and the blue showing a low one. By comparing Figs. 16 and 17 one can see that during the deformation the cell experiences remodeling of its stress-fiber network, since initially, prior to deformation, the cell’s stress-fiber network was somewhat similar to that depicted in Fig. 16, and therefore symmetric about the nucleus. Comparison of the simulation results with experimental observations by Dowling et al. (2012) indicates that the remodeling predicted by the simulation is similar to that which occurs in the cell during the shearing experiment.

Fig. 18

Graph of the force versus displacement curve for cells subject to shearing deformation by a probe. The blue data points are experimental results for a cell in an active state while the red data points are experimental results for a down-regulated cell. The full lines are the results of simulations, with the upper plot representing an active cell modeled by our coupled stress-fiber and focal adhesion formulations. The lower plot is obtained using a passive nonlinear elastic model. Results from Dowling et al. (2012)

In both the experiments and the simulations the load-deflection curve during shearing is obtained, with all results shown in Fig. 18. The upper plots in the figure, marked ‘Untreated cells’, are for active cells that are contractile and remodel. It can be seen that the simulation agrees very well with the experimental results. To emphasize the importance of the active contractility and the remodeling that occurs in the cell, shearing was also carried out for a cell treated with cytochalasin D, which disrupts the stress-fiber network and reduces its contractility. The lower plots in Fig. 18 are for such cells, and it can be seen that the behavior is not just quantitatively but qualitatively different from that of active cells. In fact the response of the cells treated with cytochalasin D can be simulated using a passive, nonlinear elastic model that stiffens slightly during deformation. Such a model is inadequate for simulating the active cells, as the shape of their load-deflection curve contrasts with that for treated cells in that the active cells exhibit stiff response followed by a reduction in tangent stiffness. The initial stiff response is caused by the active remodeling, and is thus absent from the behavior of the cells treated with cytochalasin D. These results, as well as confirming the validity of our model, emphasize the importance of capturing the active contractility and cytoskeleton remodeling that take place in cells in normal conditions.

We note that we have obtained equivalent results for cells subject to compression (Ronan et al. 2012), those being aspirated by pipetting (Reynolds et al. 2014), and for those interacting with arrays of microposts (McGarry et al. 2009; Ronan et al. 2013). We have also considered the role of contractility in regulating cell–cell junctions (Ronan et al. 2015).

4.7 Cells on Grooved Substrates

Lamers et al. (2010) have studied the behavior of osteoblasts adhered to grooved substrates. The width of the grooves, which in most cases were flat bottomed with flat, square cross-sectioned ridges, ranged from 10 nm to $2\,\upmu$m. In addition, the study encompassed flat, ungrooved substrates. Lamers et al. (2010) found increasing alignment of the cells as the pitch of the grooves increased. Of most interest to us is the degree of alignment of the stress-fibers. In the case of the narrowest grooves the distribution of orientations of the stress-fibers was indistinguishable from that observed on the flat, ungrooved substrate, and therefore was essentially isotropic. On the widest grooves, the stress-fibers aligned themselves so that none was more than $10^{\circ }$ away from being parallel to the grooves. Examples of osteoblasts from these experiments on grooves having pitches of 150 and 10 nm are shown in Fig. 19. The contrasting alignment of the stress-fibers is visible.

Fig. 19

Osteoblasts on grooved substrates. In one case, a, the pitch of the grooves is 150 nm, and in the other case, b, it is 10 nm

We have modeled this behavior, with results reported in Vigliotti et al. (2015a). For this study we utilized reaction-diffusion equations to represent signaling in the cell, according to Pathak et al. (2011). These simulations involved a 1-dimensional geometry across a groove, but permitted formation of stress-fibers in any orientation in the plane of the peaks of the grooves. As with many of our simulations, the process of developing the stress-fibers is commenced with the initiation of a signal. However, in this case, the signal emanates from the focal adhesions, which are confined to the tops of the groove ridges where adhesion ligands are to be found. Due to the time it takes for the reaction-diffusion equation to transmit the signal over the well of the groove, the signal then initiates stress-fiber polymerization on a nonsynchronous basis within the cell, with it commencing later over the well of the groove than on the tops of the ridges. The development of the stress-fiber network is further complicated by the fact that, after its initial period of activity, the signal dies away as the signaling proteins and ions are mopped up by the cell, implicitly being sequestered in the reticulum, returned to the focal adhesions, or pumped out through the cell membrane. As a consequence, the possibility arises that the signal will die before it can completely cross the well of the groove. If the diffusion distances are great enough, that is what happens, the case in point being the grooves with the widest pitches. In that case, due to the absence of a signal over the center of the well, stress-fibers cannot form there, and instead are confined to the tops of the grooves; inevitably there are many more aligned with the grooves than transverse to them. In contrast, when the grooves are narrow, the signal successfully crosses the groove well, and there can be many stress-fibers aligned transverse to the grooving direction.

Fig. 20

Simulation results for the concentration of stress-fibers for osteoblasts adhered to a grooved substrate. The scaling is such that the graph at the top is for narrow grooves and that at the bottom, i.e., the heavy dark line, is for a wide groove. In the case of the wide groove there are no stress-fibers above the well of the groove, and stress-fibers are only found on the ridges of the grooving. When the grooves are narrower stress-fibers succeed in being polymerized across the wells of the grooves

This situation is reflected in the results shown in Fig. 20, which depicts the concentration of stress-fibers across the grooves as a function of groove pitch. In the case of narrow grooves, stress-fibers are to be found above the well of the groove, whereas for the widest grooves no stress-fibers are found there. As noted above, this result translates into alignment of the stress-fibers with the grooves when the pitch of the grooves is wide, and a lack of alignment for narrow grooves. It is found that, statistically, the simulations are in agreement with the experimental results of Lamers et al. (2010) in regard to the degree of alignment of the stress-fibers.

5 Discussion

We have provided a concise description of our bio-chemo-mechanical models for stress-fiber contractility, cytoskeleton development and remodeling, the formation of focal adhesions, and the mechanics associated with these phenomena. In addition, we have described our simplistic representation of a cell signal, and given references to work where a more realistic signal model, based on reaction-diffusion equations for the signaling proteins and ions, can be found. We have illustrated how our model captures many of the observed features of mechanosensitivity in cells, and we believe that this validates and justifies our model. We note that the examples given in this chapter are all focused on single cells; however, we have exercised the model to simulate interactions between cells (Ronan et al. 2015), and in work by Legant et al. (2009) that we have not reviewed here we have successfully applied the model to tissues composed of many cells, and obtained satisfactory results.

Despite our success with the model described here, we are not entirely satisfied with it. Some of the features, such as the mechanosensitivity present in Eq. (2), though justifiable, are somewhat phenomenological and rather ad hoc. Furthermore, to capture some additional effects beyond those summarized in connection with the examples described in the present chapter it has been necessary to modify and extend the model, with the updates described by Vigliotti et al. (2015b). We expect to see further enhancements and improvements to the model in the coming years, to endow it with greater versatility and relevance to problems of mechanobiology.