On the Price of Anarchy of Highly Congested Nonatomic Network Games

Abstract

We consider nonatomic network games with one source and one destination. We examine the asymptotic behavior of the price of anarchy as the inflow increases. In accordance with some empirical observations, we show that, under suitable conditions, the price of anarchy is asymptotic to one. We show with some counterexamples that this is not always the case. The counterexamples occur in simple parallel graphs.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The study of network routing costs and their efficiency goes back to Pigou [23] who, in the first edition of his book, introduces his famous two-road model. Wardrop [31] develops a model where many players (vehicles on the road) choose a road in order to minimize their cost (travel time) and the influence of each one of them, singularly taken, is negligible. He introduces a concept of equilibrium that has become the standard in the literature on nonatomic network games.

When travelers minimize their travel time without considering the negative externalities that their behavior has on other travelers, the collective outcome of the choices of all travelers is typically inefficient, i.e., it is worse than the outcome that a benevolent planner would have achieved. Various measures have been proposed to quantify this inefficiency. Among them the price of anarchy has been the most successful. Introduced by Koutsoupias and Papadimitriou [14] and given this name by Papadimitriou [21], it is the ratio of the worst social equilibrium cost and the optimum cost. The price of anarchy has been studied by several authors and interesting bounds for it have been found under some conditions on the cost functions.

Most of the existing results about the price of anarchy consider worst-case scenarios. They are not necessarily helpful in specific situations. In a nice recent paper O’Hare et al. [19] show, both theoretically and with the aid of simulations, how the price of anarchy is affected by changes in the total inflow of players. They consider data for three cities and they write: “In each city, it can be seen that there are broadly three identifiably distinct regions of behaviour: an initial region in which the Price of Anarchy is one; an intermediate region of fluctuations; and a final region of decay, which has a similar characteristic shape across all three networks. The similarities in this general behaviour across the three cities suggest that there may be common mechanisms that drive this variation.”

The core of the paper [19] is an analysis of the intermediate fluctuations. In our paper we will mainly look at the asymptotic behavior of the price of anarchy. We consider nonatomic congestion games with single source and single destination. We show that for a large class of cost functions the price of anarchy is, indeed, asymptotic to one, as the mass of players grows. Nevertheless, we find counterexamples where its lim sup is not 1 and it can even be infinite.

Contribution. The goal of this paper is twofold. On one hand we provide some positive results that show that under some conditions the price of anarchy of nonatomic network games is indeed asymptotic to one. On the other hand, we present counterexamples where the lim sup of the price of anarchy is not one.

We first show that, for any single-source, single-destination graph, the price of anarchy is asymptotic to one whenever the cost of at least one path is bounded. Then we focus on parallel graphs and we show that the price of anarchy is asymptotic to one for a large class of costs that we characterize in terms of regularly varying functions (see [3] for properties of these functions). This class includes affine functions and cost functions that can be bounded by a pair of affine functions with the same slope.

Next, we present counterexamples where the behavior of the price of anarchy is periodic on a logarithmic scale, so that its lim sup is larger than one both as the mass of players grows unbounded and as it goes to zero. In another counterexample the lim sup of the price of anarchy is infinite. A further counterexample shows that the price of anarchy may not converge to one even for convex costs. An interesting point is that all the counterexamples concern a very simple parallel graph with just two edges, so that the bad behavior of the price of anarchy depends solely on the costs and not on the topology of the graph. This is in stark contrast with the results in [19], where the irregular behavior of the price of anarchy in the intermediate region of inflow heavily depends on the structure of the graph.

Related Literature. Wardrop’s nonatomic model has been studied by Beckmann et al. [2] and many others. The formal foundation of games with a continuum of players came with Schmeidler [30] and then with Mas Colell [16]. Nonatomic congestion games have been studied, among others, by Milchtaich [17, 18].

Various bounds for the price of anarchy in nonatomic games have been proved, under different conditions. In particular Roughgarden and Tardos [27] prove that, when the cost functions are affine, the price of anarchy in nonatomic games is at most 4/3, irrespective of the topology of the network. The bound is sharp and is attained even in very simple networks. Several authors have extended this bound to larger classes of functions. Roughgarden [25] shows that if the class of cost functions includes the constants, then the worst price of anarchy is achieved on parallel networks with just two edges. In his paper he considers bounds for the price of anarchy when the cost functions are polynomials of degree at most d. Dumrauf and Gairing [8] do the same when the degrees of the polynomials are between s and d. Roughgarden and Tardos [28] provide a unifying result for the class of standard costs, i.e., costs c that are differentiable and such that xc(x) is convex. Correa et al. [5] consider the price of anarchy for networks where edges have a capacity and costs are not necessarily convex, differentiable, or even continuous. In [7] they reinterpret and extend these results using a geometric approach. In [6] they consider the problem of minimizing the maximum latency rather than the average latency and provide results about the price of anarchy in this framework. The reader is referred to [26, 29] for a survey.

Some papers show how in real life the price of anarchy may substantially differ from the worst-case scenario, [15, 32]. González Vayá et al. [12] deal with a problem of optimal schedule for the electricity demand of a fleet of plug-in electric vehicles. Without using the term, they show that the price of anarchy goes to one as the number of vehicles grows. Cole and Tao [4] study large Walrasian auctions and large Fisher markets and show that in both cases the price of anarchy goes to one as the market size increases. Feldman et al. [10] define a concept of $(\lambda ,\mu )$-smoothness for sequences of games, and show that the price of anarchy in atomic congestion games converges to the price of anarchy of the corresponding nonatomic game, when the number of players grows. Patriksson [22] and Josefsson and Patriksson [13] perform sensitivity analysis of Wardrop equilibrium to some parameters of the model. Closer to the scope of our paper, Englert et al. [9] examine how the equilibrium of a congestion game changes when either the total mass of players is increased by $\varepsilon$ or an edge that carries an $\varepsilon$ fraction of the mass is removed. For polynomial cost functions they bound the increase of the equilibrium cost when a mass $\varepsilon$ of players is added to the system. Other recent papers, such as [20, 24], have also raised questions about the practical validity of known results about the price of anarchy.

2 The Model

Consider a finite directed multigraph $\mathscr {G}=(V,E)$, where V is a set of vertices and E is a set of edges. The graph G together with a source s and a destination t, with $s,t\in V$, is called a network. A path P is a set of consecutive edges that go from source to destination. Call $\mathscr {P}$ the set of all paths. Each path P has a flow $x_{P}\ge 0$ and call $\varvec{x}=(x_{P})_{P\in \mathscr {P}}$. The total flow from source to destination is denoted by $M\in \mathbb {R}_{+}$. A flow $\varvec{x}$ is feasible if $\sum _{P\in \mathscr {P}}x_{P}=M$. Call $\mathscr {F}_{M}$ the set of feasible flows. For each edge $e\in E$ there exists a cost function $c_{e}(\cdot ):\mathbb {R}_{+}\rightarrow \mathbb {R}_{+}$, that is assumed (weakly) increasing and continuous. Call $\varvec{c}=(c_{e})_{e\in E}$. This defines a nonatomic congestion game $\varGamma _{M}=(\mathscr {G},M,\varvec{c})$. The number M can be seen as the mass of players who play the game.

The cost of a path P with respect to a flow $\varvec{x}$ is the sum of the cost of its edges: $c_{P}(\varvec{x})=\sum _{e\in P}c_{e}(x_{e})$, where

$$ x_{e}=\sum _{\begin{array}{c} P\in \mathscr {P}:\\ e\in P \end{array}}x_{P}. $$

A flow $\varvec{x}^{*}$ is an equilibrium flow if for every $P,Q\in \mathscr {P}$ such that $x^{*}_{P}>0$ we have $c_{P}(\varvec{x}^{*}) \le c_{Q}(\varvec{x}^{*}).$ Denote $\mathscr {E}(\varGamma _{M})$ the set of all such equilibrium flows.

For each flow $\varvec{x}$ define the social cost associated to it as

$$ C(\varvec{x}) := \sum _{P\in \mathscr {P}}x_{P}c_{P}(\varvec{x})=\sum _{e\in E} x_e c_e(x_e), $$

and let ${\mathsf {Opt}}(\varGamma _{M})=\min _{\varvec{x}\in \mathscr {F}_{M}}C(\varvec{x})$ be the optimum cost of $\varGamma _{M}$. Define also the worst equilibrium cost of $\varGamma _{M}$ as ${\mathsf {WEq}}(\varGamma _{M}) = \max _{\varvec{x}\in \mathscr {E}(\varGamma _{M})}C(\varvec{x})$. Actually, in the present setting the cost $C(\varvec{x}^{*})$ is the same for every equilibrium $\varvec{x}^{*}$ (see [11]).

The price of anarchy of the game $\varGamma _{M}$ is then defined as

$$\begin{aligned} {\mathsf {PoA}}(\varGamma _{M}):=\frac{{\mathsf {WEq}}(\varGamma _{M})}{{\mathsf {Opt}}(\varGamma _{M})}. \end{aligned}$$

We will be interested in the price of anarchy of this game, as $M\rightarrow \infty$. We will show that, under suitable conditions, it is asymptotic to one. We call asymptotically well behaved the congestion games for which this happens.

3 Well Behaved Congestion Games

3.1 General Result

The following general result shows that for any network the price of anarchy is asymptotic to one when at least one path has a bounded cost.

Theorem 1

For each path $P\in \mathscr {P}$ denote

$$\begin{aligned} c_P^\infty =\sum _{e\in P}c_e^{\infty }\quad \,{with}\,\quad c_e^\infty =\lim _{z\rightarrow \infty }c_e(z) \end{aligned}$$

and suppose that $B:=\min _{P\in \mathscr {P}}c_P^\infty$ is finite. Then, $\lim _{M\rightarrow \infty } {\mathsf {PoA}}(\varGamma _M) = 1$.

Proof

Let $\varvec{x}^{*}$ be an equilibrium for $\varGamma _M$. Then if $x^{*}_{P}>0$ we have

$$\begin{aligned} c_P(\varvec{x}^{*})=\min _{Q\in \mathscr {P}}c_Q(\varvec{x}^{*})\le \min _{Q\in \mathscr {P}}c_Q^\infty = B \end{aligned}$$

and therefore

$$\begin{aligned} {\mathsf {WEq}}(\varGamma _M)=\sum _{P\in \mathscr {P}}x^{*}_P c_P(\varvec{x}^{*})\le \sum _{P\in \mathscr {P}}x^{*}_PB=MB. \end{aligned}$$

It follows that

$$\begin{aligned} {\mathsf {PoA}}(\varGamma _M)\le \frac{MB}{{\mathsf {Opt}}(\varGamma _M)}, \end{aligned}$$

so that it suffices to prove that ${\mathsf {Opt}}(\varGamma _M)/M\rightarrow B$. To this end denote $\varDelta (\mathscr {P})$ the simplex defined by $\varvec{y}=(y_P)_{P\in \mathscr {P}}\ge 0$ and $\sum _{P\in \mathscr {P}}y_P=1$, so that

$$\begin{aligned} \frac{1}{M}{\mathsf {Opt}}(\varGamma _M)&=\min _{\varvec{x}\in \mathscr {F}_M}\sum _{P\in \mathscr {P}}\frac{x_P}{M}c_P(\varvec{x})\\&=\min _{\varvec{y}\in \varDelta (\mathscr {P})}\sum _{P\in \mathscr {P}}y_Pc_P(M\varvec{y}). \end{aligned}$$

Denote $\varPhi _M(\varvec{y})=\sum _{P\in \mathscr {P}}y_Pc_P(M\varvec{y})$. Since the cost functions $c_e(\cdot )$ are non-decreasing, the family $\varPhi _M(\cdot )$ monotonically increases with M towards the limit function

$$\begin{aligned} \varPhi _\infty (\varvec{y})=\sum _{P\in \mathscr {P}:y_P>0}y_Pc_P^\infty . \end{aligned}$$

Now we use the fact that a monotonically increasing family of functions epi-converges (see [1]) and since $\varDelta (\mathscr {P})$ is compact it follows that the minimum $\min _{\varvec{y}\in \varDelta (\mathscr {P})}\varPhi _M(\varvec{y})$ converges as $M\rightarrow \infty$ towards

$$\begin{aligned} \min _{\varvec{y}\in \varDelta (\mathscr {P})}\varPhi _\infty (\varvec{y}). \end{aligned}$$

Clearly this latter optimal value is B and is attained by setting $y_P>0$ only on those paths P that attain the smallest value $c_P^\infty =B$, and therefore we conclude

$$\begin{aligned} \frac{1}{M}{\mathsf {Opt}}(\varGamma _M)=\min _{y\in \varDelta (\mathscr {P})}\varPhi _M(\varvec{y})\rightarrow B, \end{aligned}$$

as was to be proved. $\quad \square$

3.2 Parallel Graphs

In this section we examine the asymptotic behavior of the price of anarchy when the game is played on a parallel graph.

Let $\mathscr {G} = (V,E)$ be a parallel graph such that $V = \{s,t\}$ are the vertices and $E = \{e_1,e_2,\ldots ,e_{n}\}$ are the edges. For each edge $e_{i}\in E$ the function $c_i(\cdot )$ represents the cost function of the edge $e_{i}$. Call $\varGamma _{M}=(\mathscr {G},M,\varvec{c})$ the corresponding game. In the whole section we will deal with this graph.

Adding a Constant to Costs. First we prove a preservation result. We show that if the price of anarchy of a game converges to 1, then adding positive constants to each cost does not alter this asymptotic behavior.

Theorem 2

Given a game $\varGamma _{M}=(\mathscr {G},M,\varvec{c})$ and a vector $\varvec{a}\in [0,\infty )^{n}$, consider a new game $\varGamma _{M}^{\varvec{a}}(\mathscr {G},M,\varvec{c}^{\varvec{a}})$, where

$$\begin{aligned} c_{i}^{\varvec{a}}(x) = a_{i}+c_{i}(x). \end{aligned}$$

If $c_i(\cdot )$ is strictly increasing and continuous, $\lim _{x\rightarrow \infty }c_{i}(x)=\infty$ for all $e_{i}\in E$, and $\lim _{M \rightarrow \infty } {\mathsf {PoA}}(\varGamma _M) = 1$, then $\lim _{M \rightarrow \infty } {\mathsf {PoA}}(\varGamma _{M}^{\varvec{a}}) = 1$.

Regularly Varying Functions

Definition 3

Let $\beta \ge 0$. A function $\varTheta : (0, +\infty ) \rightarrow (0, +\infty )$ is called $\beta$ -regularly varying if for all $a>0$

$$\begin{aligned} \lim _{x \rightarrow \infty } \frac{\varTheta (a\cdot x)}{\varTheta (x)} = a^{\beta } \in (0,+\infty ). \end{aligned}$$

When $\beta =1$, we just say that the function is regularly varying.

The following theorem shows that asymptotically the price of anarchy goes to 1 for a large class of cost functions.

Theorem 4

Consider the game $\varGamma _{M}$ and suppose that for some $\beta >0$ there exists a $\beta$-regularly varying function $c(\cdot ) \in C^{1}$ such that the function $x\mapsto c(x)+xc'(x)$ is strictly increasing and for all $e_{i}\in E$ the function $c_i(\cdot )$ is strictly increasing and continuous with

$$\begin{aligned} \lim _{x \rightarrow \infty } \frac{c^{-1} \circ c_i(x)}{x} = \alpha _i \in (0,+\infty ] \end{aligned}$$

(1)

and that at least one $\alpha _{i}$ is finite. Then

$$\begin{aligned} \lim _{M \rightarrow \infty } {\mathsf {PoA}}(\varGamma _{M}) = 1. \end{aligned}$$

Proof

We begin by noting that if some cost $c_i(\cdot )$ is bounded, then the result follows directly from Theorem 1. Suppose now that $c_i(x)\rightarrow \infty$ when $x\rightarrow \infty$ in all links and consider first the case where all the $\alpha _i$ are finite. In this case the equilibrium flows $x^{*}_i$ must diverge to $\infty$ as $M\rightarrow \infty$ and the equilibrium is characterized by $c_i(x^{*}_i)=\lambda$. This allows to derive an upper bound for the cost of the equilibrium. That is, (1) implies that for small $\varepsilon >0$ we have

$$\begin{aligned} \frac{c^{-1}\circ c(x^{*}_i)}{x^{*}_i}=\frac{c^{-1}(\lambda )}{x^{*}_i}\in (\alpha _i-\varepsilon ,\alpha _i+\varepsilon ), \end{aligned}$$

provided M is large enough. It then follows that

$$\begin{aligned} \sum _{i=1}^n\frac{c^{-1}(\lambda )}{\alpha _i+\varepsilon }\le \sum _{i=1}^nx^{*}_i=M, \end{aligned}$$

so that, denoting

$$\begin{aligned} a(\varepsilon )=\left( \sum _{i=1}^n\frac{1}{\alpha _i+\varepsilon }\right) ^{-1}, \end{aligned}$$

we get $\lambda \le c(Ma(\varepsilon ))$ and

$$\begin{aligned} {\mathsf {WEq}}=M\lambda \le M c(Ma(\varepsilon )). \end{aligned}$$

Next we derive a lower bound for the optimal cost

$$\begin{aligned} {\mathsf {Opt}}(\varGamma _M)=\min _{x\in \mathscr {F}_M}\sum _{i=1}^n x_ic_i(x_i). \end{aligned}$$

We note that when $M\rightarrow \infty$ the optimal solutions are such that $x_i(M)\rightarrow \infty$ so that using (1) and the fact that $\alpha _i-\varepsilon >0$ we get for all M large enough

$$\begin{aligned} \min _{x\in \mathscr {F}_M}\sum _{i=1}^n x_ic_i(x_i)\ge \min _{x\in \mathscr {F}_M}\sum _{i=1}^n x_ic((\alpha _i-\varepsilon )x_i). \end{aligned}$$

The optimality condition for the latter yields

$$\begin{aligned} c((\alpha _i-\varepsilon )x_i)+(\alpha _i-\varepsilon )x_i c'((\alpha _i-\varepsilon )x_i)=\mu . \end{aligned}$$

For the sake of brevity we denote $\tilde{c}(x)=c(x)+xc'(x)$ and $y_i=(\alpha _i-\varepsilon )x_i$ so that the optimality condition becomes $\tilde{c}(y_i)=\mu$. This yields $y_i=\tilde{c}^{-1}(\mu )$ and therefore

$$\begin{aligned} M=\sum _{i=1}^n x_i=\sum _{i=1}^n\frac{\tilde{c}^{-1}(\mu )}{\alpha _i-\varepsilon }. \end{aligned}$$

Denoting

$$\begin{aligned} b(\varepsilon )=\left( \sum _{i=1}^n\frac{1}{\alpha _i-\varepsilon }\right) ^{-1}, \end{aligned}$$

we then get $\mu =\tilde{c}(Mb(\varepsilon ))$ and we obtain the following lower bound for the optimal cost

$$\begin{aligned} {\mathsf {Opt}}(\varGamma _M)\ge \min _{x\in \mathscr {F}_M}\sum _{i=1}^n x_ic((\alpha _i-\varepsilon )x_i)=Mc(\tilde{c}^{-1}(\mu ))=Mc(Mb(\varepsilon )). \end{aligned}$$

Combining the previous bounds we obtain the following estimate for the price of anarchy

$$\begin{aligned} {\mathsf {PoA}}(\varGamma _M)\le \frac{Mc(Ma(\varepsilon ))}{Mc(Mb(\varepsilon ))}. \end{aligned}$$

Letting $M\rightarrow \infty$ and using the fact that c is $\beta$-regularly varying we deduce

$$\begin{aligned} \limsup _{M\rightarrow \infty }{\mathsf {PoA}}(\varGamma _M)\le \left( \frac{a(\varepsilon )}{b(\varepsilon )}\right) ^\beta \end{aligned}$$

and since $a(\varepsilon )/b(\varepsilon )\rightarrow 1$ as $\varepsilon \rightarrow 0$ we conclude

$$\begin{aligned} \limsup _{M\rightarrow \infty }{\mathsf {PoA}}(\varGamma _M)=1. \end{aligned}$$

If some $\alpha _{i}=\infty$, then call $I_{0}:=\{i:\alpha _{i}<\infty \}$. In equilibrium

$$\begin{aligned} M = \sum _{i=1}^{n}c_{i}^{-1}(\lambda ) \ge \sum _{i\in I_{0}} c_{i}^{-1}(\lambda ) \ge \sum _{i\in I_{0}}\frac{1}{\alpha _{i}+\varepsilon } c^{-1}(\lambda ), \end{aligned}$$

hence

$$\begin{aligned} \lambda \le c\left( M \left( \sum _{i\in I_{0}} \frac{1}{\alpha _{i}+\varepsilon }\right) ^{-1}\right) . \end{aligned}$$

In the optimum proceed as before with $\alpha _{i}' \nearrow \alpha _{i}$. $\quad \square$

The following results follow easily from Theorem 4.

Corollary 5

In the game $\varGamma _{M}$ if for all $i \in E$ we have $\lim _{x \rightarrow \infty } c_i(x)/x = m_i \in (0,+\infty ]$ and at least one $m_{i}<\infty$, then

$$\begin{aligned} \lim _{M \rightarrow \infty } {\mathsf {PoA}}(\varGamma _{M}) = 1. \end{aligned}$$

Corollary 6

In the game $\varGamma _{M}$ if for all $i \in E$ we have $\lim _{x\rightarrow \infty }c_i^{\prime }(x) = m_i$ with $m_i \in (0,+\infty ]$ and at least one $m_{i}$ is finite, then

$$\begin{aligned} \lim _{M \rightarrow \infty } {\mathsf {PoA}}(\varGamma _{M}) = 1. \end{aligned}$$

Corollary 7

In the game $\varGamma _{M}$ if for all $i \in E$ for some $\beta >0$ there exists a $\beta$-regularly varying function $c(\cdot )$ such that

$$\begin{aligned} \lim _{x \rightarrow \infty } \frac{c_i(x)}{c(x)} = m_i \in (0,+\infty ], \end{aligned}$$

(2)

and at least one $m_{i}$ is finite, then

$$\begin{aligned} \lim _{M \rightarrow \infty } {\mathsf {PoA}}(\varGamma _{M}) = 1. \end{aligned}$$

Corollary 8

In the game $\varGamma _{M}$ if, for all $e_{i}\in E$, $c_{i}(x)=a_{i}+b_{i}x$, then

$$\begin{aligned} \lim _{M \rightarrow \infty } {\mathsf {PoA}}(\varGamma _{M}) = 1. \end{aligned}$$

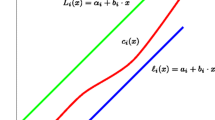
Costs Bounded by Affine Functions. The next theorem examines the case where each cost function is bounded above and below by two affine functions with the same slope.

Theorem 9

Consider the game $\varGamma _{M}$ and assume that for every $e_{i}\in E$

$$\begin{aligned} \ell _{i}(x):=a_{i}+b_{i}x \le c_{i}(x) \le \alpha _{i}+b_{i}x=:L_{i}(x). \end{aligned}$$

Then

$$\begin{aligned} \lim _{M\rightarrow \infty }{\mathsf {PoA}}(\varGamma _{M}) = 1. \end{aligned}$$

4 Ill Behaved Games

In this section we will consider some examples where the price of anarchy is not asymptotic to one, as the inflow goes to infinity.

Consider a standard Pigou graph and assume that the costs are as follows:

$$\begin{aligned} \begin{aligned} c_{1}(x)&=x, \\ c_{2}(x)&= a^{k} \quad \text {for }x \in (a^{k-1},a^{k}],\quad k\in \mathbb {Z}, \end{aligned} \end{aligned}$$

(3)

with $a\ge 2$, as in Fig. 1. In this game the cost of one edge is the identity, whereas for the other edge it is a step function that touches the identity at intervals that grow exponentially. The cost function $c_{2}$ is not continuous, but a very similar game can be constructed by approximating it with a continuous function.

Fig. 1.

Step function.

Theorem 10

Consider the game $\varGamma _{M}$ with costs as in (3). We have

$$\begin{aligned} \liminf _{M\rightarrow \infty }{\mathsf {PoA}}(\varGamma _{M})=1, \quad \limsup _{M\rightarrow \infty }{\mathsf {PoA}}(\varGamma _{M})=\frac{4+4a}{4+3a}. \end{aligned}$$

Remark 11

We can immediately see that

$$\begin{aligned} \limsup _{M\rightarrow \infty }{\mathsf {PoA}}(\varGamma _{M})=\frac{6}{5}\quad \text {for }a=2 \end{aligned}$$

and

$$\begin{aligned} \limsup _{M\rightarrow \infty }{\mathsf {PoA}}(\varGamma _{M})\rightarrow \frac{4}{3}\quad \text {as }a\rightarrow \infty . \end{aligned}$$

The proof of Theorem 10 shows that there is a periodic behavior of the price of anarchy (on a logarithmic scale). This implies that

$$\begin{aligned} \liminf _{M\rightarrow 0}{\mathsf {PoA}}(\varGamma _{M})=1, \quad \limsup _{M\rightarrow 0}{\mathsf {PoA}}(\varGamma _{M})=\frac{4+4a}{4+3a}. \end{aligned}$$

That is, even for very small values of M the price of anarchy is not necessarily close to 1.

Figure 2 plots the price of anarchy for $M\in [2a^{k},2a^{k+1}]$, when $a=3$.

Fig. 2.

Price of anarchy for $M\in [2a^{k},2a^{k+1}]$, with $a=3$, $k=1$.

The next theorem shows that the price of anarchy may fail to be asymptotic to one, even when the cost functions are all convex.

Theorem 12

There exist congestion games $\varGamma _{M}$ where the cost functions are all increasing and convex and both

$$\begin{aligned} \limsup _{M\rightarrow \infty }{\mathsf {PoA}}(\varGamma _{M})>1\quad {and} \quad \limsup _{M\rightarrow 0}{\mathsf {PoA}}(\varGamma _{M})>1. \end{aligned}$$

The next theorem shows that the lim sup of the price of anarchy may even be infinite.

Theorem 13

There exist congestion games $\varGamma _{M}$ with ${\limsup \limits _{M\rightarrow \infty }}\, {\mathsf {PoA}}(\varGamma _{M})=\infty$.

5 Conclusions

The classical result of [27] can be restated as follows. Given a nontrivial single-commodity network, for any fixed total flow M, there exists a vector $\varvec{c}$ of affine costs that depend on M, such that the price of anarchy of the corresponding game is 4/3.

In this paper we have proved that, given a single-commodity network, for any vector $\varvec{c}$ of costs that is bounded on some path P, there exists a total flow M such that the price of anarchy of the corresponding game is arbitrarily close to 1. Similar results have been obtained under different conditions on the network and the costs. What is relevant is that in our model the order of the quantifiers is reversed with respect to the classical bounds of the price of anarchy, such as [27].