The Asymptotic Behavior of the Price of Anarchy

Abstract

This paper examines the behavior of the price of anarchy as a function of the traffic inflow in nonatomic congestion games with multiple origin-destination (O/D) pairs. Empirical studies in real-world networks show that the price of anarchy is close to 1 in both light and heavy traffic, thus raising the question: can these observations be justified theoretically? We first show that this is not always the case: the price of anarchy may remain bounded away from 1 for all values of the traffic inflow, even in simple three-link networks with a single O/D pair and smooth, convex costs. On the other hand, for a large class of cost functions (including all polynomials), the price of anarchy does converge to 1 in both heavy and light traffic conditions, and irrespective of the network topology and the number of O/D pairs in the network.

1 Introduction

Almost every commuter in a major metropolitan area has experienced the frustration of being stuck in traffic. At best, this might mean being late for dinner; at worst, it means more accidents and altercations, not to mention the vastly increased damage to the environment caused by huge numbers of idling engines. To name but an infamous example, China’s G110 traffic jam in August 2010 brought to a standstill thousands of vehicles for 100 km between Hebei and Inner Mongolia. Not caused by weather or a natural disaster, this massive 10-day tie-up was instead laid at the feet of a bevy of trucks swarming on the shortest route to Beijing, thus clogging the G110 highway to a halt (while ironically carrying supplies for construction work to ease congestion). This, therefore, raises the question: how much better would things have been if all traffic had been routed by a social planner who could calculate (and enforce) the optimum traffic assignment?

In game-theoretic terms, this question boils down to the inefficiency of Nash equilibria. The most widely used quantitative measure of this inefficiency is the so-called price of anarchy (PoA): introduced by Koutsoupias and Papadimitriou (1999) and so dubbed by Papadimitriou (2001), the PoA is the ratio between the social cost of the least efficient Nash equilibria and the minimum achievable cost. By virtue of this simple definition, deriving worst-case PoA bounds has given rise to a vigorous literature at the interface of computer science, economics and operations research, with many surprising results.

In the context of network congestion, Pigou (1920) was probably the first to note the inefficiency of selfish routing, and his elementary two-road example with a PoA of 4 / 3 is one of the two prototypical examples thereof. The other is due to Braess (1968), and consists of a four-edge network where the addition of a zero-cost segment makes things just as bad as in the Pigou case. These two examples were the starting point for Roughgarden and Tardos (2002) who showed that the price of anarchy in (nonatomic) routing games with affine costs may not exceed 4 / 3. On the other hand, if the network’s cost functions are polynomials of degree at most d, the price of anarchy may become as high as $\varTheta (d/\log d)$, implying that selfish routing can be arbitrarily bad in networks with polynomial costs (Roughgarden 2003).

At the same time however, these worst-case instances are usually realized in networks with delicately tuned traffic loads and costs; if a network operates beyond this regime, it is not clear whether the price of anarchy is still high. Indeed, using both analytical and numerical methods, a recent study by O’Hare et al. (2016) suggests that the PoA is usually close to 1 for very high and very low traffic, and it fluctuates in the intermediate regime. In a similar setting, Monnot et al. (2017) recently used a huge dataset on commuting students in Singapore to estimate the so-called “empirical” PoA (a majorant of the ordinary price of anarchy); their observations yield a value between 1.11 and 1.22, suggesting that the actual value of the price of anarchy is even lower.

All this leads to the following natural questions:

• 1. Under what conditions does the PoA converge to 1 in light or heavy traffic?

• 2. Do these conditions depend on the network topology, its costs, or both?

• 3. Can general results be obtained only for networks with a single origin-destination pair or do they extend to networks with multiple such pairs?

1.1 Our Results

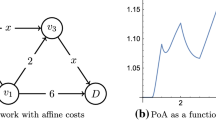
Our first result is a cautionary tale: we show that the price of anarchy may oscillate between two bounds strictly greater than 1 for all values of the traffic inflow, even in simple parallel-link networks with a single origin-destination (O/D) pair (cf. Fig. 1). The cost functions in our example are convex and differentiable, so neither convexity nor smoothness seems to play a major role in the efficiency of selfish routing. Moreover, our construction only involves a three-link network, so such phenomena may arise in any network containing such a three-link component.

Heuristically, the reason for this behavior is that the network’s cost functions exhibit higher-order oscillations which persist at any scale, for both high and low traffic. Thus, to account for such pathologies, we take a two-pronged approach:

• In the low congestion limit, we focus on cost functions that are real analytic, i.e., they are equal to their power series expansion near 0. Under this regularity assumption, we show that the PoA converges to 1, no matter the network topology or the number of O/D pairs in the network.

• At the other end of the spectrum, to tackle the high congestion limit, we introduce the concept of a benchmark function. This is a regularly varying function $c(x)$ that classifies edges into fast, slow or tight, depending on the growth rate of the cost along each edge;¹ paths are then classified as fast, slow or tight, based on their slowest edge.² We then establish the following general result: if the “most costly” O/D pair in the network admits a tight path, the network’s PoA converges to 1 under heavy traffic.

Fig. 1.

A network where selfish routing remains inefficient for both light and heavy traffic.

Among other classes of functions, polynomials satisfy all of the above requirements, leading to the following general principle:

In networks with polynomial cost functions,

the price of anarchy becomes 1 under both light and heavy traffic.

In other words, a benevolent social planner with full control of traffic assignment would not do any better than selfish agents in light or heavy traffic. Only if the traffic falls in an intermediate regime can there be a substantial gap between optimum and equilibrium states.

1.2 Related Work

Much of the literature on congestion games is devoted to the study of bounds for the price of anarchy under different conditions. Roughgarden and Tardos (2002) proved a bound of 4 / 3 in the case of affine costs, independently of the network topology. This bound is sharp in that, for every $M>0$, there exists a network with traffic inflow $M$ and affine costs such that the PoA equal to 4 / 3. Importantly, our analysis shows that the order of the quantifiers cannot be exchanged: in any network as above, the PoA gets arbitrarily close to 1 if the traffic inflow is sufficiently large.

Worst-case PoA bounds have been obtained for larger classes of cost functions. For polynomial costs with degree at most $d$, Roughgarden (2003) showed that the worst possible instance grows as $\varTheta (d/\log d)$. Dumrauf and Gairing (2006) provided sharper bounds for monomials of maximum degree $d$ and minimum degree $q$, while Roughgarden and Tardos (2004) provided a unifying result for costs that are differentiable with $xc(x)$ convex, while Correa et al. (2004; 2008) considered less regular classes of cost functions. For a survey, the reader is referred to Roughgarden (2007).

The difference between the mean value of the price of anarchy and its worst value has been studied in the context of cognitive radio networks by Law et al. (2012). Youn et al. (2008) studied the difference between optimal and actual system performance in real transportation networks, focusing in particular on Boston’s road network. They observed that the price of anarchy depends crucially on the total traffic inflow: it starts at 1, it then grows with some oscillations, and ultimately returns to 1 as the flow increases. González Vayá et al. (2015) studied optimal scheduling for the electricity demand of a fleet of plug-in electric vehicles: without using the term, they showed that the PoA goes to 1 as the number of vehicles grows. Cole and Tao (2016) showed that in large Walrasian auctions and in large Fisher markets the price of anarchy goes to one as the market size increases. Finally, Feldman et al. (2016) took a different asymptotic approach and considered atomic games where the number of players grows to infinity. Applying the notion of $(\lambda ,\mu )$-smoothness to the resulting sequence of atomic games, they showed that the price of anarchy converges to the corresponding nonatomic limit.

From an analytic standpoint, the closest antecedent to our paper is the recent work of Colini-Baldeschi et al. (2016) who studied the heavy-traffic limit of the price of anarchy in paralell-link networks with a single O/D pair. The analysis of Colini-Baldeschi et al. (2016) identified that regular variation plays an important part in heavy traffic; however, it offered no insights into the light traffic regime or the heavy-traffic limit of the PoA in non-parallel networks with more than one O/D pair. Our paper provides an in-depth answer to these questions: we show that (a) the light-traffic analogue of regular variation is real analyticity; (b) the topology of the network doesn’t matter; and (c) the advent of several O/D pairs doesn’t matter as long as they admit a common benchmark (which is always the case if the network’s costs are polynomial).

Finally, on the empirical side, our work should be compared to that of Monnot et al. (2017) who performed an empirical study of the price of anarchy based on data from thousands of commuting students in Singapore. Focusing on the network’s empirical price of anarchy (a PoA majorant), they showed that routing choices are near-optimal and the price of anarchy is much lower than traditional worst-case bounds would suggest. Interestingly, the study of Monnot et al. (2017) also suggests that the Singapore road network is often lightly congested: as such, their results can be seen as a practical validation of the light traffic results presented here (and, conversely, our results provide a theoretical justification for their empirical observations).

2 Model and Preliminaries

2.1 Network Model

Following Beckmann et al. (1956) and Roughgarden and Tardos (2002), the basic component of our model is a finite directed multi-graph $\mathcal {G}\equiv \mathcal {G}(\mathcal {V},\mathcal {E})$ with vertex set $\mathcal {V}$ and edge set $\mathcal {E}$. We further assume there is a finite set of origin-destination(O/D) pairs $i\in \mathcal {I}$, each with an individual traffic demand $m^{i}\ge 0$ which has to be routed from an origin $o^{i}\in \mathcal {V}$ to a destination $d^{i}\in \mathcal {V}$ via $\mathcal {G}$.

To route this traffic, the $i$-th O/D pair employs a set $\mathcal {P}^{i}$ of (simple) paths joining $o^{i}$ to $d^{i}$, each path $p^{}\in \mathcal {P}^{i}$ comprising a sequence of edges that meet head-to-tail in the usual way.³ For bookkeeping reasons, we also make the standing assumption that (a) $M\equiv \sum _{i} m^{i} > 0$ (so there is a positive amount of traffic in the network); and (b) the sets $\mathcal {P}^{i}$ are disjoint (which holds in particular when all pairs $(o^{i},d^{i})$ are different). Then, writing $\mathcal {P}\equiv \bigcup _{i\in \mathcal {I}} \mathcal {P}^{i}$ for the union of all such paths, the set of feasible routing flows $f= (f_{p})_{p\in \mathcal {P}}$ in the network is defined as

(2.1)

In turn, a routing flow $f\in \mathcal {F}$ induces a load on each edge $e\in \mathcal {E}$ as $x_{e}= \sum _{p\ni e} f_{p},$ and we write $x= (x_{e})_{e\in \mathcal {E}}$ for the corresponding load profile on the network.

Given all this, the delay (or latency) experienced by an infinitesimal traffic element in order to traverse edge $e$ is determined by a nondecreasing, nonzero continuous cost function $c_{e}:[0,\infty )\rightarrow [0,\infty )$. Specifically, if $x= (x_{e})_{e\in \mathcal {E}}$ is the load profile induced by a feasible routing flow $f= (f_{p})_{p\in \mathcal {P}}$, then the incurred delay on edge $e\in \mathcal {E}$ is $c_{e}(x_{e})$. Hence, with a slight abuse of notation, the associated cost of path $p\in \mathcal {P}$ is given by

$$\begin{aligned} c_{p}(f) \equiv \sum _{e\in p} c_{e}(x_{e}). \end{aligned}$$

(2.2)

Putting together all of the above, the tuple $\varGamma = (\mathcal {G},\mathcal {I},\{m^{i}\}_{i\in \mathcal {I}},\{\mathcal {P}^{i}\}_{i\in \mathcal {I}},\{c_{e}\}_{e\in \mathcal {E}})$ will be referred to as a (nonatomic) routing game.⁴

2.2 Equilibrium, Optimality, and the Price of Anarchy

In this setting, the notion of Nash equilibrium is captured by Wardrop’s first principle: at equilibrium, the delays along all utilized paths are equal and no higher than those that would be experienced by an infinitesimal traffic element going through an unused route (Wardrop 1952). Formally, a routing flow $f^{*}$ is said to be a Wardrop equilibrium (WE) of $\varGamma$ if, for all $i\in \mathcal {I}$, we have

$$\begin{aligned} c_{p}(f^{*})\le c_{p'}(f^{*}) \quad \text {for all}\,\,p,p'\in \mathcal {P}^{i}\,\mathrm{such} \,\,\mathrm{that}\,\, f^{*}_{p}>0. \end{aligned}$$

(2.3)

By the work of Beckmann et al. (1956), it is well-known that Wardrop equilibrium can be characterized equivalently as solutions of the (convex) minimization problem:

where $C_{e}(x_{e}) = \int _{0}^{x_{e}} c_{e}(w) \,dw$ denotes the primitive of $c_{e}$. On the other hand, a socially optimum (SO) flow is defined as a solution to the total cost minimization problem:

To quantify the gap between solutions to (WE) and (SO), we write

$$\begin{aligned} \text {Eq}(\varGamma ) = L(f^{*}) \quad \text {and} \quad \text {Opt}(\varGamma ) = \textstyle \min _{f\in \mathcal {F}} L(f), \end{aligned}$$

(2.4)

where $f^{*}$ is a Wardrop equilibrium of $\varGamma$. As Beckmann et al. (1956) showed, $L(f^{*})$ has the same value for all equilibria $f^{*}$. The game’s price of anarchy (PoA) is then defined as

$$\begin{aligned} {{\mathrm{PoA}}}(\varGamma ) = \frac{\text {Eq}(\varGamma )}{\text {Opt}(\varGamma )}. \end{aligned}$$

(2.5)

Obviously, ${{\mathrm{PoA}}}(\varGamma ) \ge 1$ with equality if and only if Wardrop equilibria are also socially efficient. Our main objective in what follows will be to study the asymptotics of this ratio when $M\rightarrow 0$ or $M\rightarrow \infty$.

3 A Network Where Selfish Routing is Always Inefficient

We begin by constructing a three-link network where the price of anarchy oscillates between two values strictly greater than 1, no matter the traffic inflow $M$. To that end, let $\varGamma _{M}$ be a nonatomic routing game consisting of a single O/D pair with traffic inflow $M$. This traffic is to be routed over the three-link parallel graph of Fig. 1 with cost functions

$$\begin{aligned} c_{1}(x_{1}) = x_{1}^{d} \, {\Big [1 + \tfrac{1}{2} \sin (\log x_{1})\Big ]},\end{aligned}$$

(3.1a)

$$\begin{aligned} c_{2}(x_{2}) = x_{2}^{d}, \qquad \qquad \qquad \qquad \end{aligned}$$

(3.1b)

$$\begin{aligned} c_{3}(x_{3}) = x_{3}^{d} \, {\Big [1 + \tfrac{1}{2} \cos (\log x_{3})\Big ]}, \end{aligned}$$

(3.1c)

where $d$ is an integer. It is easy to see that the cost functions (3.1) are convex and differentiable on $[0,\infty )$ for all $d\ge 2$. Furthermore, the functions $x_{e} c_{e}(x_{e})$ are strictly convex, so the problem (SO) admits a unique optimum traffic distribution. Hence, the only way for the game’s price of anarchy to be equal to 1 is if the game’s (also unique) Wardrop equilibrium coincides with the network’s socially optimum flow.

For a given value of the total inflow $M= x_{1} + x_{2} + x_{3}$, the load profile $x= (x_{1},x_{2},x_{3})$ is a Wardrop equilibrium if and only if $c_{1}(x_{1}) = c_{2}(x_{2}) = c_{3}(x_{3})$,⁵ i.e., if the normalized profile $z= x/M$ satisfies

$$\begin{aligned} z_{1}^{d} {\Big [1 + \tfrac{1}{2} \sin (\log Mz_{1})\Big ]} = z_{2}^{d} = z_{3}^{d} \, {\Big [1 + \tfrac{1}{2} \cos (\log Mz_{3})\Big ]}. \end{aligned}$$

(3.2)

Likewise, after differentiating and rearranging, the corresponding conditions for the network’s socially optimum flow are

$$\begin{aligned} z_{1}^{d} {\Big [1 + \tfrac{1}{2} \sin (\log Mz_{1}) + \tfrac{1}{2(d+1)} \cos (\log Mz_{1})\Big ]}\qquad \qquad \qquad \quad \quad \quad \nonumber \\ = z_{2}^{d} = z_{3}^{d} \, {\Big [1 + \tfrac{1}{2} \cos (\log Mz_{3}) - \tfrac{1}{2(d+1)} \sin (\log Mz_{3})\Big ]}. \end{aligned}$$

(3.3)

A simple algebraic argument shows that Eqs. 3.2 and 3.3 never admit a common solution; since Eqs. 3.2 and 3.3 are periodic in $\log M$, it also follows that the game’s price of anarchy oscillates periodically at a logarithmic scale. Thus, focusing on the period $1\le M\le e^{2\pi }$, we conclude that

$$\begin{aligned} \inf _{M\ge 0} {{\mathrm{PoA}}}(\varGamma _{M}) = \min _{1 \le M\le e^{2\pi }} {{\mathrm{PoA}}}(\varGamma _{M}) > 1, \end{aligned}$$

(3.4)

i.e., Wardrop equilibrium in the network of Fig. 1 remain strictly inefficient no matter the value of $M$.

4 Networks with a Single O/D Pair

The example of the previous section shows that the price of anarchy may be bounded away from 1 for all values of the traffic inflow, even in a three-link parallel network with a single O/D pair. That being said, the behavior of the cost model (3.1) at both ends of the congestion spectrum is fairly irregular, so the question remains: is selfish routing bad under light/heavy traffic for more “reasonable” classes of cost functions?

4.1 The Light Traffic Limit

A key observation regarding the counterexample (3.1) is that the “topologist’s trig” terms $\sin (\log x)$ and $\cos (\log x)$ are highly pathological: their oscillations become dense near 0, so the corresponding cost functions do not admit derivatives of all orders at 0. To exclude such singularities, we will instead focus on functions that are smooth enough to admit a faithful Taylor expansion at 0:

Definition 1

A function is called (real) analytic at $x_{0}$ if there exists an open neighborhood U of $x_{0}$ and real numbers $g_{k}$, $k=0,1,\cdots$, such that

$$\begin{aligned} g(x) = \sum _{k=0}^{\infty } g_{k} \, (x - x_{0})^{k} \quad \text {for all } x \in U. \end{aligned}$$

(4.1)

All polynomials are analytic, as are exponential, trigonometric, and most special functions (like the gamma function). Remarkably, under this mild regularity requirement, we have the following general result for lightly congested networks with a single O/D pair:

Theorem 1

Let $\varGamma _{M}$ be a nonatomic routing game with a single O/D pair and traffic inflow $M$. If the network’s cost functions are analytic, we have

$$\begin{aligned} \lim _{M\rightarrow 0^{+}} {{\mathrm{PoA}}}(\varGamma _{M}) = 1. \end{aligned}$$

(4.2)

Despite appearances, Theorem 1 is fairly surprising. Indeed, at first sight, one would expect that when $M\rightarrow 0$, traffic is so light that it doesn’t really matter how it is routed. This is indeed the case if, for instance, all paths in the network exhibit a positive cost for $M=0$. However, if the cost of an empty path is zero, this is no longer the case: the optimum and equilibrium assignments could be fairly different (even for low traffic), so there is no a priori reason that the price of anarchy should converge to 1 as $M\rightarrow 0$ (the example of Sect. 3 clearly illustrates this phenomenon). Theorem 1 shows that all that is needed for this to occur is for the network’s cost functions to be faithfully represented by their Taylor series. When this regularity condition is met, optimum and equilibrium costs no longer fluctuate but, instead, they converge to the same value.

4.2 The Heavy Traffic Limit

In the heavy traffic limit, Taylor expansions are no longer meaningful so we require a different criterion to rule out pathological oscillations. We do so by means of the notion of regular variation:

Definition 2

A function $g:[0,\infty ) \rightarrow (0,\infty )$ is said to be regularly varying if

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{g(tx)}{g(t)}\quad \text {is finite and nonzero for all }x\ge 0. \end{aligned}$$

(4.3)

In words, regular variation means that $g(x)$ grows at the same rate when viewed at different scales. Standard examples of regularly varying functions include all affine, polynomial and (poly) logarithmic functions. The concept itself dates back to Karamata (1933) and has been used extensively in probability and large deviations theory (see e.g. de Haan and Ferreira, 2006; Jessen and Mikosch, 2006; Resnick, 2007); for a comprehensive survey, the reader is referred to Bingham et al. (1989).

With all this at hand, we will discard growth irregularities (such as those observed in Sect. 3) by positing that each cost function $c_{e}(x)$ can be compared asymptotically to some regularly varying function $c(x)$. Specifically, given an ensemble of cost functions $\mathcal {C}= \{c_{e}\}_{e\in \mathcal {E}}$, we say that a regularly varying function $c:[0,\infty )\rightarrow (0,\infty )$ is a benchmark for $\mathcal {C}$ if the (possibly infinite) limit

$$\begin{aligned} \alpha _{e} = \lim _{x\rightarrow \infty } \frac{c_{e}(x)}{c(x)} \end{aligned}$$

(4.4)

exists for all $e\in \mathcal {E}$.

When it exists, this limit will be called the index of edge $e$, and $e$ will be called fast, slow, or tight (relative to $c$) if $\alpha _{e}$ is respectively 0, $\infty$, or in-between. Since bottlenecks in a path are caused by the slowest edges, we also define the index of a path $p\in \mathcal {P}$ as

$$\begin{aligned} \alpha _{p} = \max _{e\in p} \alpha _{e}, \end{aligned}$$

(4.5)

and we say that $p$ is fast, slow, or tight based on whether $\alpha _{p}$ is 0, $\infty$, or in-between. Finally, we say that the network is tight if the index of the network

$$\begin{aligned} \alpha =\min _{p\in \mathcal {P}} \alpha _{p} \end{aligned}$$

(4.6)

is finite and positive ($0<\alpha <\infty$).

In words, a path is fast (resp. tight/slow) if its slowest edge is fast (resp. tight/slow), and the network is tight if its fastest path is tight. In particular, tightness guarantees that the network admits a path whose cost grows asymptotically as a multiple of some regularly varying benchmark function $c(x)$. The importance of this growth requirement is illustrated by the counterexample of Sect. 3: if we slightly relax the tightness concept by asking that the network admits a path whose cost grows as $\varTheta (c(x))$, the price of anarchy may be bounded away from 1 for all values of $M$. Instead, under tightness, we have:

Theorem 2

Let $\varGamma _{M}$ be a nonatomic routing game with a single O/D pair and traffic inflow $M$. If the network is tight, then

$$\begin{aligned} \lim _{M\rightarrow \infty } {{\mathrm{PoA}}}(\varGamma _{M}) = 1. \end{aligned}$$

(4.7)

In other words, if the fastest path in the network is tight, selfish routing becomes efficient in the high congestion limit.

As an immediate corollary, we then have:

Corollary 1

In networks with polynomial costs and a single O/D pair, we have ${{\mathrm{PoA}}}(\varGamma _{M})\rightarrow 1$ as $M\rightarrow \infty$.

Proof

Let $d_{e}$ be the degree of $c_{e}$, set $d_{p} = \max _{e\in p}d_{e}$, and let $d= \min _{p\in \mathcal {P}} d_{p}$. The network is clearly tight with respect to $c(x) = x^{d}$, so Theorem 2 applies.    $\blacksquare$

Combining Theorem 1 and Corollary 1, we conclude that selfish routing becomes efficient under both light and heavy traffic in networks with polynomial costs. Beyond the polynomial case, Theorems 1 and 2 show that analyticity and regular variation can be seen as different sides of the same coin: they both ensure asymptotic regularity and they both exclude pathological oscillations (at zero and infinity respectively). As such, our results for light and heavy traffic are chiefly set apart by the notion of tightness (which only applies for heavy traffic). The reason for this qualitative difference is that costs might diverge to infinity at very different rates when the traffic inflow grows large; by contrast, all costs are finite when there is no traffic, so the notion of tightness is redundant then.

5 Networks with Multiple O/D Pairs

We now extend our analysis to networks with multiple O/D pairs. In this case, the total traffic inflow in the network is given by $M= \sum _{i\in \mathcal {I}} m^{i}$ and we write

$$\begin{aligned} \lambda ^{i} = \frac{m^{i}}{M} \end{aligned}$$

(5.1)

for the fraction of the traffic generated by the $i$-th O/D pair. In what follows, we will be assuming that the relative traffic inflow $\lambda ^{i}$ of every O/D pair $i\in \mathcal {I}$ is a fixed positive constant. At the cost of heavier notation, our analysis also extends to variable $\lambda ^{i} \equiv \lambda ^{i}(M)$ but, due to space constraints, we focus on this setting for clarity and concision.

5.1 The Light Traffic Limit

As in the previous section, we begin with the low congestion regime. Here, our main result is essentially the same as in networks with a single O/D pair:

Theorem 3

Let $\varGamma _{M}$ be a nonatomic routing game with total traffic inflow $M$. If the network’s cost functions are analytic, we have

$$\begin{aligned} \lim _{M\rightarrow 0^{+}} {{\mathrm{PoA}}}(\varGamma _{M}) = 1. \end{aligned}$$

(5.2)

In words, the advent of several O/D pairs does not change the asymptotic behavior of the price of anarchy at the light traffic limit: Theorem 3 is a direct extension of Theorem 1 (which it implies).

5.2 The Heavy Traffic Limit

In the high congestion regime, tightness plays a crucial role, but its definition must be re-examined in the presence of multiple O/D pairs. In particular, the cost of routing for different O/D pairs might grow at completely different rates as $M\rightarrow \infty$, so the definition of the network’s index must take this into account. To make this precise, we define the index of a pair $i\in \mathcal {I}$ as

$$\begin{aligned} \alpha ^{i} = \min _{p\in \mathcal {P}^{i}} \alpha _{p}, \end{aligned}$$

(5.3)

reflecting the fact that the traffic of a given O/D pair will tend to be routed along the pair’s fastest available path. The network’s index is then defined as

$$\begin{aligned} \alpha = \max _{i\in \mathcal {I}} \alpha ^{i}, \end{aligned}$$

(5.4)

and, as before, we say that the network is tight if $0<\alpha <\infty$. With all this at hand, our main result for highly congested networks is as follows:

Theorem 4

Let $\varGamma _{M}$ be a nonatomic routing game with total inflow $M$. If the network is tight, then

$$\begin{aligned} \lim _{M\rightarrow \infty } {{\mathrm{PoA}}}(\varGamma _{M}) = 1. \end{aligned}$$

(5.5)

In words, if the “most costly” O/D pair in the network admits a tight path, selfish routing becomes efficient in the high congestion limit.

Note that Theorem 2 follows directly from Theorem 4 because the definitions (4.6) and (5.4) coincide if $\mathcal {I}$ is a singleton. However, in contrast to the light traffic regime (where the presence of multiple O/D pairs does not change the result), there is more going on in the high congestion limit. Specifically, when there are multiple O/D pairs in the network, Theorem 4 posits that every O/D pair must have a path which is not slow, and at least one of the O/D pairs must be tight (i.e., its index must be finite and positive). This is a considerably lighter requirement than asking that every O/D pair be tight, so the conditions under which the price of anarchy converges to 1 are very lax in this regard.

We close this section with an immediate corollary of Theorem 4

Corollary 2

In networks with polynomial costs, $\lim _{M\rightarrow \infty } {{\mathrm{PoA}}}(\varGamma _{M}) = 1$.

Proof

Let $d_{e}$ be the degree of $c_{e}$, set $d_{p} = \max _{e\in p}d_{e}$, $d^{i}= \min _{p\in \mathcal {P}^{i}} d_{p}$ and $d= \max _{p\in \mathcal {P}} d_{p}$. Then, simply verify that the network is tight with respect to the benchmark function $c(x) = x^{d}$.    $\blacksquare$

Thus, by Theorem 3 and Corollary 2, we conclude that:

In networks with polynomial cost functions,

the price of anarchy becomes 1 under both light and heavy traffic.

6 Discussion

Our goal in this paper was to assess when selfish routing becomes efficient by examining the behavior of the price of anarchy at each end of the congestion spectrum. Under fairly mild assumptions (that always include networks with polynomial costs), we found that the price of anarchy goes to 1 in both cases, independently of the network’s topology and the number of O/D pairs in the network. What we find intriguing about this result is that it suggests that selfishness is not the real cause of increased delays under heavy traffic: from a social planner’s point of view, sophisticated tolling/rerouting schemes that target the optimum traffic assignment will not yield considerable gains over a “laissez-faire” approach where each traffic element takes the fastest available path.