Maintaining Connectivity in Sensor Networks Using Directional Antennae

Abstract

Connectivity in wireless sensor networks may be established using either omnidirectional or directional antennae. The former radiate power uniformly in all directions while the latter emit greater power in a specified direction thus achieving increased transmission range and encountering reduced interference from unwanted sources. Regardless of the type of antenna being used the transmission cost of each antenna is proportional to the coverage area of the antenna. It is of interest to design efficient algorithms that minimize the overall transmission cost while at the same time maintaining network connectivity. Consider a set S of n points in the plane modeling sensors of an ad hoc network. Each sensor is equipped with a fixed number of directional antennae modeled as a circular sector with a given spread (or angle) and range (or radius). Construct a network with the sensors as the nodes and with directed edges (u,v) connecting sensors u and v if v lies within u’s sector. We survey recent algorithms and study trade-offs on the maximum angle, sum of angles, maximum range, and the number of antennae per sensor for the problem of establishing strongly connected networks of sensors.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Connectivity in wireless sensor networks is established using either omnidirectional or directional antennae. The former transmit signals in all directions while the latter within a limited predefined angle. Directional antennae can be more efficient and transmit further in a given direction for the same amount of energy than omnidirectional ones. This is due to the fact that to a first approximation the energy transmission cost of an antenna is proportional to its coverage area. To be more specific, the coverage area of an omnidirectional antenna with range r is generally modeled by a circle of radius r and consumes energy proportional to $\pi \cdot r^2$. By contrast, a directional antennae with angular spread ϕ and range R is modeled as a circular sector of angle ϕ and radius R and consumes energy proportional to $\varphi \cdot R^2 / 2$. Thus for a given energy cost E, an omnidirectional antenna can reach distance $\sqrt{E/\pi}$, while a directional antenna with angular spread ϕ can reach distance $\sqrt{2E/\varphi}$. We think of the directional antennae as being on a “swivel” that can be oriented toward a small target area whereas the omnidirectional antennae spread their signal in all directions. Signals arriving at a sensor within the target area of multiple antennae will interfere and degrade reception. Thus for reasons of both energy efficiency and potentially reduced interference (as well as others, e.g., security), it is tempting to replace omnidirectional with directional antennae.

Replacing omnidirectional with directional antennae: Given a set of sensors positioned in the plane with omnidirectional and/or directional antennae, a directed network is formed as follows: a directed edge is placed from sensor u to sensor v if v lies within the coverage area of u (as modeled by circles or circular sectors). Note that if the radius of all omnidirectional antennae is the same then u is in the range of v if and only if v is in the range of u, i.e., the edge is bidirectional and is usually modeled be an undirected edge.

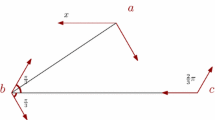
The main issue of concern when replacing omnidirectional with directional antennae is that this may alter important characteristics such as the degree, diameter, average path length of the resulting network. For example, the first network in Figure 3.2 is strongly connected with diameter two, and more than one node can potentially transmit at the same time without interference while in the omnidirectional case (Fig. 3.1) the diameter is one but only one antennae can transmit at a time without interference. In addition, and depending on the breadth and range of the directional antennae, the original topology depicted in Fig. 3.1 can be obtained only by using more than one directional antenna per sensor (see Fig. 3.3).

Fig. 3.1

Four sensors using directional antennae. For the same set of points, the resulting directed graphs depend on the antennae orientations

Fig. 3.2

Four sensors using omnidirectional antennae. They form an underlying complete network on four nodes

Fig. 3.4

Four sensors using directional antennae. Using three directional antennae per sensor in order to form an underlying complete network on four nodes

Replacing omnidirectional with directional antennae enables the sensors to reach farther using the same energy consumption. As an example consider the graphs depicted in Figs. 3.4 and 3.5. The line graph network in Fig. 3.4 with undirected edges $\{1,2\}, \{2,3\}, \{3, 4\}$ is replaced by a network of directional antennae depicted in Fig. 3.5 and having $(1,2), (1,3), (2,3), (2, 4), (3, 4), (4, 3) , (4, 2), (3, 2), (3, 1)$ as directed edges. By setting the angular spread of the directional antennae to be small a significant savings in energy are possible.

Fig. 3.4

Line graph network with undirected edges $\{1,2\}, \{2,3\}, \{3, 4\}$ resulting when four sensors 1, 2, 3, 4 use omnidirectional antennae

Fig. 3.5

Directed network resulting from Fig. 3.4 when the four sensors replace omnidirectional with directional antennae. Sensor number 3 is using two directional antennae while the rest only one

1.1 Antenna Orientation Problem

The above considerations lead to numerous questions concerning trade-offs between various factors, such as connectivity, diameter, interference, when using directional versus omnidirectional antennae in constructing sensor networks. Here we study how to maintain network connectivity when antennae angles are being reduced while at the same time the transmission range of the sensors is being kept as low as possible. More formally this raises the following optimization problem.

Consider a set S of n points in the plane that can be identified with sensors having a range $r>0$. For a given angle $0 \leq \varphi \leq 2 \pi$ and integer k, each sensor is allowed to use at most k directional antennae each of angle at most ϕ. Determine the minimum range r required so that by appropriately rotating the antennae, a directed, strongly connected network on S is formed.

Note that the range of a sensor must be at least the length of the longest edge of a minimum spanning tree on the set S, since this is the smallest range required just to attain connectivity.

1.2 Preliminaries and Notation

Consider a set S of n points in the plane and an integer $k \geq 1$. We give the following definitions.

Definition 1

$r_k (S, \varphi)$ is the minimum range of directed antennae of angular spread at most ϕ so that if every sensor in S uses at most k such antennae (under an appropriate rotation) a strongly connected network on S results.

A special case is when $\varphi = 0$, for which we use the simpler notation $r_k (S)$ instead of $r_k (S, 0)$. Clearly, different directed graphs can be produced depending on the range and direction of the directional antennae. This gives rise to the following definition.

Definition 2

Let ${\cal D}_k (S)$ be the set of all strongly connected graphs on S with out-degree at most k.

For any graph $G \in {\cal D}_k (S)$, let $r_k (G)$ be the maximum length of an edge in G. It is easy to see that $r_k (S) : = \min_{G \in {\cal D}_k (S)} r_k (G)$. It is useful to relate $r_k(S)$ to another quantity which arises from a minimum spanning tree (MST) on S.

Definition 3

Let MST (S) denote the set of all MSTs on S.

Definition 4

For $T \in \textrm{MST} (S)$ let $r(T)$ denote the length of longest edge of T and let $r_{\mathrm{MST}}(S) = \min \{ r(T) : T \in \mathrm{MST} (S)\}.$

For a set S of size n, it is easily seen that $r_{\mathrm{MST}}(S)$ can be computed in $O(n^2)$ time. Further, for any angle $\varphi \geq 0$, it is clear that $r_{\mathrm{MST}}(S) \leq r_k (S, \varphi )$ since every strongly connected, directed graph on S has an underlying spanning tree.

1.3 Related Work

When each sensor has one antenna and the angle $\varphi = 0$ then our problem is easily seen to be equivalent to finding a Hamiltonian cycle that minimizes the maximum length of an edge. This is the well-known bottleneck traveling salesman problem.

1.3.1 Bottleneck Traveling Salesman Problem

Let $1,2,\ldots,n$ be a set of n labeled vertices with associated edge weights $w(i,j)$, for all i, j. The bottleneck traveling salesman problem (BTSP) asks to find a Hamiltonian cycle in the complete (weighted) graph on the n points which minimizes the maximum weight of an edge, i.e.,

$$\min \{ \max_{(i,j) \in H} w(i,j): \hbox{<Emphasis Type="Italic">H</Emphasis> is a Hamiltonian cycle\}}$$

Parker and Rardin [31] study the case where the weights satisfy the triangle inequality and they give a two-approximation algorithm for this problem. (They also show that no polynomial time $(2 -\varepsilon)$-approximation algorithm is possible for metric BTSP unless $P=NP$.) Clearly, their approximation result applies to our problem for the special case of one antennae and $\varphi =0$. The proof uses a result in [12] that the square of every two-connected graph is Hamiltonian. (The square $G^{(2)}$ of a graph $G = (V,E)$ has the same node set V and edge set $E^{(2)}$ defined by $\{ u,v\} \in E^{(2)} \Leftrightarrow \exists w \in V (\{u,w\} \in E \& \{w,v\} \in E)$.) In fact the latter paper also gives an algorithm for constructing such a Hamiltonian cycle. A generalization of this problem to finding strongly connected subgraphs with minimum maximum edge weight is studied by Punnen [32].

1.3.2 MST and Out-Degrees of Nodes

It is easy to see that the degree structure of an MST on a point set is constrained by proximity. If a vertex has many neighbors then some of them have to be too close together and can thus be connected directly. This can be used to show that for a given point set there is always a Euclidean minimum spanning tree of maximum degree six. In turn, this can be improved further to provide an MST with max degree five [28]. Since for large enough r every set of sensors in the plane has a Euclidean spanning tree of degree at most five and maximum range r, it is easy to see that given such minimum r and $k \geq 5, r_k (S)=r$. A useful parameter is the maximum degree of a spanning tree. This gives rise to the following definition.

Definition 5

For $k \geq 2$, a maximum degree k spanning tree (abbreviated $Dk-ST$) is a spanning tree all of whose vertices have degree at most k.

Related literature concerns trade-offs between maximum degree and minimum weight of the spanning tree. For example, [2] gives a quasi-polynomial time approximation scheme for the minimum weight Euclidean $D3-ST$. Similarly, [21] and [6] obtain approximations for minimum weight $D3-ST$ and $D4-ST$. In addition, [13] shows that it is an NP-hard problem to decide for a given set S of n points in the Euclidean plane and a given real parameter w, whether S admits a spanning tree of maximum node degree four (i.e., $D4-ST$) whose sum of edge lengths does not exceed w. Related is also [22] which gives a simple algorithm to find a spanning tree that simultaneously approximates a shortest path tree and a minimum spanning tree. In particular, given the two trees and a $\gamma > 0$, the algorithm returns a spanning tree in which the distance between any node and the root is at most $1 + \gamma \sqrt{2}$ times the shortest path distance, and the total weight of the tree is at most $1 + \sqrt{2} / \gamma$ times the weight of a minimum spanning tree.

Of interest here is the connection between strongly connected geometric spanners with given out-degree on a point set and the maximum length edge of an MST. Beyond the connection of BTSP mentioned above we know of no other related literature on this specific question.

1.3.3 Enhancing Network Performance Using Directional Antennae

Directional antennae are known to enhance ad hoc network capacity and performance and when replacing omnidirectional with directional antennae one can reduce the total energy consumption of the network. A theoretical model to this effect is presented in [16] showing that when n omnidirectional antennae are optimally placed and assigned optimally chosen traffic patterns the transport capacity is $\varTheta \left(\sqrt{W/n}\right)$, where each antenna can transmit W bits per second over the common channel(s). When both transmission and reception are directional, [39] proves an $\sqrt{2\pi /\alpha \beta}$ capacity gain as well as corresponding throughput improvement factors, where α is the transmission angle and β is a parameter indicating that $\beta/2 \pi$ is the average proportion of the number of receivers inside the transmission zone that will get interfered with.

Additional experimental studies confirm the importance of using directional antennae in ad hoc networking for enhancing channel capacity and improving multiaccess control. For example, research in [33] considers several enhancements, including “aggressive” and “conservative” channel access models for directional antennae, link power control, and neighbor discovery and analyzes them via simulation. [38] and [37] consider how independent communications between directional antennae can occur in parallel and calculate interference-based capacity bounds for a generic antenna model as well as a real-world antenna model and analyze how these bounds are affected by important antenna parameters like gain and angle. The authors of [3] propose a distributed receiver-oriented multiple access (ROMA) channel access scheduling protocol for ad hoc networks with directional antennae, each of which can form multiple beams and commence several simultaneous communication sessions. Finally, [24] considers energy consumption thresholds in conjunction to k-connectivity in networks of sensors with omnidirectional and directional antennae, while [23] studies how directional antennae affect overall coverage and connectivity.

A related problem that has been addressed in the literature is one that studies connectivity requirements on undirected graphs that will guarantee highest edge connectivity of its orientation, c.f. [29] and [14].

1.3.4 Other Applications

It is interesting to note that beyond reducing the energy consumption, directional antennae can enhance security. Unlike omnidirectional antennae that spread their signal in all directions over an angle 2π, directional antennae can attain better security because they direct their beam toward the target thus avoiding potential risks along the transmission path. In particular, in a hostile environment a directional antenna can decrease the radiation region within which nodes could receive the electromagnetic signals with high quality. For example, this has led [17] to the design of several authentication protocols based on directional antennae. In [27] they employ the average probability of detection to estimate the overall security benefit level of directional transmission over the omnidirectional one. In [18] they examine the possibility of key agreement using variable directional antennae. In [30] the use of directional antennae and beam steering techniques in order to improve performance of 802.11 links is investigated in the context of communication between a moving vehicle and roadside access points.

1.4 Outline of the Presentation

The following is an outline of the main issues that will be addressed in this survey. In Sect. 3.2 we discuss approximation algorithms to the main problem introduced above. The constructions are mainly based on an appropriately defined MST of the set of points. Section 3.2.1 focuses on the case of a single antenna per sensor while Sect. 3.2.2 on k antennae per sensor, for a given $2 \leq k \leq 4$. (Note that the case $k \geq 5$ is handled by using a degree five MST.) In Sect. 3.3 we discuss NP-completeness results for the cases of one and two antennae. In Sect. 3.4 we investigate a variant of the main problem whereby we want to minimize the sum of the angles of the antennae given a bound on their radius. Unlike Sect. 3.2 where we have the flexibility to select and adapt an MST on the given point set S, Sect. 3.5 considers the case whereby the underlying network is given in advance as a planar spanner on the set S and we study number of antennae and stretch factor trade-offs between the original graph and the resulting planar spanner. In addition throughout the chapter we propose several open problems and discuss related questions of interest.

2 Orienting the Sensors of a Point Set

In this section we consider several algorithms for orienting antennae so that the resulting spanner is strongly connected. Moreover we look at trade-offs between antenna range and breadth.

2.1 Sensors with One Antenna

The first paper to address the problem of converting a connected (undirected) graph resulting from omnidirectional sensors to a strongly connected graph of directional sensors having only one directional antenna each was [5].

2.1.1 Sensors on the Line

The first scenario to be considered is for sensors on a line. Assume that each sensor’s directional antenna has angle ϕ. Further assume that $\varphi \geq \pi$. The problem of minimizing the range in this case can be seen to be equivalent to the same problem for the omnidirectional case, simply by pointing the antennae so as to cover the same nodes as those covered by the omnidirectional antenna as depicted in Fig. 3.6. Clearly a range equal to the maximum distance between any pair of adjacent sensors is necessary and sufficient.

Fig. 3.6

Antenna orientation for a set of sensors on a line when the angle $\boldsymbol\varphi \geq \boldsymbol\pi$

When the angle ϕ of the antennae is less than π then a slightly more complicated orientation of the antennae is required so as to achieve strong connectivity with minimum range.

Theorem 1 ([5])

Consider a set of $n>2$ points $x_i, i=1,2,\ldots ,n$, sorted according to their location on the line. For any $\pi > \varphi \geq 0$ and $r > 0$, there exists an orientation of sectors of angle ϕ and radius r at the points so that the transmission graph is strongly connected if and only if the distance between points i and $i+2$ is at most r, for any $i=1,2,\ldots ,n-2$.

Proof

Assume $d(x_i,x_{i+2}) > r$, for some $i \leq n-2$. Consider the antenna at $x_{i+1}$. There are two cases to consider. First, if the antenna at $x_{i+1}$ is directed to the left then the portion of the graph to its left cannot be connected to the portion of the graph to the right; second, if the antenna at $x_{i+1}$ is directed to the right then the portion of the graph to its right cannot be connected to the portion of the graph to the left. In either case the graph becomes disconnected.

Conversely, assume $d(x_i,x_{i+2}) \leq r$, for all $i \leq n-2$. Consider the following antenna orientation for an even number of sensors (see Fig. 3.7). (The odd case is handled similarly.)

• 1. antennas $x_1, x_3,x_5,\ldots$ labeled with odd integers are oriented right and

• 2. antennas $x_2,x_4,x_6, \ldots$ labeled with even integers are oriented left.

Fig. 3.7

Antenna orientation for a set of sensors on a line when the angle $\boldsymbol\varphi < \boldsymbol\pi$

It is easy to see that the resulting orientation leads to a strongly connected graph. This completes the proof of Theorem 1.

2.1.2 Sensors on the Plane

The case of sensors on the plane is more challenging. As was noted above the case of $\varphi = 0$ is equivalent to the Euclidean BTSP and thus the minimum range can be approximated to within a factor of 2. In [5] the authors present a polynomial time algorithm for the case when the sector angle of the antennae is at least $8\pi/5$. For smaller sector angles, they present algorithms that approximate the minimum radius. We present the proof of this last result below.

Theorem 2 (Caragiannis et al. [5])

Given an angle ϕ with $\pi\leq \varphi< 8\pi/5$ and a set S of points in the plane, there exists a polynomial time algorithm that computes an orientation of sectors of angle ϕ and radius $2\sin{\left(\pi-\frac{\varphi}{2}\right)}\cdot r_1(S,\varphi)$ so that the transmission graph is strongly connected.

Proof

Consider a set S of nodes on the Euclidean plane and let T be a minimum spanning tree of S. Let $r=r_{\mathrm{MST}}(S)$ be the longest edge of T. We will use sectors of angle ϕ and radius $d(\varphi)=2r\sin{\left(\pi-\frac{\varphi}{2}\right)}$ and we will show how to orient them so that the transmission graph induced is a strongly connected subgraph over S. The theorem will then follow since r is a lower bound on $r_1 (S,\varphi)$.

We first construct a matching M consisting of (mutually non-adjacent) edges of T with the following additional property: any non-leaf node of T is adjacent to an edge of M. This can be done as follows. Initially, M is empty. We root T at an arbitrary node s. We pick an edge between s and one of its children and insert it in M. Then, we visit the remaining nodes of T in a BFS (breadth first search) manner. When visiting a node u, if u is either a leaf node or a non-leaf node such that the edge between it and its parent is in M, we do nothing. Otherwise, we pick an edge between u and one of its children and insert it to M.

We denote by Λ the leaves of T which are not adjacent to edges of M. We also say that the endpoints of an edge in M form a couple. We use sectors of angle ϕ and radius $d(\varphi)$ at each point and orient them as follows. At each node $u\in \varLambda$, the sector is oriented so that it induces the directed edge from u to its parent in T in the corresponding transmission graph G. For each two points u and v forming a couple, we orient the sector at u so that it contains all points p at distance $d(\varphi)$ from u for which the counterclockwise angle $\hat{vup}$ is in $[0,\varphi]$, see Fig. 3.8.

Fig. 3.8

The orientation of sectors at two nodes u,v forming a couple, and a neighbor w of u that is not contained in the sector of u. The dashed circles have radius r and denote the range in which the neighbors of u and v lie

We first show that the transmission graph G defined in this way has the following property, denoted by (P), and stated in the Claim below.

Claim (P).

For any two points u and v forming a couple, G contains the two opposite directed edges between u and v, and, for each neighbor w of either u or v in T, it contains a directed edge from either u or v to w.

Consider a point w corresponding to a neighbor of u in T (the argument for the case where w is a neighbor of v is symmetric). Clearly, w is at distance $|uw|\leq r$ from u. Also, note that since $\varphi <8\pi/5$, we have that the radius of the sectors is $d(\varphi)=2r\sin{\left(\pi- \frac{\varphi}{2}\right)}\geq 2r\sin{\frac{\pi}{5}}>2r\sin{\frac{\pi}{6}}=r$. Hence, w is contained in the sector of u if the counterclockwise angle $\hat{vuw}$ is at most ϕ; in this case, the graph G contains a directed edge from u to w. Now, assume that the angle $\hat{vuw}$ is $x>\varphi$ (see Fig. 3.8). By the law of cosines in the triangle defined by points u, v, and w, we have that

$$\begin{array}{lll} |vw| &=& \sqrt{|uw|^2+|uv|^2-2|uw||uv|\cos{x}}\\ &\leq & r\sqrt{2-2\cos{x}}\\ &=& 2r\sin{\frac{x}{2}}\\ &\leq & 2r\sin{\left(\pi-\frac{\varphi}{2}\right)}\\ &=& d(\varphi) \end{array}$$

Since the counterclockwise angle $\hat{vuw}$ is at least π, the counterclockwise angle $\hat{uvw}$ is at most $\pi\leq \varphi$ and, hence, w is contained in the sector of v; in this case, the graph G contains a directed edge from v to w. In order to complete the proof of property (P), observe that since $|uv|\leq r\leq d(\varphi)$ the point v is contained in the sector of u (and vice versa).

Now, in order to complete the proof of the theorem, we will show that for any two neighbors u and v in T, there exist a directed path from u to v and a directed path from v to u in G. Without loss of generality, assume that u is closer to the root s of T than v. If the edge between u and v belongs to M (i.e., u and v form a couple), property (P) guarantees that there exist two opposite directed edges between u and v in the transmission graph G. Otherwise, let w ₁ be the node with which u forms a couple. Since v is a neighbor of u in T, there is either a directed edge from u to v in G or a directed edge from w ₁ to v in G. Then, there is also a directed edge from u to w ₁ in G which means that there exists a directed path from u to v. If v is a leaf (i.e., it belongs to Λ), then its sector is oriented so that it induces a directed edge to its parent u. Otherwise, let w ₂ be the node with which v forms a couple. Since u is a neighbor of v in T, there is either a directed edge from v to u in G or a directed edge from w ₂ to u in G. Then, there is also a directed edge from v to w ₂ in G which means that there exists a directed path from v to u.

2.1.3 Further Questions and Open Problems

In Sect. 3.3 we present a lower bound from [5] that shows this problem is NP-hard for angles smaller than $2\pi/3$. This leaves the complexity of the problem open for angles between $2\pi/3$ and $8\pi/5$. Related problems that deserve investigation include the complexity of gossiping and broadcasting as well as other related communication tasks in this geometric setting.

2.2 Sensors with Multiple Antennae

We are interested in the problem of providing an algorithm for orienting the antennae and ultimately for estimating the value of $r_k (S, \varphi )$. Without loss of generality antennae ranges will be normalized to the length of the longest edge in any MST, i.e., $r_{\mathrm{MST}} (S) = 1$. The main result concerns the case $\varphi = 0$ and was proven in [10]:

Theorem 3 (Dobrev et al. [10])

Consider a set S of n sensors in the plane, and suppose each sensor has k, $1 \leq k \leq 5$, directional antennae. Then the antennae can be oriented at each sensor so that the resulting spanning graph is strongly connected and the range of each antenna is at most $2\cdot\sin\left(\frac{\pi}{k+1} \right)$ times the optimal. Moreover, given an MST on the set of points the spanner can be constructed with additional $O(n)$ overhead.

The proof in [10] considers five cases depending on the number of antennae that can be used by each sensor. As noted in the introduction, the case k = 1 was derived in [31]. The case k = 5 follows easily from the fact that there is an MST with maximum vertex degree five. This leaves the remaining three cases for $k = 2, 3, 4$. Due to space limitations we will not give the complete proof here. Instead we will discuss only the simplest case k = 4.

2.2.1 Preliminary Definitions

Before proceeding with presentation of the main results we introduce some notation which is specific to the following proofs. $D(u;r)$ is the open disk with radius r. d $(\cdot, \cdot)$ denotes the usual Euclidean distance between two points. In addition, we define the concept of Antenna-Tree (A-Tree, for short) which isolates the particular properties of an MST that we need in the course of the proof.

Definition 6

An A-Tree is a tree T embedded in the plane satisfying the following three rules:

• 1. Its maximum degree is five.

• 2. The minimum angle among nodes with a common parent is at least $\pi/3$.

• 3. For any point u and any edge $\{u,v\}$ of T, the open disk $D(v; d(u,v))$ does not have a point $w \not= v$ which is also a neighbor of u in T.

It is well known and easy to prove that for any set of points there is an MST on the set of points which satisfies Definition 6. Recall that we consider normalized ranges (i.e., we assume $r(T)=1$).

Definition 7

For each real $r > 0$, we define the geometric rth power of a A-Tree T, denoted by $T^{(r)}$, as the graph obtained from T by adding all edges between vertices of (Euclidean) distance at most r.

For simplicity, in the sequel we slightly abuse terminology and refer to the geometric rth power as the rth power.

Definition 8

Let G be a graph. An orientation $\overrightarrow{G}$ of G is a digraph obtained from G by orienting every edge of G in at least one direction.

As usual, we denote with $(u,v)$ a directed edge from u to v, whereas $\{u,v\}$ denotes an undirected edge between u and v. Let $d^+ (\overrightarrow{G} ,u)$ be the out-degree of u in $\overrightarrow{G}$ and $\varDelta^+(\overrightarrow{G})$ the maximum out-degree of a vertex in $\overrightarrow{G}$.

2.2.2 Maximum Out-Degree four

In this section we prove that there always exists a subgraph of $T^{(2\sin{\pi/5})}$ that can be oriented in such a way that it is strongly connected and its maximum out-degree is four. A precise statement of the theorem is as follows.

Theorem 4 (Dobrev et al. [10])

Let T be an A-Tree. Then there exists a spanning subgraph $G \subseteq T^{(2\sin{\pi/5})}$ such that $\overrightarrow{G}$ is strongly connected and $\varDelta^+(\overrightarrow{G}) \leq 4$. Moreover, $d^+ (\overrightarrow{G} ,u) \leq 1$ for each leaf u of T and every edge of T incident to a leaf is contained in G.

Proof

We first introduce a definition that we will use in the course of the proof. We say that two consecutive neighbors of a vertex are close if the smaller angle they form with their common vertex is at most $2\pi/5$. Observe that if v and w are close, then $|v,w| \leq 2\sin{\pi/5}$. In all the figures in this section an angular sign with a dot depicts close neighbors. The proof is by induction on the diameter of the tree. First, we do the base case. Let k be the diameter of T. If $k\leq 1$, let $G = T$ and the result follows trivially. If k = 2, then T is an A-Tree which is a star with $2 \leq d\leq 5$ leaves. Two cases can occur:

• $d <5$. Let $G=T$ and orient every edge in both directions. This results in a strongly connected digraph which trivially satisfies the hypothesis of the theorem.

• d = 5. Let u be the center of T. Since T is a star, two consecutive neighbors of u, say, v and w, are close. Let $G=T \cup \{\{v, w\}\}$ and orient edges of G as depicted in Fig. 3.9.¹ It is easy to check that G satisfies the hypothesis of the theorem.

Fig. 3.9

T is a tree with five leaves and diameter k = 2

Next we continue with the inductive step. Let T′ be the tree obtained from T by removing all leaves. Since removal of leaves does not violate the property of being an A-Tree, T′ is also an A-Tree and has diameter less than the diameter of T. Thus, by inductive hypothesis there exists $G' \subseteq T'^{(2\sin{\pi/5})}$ such that $\overrightarrow{G'}$ is strongly connected, $\varDelta^+(\overrightarrow{G'}) \leq 4$. Moreover, $d^+ (\overrightarrow{G} ,u) \leq 1$ for each leaf u of T′ and every edge of T′ incident to a leaf is contained in G′.

Let u be a leaf of T′, u ₀ be the neighbor of u in T′, and $u_1, .., u_c$ be the c neighbors of u in $T\setminus T'$ in clockwise order around u starting from u ₀. Two cases can occur:

• $c \leq 3$. Let $G = G' \cup \{\{u,u_1\},..,\{u,u_c\}\}$ and orient these c edges in both directions. $\overrightarrow{G}$ satisfies the hypothesis since $G \subseteq T^{(2\sin{\pi/5})}$, $\varDelta^+(\overrightarrow{G}) \leq 4$, $d^+ (\overrightarrow{G} ,u) \leq 1$ for each leaf u of T and every edge of T incident to a leaf is contained in G.

• c = 4. We consider two cases. In the first case suppose that two consecutive neighbors of u in $T\setminus T'$ are close. Consider u _k and $u_{k+1}$ are close, where $1\leq k <4$. Define $G = G'\cup \{\{u,u_1\}, \{u,u_2\}, \{u,u_3\}, \{u,u_4\}, \{u_k,u_{k+1}\}\}$ and orient edges of G as depicted in Fig. 3.10. In the second case, either u ₀ and u ₁ are close or u ₀ and u ₄ are close. Without loss of generality, let assume that u ₀ and u ₁ are close. Thus, let $G = \{G' \setminus \{u,u_0\}\} \cup \{\{u,u_1\}, \{u,u_2\},\{u,u_3\}, \{u,u_4\},\{u_0,u_1\}\},$ but now the orientation of G will depend on the orientation of $\{u, u_0\}$ in G′. Thus, if $(u_0,u)$ is in $\overrightarrow{G'}$, then orient edges of G as depicted in Fig. 3.11. Otherwise if $(u,u_0)$ is in $\overrightarrow{G'}$, then orient edges of G as depicted in Fig. 3.12. $\overrightarrow{G}$ satisfies the hypothesis since $G \subseteq T^{(2\sin{\pi/5})}$, $\varDelta^+(\overrightarrow{G}) \leq 4$, $d^+ (\overrightarrow{G} ,u) \leq 1$ for each leaf u of T and every edge of T incident to a leaf is contained in G.

Fig. 3.10

Depicting the inductive step when u has four neighbors in $T'\setminus T$ and u _k and $u_{k+1}$ are close, where k = 2. (The dotted curve is used to separate the tree T′ from T)

Fig. 3.11

Depicting the inductive step when u has four neighbors in $T'\setminus T$, u ₀ and $u_{1}$ are close and $(u_0,u)$ is in the orientation of G′ (The dashed edge $\{u_0,u\}$ indicates that it does not exist in G but exists in G′ and the dotted curve is used to separate the tree T′ from T)

Fig. 3.12

Depicting the inductive step when u has four neighbors in $T'\setminus T$, u ₀ and u ₁ are close and $(u,u_0)$ is in the orientation of G′ (The dashed edge $\{u_0,u\}$ indicates that it does not exist in G but exists in G′ and the dotted curve is used to separate the tree T′ from T)

This completes the proof of the theorem.

The above implies immediately the case k = 4 of Theorem 3. The remaining cases of $k =3$ and k = 2 are similar but more complex. The interested reader can find details in [10].

2.2.3 Further Questions and Open Problems

There are several interesting open problems all related to the optimality of the range $2 \sin\left( \frac{\pi}{k+1} \right)$ which was derived in Theorem 3. This value is obviously optimal for k = 5 but the cases $1\leq k \leq 4$ remain open. Additional questions concern studying the problem in d-dimensional Euclidean space, $d \geq 3$, and more generally in normed spaces. The case d = 3 would also be of particular interest to sensor networks.

3 Lower Bounds

In this section we discuss the only known lower bounds for the problem.

3.1 One Antenna Per Sensor

When the sector angle is smaller than $2\pi/3$, the authors of [5] show that the problem of determining the minimum radius in order to achieve strong connectivity is NP-hard.

Theorem 5 (Caragiannis et al. [5])

For any constant $\varepsilon>0$, given ϕ such that $0\leq \varphi < 2\pi/3 - \varepsilon$, $r > 0$, and a set of points on the plane, determining whether there exists an orientation of sectors of angle ϕ and radius r so that the transmission graph is strongly connected is NP-complete.

A simple proof is by reduction from the well-known NP-hard problem for finding Hamiltonian cycles in degree three planar graphs [15]. In particular, a weaker statement for sector angles smaller than $\pi/2$ follows by the same reduction used in [19] in order to prove that the Hamiltonian circuit problem in grid graphs is NP-complete. Consider an instance of the problem consisting of points with integer coordinates on the Euclidean plane (these can be thought of as the nodes of the grid proximity graph between them). Then, if there exists an orientation of sector angles of radius 1 and angle $\varphi<\pi/2$ at the nodes so that the corresponding transmission graph is strongly connected, then this must also be a Hamiltonian circuit of the proximity graph. The construction of [19] can be thought of as reducing the Hamiltonian circuit problem on bipartite planar graphs of maximum degree three (which is proved in [19] to be NP-complete) to an instance of the problem with a grid graph as a proximity graph such that there exists a Hamiltonian circuit in the grid graph if and only if the original graph has a Hamiltonian circuit. The proof of [5] uses a slightly more involved reduction with different gadgets in order to show that the problem is NP-complete for sector angles smaller than $2\pi/3$.

3.2 Two Antennae Per Sensor

For two antennae the best known lower bound is from [10] and can be stated as follows.

Theorem 6 (Dobrev et al. [10])

For k = 2 antennae, if the angular sum of the antennae is less than α then it is NP-hard to approximate the optimal radius to within a factor of x, where x and α are the solutions of equations $x=2\sin ( \alpha)=1+2\cos(2\alpha)$.

Observe that by using the identity $\cos (2 \alpha) = 1 - 2 \sin^2 \alpha$ above and by solving the resulting quadratic equation with unknown $\sin \alpha$ we obtain numerical solutions $x\approx 1.30, \alpha\approx 0.45\pi$.

As before, the proof is by reduction from the well-known NP-hard problem for finding Hamiltonian cycles in degree three planar graphs [15]. In particular, the construction in [10] takes a degree three planar graph $G=(V,E)$ and replaces each vertex $v \in V$ by a vertex graph (meta-vertex) G _v and each edge $e \in E$ of G by an edge graph (meta-edge) G _e. Figure 3.13 shows that how meta-edges are connected with meta-vertices. Further details of the construction can be found in [10].

Fig. 3.13

Connecting meta-edges with meta-vertices. The dashed ovals show the places where embedding is constrained

3.2.1 Further Questions and Open Problems

It is interesting to note that in addition to the question of improving the lower bounds in Theorems 5 and 6 no lower bound or NP-completeness result is known for the cases of three or four antennae.

4 Sum of Angles of Antennae

A variant of the main problem is considered in a subsequent paper [4]. As before each sensor has fixed number of directional antennae and we are interested in achieving strong connectivity while minimizing the sum (taken over all sensors) of angles of the antennae under the assumption that the range is set at the length of the longest edge in any MST (normalized to 1). The authors present trade-offs between the antennae range and specified sums of antennae, given that we have k directional antennae per sensor for $1\leq k \leq 5$. The following result is proven in [4].

Lemma 1 (Caragiannis et al. [4])

Assume that a node u has degree d and the sensor at u is equipped with k antennae, where $1 \leq k \leq d$, of range at least the maximum edge length of an edge from u to its neighbors. Then $2(d-k)\pi/d$ is always sufficient and sometimes necessary bound on the sum of the angles of the antennae at u so that there is an edge from u to all its neighbors in an MST.

Proof

The result is trivially true for $k = d$ since we can satisfy the claim by directing a separate antenna of angle 0 to each node adjacent to u. So we can assume that $k \leq d - 1$. To prove the necessity of the claim take a point at the center of a circle and with d adjacent neighbors forming a regular d-gon on the perimeter of the circle of radius equal to the maximum edge length of the given spanning tree on S. Thus each angle formed between two consecutive neighbors on the circle is exactly $2\pi/d$. It is easy to see that for this configuration a sum of $2(d - k)\pi/d$ is always necessary.

To prove that sum $2(d - k)\pi/d$ is always sufficient we argue as follows. Consider the point u which has d neighbors and consider the sum σ of the largest k angles formed by $k + 1$ consecutive points of the regular polygon on the perimeter of the circle. We claim that $\sigma \geq 2k\pi/d$. Indeed, let the d consecutive angles be $\alpha_0,\alpha_1,...,\alpha_{d-1}$. (see Fig. 3.14). Consider the d sums $\alpha_i+\alpha_{i+1}+...+\alpha_{i+k-1}$, for $i = 0,...,d-1$, where addition on the indices is modulo d. Observe, that

$$2k\pi=\sum_{i=0}^{d-1}(\alpha_{i}+\alpha_{i+1}+...+\alpha_{i+k-1}) \leq d\sigma$$

Fig. 3.14

Example of a vertex of degree d = 5 and corresponding angles $\alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5$ listed in a clockwise order

It follows that the remaining angles sum to at most $2\pi -\sigma \leq 2\pi-2k\pi/d =2\pi(d-k)/d$. Now consider the $k + 1$ consecutive points, say $p_1,p_2,...,p_{k+1}$, such that the sum σ of the k consecutive angles formed is at least $2k\pi/d$. Use $k-1$ antennae each of size 0 rad to cover each of the points $p_2,...,p_k$, respectively, and an angle of size $2\pi(d-k)/d$ to cover the remaining $n-k+1$ points. This proves the lemma.

The next simple result is an immediate consequence of Lemma 1 and indicates how antennae spreads affect the range in order to accomplish strong connectivity.

Definition 9

Let ϕ _k be a given non-negative value in $[0, 2\pi)$ such that the sum of angles of k antennae at each sensor location is bounded by ϕ _k . Further, let $r_{k,\varphi_k}$ denote the minimum radius (or range) of directional antennae for a given k and ϕ _k that achieves strong connectivity under some rotation of the antennae.

We can prove the following result.

Theorem 7 (Caragiannis et al. [4])

For any $1 \leq k \leq 5$, if $\varphi_k \geq \frac{2(5-k)\pi}{5}$ then $r_{k,\varphi_k} =1$.

Proof

We prove the theorem by showing that if $\varphi_k \geq 2(5-k)\pi / 5$ then the antennae can be oriented in such a way that for every vertex u there is a directed edge from u to all its neighbors.

Consider the case k = 2 of two antennae per sensor and take a vertex u of degree d. We know from Lemma 1 that for $k=2\leq d$ antennae, $2(d-2) \pi / d$ is always sufficient and sometimes necessary on the sum of the angles of the antennae at u so that there is a directional antenna from u pointing to all its neighbors. Observe that $2(d-2) \pi / d \leq 6\pi/5$ is always true. Now take an MST with max degree five. Do a preorder traversal that comes back to the starting vertex (any starting vertex will do). For any vertex u arrange the two antennae at u so that there is always a directed edge from u to all its neighbors (if the degree of vertex is 2 you need only one antenna at that vertex). It is now easy to show by following the “underlying” preorder traversal on this tree that the resulting graph is strongly connected.

Consider the case k = 3 of three antennae per sensor. First, assume the sum of the three angles is at least $4 \pi /5$. Consider an arbitrary vertex u of the MST. We are interested in showing that for this angle there is always a link from u to all its neighbors. If the degree of u is at most three the proof is easy. If the degree is four then by Lemma 1, $2(4-3)\pi/4 = \pi /2$ is sufficient. Finally, if the degree of u is five then again by Lemma 1 then $2(5-3)\pi/5 = 4\pi /5$ is sufficient. Thus, in all cases a sum of $4\pi/5$ is sufficient.

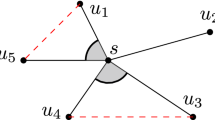
Consider the case k = 4 of four antennae per sensor. First, assume that the sum of the four angles is at least $2 \pi /5$. Consider an arbitrary vertex, say u, of the MST. If it has degree at most four then clearly four antennae each of angle 0 is sufficient. If it has degree five then an angle between two adjacent neighbors of u, say $u_0,u_1$, must be $\leq 2 \pi /5$ (see left picture in Fig. 3.15). Therefore use the angle $2 \pi /5$ to cover both of these sensors and the remaining three antennae (each of spread 0) to reach from u the remaining three neighbors.

Fig. 3.15

Orienting antennae around u

Finally, for the case k = 5 of five antennae per sensor the result follows immediately from the fact that the underlying MST has maximum degree five. This proves the theorem.

In fact, the result of Theorem 3 can be used to provide better trade-offs on the maximum antennae range and sum of angles. We mention without proof that as consequence of Lemma 1 and Theorem 3 we can construct Table 3.1, which shows trade-offs on the number, max range, max angle, and sum of angles of k antennae, being used per sensor for the problem of converting networks of omnidirectional sensors into strongly connected networks of sensors.

Table 3.1 Trade-offs on the number, max range, max angle, and sum of angles of k antennae being used by a sensor

4.1 Further Questions and Open Problems

There are two versions of the antennae orientation problem that have been studied. In the first, we are concerned with minimizing the max sensor angle. In the second, discussed in this section, we looked at minimizing the sum of the angles. Aside from the results outlined in Table 3.1, nothing better is known concerning the optimality of the sum of the sensor angles for a given sensor range. Interesting open questions for these problems arise when one has to “respect” a given underlying network of sensors. One such problem is investigated in the next section.

5 Orienting Planar Spanners

All the constructions previously considered relied on orienting antennae of a set S of sensors in the plane. Regardless of the construction, the underlying structure connecting the sensors was always an MST on S. However, there are instances where an MST on the point set may not be available because of locality restrictions on the sensors. This is, for example, the case when the spanner results from application of a local planarizing algorithm on a unit disk graph (e.g., see [7,26]). Thus, in this section we consider the case whereby the underlying network is a given planar spanner on the set S. In particular we have the following problem.

Let $G (V, E, F)$ be a planar geometric graph with V as set of vertices, E as set of edges and F as set of faces. We would like to orient edges in E so that the resulting digraph is strongly connected as well as study trade-offs between the number of directed edges and stretch factor of the resulting graphs.

A trivial algorithm is to orient each edge in E in both directions. In this case, the number of directed edges is $2| E|$ and the stretch factor is 1. Is it possible to orient some edges in only one direction so that the resulting digraph is strongly connected with bounded stretch factor? The answer is yes and an intuitive idea of our approach is based on a c-coloring of faces in F, for some integer c. The idea of using face coloring was used in [40] to construct directed cycles. Intuitively we give directions to edges depending on the color of their incident faces.

5.1 Basic Construction

Theorem 8 (Kranakis et al. [25])

Let $G (V, E, F)$ be a planar geometric graph having no cut edges. Suppose G has a face c-coloring for some integer c. There exists a strongly connected orientation G with at most

$$\left( 2 - \frac{4c-6}{c(c-1)} \right) \cdot |E|$$

((3.1))

directed edges, so that its stretch factor is $\varPhi (G) - 1$, where $\varPhi (G)$ is the largest degree of a face of G.

Before giving the proof, we introduce some useful ideas and results that will be required. Consider a planar geometric graph $G (V, E, F)$ and a face c-coloring C of G with colors $\{1, 2, \ldots, c\}$.

Definition 10

Let G be the orientation resulting from giving two opposite directions to each edge in E.

Definition 11

For each directed edge $(u, v)$, we define L _{u v} as the face which is incident to $\{u, v\}$ on the left of $(u, v)$, and similarly R _{u v} as the face which is incident to $\{u, v\}$ on the right of $(u, v)$.

Observe that for given embedding of G, L _{u v} , and R _{u v} are well defined. Since G has no cut edges, $L_{u v} \neq R_{_{u v}}$. This will be always assumed in the proofs below without specifically recalling it again. We classify directed edges according to the colors of their incident faces.

Definition 12

Let $E_{(i, j)}$ be the set of directed edges $(u, v)$ in G such that $C (L_{u v}) = i$ and $C (R_{u v}) = j$.

It is easy to see that each directed edge is exactly in one such set. Hence, the following lemma is evident and can be given without proof.

Lemma 2

For any face c-coloring of a planar geometric graph G,

$$\sum_{i = 1}^c \sum_{j = 1, j \neq i}^c |E_{(i, j)} | = 2| E|$$

Definition 13

For any of $c (c - 1)$ ordered pairs of two different colors a and b of the coloring C, we define the digraph $D (G ; a, b)$ as follows: The vertex set of the digraph D is V and the edge set of D is

$$\bigcup_{i \in [1, c]] \setminus \{b\}, j \in [1, c] \setminus \{a\}} E_{(i, j)}$$

Along with this definition, for $i \neq b$, $j \neq a$, and $i \neq j$, we say that $E_{(i, j)}$ is in $D (G ; a, b)$. Next consider the following characteristic function

$$\chi_{a, b} (E_{(i, j)}) = \left\{ \begin{array}{ll} 1 & \hbox{ if } E_{(i, j)} \hbox{ is in } D (G ; a, b), \hbox{and}\\ 0 & \hbox{ otherwise} . \end{array} \right.$$

We claim that every set $E_{(i, j)}$ is in exactly $c^2 - 3 c + 3$ different digraphs $D (G ; a, b)$ for some $a \neq b$.

Lemma 3

For any face c-coloring of a planar geometric graph G,

$$\sum_{a = 1}^c \sum_{b = 1, b \not{=} a}^c \chi_{a, b} (E_{(i, j)}) = c^2 - 3 c + 3.$$

Proof

Let $i, j \in [1, c]$, $i \neq j$ be fixed. For any two distinct colors a and b of the c-coloring of G, $\chi_{a, b} (E_{(i, j)}) = 1$ only if either $i = a$ or $j = b$, or i and j are different from a and b. There are $(c - 1) + (c - 2) + (c - 2) (c - 3)$ such colorings. The lemma follows by simple counting.

The following lemma gives a key property of the digraph $D (G ; a, b)$.

Lemma 4

Given a face c-coloring of a planar geometric graph G with no cut edges, and the corresponding digraph $D (G ; a, b)$. Every face of $D (G ; a, b)$, which has color a, constitutes a counterclockwise-directed cycle, and every face which has color b constitutes a clockwise-directed cycle. All edges on such cycles are unidirectional. Moreover, each edge of $D (G ; a, b)$ incident to faces having colors different from either a or b is bidirectional.

Proof

Let G be a planar geometric graph with a face c-coloring C with colors a, b, and $c - 2$ other colors. Consider $D (G ; a, b)$. The sets $E_{(a, x)}$ are in $D (G ; a, b)$ for each color $x \neq a$. Let f be a face and let $\{u, v\}$ be an edge of f so that $L_{u v} = f$. Let f′ be the other face incident to $\{u, v\}$; hence $R_{u v} = f'$. Since G has no cut edges, $f \neq f'$, and, since $C (f') \neq a$, the directed edge $(u, v) \in \bigcup_{x \not{=} a} E_{(a, x)}$ and hence the edge $(u, v)$ is in $D (G ; a, b)$. Since $\{u, v\}$ was an arbitrary edge of f, f will induce a counterclockwise cycle in $D (G ; a, b)$ (see Fig. 3.16). The fact that every face which has color b induces a clockwise cycle in $D (G ; a, b)$ is similar. Finally consider an edge $\{u, v\}$ such that $C (L_{u v}) \neq a, b$ and $C (R_{u v}) \neq a, b$ (see Fig. 3.17). Hence $(u, v) \in E_{(c, d)}$ which is in $D (G ; a, b)$ and similarly $(v, u) \in E_{(d, c)}$ which is also in $D (G ; a, b)$. This proves the lemma.

Fig. 3.16

$(u,v)$ is in $D(G; a,b)$ if $C(L_{uv}) =a$ and therefore the edges in the face L _uv form a counterclockwise-directed cycle in $D(:G,a,b)$

Fig. 3.17

A bidirectional edge is in $D(G; a,b)$ if its incident faces have color different than a and b

We are ready to prove Theorem 8.

Proof (Theorem 8)

Let G be a planar geometric graph having no cut edges. Let C be a face c-coloring of G with colors a, b and other $c - 2$ colors. Suppose colors a and b are such that the corresponding digraph $D (G ; a, b)$ has the minimum number of directed edges. Consider $\overline{D}$ the average number of directed edges in all digraphs arising from C. Thus,

$$\begin{array}{lll}\overline{D} = \frac{1}{c (c - 1)} \sum_{a = 1}^c \sum_{b = 1, b \not{=} a}^c ||D (G ; a, b) ||, \hbox{where}\\ ||D (G ; a, b) || = \sum_{i = 1}^c \sum_{j = 1, j \not{=} i}^c \chi_{a, b} (E_{(i, j)}) |E_{(i, j)} | \end{array}$$

By Lemma 2 and Lemma 3,

$$\begin{array}{lll} \overline{D} &= & \frac{1}{c (c - 1)} \sum_{a = 1}^c \sum_{b = 1, b \not{=} a}^c \sum_{i = 1}^c \sum_{j = 1, j \not{=} i}^c \chi_{a, b} (E_{(i, j)}) |E_{(i, j)} |\\ &= & \frac{1}{c (c - 1)} \sum_{i = 1}^c \sum_{j = 1, j \not{=} i}^c (c^2 - 3 c + 3) |E_{(i, j)} |\\ & = & \frac{2 (c^2 - 3 c + 3)}{c (c - 1)} |E|\\ & = & \left( 2 - \frac{4c-6}{c(c-1)} \right) \cdot |E| \end{array}$$

Hence $D (G ; a, b)$ has at most the desired number of directed edges.

To prove the strong connectivity of $D (G ; a, b)$, consider any path, say $u = u_0, u_1, \ldots, u_n = v$, in the graph G from u to v. We prove that there exists a directed path from u to v in $D (G ; a, b)$. It is enough to prove that for all i there is always a directed path from u _i to $u_{i + 1}$ for any edge $\{u_i, u_{i + 1} \}$ of the above path. We distinguish several cases.

• Case 1. $C (L_{u_i u_{i + 1}}) = a$. Then $(u_i, u_{i + 1}) \in E_{(a, \omega)}$ where $\omega = C (R_{u_{i u_{i + 1}}}) .$ Since $E_{(a, \omega)}$ is in $D (G ; a, b)$, the edge $(u_i, u_{i + 1})$ is in $D (G ; a, b)$. Moreover, the stretch factor of $\{u_i, u_{i + 1} \}$ is one.

• Case 2. $C (L_{u_i u_{i + 1}}) = b$. Hence, $(u_i, u_{i + 1})$ is not in $D (G ; a, b)$. However, by Lemma 4, the face $L_{u_i u_{i + 1}} = R_{u_{i + 1} u_i}$ constitutes a clockwise-directed cycle and therefore, a directed path from u _i to $u_{i + 1}$. It is easy to see that the stretch factor of $\{u_{i, u_{i + 1}} \}$ is not more than the size of the face $L_{u_i u_{i + 1}}$ minus one, which is at most $\varPhi (G) - 1$.

• Case 3. $C (L_{u_i u_{i + 1}}) \neq a, b$. Suppose $C (L_{u_i u_{i + 1}}) = c$. Three cases can occur.

  • $C (R_{u_i u_{i + 1}}) = a$. Hence, $(u_i, u_{i + 1})$ is not in $D (G ; a, b)$. However, by Lemma 4, there exists a counterclockwise-directed cycle around face $R_{u_i u_{i + 1}} = L_{u_{i + 1} u_i}$, and consequently a directed path from u _i to $u_{i + 1}$. The stretch factor is at most the size of face $R_{u_i u_{i + 1}}$ minus one, which is at most $\varPhi (G) - 1$.

  • $C (R_{u_i u_{i + 1}}) = b$. By Lemma 4, there exists a clockwise-directed cycle around face $R_{u_i u_{i + 1}}$. This cycle contains $(u_i u_{i + 1})$, and in addition the stretch factor of $\{u_i, u_{i + 1} \}$ is one.

  • $C (R_{u_i u_{i + 1}}) = d \neq a, b, c$. By construction, $D (G ; a, b)$ has both edges $(u_i, u_{i + 1})$ and $(u_{i + 1}, u_i)$. Again, the stretch factor of $\{u_i, u_{i + 1} \}$ is one.

This proves the theorem.

As indicated in Theorem 8 the number of directed edges in the strongly oriented graph depends on the number c of colors according to the formula $\left( 2 - \frac{4c-6}{c(c-1)} \right) \cdot |E|$. Thus, for specific values of c we have the following table of values:

$$\begin{array}{|c|c|c|c|c|c|} c & 3 & 4 & 5 & 6 & 7 \\ 2 - (4c-6)/c(c-1) & 1 & 7/6 & 13/10 & 7/5 & 31/21 \\ \end{array}$$

Regarding the complexity of the algorithm, this depends on the number c of colors being used. For example, computing a four coloring can be done in $O (n^2)$ [35]. Finding the digraph with minimum number of directed edges among the 12 possible digraphs can be done in linear time. Therefore, for c = 4 it can be computed in $O (n^2)$. For c = 5 a five coloring can be found in linear time $O(n)$. For the case of geometric planar subgraphs of unit disk graphs and location aware nodes there is a local seven coloring (see [9]). For more information on colorings the reader is advised to look at [20].

5.1.1 Further Questions and Open Problems

Observe that it is required that the underlying geometric graph in Theorem 8 does not have any cut edges. Although it is well known how to construct planar graphs with no cut edges starting from a set of points (e.g., Delaunay triangulation) there are no known constructions in the literature of “local” spanners from UDGs which also guarantee planarity, network connectivity, and no cut edges at the same time. Constructions of spanners obtained by deleting edges from the original graph can be found in Cheriyan et al. [8] and Dong et al. [11] but the algorithms are not local and the spanners not planar. Similarly, existing constructions for augmenting (i.e., adding edges) graphs into spanners with no cut edges (see Rappaport [34], Abellanas et al. [1], Rutter et al. [36]) are not local algorithms and the resulting spanners not planar.

6 Conclusion

We considered the problem of converting a planar (undirected) graph constructed using omnidirectional antennae into a planar-directed graph constructed using directional antennae. In our approach we considered trade-offs on the number of antennae, antennae angle, sum of angles of antennae, stretch factor, lower and upper bounds on the feasibility of achieving connectivity. In addition to closing several existing gaps between upper and lower bounds for the algorithms we proposed there remain several open problems concerning topology control whose solution can help to illuminate the relation between networks of omnidirectional and directional antennae. Also of interest is the question of minimizing the amount of energy required to maintain connectivity given one or more directional antennae of a given angular spread in replace of a single omnidirectional antennae.