Improved algorithms in directional wireless sensor networks

Abstract

Recent advances in wireless sensor networks (WSNs) allow directional antennas to be used instead of omni-directional antennas. However, the problem of maintaining (symmetric) connectivity in directional wireless sensor networks is significantly harder. Contributing to this field of research, in this paper, we study two problems in WSNs equipped with k directional antennas ($3 \le k \le 4$). The first problem, called antenna orientation (AO) is that given a set S of nodes equipped with omni-directional antennas of unit range, the goal is to replace omni-directional antennas by directional antennas with beam-width $\theta \ge 0$ and to find a way to orient them such that the required range to yield a symmetric connected communication graph (SCCG) is minimized. For this problem, we propose an $O(n \log n)$ time algorithm yielding $r = 2sin\left( \frac{180^\circ }{k}\right)$. The second problem, called antenna orientation and power assignment (AOPA) is to determine for each node u an orientation of its antennas and a range $r_u$ in order to induce an SCCG such that the total power assignment $\sum _u r_u^\beta$ is minimized, where $\beta$ is a distant-power gradient. We show that our solution for the AO problem also induces an O(1)-approximation algorithm for the AOPA problem. Simulation results demonstrate that our algorithms have better performance than previous approaches, especially in case $k = 3$.

1 Introduction

Wireless sensor networks (WSNs) have received significant attention of many researchers due to their vast applications in various areas. As the amount of battery equipped with each node is limited, reducing energy consumption is one of the most studied problems concerning WSNs. One of the main approaches to resolve this problem is topology control, especially in omni-directional WSNs (Kirousis et al. 2000; Li et al. 2001; Calinescu et al. 2003; Ye and Zhang 2004; Lloyd et al. 2005; Calinescu and Wan 2006; Lloyd et al. 2006; Caragiannis et al. 2006; Wang et al. 2010). Besides topology control, appropriate power assignments can be exploited to obtain wireless networks that are fault-tolerant and have low interference (Lam et al. 2011).

In contrast to a low-gain omni-directional antenna, a high-gain directional antenna has a limited broadcast region defined by a range r and a beam-width $\theta$. Replacing omni-directional antennas by directional ones can bring some noticeable advantages, such as reduced energy consumption, minimized interference and increased communication security (see Aschner et al. 2012; Kranakis et al. 2015 and references therein). A natural way to reduce energy usage of a directional wireless sensor network (DWSN) is to reduce the power range of the antennas. However, a very low range may cause the communication graph to be disconnected. Therefore, the AO problem whose goal is to find a way to orient the antennas with a smallest possible range is an interesting problem to investigate.

Formally, we consider a Directional Wireless Sensor Network (DWSN) as a set S of nodes in the plane. Let k, $3 \le k \le 4$, be an integer, and $\theta$, $0 \le \theta \le 360^\circ$, a beam-width angle. Each sensor u in a DWSN is equipped with k directional antennas having a beam-width $\theta$ and a transmission range r(u). The broadcasting region of an antenna of u is defined by a sector centering at u with radius r(u) and beam-width $\theta$ and the orientation of the bisector of $\theta$ (in case of $\theta = 0$, the sector and its bisector are degenerated to a segment). Two nodes u and v are said to be symmetrically connected if these two conditions are both satisfied: (1) u lies inside the broadcasting region of one of k antennas of v and vice versa, and (2) the Euclidean distance between u and v is no greater than min(r(u), r(v)).

1.1 Our results

We obtain the following results for beam-width $\theta = 0$, however, these results also hold for any angle $\theta \ge 0$.

• 1. In Dobrev et al. (2012), the authors present an elegant algorithm that yields state-of-the-art results for the required range $r = 2sin\left( \frac{180^\circ }{k + 1}\right)$ to induce a strongly connected communication graph for a DWSN spanned by a unit disk graph (UDG). Our main technical result is to modify this approach in order to yield an SCCG where the required range is $r = 2sin\left( \frac{180^\circ }{k}\right)$.       Similar to many typical approaches in constructing a geometric spanning tree, Dobrev et al. first use a minimum spanning tree (MST) with maximum degree 5 as a backbone. They then choose an arbitrary node to root the tree and added nodes to the communication graph according to their levels in the MST in such a way that the outdegree of newly-added nodes is at most 1. In the proof of their results, they demonstrate the existence of pairs of children of a node (in a rooted MST) such that their distances are bounded by $2sin\left( \frac{180^\circ }{k + 1}\right)$. Note that the range obtained by Dobrev et al., and also throughout this paper, is computed after normalizing the maximum edge length of the MST to 1.       We follow the same approach. To adapt this approach for symmetric connectivity, we try to guarantee that the maximum degree of a newly-added node is 2 for both $k = 3$ and $k = 4$. For the case $k = 4$, we obtain the desired range using a subtle orientation. However, the problem is much more involved for $k = 3$. Inspired by the study of Biniaz (2020), we exploit the grandchildren (if exist) of a node to establish symmetric connectivity between this node and their children as well as their grandchildren.

• 2. We prove that our solution for the AO problem also induces an O(1)-approximation algorithm for the AOPA problem. Using the method presented in Aschner et al. (2013) and Tran and Huynh (2020), we obtain the bound $k_{max} \le 4$, where $k_{max}$ is the maximum number of times that an edge is used to estimate the range of a node in the induced communication graph. This result implies that the approximation ratio obtained for the AOPA problem for $k = 3$ and $k = 4$ is $4 \times r_k^\beta$, where $r_k$ is the required range in our solution for the AO problem, which is $2sin\left( \frac{180^\circ }{k}\right)$.

Comparison of our algorithm with the algorithm byBiniaz (2020): Our algorithms achieve the same theoretical results as Biniaz’s for the AO problem using a different approach, i.e., our algorithms are top-down whereas Biniaz’s are bottom-up. Although sharing the same theoretical performance guarantee, simulation results show that our algorithms outperform previous approaches in practice. Our minimum required ranges for the AO problem are nearly optimal. Finally, we also investigate the AOPA problems, which is not considered in Biniaz (2020).

Theorem 1

Given a set of nodes S in the plane, each node is equipped with k directional antennas, $3 \le k \le 4$, with beam-width $\theta \ge 0$. Then there always exists an orientation of these antennas so that the communication graph G of S is symmetric connected and the maximum range assignment for each node is $2sin\left( \frac{180^\circ }{k}\right)$.

Theorem 2

Given a set of nodes S in the plane, each node is equipped with k directional antennas, $3 \le k \le 4$, with beam-width $\theta \ge 0$. Let $Cost(AOPA_S)$ be the total power assignment of an orientation algorithm for the set of nodes S and $OPT(AOPA_S)$ be the optimal total power assignment over all orientation algorithms for S, then

$$\begin{aligned} Cost(AOPA_S) \le 4 \times 2sin\left( \frac{180^\circ }{k}\right) ^{\beta } \times Cost_\beta (T), \end{aligned}$$

where $\beta$ is the distant-power gradient, T is an MST of S and $Cost_\beta (T):= \sum _{e \in T} |e|^\beta \le OPT(AOPA_S)$.

1.2 Related work

1.2.1 Related work on strong connectivity

In Caragiannis et al. (2008), the authors initiated the line of research in DWSNs. In that paper, the authors proved that if each node in DWSN is equipped with one directional antenna having beam-width $\theta \ge 288^\circ$ ($8\pi /5$), the problem of maintaining a strongly connected communication graph is solvable in polynomial time. Bhattacharya et al. (2009) addressed the problem of minimizing the sum of transmission angle over all antennas of one node to ensure that the communication graph is strongly connected given a fixed transmission range r. Dobrev et al. (2012) gave an elegant algorithm to achieve a communication graph that requires a range of $2sin\left( \frac{180^\circ }{k + 1}\right)$ to maintain strong connectivity.

1.2.2 Related work on symmetric connectivity

In regard to symmetric connectivity, when $\theta \ge 0$, the AO problem for DWSNs is equivalent to the Euclidean Degree-Bounded Bottleneck Spanning Tree problem. Andersen and Ras (2016) showed that the problem is NP-Hard for $k = 3$ by a reduction from the Hamiltonian path problem for grid graphs with maximum degree 3. For $k = 4$, while the approximation ratio is reduced to $\sqrt{3}$ (Andersen and Ras 2016; Tran and Huynh 2020) and then to $\sqrt{2}$ (Biniaz 2020 and Theorem 3), its NP hardness still remains open.

In case $\theta > 0$, when $k = 1$, multiple research papers have been presented. Carmi et al. (2011) showed that a DWSN where each antenna has beam-width $\theta \ge 60^\circ$ always admits an SCCG. In Aschner et al. (2013), the authors proposed an orientation such that the induced SCCG requires a range of $14\sqrt{2}$ and a hop-distance of 8 when $\theta = 90^\circ$. Later, Tran et al. (2017a) gave an algorithm yielding an SCCG with required range of 9 but hop-distance is unbounded. When $\theta = 120^\circ$, Aschner and Katz (2017) presented a 6-hop spanner where the bottleneck range is at most 7. Moreover, if our objective is to optimize only one of these two measures, a better constant can be achieved (i.e. a 3-hop spanner or an SCCG with required range 5).

When $k \ge 2$, very few studies can be found in the literature. When $k = 2$, Tran et al. (2017b) were the first researchers who studied this case. In that paper, the authors proposed an algorithm yielding an SCCG where the required range is 4 and 5 for $\theta = 60^\circ$ and $\theta = 45^\circ$, respectively. In case $3 \le k \le 4$ and $\theta > 0$, to the best of our knowledge, no study has been found.

In this paper, our focus is to investigate the antenna orientation (AO) and the antenna orientation and power assignment (AOPA) problems for DWSNs in which each node is equipped with $3 \le k \le 4$ antennas with beam-width $\theta \ge 0$. Our algorithms are a significant improvement over Tran’s algorithms presented in Tran and Huynh (2020) (for the conference version, see Tran and Huynh 2018) in terms of both the minimum required range and the total power assignment. Our approach is top-down whereas Tran et al.’s algorithms are bottom-up. For the AOPA problem, the NP-hardness was obtained by Tran and Huynh (2020) for $k = 3$ and $k = 4$, while the NP-hardness result for the problem in case $k = 2$ can be easily derived from the Hamiltonian Path problem in grid graphs (Papadimitriou and Vazirani 1984).

2 Preliminaries

In this section, we recall some properties of Euclidean Minimum Spanning Trees (MSTs) and include some definitions and notations using in the rest of the paper. Let $MST_5$ be the MST where the maximum degree of each vertex is 5. It is well known that a set S of points in the plane admits an $MST_5 T$ such that (see Monma and Suri 1992):

• 1. The minimum angle among nodes with a common parent is at least $60^\circ$,

• 2. For any point u and any edge $\{u, v\}$ of T, the disk D(v; d(u, v)) does not contain a point $w \ne v$ which is also a neighbor of u in T.

An $MST_5$ of a set of points can be constructed from an arbitrary MST by using Wu et al.’s technique in Wu et al. (2006) in polynomial time.

Definition 1

Given a graph G and a node u in G, $\deg _G(u)$ denotes the degree of u in G.

Definition 2

Given two pairs (a, b) and (c, d), we say that they are separated if a, b, c and d are four distinct nodes.

Definition 3

Given an MST T with height h, we define an l-node, $1 \le l \le h$, as a node of T whose level from root node is l where the level of the root node is 0.

For the sake of simplicity, we introduce here some conventions used in this paper. First, given two nodes u and v in a DWSN, the terms “add edge uv", “connect u to v” and “orient one antenna of u to v and orient one antenna of v to u" are all equivalent. Second, unless specially stated, $\angle (uvw)$ denotes the convex angle formed by the two segments $\overline{uv}$ and $\overline{vw}$. Third, any MST mentioned in this work is an $MST_5$. Finally, neighbors of a node are listed in clockwise order.

3 Algorithm for the AO problem when $k=4$

In this section we derive the algorithm for the AO problem.

Definition 4

Let u and v be two consecutive neighbors of a node p in a tree. We say that u and v are angle-close (or a-close for short) if $\angle (upv) \le 90^\circ$, and angle-far (or a-far for short) otherwise. It is obvious that u and v are a-close implies that $d(u, v) \le \sqrt{2}$.

Lemma 1

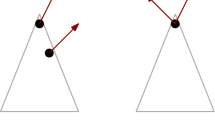
Let s be a node that has 5 neighbors in an MST. Then there does not exist any 3 consecutive sectors that are a-far. In other words, there exist two separated pairs of neighbors of s that are a-close (see Fig. 1).

Proof

The proof is by contradiction. Assume that s has 3 consecutive a-far pairs. Then the sum of the angles formed by them are larger $270^\circ$, thus the sum of two remaining sectors are smaller than $90^\circ$. However, every sector is at least $60^\circ$, or the sum of these two sectors is larger than $120^\circ > 90^\circ$, which is contradiction. $\square$

Theorem 3

Given a set S of nodes in the plane, each node is equipped with 4 directional antennas with beam-width $\theta \ge 0$. Let T be the MST spanning the UDG of S. Then there always exists an orientation of these antennas so that the communication graph G of S is symmetric connected and the maximum power range assignment for each node is $\sqrt{2}$. Moreover, for each leaf node u in T, $\deg _G(u) \le 2$ and if $\deg _G(u) = 2$, u is directly connected with its parent (in T) in the communication graph G.

Proof

The proof is by induction on the height h of T. First, we do the base case for $h \le 1$. If $h = 0$, the result is trivial. If $h = 1$, let s be the root of T, then $1 \le \deg (s) \le 5$. We have two cases:

• 1. $\deg (s) < 5$. In this case, we just connect s to its neighbors. It is obvious that the communication graph is symmetric connected.

• 2. $\deg (s) = 5$. Let $u_1, u_2, \dots , u_5$ be five neighbors of s. By Lemma 1, there must exists one pair of s’s neighbors that are a-close. W.l.o.g., let $u_1$ and $u_5$ be a-close. We can add the edges $su_1$, $su_2$, $su_3$, $su_4$ and $u_1u_5$ to G as in Fig. 2. Observe that the longest edge is $u_1u_5$ and by Definition 4, the length of this edge is at most $\sqrt{2}$. Thus, this orientation satisfies Theorem 3.

Fig. 1

Illustration of Lemma 1. $(u_1,u_5)$ and $(u_3,u_4)$ are two separated a-close pairs

Fig. 2

Base case for $k = 4$

We now prove the induction step. To this end, let T be an MST with height $h \ge 2$, we remove all h-nodes of T to produce a tree $T'$ whose height is $h - 1$. The tree $T'$ is still an MST and by the induction hypothesis, there exists an orientation yielding a communication graph $G'$ that satisfies Theorem 3. Now let $G = G'$, we add all of the h-nodes back and connect them to G. As our orientation is applied to $(h-1)$-nodes independently, let u in $T'$ be an arbitrary $(h-1)$-node. We describe the process of connecting u’s children to u in G. Let d be the number of neighbors of u that are the h-nodes added in this step, $0 \le d \le 4$. We have three cases:

• 1. $d \le 2$. Since u has at least 2 remaining free antennas, we can freely connect u to its children. It is obvious that the orientation satisfies Theorem 3.

• 2. $d = 3$. We have two subcases:

  • (a) Node u is connected with one node in $T'$. In Fig. 2, u may be one of the nodes $u_2, u_3, u_4, u_5$. Let u be for instance $u_5$. To maintain symmetric connectivity, we just connect $u_5$ to its children.

  • (b) Node u is connected with two nodes in $T'$. One of these two nodes must be the parent s of u in $T'$ (and T also). In Fig. 2, node u is $u_1$ is in this case. Let $v_0 = s, v_1, v_2$ and $v_3$ be the neighbors of $u_1$ in T. By the pigeonhole principle, there must exist one a-close pair of consecutive $v_i$. If $v_0$ is not a-close with any other $v_i$ then, W.l.o.g., let’s assume that $v_1$ and $v_2$ are a-close, we add the edges $u_1v_1$, $u_1v_3$ and $v_1v_2$ as in Fig. 3a. Otherwise, assume that $v_0$ and $v_1$ are a-close, we remove the edge $v_0u_1$ and add the edges $v_0v_1$, $u_1v_1$, $u_1v_2$ and $u_1v_3$ to G (see Fig. 3b).

• 3. $d = 4$. Then we have two subcases:

  • (a) Node u is connected with one node in $T'$. As in Fig. 2, u is one of the nodes $u_2, u_3, u_4, u_5$ in this case. W.l.o.g. let u be $u_5$. Let $v_1, v_2, v_3$ and $v_4$ be the children of $u_5$ in T, by Lemma 1 and W.l.o.g., assume that $v_1$ and $v_2$ are a-close, we connect $u_5$ with $v_1$, $v_3$ and $v_4$, and connect $v_1$ with $v_2$ as in Fig. 4.

  • (b) Node u is connected with two nodes in $T'$. One of these two nodes must be the parent s of u in T. In Fig. 2, node $u_1$ is u in this case. Let $v_0 = s, v_1, v_2, v_3$ and $v_4$ be five neighbors of $u_1$ in T. There are 2 cases:

    • i. $v_1, v_2$ and $v_3, v_4$ are a-close. We add the edges $v_1v_2$, $v_3v_4$, $u_1v_1$ and $u_1v_3$ to G as in Fig. 5a.

    • ii. $v_0$ is a-close with either $v_1$ or $v_4$. W.l.o.g., let $v_0$ be a-close to $v_4$. By Lemma 1, there is another pair that are a-close and separated with $(v_0, v_4)$. Suppose that $v_1$ and $v_2$ are a-close. We remove edge $u_1v_0$, and then connect $v_0$ with $v_4$, $v_1$ with $v_2$, $u_1$ with $v_1$, $u_1$ with $v_3$ and $u_1$ with $v_4$ (see Fig. 5b).

$\square$

Fig. 3

Case $k = 4$, $d = 3$, node $u = u_1$ is connected with two nodes in $T'$ and a $v_1, v_2$ are a-close, b $v_0, v_1$ are a-close

Fig. 4

Case $k = 4$, $d = 4$, node $u = u_5$ is connected with one node in $T'$ and $v_1, v_2$ are a-close

Fig. 5

Case $k = 4$, $d = 4$, node $u = u_1$ is connected with two nodes in $T'$ and a $v_1, v_2$ and $v_3, v_4$ are a-close, b $v_1, v_2$ and $v_0, v_4$ are a-close

4 Algorithm for the AO problem when $k=3$

In this section, we present the algorithm for the AO problem when $k=3$. We first define the closeness of nodes by the distance between them instead of by the angle.

Definition 5

Let u and v be two nodes in an MST. We say that u and v are distance-close (or d-close for short) if the distance between them is at most $\sqrt{3}$, and distance-far (or d-far for short) otherwise. It is easy to see that if u and v are two d-far consecutive neighbors of p, then $\angle (upv) > 120^\circ$.

Lemma 2

Let s be any node in an MST. The following statements hold:

• (1) If $\deg (s) = 3$, then at least two consecutive neighbors of s are d-close.

• (2) If $\deg (s) = 4$, then there exist two separated pairs of neighbors of s that are both d-close.

• (3) If $\deg (s) = 5$, then all consecutive neighbors of s are d-close.

Proof

• (1) If $\deg (s) = 3$, then the smallest angle is at most $120^\circ$, hence two neighbors of s defining this angle are d-close.

• (2) If $\deg (s) = 4$, then there is at most one angle larger than $120^\circ$, because if there are two angles larger than $120^\circ$, then the sum of these four angles must be larger than $2 \cdot 120^\circ + 2 \cdot 60^\circ = 360^\circ$, which is impossible. Thus, there must exist two nonadjacent angles smaller than $120^\circ$, and the pairs of neighbors defining these angles are d-close.

• (3) If $\deg (s) = 5$, then the largest angle is at most $120^\circ$, hence all consecutive neighbors of s are d-close.

$\square$

Claim

(Biniaz 2020) Let u and v be two neighbors in an MST, p and q be a child of u and v, respectively. Assume that both p and q lie on the same half plane defined by the line through uv. If $\angle (puv) + \angle (qvu) \le 210^\circ$, then $|pq| \le \sqrt{3}\cdot \max \{|pu|,|uv|,|vq|\}$.

The following claim is a summarized version of Lemma 2.8 in Dobrev et al. (2012).

Claim

(Dobrev et al. 2012) Let u, v and w be three consecutive children with parent p in an MST such that $\angle (upv) + \angle (vpw) \le 180^\circ$. The following statements hold true:

• (1) If $\deg (v)=3$ and the only two children of v are d-far, then at least one of them is d-close to either u or w.

• (2) If $\deg (v) \ge 4$, then at least one child of v is d-close to either u or w.

Lemma 3

Let p and q be two neighbors in an MST, having degree 5 and degree 4, respectively. Let $v_0, v_1, v_2, v_3=q$ and $v_4$ be the 5 neighbors of p, and $w_0 = p, w_1, w_2$ and $w_3$ be the 4 neighbors of q. Then only one of the following five cases can occur:

• (1) $w_1, v_2$ and $w_3, v_4$ are both d-close.

• (2) If $w_1, v_2$ are d-far and $w_1, w_2$ are d-close, then $w_3, v_4$ are d-close.

• (3) If $w_1, v_2$ and $w_1, w_2$ are both d-far, then $w_2, v_4$ and $w_3, v_0$ are both d-close.

• (4) If $w_3, v_4$ are d-far and $w_3, w_2$ are d-close, then $w_1, v_2$ are d-close.

• (5) If $w_3, v_4$ and $w_3, w_2$ are both d-far, then $w_2, v_2$ and $w_1, v_1$ are both d-close.

Proof

• (1) If $w_1, v_2$ and $w_3, v_4$ are d-close, we are done.

• (2) If $w_1, v_2$ are d-far, since $\angle (v_2w_0v_3) + \angle (v_3w_0v_4) \le 180^\circ$, by Claim 4, $w_3, v_4$ must be d-close. (Notice that $w_1$ and $w_3$ are obviously far, thus we can ignore $w_2$ and apply case 1 of Claim 4).

• (3) If $w_1, v_2$ are d-far, we first prove the claim that $w_1$ and $v_2$ are on the same side of the line $v_3w_0$.

Claim

Let p and q be two neighbors in an MST, having degree 5 and degree 4, respectively. Let $v_0, v_1, v_2, v_3=q$ and $v_4$ be the 5 neighbors of p, and $w_0 = p, w_1, w_2$ and $w_3$ be the 4 neighbors of q. If $w_1, w_2$ are d-far, then $w_2$ and $v_4$ lie on the same half plane defined by the line through $v_3w_0$.

Proof

Place a 2-dimensional Cartesian coordinate system on the plane such that $v_3$ is the origin O of the system and $w_0$ is on the horizontal axe Ox. Suppose that $w_0$ is on the right of $v_3$. Since we list the neighbors of p in clockwise order, $v_4$ must be above Ox. As $w_1, w_2$ are d-far, clockwise the angle $\angle (w_0v_3w_2) = \angle (w_0v_3w_1) + \angle (w_1v_3w_2)$ is $> 60^\circ + 120^\circ = 180^\circ$. Thus $w_2$ is above Ox. Therefore $w_2$ and $v_4$ are on the same half plane defined by the line $v_3w_0$. $\square$

Since $w_1, v_2$ are d-far and $w_1, v_2$ are on the same half plane defined by the line $v_3w_0$, by Claim 4, $\angle (w_1v_3w_0) + \angle (v_3w_0v_2) > 210^\circ$. In addition, if $w_1, w_2$ are d-far, $\angle (w_2v_3w_1) > 120^\circ$. Therefore, $\angle (w_2v_3w_0) + \angle (v_4w_0v_3) = [360^\circ - (\angle (w_2v_3w_1) + \angle (w_1v_3w_0))] + [360^\circ - (\angle (v_3w_0v_2) + \angle (v_2w_0v_1) + \angle (v_1w_0v_0) + \angle (v_0w_0v_4))] \le 2 \cdot 360^\circ - \angle (w_2v_3w_1) - (\angle (w_1v_3w_0) + \angle (v_3w_0v_2)) - 3 \cdot 60^\circ < 2 \cdot 360^\circ - 120^\circ - 210^\circ - 3 \cdot 60^\circ = 210^\circ$. Hence by Claim 4 and Claim 4, $w_2, v_4$ are d-close (see Fig. 6). Analogously, one can prove that $w_3, v_0$ are d-close.

• (4) This case can be shown as case (2) by relabeling.

• (5) This case can be shown as case (3) by relabeling.

$\square$

Lemma 4

Let p and q be two neighbors in an MST, each be of degree 5. Let $v_0, v_1, v_2, v_3=q$ and $v_4$ be the 5 neighbors of p and $w_0 = p, w_1, w_2, w_3$ and $w_4$ be the 5 neighbors of q. Then only one of following three cases can to occur.

• (1) $w_1, v_2$ and $w_4, v_4$ are both d-close.

• (2) If $w_1, v_2$ are d-far, then $w_4, v_0$ and $w_3, v_4$ are both d-close.

• (3) If $w_4, v_4$ are d-far, then $w_1, v_1$ and $w_2, v_2$ are both d-close.

Proof

It is easy to see that $w_1, w_2, v_1$ and $v_2$ are on the same side of the line $v_3w_0$. The same holds for the nodes $w_3, w_4, v_0, v_4$.

• (1) If $w_1, v_2$ and $w_4, v_4$ are d-close, we are done.

• (2) If $w_1, v_2$ are d-far then by Claim 4, $\angle (w_1v_3w_0) + \angle (v_3w_0v_2) > 210^\circ$. Thus, $\angle (w_3v_3w_0) + \angle (v_4w_0v_3) = [360^\circ - (\angle (w_3v_3w_2) + \angle (w_2v_3w_1) + \angle (w_1v_3w_0))] + [360^\circ - (\angle (v_3w_0v_2) + \angle (v_2w_0v_1) + \angle (v_1w_0v_0) + \angle (v_0w_0v_4))] \le 2 \cdot 360^\circ - (\angle (w_1v_3w_0) + \angle (v_3w_0v_2)) - 5 \cdot 60^\circ < 2 \cdot 360^\circ - 210^\circ - 5 \cdot 60^\circ = 210^\circ$. Hence by Claim 4, $w_3, v_4$ are d-close (see Fig. 7). Analogously, one can prove that $w_4, v_0$ are d-close.

• (3) If $w_4, v_4$ are d-far, after a suitable relabelling, we can obtain the previous case. Therefore, the proof is complete.

$\square$

Fig. 6

Illustration of Lemma 3, case (3)

Fig. 7

Illustration of Lemma 4, case (2)

Theorem 4

Given a set of nodes S in the plane, each node is equipped with 3 directional antennas with beam-width $\theta \ge 0$. Let T be the MST spanning the UDG of S. Then there always exists an orientation of these antennas so that the communication graph G of S is symmetric connected and the maximum range assignment for each node is $\sqrt{3}$. Moreover, for each leaf node u in T, $\deg _G(u) \le 2$ and if $\deg _G(u) = 2$, u is connected with its parent in T in the communication graph G.

Proof

The proof is by induction on the height h of T. First, we do the base case for $h \le 1$. If $h = 0$, the result is trivial. If $h = 1$, let s be the root of the tree. Then $1 \le \deg (s) \le 5$. We have three cases:

• 1. $\deg (s) < 4$. We just connect s with its neighbors. Observe that this communication graph is symmetric connected.

• 2. $\deg (s) = 4$. Let $u_1, u_2, \dots , u_4$ be four neighbors of s. By Lemma 2, there must exist one pair of neighbors that are d-close. W.l.o.g., let $u_1$ and $u_2$ be d-close. We add the edges $u_1u_2$, $su_1$, $su_3$ and $su_4$ to G. Observe that the longest edge is $u_1u_2$ and by Definition 5, the length of this edge is at most $\sqrt{3}$. Thus this orientation satisfies Theorem 4.

• 3. $\deg (s) = 5$. Let $u_1, u_2, \dots , u_5$ be five neighbors of s. By Lemma 2, all consecutive neighbors of s are d-close. Therefore, we can add the edges $u_1u_5$, $u_3u_4$, $su_1$, $su_2$ and $su_3$ to G (see Fig. 8). Observe that the longest edge is either $u_1u_5$ or $u_3u_4$ and by Definition 5, the lengths of these edges are at most $\sqrt{3}$. Thus this orientation satisfies Theorem 4.

Fig. 8

Base case for $k = 3$

Fig. 9

Case $k=3$, $d=2$, $u=u_1$

Fig. 10

Case $k=3$, $d=3$. a $u=u_5$, b $u=u_1$

We now prove the induction step. Given a tree T with height $h \ge 2$, we remove all $(h-1)$-nodes and h-nodes of T to produce a tree $T'$ whose height is $h - 2$. The tree $T'$ is still an MST and by the induction hypothesis, there exists an orientation yielding a communication graph $G'$ satisfied Theorem 4. Letting $G = G'$ we add back all of these $(h-1)$-nodes and some h-nodes (if needed) to T and connect them to G, and finally, connect all remaining h-nodes to G. Since the orientation is independent between the $(h-2)$-nodes in $T'$, we only describe the process for a fixed $(h-2)$-node u. First, we describe the process of connecting u’s children (which are $(h-1)$-nodes of T) to G. Let d be the number of neighbors of u that are the $(h-1)$-nodes added in this step, $0 \le d \le 4$. We have four cases:

• 1. $d \le 1$. Let v be the only child of u (if exists). Since u has at least 1 remaining free antenna, we can always add edge uv to G. It is obvious that the orientation satisfies Theorem 4.

• 2. $d = 2$. Then we have two subcases:

  • (a) If u is connected with one node in $T'$, we just add the edges between u and its two children to G.

  • (b) If u is connected with two nodes in $T'$ then one of these two nodes must be the parent s of u in T. As in Fig. 8, node u is $u_1$ is in this case. Let $v_0 = s, v_1$ and $v_2$ be the neighbors of $u_1$ in T. By Lemma 2, there must exist one d-close pair of consecutive $v_i$. If $v_1, v_2$ are d-close, we add the edges $u_1v_1$ and $v_1v_2$ to G as in Fig. 9a. Otherwise, assume that $v_0$ and $v_1$ are d-close, we remove the edge $v_0u_1$ and add the edges $v_0v_1$, $u_1v_1$ and $u_1v_2$ to G as in Fig. 9b.

• 3. $d = 3$. Now we have two subcases:

  • (a) Node u is connected with one node in $T'$. In Fig. 8, node u is $u_5$ is in this case. Let $v_1, v_2$ and $v_3$ be the children of $u = u_5$ in T. By Lemma 2, there must exist two separated d-close pairs of consecutive $v_i$. W.l.o.g., suppose that $v_1, v_2$ are d-close, we add the edges $v_1v_2$, $u_5v_1$ and $u_5v_3$ to G (see Fig. 10a).

  • (b) If u is connected with two nodes in $T'$, then one of these two nodes must be the parent s of u in T. In Fig. 8, node u is $u_1$ is in this case. Let $v_0 = s, v_1, v_2$ and $v_3$ be the neighbors of $u_1$ in T. By Lemma 2, there must exist two separated d-close pairs of consecutive $v_i$’s. W.l.o.g., suppose that $v_0, v_1$ and $v_2, v_3$ are d-close, we remove edge $v_0u_1$ and add the edges $v_0v_1$, $u_1v_1$, $u_1v_2$ and $v_2v_3$ to G (see Fig. 10b).

• 4. $d = 4$. We have two subcases:

  • (a) Node u is connected with one node in $T'$. In Fig. 8, node u is $u_5$ is in this case. Let $v_1, v_2, v_3$ and $v_4$ be the children of $u_5$ in T. By Lemma 2, every pair of consecutive neighbors of $u_5$ are d-close. We add the edges $v_1v_2$, $v_3v_4$, $u_5v_1$ and $u_5v_3$ to G as in Fig. 11.

  • (b) If u is connected with two nodes in $T'$, then one of these two nodes must be the parent s of u in T. In Fig. 8, node u is $u_1$ is in this case. Let $v_0 = s, v_1, v_2, v_3$ and $v_4$ be the neighbors of $u_1$ in T. This is the most involved case. To handle it, our method is to make use of the children of $v_3$. We separate this case into four subcases corresponding to the degree of $v_3$.

    • i. $\deg (v_3) \le 2$. Let w be the only child of $v_3$, if exists. We remove edge $u_1v_0$ and add the edges $v_0v_1$, $u_1v_1$, $u_1v_2$, $v_2v_3$, $v_3v_4$ and $v_3w$ (see Fig. 12).

    • ii. $\deg (v_3) = 3$. Let $w_0 = u_1, w_1$ and $w_2$ be the three neighbors of $v_3$. We consider two subcases.

      • A. $w_1, w_2$ are d-close. We can remove edge $u_1v_0$ and add the edges $v_0v_1$, $u_1v_1$, $u_1v_4$, $v_3v_4$, $v_3w_1$, $v_3v_2$ and $w_1w_2$ (see Fig. 13a).

      • B. $w_1, w_2$ are d-far. Since $\angle (v_2w_0v_3) + \angle (v_3w_0v_4) \le 180^\circ$, by Claim 4, either $w_1, v_2$ or $w_2, v_4$ are d-close. W.l.o.g., suppose that $w_1, v_2$ are d-close, we can remove edge $u_1v_0$ and add the edges $v_0v_1$, $u_1v_1$, $u_1v_4$, $v_3v_4$, $v_3w_1$, $v_3w_2$ and $w_1v_2$ (see Fig. 13b).

    • iii. $\deg (v_3) = 4$. Let $w_0 = u_1, w_1, w_2$ and $w_3$ be the four neighbors of $v_3$. We have five subcases corresponding to the five cases of Lemma 3.

      • A. $w_1, v_2$ and $w_3, v_4$ are both d-close. In this case, we can remove edge $u_1v_0$ and add the edges $v_0v_1$, $u_1v_1$, $u_1v_4$, $w_3v_4$, $v_3w_3$, $v_3w_1$, $v_3w_2$ and $w_1v_2$ (see Fig. 14a).

      • B. $w_1, v_2$ are d-far and $w_1, w_2$ are d-close whereas $w_3, v_4$ are d-close. To handle this case, we do the same as the previous case, but replacing the last two edges by $v_3v_2$ and $w_1w_2$.

      • C. $w_1, v_2$ and $w_1, w_2$ are both d-far. By Lemma 3, $w_2, v_4$ and $w_3, v_0$ are d-close. We can remove edge $u_1v_0$ and add the edges $u_1v_2$, $u_1v_4$, $v_1v_2$, $v_3w_1$, $v_3w_2$, $v_3w_3$, $w_3v_0$ and $w_2v_4$ to obtain a symmetric connected graph (see Fig. 14b).

      • D. $w_3, v_4$ are d-far and $w_3, w_2$ are d-close whereas $w_1, v_2$ are d-close. After a suitable relabeling, the graph will turn to case 4(b)iiiB.

      • E. $w_3, v_4$ and $w_3, w_2$ are both d-far whereas $w_2, v_2$ and $w_1, v_1$ are both d-close. After a suitable relabeling, this subcase is similar to subcase 4(b)iiiC.

    • iv. $\deg (v_3) = 5$. Let $w_0 = u_1, w_1, w_2, w_3$ and $w_4$ be four neighbors of $v_3$. We have three subcases corresponding to the three cases of Lemma 4. Notice that by Lemma 2, all pairs $w_i, w_{(i+1) \mod 5}$ are d-close.

      • A. $w_1, v_2$ and $w_4, v_4$ are both d-close. In this case, we can remove edge $u_1v_0$ and add the edges $v_0v_1$, $u_1v_1$, $u_1v_4$, $w_1v_2$, $v_3w_1$, $v_3w_3$, $v_3w_4$, $w_2w_3$ and $w_4v_4$ (see Fig. 15a).

      • B. $w_1, v_2$ are d-far whereas $w_4, v_0$ and $w_3, v_4$ are both d-close. We can remove edge $u_1v_0$ and add the edges $u_1v_2$, $u_1v_4$, $v_1v_2$, $v_3w_2$, $v_3w_3$, $v_3w_4$, $w_1w_2$, $w_3v_4$ and $w_4v_0$ to obtain a symmetric connected graph (see Fig. 15b).

      • C. $w_4, v_4$ are d-far whereas $w_1, v_1$ and $w_2, v_2$ are both d-close. After a suitable relabeling, this case is the same as case 4(b)ivB.

Finally, we connect all of the remaining h-nodes of T to G by considering each group of nodes that have a common parent. Observe that this scenario is similar to that of the $(h-1)$-nodes, except the fact that the last three subcases of Case 4b cannot occur (because an h-node does not have any children). Thus, we can treat these nodes as the $(h-1)$-nodes when connecting them to G. Therefore, the proof of Theorem 4 is complete. $\square$

Fig. 11

Case $k=3$, $d=4$, $u = u_5$ is connected with one node in previous step

Fig. 12

Case $k=3$, $d=4$, $u = u_1$ is connected with two nodes in previous step and $v_3$ has only one child

Fig. 13

Case $k=3$, $d=4$, $u = u_1$ is connected with two nodes in previous step and $v_3$ has two children. a $w_1, w_2$ are d-close, b $w_1, w_2$ are d-far

Fig. 14

Case $k=3$, $d=4$, $u = u_1$ is connected with two nodes in previous step and $v_3$ has three children. a $w_1, v_2$ and $w_3, v_4$ are both d-close, b $w_1, v_2$ are d-far and $w_1, w_2$ are d-close whereas $w_3, v_4$ are d-close

Fig. 15

Case $k=3$, $d=4$, $u = u_1$ is connected with two nodes in previous step and $v_3$ has four children. a $w_1, v_2$ and $w_4, v_4$ are both d-close, b $w_1, v_2$ are d-far whereas $w_4, v_0$ and $w_3, v_4$ are both d-close

Combining Theorems 3 and 4, we conclude the Proof of Theorem 1.

Remark 1

The most complicated part in subcases 4(b)iiiC, 4(b)iiiE, 4(b)ivB and 4(b)ivC is to maintain the connection between s and $u_1$, since it is the only connection between the nodes v’s and w’s with the remaining nodes of the network. Fortunately, this is achieved by the 5-hop path $sw_3v_3w_2v_4u_1$ as in Fig. 14b and $sw_4v_3w_3v_4u_1$ as in Fig. 15b.

Remark 2

Notice that one of the key ideas of these two algorithms is to force a leaf node to have as few connections as possible, and if such as leaf node is added and has degree 2, then it must connect directly with its parent. This gives us a flexible edge that can be replaced later if necessary.

5 Main algorithm

In this section, we present Algorithm 1 that yields a SCCG for k, $3 \le k \le 4$, antennas and the range is bounded by $2sin\left( \frac{180^\circ }{k}\right)$. The algorithm calls the recursive Procedure FourAntennas and ThreeAntennas for $k = 3$ and $k = 4$, respectively. In order to enhance readability, we describe the process of connecting node $v_3$ and its children in Case 4b when $k = 3$ in the procedure ConnectBridgeNode. Notice that the addition operation in the index of a neighbor of a node is done modulo the number of neighbors of this node.

Runtime Analysis: It is easy to see that Procedure FourAntennas and ThreeAntennas run in O(n). The time to construct a Euclidean MST with max degree 5 spanning the UDG of a set of points S is O(nlogn). Thus, the time complexity of Algorithm 1 is O(nlogn). The correctness of the algorithm follows from Theorem 1.

6 Antenna orientation and power assignment (AOPA)

Let S be a set of nodes in the plane such that each node is equipped with k directional antennas with beam-width $\theta \ge 0$ ($k = 3$ or $k = 4$). Let r(u) be the range assigned to a node u in S. The goal of the AOPA problem is to find a range assignment for every node u in S such that (i) there exists a way to orient the antennas of the nodes in order to yield a symmetric connected communication graph, and (ii) $\sum _{u \in P}{r(u)^\beta }$ is minimized, where $\beta \ge 1$ is the distance-power gradient (in a WSN, typically, $2 \le \beta \le 5)$.

In this section, we show that our antenna orientation algorithms for both $k = 3$ and $k = 4$ also yield O(1)-approximation algorithms for the AOPA problem. Let T be an MST with maximum degree 5 spanning S and G be the communication graph obtained by one of the two algorithms above. We define that an edge in T is used to estimate length of an edge in G as below.

Definition 6

Let $\overline{pc}$ be an edge between a node p and its child c in an MST T. Let u and v be two nodes connected directly in the communication graph G (u and/or v may coincide with p and/or c). If $|\overline{pc}| \le r_k \cdot |\overline{uv}|$, then we say that edge $\overline{pc}$ can be used to estimate the length of edge $\overline{uv}$, where $3 \le k \le 4$ denotes the number of antennas equipped with a node in the WSN and $r_k = 2sin\left( \frac{180^\circ }{k}\right)$.

We say that an edge $\bar{e}$ in T is used to estimate the power assigned to a node u if it is used to estimate length of the longest edge in G incident to u.

We first show how to estimate the total power in terms of a given MST T (of degree 5) spanning S. Let r(u) denote the range assigned to node u. Let $\bar{e}$ denote the edge in T that is used to estimate the power assigned to u. The power P(u) assigned to u can be bounded by $P(u) \le (r_k \times |\bar{e}|)^\beta$.

Let $Cost(AOPA_S)$ be the total power assignment of an orientation algorithm for the set of nodes S. We can bound this value by

$$\begin{aligned} Cost(AOPA_S) = \sum _{u \in S} P(u) \le \sum _{e \in T}{k_e \times (r_k \times |e|)^\beta }, \end{aligned}$$

where $k_e$ is the number of times an edge e in T is used to estimate the power assigned to a node in S. Let $k_{max}$ be the maximum number of times that an edge is used to estimate power of a node in S. We have:

$$\begin{aligned} Cost(AOPA_S)&\le k_{max} \times \sum _{e \in T}{(r_k \times |e|)^\beta } \\&\le k_{max} \times r_k^\beta \sum _{e \in T}{|e|^\beta } \\&\le k_{max} \times r_k^{\beta } \times Cost_{\beta }(T). \end{aligned}$$

In the following we say that u connects with v if u connects directly with v. We also say u disconnects with v if the edge $\overline{uv}$ is removed from the communication graph G, unless otherwise stated. An edge of G is said to be long if it is not an edge in T, and short otherwise. We refer to “step i” in the following proof as the i-th time that the Procedure FourAntennas or ThreeAntennas is recursively called.

First we have some observations about our two algorithms.

Observation 1

A long edge is never removed.

Observation 2

If a short edge $\overline{su}$, where s is parent of u in T, is removed from G at step i (i.e., the $i-th$ recursive call of Procedure ThreeAntennas or FourAntennas), then this edge must have been added to G at step $i - 1$ ($i \ge 2)$ and degree of u in G at step $i - 1$ must be 2.

Observation 3

If a short edge $\overline{su}$ is removed from G at step i, then at the end of both algorithms, u must connect directly (in G) with another child $u'$ of s, and s must connect directly (in G) with a child v of u.

6.1 Case $k = 4$

For this case we have an additional observation concerning our algorithm for $k = 4$.

Observation 4

If a parent s never connects with its child u in G, then u must connect with s via another child $u'$ of s.

Theorem 5

Let e be an edge between a parent s and a child u in T. According to the algorithm in Sect. 3, the number of times that e is used to estimate power of a node in G is at most 4.

Proof

We separate the proof into three cases corresponding to the status of the edge $\overline{su}$ in G.

• If s connects with u at step i, and this connection still remains till the end the algorithm, then $e = \overline{su}$ is used to estimate the length of at most two edges su and $uu'$, where $u'$ is another child of s, hence e is used to estimate power of at most three nodes: s, u and $u'$ (see Fig. 2 where $u = u_1$ and $u' = u_5$).

• If s connects with u at step i, and s disconnects with u at step $i + 1$ (Observation 2), then according to Observation 3, $e = \overline{su}$ is used to estimate length of at most two edges sv and $uu'$, where $u'$ is another child of s and v is a child of u, hence e is used to estimate power of at most four nodes: s, u, $u'$ and v (see Figs. 3b and 5b; in Fig. 3b, $u = u_1$, $u' = u_5$ and $v = v_1$ and in Fig. 5b, $u = u_1$, $u' = u_5$ and $v = v_4$).

• If s never connects with u in G, then u must connect with s via another child $u'$ of s (Observation 4). Hence $e = \overline{su}$ is used to estimate the length of at most one edge $uu'$ or in other words, the power of two nodes u and $u'$ (see Figs. 2 and 4 where $u = u_5$ and $u' = u_1$).

$\square$

Corollary 1

The algorithm for $k = 4$ in Sect. 3 yields a communication graph G with a total power assignment that satisfies $Cost(AOPA_S) \le 4 \times \sqrt{2}^{\beta } \times Cost_\beta (T)$.

6.2 Case $k = 3$

In this subsection, we define a bridge node to be a node having the role of node $v_3$ in the algorithm for $k = 3$ in Sect. 4. Notice that a bridge node never connects with its parent in the communication graph G. Additionally, we see that Observation 4 still holds for the algorithm for $k = 3$ if u is not a bridge node.

Theorem 6

Let e be an edge between a parent s and a child u in T. According to the algorithm in Sect. 4, the number of times that e is used to estimate the power of a node in G is at most 4.

Proof

Similar to case $k = 4$, we separate the proof into three cases corresponding to the status of edge $\overline{su}$ in G.

• If s connects with u at step i, and this connection still remains till the end of the algorithm, then $e = \overline{su}$ is used to estimate the length of at most two edges su and $uu'$, where $u'$ is another child of s, hence e is used to estimate the power of at most three nodes: s, u and $u'$ (see Fig. 8 where $u = u_1$ and $u' = u_5$).

• If s connects with u at step i, and then disconnected with u at step $i + 1$ (Observation 2), then according to Observation 3, $e = \overline{su}$ is used to estimate the length of at most two edges sv and $uu'$, where $u'$ is another child of s and v is a child of u, hence e is used to estimate the power of at most four nodes: s, u, $u'$ and v (see Figs. 9b, 10b and 11 where, $u = u_1$, $u' = u_5$ and $v = v_1$).

• If s never connects with u in G, and u is not a bridge node, then u must connect with s via another child $u'$ of s, hence $e = \overline{su}$ is used to estimate the length of at most one edge $uu'$ or in other words, the power of two nodes u and $u'$ (see Figs. 8 and 10 where $u = u_5$ and $u' = u_1$).

• If u is a bridge node, we claim that edge $e = \overline{su}$ is used to estimate power of at most four nodes.

To prove the claim, it is easy to see that the edge between a bridge node v and its parent u can only be used to estimate the power of nodes participating in connecting children of u and the children of v to G. Therefore analyzing $k_e$ for $e = u_1v_3$ in four the subcases of case 4b in the proof of Theorem 4 is sufficient to prove the claim.

• 1. $\deg (v_3) \le 2$. In this case, e can be used to estimate the length of at most two edges $v_3v_2$ and $v_3v_4$, or the power of three nodes $v_2$, $v_3$ and $v_4$ (see Fig. 12).

• 2. $\deg (v_3) = 3$. Let $w_0 = u_1, w_1$ and $w_2$ be the three neighbors of $v_3$. We have two subcases.

  • (a) $w_1, w_2$ are d-close. In this case, e can be used to estimate the length of at most two edges $v_3v_2$ and $v_3v_4$, or the power of three nodes $v_2$, $v_3$ and $v_4$ (see Fig. 13a).

  • (b) $w_1, w_2$ are d-far. In this case, e can be used to estimate the length of at most two edges $v_3v_4$ and $w_1v_2$, or the power of four nodes $v_3$, $v_4$, $w_1$ and $v_2$ (see Fig. 13b).

• 3. $\deg (v_3) = 4$. Let $w_0 = u_1, w_1, w_2$ and $w_3$ be the four neighbors of $v_3$. Now we have five subcases corresponding to the five cases of Lemma 3.

  • (a) $w_1, v_2$ and $w_3, v_4$ are both d-close. In this case, e can be used to estimate length of at most two edges $w_3v_4$ and $w_1v_2$, or power of four nodes $w_3$, $v_4$, $w_1$ and $v_2$ (see Fig. 14a).

  • (b) $w_1, v_2$ are d-far and $w_1, w_2$ are d-close whereas $w_3, v_4$ are d-close. In this case, e can be used to estimate the length of at most two edges $w_3v_4$ and $v_3v_2$, or the power of four nodes $w_3$, $v_4$, $v_3$ and $v_2$.

  • (c) $w_1, v_2$ and $w_1, w_2$ are both d-far. In this case, e can be used to estimate the length of at most two edges $w_2v_4$ and $w_3v_0$, or the power of four nodes $w_2$, $v_4$, $w_3$ and $v_0$ (see Fig. 14b).

  • (d) $w_3, v_4$ are d-far and $w_3, w_2$ are d-close whereas $w_1, v_2$ are d-close. This case is analogous to Case 3b.

  • (e) $w_3, v_4$ and $w_3, w_2$ are both d-far whereas $w_2, v_2$ and $w_1, v_1$ are both d-close. This case is analogous to Case 3c.

• 4. $\deg (v_3) = 5$. Let $w_0 = u_1, w_1, w_2, w_3$ and $w_4$ be four neighbors of $v_3$. Now we have three sub cases corresponding to three cases of Lemma 4.

  • (a) $w_1, v_2$ and $w_4, v_4$ are both d-close. In this case, e can be used to estimate length of at most two edges $w_4v_4$ and $w_1v_2$, or power of four nodes $w_4$, $v_4$, $w_1$ and $v_2$ (see Fig. 15a).

  • (b) $w_1, v_2$ are d-far whereas $w_4, v_0$ and $w_3, v_4$ are both d-close. In this case, e can be used to estimate length of at most two edges $w_3v_4$ and $w_4v_0$, or power of four nodes $w_3$, $v_4$, $w_4$ and $v_0$ (see Fig. 15b).

  • (c) $w_4, v_4$ are d-far whereas $w_1, v_1$ and $w_2, v_2$ are both d-close. This case is analogous to case 4b.

  This concludes the proof of the claim and hence the proof of Theorem 6 is complete.

$\square$

Corollary 2

The algorithm for $k = 3$ in Sect. 4 yields a communication graph G with a total power assignment that satisfies $Cost(AOPA_S) \le 4 \times \sqrt{3}^{\beta } \times Cost_\beta (T)$.

Combining Corollaries 1 and 2, we conclude the proof of Theorem 2.

Remark 3

Although our bound for $k_{max}$ is greater than the one obtained by Tran et al., the required range obtained by our algorithms is smaller. In particular, if $\beta \ge 2$, our approximation ratio for the AOPA problems is better.

7 Simulation

In this section, we perform simulation over 5000 instances of sparse, medium, and dense WSNs of 100 nodes in the plane of size $1000 \times 1000$. A UDG spanning a WSN is considered to be sparse, medium, or dense if the number of its edges is less than 4n, in the range of $[4n, n^2/4)$, or at least $n^2/4$, respectively, where n is the number of nodes. For every instance, we run Tran et al.’s algorithms (Tran and Huynh 2020), Biniaz’s algorithms (Biniaz 2020) and our algorithms to yield a symmetric connected communication graph for $k = 3$ and $k = 4$. We then get the ratio of the required range over the length of the longest MST edge. Tables 1 and 2 show the simulation results.

The simulation results show that our algorithms perform better than Tran et al.’s in both metrics, especially in case $k = 3$, which is expected as the theoretical analysis shows. The reason is that our algorithms try to maintain the structure of the MST as much as possible by exploiting more geometric properties of a Euclidean MST. The shortcut edges are chosen more carefully to replace the original edges of the MST in order to save the communication cost. In Table 1, the required ranges of our algorithms are nearly equal to the lengths of the longest MST edges that are also the optimal ranges to induce symmetric connected communication graphs when using omni-directional antennas. In other words, our algorithms provide nearly optimal required ranges in order to establish SCCG for DWSNs. In addition, Table 2 shows that the results of our algorithms are closer to the optimal ones than those obtained by the algorithms in Biniaz (2020) for the AOPA problems. In case $k = 3$, even when $\beta$ is close to 6, our algorithm still achieves a sub-2 ratio, in contrast with other methods. Another observation is that all algorithms perform almost the same for different types of density of input graphs, which shows that these algorithms have density robustness property.

Table 1 Average ratio of required range and length of the longest MST edge

Table 2 Average ratio of total power assignment and $Cost_\beta (MST)$

8 Conclusion

In this paper, we have proposed algorithms which, when given a set of sensor nodes in the plane equipped with 3 or 4 directional antennas having beam-width $\theta \ge 0$, produce orientations such that the induced communication graphs are symmetric connected and the required ranges are at most $2sin\left( \frac{180^\circ }{k}\right)$. We also prove that not only do our algorithms improve on the required transmission ranges, they also give smaller total power assignments than in Tran and Huynh (2020). The results demonstrate that our method outperforms previous approaches in both theoretical and empirical aspects. To conclude this work, we point out that there are several interesting open problems for further research such as (1) maintaining symmetric connectivity for DWSNs whose nodes are equipped with more than 2 antennas having a positive transmission angle $\theta > 0$, (2) constructing fault-tolerant symmetric connected communication networks, and (3) investigating connectivity and interference for DWSNs in more realistic interference models such as SINR.