Abstract
We introduce forest straight-line programs (FSLPs) as a compressed representation of unranked ordered node-labelled trees. FSLPs are based on the operations of forest algebra and generalize tree straight-line programs. We compare the succinctness of FSLPs with two other compression schemes for unranked trees: top dags and tree straight-line programs of first-child/next sibling encodings. Efficient translations between these formalisms are provided. Finally, we show that equality of unranked trees in the setting where certain symbols are associative or commutative can be tested in polynomial time. This generalizes previous results for testing isomorphism of compressed unordered ranked trees.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Generally speaking, grammar-based compression represents an object succinctly by means of a small context-free grammar. In many grammar-based compression formalisms such a grammar can be exponentially smaller than the object. Henceforth, there is a great interest in problems that can be solved in polynomial time on the grammar, while requiring at least linear time on the original uncompressed object. One of the most well-known and fundamental such problems is testing equality of the strings produced by two context-free string grammars, each producing exactly one string (such grammars are also known as straight-line programs — in this paper we use the term string straight-line program, SSLP for short). Polynomial time solutions to this problem were discovered, in different contexts by different groups of people, see the survey [14] for references.
Grammar-based compression has been generalized from strings to ordered ranked node-labelled trees, by means of linear context-free tree grammars generating exactly one tree [6]. Such grammars are also known as tree straight-line programs, TSLPs for short. Equality of the trees produced by two TSLPs can also be checked in polynomial time: one constructs SSLPs for the pre-order traversals of the trees, and then applies the above mentioned result for SSLPs, see [6]. The tree case becomes more complex when unordered ranked trees are considered. Such trees can be represented using TSLPs, by simply ignoring the order of children in the produced tree. Checking isomorphism of unordered ranked trees generated by TSLPs was recently shown to be solvable in polynomial time [16]. The solution transforms the TSLPs so that they generate canonical representations of the original trees and then checks equality of these canonical forms.
The aforementioned result for ranked trees cannot be applied to unranked trees (where the number of children of a node is not bounded), which arise for instance in XML document trees. This is unfortunate, because (i) grammar-based compression is particularly effective for XML document trees (see [15]), and (ii) XML document trees can often be considered unordered (one speaks of “data-centric XML”, see e.g. [1, 3, 5, 20]), allowing even stronger grammar-based compressions [17].
In this paper we introduce a generalization of TSLPs and SSLPs that allows to produce ordered unranked node-labelled trees and forests (i.e., ordered sequences of trees) that we call forest straight-line programs, FSLPs for short. In contrast to TSLPs, FSLPs can compress very wide and flat trees. For instance, the tree \(f(a,a,\ldots , a)\) with n many a’s is not compressible with TSLPs but can be produced by an FSLP of size \(O(\log n)\). FSLPs are based on the operations of horizontal and vertical forest composition from forest algebras [4]. The main contributions of this paper are the following:
Comparison with Other Formalisms. We compare the succinctness of FSLPs with two other grammar-based formalisms for compressing unranked node-labelled ordered trees: TSLPs for “first-child/next-sibling” (fcns) encodings and top dags. The fcns-encoding is the standard way of transforming an unranked tree into a binary tree. Then the resulting binary tree can be succinctly represented by a TSLP. This approach was used to apply the TreeRePair-compressor from [15] to unranked trees. We prove that FSLPs and TSLPs for fcns-encodings are equally succinct up to constant multiplicative factors and that one can change between both representations in linear time (Propositions 9 and 10).
Top dags are another formalism for compressing unranked trees [2]. Top dags use horizontal and vertical merge operations for tree construction, which are very similar to the horizontal and vertical concatenation operations from FSLPs. Whereas a top dag can be transformed in linear time into an equivalent FSLP with a constant multiplicative blow-up (Proposition 6), the reverse transformation (from an FSLP to a top dag) needs time \(O(\sigma \cdot n)\) and involves a multiplicative blow-up of size \(O(\sigma )\) where \(\sigma \) is the number of node labels of the tree (Proposition 7). A simple example (Example 8) shows that this \(\sigma \)-factor is unavoidable. The reason for the \(\sigma \)-factor is a technical restriction in the definition of top dags: In contrast to FSLPs, top dags only allow sharing of common subtrees but not of common subforests. Hence, sharing between (large) subtrees which only differ in their root labels may be impossible at all (as illustrated by Example 8), and this leads to the \(\sigma \)-blow-up in comparison to FSLPs. The impossibility of sharing subforests would also complicate the technical details of our main algorithmic results for FSLPs (in particular Proposition 10 and Theorem 13 which is discussed below) for which we make heavy use of a particular normal form for FSLPs that exploits the sharing of proper subforests. We therefore believe that at least for our purposes, FSLPs are a more adequate formalism than top dags.
Testing Equality Modulo Associativity and Commutativity. Our main algorithmic result for FSLPs can be formulated as follows: Fix a set \(\varSigma \) of node labels and take a subset \(\mathcal {C} \subseteq \varSigma \) of “commutative” node labels and a subset \(\mathcal {A} \subseteq \varSigma \) of “associative” node labels. This means that for all \(a \in \mathcal {A}\), \(c \in \mathcal {C}\) and all trees \(t_1, t_2, \ldots , t_n\) (i) we do not distinguish between the trees \(c(t_1, \ldots , t_n)\) and \(c(t_{\sigma (1)}, \ldots , t_{\sigma (n)} )\), where \(\sigma \) is any permutation (commutativity), and (ii) we do not distinguish the trees \(a(t_1, \ldots , t_n)\) and \(a(t_1, \ldots , t_{i-1}, a(t_i,\ldots , t_{j-1}), t_j, \ldots , t_n)\) for \(1 \le i \le j \le n+1\) (associativity). We then show that for two given FSLPs \(F_1\) and \(F_2\) that produce trees \(t_1\) and \(t_2\) (of possible exponential size), one can check in polynomial time whether \(t_1\) and \(t_2\) are equal modulo commutativity and associativity (Theorem 13). Note that unordered tree isomorphism corresponds to the case \(\mathcal {C} = \varSigma \) and \(\mathcal {A}=\emptyset \) (in particular we generalize the result from [16] for ranked unordered trees). Theorem 13 also holds if the trees \(t_1\) and \(t_2\) are given by top dags or TSLPs for the fcns-encodings, since these formalisms can be transformed efficiently into FSLPs. Theorem 13 also shows the utility of FSLPs even if one is only interested in say binary trees, which are represented by TSLPs. The law of associativity will yield very wide and flat trees that are no longer compressible with TSLPs but are still compressible with FSLPs.
Missing proofs can be found in the arXiv version of this paper [11].
2 Straight-Line Programs over Algebras
We will produce strings, trees and forests by algebraic expressions over certain algebras. These expressions will be compressed by directed acyclic graphs. In this section, we introduce the general framework, which will be reused several times in this paper.
An algebraic structure is a tuple \(\mathcal {A} = (A, f_1, \ldots , f_k)\) where A is the universe and every \(f_i :A^{n_i} \rightarrow A\) is an operation of a certain arity \(n_i\). In this paper, the arity of all operations will be at most two. If \(n_i = 0\), then \(f_i\) is called a constant. Moreover, it will be convenient to allow partial operations for the \(f_i\). Algebraic expressions over \(\mathcal {A}\) are defined in the usual way: if \(e_1, \ldots , e_{n_i}\) are algebraic expressions over \(\mathcal {A}\), then also \(f_i(e_1, \ldots , e_{n_i})\) is an algebraic expressions over \(\mathcal {A}\). For an algebraic expression e, \(\llbracket e \rrbracket \in A\) denotes the element to which e evaluates (it can be undefined).
A straight-line program (SLP for short) over \(\mathcal {A}\) is a tuple \(P = (V, S, \rho )\), where V is a set of variables, \(S \in V\) is the start variable, and \(\rho \) maps every variable \(A \in V\) to an expression of the form \(f_i(A_1, \ldots , A_{n_i})\) (the so called right-hand side of A) such that \(A_1,\ldots ,A_{n_i} \in V\) and the edge relation \(E(P) =\{(A, B) \in V \times V {\mid } B\ \text {occurs in}\ \rho (A) \}\) is acyclic. This allows to define for every variable \(A \in V\) its value \(\llbracket A \rrbracket _{P}\) inductively by \(\llbracket A \rrbracket _{P} = f_i(\llbracket A_1 \rrbracket _{P}, \ldots , \llbracket A_{n_i} \rrbracket _{P})\) if \(\rho (A) = f_i(A_1, \ldots , A_{n_i})\). Since the \(f_i\) can be partially defined, the value of a variable can be undefined. The SLP P will be called valid if all values \(\llbracket A \rrbracket _{P}\) (\(A \in V\)) are defined. In our concrete setting, validity of an SLP can be tested by a simple syntax check. The value of P is \(\llbracket P \rrbracket = \llbracket S \rrbracket _{P}\). Usually, we prove properties of SLPs by induction along the partial order \(E(P)^*\).
It will be convenient to allow for the right-hand sides \(\rho (A)\) algebraic expressions over \(\mathcal {A}\), where the variables from V can appear as atomic expressions. By introducing additional variables, we can transform such an SLP into an equivalent SLP of the original form. We define the size |P| of an SLP P as the total number of occurrences of operations \(f_1,\ldots , f_k\) in all right-hand sides (which is the number of variables if all right-hand sides have the standard form \(f_i(A_1, \ldots , A_{n_i})\)).
Sometimes it is useful to view an SLP \(P = (V,S,\rho )\) as a directed acyclic graph (dag) (V, E(P)), together with the distinguished output node S, and the node labelling that associates the label \(f_i\) with the node \(A \in V\) if \(\rho (A) = f_i(A_1, \ldots , A_{n_i})\). Note that the outgoing edges \((A,A_1), \ldots , (A,A_{n_i})\) have to be ordered since \(f_i\) is in general not commutative and that multi-edges have to be allowed. Such dags are also known as algebraic circuits in the literature.
String Straight-Line Programs. A widely studied type of SLPs are SLPs over a free monoid \((\varSigma ^*, \cdot , \varepsilon , (a)_{a \in \varSigma })\), where \(\cdot \) is the concatenation operator (which, as usual, is not written explicitly in expressions) and the empty string \(\varepsilon \) and every alphabet symbol \(a \in \varSigma \) are added as constants. We use the term string straight-line programs (SSLPs for short) for these SLPs. If we want to emphasize the alphabet \(\varSigma \), we speak of an SSLP over \(\varSigma \). In many papers, SSLPs are just called straight-line programs; see [14] for a survey. Occasionally we consider SSLPs without a start variable S and then write \((V,\rho )\).
Example 1
Consider the SSLP \(G = (\{S,A,B,C\},S,\rho )\) over the alphabet \(\{a,b\}\) with \(\rho (S) = AAB\), \(\rho (A) = CBB\), \(\rho (B) = CaC\), \(\rho (C) = b\). We have \(\llbracket B \rrbracket _{G} = bab\), \(\llbracket A \rrbracket _{G} = bbabbab\), and \(\llbracket G \rrbracket = bbabbabbbabbabbab\). The size of G is 8 (six concatenation operators are used in the right-hand sides, and there are two occurrences of constants).
In the next two sections, we introduce two types of algebras for trees and forests.
3 Forest Algebras and Forest Straight-Line Programs
Trees and Forests. Let us fix a finite set \(\varSigma \) of node labels for the rest of the paper. We consider \(\varSigma \)-labelled rooted ordered trees, where “ordered” means that the children of a node are totally ordered. Every node has a label from \(\varSigma \). Note that we make no rank assumption: the number of children of a node (also called its degree) is not determined by its node label. The set of nodes (resp. edges) of t is denoted by V(t) (resp., E(t)). A forest is a (possibly empty) sequence of trees. The size |f| of a forest is the total number of nodes in f. The set of all \(\varSigma \)-labelled forests is denoted by \(\mathcal {F}_0(\varSigma )\) and the set of all \(\varSigma \)-labelled trees is denoted by \(\mathcal {T}_0(\varSigma )\). As usual, we can identify trees with expressions built up from symbols in \(\varSigma \) and parentheses. Formally, \(\mathcal {F}_0(\varSigma )\) and \(\mathcal {T}_0(\varSigma )\) can be inductively defined as the following sets of strings over the alphabet \(\varSigma \cup \{(, )\}\).
-
If \(t_1, \ldots , t_n\) are \(\varSigma \)-labelled trees with \(n \ge 0\), then the string \(t_1 t_2 \cdots t_n\) is a \(\varSigma \)-labelled forest (in particular, the empty string \(\varepsilon \) is a \(\varSigma \)-labelled forest).
-
If f is a \(\varSigma \)-labelled forest and \(a \in \varSigma \), then \(a(f)\) is a \(\varSigma \)-labelled tree (where the singleton tree \(a()\) is usually written as a).
Let us fix a distinguished symbol \(x \not \in \varSigma \) for the rest of the paper (called the parameter). The set of forests \(f \in \mathcal {F}_0(\varSigma \cup \{x\})\) such that x has a unique occurrence in f and this occurrence is at a leaf node is denoted by \(\mathcal {F}_1(\varSigma )\). Let \(\mathcal {T}_1(\varSigma ) = \mathcal {F}_1(\varSigma ) \cap \mathcal {T}_0(\varSigma \cup \{x\})\). Elements of \(\mathcal {T}_1(\varSigma )\) (resp., \(\mathcal {F}_1(\varSigma )\)) are called tree contexts (resp., forest contexts). We finally define \(\mathcal {F}(\varSigma ) = \mathcal {F}_0(\varSigma ) \cup \mathcal {F}_1(\varSigma )\) and \(\mathcal {T}(\varSigma ) = \mathcal {T}_0(\varSigma ) \cup \mathcal {T}_1(\varSigma )\). Following [4], we define the forest algebra  as follows:
as follows:
-
\(\mathop {\boxdot }\) is the horizontal concatenation operator: for forests \(f_1, f_2 \in \mathcal {F}(\varSigma )\), \(f_1 \mathop {\boxdot }f_2\) is defined if \(f_1 \in \mathcal {F}_0(\varSigma )\) or \(f_2 \in \mathcal {F}_0(\varSigma )\) and in this case we set \(f_1 \mathop {\boxdot }f_2 = f_1 f_2\) (i.e., we concatenate the corresponding sequences of trees).
-
 is the vertical concatenation operator: for forests \(f_1, f_2 \in \mathcal {F}(\varSigma )\),
is the vertical concatenation operator: for forests \(f_1, f_2 \in \mathcal {F}(\varSigma )\),  is defined if \(f_1 \in \mathcal {F}_1(\varSigma )\) and in this case
is defined if \(f_1 \in \mathcal {F}_1(\varSigma )\) and in this case  is obtained by replacing in \(f_1\) the unique occurrence of the parameter x by the forest \(f_2\).
is obtained by replacing in \(f_1\) the unique occurrence of the parameter x by the forest \(f_2\). -
Every \(a \in \varSigma \) is identified with the unary function \(a : \mathcal {F}(\varSigma ) \rightarrow \mathcal {T}(\varSigma )\) that produces \(a (f )\) when applied to \(f \in \mathcal {F}(\varSigma )\).
-
\(\varepsilon \in \mathcal {F}_0(\varSigma )\) and \(x \in \mathcal {F}_1(\varSigma )\) are constants of the forest algebra.
For better readability, we also write \(f\langle g \rangle \) instead of  , fg instead of \(f \mathop {\boxdot }g\), and a instead of \(a ( \varepsilon )\). Note that a forest \(f \in \mathcal {F}(\varSigma )\) can be also viewed as an algebraic expression over \(\mathsf {FA}(\varSigma )\), which evaluates to f itself (analogously to the free term algebra).
, fg instead of \(f \mathop {\boxdot }g\), and a instead of \(a ( \varepsilon )\). Note that a forest \(f \in \mathcal {F}(\varSigma )\) can be also viewed as an algebraic expression over \(\mathsf {FA}(\varSigma )\), which evaluates to f itself (analogously to the free term algebra).
First-Child/Next-Sibling Encoding. The first-child/next-sibling encoding transforms a forest over some alphabet \(\varSigma \) into a binary tree over \(\varSigma \uplus \{\bot \}\). We define \(\text {fcns}:\mathcal {F}_0(\varSigma ) \rightarrow \mathcal {T}_0(\varSigma \uplus \{\bot \})\) inductively by: (i) \(\text {fcns}(\varepsilon ) = \bot \) and (ii) \(\text {fcns}(a(f )g) = a(\text {fcns}(f) \text {fcns}(g) )\) for \(f, g \in \mathcal {F}_0(\varSigma )\), \(a \in \varSigma \). Thus, the left (resp., right) child of a node in \(\text {fcns}(f)\) is the first child (resp., right sibling) of the node in f or a \(\bot \)-labelled leaf if it does not exist.
Example 2
If \(f = a (bc)d(e )\) then
Forest Straight-Line Programs. A forest straight-line program over \(\varSigma \), FSLP for short, is a valid straight-line program over the algebra \(\mathsf {FA}(\varSigma )\) such that \(\llbracket F \rrbracket \in \mathcal {F}_0(\varSigma )\). Iterated vertical and horizontal concatenations allow to generate forests, whose depth and width is exponential in the FSLP size. For an FSLP \(F = (V,S,\rho )\) and \(i \in \{0,1\}\) we define \(V_i = \{ A \in V \mid \llbracket A \rrbracket _{F} \in \mathcal {F}_i(\varSigma ) \}\).
Example 3
Consider the FSLP \(F = (\{S,A_0,A_1, \ldots , A_n,B_0,B_1, \ldots , B_n\}, S, \rho )\) over \(\{a,b,c\}\) with \(\rho \) defined by \(\rho (A_0) = a\), \(\rho (A_i) = A_{i-1} A_{i-1}\) for \(1 \le i \le n\), \(\rho (B_0) = b ( A_n x A_n )\), \(\rho (B_i) = B_{i-1} \langle B_{i-1} \rangle \) for \(1 \le i \le n\), and \(\rho (S) = B_n \langle c \rangle \). We have \(\llbracket F \rrbracket = b (a^{2^n} b (a^{2^n} \cdots b (a^{2^n} c \, a^{2^n} )\cdots a^{2^n} )a^{2^n} )\), where b occurs \(2^n\) many times. A more involved example can be found in the arXiv version of this paper [11].
FSLPs generalize tree straight-line programs (TSLPs for short) that have been used for the compression of ranked trees before, see e.g. [6, 15]. We only need TSLPs for binary trees. A TSLP over \(\varSigma \) can then be defined as an FSLP \(T = (V,S,\rho )\) such that for every \(A \in V\), \(\rho (A)\) has the form a, \(a ( BC )\), \(a ( xB )\), \(a ( Bx )\), or \(B \langle C \rangle \) with \(a \in \varSigma \), \(B,C \in V\). TSLPs can be used in order to compress the fcns-encoding of an unranked tree; see also [15]. It is not hard to see that an FSLP F that produces a binary tree can be transformed into a TSLP T such that \(\llbracket F \rrbracket = \llbracket T \rrbracket \) and \(|T| \in O(|F|)\). This is an easy corollary of our normal form for FSLPs that we introduce next (see also the proof of Proposition 9).
Normal Form FSLPs. In this paragraph, we introduce a normal form for FSLPs that turns out to be crucial in the rest of the paper. An FSLP \(F=(V, S, \rho )\) is in normal form if \(V_0 = V_0^{\top } \uplus V_0^{\bot }\) and all right-hand sides have one of the following forms:
-
\(\rho (A) = \varepsilon \), where \(A \in V_0^\top \),
-
\(\rho (A) = BC\), where \(A \in V_0^\top , B, C \in V_0\),
-
\(\rho (A) = B \langle C \rangle \), where \(B \in V_1\) and either \(A, C \in V_0^\bot \) or \(A,C \in V_1\),
-
\(\rho (A) = a ( B )\), where \(A \in V_0^\bot \), \(a \in \varSigma \) and \(B \in V_0\),
-
\(\rho (A) = a ( B x C )\), where \(A \in V_1\), \(a \in \varSigma \) and \(B, C \in V_0\).
Note that the partition \(V_0 = V_0^{\top } \uplus V_0^{\bot }\) is uniquely determined by \(\rho \). Also note that variables from \(V_1\) produce tree contexts and variables from \(V_0^{\bot }\) produce trees, whereas variables from \(V_0^{\top }\) produce forests with arbitrarily many trees.
Let \(F=(V,S,\rho )\) be a normal form FSLP. Every variable \(A \in V_1\) produces a vertical concatenation of (possibly exponentially many) variables, whose right-hand sides have the form \(a ( B x C )\). This vertical concatenation is called the spine of A. Formally, we split \(V_1\) into \(V_1^{\top } = \{ A \in V_1 \mid \exists B, C \in V_1 : \rho (A) = B\langle C\rangle \}\) and \(V_1^{\bot } = V_1 \setminus V_1^{\top }\). We then define the vertical SSLP  over \(V_1^{\bot }\) with \(\rho _1(A) = BC\) whenever \(\rho (A) = B\langle C\rangle \). For every \(A \in V_1\) the string
over \(V_1^{\bot }\) with \(\rho _1(A) = BC\) whenever \(\rho (A) = B\langle C\rangle \). For every \(A \in V_1\) the string  is called the spine of A (in F), denoted by \(\text {spine}_{F}(A)\) or just \(\text {spine}(A)\) if F is clear from the context. We also define the horizontal SSLP \(F^{\mathop {\boxdot }} = (V_0^{\top }, \rho _0)\) over \(V_0^{\bot }\), where \(\rho _0\) is the restriction of \(\rho \) to \(V_0^{\top }\). For every \(A \in V_0\) we use \(\text {hor}(A)\) to denote the string \(\llbracket A \rrbracket _{F^{\mathop {\boxdot }}} \in (V_0^{\bot })^*\). Note that \(\text {spine}(A) = A\) (resp., \(\text {hor}(A) = A\)) for every \(A \in V_1^{\bot }\) (resp., \(A \in V_0^\bot \)).
is called the spine of A (in F), denoted by \(\text {spine}_{F}(A)\) or just \(\text {spine}(A)\) if F is clear from the context. We also define the horizontal SSLP \(F^{\mathop {\boxdot }} = (V_0^{\top }, \rho _0)\) over \(V_0^{\bot }\), where \(\rho _0\) is the restriction of \(\rho \) to \(V_0^{\top }\). For every \(A \in V_0\) we use \(\text {hor}(A)\) to denote the string \(\llbracket A \rrbracket _{F^{\mathop {\boxdot }}} \in (V_0^{\bot })^*\). Note that \(\text {spine}(A) = A\) (resp., \(\text {hor}(A) = A\)) for every \(A \in V_1^{\bot }\) (resp., \(A \in V_0^\bot \)).
The intuition behind the normal form can be explained as follows: Consider a tree context \(t \in \mathcal {T}_1(\varSigma ) \setminus \{x\}\). By decomposing t along the nodes on the unique path from the root to the x-labelled leaf, we can write t as a vertical concatenation of tree contexts \(a_1 (f_1 x g_1 ), \ldots , a_n (f_n x g_n )\) for forests \(f_1, g_1, \ldots , f_n, g_n\) and symbols \(a_1, \ldots , a_n\). In a normal form FSLP one would produce t by first deriving a vertical concatenation \(A_1 \langle \cdots \langle A_n \rangle \cdots \rangle \). Every \(A_i\) is then derived to \(a_i ( B_i x C_i )\), where \(B_i\) (resp., \(C_i\)) produces the forest \(f_i\) (resp., \(g_i\)). Computing an FSLP for this decomposition for a tree context that is already given by an FSLP is the main step in the proof of the normal form theorem below. Another insight is that proper forest contexts from \(\mathcal {F}_1(\varSigma ) \setminus \mathcal {T}_1(\varSigma )\) can be eliminated without significant size blow-up.
Theorem 4
From a given FSLP F one can construct in linear time an FSLP \(F'\) in normal form such that \(\llbracket F' \rrbracket = \llbracket F \rrbracket \) and \(|F'| \in O(|F|)\).
4 Cluster Algebras and Top Dags
In this section we introduce top dags [2, 12] as an alternative grammar-based formalism for the compression of unranked trees. A cluster of rank 0 is a tree \(t \in \mathcal {T}_0(\varSigma )\) of size at least two. A cluster of rank 1 is a tree \(t \in \mathcal {T}_0(\varSigma )\) of size at least two together with a distinguished leaf node that we call the bottom boundary node of t. In both cases, the root of t is called the top boundary node of t. Note that in contrast to forest contexts there is no parameter x. Instead, one of the \(\varSigma \)-labelled leaf nodes may be declared as the bottom boundary node. When writing a cluster of rank 1 in term representation, we underline the bottom boundary node. For instance \(a (b \, c (\underline{a} \, b ))\) is a cluster of rank 1. An atomic cluster is of the form \(a (b )\) or \(a (\underline{b} )\) for \(a,b \in \varSigma \). Let \(\mathcal {C}_i(\varSigma )\) be the set of all clusters of rank \(i \in \{0,1\}\) and let \(\mathcal {C}(\varSigma ) = \mathcal {C}_0(\varSigma ) \cup \mathcal {C}_1(\varSigma )\). We write \(\text {rank}(s) = i\) if \(s \in \mathcal {C}_i(\varSigma )\) for \(i \in \{0,1\}\). We define the cluster algebra  as follows:
as follows:
-
 is the horizontal merge operator:
is the horizontal merge operator:  is only defined if \(\text {rank}(s)\,+\,\text {rank}(t)\le 1\) and s, t are of the form \(s = a (f )\), \(t = a (g )\), i.e., the root labels coincide. Then
is only defined if \(\text {rank}(s)\,+\,\text {rank}(t)\le 1\) and s, t are of the form \(s = a (f )\), \(t = a (g )\), i.e., the root labels coincide. Then 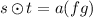 . Note that at most one symbol in the forest fg is underlined. The rank of
. Note that at most one symbol in the forest fg is underlined. The rank of  is \(\text {rank}(s)+\text {rank}(t)\). For instance,
is \(\text {rank}(s)+\text {rank}(t)\). For instance,  .
. -
 is the vertical merge operator:
is the vertical merge operator:  is only defined if \(s \in \mathcal {C}_1(\varSigma )\) and the label of the root of t (say a) is equal to the label of the bottom boundary node of s. We then obtain
is only defined if \(s \in \mathcal {C}_1(\varSigma )\) and the label of the root of t (say a) is equal to the label of the bottom boundary node of s. We then obtain  by replacing the unique occurrence of \(\underline{a}\) in s by t. The rank of
by replacing the unique occurrence of \(\underline{a}\) in s by t. The rank of 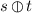 is \(\text {rank}(t)\). For instance,
is \(\text {rank}(t)\). For instance,  .
. -
The atomic clusters \(a (b )\) and \(a (\underline{b} )\) are constants of the cluster algebra.
A top tree for a tree \(t \in \mathcal {T}_0\) is an algebraic expression e over the algebra \(\mathsf {CA}(\varSigma )\) such that \(\llbracket e \rrbracket = t\). A top dag over \(\varSigma \) is a straight-line program D over the algebra \(\mathsf {CA}(\varSigma )\) such that \(\llbracket D \rrbracket \in \mathcal {T}_0(\varSigma )\). In our terminology, cluster straight-line program would be a more appropriate name, but we prefer to call them top dags.
Example 5
Consider the top dag \(D = (\{S,A_0, \ldots , A_n,B_0, \ldots , B_n\},S,\rho )\), where \(\rho (A_0) = b (a )\),  for \(1 \le i \le n\),
for \(1 \le i \le n\),  ,
,  for \(1 \le i \le n\), and
for \(1 \le i \le n\), and  . We have \(\llbracket D \rrbracket = b (a^{2^n} b (a^{2^n} \cdots b (a^{2^n} b (c )\, a^{2^n} )\cdots a^{2^n} )a^{2^n} )\), where b occurs \(2^n+1\) many times.
. We have \(\llbracket D \rrbracket = b (a^{2^n} b (a^{2^n} \cdots b (a^{2^n} b (c )\, a^{2^n} )\cdots a^{2^n} )a^{2^n} )\), where b occurs \(2^n+1\) many times.
5 Relative Succinctness
We have now three grammar-based formalisms for the compression of unranked trees: FSLPs, top dags, and TSLPs for fcns-encodings. In this section we study their relative succinctness. It turns out that up to multiplicative factors of size \(|\varSigma |\) (number of node labels) all three formalisms are equally succinct. Moreover, the transformations between the formalisms can be computed very efficiently. This allows us to transfer algorithmic results for FSLPs to top dags and TSLPs for fcns encodings, and vice versa. We start with top dags:
Proposition 6
For a given top dag D one can compute in linear time an FSLP F such that \(\llbracket F \rrbracket = \llbracket D \rrbracket \) and \(|F| \in O(|D|)\).
Proposition 7
For a given FSLP F with \(\llbracket F \rrbracket \in \mathcal {T}_0(\varSigma )\) and \(|\llbracket F \rrbracket | \ge 2\) one can compute in time \(O(|\varSigma | \cdot |F|)\) a top dag D such that \(\llbracket D \rrbracket = \llbracket F \rrbracket \) and \(|D| \in O(|\varSigma | \cdot |F|)\).
The following example shows that the size bound in Proposition 7 is sharp:
Example 8
Let \(\varSigma = \{a, a_1,\ldots ,a_\sigma \}\) and for \(n \ge 1\) let \(t_{n} = a (a_1 (a^m )\cdots a_\sigma (a^m ))\) with \(m = 2^n\). For every \(n > \sigma \) the tree \(t_n\) can be produced by an FSLP of size O(n): using \(n = \log m\) many variables we can produce the forest \(a^{m}\) and then O(n) many additional variables suffice to produce \(t_{n}\). On the other hand, every top dag for \(t_{n}\) has size \(\varOmega (\sigma \cdot n)\): consider a top tree e that evaluates to \(t_{n}\). Then e must contain a subexpression \(e_i\) that evaluates to the subtree \(a_i(a^m)\) (\(1 \le i \le \sigma \)) of \(t_{n}\). The subexpression \(e_i\) has to produce \(a_i(a^m)\) using the  -operation from copies of \(a_i (a )\). Hence, the expression for \(a_i (a^m)\) has size \(n = \log _2 m\) and different \(e_i\) contain no identical subexpressions. Therefore every top dag for \(t_n\) has size at least \(\sigma \cdot n\).
-operation from copies of \(a_i (a )\). Hence, the expression for \(a_i (a^m)\) has size \(n = \log _2 m\) and different \(e_i\) contain no identical subexpressions. Therefore every top dag for \(t_n\) has size at least \(\sigma \cdot n\).
In contrast, FSLPs and TSLPs for fcns-encodings turn out to be equally succinct up to constant factors:
Proposition 9
Let \(f \in \mathcal {F}(\varSigma )\) be a forest and let F be an FSLP (or TSLP) over \(\varSigma \uplus \{\bot \}\) with \(\llbracket F \rrbracket = \text {fcns}(f)\). Then we can transform F in linear time into an FSLP \(F'\) over \(\varSigma \) with \(\llbracket F' \rrbracket = f\) and \(|F'| \in O(|F|)\).
Proposition 10
For every FSLP F over \(\varSigma \), we can construct in linear time a TSLP T over \(\varSigma \cup \{\bot \}\) with \(\llbracket T \rrbracket = \text {fcns}(\llbracket F \rrbracket )\) and \(|T| \in O(|F|)\).
Proposition 10 and the construction from [7, Proposition 8.3.2] allow to reduce the evaluation of forest automata on FSLPs (for a definition of forest and tree automata, see [7]) to the evaluation of ordinary tree automata on binary trees. The latter problem can be solved in polynomial time [18], which yields:
Corollary 11
Given a forest automaton A and an FSLP (or top dag) F we can check in polynomial time whether A accepts \(\llbracket F \rrbracket \).
In [2], a linear time algorithm is presented that constructs from a tree of size n with \(\sigma \) many node labels a top dag of size \(O(n / \log ^{0.19}_\sigma n)\). In [12] this bound was improved to \(O(n \log \log n / \log _\sigma n)\) (for the same algorithm as in [2]). In [19] we recently presented an alternative construction that achieves the information-theoretic optimum of \(O(n / \log _\sigma n)\) (another optimal construction was presented in [9]). Moreover, as in [2], the constructed top dag satisfies the additional size bound \(O(d \cdot \log n)\), where d is the size of the minimal dag of t. With Propositions 6 and 10 we get:
Corollary 12
Given a tree t of size n with \(\sigma \) many node labels, one can construct in linear time an FSLP for t (or an TSLP for \(\text {fcns}(t)\)) of size \(O(n / \log _\sigma n) \cap O(d \cdot \log n)\), where d is the size of the minimal dag of t.
6 Testing Equality Modulo Associativity and Commutativity
In this section we will give an algorithmic application which proves the utility of FSLPs (even if we deal with binary trees). We fix two subsets \(\mathcal {A} \subseteq \varSigma \) (the set of associative symbols) and \(\mathcal {C} \subseteq \varSigma \) (the set of commutative symbols). This means that we impose the following identities for all \(a \in \mathcal {A}\), \(c \in \mathcal {C}\), all trees \(t_1, \ldots , t_n \in \mathcal {T}_0(\varSigma )\), all permutations \(\sigma :\{1, \ldots , n\} \rightarrow \{1,\ldots ,n\}\), and all \(1 \le i \le j \le n+1\):
Note that the standard law of associativity for a binary symbol \(\circ \) (i.e., \(x \circ (y \circ z) = (x \circ y) \circ z\)) can be captured by making \(\circ \) an (unranked) associative symbol in the sense of (1). Our main result is:
Theorem 13
For trees s, t we can test in polynomial time whether s and t are equal modulo the identities in (1) and (2), if s and t are given succinctly by one of the following three formalisms: (i) FSLPs, (ii) top dags, (iii) TSLPs for the fcns-encodings of s, t.
6.1 Associative Symbols
Below, we define the associative normal form \(\text {nf}_{\mathcal {A}}(f)\) of a forest f and show that from an FSLP F we can compute in linear time an FSLP \(F'\) with \(\llbracket F' \rrbracket = \text {nf}_{\mathcal {A}}(\llbracket F \rrbracket )\). For trees \(s, t \in \mathcal {T}_0(\varSigma )\) we have that \(s = t\) modulo the identities in (1) if and only if \(\text {nf}_{\mathcal {A}}(s) = \text {nf}_{\mathcal {A}}(t)\). The generalization to forests is needed for the induction, where a slight technical problem arises. Whether the forests \(t_1 \cdots t_{i-1} a (t_i \cdots t_{j-1} )t_{j} \cdots t_n\) and \(t_1 \cdots t_n\) are equal modulo the identities in (1) actually depends on the symbol on top of these two forests. If it is an a, and \(a\in \mathcal {A}\), then the two forests are equal modulo associativity, otherwise not. To cope with this problem, we use for every associative symbol \(a \in \mathcal {A}\) a function \(\phi _a :\mathcal {F}_0(\varSigma ) \rightarrow \mathcal {F}_0(\varSigma )\) that pulls up occurrences of a whenever possible.
Let \(\bullet \notin \varSigma \) be a new symbol. For every \(a \in \varSigma \cup \{ \bullet \}\) let \(\phi _a:\mathcal {F}_0(\varSigma ) \rightarrow \mathcal {F}_0(\varSigma )\) be defined as follows, where \(f \in \mathcal {F}_0(\varSigma )\) and \(t_1, \ldots , t_n \in \mathcal {T}_0(\varSigma )\):
In particular, \(\phi _a(\varepsilon ) = \varepsilon \). Moreover, define \(\text {nf}_{\mathcal {A}}:\mathcal {F}_0(\varSigma ) \rightarrow \mathcal {F}_0(\varSigma )\) by \(\text {nf}_{\mathcal {A}}(f) = \phi _\bullet (f)\).
Example 14
Let \(t = a (a (cd )b (cd )a (e ))\) and \(\mathcal {A} = \{a\}\). We obtain
To show the following simple lemma one considers the terminating and confluent rewriting system obtained by directing the Eq. (1) from right to left.
Lemma 15
For two forests \(f_1, f_2 \in \mathcal {F}_0(\varSigma )\), \(\text {nf}_{\mathcal {A}}(f_1) = \text {nf}_{\mathcal {A}}(f_2)\) if and only if \(f_1\) and \(f_2\) are equal modulo the identities in (1) for all \(a \in \mathcal {A}\).
Lemma 16
From a given FSLP \(F = (V,S,\rho )\) over \(\varSigma \) one can construct in time \(\mathcal {O}(|F|\cdot |\varSigma |)\) an FSLP \(F'\) with \(\llbracket F' \rrbracket = \text {nf}_{\mathcal {A}}(\llbracket F \rrbracket )\).
For the proof of Lemma 16 one introduces new variables \(A_a\) for all \(a \in \varSigma \cup \{\bullet \}\) and defines the right-hand sides of \(F'\) such that \(\llbracket A_a \rrbracket _{F'} = \phi _a(\llbracket A \rrbracket _{F})\) for all \(A \in V_0\) and \(\llbracket B_a \langle \phi _{b}(f) \rangle \rrbracket _{F'} = \phi _a(\llbracket B \langle f \rangle \rrbracket _{F})\) for all \(B \in V_1\), \(f \in \mathcal {F}_0(\varSigma )\), where b is the label of the parent node of the parameter x in \(\llbracket B \rrbracket _{F}\). This parent node exists if we assume the FSLP F to be in normal form.
6.2 Commutative Symbols
To test whether two trees over \(\varSigma \) are equivalent with respect to commutativity, we define a commutative normal form \(\text {nf}_{\mathcal {C}}(t)\) of a tree \(t \in \mathcal {T}_0(\varSigma )\) such that \(\text {nf}_{\mathcal {C}}(t_1) = \text {nf}_{\mathcal {C}}(t_2)\) if and only if \(t_1\) and \(t_2\) are equivalent with respect to the identities in (2) for all \(c \in \mathcal {C}\).
We start with a general definition: Let \(\varDelta \) be a possibly infinite alphabet together with a total order <. Let \(\le \) be the reflexive closure of <. Define the function \(\text {sort}^{<}:\varDelta ^* \rightarrow \varDelta ^*\) by \(\text {sort}^{<}(a_1\cdots a_n) = a_{i_1}\cdots a_{i_n}\) with \(\{i_1,\ldots ,i_n\} = \{1,\ldots ,n\}\) and \(a_{i_1} \le \cdots \le a_{i_n}\).
Lemma 17
Let G be an SSLP over \(\varDelta \) and let < be some total order on \(\varDelta \). We can construct in time \(\mathcal {O}(|\varDelta |\cdot |G|)\) an SSLP \(G'\) such that \(\llbracket G' \rrbracket = \text {sort}^{<}(\llbracket G \rrbracket )\).
In order to define the commutative normal form, we need a total order on \(\mathcal {F}_0(\varSigma )\). Recall that elements of \(\mathcal {F}_0(\varSigma )\) are particular strings over the alphabet \(\varGamma := \varSigma \cup \{(, )\}\). Fix an arbitrary total order on \(\varGamma \) and let \(<_{\text {llex}}\) be the length-lexicographic order on \(\varGamma ^*\) induced by <: for \(x,y \in \varGamma ^*\) we have \(x <_{\text {llex}} y\) if \(|x| < |y|\) or (\(|x|=|y|\), \(x = u a v\), \(y = u b v'\), and \(a < b\) for \(u,v,v' \in \varGamma ^*\) and \(a,b \in \varGamma \)). We now consider the restriction of \(<_{\text {llex}}\) to \(\mathcal {F}_0(\varSigma ) \subseteq \varGamma ^*\). For the proof of the following lemma one first constructs SSLPs for the strings \(\llbracket F_1 \rrbracket , \llbracket F_2 \rrbracket \in \varGamma ^*\) (the construction is similar to the case of TSLPs, see [6]) and then uses [16, Lemma 3] according to which SSLP-encoded strings can be compared in polynomial time with respect to \(<_{\text {llex}}\).
Lemma 18
For two FSLPs \(F_1\) and \(F_2\) we can check in polynomial time whether \(\llbracket F_1 \rrbracket = \llbracket F_2 \rrbracket \), \(\llbracket F_1 \rrbracket <_{\text {llex}} \llbracket F_2 \rrbracket \) or \(\llbracket F_2 \rrbracket <_{\text {llex}} \llbracket F_1 \rrbracket \).
From the restriction of \(<_{\text {llex}}\) to \(\mathcal {T}_0(\varSigma ) \subseteq \varGamma ^*\) we obtain the function \(\text {sort}^{<_{\text {llex}}}\) on \(\mathcal {T}_0(\varSigma )^* = \mathcal {F}_0(\varSigma )\). We define \(\text {nf}_{\mathcal {C}}:\mathcal {F}_0(\varSigma ) \rightarrow \mathcal {F}_0(\varSigma )\) by
Obviously, \(f_1, f_2 \in \mathcal {F}(\varSigma )\) are equal modulo the identities in (2) for all \(c \in \mathcal {C}\) if and only if \(\text {nf}_{\mathcal {C}}(f_1) = \text {nf}_{\mathcal {C}}(f_2)\). Using this fact and Lemma 15 it is not hard to show:
Lemma 19
For \(f_1, f_2 \in \mathcal {F}_0(\varSigma )\) we have \(\text {nf}_{\mathcal {C}}(\text {nf}_{\mathcal {A}}(f_1)) = \text {nf}_{\mathcal {C}}(\text {nf}_{\mathcal {A}}(f_2))\) if and only if \(f_1\) and \(f_2\) are equal modulo the identities in (1) and (2) for all \(a \in \mathcal {A}\), \(c \in \mathcal {C}\).
For our main technical result (Theorem 21) we need a strengthening of our FSLP normal form. Recall the notion of the spine from Sect. 3. We say that an FSLP \(F = (V,S,\rho )\) is in strong normal form if it is in normal form and for every \(A \in V_0^\bot \) with \(\rho (A) = B \langle C \rangle \) either \(B \in V_1^\bot \) or \(|\llbracket C \rrbracket _{F}| \ge |\llbracket D \rrbracket _{F}| - 1\) for every \(D \in V_1^\bot \) which occurs in \(\text {spine}(B)\) (note that \(|\llbracket D \rrbracket _{F}| - 1\) is the number of nodes in \(\llbracket D \rrbracket _{F}\) except for the parameter x).
Lemma 20
From a given FSLP \(F = (V,S,\rho )\) in normal form we can construct in polynomial time an FSLP \(F' = (V',S,\rho ')\) in strong normal form with \(\llbracket F \rrbracket = \llbracket F' \rrbracket \).
For the proof of Lemma 20 we modify the right-hand sides of variables \(A \in V_0^\bot \) with \(\rho (A) = B \langle C \rangle \) and \(|\text {spine}(B)| \ge 2\). Basically, we replace the vertical concatenations \(B \langle C \rangle \) by polynomially many vertical concatenations \(B_i \langle C_i \rangle \) which satisfy the condition of the strong normal form. We can now prove the main technical result of this section:
Theorem 21
From a given FSLP F we can construct in polynomial time an FSLP \(F'\) with \(\llbracket F' \rrbracket = \text {nf}_{\mathcal {C}}(\llbracket F \rrbracket )\).
Proof
Let \(F = (V,S,\rho )\). By Theorem 4 and Lemma 20 we may assume that F is in strong normal form. For every \(A \in V_1\) let
We want to construct an FSLP \(F' = (V',S,\rho ')\) with \(V_0 \subseteq V_0'\) and \(V_1 = V_1'\) such that
-
(1)
\(\llbracket A \rrbracket _{F'} = \text {nf}_{\mathcal {C}}(\llbracket A \rrbracket _{F})\) for all \(A \in V_0\),
-
(2)
\(\llbracket A \rrbracket _{F'} \langle \text {nf}_{\mathcal {C}}(t) \rangle = \text {nf}_{\mathcal {C}}(\llbracket A \rrbracket _{F} \langle t \rangle )\) for all \(A \in V_1\), \(t \in \text {args}(A)\).
From (1) we obtain \(\llbracket F' \rrbracket = \llbracket S \rrbracket _{F'} = \text {nf}_{\mathcal {C}}(\llbracket S \rrbracket _{F}) = \text {nf}_{\mathcal {C}}(\llbracket F \rrbracket )\) which concludes the proof.
To define \(\rho '\), let \(V^c = V_0^c \cup V_1^c\) with \(V_1^c = \{A \in V_1 \mid \rho (A) = a ( BxC )\ \text {with}\ a \in \mathcal {C}\}\) and \(V_0^c = \{A \in V_0 \mid \rho (A) = a ( B ) \ \text {with}\ a \in \mathcal {C}\ \text {or}\ \rho (A) = D \langle C \rangle \text { with } D \in V_1^c \}\) be the set of commutative variables. We set \(\rho '(A) = \rho (A)\) for \(A \in V \setminus V^c\). For \(A \in V^c\) we define \(\rho '(A)\) by induction along the partial order of the dag:
-
1.
\(\rho (A) = a ( B )\): Let \(M_{A}\) be the set of all \(C \in V_0^\bot \) which are below A in the dag, and let \(w = \text {hor}(B) = \llbracket B \rrbracket _{F^{\mathop {\boxdot }}} \in M_{A}^*\). By induction, \(\rho '\) is already defined on \(M_{A}\), and thus \(\llbracket C \rrbracket _{F'}\) is defined for every \(C \in M_{A}\). By Lemma 18, we can compute in polynomial time a total order < on \(M_{A}\) such that \(C < D\) implies \(\llbracket C \rrbracket _{F'} \le _\text {llex}\llbracket D \rrbracket _{F'}\) for all \(C,D \in M_{A}\). By Lemma 17, we can construct in linear time an SSLP \(G_w = (V_w,S_w,\rho _w)\) with \(\llbracket G_w \rrbracket = \text {sort}^{<}(w)\), and we may assume that all variables \(D \in V_w\) are new. We add these variables to \(V_0'\) together with their right hand sides \(\rho '(D) = \rho _w(D)\), and we finally set \(\rho '(A) = a ( S_w )\).
-
2.
\(\rho (A) = B \langle C \rangle \): Let \(\rho (B) = a ( DxE )\). We define \(G_w = (V_w,S_w,\rho _w)\) as before, but with \(w = \llbracket DCE \rrbracket _{F^{\mathop {\boxdot }}}\) instead of \(w = \llbracket B \rrbracket _{F^{\mathop {\boxdot }}}\), and we set \(\rho '(A) = a ( S_w )\).
-
3.
\(\rho (A) = a ( BxC )\): We define \(G_w = (V_w,S_w,\rho _w)\) as before, this time with \(w = \llbracket BC \rrbracket _{F^{\mathop {\boxdot }}}\), and we set \(\rho '(B) = a ( S_w x )\).
The main idea is that the strong normal form ensures that in right-hand sides of the form \(a ( DxE )\) with \(a \in \mathcal {C}\) one can move the parameter x to the last position (see point 3 above), since only trees that are larger than all trees produced from D and E are substituted for x. \(\square \)
Proof of Theorem 13. By Propositions 6 and 9 it suffices to show Theorem 13 for the case that \(t_1\) and \(t_2\) are given by FSLPs \(F_1\) and \(F_2\), respectively. By Lemma 19 and Lemma 18 it suffices to compute in polynomial time FSLPs \(F'_1\) and \(F'_2\) for \(\text {nf}_{\mathcal {C}}(\text {nf}_{\mathcal {A}}(t_1))\) and \(\text {nf}_{\mathcal {C}}(\text {nf}_{\mathcal {A}}(t_2))\). This can be achieved using Lemma 16 and Theorem 21. \(\square \)
7 Future Work
We have shown that simple algebraic manipulations (laws of associativity and commutativity) can be carried out efficiently on grammar-compressed trees. In the future, we plan to investigate other algebraic laws. We are optimistic that our approach can be extended by idempotent symbols (meaning that \(a(f t t g)= a(f t g)\) for forests f, g and a tree t).
Another interesting open problem concerns context unification modulo associative and commutative symbols. The decidability of (plain) context-unification was a long standing open problem that was finally solved by Jeż [13], who showed the existence of a polynomial space algorithm. Jeż’s algorithm uses his recompression technique for TSLPs. One might try to extend this technique to FSLPs with the goal of proving decidability of context unification for terms that also contain associative and commutative symbols. For first-order unification and matching [10], context matching [10], and one-context unification [8] there exist algorithms for TSLP-compressed trees that match the complexity of their uncompressed counterparts. One might also try to extend these results to the associative and commutative setting.
References
Abiteboul, S., Bourhis, P., Vianu, V.: Highly expressive query languages for unordered data trees. Theor. Comput. Syst. 57(4), 927–966 (2015)
Bille, P., Gørtz, I.L., Landau, G.M., Weimann, O.: Tree compression with top trees. Inf. Comput. 243, 166–177 (2015)
Boiret, A., Hugot, V., Niehren, J., Treinen, R.: Logics for unordered trees with data constraints on siblings. In: Dediu, A.-H., Formenti, E., Martín-Vide, C., Truthe, B. (eds.) LATA 2015. LNCS, vol. 8977, pp. 175–187. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-15579-1_13
Bojańczyk, M., Walukiewicz, I.: Forest algebras. In: Proceedings of Logic and Automata: History and Perspectives [in Honor of Wolfgang Thomas], Texts in Logic and Games, vol. 2, pp. 107–132. Amsterdam University Press (2008)
Boneva, I., Ciucanu, R., Staworko, S.: Schemas for unordered XML on a DIME. Theory Comput. Syst. 57(2), 337–376 (2015)
Busatto, G., Lohrey, M., Maneth, S.: Efficient memory representation of XML document trees. Inf. Syst. 33(4–5), 456–474 (2008)
Comon, H., Dauchet, M., Gilleron, R., Jacquemard, F., Löding, C., Lugiez, D., Tison, S., Tommasi, M.: Tree automata techniques and applications. http://www.grappa.univ-lille3.fr/tata (2007)
Creus, C., Gascón, A., Godoy, G.: One-context unification with STG-compressed terms is in NP. In: Proceedings of RTA 2012, LIPIcs 15, pp. 149–164. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2012)
Dudek, B., Gawrychowski, P.: Slowing down top trees for better worst-case bounds (2018). https://arxiv.org/abs/1801.01059
Gascón, A., Godoy, G., Schmidt-Schauß, M.: Unification and matching on compressed terms. ACM Trans. Comput. Logic 12(4), 26:1–26:37 (2011)
Gascón, A., Lohrey, M., Maneth, S., Reh, P., Sieber, K.: Grammar-based compression of unranked trees (2018). https://arxiv.org/abs/1802.05490
Hübschle-Schneider, L., Raman, R.: Tree compression with top trees revisited. In: Bampis, E. (ed.) SEA 2015. LNCS, vol. 9125, pp. 15–27. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-20086-6_2
Jeż, A.: Context unification is in PSPACE. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014. LNCS, vol. 8573, pp. 244–255. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43951-7_21
Lohrey, M.: Algorithmics on SLP-compressed strings: a survey. Groups Complex. Cryptol. 4(2), 241–299 (2012)
Lohrey, M., Maneth, S., Mennicke, R.: XML tree structure compression using RePair. Inf. Syst. 38(8), 1150–1167 (2013)
Lohrey, M., Maneth, S., Peternek, F.: Compressed tree canonization. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 337–349. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_27
Lohrey, M., Maneth, S., Reh, C.P.: Compression of unordered XML trees. In: Proceedings of ICDT 2017, LIPIcs 68, pp. 18:1–18:17. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2017)
Lohrey, M., Maneth, S., Schmidt-Schauß, M.: Parameter reduction and automata evaluation for grammar-compressed trees. J. Comput. Syst. Sci. 78(5), 1651–1669 (2012)
Lohrey, M., Reh, P., Sieber, K.: Optimal top dag construction (2017). https://arxiv.org/abs/1712.05822
Sundaram, S., Madria, S.K.: A change detection system for unordered XML data using a relational model. Data Knowl. Eng. 72, 257–284 (2012)
Acknowledgements
The first author was supported by the EPSRC grant EP/N510129/1 at the Alan Turing Institute and the EPSRC grant EP/J017728/2 at University of Edinburgh. The second author was supported by the DFG research project LO748/10-1.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Gascón, A., Lohrey, M., Maneth, S., Reh, C.P., Sieber, K. (2018). Grammar-Based Compression of Unranked Trees. In: Fomin, F., Podolskii, V. (eds) Computer Science – Theory and Applications. CSR 2018. Lecture Notes in Computer Science(), vol 10846. Springer, Cham. https://doi.org/10.1007/978-3-319-90530-3_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-90530-3_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-90529-7
Online ISBN: 978-3-319-90530-3
eBook Packages: Computer ScienceComputer Science (R0)





 is the vertical concatenation operator: for forests
is the vertical concatenation operator: for forests  is defined if
is defined if  is obtained by replacing in
is obtained by replacing in  is the horizontal merge operator:
is the horizontal merge operator:  is only defined if
is only defined if 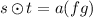 . Note that at most one symbol in the forest fg is underlined. The rank of
. Note that at most one symbol in the forest fg is underlined. The rank of  is
is  .
. is the vertical merge operator:
is the vertical merge operator:  is only defined if
is only defined if  by replacing the unique occurrence of
by replacing the unique occurrence of 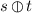 is
is  .
.